Часто, строя
проекции предмета, можно сразу определить
форму какого-либо элемента изображения,
если его очертания состоят из прямых
линий или окружностей. Но положение
такого элемента относительно остального
изображения или сами очертания
элемента (когда они криволинейные)
приходится определять по проекциям
одной или нескольких точек на
поверхности предмета.
Общий метод
определения точки на проекциях участка
поверхности, несущей эту точку, состоит
в следующем:
Через точку на
поверхности проводят вспомогательную
линию, проекции которой легко определяются
на данной поверхности.
На проекциях
вспомогательной линии находят с помощью
проекционной связи недостающую
проекцию точки.
Вспомогательная
линия должна быть простейшей для данной
поверхности. Для плоскости это всегда
отрезок прямой, опирающейся концами
на края плоского участка или на ребра
грани. Для поверхности вращения, если
ось вращения перпендикулярна к одной
из плоскостей проекций, может быть
использована окружность, полученная в
пересечении этой поверхности с
плоскостью, перпендикулярной к оси
вращения. Разумеется, вспомогательная
плоскость проводится через
рассматриваемую точку.
На конусе или
цилиндре, в частности, также можно
воспользоваться прямолинейной образующей.
Рассмотрим сказанное
на примерах. На гранях пирамиды,
показанной на рис. 5, даны фронтальная
проекция точки М и горизонтальная
проекция точки. N.
Найдем недостающие проекции этих
точек.
Через точку N
проведем прямую 1—2, начав с ее фронтальной
проекции 12—22.
Найдя затем горизонтальную проекцию
11—21,
проведем вниз линию связи и отметим
недостающую проекцию.
Для точки М был
выбран отрезок, пересекающийся с боковым
ребром AD и нижним ребром АВ. Через ребро
BD проводить вспомогательную прямую
было бы нежелательно, так как BD —
профильная прямая и проекцию точки на
ней пришлось бы находить путем
дополнительных построений, используя
пропорциональное деление проекций
отрезка проекциями принадлежащей
ему точки.
Для точки N, заданной
своей горизонтальной проекцией N1
используем вспомогательную прямую 3 —
D, одним из концов которой будет вершина
пирамиды. Построения будут такими же,
как для точки М, но начнутся они с
горизонтальной проекции.
На рис. 6 точки А
задана своей фронтальной проекцией на
поверхности сферы. Проведя через эту
точку горизонтальную плоскость Σ
(проекция Σ2
проходит через А2),
получим в пересечении со сферой
окружность, радиус г которой измеряется
прямо на проекции Σ2,
как показано на чертеже. Сама окружность
проецируется в натуральную величину
на виде сверху. Проведя окружность,
отмечаем на ней недостающую проекцию
А1.
На рис. 7 показан
усеченный конус, а точка К задана на
горизонтальной проекции. Если бы через
точку К была проведена плоскость,
перпендикулярная оси конуса, она дала
бы в пересечении с конусом окружность,
проецирующуюся в натуральную величину
на виде сверху и проходящую через
горизонтальную проекцию К. Проведем
эту окружность, измерим ее радиус, и
тогда несложно будет найти на фронтальной
проекции уровень вспомогательной
горизонтальной плоскости, дающей в
пересечении с конусом эту самую
окружность. Отменив этот уровень,
обозначим на нем недостающую
проекцию K2
как показано на чертеже.
На рис. 8 и 9 показано,
как строятся недостающие горизонтальная
и профильная проекция точки Е на конусе
и цилиндре с помощью образующих
(прямая 1—2 на обоих чертежах).
Построения начинаются с фронтальной
проекции образующей, проходящей
через заданную фронтальную проекцию
точки Е. Затем строятся горизонтальная
и профильная проекции образующей, а на
них отмечаются одноименные проекции
точки Е. Здесь следует обратить внимание,
что профильные проекции указанной
образующей и самой точки при наличии
двух других проекций легко определяются
без проведения внешних осей проекций
(например, 13—23
на рис. 8 и Е3
на рис. 9).
§ 18. Конус
18.1.Определение конуса и его элементов
Определение. Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащей его катет, называется прямым круговым конусом (рис. 165, 166).
Отрезок оси вращения, заключённый внутри конуса, называется осью конуса.
Круг, образованный при вращении второго катета, называется основанием конуса. Длина этого катета называется радиусом основания конуса или, короче, радиусом конуса. Вершина острого угла вращающегося треугольника, лежащая на оси вращения, называется вершиной конуса. На рисунках 165, б и 166 вершиной конуса является точка Р.
Высотой конуса называется отрезок, проведённый из вершины конуса перпендикулярно его основанию. Длину этого перпендикуляра также называют высотой конуса. Высота конуса имеет своим основанием центр круга — основания конуса — и совпадает с осью конуса.
Отрезки, соединяющие вершину конуса с точками окружности его основания, называются образующими конуса. Все образующие конуса равны между собой (почему?).
Как и в случае с цилиндром, можно рассматривать конус в более широком, чем у нас, понимании, когда в основании конуса может быть, например, эллипс (эллиптический конус), парабола (параболический конус). Мы будем изучать только определённый выше прямой круговой конус (конус вращения), поэтому слова «прямой круговой» мы будем опускать.
Рис. 165
Рис. 166
Рис. 167
Поверхность, полученная при вращении гипотенузы, называется боковой поверхностью конуса, а её площадь — площадью боковой поверхности конуса и обозначается Sбок. Боковая поверхность конуса является объединением всех его образующих.
Объединение боковой поверхности конуса и его основания называется полной поверхностью конуса, а её площадь называется площадью полной поверхности конуса или, короче, площадью поверхности конуса и обозначается Sкон. Из этого определения следует, что
Sкон = Sбок + Sосн.
Если вокруг данной прямой — оси — вращать пересекающую её прямую, то при этом вращении образуется поверхность, которую называют круговой конической поверхностью или конической поверхностью вращения. Уравнение 


18.2. Сечения конуса
Определение. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса.
Рис. 168
Рис. 169
Рис. 170
Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники. На рисунке 168 осевым сечением конуса является треугольник ABP (АР = ВР). Угол АPВ называют углом при вершине осевого сечения конуса.
Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.
Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP).
Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).
Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением.
Рис. 171

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.
ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60°; б) в 90°. Найти площадь сечения.
Решение. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.
Хорда АВ окружности основания стягивает дугу в 60°, значит, △ AOB — правильный и АВ = R.
Рис. 172
Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S△ ABP = 



Тогда S△ ABP = 

Ответ: а) 
18.3. Касательная плоскость к конусу
Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.
Рис. 173
Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.
Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.
18.4. Изображение конуса
Рис. 174
Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).
Для достижения наглядности изображения невидимые линии изображают штрихами.
Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.
18.5. Развёртка и площадь поверхности конуса
Пусть l — длина образующей, R — радиус основания конуса с вершиной Р.
Рис. 175
Рис. 176
Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a), то получим развёртку поверхности конуса (рис. 176, б), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):
α = 
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.
Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле
Sбок = 
где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = 
Sбок = πRl.(2)
Таким образом, доказана следующая теорема.
Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼
Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.
Sкон = πRl + πR2.(3)
Следствие. Пусть конус образован вращением прямоугольного треугольника ABC вокруг катета АС (рис. 177). Тогда Sбок = π•BC•АВ. Если D — середина отрезка АВ, то AB = 2AD, поэтому
Sбок = 2 π ВС•AD.(4)
Рис. 177
Проведём DE ⟂ АB (E ∈ l = AС). Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А) имеем


Тогда соотношение (4) принимает вид
Sбок = (2π•DE)•AC,(6)
т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.
Это следствие будет использовано в п. 19.7.
18.6. Свойства параллельных сечений конуса
Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Рис. 178
Доказательство. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α, параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).
Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β, α || β, то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O1 = α ∩ РО. Обозначим этот круг F1.
Рассмотрим гомотетию 
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия 



где k — коэффициент гомотетии 
А поскольку гомотетия является подобием, то круг F1, являющийся параллельным сечением конуса, подобен его основанию.
Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO1 : РО, где РO1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
Sсечен : Sоснов = k2 = 
Теорема доказана. ▼
18.7.Вписанные в конус и описанные около конуса пирамиды
Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.
Для построения изображения правильной пирамиды, вписанной в конус:
—строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;
—соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;
—выделяют видимые и невидимые (штрихами) линии изображаемых фигур.
На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:
—прямоугольный треугольник (см. рис. 179);
—правильный треугольник (см. рис. 180);
—квадрат (см. рис. 181);
—правильный шестиугольник (см. рис. 182).
Рис. 179
Рис. 180
Рис. 181
Рис. 182
Определение. Пирамида называется описанной около конуса, если у них вершина общая, а основание пирамиды описано около основания конуса. В этом случае конус называют вписанным в пирамиду (рис. 183).
Рис. 183
Рис. 184
ЗАДАЧА (3.080). В равносторонний конус вписана правильная пирамида. Найти отношение площадей боковых поверхностей пирамиды и конуса, если пирамида: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решение. Рассмотрим случай а). Пусть R — радиус основания равностороннего конуса, РАВС — правильная пирамида, вписанная в этот конус (рис. 184); △ DPE — осевое сечение конуса, CF — медиана △ АBС. Тогда в △ АВС (правильный): АВ = R



PF = 

Так как CF — медиана △ АВС, то PF — высота равнобедренного треугольника АВР. Поэтому
S△ ABP = 




Обозначим: S1 — площадь боковой поверхности пирамиды, S2 — площадь боковой поверхности конуса. Тогда
S1 = 3S△ ABP = 
S
2 = πR•PA = πR•2R = 2πR2.
Следовательно,
S1 : S2 = 

Ответ: а) 


18.8. Усечённый конус
Рис. 185
Пусть дан конус с вершиной Р. Проведём плоскость α, параллельную плоскости основания конуса и пересекающую этот конус (рис. 185). Эта плоскость пересекает данный конус по кругу и разбивает его на два тела: одно из них является конусом, а другое (расположенное между плоскостью основания данного конуса и секущей плоскостью) называют усечённым конусом. Таким образом, усечённый конус представляет собой часть полного конуса, заключённую между его основанием и параллельной ему плоскостью. Основание данного конуса и круг, полученный в сечении этого конуса плоскостью α, называются соответственно нижним и верхним основаниями усечённого конуса. Высотой усечённого конуса называется перпендикуляр, проведённый из какой-либо точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённого конуса. (Часто за высоту усечённого конуса принимают отрезок, соединяющий центры его оснований.)
Рис. 186
Рис. 187
Часть боковой поверхности данного конуса, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса, а отрезки образующих конуса, заключённые между основаниями усечённого конуса, называются образующими усечённого конуса. Так как все образующие данного конуса равны и равны все образующие отсечённого конуса, то равны все образующие усечённого конуса.
Построение изображения усечённого конуса следует начинать с изображения того конуса, из которого получился усечённый конус (рис. 186).
На рисунке 187 показана развёртка усечённого конуса.
Из теоремы 28 следует, что основания усечённого конуса — подобные круги.
Определения усечённой пирамиды, вписанной в усечённый конус и описанной около него, аналогичны определениям пирамиды, вписанной в конус и описанной около него.
Заметим, что построение изображений усечённой пирамиды, вписанной в усечённый конус и описанной около него, следует начинать с изображений того конуса или той пирамиды, из которых получены соответственно усечённые конус и пирамида.
Полной поверхностью усечённого конуса называется объединение боковой поверхности этого конуса и двух его оснований. Иногда полную поверхность усечённого конуса называют его поверхностью, а её площадь — площадью поверхности усечённого конуса. Эта площадь равна сумме площадей боковой поверхности и оснований усечённого конуса.
Усечённый конус может быть образован также вращением прямоугольной трапеции вокруг боковой стороны трапеции, перпендикулярной её основанию.
Рис. 188
На рисунке 188 изображён усечённый конус, образованный вращением прямоугольной трапеции ABCD вокруг стороны CD. При этом боковая поверхность усечённого конуса образована вращением боковой стороны АВ, а основания его — вращением оснований AD и ВС трапеции.
18.9. Поверхность усечённого конуса
Выразим площадь Sбок боковой поверхности усечённого конуса через длину l его образующей и радиусы R и r оснований (R > r).
Рис. 189
Пусть точка Р — вершина конуса, из которого получен усечённый конус; точки О, O1 — центры оснований усечённого конуса; AA1 = l — одна из образующих усечённого конуса (рис. 189).
Используя формулу (2) п. 18.5, получаем
Sбок = πR•PA – πr•РA1 =
= πR(РA1 + А1A) – πr•PA1 =
= πR•A1A + π(R – r)•PA1.
Учитывая, что A1A = l, имеем
Sбок = πRl + π(R – r)PA1.(7)
Выразим PA1 через l, R и r. Так как O1A1 || OA и OO1 — высота усечённого конуса, то прямоугольные треугольники POA и PO1A1 подобны. Поэтому АО : А1O1 = PA : PA1 или
R : r = (PA1 + A1A) : PA1, откуда
R•PA1 = r(PA1 + l) ⇒ (R – r)PA1 = rl ⇒ PA1 = 
Подставив это значение РА1 в (7), получаем
Sбок = π(R + r)l.(8)
Таким образом, доказана следующая теорема.
Теорема 29. Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую. ▼
Площадь полной поверхности усечённого конуса находится по формуле:
Sполн = π•(R + r)•l + π•R2 + π•r2.
Следствие. Пусть усечённый конус образован вращением прямоугольной трапеции ABCD вокруг её высоты AD (рис. 190). Тогда Sбок = π (АВ + DC)•ВС. Если KЕ — средняя линия трапеции, то АВ + DC = 2KE, поэтому
Sбок = 2π•KE•BC.(9)
Рис. 190
Проведём EF ⟂ ВС. Из подобия прямоугольных треугольников ВСН и EFK имеем
BC : EF = BH : KE ⇒ ⇒ KE•BC = EF•BH.(10)
Тогда равенство (9) принимает вид
Sбок = (2π•EF)•ВH,(11)
т. е. боковая поверхность усечённого конуса равна произведению его высоты на длину окружности, радиус которой равен серединному перпендикуляру, проведённому из точки оси конуса к его образующей.
18.10. Объёмы конуса и усечённого конуса
Найдём объём конуса, высота которого равна h и радиус основания — R. Для этого расположим этот конус и правильную четырёхугольную пирамиду, высота которой равна h и сторона основания — R, так, чтобы их основания находились на одной и той же плоскости α, а вершины — также в одной и той же плоскости β, параллельной плоскости α и удалённой от неё на расстояние h (рис. 191).
Рис. 191
Каждая плоскость, параллельная данным плоскостям и пересекающая конус, пересекает также пирамиду; причём площади сечений, образованных при пересечении обоих тел, относятся к площадям оснований этих тел, как квадраты их расстояний от вершин. А так как секущие плоскости для пирамиды и для конуса равноудалены от их вершин, то 




Vкон : Vпир = π : 1 или Vкон : 
Vкон = 
Рис. 192
Самостоятельно рассмотрите усечённые конус и пирамиду, расположенные в соответствии с условиями принципа Кавальери. Тогда вы получите формулу вычисления объёма усечённого конуса:
Vус. кон = 
Эту же формулу вы можете вывести, если используете идею подобия так же, как это сделано в случае с выводом формулы площади боковой поверхности усечённого конуса.
Используя принцип Кавальери, докажите, что объём каждого из тел, на которые конус разбивается его сечением плоскостью, проходящей через вершину (рис. 192), может быть вычислен по формуле V = 
Нахождение проекций точек на поверхности конуса
Для нахождения недостающих проекций точек на поверхности конуса могут применяться следующие линии, принадлежащие поверхности конуса: окружность — параллель конуса (рис. 2.7, а), прямая — образующая конуса (рис. 2.7, б). Рассмотрим оба способа.
Пример 2.1. На поверхности конуса заданы проекции А2 и В, (см. рис. 2.7). Найдите недостающие проекции точек Ли В на поверхности конуса.
Рис. 2.7. Нахождение проекций точек на поверхности конуса
Способ 1. На рис. 2.7, а точка А задана проекцией А. Для нахождения недостающих проекций точки А воспользуемся вышеизложенным алгоритмом.
- 1. Через заданную проекцию точки Аг проводим линию, принадлежащую поверхности конуса — параллель.
- 2. Строим проекции параллели на других изображениях конуса. Па виде сверху она представляет собой окружность радиусом Rvна виде слева — отрезок.
- 3. На проекциях линии находим соответствующие проекции точек.
- 4. На пересечении окружности радиусом Л., с вертикальной линией связи, опущенной из А2, отмечаем проекцию Л,.
- 5. На виде сверху измеряем координату от проекции А, до горизонтальной оси и откладываем ее на проведенной линии связи на виде слева — получаем проекцию Л3.
- 6. Отмечаем проекцию А.л как невидимую. Проекция А., задана как видимая, следовательно, точка лежит в той части конической поверхности, которая обращена к наблюдателю (на виде сверху это часть, расположенная ниже горизонтальной оси). Таким образом, на виде слева ее проекция не видна.
Способ 2. Па рис. 2.7, 6 точка В задана проекцией В,. Построение недостающих проекций аналогично построению проекций точки А, за исключением того, что вместо окружности используется образующая конуса, пересекающая его основание в точке 1.
Коническая поверхность вращения
Коническая поверхность вращения — это линейчатая поверхность, образованная вращением прямолинейной образующей, которая пересекает криво-линейную направляющую (окружность) и проходит через неподвижную точку оси вращения, называемую вершиной.
Конусом называют геометрическое тело, ограниченное конической поверхностью и плоскостью основания, пересекающего все его образующие.
Конус называют прямым, если ось вращения перпендикулярна его основанию. Конус называют круговым, так как направляющей является окружность Конус с двумя параллельными основаниями, т.е. конус со срезанной вершиной, называют усеченным.
Построение проекций прямого кругового конуса
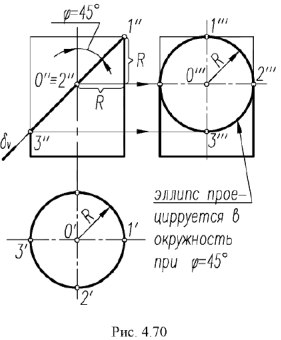
На рис. 4.71 показан пример построения проекций прямою кругового конуса с горизонтально-проецирующей осью вращения 

Для построения проекций конуса требуется выполнить графо-аналитические действия в следующем порядке:
1-е действие. По заданному условию построить горизонтальную проекцию очерка прямого кругового конуса, которая представляет собой окружность заданного радиуса 
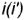
2-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса:
- Круг радиуса
является невидимой проекцией основания конуса.
- Круг радиуса
с вершиной конуса
является видимой проекцией боковой поверхности конуса.
- Обозначить на горизонтальной проекции характерные образующие конуса
и
которые будут определять очерки фронтальной и профильной проекций конуса.
3-е действие. Построить фронтальную проекцию (очерк) конуса, которая представляет собой треугольник 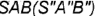
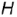
4-е действие. Построить профильную проекцию (очерк) конуса:
- ‘Задать на окружности горизонтальной проекции конуса положение базовой линии (б.о.), совпадающей с горизонтальной линией оси этой окружности.
- Выбрать положение базовой оси
(б.о.), которая будет совпадать с вертикальной осью
вращения на профильной проекции конуса.
- Профильная проекция конуса представляет собой треугольник
ограниченный:
слева и справа очерковыми образующими 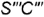
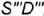
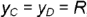
вершиной 
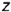
профильными проекциями характерных образующих 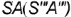
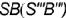
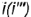
. Запомните характерные признаки очерков прямого круговою конуса на чертеже — окружность основания и два треугольника.
. Характерные признаки очерков прямого кругового усеченного конуса окружность основания и две равнобокие трапеции.
Построение проекции точек, лежащих на поверхности конуса
Принадлежность точки поверхности конуса определяется ее принадлежностью образующей поверхности и принадлежностью круговым параллелям (окружностям), по которой точка вращается вокруг оси конуса. Следовательно, проекции точки можно строить либо по принадлежности образующей, либо по принадлежности круговой параллели.
На рис. 4.71 показан пример построения горизонтальных и профильных проекций точек 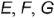
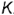
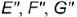
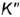
Посфоение горизонтальных проекций заданных точек:
горизонтальные проекции точек 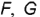
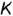
Рассмотрим графический алгоритм для построения горизонтальных проекции точек, лежащих на боковой поверхности конуса (на примере заданной точки , по их при надежности круговым параллелям:
Графический алгоритм I:
1-е действие. Провести фронтальную проекцию вспомогательной круговой параллели 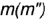
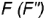
2-е действие. Провести окружность горизонтальной проекции параллели 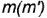
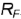
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки 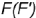
Повторить действия графического алгоритма 1 и построить аналогично горизонтальные проекции 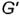
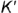
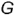
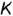
Построение профильных проекций заданных точек. Точки 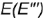
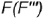
точка 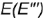
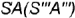
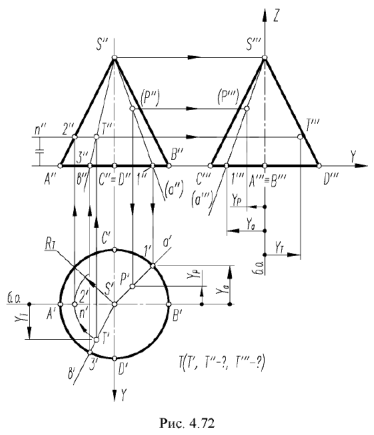
На рис. 4.72 показан пример построения горизонтальной и профильной проекции точки 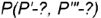
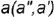
- Построение горизонтальной проекции точки по принадлежности образующей выполняется по графическому алгоритму II:
1-е действие. Провести через вершину конуса 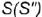
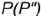
2-е действие. Построить горизонтальную проекцию образующей 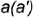
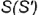
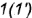
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки 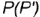
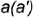
- Построение профильной проекции невидимой точки
выполняется по принадлежности образующей
, построенной но координате
.
На рис. 4.72 показано построение фронтальной и профильной проекции точки по ее заданной горизонтальной проекции. Построение выполнено по приведенным алгоритмам I и II, но в обратном порядке:
1-е действие. Провести на горизонтальной проекции конуса радиусом 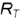
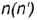
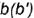
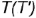
2-е действие. Построить фронтальные проекции вспомогательной параллели 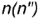
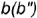
параллель 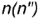
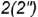
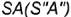
образующую 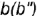
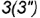
3-е действие. Построить по вертикальной линии связи фронтальную проекцию точки 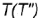
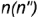
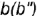
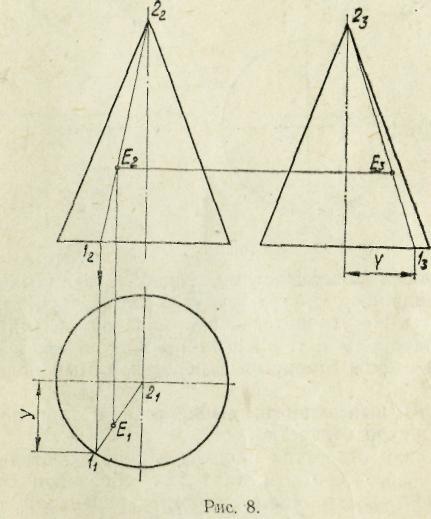
Конические сечения
Рассмотрим пять возможных случаев расположения секущей плоскости относительно оси конуса и его образующих, определяющих форму линии ее пересечения с поверхностью конуса (математические доказательства не приводятся):
1-й случаи. Гели секущая плоскость проходит через вершину конуса, то эта плоскость пересекает коническую поверхность по двум образующим 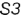

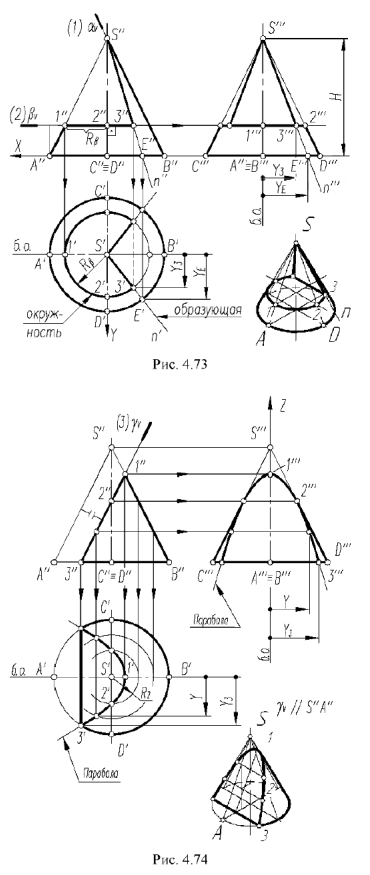
2-й случай. Если секущая плоскость расположена перпендикулярно оси конуса, то эта плоскость пересекает коническую поверхность но окружности (горизонтальная плоскость рис. 4.73).
3-й случай. Если секущая плоскость расположена параллельно одной образующей конуса, то эта плоскость пересекает коническую поверхность по параболе (фронтально-проецирующая плоскость 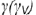

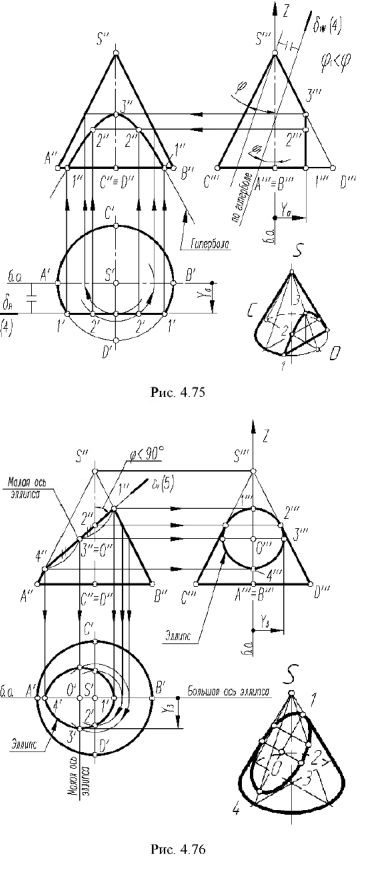
4-и случай. Если секущая плоскость расположена параллельно двум образующим конуса, то эта плоскость пересекает коническую поверхность по гиперболе (фронтальная плоскость 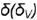

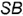
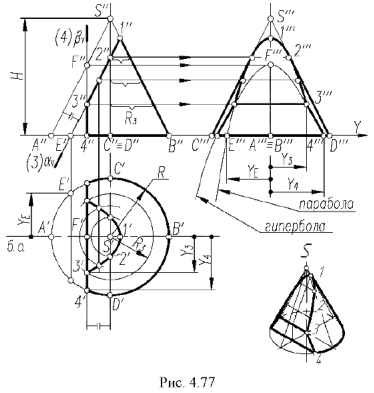
5-й случай. Если плоскость пересекает все образующие конуса под углом, отличным от прямого (или иначе, не параллельна ни одной образующей конуса), то эта плоскость пересекает коническую поверхность по эллипсу (фронтально-проецирующая плоскость ), рис 4.76).
Рассмотрим построение на проекциях конуса линии пересечения для всех пяти случаев сечений.
1-й и 2-й случаи. На рис. 4.73 показано построение проекций прямого кругового конуса с вырезом, образованным сечениями конической поверхности фронтально-проецирующей плоскостью 

Плоскость 

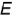
Плоскость пересекает поверхность конуса по окружности радиуса ограниченной линией 3-3 пересечения плоскостей выреза.
Построение горизонтальной и профильной проекций конуса с вырезом и оформление очерков этих проекций видно из чертежа.
3-й случай. На рис. 4.74 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью 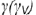

Плоскость пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена)
Построение проекций этих точек выполнено по их принадлежности:
- проекции промежуточной точки построены по ее принадлежности соответствующей параллели (профильные проекции — по координате
).
Оформление очерков проекций видно из чертежа.
4-й случай. На рис. 4.75 показано построение проекций конуса со срезом фронтальной плоскостью 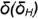


Плоскость 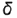
Оформление очерков проекций видно из чертежа.
На рис 4 75 на профильной проекции конуса показано положение секущей плоскости 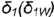
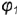
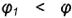
5-й ыучай. На рис. 4.76 показано построение проекции конуса со срезом фронтально-проецирующей плоскостью 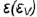
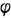
Плоскость 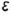
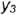
Оформление очерков проекций видно из чертежа.
. Количество взятых промежуточных точек должно быть минимальным, но достаточным, чтобы построить на проекциях конуса формы кривых второго порядка (параболы, гиперболы и эллипса), которые выполняют на чертеже по построенным характерным и промежуточным точкам с помощью лекала.
Построении проекции прямого конуса со срезами плоскостями частного положения
На рис. 4.77 показан пример построения проекций прямого круговою конуса со срезами фронтально-проецирующей плоскостью 

Для построения проекций конуса со срезами следует выполнить графический алгоритм, определяющий порядок действий при решении всех подобных задач.
1-е действие. Построить на чертеже тонкими линиями по заданному радиусу основания 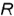
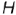


2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выпол-иить графический анализ сечений:
1. Фронтально-проецирующая плоскость 
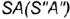
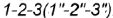
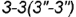


- Профильная плоскость
параллельна двум образующим конуса
и
и пересекает его поверхность по участку гиперболы
, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов
и
и плоскости
с основанием конуса (4-4).
3-е действие. Достроить горизонтальную проекцию конуса со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек и определить видимость плоскостей срезов:
1. Плоскость среза 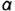
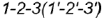
- Плоскость среза
определяет вертикальный видимый отрезок
вырожденной в линию проекции профильной плоскости, точки
которой лежат на очерковой окружности основания конуса.
. Поскольку горизонтальная проекция имеет вертикальную симметрию, точки обозначены на одной ее половине (нижней).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса для определения ее очерка и внутреннего контура:
- Горизонтальный очерк определяют участок окружности и отрезок
.
- Внутренний контур определяет видимый участок параболы
.
5-е действие. Достроить профильную проекцию конуса со срезами, пост-роив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
1. Плоскость среза а определяет видимый участок параболы , построенный по профильным проекциям обозначенных точек:
- Плоскость среза
определяют видимые участки гиперболы
, ограниченные видимым отрезком
(построен) и видимым отрезком
. точки которого построены но координате
.
6-е действие. Выполнить графический анализ построенной профильной проекции конуса для определения ее очерка и внутреннего контура.
- Профильный очерк определяют:
- Внутренний контур определяют:
7-е действие. Оформить чертеж конуса, выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой его проекции (оставить сплошными тонкими линиями полные очерки проекций и линии построения).
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Сечение поверхности конуса плоскостью общего положения
При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.
Ниже мы рассмотрим задачу, в которой требуется построить проекции и натуральную величину сечения конуса ω плоскостью α . Начальные данные представлены на рисунке ниже.
Определение высшей и низшей точки сечения. Границы видимости
Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.
Через ось конической поверхности проведем вспомогательную плоскость γ, параллельную П2. Она пересекает конус ω по двум образующим, а плоскость α по фронтали fγ. Точки 1 и 2 пересечения fγ с образующими являются граничными точками. Они делят сечение на видимую и невидимую части.
Определим высшую и низшую точки линии пересечения. Для этого через ось конуса перпендикулярно h0α введем дополнительную секущую плоскость β. Она пересекает коническую поверхность по образующим SL и SK, а плоскость α по прямой MN. Искомые точки 3 = SL ∩ MN и 4 = SK ∩ MN определяют большую ось эллипса. Его центр находится в точке O, которая делит отрезок 3–4 пополам.
Определение промежуточных точек и построение проекций эллипса
Чтобы построить проекции сечения наиболее точно, найдем ряд дополнительных точек. В случае с эллипсом целесообразно определить величину его малого диаметра. Для этого через центр O проводим вспомогательную горизонтальную плоскость δ. Она пересекает коническую поверхность по окружности диаметром AB, а плоскость α – по горизонтали hδ. Строим горизонтальные проекции окружности и прямой hδ. Их пересечение определяет точки 5′ и 6′ малого диаметра эллипса.
Для построения промежуточных точек 7 и 8 вводим вспомогательную горизонтальную плоскость ε. Проекции 7′ и 8′ определяются аналогично 5′ и 6′, как это показано на рисунке.
Соединив найденные точки плавной кривой, мы получили контур эллиптического сечения. На рисунке он обозначен красным цветом. Фронтальная проекция контура меняет свою видимость в точках 1 и 2, как это было отмечено выше.
Построение натуральной величины сечения методом совмещения
Чтобы найти натуральную величину сечения, повернем плоскость α до совмещения её с горизонтальной плоскостью. В качестве оси вращения будем использовать след h0α. Его положение в процессе преобразований останется неизменным.
Построение начинается с определения направления фронтального следа f1α. На прямой f0α возьмем произвольную точку E и определим её проекцию E’. Из E’ опустим перпендикуляр к h0α. Пересечение данного перпендикуляра с окружностью радиусом XαE» определяет положение точки E’1. Через Xα и E’1 проводим f1α.
Строим проекцию горизонтали h’1δ ∥ h0α, как это показано на рисунке. Точки O’1 и 5′1, 6′1 лежат на пересечении h’1δ с прямыми, проведенными перпендикулярно h0α из O’ и 5′, 6′. Аналогично на горизонтали h’1ε находим 7′1 и 8′1.
Строим проекции фронталей f’1γ ∥ f1α, f’3 ∥ f1α и f’4 ∥ f1α. Точки 1′1, 2′1, 3′1 и 4′1 лежат на пересечении этих фронталей с перпендикулярами, восстановленными к h0α из 1′, 2′, 3′ и 4′ соответственно.
Форум программистов Vingrad
| Модераторы: Poseidon |
Поиск: |
  
|
|
Опции темы |
| CompWorm |
|
||

Допеределыватель Профиль
Репутация: нет
|
Доброго времени суток. задача состоит в написании функции проверки нахождения точки в усечённом конусе. итак, мой конус задан 6 координатами центров и, соответственно, двумя радиусами отсекающих окружностей: то есть, конус может быть и наклоненным, а отсекающие окружности, само собой, остаются взаимно перпендикулярными. формула поверхности конуса второко порядка такая: вопрос… как этим пользоваться? как связать X1, Y1, Z1, R1, X2, Y2, Z2, R2, x, y, z с этой формулой? я так понимаю, как-то надо заюзать нормали этой поверхности… Это сообщение отредактировал(а) CompWorm — 5.6.2009, 22:46 ——————— >>> Indie Games Club! <<< |
||
|
|||
| Курсант |
|
||

Опытный Профиль
Репутация: 3
|
Пардон, ошибся… Подумаю Ага, подумал Нужно: 1. Построить прямую, проходящую через точки (x1, y1, z1) и (x2, y2, z2) Это коэффициент будет… Дальше берем расстояние от точки (x, y, z) до прямой (x1, y1, z1)-(x2, y2, z2) и сравниваем с выражением ax+b, где x — расстояние от (пересечения нормали построенной в п.2 с этой прямой) до (точки (x1, y1, z1))… Уффф, кажется все… Щас рисунок попробую сделать… Это сообщение отредактировал(а) Курсант — 6.6.2009, 19:13 Присоединённый файл ( Кол-во скачиваний: 16 ) ——————— Мобильная библиотека — онлайн книги для мобильного |
||
|
|||
| Курсант |
|
||

Опытный Профиль
Репутация: 3
|
Еще есть вариант… У Вас есть две точки и нормаль (нормаль это прямая проходящая через две твои точки)… Поэтому в каждой точке можно построить по одной плоскости, делящей пространство на полупространства… Уравнения полупространств наверняка как-то получить можно… очевидно что уравнение плоскости будет ( … = 0 ) , тогда уравнения полупространств будут соответственно ( … > 0 ) и ( … < 0 )… Аналогично поверхность конуса делит пространство на подпространства, где ( … = 0 ) — уравнение поверхности, и далее ( … < 0 ) и ( … > 0 ) — это соответственно внутреннее и внешнее подпространства поверхности… Вот Вам надо написать три функции — определения нахождения точки в каждом из трех подпространств… Если все три функции вернули тру, значит точка внутри фигуры, если нет — значит вне фигуры… Такое вот предположение… Не ругайтесь, если оно глупой (ан гем я сам забыл сто лет назад), то можно воспользоваться первым вариантом… Добавлено @ 22:27 При этом первое подпространство будет задано неравенством z > z1′ , второе будет задаваться неравенством z < z2′ , и каноническое уравнение конуса второго порядка будет задано уравнением, которое Вы написали выше.. подпространства его будут: внутреннее — < 0 и внешнее — > 0 … вот этими то объектами Вы и сможете все это дело определить… Это сообщение отредактировал(а) Курсант — 6.6.2009, 22:29 ——————— Мобильная библиотека — онлайн книги для мобильного |
||
|
|||
| CompWorm |
|
||

Допеределыватель Профиль
Репутация: нет
|
спасибо, Курсант, допишу свой третий вариант (это фактически доработанный твой первый)… 1) перевести систему координат из стандартной 3D (x, y, z) в 2) теперь наши точки имеют координаты (x’, y’) , (x1′, y1′)-(x2′, y2′). теперь совсем просто проверить, находится ли наша точки между отсекающими кругами: она между ними, если (x1′<x'<x2′) или (x2′<x'<x1′) в противном случае, точка точно за отсекающими кругами. 3) теперь от поверхности конуса осталась только прямая ВСЁ! —————————————————— то есть далее речь пойдет о формулах и конкретных математических расчетах. надеюсь, кто-нибудь мне в этом поможет. мой метод кажется мне очень простым, но я не уверен в том что он окажется быстрее в плане расчетов двух методов предложенных Курсантом. мне кажется, с использованием уравнения поверхности это выйдет быстрее!!! очень хотелось бы добить именно этот вариант… давайте распишим математику и увидим, какой метод лучше. 1) перевод координат… хммм… понятия не имею, как это реализовать)))))))))) подскажите? когда нашли y3′ от x’ — проверяем, если if (y3′ > y’) то точка в конусе. в противном случае false подскажите, как мне координаты перевести в первом пункте ? Это сообщение отредактировал(а) CompWorm — 7.6.2009, 13:03 ——————— >>> Indie Games Club! <<< |
||
|
|||
| Курсант |
|
||

Опытный Профиль
Репутация: 3
|
http://gis-lab.info/qa/datum-transform-methods.html Вот здесь описан переход к другой системе координат через ее известные смещение/поворот относительно исходной… Нормаль все равно прийдется строить мне кажется… Я не помню точно, но мне кажется Вам прийдется найти три единичных вектора. Тогда в этой СК значения Z для всех точек будет равным нулю, и можно будет поверхность вырождать в трапецию… И все таки мне все больше начинает нравится второй вариант — можно найти всего одну СК, в которой точки (1) и (2) вырождаются в точки на оси z, уравнение поверхности вырождается в каноническое, которое Вы привели, внутренняя область конуса вырождается соответственно в неравенство (x^2/a^2 + y^2/b^2 — z^2/c^2 < 0) а полупространства вырождаются в уравнения z {принадлежит} (z1’…z2′)… то есть совпадение точки и полупространств вычислить будет элементарно… Вершина находится элементарно, раз у вас есть координаты и радиусы, углы поворота осей может найдете из приведенной ссылки. Это сообщение отредактировал(а) Курсант — 7.6.2009, 23:15 ——————— Мобильная библиотека — онлайн книги для мобильного |
||
|
|||
| CompWorm |
|
||||

Допеределыватель Профиль
Репутация: нет
|
Курсант, ха ха, я конечно дубина)))) как только я эти матрицы поворота и смещения увидел — сразу вспомнил, что они у меня в одной книжке были))
вот, да! мне тоже))) сместить просто — берм центр одного из отсекающих кругов, например 1 и вычетаем его x, y, z из коорднинат искомой точки, точки 1 и 2. для поворота надо использовать матрицу поворота. с углами поворота замута тоже, но думаю можно вычисить из катетов и акрсинусов всяких.
а как быть с концом конуса??? достраивать? ну допустим)) тогда есть мысль — подставить в каноническое уравнение координаты от искомой точки y` и z` ( где z {принадлежит} (z1’…z2′) ) y’=0 к стати оси как тут , найдя точки X поверхности (их будет две на одной и другой стороне) и проверить, принадлежит ли x’ этому промежутку? так? Это сообщение отредактировал(а) CompWorm — 9.6.2009, 23:04 ——————— >>> Indie Games Club! <<< |
||||
|
|||||
| Курсант |
|
||

Опытный Профиль
Репутация: 3
|
За плюсик пасибо Что касается преобразований — я немного другое имел ввиду… Найти систему координат конуса, вот что я имел ввиду… Систему координат, в которой начало координат в вершине конуса, ось z направлена по прямой (1) — (2)… Вот по координатам точек этой прямой можно найти два угла поворота системы координат конуса относительно исходной. А по «раствору» конуса можно определить коэфф-ты a, b, c для его канонического уравнения в этой системе координат. Усе. Теперь у Вас есть вектор смещения СК конуса относительно исходной СК (координаты вершины конуса и будут составляющими этого вектора). Углы поворота тоже можно вычислить через угол наклона оси конуса… Дальше преобразовывайте координаты точки из исходной СК в СК конуса, и уже в ней, имея коэффициенты a, b, c, а также значения z1 и z2 (где z1 и z2 есть расстояния центров отсекающих кругов от вершины конуса) можно определить, внутри конуса точка или снаружи… Если трудно — всегда можно вернуться к первому варианту — построению нормали, проходящей через точку. Всего то… Добавлено @ 23:49 З.Ы. Есть предположение у меня, что по координатам двух точек не получится найти углов наклона прямой. Хотя возможно что: Как по координатам синусы углов между прямыми и плоскостями, проекциями и т.п. найти думаю сможете? Там по т. Пифагора все проекции очень миленько высчитываются… Щас спать пора, а завтра может допишу Вот графический комментарий… Сначала поворачиваем вокруг оси X на угол альфа, а потом вокруг получившейся оси Y’ на угол бета. То есть в моем понимании, угол поворота вокруг оси X , будет равен Это сообщение отредактировал(а) Курсант — 10.6.2009, 14:42 Присоединённый файл ( Кол-во скачиваний: 6 ) ——————— Мобильная библиотека — онлайн книги для мобильного |
||
|
|||
| CompWorm |
|
||

Допеределыватель Профиль
Репутация: нет
|
хе хе! ну а матрицы то на что! я почесал репу и пришел к такому мнению: ты прав, достаточно два любых поворота, но нас сами углы как таковые не интересуют, ибо если сместить R2 в точку (0,0,0), где R2>R1, то координаты точки R1 мы знаем! давай считать, что расстояние между R1 и R2 известно и равно L. |x1| | | | | | x’ | то есть, помножив известные x1,y1,z1 на две матрицы поворота (вокруг Z и вокруг Y например) получим известные координаты (0,0,-L). соответственно нам надо отсюда найти элементы произведения |Z| на |Y|. с матрицами я не в ладах, но думаю так можно)))) я тебя малость не дождаля и решил от скуки расписать своё решение из предыдущего поста. посмотри рисунок, который я приложил. считаем, что координаты уже преобразованы и конус торчит как на рисунке 2. расстояние от начала координат до первой отсекающей окружности я обозначил как Lo и Lo=-Z теперь решаем каноническое уравнение (рисунок 1). здесь считаем, что a=b; c=L+Lo; x=y. решив его находим два игрика Yo и Y1, равные, соответственно, двум иксам. это и есть промежуток для сравнения. сравнение такое: Z {принадлежит} (Lo, Lo+L) всё ——————— Это сообщение отредактировал(а) CompWorm — 10.6.2009, 15:25 Присоединённый файл ( Кол-во скачиваний: 8 ) ——————— >>> Indie Games Club! <<< |
||
|
|||
| Курсант |
|
||

Опытный Профиль
Репутация: 3
|
Я считаю, что удобнее будет центр СК помещать в вершине конуса. Тогда вектор смещения исходной СК в СК конуса будет равен (координаты вершины конуса) — (координаты начала координат, т.е. (0, 0, 0) ) Удобнее потому, что если у тебя центр СК будет в точке x1, y1, z1 то уравнение конуса будет иметь вид (x-x1)^2/a^2 + (y-y1)^2/b^2 — (z-z1)^2/c^2 = 0, а это трабла полная… Проще центр СК иметь в точке вершины конуса, тогда уравнение будет x^2 + y^2 — z^2/((расстояние от т.1 до вершины)/R1)^2 = 0, то есть a=1, b=1, c=(расст. от т.1 до вершины конуса)/R1… А по отношениям длин проекций (см пост выше) можно построить сразу и матрицу направляющих косинусов… как в той википедии которую ты разместил в предыд посте… Вектор сдвига есть, матрица поворота есть. Сначала пересчитывай точку (x y z) в сдвинутой СК, потом пересчитывай эту точку из сдвинутой СК в сдвинуто-повернутую, путем умножения на матрицу направляющих косинусов — вуаля, у тебя есть координаты точки относительно канонического конуса и двух плоскостей… Проверяй условия вхождения точки одновременно в три объемных области, если хоть одна область не содержит точку, то вне, а если все содержат, то внутри. Чтобы пересчитать точку (x, y, z) в СК конуса, в любом случае нужны вектор смещения и поворотная матрица. Это сообщение отредактировал(а) Курсант — 10.6.2009, 20:44 ——————— Мобильная библиотека — онлайн книги для мобильного |
||
|
|||
| CompWorm |
|
||

Допеределыватель Профиль
Репутация: нет
|
я так и делаю. просто сначала мне надо найти Lo, а потом делаем СК стандартной для канонического уравнения, ка ты и пишешь. на счет остального, соглашусь и подумаю над этим. спасибо. скорее всего это и будет идеальный вариант. последнее, вопрос про формулу сечения конуса, о чем я писал выше… не в курсе какая она? может её как-то можно использовать без преобразований СК ——————— >>> Indie Games Club! <<< |
||
|
|||
| Курсант |
|
||

Опытный Профиль
Репутация: 3
|
Лучше не стоит — это опять надо будет по теореме Пифагора длины вычислять, и тому подобное.. Лучше не стоит.. Сначала лучше ную матрицу, потом каноническое уравнение… Тем более что от поворота все равно никуда не деться — как минимум одну точку поворачивать надо… ——————— Мобильная библиотека — онлайн книги для мобильного |
||
|
|||
  
|
| Правила форума «Центр помощи» | |
|
|
ВНИМАНИЕ! Прежде чем создавать темы, или писать сообщения в данный раздел, ознакомьтесь, пожалуйста, с Правилами форума и конкретно этого раздела.
Более подробно с правилами данного раздела Вы можете ознакомится в этой теме. Если Вам помогли и атмосфера форума Вам понравилась, то заходите к нам чаще! С уважением, Poseidon, Rodman |
| 0 Пользователей читают эту тему (0 Гостей и 0 Скрытых Пользователей) |
| 0 Пользователей: |
| « Предыдущая тема | Центр помощи | Следующая тема » |
Наверх

Развертка усеченного конуса является одним часто задаваемым заданием по инженерной графике для студентов в учебных заведениях.
Рассмотрим пошаговое построение с подробным описанием согласно этому заданию: дан конус высотой 120 мм и диаметром 100 мм. Необходимо провести линию сечения под углом 45 0 на расстоянии 60 мм от оси фигуры.
Приступим к выполнению:
1.) Чертим третий вид конуса;
2.) Разбиваем вид сверху на 12 составляющих частей. Это необходимо для построения развертки;
3.) Находим точки сечения на нижнем рисунке;
4.) Подписываем точки полученного сечения на видовых проекциях;
5.) Переносим точки сечения на третью проекцию (вид слева);
6.) Обводим толстыми видимыми линиями полученную фигуру;
7.) Строим развертку, если бы она не имела выреза. Отмеряется расстояние от вершины конуса до основания и от центральной оси чертится 12 участков;
8.) Обозначаем на развертке участки для лучшего представления о том где строить точки;
9.) Отмеряем расстояние на конусе (фронтальной проекции) циркулем и чертим таким же размером на развертке и подписываем полученную точку. По такому принципу осуществляется нахождение точек на развертке;
10.) Обводим толстыми линиями чертежа полученную развертку усеченного конуса.
Вы также можете посмотреть видео:
Просмотрели 1 827











































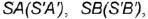
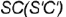 и
и 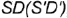 которые будут определять очерки фронтальной и профильной проекций конуса.
которые будут определять очерки фронтальной и профильной проекций конуса.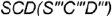 ограниченный:
ограниченный: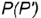
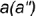
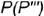 выполняется по принадлежности образующей
выполняется по принадлежности образующей 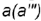 , построенной но координате
, построенной но координате  .
.
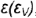
 ).
).
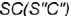 и
и 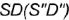 и пересекает его поверхность по участку гиперболы
и пересекает его поверхность по участку гиперболы 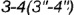 , которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов
, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов 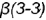 и плоскости
и плоскости 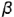 определяет вертикальный видимый отрезок
определяет вертикальный видимый отрезок 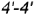 вырожденной в линию проекции профильной плоскости, точки
вырожденной в линию проекции профильной плоскости, точки 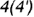 которой лежат на очерковой окружности основания конуса.
которой лежат на очерковой окружности основания конуса.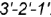 .
.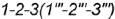
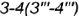 , ограниченные видимым отрезком
, ограниченные видимым отрезком 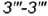 (построен) и видимым отрезком
(построен) и видимым отрезком 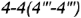 . точки которого построены но координате
. точки которого построены но координате 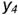 .
.





















 (её концы нас не интересуют. это учтено в пункте 2) нам нужно найти Y3′ этой прямой в точке X3’=x’ (абсцисса нашей искомой точки) и если Y3′>y’ то наша точка под прямой.
(её концы нас не интересуют. это учтено в пункте 2) нам нужно найти Y3′ этой прямой в точке X3’=x’ (абсцисса нашей искомой точки) и если Y3′>y’ то наша точка под прямой.
 )
)































