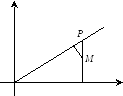Как найти точку начала координат гиперболы - Исправление недочетов и поиск решений вместе с Examum.ru

Гипербола: определение, свойства, построение

Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек F_1 и F_2 есть величина постоянная (2a) , меньшая расстояния (2c) между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.

Фокальное свойство гиперболы

Точки F_1 и F_2 называются фокусами гиперболы, расстояние 2c=F_1F_2 между ними — фокусным расстоянием, середина отрезка F_1F_2 — центром гиперболы, число — длиной действительной оси гиперболы (соответственно, — действительной полуосью гиперболы). Отрезки F_1M и F_2M , соединяющие произвольную точку гиперболы с ее фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение $e=frac{c}{a}$ , где $c=sqrt{a^2+b^2}$ , называется эксцентриситетом гиперболы. Из определения (2a<2c) следует, что e>1 .

Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:

$frac{x^2}{a^2}-frac{y^2}{b^2}=1.$

(3.50)

Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F_1 к точке F_2 ); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).

Гипербола и фокальное свойство гипербол

Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов F_1(-c,0) и F_2(c,0) . Для произвольной точки M(x,y) , принадлежащей гиперболе, имеем:

$left||overrightarrow{F_1M}|-|overrightarrow{F_2M}|right|=2a.$

Записывая это уравнение в координатной форме, получаем:

$sqrt{(x+c)^2+y^2}-sqrt{(x-c)^2+y^2}=pm2a.$

Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:

$frac{x^2}{a^2}-frac{y^2}{b^2}=1,,$

где $b=sqrt{c^2-a^2}$ , т.е. выбранная система координат является канонической.

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.

Директориальное свойство гиперболы

Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии $a^2!!not{phantom{|}},c$ от нее (рис.3.41,а). При a=0 , когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.

Гиперболу с эксцентриситетом e=1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство гиперболы). Здесь и — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

Директрисы гиперболы и директориальное свойство

В самом деле, например, для фокуса F_2 и директрисы d_2 (рис.3.41,а) условие $frac{r_2}{rho_2}=e$ можно записать в координатной форме:

$sqrt{(x-c)^2+y^2}=eleft(x-frac{a^2}{c}right)$

Избавляясь от иррациональности и заменяя $e=frac{c}{a},~c^2-a^2=b^2$ , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса F_1 и директрисы d_1 :

$frac{r_1}{rho_1}=e quad Leftrightarrow quad sqrt{(x+c)^2+y^2}= eleft(x+frac{a^2}{c} right).$

Уравнение гиперболы в полярной системе координат

Уравнение правой ветви гиперболы в полярной системе координат F_2rvarphi (рис.3.41,б) имеет вид

$r=frac{p}{1-ecdotcosvarphi}$ , где $p=frac{p^2}{a}$ — фокальный параметр гиперболы.

В самом деле, выберем в качестве полюса полярной системы координат правый фокус F_2 гиперболы, а в качестве полярной оси — луч с началом в точке F_2 , принадлежащий прямой F_1F_2 , но не содержащий точки F_1 (рис.3.41,б). Тогда для произвольной точки M(r,varphi) , принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем F_1M-r=2a . Выражаем расстояние между точками M(r,varphi) и F_1(2c,pi) (см. пункт 2 замечаний 2.8):

$F_1M=sqrt{(2c)^2+r^2-2cdot(2c)^2cdot rcdotcos(varphi-pi)}=sqrt{r^2+4cdot ccdot rcdotcosvarphi+4cdot c^2}.$

Следовательно, в координатной форме уравнение гиперболы имеет вид

$sqrt{r^2+4cdot ccdot rcdotcosvarphi+4cdot c^2}-r=2a.$

Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:

$r^2+4crcdotcosvarphi+4c^2=4a^2+4ar+r^2 quad Leftrightarrow quad aleft(1-frac{c}{a}cosvarphiright)r=c^2-a^2.$

Выражаем полярный радиус и делаем замены $e=frac{c}{a},~b^2=c^2-a^2,~p=frac{b^2}{a}$ :

$r=frac{c^2-a^2}{a(1-ecosvarphi)} quad Leftrightarrow quad r=frac{b^2}{a(1-ecosvarphi)} quad Leftrightarrow quad r=frac{p}{1-ecosvarphi},$

что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( e>1 для гиперболы, 0leqslant e<1 для эллипса).

Геометрический смысл коэффициентов в уравнении гиперболы

Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение y=0 , находим абсциссы точек пересечения: x=pm a . Следовательно, вершины имеют координаты (-a,0),,(a,0) . Длина отрезка, соединяющего вершины, равна . Этот отрезок называется действительной осью гиперболы, а число — действительной полуосью гиперболы. Подставляя x=0 , получаем y=pm ib . Длина отрезка оси ординат, соединяющего точки (0,-b),,(0,b) , равна . Этот отрезок называется мнимой осью гиперболы, а число — мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.

Замечания 3.10.

1. Прямые x=pm a,~y=pm b ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).

2. Прямые $y=pmfrac{b}{a},x$ , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).

Для равносторонней гиперболы, описываемой уравнением $frac{x^2}{a^2}-frac{y^2}{a^2}=1$ (т.е. при a=b ), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат Ox'y' (рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид $y'=frac{a^2}{2x'}$ (гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).

Асимптоты гиперболы и равносторонняя гипербола

В самом деле, повернем каноническую систему координат на угол $varphi=-frac{pi}{4}$ (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами

$left{!begin{aligned}x&=frac{sqrt{2}}{2}cdot x'+frac{sqrt{2}}{2}cdot y',\ y&=-frac{sqrt{2}}{2}cdot x'+frac{sqrt{2}}{2}cdot y'end{aligned}right. quad Leftrightarrow quad left{!begin{aligned}x&=frac{sqrt{2}}{2}cdot(x'+y'),\ y&=frac{sqrt{2}}{2}cdot(y'-x')end{aligned}right.$

Подставляя эти выражения в уравнение $frac{x^2}{a^2}-frac{y^2}{a^2}=1$ равносторонней гиперболы и приводя подобные члены, получаем

$frac{frac{1}{2}(x'+y')^2}{a^2}-frac{frac{1}{2}(y'-x')^2}{a^2}=1 quad Leftrightarrow quad 2cdot x'cdot y'=a^2 quad Leftrightarrow quad y'=frac{a^2}{2cdot x'}.$

3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.

Действительно, если точка M(x,y) принадлежит гиперболе $frac{x^2}{a^2}-frac{y^2}{b^2}=1$ . то и точки M'(x,y) и M''(-x,y) , симметричные точке относительно координатных осей, также принадлежат той же гиперболе.

Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.

4. Из уравнения гиперболы в полярных координатах $r=frac{p}{1-ecosvarphi}$ (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси ( r=p при $varphi=frac{pi}{2}$ ).

5. Эксцентриситет характеризует форму гиперболы. Чем больше , тем шире ветви гиперболы, а чем ближе к единице, тем ветви гиперболы уже (рис.3.43,а).

Действительно, величина gamma угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника: $operatorname{tg}frac{gamma}{2}=frac{b}{2}$ . Учитывая, что $e=frac{c}{a}$ и c^2=a^2+b^2 , получаем

$e^2=frac{c^2}{a^2}=frac{a^2+b^2}{a^2}=1+{left(frac{b}{a}right)!}^2=1+operatorname{tg}^2frac{gamma}{2}.$

Чем больше , тем больше угол gamma . Для равносторонней гиперболы (a=b) имеем e=sqrt{2} и $gamma=frac{pi}{2}$ . Для e>sqrt{2} угол gamma тупой, а для 1<e<sqrt{2} угол gamma острый (рис.3.43,а).

Эксцентриситет гиперболы и сопряжённая гипербола

6. Две гиперболы, определяемые в одной и той же системе координат уравнениями $frac{x^2}{a^2}-frac{y^2}{b^2}=1$ и $-frac{x^2}{a^2}+frac{y^2}{b^2}=1$ называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы $-frac{x^2}{a^2}+frac{y^2}{b^2}=1$ приводится к каноническому при помощи переименования координатных осей (3.38).

7. Уравнение $frac{(x-x_0)^2}{a^2}-frac{(y-y_0)^2}{b^2}=1$ определяет гиперболу с центром в точке O'(x_0,y_0) , оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение $-frac{(x-x_0)^2}{a^2}+frac{(y-y_0)^2}{b^2}=1$ определяет сопряженную гиперболу с центром в точке O'(x_0,y_0) .

Параметрическое уравнение гиперболы

Параметрическое уравнение гиперболы в канонической системе координат имеет вид

$begin{cases}x=acdotoperatorname{ch}t,\y=bcdotoperatorname{sh}t,end{cases}tinmathbb{R},$

где $operatorname{ch}t=frac{e^t+e^{-t}}{2}$ — гиперболический косинус, a $operatorname{sh}t=frac{e^t-e^{-t}}{2}$ гиперболический синус.

Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству $operatorname{ch}^2t-operatorname{sh}^2t=1$ .

Построение гиперболы в канонической системе координат

Пример 3.21. Изобразить гиперболу $frac{x^2}{2^2}-frac{y^2}{3^2}=1$ в канонической системе координат Oxy . Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.

Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: a=2 — действительная полуось, b=3 — мнимая полуось гиперболы. Строим основной прямоугольник со сторонами 2a=4,~2b=6 с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя x=4 в уравнение гиперболы, получаем

$frac{4^2}{2^2}-frac{y^2}{3^2}=1 quad Leftrightarrow quad y^2=27 quad Leftrightarrow quad y=pm3sqrt{3}.$

Следовательно, точки с координатами (4;3sqrt{3}) и (4;-3sqrt{3}) принадлежат гиперболе. Вычисляем фокусное расстояние

$2cdot c=2cdotsqrt{a^2+b^2}=2cdotsqrt{2^2+3^2}=2sqrt{13}$

эксцентриситет $e=frac{c}{a}=frac{sqrt{13}}{2}$ ; фокальныи параметр $p=frac{b^2}{a}=frac{3^2}{2}=4,!5$ . Составляем уравнения асимптот $y=pmfrac{b}{a},x$ , то есть $y=pmfrac{3}{2},x$ , и уравнения директрис: $x=pmfrac{a^2}{c}=frac{4}{sqrt{13}}$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).

Математическая гипербола.

Функция заданная формулой (y=frac{k}{x}), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac{k}{x}) называют гиперболой. Где х является независимой переменной, а у — зависимой.

Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти.
гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти

гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти

2.Асимптоты гиперболы. Чтобы найти асимптоты гиперболы необходимо,иногда, уравнение гиперболы упростить. Рассмотрим на примере:
Пример №1:
$$y=frac{1}{x}$$
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х не равен 0.
$$yneqcolor{red} {frac{1}{x}}+0$$
(frac{1}{x}) дробь отбрасываем, для того чтобы найти вторую асимптоту.
Остается простое число
y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.

Пример №2:
$$y=frac{1}{x+2}-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота

Находим вторую асимптоту.

$$y=color{red} {frac{1}{x+2}}-1$$

Дробь (color{red} {frac{1}{x+2}}) отбрасываем
Остается y≠ -1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):

Пример №3:

$$begin{align*}
&y=frac{2+x}{1+x} \\
&y=frac{color{red} {1+1}+x}{1+x} \\
&y=frac{1}{1+x}+frac{1+x}{1+x}\\
&y=frac{1}{1+x}+1\\
&y=frac{1}{color{red} {1+x}}+1
end{align*}$$

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.

Находим вторую асимптоту.

$$y=color{red}{frac{1}{1+x}}+1$$

(color{red}{frac{1}{1+x}}) Дробь убираем.

Остается y≠1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:

$$y=frac{1}{x}$$

Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.

4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:

$$y=frac{1}{x}$$

Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.

Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.

$$f(-x)=frac{1}{-x}=-frac{1}{x}=-f(x)$$

6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:

$$y=frac{-1}{x-1}-1$$

а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.

Находим вторую асимптоту.

$$y=color{red} {frac{-1}{x-1}}-1$$

Дробь (color{red} {frac{-1}{x-1}}) удаляем.

Остается y≠ -1 это вторая асимптота.

б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.

в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5

г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).

д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).

е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k<0 функция возрастающая.

8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
реклама

Источник

Гипербола и её форма.

Начать изучение
Фокусы, эксцентриситет и директрисы гиперболы.

Начать изучение
Точки гиперболы и их свойства.

Начать изучение
Уравнение касательной к гиперболе.

Начать изучение

Гипербола и её форма.

Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1.label{ref9}
$$

Из этого уравнения видно, что для всех точек гиперболы (|x| geq a), то есть все точки гиперболы лежат вне вертикальной полосы ширины (2a) (рис. 8.6). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами ((a, 0)) и ((-a, 0)), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа (a) и (b) называются соответственно вещественной и мнимой полуосями гиперболы.

Рис. 8.6. Гипербола.

Утверждение.

Для гиперболы оси канонической системы координат являются осями симметрии, а начало канонической системы — центром симметрии.

Доказательство.

Доказательство аналогично доказательству соответствующего утверждения для эллипса.

Для исследования формы гиперболы найдем ее пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде (y=kx), поскольку мы уже знаем, что прямая (x=0) не пересекает гиперболу. Абсциссы точек перечения находятся из уравнения
$$
frac{x^{2}}{a^{2}}-frac{k^{2}x^{2}}{b^{2}}=1.
$$
Поэтому, если (b^{2}-a^{2}k^{2} > 0), то
$$
x=pm frac{ab}{sqrt{b^{2}-a^{2}k^{2}}}.
$$
Это позволяет указать координаты точек пересечения ((ab/v, abk/v)) и ((-ab/v, -abk/v)), где обозначено (v=(b^{2}-a^{2}k^{2})^{1/2}). В силу симметрии достаточно проследить за движением первой из точек при изменении (k) (рис. 8.7).

Рис. 8.7. Пересечение прямой и гиперболы.

Числитель дроби (ab/v) постоянен, а знаменатель принимает наибольшее значение при (k=0). Следовательно, наименьшую абсциссу имеет вершина ((a, 0)). С ростом (k) знаменатель убывает, и (x) растет, стремясь к бесконечности, когда (k) приближается к числу (b/a). Прямая (y=bx/a) с угловым коэффициентом (b/a) не пересекает гиперболу, и прямые с большими угловыми коэффициентами ее тем более не пересекают. Любая прямая с меньшим положительным угловым коэффициентом пересекает гиперболу.

Если мы будем поворачивать прямую от горизонтального положения по часовой стрелке, то (k) будет убывать, (k^{2}) расти, и прямая будет пересекать гиперболу во все удаляющихся точках, пока не займет положения с угловым коэффициентом (-b/a).

К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из приведенных рассуждений вытекает, что гипербола имеет вид, изображенный на рис. 8.7.

Определение.

Прямые с уравнениями (y=bx/a) и (y=-bx/a) в канонической системе координат называются асимптотами гиперболы.

Запишем уравнения асимптот в виде (bx-ay=0) и (bx+ay=0). Расстояния от точки (M(x, y)) до асимптот равны соответственно
$$
h_{1}=frac{|bx-ay|}{sqrt{a^{2}+b^{2}}}, h_{2}=frac{|bx+ay|}{sqrt{a^{2}+b^{2}}}.nonumber
$$
Если точка (M) находится на гиперболе, то (b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2}), и
$$
h_{1}h_{2}=frac{|b^{2}x^{2}-a^{2}y^{2}|}{a^{2}+b^{2}}=frac{a^{2}b^{2}}{a^{2}+b^{2}}.nonumber
$$

Утверждение.

Произведение расстояний от точки гиперболы до асимптот постоянно и равно (a^{2}b^{2}/(a^{2}+b^{2})).

Отсюда следует важное свойство асимптот.

Свойство.

Если точка движется по гиперболе так, что ее абсцисса по абсолютной величине неограниченно возрастает, то расстояние от точки до одной из асимптот стремится к нулю.

Доказательство.

Действительно, хотя бы одно из расстояний (h_{1}) или (h_{2}) при этих условиях должно неограниченно возрастать, и, если бы предложение было неверно, произведение не было бы постоянно.

Фокусы, эксцентриситет и директрисы гиперболы.

Определение.

Введем число (c), положив
$$
c^{2}=a^{2}+b^{2}label{ref10}
$$
и (c > 0). Фокусами гиперболы называются точки (F_{1}) и (F_{2}) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат.

Рис. 8.8. Фокусы гиперболы.

Отношение (varepsilon=c/a), как и для эллипса, называется эксцентриситетом. У гиперболы (varepsilon > 1).

Утверждение 9.

Расстояния от произвольной точки (M(x, y)) на гиперболе до каждого из фокусов следующим образом зависят от ее абсциссы (x):
$$
r_{1}=|F_{1}M|=|a-varepsilon x|, r_{2}=|F_{2}M|=|a+varepsilon x|.label{ref11}
$$

Рис. 8.9. Расстояние от точки на гиперболе до ее фокусов.

Доказательство.

Доказательство этого утверждения почти дословно совпадает с доказательством аналогичного утверждения для эллипса.

Заметим, что равенства eqref{ref11} можно подробнее записать так:

для правой ветви гиперболы ((x geq a))
$$
r_{1}=varepsilon x-a, r_{2}=varepsilon x+a;nonumber
$$
для левой ветви гиперболы ((x leq -a))
$$
r_{1}= a-varepsilon x, r_{2}=-varepsilon x-a;nonumber
$$

Итак, для правой ветви (r_{2}-r_{1}=2a), а для левой ветви (r_{1}-r_{2}=2a). В обоих случаях
$$
|r_{2}-r_{1}|=2a.label{ref12}
$$

Директрисами гиперболы называются прямые, задаваемые в канонической системе координат уравнениями
$$
x=frac{a}{varepsilon}, x=-frac{a}{varepsilon}.label{ref13}
$$

Директрисы лежат ближе к центру, чем вершины, и, следовательно, не пересекают гиперболу. Директриса и фокус, лежащие по одну сторону от центра, считаются соответствующими друг другу.

Точки гиперболы и их свойства.

Утверждение 10.

Для того чтобы точка (M) лежала на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы (2a).

Доказательство.

Необходимость условия уже доказана. Для доказательства достаточности условия его нужно представить в виде
$$
sqrt{(x-c)^{2}+y^{2}}=pm 2a+sqrt{(x+c)^{2}+y^{2}}nonumber
$$
Дальнейшее отличается от доказательства соответствующего утверждения для эллипса только тем, что нужно воспользоваться равенством (c^{2}=a^{2}+b^{2}), а не (c^{2}=a^{2}-b^{2}).

Утверждение 11.

Для того чтобы точка лежала на гиперболе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету (varepsilon) (рис. 8.10).

Рис. 8.10.

Доказательство.

Доказательство повторяет доказательство предложения 4. Докажем, например, необходимость условия для фокуса (F_{2}(-c, 0)). Пусть (M'(x, y)) — точка гиперболы. Расстояние от (M’) до директрисы с уравнением (x=-a/varepsilon) по формуле (9) § 3 гл. II равно
$$
d’=left|x+frac{a}{varepsilon}right|=frac{1}{varepsilon}|varepsilon x+a|.nonumber
$$

Из формулы eqref{ref11} мы видим теперь, что (r’/d’=varepsilon).

Уравнение касательной к гиперболе.

Уравнение касательной к гиперболе в точке (M_{0}(x_{0}, y_{0})), лежащей на ней, выводится так же, как соответствующее уравнение касательной для эллипса. Оно имеет вид
$$
frac{xx_{0}}{a^{2}}-frac{yy_{0}}{b^{2}}=1.label{ref14}
$$

Утверждение 12.

Касательная к гиперболе в точке (M_{0}(x_{0}, y_{0})) есть биссектриса угла между отрезками, соединяющими эту точку с фокусами.

Доказательство.

Доказательство почти не отличается от доказательства соответствующего утверждения для эллипса.

Источник

Определение.
Пусть на плоскости заданы две точки F₁
и F₂,
расстояние между которыми равно 2c.
Пусть, кроме того, задано положительное
число a,
меньшее c.
Гиперболой
называется множество точек той же
плоскости, для каждой из которых модуль
разности расстояний до точек F₁
и F₂,
называемых фокусами
гиперболы, есть число постоянное, равное
2а.

Вывод канонического уравнения

Для вывода уравнения
гиперболы, которое мы впоследствии
назовём каноническим, выберем на
плоскости прямоугольную декартову
систему координат следующим образом:
ось

проведем через фокусы гиперболы, а ось

–
перпендикулярно ей через середину
отрезка F₁F₂
(рис. 3.1). По определению гиперболе
удовлетворяют те, и только те точки М
плоскости, для которых

Рис. 3.1.

.
(1)

Чтобы получить
уравнение гиперболы остаётся только
записать равенство (1) в координатах. В
выбранной системе координат фокусы
гиперболы имеют следующие координаты:
F₁
(–c;
0); F₂
(c;
0). Координаты произвольной (или текущей)
точки множества всегда обозначаются x
и y.
Таким образом, M(x;
y).
Так как

то уравнение (1)
равносильно следующему:

,
(2)

которое, в свою
очередь, равносильно уравнению:

.
(3)

Оба эти уравнения
являются уравнениями гиперболы, но они
имеют громоздкий вид, неудобны для
использования и для запоминания, поэтому
мы преобразуем их к более простому виду.
Проведем следующую цепочку преобразований:

(3)

Учитывая, что
,
разделив последнее уравнение на
,
получаем:

.
(4′)

Так как
,
то
,
поэтому найдется такое положительное
число
,
что
.
Теперь уравнение (4′) примет вид:

.
(4)

Мы доказали: если
точка принадлежит гиперболе, то её
координаты удовлетворяют уравнению
(3) или (4).

Докажем обратное:
если координаты точки удовлетворяют
уравнению (4) или (3), то она принадлежит
гиперболе. Итак,

{M
(x;
y)
удовлетворяет (4)}

.
(5)

Аналогично получаем:

.
(6)

Находим разность
расстояний:

[(4)

]=

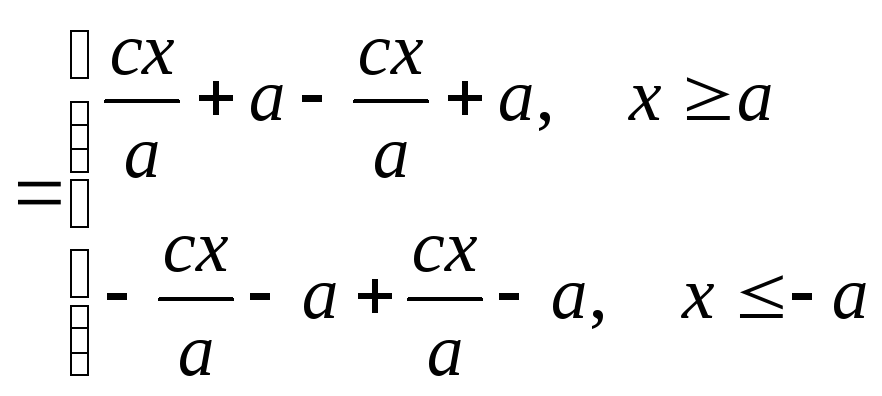
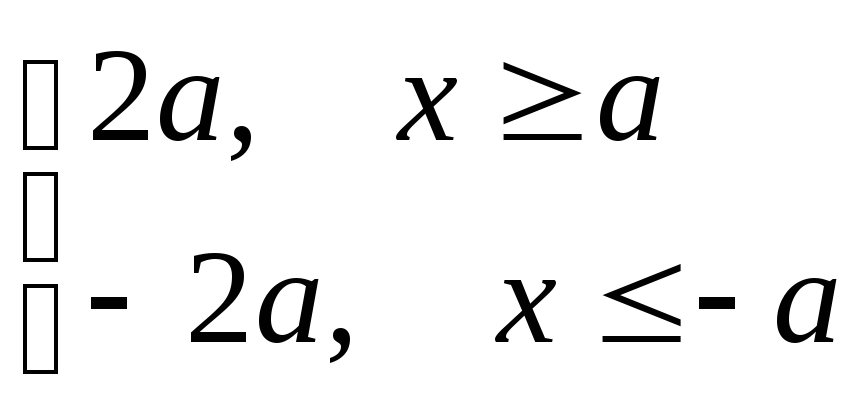
Таким образом, (4)
– уравнение гиперболы, которое и
называется её каноническим
уравнением.

Исследование формы гиперболы по ее каноническому уравнению

1. Симметрия.
Так как координаты x
и y
в уравнение
(4) входят только в чётных степенях, то

{M₁(x₀;
y₀)
Г}

{M₂(–x₀;
y₀)
Г, M₃(–x₀;
–y₀)
Г; M₄(x₀;
–y₀)Г}.

Это означает, что
гипербола (4) симметрична относительно
координатных осей и начала координат.
Оси симметрии гиперболы называются
осями
гиперболы,
центр симметрии – ее центром.

2. Пересечение
с осями. Если
y
= 0, то (4)

{x
= a}.
Значит, гипербола пересекает ось

в точках A₁
(–a;
0) и A₂
= (a;
0), которые называются вершинами
гиперболы. Если же x
= 0, то (4) решений не имеет, т.е. ось

гипербола не пересекает. Та ось гиперболы,
которую она пересекает, называется её
действительной
осью, а та, которую не пересекает –
мнимой.
Числа a
и b
называются полуосями
гиперболы, действительной и мнимой
соответственно.

3. В силу симметрии
гиперболы ее достаточно нарисовать в
первой координатной четверти, а затем
продолжить рисунок по симметрии. Если
,
,
то из (4) можно выразить y:

.
(7)

Если x
= a,
то y
= 0, если же
,
то и
.
Вычислим производную:

Если
,
то
,
поэтому гипербола в вершине имеет
вертикальную касательную.

. Асимптотами
гиперболы (4) называются прямые
.
Рассмотрим ту из них, которая проходит
в первой четверти:

.
(8)

равнивая (7) и (8), видим, что
:

,
значит, гипербола расположена ниже
своей асимптоты. Кроме того, ели М
– точка гиперболы, Р
– точка её асимптоты Рис.
3.2. с такой же
первой координатой,

–расстояние
от М до
гиперболы (рис.3.2), то

С
ледовательно,
при неограниченном удалении от начала
координат гипербола бесконечно близко
приближается к своей асимптоте, не
пересекая ее.

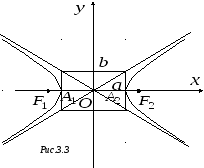
Теперь можно
приступить к рисованию. По обе стороны
от начала координат откладываем на
действительной оси действительные
полуоси, а на мнимой – мнимые. Рисуем
прямоугольник, стороны которого проходят
через полученные точки параллельно
осям координат. Точки пересечения
прямоугольника с действительной осью
– это вершины гиперболы

и
.
Затем проводим диагонали прямоугольника
и продляем их – это асимптоты гиперболы.
Рисуем гиперболу сначала в первой
четверти, начиная от вершины и неограниченно
приближая её к асимптоте, а затем
продолжаем по симметрии в остальные
координатные четверти (рис. 3.3).

В заключение
параграфа отметим, что уравнение

задаёт гиперболу, действительной осью
которой является ось
,
а школьное уравнение

при

–
это уравнение гиперболы с перпендикулярными
асимптотами, составленное относительно
её асимптот.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

515 Составить уравнение гиперболы,
фокусы которой расположены на оси абсцисс
симметрично относительно начала координат, зная,
кроме того, что:
515.1 ее оси 2a=10 и 2b=8;
515.2 расстояние между
фокусами 2c=10 и ось 2b=8;
515.3 расстояние между
фокусами 2c=6 и эксцентриситет e=3/2;
515.4 ось 2a=16 и
эксцентриситет e=5/4;
515.5 уравнения асимптот

и расстояние между фокусами 2c=20;
515.6 расстояние между
директрисами равно 228/13 и расстояние между
фокусами 2c=26;
515.7 расстояние между
директрисами равно 32/5 и ось 2b=6;
515.8 расстояние между
директрисами равно 8/3 и эксцентриситет e=3/2;
515.9 уравнения асимптот

и расстояние между директрисами
равно 64/5; 516 Составить
уравнение гиперболы, фокусы которого
расположены на оси ординат симметрично
относительно начала координат, зная, кроме того,
что: 516.1 ее полуоси a=6, b=18
(буквой а мы обозначаем полуось гиперболы,
расположенной на оси абсцисс); 516.2 расстояние между
фокусами 2с=10 и эксцентриситет e=5/3;
516.3 уравнения асимптот

и расстояние между вершинами равно
48; 516.4 расстояние между
директрисами равно 50/7 и эксценриситет e=7/5; 516.5 уравнения асимптот

и расстояние между директрисами
равно 32/5. 517 Определить полуоси
а и b каждой из следующих гипербол: 517.1

; 517.2

; 517.3

; 517.4

; 517.5

; 517.6

; 517.7

. 518 Дана гипербола

. Найти: полуоси а и b, фокусы,
эксцентриситет, уравнения асимптот, уравнения
директрис. 519 Дана гипербола

. Найти: полуоси а и b, фокусы,
эксцентриситет, уравнения асимптот, уравнения
директрис. 520 Вычислить площадь
треугольника, образованного асимптотами
гиперболы

и прямой

. 521 Установить, какие
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже. 521.1

; 521.2

; 521.3

; 521.4

. 522 Дана точка M₁(10;

) на гиперболе

. Составить
уравнения прямых, на которых лежат фокальные
радиусы точки М₁. 523 Убедившись, что
точка М₁(-5; 9/4) лежит
на гиперболе

, определить фокальные радиусы точки
М₁. 524 Эксцентриситет
гиперболы e=2, фокальный радиус ее точки М,
проведенный из некоторого фокуса, равен 16.
Вычислить расстояние от точки М до односторонней
с этим фокусом директрисы. 525 Эксцентриситет
гиперболы e=3, расстояние от точки М гиперболы до
директрисы e=3, расстояние от точки М гиперболы до
директрисы равно 4. Вычислить расстояние от точки
М до фокуса, одностороннего с этой директрисой. 526 Эксцентриситет
гиперболы e=2, центр ее лежит в начале координат,
один из фокусов F(12; 0). Вычислить расстояние от
точки М₁ гиперболы
с абсциссой, равной 13, до директрисы,
соответствующей заданному фокусу. 527 Эксцентриситет
гиперболы e=3/2, центр ее лежит в начале координат,
одна из директрис дана уравнением x=-8. Вычислить
расстояние от точки М₁ гиперболы с абсциссой, равной 10, до
фокуса, соответствующего заданной директрисе. 528 Определить точки
гиперболы

, расстояние от которых до
правого фокуса равно 4,5. 529 Определить точки
гиперболы

, расстояние которых до
левого фокуса равно 7. 530 Через левый фокус
гиперболы

проведен перпендикуляр к
ее оси, содержащей вершины. Определить
расстояние от фокусов до точек пересечения этого
перпендикуляра с гиперболой. 531 Пользуясь одним
циркулем, построить фокусы гиперболы

(считая,
что оси координат изображены и масштабная
единица задана). 532 Составить
уравнение гиперболы, фокусы которой лежат на оси
абсцисс симметрично относительно начала
координат, если даны: 532.1 точки M₁(6;
-1), M₂(-8;

) гиперболы; 532.2 точка М₁(-5;
3) гиперболы и эксцентриситет e=

; 532.3 точка М₁(9/2;
-1) гиперболы с уравнения асимптот

; 532.4 точка М₁(-3;
5/2) гиперболы и уравнения
директрис

; 532.5 уравнения асимптот

и уравнения директрис

.
533 Определить
эксцентриситет равносторонней гиперболы. 534 Определить
эксцентриситет гиперболы, если отрезок между ее
вершинами виден из фокусов сопряженной
гиперболы под углом 60⁰. 535 Фокусы гиперболы
совпадают с фокусами эллипса

. Составить
уравнение гиперболы, если ее эксцентриситет e=2. 536 Составить
уравнение гиперболы, фокусы которой лежат в
вершинах эллипса

, а директрисы
проходят через фокусы этого эллипса. 537 Доказать, что
расстояние от фокуса гиперболы

до ее
асимптоты равно b. 538 Доказать, что
произведение расстояний от любой точки
гиперболы

до двух ее асимптот есть
величина постоянная, равная

. 539 Доказать, что
площадь параллелограмма, ограниченного
асимптотами гиперболы

и
прямыми, проведенными через любую ее точку
параллельно асимптотами, есть величина
постоянная, равная ab/2. 540 Составить
уравнение гиперболы, если известны ее полуоси a и
b, центр C(x₀; y₀) и фокусы расположены на прямой: 540.1 параллельной оси Ox; 540.2 параллельной оси Oy. 541 Установить, что
каждое из следующих уравнений определяет
гиперболу, и найти координаты ее центра С,
полуоси, эксцентриситет, уравнения асимптот и
уравнения директрис: 541.1

; 541.2

; 541.3

. 542 Установить, какие
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
542.1

;
542.2

; 542.3

; 542.4

. 543 Составить
уравнение гиперболы, зная, что: 543.1 расстояние между ее
вершинами равно 24 и фокусы суть F₁(-10;
2), F₂(16; 2); 543.2 фокусы суть F₁(3; 4), F₂(-3; -4) и
расстояние между директрисами равно 3,6; 543.3 угол между
асимптотами равен 90⁰ и фокусы суть F₁(4; -4), F₂(-2;
2). 544 Составить
уравнение гиперболы, если известны ее
эксцентриситет e=5/4, фокус F(5; 0) и уравнение
соответствующей директрисы

. 545 Составить
уравнение гиперболы, если известны ее
эксцентриситет e=13/12, фокус F(0; 13) и уравнение
соответствующей директирсы

. 546 Точка А(-3; -5) лежит
на гиперболе, фокус которой F(-2; -3), а
соответствующая директриса дана уравнением

. Составить уравнение этой гиперболы. 547 Составить
уравнение гиперболы, если известны ее
эксцентриситет e=

, фокус F(2; -3) и
уравнение соответствующей директрисы

. 548 Точка М₁(1;
-2) лежит на гиперболе, фокус
которой F(-2; 2), а соответстующая директриса дана
уравнением

. Составить уравнение этой гиперболы. 549 Дано уравнение
равносторонней гиперболы

. Найти
ее уравнение в новой системе, приняв за оси
координат ее асимптоты. 550 Установив, что
каждое из следующих уравнений определяет
гиперболу, найти для каждой из них центр, полуоси,
уравнения асимптот и построить их на чертеже: 550.1

; 550.2

; 550.3

. 551 Найти точку
пересечения прямой

и гиперболы

. 552 Найти точки
пересечения прямой

и гиперболы

. 553 Найти точки
пересечения прямой

и гиперболы

. 554 В следующих случаях
определить, как расположена прямая относительно
гиперболы: пересекает ли, касается или проходит
вне ее: 554.1

; 554.2

; 554.3

. 555 Определить, при
каких значениях m прямая

: 555.1 пересекает
гиперболу

: 555.2 касается ее; 555.3 проходит вне этой
гиперболы. 556 Вывести условие,
при котором прямая

касается гиперболы

. 557 Составить
уравнение касательной к гиперболе

в ее
точке M₁(x₁; y₁). 558 Доказать, что
касательные к гипербле, проведенные в концах
одного и того же диаметра, параллельны. 559 Составить
уравнения касательных к гиперболе

, перпендикулярных
к прямой

. 560 Составить
уравнения касательных к гиперболе

, параллельных
прямой

. 561 Провести
касательные к гиперболе

параллельно
прямой

и вычислить расстояние d между ними. 562 На гиперболе

найти точку М₁, ближайшую к прямой

, и
вычислить расстояние d от точки М₁ до этой прямой. 563 Составить
уравнение касательной к гиперболе

, проведенных
из точки А(-1; -7). 564 Из точки С(1; -10)
проведены касательные к гиперболе

. Составить
уравнение хорды, соединяющей точки касания. 565 Из точки Р(1; -5)
проведены касательные к гиперболе

. Вычислить
расстояние d от точки Р до хорды гиперболы,
соединяющей точки касания. 566 Гипербола проходит
через точку А(

; 3) и касается прямой

. Составить
уравнение этой гиперболы при условии, что ее оси
совпадают с осями координат. 567 Составить
уравнение гиперболы, касающейся прямых

, при
условии, что ее оси совпадают с осями координат. 568 Убедившись, что
точки пересечения эллипса

и
гиперболы

являются вершинами прямоугольника,
составить уравнения его сторон. 569 Даны гиперболы

и какая-нибудь ее касательная, Р –
точка пересечения касательной с осью Ох, Q –
проекция точки касания на ту же ось. Доказать, что

. 570 Доказать, что
фокусы гиперболы расположены по разные стороны
от любой ее касательной. 571 Доказать, что
произведение расстояний от фокусов до любой
касательной к гиперболе

есть
величина постоянная, равная b². 572 Прямая

касается
гиперболы, фокусы которой находятся в точках F₁(-3;
0), F₂(3; 0). Составить
уравнение этой гиперболы. 573 Составить
уравнение гиперболы, фокусы которой расположены
на оси абсцисс симметрично относительно начала
координат, если известны уравнение касательной к
гиперболе

и расстояние между ее
вершинами 2а=8. 574 Доказать, что
прямая, касающаяся гиперболы в некоторой точке М,
составляет равные углы с фокальными радиусами F₁M, F₂M и проходит
внутри угла F₁MF₂. 575 Из правого фокусы
гиперболы

под углом

(

) к
оси Ох направлен луч света. Известно, что

. Дойдя
до гиперболы, луч от нее отразился. Составить
уравнение прямой, на которой лежит отраженный
луч. 576 Доказать, что
эллипс и гипербола, имеющие общие фокусы,
пересекаются под прямым углом. 577 Коэффициент
равномерного сжатия плоскости к оси Ох равен 4/3.
Определить уравнение линии, в котороую при этом
сжатии преобразуется гипербола

. 578 Коэффициент
равномерного сжатия плоскости к оси Оу равен 4/5.
Определить уравнение линии, в которую при этом
сжатии преобразуется гипербола

. 579 Найти уравнение
линии, в которую преобразуется гипербола

при двух последовательных
равноменых сжатиях плоскости к координатным
осям, если коэффициенты равномерного сжатия
плоскости к осям Ох и Оу соответствуют 2/3 и 5/3. 580 Определить
коэффициент q равномерного сжатия плоскости к
оси Ох, при котором гипербола

преобразуется
в гиперболу

. 581 Определить
коэффициент q равномерного сжатия плоскости к
оси Оу, при котором гипербола

преобразуется
в гиперболу

. 582 Определить
коэффициенты q₁, q₂ двух последовательных равномерных
сжатий плоскости к осям Ох и Оу, при которых
гипербола

преобразуется в гиперболу

Источник