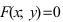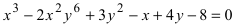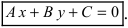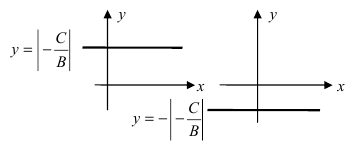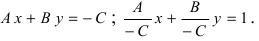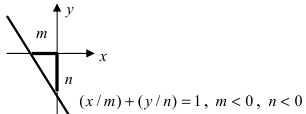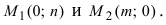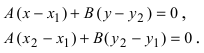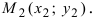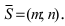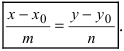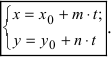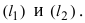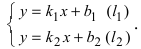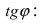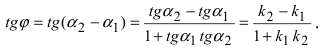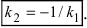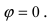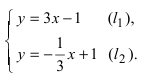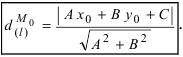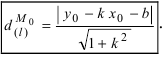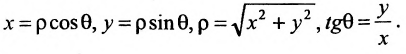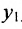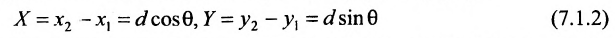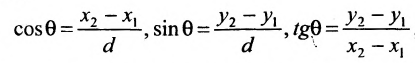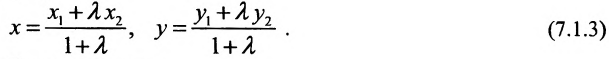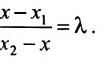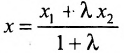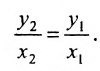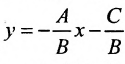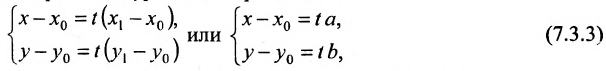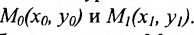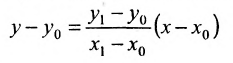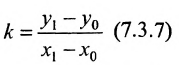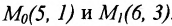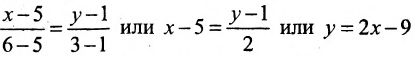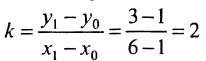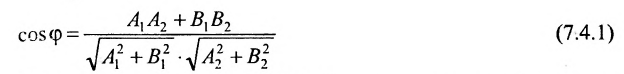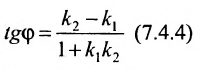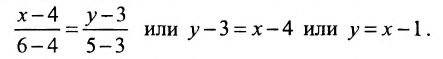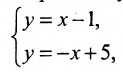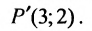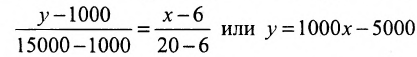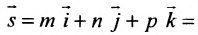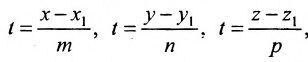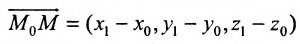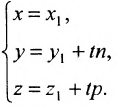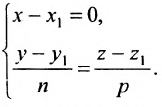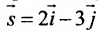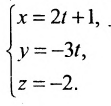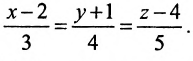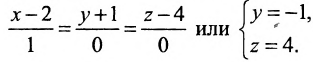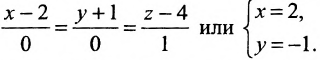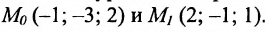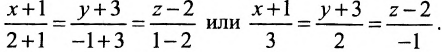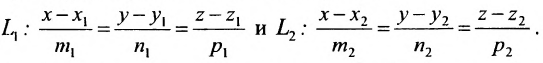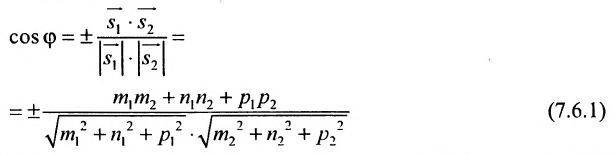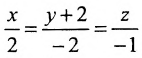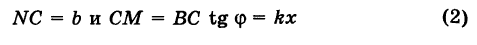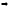Есть две паралельные прямые, заданные уравнениями:
a1x + b1y + c1 = 0,
a2x + b2y + c2 = 0.
Как определить, находится ли точка P(x, y) между ними?
задан 18 дек 2015 в 9:57
9
Например, можно сделать вот как:
Пусть n — общий вектор нормали ваших прямых, A1 и A2 — точки на 1-ой и 2-ой прямых соответственно, X — проверяемая точка. Вычислите скалярные произведения (XA1, n) и (XA2, n). Точка лежит внутри, если эти произведения имеют противоположный знак.
Для случая не обязательно параллельных прямых и тупого угла, у нас появляется два вектора нормали n1 и n2. Тогда нужно установить следующие величины: isFirstDirectionPositive — знак скалярного произведение (XA1, n1) (соответственно, результата подстановки точки в уравнение первой прямой), isSecondDirectionPositive — знак скалярного произведения (XA2, n2) (соответственно, результата подстановки точки в уравнение второй прямой), и isAngleBetweenNormalsAcute — знак скалярного произведения (n1, n2). Вам нужно, чтобы произведение всех трёх знаков было положительным.
ответ дан 18 дек 2015 в 10:18
VladDVladD
206k27 золотых знаков289 серебряных знаков521 бронзовый знак
7
Т.к. уравнение прямой на плоскости, проходящей через точку имеет вид Ax + Bу + С = 0, то если Ax + Bу + С больше нуля — точка находится выше прямой, если Ax + Bу + С меньше нуля — ниже.
Исходя из этого, по логике, надо подставить координаты заданной точки в оба уравнения, и, если результат одного уравнения будет больше нуля, а у другого меньше — значит точка находится между прямыми. Конечно с учетом того, что прямые параллельны
ответ дан 18 дек 2015 в 10:25
Алексей ШиманскийАлексей Шиманский
72.3k11 золотых знаков87 серебряных знаков173 бронзовых знака
7
a1x + b1y + c1 = 0 && a2x + b2y + c2 = 0
Они параллельны только если коэффициенты кратны. Т. е. надо привести прямые к одинаковым коэффициентам
ax + by + d1 = 0 && ax + by + d2 = 0
В таком виде вопрос сводится к одномерному после подстановки x.
ответ дан 18 дек 2015 в 10:19
Qwertiy♦Qwertiy
121k24 золотых знака121 серебряный знак291 бронзовый знак
1
Всем спасибо! Подсказали еще один ответ:
var sign1 = ((a1 * x + b1 * y + c1) * (a2 * x + b2 * y + c2)) < 0;
var sign2 = (a1 * a2 + b1 * b2) < 0;
return this.xor(sign1, sign2);
здесь xor операция исключающая ИЛИ
ответ дан 18 дек 2015 в 10:41
4
Предствами уравнения в форме угловых коэффициентов и смещений:
y = k1x + b1, где: k1 = -A1B1, b1 = -C1B1
y = k2x + b2, где: k2 = -A2B2, b2 = -C2B2
Тогда, так как прямые параллельны то k1 = k2 = k. Теперь попробуем провести через P другую прямую также параллельную исходным, ее уравнение будет иметь вид:
yP = kxP + bP, от куда bP = yP — kxP
Прямая с токой P будет лежать между двумя исходными, если смещение bP будет находится между смещениями b1 и b2:
b1 ≤ b2 → b1 ≥ bP ∧ bP ≤ b2
b1 ≥ b2 → b2 ≥ bP ∧ bP ≤ b1
ответ дан 18 дек 2015 в 10:56
CerboCerbo
6,8532 золотых знака23 серебряных знака43 бронзовых знака
Если прямые пересекаются, то точка — либо на одной из прямых, либо между ними.
Если параллельны, то сверяются знаки при подстановке точки в уравнения.
eps = 1e-7;
comp = eps*(a1*a1 + b1*b1)*(a2*a2+b2*b2);
det = a1*b2 - a2*b1;
val = (a1*b1+a2*b2)(a1*x+b1*y+c1)(a2*x+b2*y+c2);
if (det*det < comp) return (val < comp) ? 0: 1;
return (a1*b1+a2*b2)(a1*x+b1*y+c1)(a2*x+b2*y+c2) < 0 ? 1 :0;
ответ дан 20 дек 2015 в 5:37
Потенциал. Разность потенциалов.
Разность потенциалов (напряжение) между 2-мя точками поля равняется отношению работы поля по перемещению заряда из начальной точки в конечную к этому заряду:
,
Так как работа по перемещению заряда в потенциальном поле не зависит от формы траектории, то, зная напряжение между двумя точками, мы определим работу, которая совершается полем по перемещению единичного заряда.
Если есть несколько точечных зарядов, значит, потенциал поля в некоторой точке пространства определяется как алгебраическая сумма потенциалов электрических полей каждого заряда в данной точке:
.
Эквипотенциальной поверхностью, или поверхностью равного потенциала, является поверхность, для любых точек которой разность потенциалов равна нулю. Это означяет, что работа по перемещению заряда по такой поверхности равна нулю, следовательно, линии напряженности электрического поля перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности однородного поля представляют собой плоскости, а точечного заряда — концентрические сферы.
Вектор напряженности 

Напряжение и напряженность однородного поля .
В однородном электрическом поле напряженность E в каждой точке одинакова, и работа A по перемещению заряда q параллельно на расстояние d между двумя точками с потенциалами φ1, и φ2 равна:
,
.
Т.о., напряженность поля пропорциональна разности потенциалов и направлена в сторону уменьшения потенциала. Поэтому положительный заряд будет двигаться в сторону уменьшения потенциала, а отрицательный — в сторону его увеличения.
Единицей напряжения (разности потенциалов) является вольт. Исходя из формулы 

Электрический потенциал простыми словами: формулы, единица измерения
Электрический потенциал – это скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.
Если вы хотите расширить свои знания об электрическом потенциале или сначала узнать, что такое электрический потенциал, то вы пришли по адресу.
Простое объяснение
В классической механике рассмотрение проблемы с точки зрения энергии может значительно упростить ситуацию по сравнению с рассмотрением ее с точки зрения сил, действующих на систему. В частности, в этом контексте существенную роль играет тот факт, что энергия является сохраняющейся переменной.
Также в классической электродинамике рассмотрение на энергетическом уровне оказывается очень полезным. Поэтому электрический потенциал φ (также называемый электростатическим потенциалом) определяется как отношение потенциальной энергии Eпот пробного электрического заряда и его величины электрического заряда q: φ = Eпот / q .
Возможность определения такого электрического потенциала обусловлена тем, что электрическое поле E распределения заряда и результирующая электростатическая сила Fc на пробном электрическом заряде является консервативной силой, подобной гравитационной силе.
Электрический потенциал имеет единицу измерения вольт В или также джоуль на кулон Дж / Кл .
Формулы
В этом разделе мы познакомим вас с двумя важными формулами для электрического потенциала определенных распределений электрических зарядов. Мы также кратко обсудим аналогию между электрическим потенциалом и гравитацией.
Пластинчатый конденсатор
Мы рассматриваем ситуацию, когда две плоские пластины расположены параллельно на расстоянии d друг от друга. Кроме того, пусть одна из двух пластин заряжена положительно, а другая – отрицательно. Такая комбинация также называется пластинчатым конденсатором. Обозначим точку на положительной пластине через A, а точку на отрицательной пластине через B. Тогда для разности потенциалов между этими двумя точками получим:
Здесь E – величина электрического поля между двумя пластинами, которое предполагается однородным. Такая разность потенциалов также называется электрическим напряжением, которое существует между этими двумя точками.
Из этого уравнения видно, что электрический потенциал на положительно заряженной пластине (пластина A) выше, чем потенциал на отрицательно заряженной пластине (пластина B). Поэтому положительный заряд в пластинчатом конденсаторе перемещается к отрицательной пластине. В общем случае электрическое поле – а значит, и направление движения положительного заряда – направлено в ту сторону, в которой электрический потенциал убывает быстрее всего.
Рис. 1. Пластинчатый конденсатор
Аналогия с гравитационным полем
Если умножить уравнение (приведенное выше в статье) на величину электрического заряда q пробного электрического заряда и предположить, что отрицательно заряженная пластина имеет электрический потенциал, равный нулю, то электрическая потенциальная энергия на расстоянии h от пластины равна:
Eпот. эл = q * φ = q * E * h
Здесь φ обозначает электрический потенциал в точке пробного электрического заряда.
Сравним это уравнение с потенциальной энергией в однородном гравитационном поле:
Eпот. гр = m * g * h .
Мы определяем, что количество заряда электрического q играет роль массы m, а величина электрического поля E играет роль гравитационного ускорения g. Масса, находящаяся на высоте h над землей, ускоряется по направлению к земле под действием земного притяжения.
Таким образом, масса движется в том направлении, в котором уменьшается ее потенциальная энергия. Аналогично, положительный электрический заряд движется в направлении, в котором его электрическая потенциальная энергия будет уменьшаться. Поскольку электрическая потенциальная энергия и электрический потенциал линейно связаны, это наблюдение аналогично тому, что положительно заряженная частица движется в направлении уменьшения электрического потенциала.
Рис. 2. Аналогия с гравитационным полем
Подобно потенциальной энергии, только разность потенциалов имеет физический смысл, поскольку при определении электрического потенциала необходимо произвольно определить точку отсчета, от которой затем можно обозначить другие точки в пространстве. В этом смысле электрический потенциал сам по себе не имеет реального физического смысла, поскольку для данной точки в пространстве его значение можно изменить, выбрав другую точку отсчета. Таким образом, электрический потенциал ведет себя подобно высоте, потому что вы не можете говорить о высоте, пока у вас нет точки отсчета.
На топографической карте – пути, вдоль которых высота не меняется, называются изолиниями. Аналогично, пути, вдоль которых электрический потенциал постоянен, называются эквипотенциальными линиями.
Заряженные частицы
Предположим, что частица с зарядом q находится в начале выбранной нами системы координат. Пусть положение другой точки равно r и пусть r – расстояние между двумя точками. Для электрического потенциала в точке r действует следующее соотношение:
φ (r) = q / 4 * π * ε0 * r ,
здесь ε0 – электрическая постоянная.
В этом уравнении предполагается, что под действием электрического поля положительный пробный электрический заряд переносится из бесконечности в положение r.
Примеры задач
Наконец, давайте вместе рассчитаем небольшой пример. Предположим, что электрон ускоряется от отрицательно заряженной пластины к положительно заряженной через разность потенциалов 2000 В. Как изменяется потенциальная энергия электрона?
Для разности электрических потенциалов между двумя пластинами: φB – φA = ΔEпот / q , преобразованной в искомое изменение потенциальной энергии, получаем:
Величина электрического заряда электрона равна qe = e = – 1,6 * 10 -19 Кл и поэтому получаем:
ΔEпот = e * ( φB – φA ) = – 1,6 * 10 -19 Кл * 2000 В = -3,2 * 10 -19 Дж.
Обратите внимание, что [ В ] = Дж / Кл. Кроме того, мы предположили, что пластина с точкой B заряжена положительно, поэтому перед 2000 В нет знака минус. Расчет показывает, что потенциальная энергия электрона уменьшается.
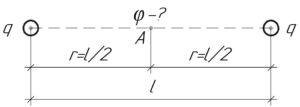
Найти потенциал электрического поля в точке, лежащей посредине между двумя
Найти потенциал электрического поля в точке, лежащей посредине между двумя зарядами по 50 нКл, расположенными на расстоянии 1 м в вакууме.
Задача №6.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
Так как заряды одинаковы, и они находятся на одинаковом расстоянии (r) от точки A, в которой нужно определить потенциал, значит потенциалы электрических полей в точке A, создаваемых каждым зарядом, также одинаковы. Это видно из формулы:
Здесь (k) – коэффициент пропорциональности, равный 9·10 9 Н·м 2 /Кл 2 .
Учитывая, что точка A находится посредине между двумя зарядами ((r=frac)), то:
Искомый потенциал (varphi) равен сумме потенциалов электрических полей в точке A, создаваемых каждым зарядом, поскольку потенциал – величина скалярная. Учитывая вышесказанное, имеем:
В итоге решение задачи в общем виде выглядит так:
Ответ: 1,8 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Как определяется место нуля и по каким формулам вычисляется угол наклона для теодолита 2Т30
Место нуля определяется так
: теодолит устанавливают, приводят в рабочее положение, находят хорошо видимую точку и наводят на неё трубу при круге лево. При наличии уровня при вертикальном круге, приводят пузырек его в нуль- пункт и берут отсчет по вертикальному кругу. Теперь переворачиваем теодолит через зенит, теодолит на 180° и при круге право наводимся на ту же точку. Пузырек – приводят в нуль-пункт и берут второй отсчет вертикальному кругу.
Место нуля
вычисляется по формуле: М0=(П+Л+180)/2 где П и Л –отсчеты по вертикальному кругу.
Угол наклона теодолита вычисляют по формуле: υ=Л-М0; υ=М0-П-180; υ=(Л-П-180)/2.
Какие основные поверки выполняются перед производством измерений теодолитом.
Поверки- это действия, которыми контролируют правильность взаимного расположения основных осей прибора, если при выполнении поверок обнаруживается несоответствие взаимного расположения частей прибора, его юстируют исправительными винтами.
Д ля начала работы с теодолитом внешним осмотром проверяют его устойчивость на штативе, плавонсть хода подъемн и наводяших винтов, прочность фиксации врашающихся частей закрепительными винтами.
1)Ось UU цилиндрического уровня горизонтального круга должна быть перпендикулярна оси VV врашения прибора.
2) Визирная ось РР трубы должна быть перпендикульрная оси НН вращения трубы.
3) Ось НН вращения трубы должна быть перпендикулярна оси вращения прибора.
4) Вертикальная нить АА сетки зрительной трубы должна быть перпендикулярна оси НН и её вращения.
5) Компенсатор вертикального круга должен обеспечивать неизменный отсчет по вертикальному кругу при наклонах вертикалной оси теодолите в пределах ± 2 минуты для теодолитов 3Т5К.
Прямая геодезическая задача.
Задача, в которой по данному дирекционному углу и заданному положению прямой, образованной точками, нужно найти сами координаты точек.
46. Обратная геодезическая задача.-
это задача, в которой даны координаты точек и по этим данным требуется найти прямой или обратный дирекционый угол, а также горизонтальное положение прямой, образованной этими точками.
Источник
Измерение вертикальных углов. Место нуля и его поверка
Вертикальным углом, или углом наклона, называют угол между направлением на наблюдаемую точку и ее горизонтальной проекцией. Если наблюдаемая точка расположена выше уровня горизонтальной оси вращения трубы, то угол будет п о л о ж и т е л ь н ы й, а если ниже – о т р и ц а т е л ь н ы й.
Измерение вертикальных углов (углов наклона) выполняется при помощи вертикального круга теодолита (рисунок 5.14). Лимб вертикального круга жестко скреплен с осью трубы и вращается вместе с ней. Алидада расположена на оси вращения трубы, но не скреплена с ней и при вращении остается неподвижной. В технических теодолитах вертикальный круг оцифрован от 0 до 360о. Диаметр 0–180о располагается параллельно визирной оси трубы.
Для удобства вычисления вертикальных углов ставится условие: когда визирная ось зрительной трубы горизонтальна и пузырек уровня алидады вертикального круга находится на середине, нулевые деления алидады должны совпадать с нулевыми делениями лимба (то есть отсчет будет равен 0о). Однако это условие может быть нарушено, и отсчет будет отличаться от нуля.
Рисунок 5.14 – Схема измерения вертикальных углов
Отсчет по вертикальному кругу, когда визирная ось трубы горизонтальна, а пузырек уровня при алидаде находится в нуль-пункте, называется местом нуля вертикального круга и обозначается М0.
О п р е д е л е н и е у г л о в н а к л о н а. Зрительную трубу при круге право (КП) наводят на некоторую точку М (см. рисунок 5.14). Приводят пузырек уровня алидады вертикального круга в нуль-пункт и берут отсчет П по вертикальному кругу. Как видно из рисунка, этот отсчет будет больше угла наклона на величину М0. То есть измеренный угол
υ = П – М0. (5.4)
Такие же действия выполняют при круге лево (КЛ). Отсчет Л (см. рисунок 5.14) также будет больше на величину М0. Угол наклона в этом случае
υ = М0 + (360о – Л). (5.5)
В тех случаях, когда из малых отсчетов приходится вычитать большие, то к малым прибавляют 360о. Тогда полученная формула примет вид
υ = М0 – Л. (5.6)
Решив уравнения (5.4) и (5.6) относительно υ и М0, найдем:
υ = (П – Л) / 2; (5.7)
М0 = (П + Л) / 2. (5.8)
В теодолите Т-30 деления вертикального круга подписаны против хода часовой стрелки и отсчитывание выполняется по одной стороне круга, поэтому для вычисления значений М0 и υ применяют формулы
М0 = (П + Л +180о) / 2; (5.9)
υ = Л – М0 = М0 – П – 180о; (5.10)
υ = (Л – П – 180о) / 2 (5.11)
При вычислениям по этим формулам к значениям Л, П и М0, меньшим 90о,следует прибавлять 360о.
П о р я д о к и з м е р е н и я в е р т и к а л ь н ы х у г л о в. Устанавливают теодолит в рабочее положение. Затем наводят пересечение сетки нитей при круге лево (КЛ) на наблюдаемую точку. Приводят пузырек уровня алидады вертикального круга в нуль-пункт и берут отсчет по вертикальному кругу (Л). Затем переводят трубу через зенит и те же действия повторяют при круге право, получая отсчет (П). По результатам измерений, используя формулы (5.4) – (5.8), вычисляют М0 и вертикальный угол υ.
При измерении углов наклона теодолитом Т-30 перед снятием отсчета по вертикальному кругу необходимо с помощью подъемных винтов привести на середину ампулы пузырек уровня при алидаде горизонтального круга (уровень при алидаде вертикального круга отсутствует). М0 и угол наклона вычисляют по формулам (5.9) – (5.11).
При измерении углов наклона приборами с компенсатором (теодолит Т5К, электронный тахеометр), заменяющим уровень при алидаде вертикального круга, отсчет берут спустя 2 с после наведения трубы на предмет, так как прибор находится в рабочем положении, если пузырек круглого приведен в нуль-пункт вращением подъемных винтов.
Правильность измерения контролируется постоянством М0, колебания которого не должны превышать двойной точности отсчетного устройства теодолита. Поверка выполняется в следующем порядке. Наблюдают одну и ту же точку при круге право и круге лево. Определяют величину М0. Если она окажется больше двойной точности отсчетного устройства теодолита, то производят исправление М0. Для этого у теодолита Т-5 устанавливают вращением трубы отсчет равный М0. Пузырек уровня алидады вертикального круга при этом должен быть в нуль-пункте.
Затем с помощью микрометренного винта алидады устанавливают отсчет по вертикальному кругу, равный 0о, при этом пузырек уровня сойдет с нуль-пункта. Действуя исправительными винтами уровня, приводят пузырек в нуль-пункт. Для контроля поверку повторяют.
У теодолита Т-30 исправление М0 выполняют следующим образом. Устанавливают при круге лево на вертикальном круге отсчет, равный углу наклона υ = Л – М0, при помощи наводящего винта. При этом горизонтальный штрих сетки нитей сойдет с наблюдаемой точки. После этого, ослабив боковые исправительные винты сетки нитей и действуя вертикальными исправительными винтами, совмещают горизонтальный штрих сетки нитей с изображением наблюдаемой точки. После закрепления оправы сетки нитей поверку повторяют.
Т о ч н о с т ь и з м е р е н и я в е р т и к а л ь н ы х у г л о в. Средняя квадратическая погрешность mυ измерения вертикального угла составляет не более 1,5mβ аналогичной ошибки горизонтального угла. Надежному измерению вертикального угла способствует выполнение следующих условий: аккуратное обращение с теодолитом, регулярный контроль разворота сетки нитей и ошибки М0, визирование целей при двух положениях круга. Значение М0 должно быть неизменным в пределах двойной точности прибора. При колеблющихся изображениях целей (из-за конвекции воздуха при нагреве почвы) наблюдения лучше прекратить, прохождение визирного луча следует фиксировать не ближе 1 м от местных предметов, соблюдать точное центрирование.
ИЗУЧЕНИЕ И УСТРОЙСТВО ТЕОДОЛИТА
На подставке (1) с тремя подъёмными винтами (9) крепится угломерный круг (2), называемый лимбом, на котором нанесены деления от 0 до 360 о с возрастанием отсчётов по ходу часовой стрелки.
На колонках алидады (4) крепится зрительная труба(5), которая может вращаться вокруг оси вращения трубы НН1. На одном из концов оси вращения зрительной трубы расположен вертикальный круг, состоящий из лимба (6) и алидады (7). Вертикальный круг предназначен для измерения углов наклона. При наблюдении в зрительную трубу наблюдатель смотрит в окуляр (11), противоположная часть трубы (10) называется объективом. В окуляре имеется нарезанная на стекле сетка нитей.
Зрительная труба может быть повернута вокруг своей оси вращения. Поворот зрительной трубы на 180 o называется переводом зрительной трубы через зенит. При расположении наблюдателя со стороны окуляра вертикальный круг находиться справа или слева от нее.
ЦЕНА ДЕЛЕНИЯ ЛИМБА И ТОЧНОСТЬ ОТСЧИТЫВАНИЯ ПО ГОРИЗОНТАЛЬНОМУ И ВЕРТИКАЛЬНОМУ КРУГУ
Теодолит 2Т30 имеет шкаловой отсчётный микроскоп. В верхней части поля зрения микроскопа, обозначенного буквой В (рис. 4), видны штрихи лимба вертикального круга, а в нижней части поля зрения, обозначенного буквой Г, видны штрихи лимба горизонтального круга.
Отсчёт по горизонтальному кругу проводится в следующем порядке: сначала считывается с лимба число градусов (по штриху лимба, попадающему на отсчётную шкалу), затем по отсчётной шкале берется отсчёт с точностью 0.1 деления шкалы, что соответствует 0.5′. Таким образом, точность отсчитывания по шкалам горизонтального и вертикального кругов составляет t = 0.5′. Индексом для отсчитывания минут служит штрих градусного деления лимба, находящийся на отсчётной шкале. На рис. 4 отсчёт по горизонтальному кругу равен 125 о 06,0′.
При отсчитывании по вертикальному кругу различают два вида отсчётов. Если вертикальный круг находится справа от зрительной трубы (при расположении наблюдателя со стороны окуляра), то такой отсчёт называется отсчётом при «круге право» (КП). Если же вертикальный круг находится слева от зрительной трубы (при расположении наблюдателя со стороны окуляра), то такой отсчёт называется отсчётом при «круге лево» (КЛ).
ПОВЕРКИ И ЮСТИРОВКИ ТЕОДОЛИТА 2Т30
Для исключения возникновения условий, порождающих приборные ошибки, должны производиться поверки и юстировки (исправления) геодезических приборов.
Поверками геодезических приборов
называется обследование приборов, устанавливающее выполнение конструктивных и геометрических требований к положению отдельных осей и блоков приборов. Поверки выполнения геометрических требований к положению отдельных осей теодолита состоят в проверке взаимной параллельности или взаимной перпендикулярности соответствующих пар осей прибора. У теодолитов 2Т30 и 2Т30П вышеуказанные требования проверяются для 4-х пар таких осей.
Геометрическое условие 1-й поверки:
ОСЬ ЦИЛИНДРИЧЕСКОГО УРОВНЯ ДОЛЖНА БЫТЬ ПЕРПЕНДИКУЛЯРНА К ВЕРТИКАЛЬНОЙ ОСИ ВРАЩЕНИЯ ПРИБОРА.
Проверка выполнения условия:
Порядок исправления (юстировка):
При отклонении более чем на одно деление исправительными винтами цилиндрического уровня пузырёк перемещают к середине ампулы на половину дуги отклонения; на вторую половину дуги отклонения пузырёк уровня перемещают при помощи тех же подъёмных винтов. Для контроля поверку повторяют
.
Прежде чем делать другие поверки, приводят плоскость лимба в горизонтальное положение
(ось вращения прибора в вертикальное положение). Для этого устанавливают уровень параллельно двум подъёмным винтами с их помощью приводят пузырек уровня на середину. Поворачивают алидаду на 90 o и третьим подъёмным винтом приводят пузырёк уровня в нульпункт. После приведения плоскости лимба в горизонтальное положение, при вращении алидады вокруг основной оси прибора, пузырёк уровня не должен отклоняться от нульпункта более чем на одно деление.
Геометрическое условие 2-й поверки:
ГОРИЗОНТАЛЬНАЯ НИТЬ СЕТКИ НИТЕЙ ДОЛЖНА БЫТЬ ПЕРПЕНДИКУЛЯРНА К ВЕРТИКАЛЬНОЙ ОСИ ВРАЩЕНИЯ ПРИБОРА, А ВЕРТИКАЛЬНАЯ НИТЬ СЕТКИ НИТЕЙ ДОЛЖНА НАХОДИТЬСЯ В ПЛОСКОСТИ, ПЕРПЕНДИКУЛЯРНОЙ К ОСИ ВРАЩЕНИЯ ЗРИТЕЛЬНОЙ ТРУБЫ.
Проверка выполнений условия:
Вертикальную нить сетки нитей наводят на нить отвеса. Если вертикальная нить будет совпадать с нитью отвеса, условие выполнено.
Порядок исправления (юстировка):
При отклонении вертикальной нити сетки нитей от нити отвеса отвёрткой ослабляют 4 крепёжных винта окуляра, расположенные под колпачком 12 (рис. 4). Затем поворачивают окулярную часть трубы до совмещения (или до параллельного положения) видимых в окуляр вертикальной нити отвеса и нити сетки, после чего винты вновь закрепляют. Поверку повторяют
.
Геометрическое условие 3-й поверки:
ВИЗИРНАЯ ОСЬ ЗРИТЕЛЬНОЙ ТРУБЫ ДОЛЖНА БЫТЬ ПЕРПЕНДИКУЛЯРНА К ОСИ ВРАЩЕНИЯ ЗРИТЕЛЬНОЙ ТРУБЫ.
Проверка выполнений условия:
Угол С между визирной осью и перпендикуляром к оси вращения трубы (рис. 5) называется коллимационной ошибкой. Для выявления коллимационной ошибки выбирают удалённую, хорошо видимую точку, расположенную так, чтобы линия визирования была примерно горизонтальна. Наводят пересечение сетки нитей на эту точку визирования и производят отсчёт по горизонтальному кругу. Например, при КЛ отсчёт равен 18 o 30,0′ (КЛ = 18 o 30,0′). Переводят трубу через зенит, открепляют алидаду, наводят пересечение сетки нитей на ту же точку визирования при «круге право» и производят отсчёт. Например, КП = 198 o 36,0′.
Величину коллимационной ошибки С вычисляют по формуле:
Допускаемое отклонение от требования к выполнению условия: Коллимационная ошибка С не должна превышать двойную точность отсчёта по шкале прибора. Рассчитаем коллимационную ошибку С для 2-х пар значений.
Условие не выполняется.
Порядок исправления (юстировка):
Вычисляют исправленный отсчёт по горизонтальному кругу, в котором число градусов берется из последнего отсчёта, а количество минут вычисляется как среднее арифметическое из числа минут обоих отсчетов. В первом примере исправленный отсчёт будет равен:
Этот отсчёт наводящим винтом алидады устанавливают на горизонтальном круге. Пересечение сетки нитей сойдёт с точки визирования, на которую до этого была наведена точка пересечения сетки нитей. Следует переместить сетку нитей так, чтобы перекрестие сетки нитей вновь установилось на точку визирования. Для этого используются 4 исправительных винта с отверстиями для шпильки. Исправительные винты расположены под колпачком 12 (рис. 4). Шпилькой ослабляют вертикальные винты и боковыми винтами перемещают сетку нитей до того, пока перекрестие сетки не встанет на точку визирования. Вертикальные винты вновь затягивают и поверку повторяют
.
Примечание. Значения углов, полученных как среднее из результатов измерений при двух положениях зрительной трубы (КП и КЛ), свободны от влияния коллимационной ошибки.
Геометрическое условие 4-й поверки:
ОСЬ ВРАЩЕНИЯ ЗРИТЕЛЬНОЙ ТРУБЫ ДОЛЖНА БЫТЬ ПЕРПЕНДИКУЛЯРНА К ВЕРТИКАЛЬНОЙ ОСИ ВРАЩЕНИЯ ТЕОДОЛИТА.
Проверка выполнений условия:
Порядок исправления (юстировка):
Если это условие не выполняется, то следует провести исправление прибора в мастерской.
Вертикальный круг
Вертикальный круг, астрономический инструмент, служащий для измерения высот (или зенитных расстояний) светил. Он состоит из астрономической трубы (см.) и круга, возможно точнее разделенного на градусы и доли градуса (самое малое деление 5-2 минуты дуги); труба и круг накрепко соединены со стальной осью, перпендикулярной к оси трубы и к кругу и направленной горизонтально; муфта, в которой вращается эта ось, прикреплена к вертикальной оси, вращающейся в колонне, которая тремя ножками стоит на солидном фундаменте. К муфте горизонтальной оси прикреплена рама, несущая 2, 4, 6 микроскопов, направленных на лимб круга с делениями; эти микроскопы снабжены микрометрами (см.), при помощи которых можно очень точно (в больших инструментах до 0,1 секунды дуги) определять взаимное положение микроскопов и круга. На раме находится чувствительный уровень, указывающий мельчайшие изменения в положении рамы относительно вертикальной линии; на горизонтальной оси находится другой уровень для определения малой наклонности ее к горизонту. Для измерения угла поворота инструмента около вертикальной оси служит особый круг в нижней части инструмента; он имеет вспомогательное значение при наблюдениях. В фокусной плоскости трубы находится крест из паутинных нитей. При определении зенитного расстояния какого-либо предмета, труба наводится на него так, чтобы изображение его совпало с точкой пересечения нитей и микрометрами определяется соответственное положение круга; потом инструмент поворачивается около вертикальной оси на 180°; труба оказывается направленной на то же зенитное расстояние, но по другую сторону от вертикальной линии и теперь ее повертывают около горизонтальной оси, переводя через вертикальное положение, вновь наводят на наблюдаемый предмет и вновь на микрометрах отсчитывают положение круга; половина разности отсчетов при обоих положениях трубы есть искомое зенитное расстояние. При этих операциях отсчитываются также положения пузырька уровня на раме и принимаются во внимание различные ошибки, происходящие от несовершенства инструмента. Особенно важны и трудны для исследования ошибки делений круга. Если наблюдается небесное светило, то нужно принять во внимание изменение его зенитного расстояния с течением времени. В результате получается так называемое видимое зенитное расстояние наблюдаемого предмета в момент наблюдения, из которого затем соответственными вычислениями получаются другие величины, служащие для определения либо положения светила на небесной сфере, либо положения места наблюдения на земной поверхности. В астрономии вертикальный круг применяется для определения зенитного расстояния светил вблизи от меридиана; из них можно вычислить зенитное расстояние в меридиане, а зная зенитное расстояние полюса мира в месте наблюдения, получают полярные расстояния светил; вычитая полярное расстояние из 90°, получают склонение (см. небесная сфера). Переносные вертикальные круги небольшого размера применяются в экспедициях для определения географических широт (см. земля).
С. Бл.
УСТАНОВКА ПРИБОРА В РАБОЧЕЕ ПОЛОЖЕНИЕ
Перед измерением горизонтального угла теодолит устанавливается в рабочее положение. Точка установки прибора называется станцией. Установка теодолита в рабочее положение
складывается из: а)
центрирования теодолита
, заключающегося в установке центра лимба над вершиной измеряемого угла с помощью нитяного отвеса; б)
приведение плоскости лимба
в горизонтальное положение с помощью уровня горизонтального круга и подъёмных винтов; в)
установка зрительной трубы для наблюдения
по глазу и по предмету. Установка трубы по глазу производится вращением диоптрийного кольца окуляра до наилучшей видимости сетки нитей, при этом труба должна быть наведена на светлый фон. Установка трубы по предмету производится с помощью кремальеры, вращая которую добиваются чёткого изображения предмета в поле зрения трубы.
ИЗМЕРЕНИЕ УГЛОВ
Измерение горизонтального угла
Измерение угла выполняется способом приёмов
. При закреплённом лимбе, открепив закрепительный винт алидады, поворачивают алидаду, приблизительно наводят зрительную трубу (с учётом возрастания отсчётов по лимбу по ходу часовой стрелки) на правую точку 1 (рис. 6).
Зажимают закрепительные винты алидады и зрительной трубы и окончательное наведение точки пересечения сетки нитей на точку местности выполняют с помощью наводящих винтов алидады и зрительной трубы. После этого производят отсчёт по горизонтальному кругу. Отсчёт записывается в журнал (табл. 1).
Контроль:
если расхождение значений угла в полу приёмах более двойной точности отсчитывания, т.е. более 1? для теодолитов 2Т30 и 2Т30П, запись в журнале зачёркивается, отсчёт на лимбе сбивается и измерения повторяются.
Измерение угла наклона
Углом наклона визирной оси
называется угол, составленный линией визирования с горизонтальной плоскостью, проходящей через ось вращения зрительной трубы (рис. 7).
Перед измерением угла наклона теодолит устанавливают в рабочее положение и наводят среднюю горизонтальную нить сетки на точку, например, при КП. Если при этом пузырёк уровня отойдёт от середины, то его необходимо установить на середину подъёмным винтом, расположенным по направлению линии визирования, и затем проверить наведение горизонтальной линии на точку. Перед отсчётом горизонтальная нить должна быть наведена на точку местности, а пузырёк уровня должен быть в нуль-пункте. Производят отсчёт по вертикальному кругу и записывают его в журнал (табл. 2).
Переводят трубу через зенит и аналогичные действия выполняют при другом положении вертикального круга при КЛ. Отсчёт записывают в журнал. Затем вычисляют место нуля (МО) вертикального круга.
Местом нуля (МО)
называется отсчёт по вертикальному кругу, когда визирная ось зрительной трубы горизонтальна, а пузырёк уровня находится в нуль-пункте.
Место нуля (МО) и угол наклона вычисляются по следующим формулам:
Контроль:
правильностью измерения вертикальных углов служит постоянство МО, колебание которого не должно превышать двойной точности отсчёта по шкале прибора, т.е. 1′ (для теодолитов 2Т30 и 2Т30П).
Источник
ДОМОСТРОЙСантехника и строительство
Место нуля (МО)
– это отсчет по лимбу вертикального круга, соответствующий горизонтальному положению визирной оси зрительной трубы и отвесному положению вертикальной оси теодолита.
При измерении вертикальных углов необходимо следить за положением пузырька уровня при алидаде горизонтального круга и, в случае смещения пузырька с нуль-пункта, приводить его на нуль-пункт подъемными винтами.
Приведя с помощью уровня и подъемных винтов (у теодолитов Т30 и 2Т30 один цилиндрический уровень, которым пользуются при измерении горизонтальных и вертикальных углов) ось вращения теодолита в отвесное положение, наблюдают любую неподвижную и хорошо видимую точку при Л и П, производят отсчеты по вертикальному кругу и вычисляют значения места нуля по формулам
– ( Т30), – (2Т30),
При выполнении проверки необходимо наблюдать две различные точки. Из наблюдений вычисляют значение места нуля для каждой точки. Из полученных результатов, если они различаются не более чем на величину двойной точности прибора, образуют среднее арифметическое, которое принимается как окончательное значение места нуля. Для сведения места нуля к 0° удобнее всего при Л
навести трубу на любую точку. Взять отсчет по вертикальному кругу
Л
, и, вращением наводящего винта трубы, установить на вертикальном круге отсчет, равный
Л – МО
. При этом центр сетки сместится по вертикали с наблюдаемой точки. Его необходимо вернуть на точку, действуя вертикальными исправительными винтами сетки, предварительно слегка ослабив боковые исправительные винты. Проверку следует повторить. После выполнения условия проверки все исправительные винты сетки должны быть затянуты и предохранительный колпачок, закрывающий доступ к юстировочным винтам сетки, должен быть навинчен на трубу.
2)Геодезические работы при изысканиях сооружений линейного типа Наиболее сложный комплекс геодезических работ выполняется при изысканиях автомобильных дорог. В промышленном и гражданском строительстве это подъездные пути к строительным площадкам (автомобильные дороги небольшой протяженности). В отличие от линий канализаций, водопроводов, связи, каналов, электролиний и др., при строительстве автомобильных дорог в углы поворота вписываются круговые кривые. Таким образом трасса автодороги это совокупность прямых и кривых участков. Поэтому в дальнейшем будут излагаться работы применительно к изысканиям и проектированию автодороги.
Определение места нуля вертикального круга и углов наклона.
Из отсчетов по вертикальному кругу при «круге право» (КП) и «круге лево» (КЛ) на один и тот же отсчет дважды вычисляется место нуля (МО):
МО = (КП + КЛ)/2
Пример:При наведении со станции II на станцию I
Полученное значение МО записывают в «шапке» журнала тахеометрической съемки.
При визировании на предыдущую и последующую точки высотно-теодолитного хода углы наклона ν вычисляют с контролем по формуле:
Пример:При визировании со станции II на станцию I угол наклона
В журнале тахеометрической съемки углы наклона вычислены только для первой точки наведения для каждой станции. Значения ν для остальных точек наведения следует вычислить самостоятельно.
Вычисление горизонтальных проложений и превышений.
Значения горизонтальных расстояний между вершинами высотно-теодолитного хода находятся в графе 6 таблицы 4. Их также переписывают в графу 5 таблицы 5. Вычисление горизонтальных проложений d от станций до реечных точек производят в журнале тахеометрической съемки в графе 6 таблицы 6 по значениям расстояний D, полученных по нитяному дальномеру:
d = D cos²ν
Превышения h вычисляют по формуле:
h = d tgν
и записывают в графу 7 таблицы 6.
Вычисление отметок станций.
Вычисление отметок станций выполняют в «Ведомости увязки превышений высотно-теодолитного хода и вычисления отметок станций» (табл. 5). Вычисления нужно провести только в графе 8, причем в этой графе сначала записывают отметку первой точки I, которая задается преподавателем. Но если отметка не дана, то ее вычисляют также, как это показано в задании 2 раздела исходные данные. Данные в остальных графах являются общими для всех вариантов. Отметки реечных точек на каждой станции получают путем алгебраического сложения отметки данной станции с соответствующим исправленным превышением hиспр. Эти отметки также записывают в «шапку» таблицы 6 соответственно для каждой станции. Контролем правильности является получение второй раз (в конце графы 
Также отметки точек вычисляют в графе 8 таблицы 6. Отметки точек наблюдения вычисляются так же, как и отметки станций в таблице 5, т.е. путем алгебраического сложения отметки данной точки наблюдения с соответствующим превышением, начиная с отметки станции, на которой ведется съемка.
В журнале тахеометрической съемки (табл. 6) для примера вычислены значения горизонтального проложения d и превышения h только для первых точек наблюдения на каждой станции. Значения d и h на остальных точках наблюдения следует вычислить самостоятельно. Отметки Н в графе 8 таблицы 6 первых точек наблюдения, а также отметки Н станций в графе 8 таблицы 5 вычислены для одного из вариантов студенческой работы.
Ведомость увязки превышений высотно-теодолитного хода и вычисления отметок станций.
| Номера станций | Горизон-тальные проложе-ния, d | Превышения | Поправки в превы-шения | Исправлен- ные превыше- ния hиспр | Отметки станций H | Номера станций | ||
| hчерн | hкрасн | hср | ||||||
| I | 34,13 | 4,55 | 4,57 | 4,56 | -0,01 | +4,55 | 106,48 | I |
| II | 111,03 | II | ||||||
| 37,83 | — 5,29 | — 5,31 | — 5,30 | -0,01 | -5,31 | |||
| III | 105,72 | III | ||||||
| 30,35 | — 1,95 | — 1,97 | — 1,96 | -0,01 | — 1,97 | |||
| IV | 103,75 | IV | ||||||
| 34,90 | — 1,58 | — 1,56 | — 1,57 | -0,01 | — 1,58 | |||
| V | 102,17 | V | ||||||
| 32,82 | 4,31 | 4,33 | 4,32 | -0,01 | +4,31 | |||
| I | 106,48 | I | ||||||
| P= | 170,03 | +0,05 | -0,05 | 0,00 | ||||
| f h= Σ hср – ΣhT = 0.05 – 0 = +0.05 f h доп = P100 – периметр хода выраженный в сотнях метров; n – число сторон хода. |
Журнал тахеометрической съемкиТаблица 6
| Станция I Высота прибора 1,57м Круг КЛ Ориентирована на II М0=(КЛ+КП)/2=2′ Отметка 106,48м | |||||||
| № точки | Дальномерное расстояние D, м | Отчеты | Угол наклона ν | Горизонтальное проложение d=D*cos 2 *ν | Превышение hp=d*tgν м | Отметка, м | Примечания |
| ГК | ВК | ||||||
| 15,1 | 231°57,4′ | 3°21,9′ | 3°19,9′ | 15,04 | 0,87 | 107,35 | |
| 21,3 | 256°2,7′ | 12°27,3′ | |||||
| 20,5 | 297°33,6′ | 13°37′ | |||||
| 17,8 | 217°9,2′ | 1°47,9′ | |||||
| 25,1 | 38°18′ | -1°56,3′ | |||||
| 23,85 | 191°00′ | -2°19′ |
| Станция II Высота прибора 1,62м Круг КЛ Ориентирована на III М0=(КЛ+КП)/2=2′ Отметка 111,03м | |||||||
| № точки | Дальномерное расстояние D, м | Отчеты | Угол наклона ν | Горизонтальное проложение d=D*cos 2 *ν | Превышение hn=d*tgν м | Отметка, м | Примечания |
| ГК | ВК | ||||||
| 4,8 | 132°19′ | -1°05′ | -1°07′ | 4,79 | -0,09 | 110,94 | |
| 13,9 | 122°25,2′ | 0°02′ | |||||
| 12,7 | 302°53,2′ | -0°24,6′ | |||||
| 14,7 | 282°23′ | -0°19,6′ | |||||
| 18,6 | 295°13′ | -0°50,6′ | |||||
| 27,2 | 42°40′ | -12°26′ | |||||
| 23,6 | 20°52,3′ | -13°08,3′ |
| Станция III Высота прибора 1.57м Круг КЛ Ориентирована на IV М0=(КЛ+КП)/2=2′ Отметка 105,72 м | |||||||
| № точки | Дальномерное расстояние D, м | Отчеты | Угол наклона ν | Горизонтальное проложение d=D*cos 2 *ν | Превышение hn=d*tgν м | Отметка, м | Примечания |
| ГК | ВК | ||||||
| 6,8 | 261°01,9′ | -1°35′ | -1°37′ | 6,79 | -0,19 | 105,53 | |
| 9,2 | 285°40,5′ | -2°22,9′ | |||||
| 113°25,1′ | 4°08′ | ||||||
| 152°09′ | 8°26,3′ | ||||||
| 13,5 | 200°33,4′ | 6°51,9′ | |||||
| 19,4 | 211°34,9′ | 4°54′ | |||||
| 30,86 | 143° 00′ | 3° 01,6′ |
| Станция V Высота прибора 1.51м Круг КЛ Ориентирована на I М0=(КЛ+КП)/2=2′ Отметка 102,17 м | |||||||
| № точки | Дальномерное расстояние D, м | Отчеты | Угол наклона ν | Горизонтальное проложение d=D*cos 2 *ν | Превышение hn=d*tgν м | Отметка, м | Примечания |
| ГК | ВК | ||||||
| 39,8 | 32°21,1′ | 4°25′ | 4°23′ | 39,57 | 3,03 | 105,2 | |
| 22,5 | 29°28,3′ | 2°27′ | |||||
| 5,6 | 353°52,7′ | 10°26,9′ | |||||
| 3,9 | 21°18′ | 13°10,6′ | |||||
| 9,4 | 243°03,1′ | -4°26′ | |||||
| 171°43,2′ | -6°50,3′ |
| Станция IV Высота прибора 1.50 м Круг КЛ Ориентирована на V М0=(КЛ+КП)/2=2′ Отметка 103,75 м | |||||||
| № точки | Дальномерное расстояние D, м | Отчеты | Угол наклона ν | Горизонтальное проложение d=D*cos 2 *ν | Превышение hn=d*tgν м | Отметка, м | Примечания |
| ГК | ВК | ||||||
| 10,66 | 292°00¢ | — 6°50,3¢ | — 6°52,3¢ | 10,51 | -1,27 | 102,48 | |
| 40,37 | 225°12¢ | — 0°52,5¢ |
Продолжение таблицы 6
Построение топографического плана
Построение координатной сетки
Координатную сетку в виде квадратов со сторонами по 10 см. вычерчивают на листе чертёжной бумаги размером не менее 40×40 см. Необходимое количество квадратов сетки рассчитывают, исходя из полученных значений координат вершин полигона (ведомость вычисления координат вершин теодолитного хода – графы 11 и 12).
Пример: (Xсев – Xюжн)/50 = количество горизонтальных квадратов.
Где Xсев – абсцисса самой северной точки полигона, а Xюжн – абсцисса самой южной точки.
Сетку вычерчивают остро отточенным карандашом. Расхождение между диагоналями квадратов сетки не должно превышать 0,2 мм. В противном случае сетку чертят заново.
Источник
Измерение горизонтальных и вертикальных углов в ходах постоянного съемочного обоснования производится отъюстированными теодолитами.
3.2.1. Измерение горизонтальных углов
Измерение горизонтальных углов постоянного съемочного обоснования рекомендуется выполнять по трехштативной системе. Если трехштативную систему применить нельзя, угол следует измерять на веху, устанавливаемую по круглому уровню (см.рис.3.22)
Таблица 3. 3
| Точка | Отсчеты | Вычисленный угол из полуприема | Среднее значение угла | |||
| стояния | визирования | Круг | I | II | 1+И
2 |
|
| 2 3
2 3 |
П Л | 10°28,0′ 107 18,5
197°55,5′ 294 45,0 |
28,2′ 18,0
55,3 44,8 |
28,1′ (1) 28,2 (2)
55,4 (4) 44,9 (3) |
96°50,У 96°49,5′ | 96°49,8′ |
либо на отвес, прикрепленный к штативу и центрированный над точкой.
Устанавливают теодолит над вершиной измеряемого угла в рабочее положение, центрируют его при помощи нитяного отвеса или оптического центрира с точностью 2 мм. С такой же точностью центрируют и марки, устанавливаемые над наблюдаемыми точками. Каждый горизонтальный угол измеряют одним полным приемом с перестановкой лимба между полуприемами на величину, близкую к 90°. Измерения всегда начинают при вертикальном круге лево (Л). Для этого закрепляют лимб и, вращая алидаду, наводят центральную точку сетки нитей зрительной трубы или биссектор на заднюю (правую) веху или марку, при этом пользуются наводящими винтами зрительной трубы и алидады горизонтального круга, после этого при том же положении вертикального круга визируют на переднюю (левую) веху или марку. При визировании по каждому направлению производят два наведения биссектора на предмет и соответственно делают два отсчета по шкалам микрометра, округляют их до целого (наименьшего) деления микроскопа (верньера) и записывают в журнал (табл. 3.3). На этом заканчивается первый полуприем.
Переводят зрительную трубу через зенит и переставляют лимб па величину, близкую к 90°, для второго полуприема и повторяют визирование при положении вертикального круга право (П). При этом алидаду перемещают в противоположную сторону, наводят пересечение нитей на переднюю веху (марку), а потом на заднюю и делают отсчеты, записывают в журнал (см. табл. 3.3).
Для получения значения правого по ходу горизонтального угла необходимо из среднего отсчета, полученного при визировании на заднюю точку, вычесть средний отсчет, полученный при визировании на переднюю точку. Для получения левого по ходу угла из среднего отсчета на переднюю точку вычитают средний отсчет на заднюю точку. Все записи по измерению углов заносятся в специальный полевой журнал (табл. 3.3).
Записи в журналах ведутся карандашом, цифры должны быть отчетливыми, т. е. не допускающими различных толкований, неправильная запись зачеркивается, но так, чтобы она читалась, а выше зачеркнутого записывается исправленный результат. Подчистки резинкой, скребком, бритвой не допускаются.
Страницы в полевом журнале перед наблюдением должны быть пронумерованы и подписаны наблюдателем и начальником партии.
По окончании работ по измерению горизонтальных углов на данном объекте составляют схему, на которую выписывают углы до десятых долей минуты. Невязки не должны превышать величины, подсчитанной по формуле
/h«on = 1’V«I (3.4)
где п — число измеренных углов в полигоне или ходе.
На узловых и исходных пунктах горизонтальные углы измеряют одним полным круговым приемом
При измерении углов по способу круговых приемов алидаду, как при положении круг право П, так и при лево JI вращают по ходу часовой стрелки. При визировании по каждому направлению делают два наведения биссектора на визирную цель и производят соответственно по микрометру два отсчета, округляя их до целого деления микрометра (верньера). При движении алидады по ходу часовой стрелки в первом полуприеме зрительную трубу вначале наводят на крайнюю левую точку хода, а затем на все последующие по порядку: полуприем заканчивают наведением на начальную точку. Затем зрительную трубу переводят через зенит и движением алидады по ходу часовой стрелки вновь наводят на крайнюю левую точку хода, повторяя наблюдения на все последующие точки в том же порядке, как и в первом полуприеме.
Таким образом, для исключения систематического влияния от увлекания алидадой лимба в обоих полуприемах алидаду вращают в одном и том же направлении (по ходу часовой стрелки). Перед началом измерения алидаду поворачивают в направлении измерения углов на 10—15 оборотов.
Важнейшим условием получения хороших результатов в угловых измерениях является устойчивость теодолита, визирных марок или вех, поэтому штатив должен быть прочным.
Во избежание кручения штатива от нагревания солнцем при измерении углов применяют зонт, защищая им не только теодолит, но и весь штатив. При установке на асфальте в жаркую погоду или на тающем льду весной необходимо концы ножек штатива засыпать землей или снегом, чтобы металлические концы не плавили асфальт или лед и штатив не опускался.
Кроме того, необходимо обращать внимание на правильную работу подъемных винтов, так как даже небольшой люфт в осях вызывает смещение теодолита при вращении лимба или алидады.
При измерении горизонтальных углов визирный луч не должен проходить ниже 0,5 м от поверхности земли, асфальта и не ближе 0,5 м от вертикальной поверхности предметов.
При измерении горизонтальных углов в ходах постоянного съемочного обоснования руководствуются следующими правилами. Окуляр микроскопа устанавливают на наиболее резкое изображение штрихов круга, следя за тем чтобы не было параллакса. В случае разницы в изображении штрихов ставят окуляр на среднюю резкость изображения. Окуляр зрительной трубы устанавливают на резкое изображение сетки нитей и добиваются четкого изображения наблюдаемых предметов в поле зрения трубы и отсутствия параллакса. Желательно, чтобы при измерении углов установка окуляра и фокусировка трубы оставались неизменными.
Рукоятку оптического микрометра следует вращать только по ходу часовой стрелки (при совмещении штрихов). Во время измерения углов наводящие винты алидады горизонтального круга следует ставить на середину резьбы и выполнять наведения только на ввинчивание винта, при этом закрепительные винты не следует сильно закреплять.
Основными погрешностями при измерении углов являются следующие:
Погрешности, возникающие непосредственно в процессе измерения угла. К ним относятся погрешности визирования, отсчета, влияиия остаточных погрешностей после юстировки прибора, погрешности смещения штатива и теодолита во время измерений, а также личные погрешности наблюдателя.
1. Инструментальные погрешности.
Влияние коллимационной ошибки ДС на измеренное направление
ДС=——, (3.5)
cos а
где С — коллимационная ошибка теодолита, а — угол наклона трубы при визировании на пункт.
Эта погрешность компенсируется, если наблюдать при разных положениях вертикального круга (П и Л), а коллимационная ошибка остается постоянной во время измерений. Если коллимационная ошибка изменяется (например, при различной фокусировке), то остаточное влияние ее тем больше, чем больше изменение С и чем больше угол наклона а. В этом случае угол будет содержать погрешность
1 ( sic) «!c) Л
дС = ± (-J—!_ 1 (3.6)
2 V cos а2 cosc^ /
где 6}С> и б|с) — изменение коллимационной ошибки при переходе от измерений при круге право П к измерению при круге лево Л для направлений 1 и 2, определяющих измеряемый угол. Из формулы видно, что влияние коллимационной ошибки на измеренный угол тем больше, чем больше разница в величинах 6(с) и в абсолютных величинах углов а.
Влияние наклона оси вращения трубы теодолита на измеряемое направление равно
(О = t tg а, (3.7)
где i — угол наклона оси вращения трубы, a — угол наклона трубы.
В случае когда вертикальная ось вращения теодолита приведена в отвесное положение, это влияние будет исключено в среднем из двух измере-нин при различных положениях трубы .(П и Л) при условии, что угол между осью вращения трубы и вертикальной осью вращения теодолита остается неизменным.
Если вертикальная ось вращения теодолита несколько отклоняется от отвесного положения, то это вызовет появление погрешности, определяемой формулой
,М = 1/2(6® tga2-6«tga2), (3.8)
где б}’1 и —среднее значение угла наклона оси вращения *трубы при П и Л для направлений 1, 2, определяющих угол; ai и а2 — углы наклона трубы.
Влияние рефракции при наблюдениях вертикальных углов в прямом и обратном направлениях уменьшается. При измерении углов постоянного съемочного обоснования, где при сравнительно коротких сторонах разность в углах наклона может достигать несколько градусов, следует особенно тщательно приводить ось вращения теодолита в отвесное положение.
К другим инструментальным погрешностям относятся азимутальные, для уменьшения которых следует надежно устанавливать штатив над центром пункта, крепко затягивать винты, скрепляющие ножки штатива с головкой и места соединения раздвижных ножек, а также проверять регулировку вращения подъемных винтов. Рекомендуется перед измерением углов теодолит исследовать в отношении азимутальных сдвигов в условиях, близких к полевым.
2. Погрешности от воздействия внешней среды.
К этим погрешностям следует отнести влияние нагревания теодолита
лучами солнца, изменения температуры воздуха, колебания изображений и т. д.
Погрешности, возникающие под влиянием неравномерного нагрева прибора, можно значительно уменьшить, закрывая теодолит зонтом от воздействия прямых лучей солнца.
Для уменьшения погрешностей, вызванных колебаниями изображения, необходимо измерение углов производить в часы наиболее спокойных изображений. При ветре средней силы рекомендуется теодолит и штатив прикрыть зонтом со стороны ветра. Визирный луч не должен проходить низко над землей и близко от местного предмета, так как в случае несоблюдения этого условия на визирный луч будет влиять рефракция, значительно искажающая результат измерения угла.
3.Погрешности центрирования и редукции теодолита и марок над пунктами.
Для ослабления влияния погрешностей центрирования и редукций необходимо применять трехштатипную систему. В случае когда теодолит и марки центрируются с одинаковой точностью (например, 1 мм), совместное влияние погрешности центрирования редукции (при ходе с равными сторонами S) будет равно
. тсг= — -л/2, (3.9)
5
а в случае хода с разными сторонами
3.2.2. Измерение вертикальных углов
При развитии сетей постоянного съемочного обоснования в горной и всхолмленной местности определение высот пунктов этих сетей, кроме геометрического, допускается выполнять тригонометрическим (геодезическим) нивелированием при длине хода не более 1 км.
Тригонометрическое нивелирование производится измерением вертикальных углов, приведенными выше теодолитами, одним полным приемом по трем горизонтальным нитям при двух положениях вертикального круга при круге П и Л. Колебание места нуля сетки (МО) при повторных его определениях не должно быть более 20″, Высоты теодолитов и визирных целей должны измеряться дважды с точностью до 1 см. Превышения между пунктами постоянного съемочного обоснования определяются в прямом и обратном направлениях.
Расхождения между прямыми и обратными превышениями не должны превышать 10 см на 1 км расстояния.
Допустимые невязки в ходах тригонометрического нивелирования не должны превышать 10 У L> где L — длина хода в километрах.
Для измерения вертикального угла (угла наклона) последовательно наводят пересечение вертикальной нити с каждой из трех горизонтальных нитей сетки зрительной трубы на точку, отмеченную на вехе или рейке, соответствующую высоте теодолита. Делают отсчеты по вертикальному кругу, при положении пузырька уровня, при вертикальном круге в нуль-пункте.
При измерении вертикальных углов теодолитом с компенсатором. заменяющим уровень при алидаде вертикального круга,, отсчет по вертикальному кругу производится после визирования зрительной трубой теодолита на точку вешки (рей!<�и), соответствующую высоте теодолита.
Вычисление углов наклона производится по формулам:
для теодолита Т15
Л — П —180° _ /Q , ov
а=-; а = Л—МО; (3.12)
или а = МО—П—180°.
В формуле (3.12) к величинам, меньшим 90°, следует предварительно прибавлять 360°;
сс = 90°—г или а = 2— 90°.
В формулах (3.12) — (3.15) П и Л — отсчеты по вертикальному кругу при положении его соответственно справа и слева от наблюдателя; МО — место нуля, а — угол наклона, Мг — место зенита, z — зенитное расстояние.
При измерении углов как вертикальных, так и горизонтальных, практически невозможно определить температуру вдоль каждого направления.
— Имеющиеся данные о распределении температуры в приземном слое воздуха позволяют установить, что влияние рефракции сильнее сказывается на зенитные расстояния и значительно меньше на горизонтальные углы.
Практика работ подтвердила это обстоятельство. Установлено, что вертикальная рефракция может искажать зенитные расстояния до 2′ и более, в то время как влияние боковой рефракции на горизонтальные углы в исключительных случаях может достигнуть всего десяти секунд дуги.
В числе аномальных могут оказаться и направления, проходящие близ нагретых солнечным лучом сооружений, стоек сигнала и т. п. .
Следовательно, измерение вертикальных углов необходимо делать обязательно в прямом и в обратном направлениях, что повысит точность в два раза.
Измерение горизонтальных углов рекомендуется выполнять по теневой стороне улицы в удалении от стен здания. Пользоваться зонтом, что позволит уменьшить вращение штатива от нагрева солнцем.
Прямая линия на плоскости и в пространстве с примерами решения
Содержание:
Общее уравнение прямой:
Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами х и у по этой плоскости порождает линию.
Определение: Любое соотношение
Определение: Порядок линии определяется по высшему показателю степени переменных х и у или по сумме показателей степени в произведении этих величин.
Пример:
а) 2х + Зу-5 = 0 — линия первого порядка; точка A(l; 1) удовлетворяет этому соотношению, а точка, например, В(1; 0) — ему не удовлетворяет;
б)
в) 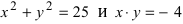
Рассмотрим другое определение линии:
Определение: Геометрическое место точек, координаты которых удовлетворяют уравнению F(x; у)=0, называется линией, а само уравнение F(x; у) = 0 — уравнением линии.
Определение: Общим уравнением прямой называется уравнение первого порядка вида
Рассмотрим частные случаи этого уравнения:
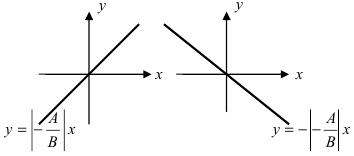
а) С = 0; 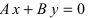
Рис. 20. Прямая, проходящая через начало координат.
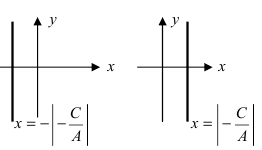
б) 5 = 0; Ах+С=0 — прямая проходит параллельно оси ординат Оу (Рис. 21):
Рис. 21. Прямая, проходящая параллельно оси ординат Оу.
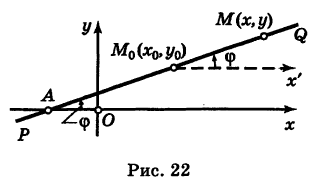
в) А = 0; Ву+С=0 — прямая проходит параллельно оси абсцисс Ох (Рис. 22):
Рис. 22. Прямая, проходящая параллельно оси абсцисс Ох.
Виды уравнений прямой
1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой 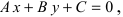
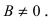
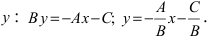
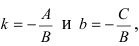
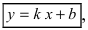
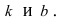
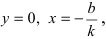
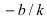
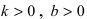
Рис. 23. Отрезки, отсекаемые прямой на координатных осях.
Из рисунка видно, что 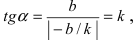
2. Уравнение прямой в отрезках.
Пусть в общем уравнении прямой параметр 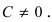
Обозначим через 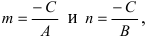
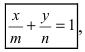
Рис. 24. Отрезки, отсекаемые прямой на координатных осях.
При у=о, х=m, т.е. прямая отсекает на оси абсцисс отрезок m. Следовательно, прямая проходит через 2 точки:
3. Уравнение прямой, проходящей через две заданные точки. Пусть дано общее уравнение прямой Ах + Ву + С = 0, которая проходит через две известные точки 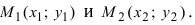
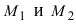
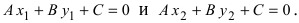
Пусть 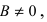
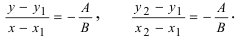
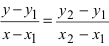
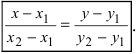
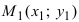
4. Уравнение прямой, проходящей через заданную точку 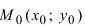
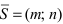
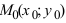
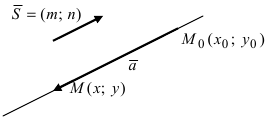
Определение: Вектор 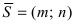
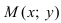
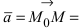
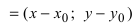
Рис. 25. Прямая, проходящая через данную точку параллельно направляющему вектору.
В силу того, что вектора 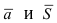
Определение: Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо каноническим уравнением прямой.
5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру t, то получим параметрическое уравнение прямой
Основные задачи о прямой на плоскости
1. Координаты точки пересечения двух прямых. Пусть две прямые заданы общими уравнениями 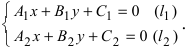
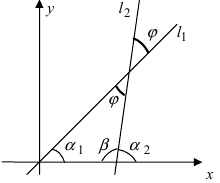
2. Угол между двумя пересекающимися прямыми. Пусть даны две пересекающиеся прямые, заданные уравнениями с угловыми коэффициентами
Требуется найти угол между этими прямыми (Рис. 26):
Рис. 26. Угол между двумя прямыми.
Из рисунка видно, что 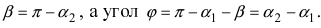
Наименьший угол между пересекающимися прямыми определим формулой 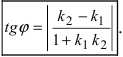
Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением
Пример:
Определить угол между прямыми
Решение:
В силу того, что 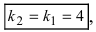
Пример:
Выяснить взаимное расположение прямых
Решение:
Так как угловые коэффициенты 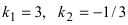
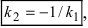
3. Расстояние от точки до прямой. Расстояние от точки до прямой определятся вдоль перпендикуляра, опущенного из точки 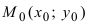
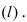
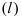
Если прямая 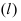
Прямая линия на плоскости и в пространстве. Системы координат на плоскости
Рассмотрим произвольную прямую. Выберем на этой прямой начальную точку, обозначаемую буквой О, определим положительное направление, выберем некоторый отрезок в качестве линейной единицы, благодаря чему прямая станет осью. После этого условимся называть координатой любой точки М на этой оси величину отрезка 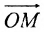
Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке, т.е. указано, какая из них считается первой, а какая — второй. Точка пересечения осей называется началом координат и обозначается через О, а сами оси — координатными осями, причем первую из них называют также осью абсцисс и обозначают через Ох, а вторую — осью ординат, обозначаемую Оу.
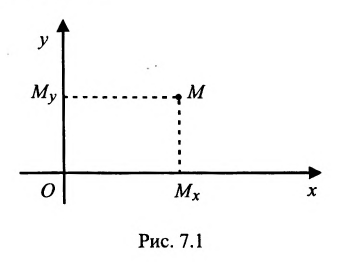
Пусть М- произвольная точка плоскости. Спроектируем точку M на координатные оси, т.е., проведем через М перпендикуляры к осям Ох и Оу; основания этих перпендикуляров обозначим соответственно 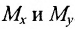
Координатами точки М в заданной системе называются числа 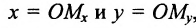
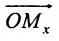
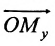
Если задана декартова прямоугольная система координат, то каждая точка М плоскости в этой системе имеет одну вполне определенную пару координат х, у — М(х, у). И обратно, для любых х и у на плоскости найдется одна вполне определенная точка с абсциссой х и ординатой у.
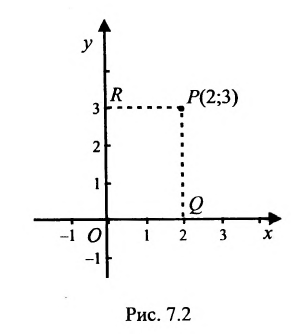
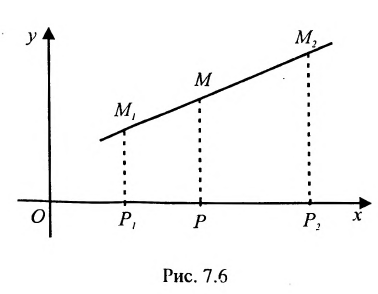
На рис. 7.2 положение точки Р полностью определяется ее координатами (2;3).
Две координатные оси разделяют всю плоскость на четыре части, называемыми координатными плоскостями, определяемыми соответственно:
Декартова прямоугольная система координат является наиболее употребительной. Однако, в отдельных случаях могут оказаться более удобными или косоугольная декартова или полярная системы координат.
Косоугольная система координат от прямоугольной декартовой системы координат отличается только произвольным углом между осями координат.
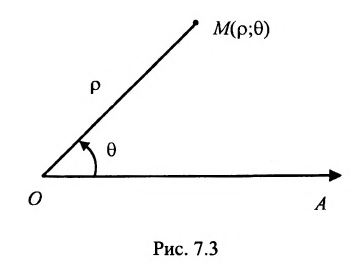
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча OA, называемого полярной осью, масштаба для измерения длин и направления- вращения в плоскости, считаемого положительным (рис. 7.3).
Каждая точка М в полярной системе координат задается парой координат 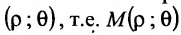
Декартова прямоугольная система координат связана с полярной системой формулами:
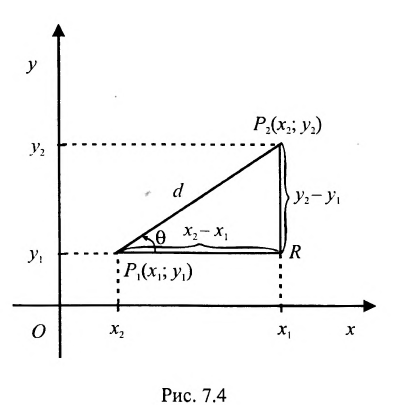
Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками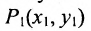
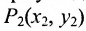
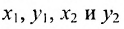
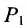
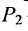
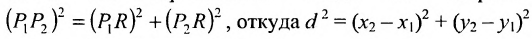
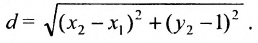
Это и есть формула для вычисления расстояния между двумя точками.
Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки 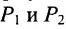
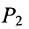
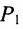
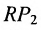
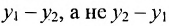
Расстояние между точками, вычисляемое по формуле (7.1.1), от этого не изменится, так как 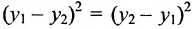
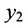
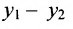
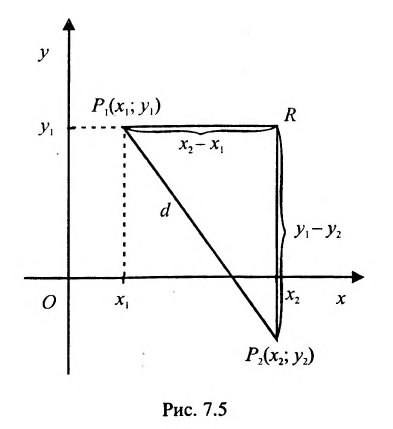
Если обозначить через 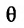
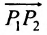
выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Из формул (7.1.2) получаем формулы:
позволяющие определить полярный угол отрезка по координатам его конца и начала. Кроме того, если u — произвольная ось, а 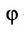
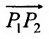
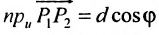
Пусть на плоскости даны две произвольные точки, из которых одна считается первой, другая — второй. Обозначим их в заданном порядке через 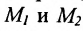
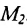
Определение 7.1.1. Число 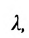
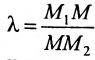
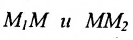
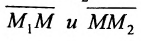
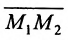
Число 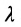
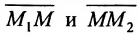
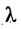
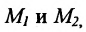
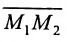
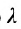
Задача о делении отрезка в данном отношении формулируется следующим образом:
Считая известными координаты двух точек 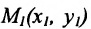
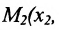
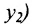
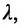
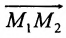
Решение задачи определяется следующей теоремой.
Теорема 7.1.1. Если точка М(х, у) делит направленный отрезок 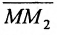
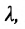
Доказательство:
Спроектируем точки 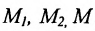
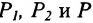
Подставив в (7.1.4) величины отрезков 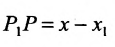
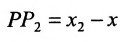
Разрешая это уравнение относительно х, находим:
Вторая формула (7.1.3) получается аналогично.
Если 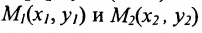
середина отрезка 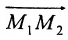
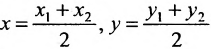
получаются из (7.1.3) при 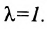
Основная теорема о прямой линии на плоскости
Предположим, что в данной плоскости задана прямоугольная система координат и некоторая прямая l.
Всякий ненулевой вектор, коллинеарный данной прямой, называется её направляющим вектором. Всякие два направляющих вектора 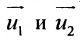
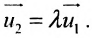
Для всех направляющих векторов 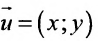
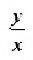
Действительно, если 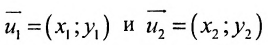
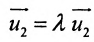
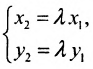
Угловой коэффициент прямой можно определить и по-другому: как тангенс угла, образованного положительным направлением оси абсцисс и заданной прямой.
Справедлива следующая теорема.
Теорема 7.3,1. Всякая прямая на плоскости определяется уравнением первой степени с двумя переменными х и у; и обратно, всякое уравнение первой степени с двумя переменными х и у определяет некоторую прямую на плоскости.
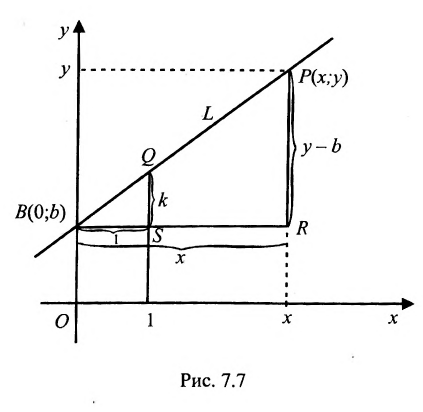
Доказательство: Пусть В = (О,b>- точка пересечения прямой L с осью у, а Р = (х,у) — любая другая точка на этой прямой. Проведем через точку В прямую, параллельную оси х, а через точку Р — прямую, параллельную оси у; проведем также прямую х = 1. Пусть k -угловой коэффициент прямой L (см. рис. 7.7). Случай к =0 не исключается.
Так как треугольники BSQ и BRP подобны, то 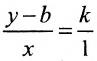
Следовательно, если точка Р принадлежит прямой L, то ее координаты удовлетворяют уравнению (7.2.1). Обратно, нетрудно показать, что если х и у связаны уравнением (7.2.1), то точка Р принадлежит прямой L, проходящей через точку (0;b) и имеющей угловой коэффициент k.
Таким образом, уравнение любой прямой можно записать в виде:
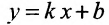
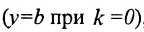
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени ио х и у можно привести к виду (7.2.2) либо (7.2.3).
Докажем обратное утверждение. Предположим, что задано произвольное уравнение первой степени:
Если 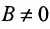
т.е. в виде (7.2.2). При В = 0 уравнение (7.2.3) сводится к уравнению
или 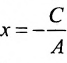
Таким образом, любая прямая описывается уравнением первой степени с неизвестными х и у, и обратно, каждое уравнение первой степени с неизвестными х и v определяет некоторую прямую.
Уравнение (7.2.4) называется общим уравнением прямой. Так
как 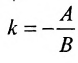
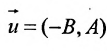
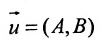
1. 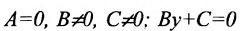
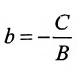
2. 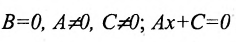
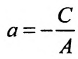
3. 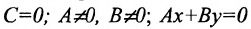
4. А=0; С=0; Ву-0 или у = 0 — это уравнение оси абсцисс Ох.
5. В=0;С=0; Ах=0 или х = 0 — это уравнение оси ординат Оу.
Различные виды уравнений прямой на плоскости
Положение прямой на плоскости относительно системы координат можно задать различными способами. Например, прямая однозначно определяется: двумя различными точками; точкой и направляющим вектором; отрезками, отсекаемыми прямой на осях координат и др. Однако, обязательно, должна быть точка, лежащая на этой прямой.
Пусть в уравнении (7.2.4) ни один из коэффициентов А, В, С не равен нулю. Перенесем свободные члены вправо и разделим на (-С). Получим уравнение прямой в отрезках:
где 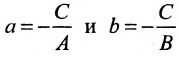
Рассмотрим прямую l на плоскости и выберем на этой прямой какие-нибудь точки 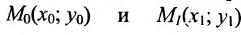
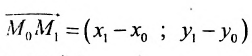
Геометрическое место концов всевозможных векторов вида 
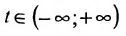
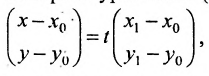
где 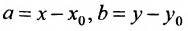
Система (7.3.3) равносильна уравнению
называемым каноническим уравнением прямой на плоскости. Из системы (7.3.3) можно получить уравнение
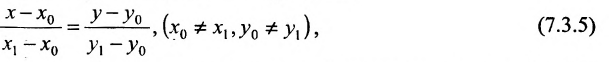
Если абсциссы точек 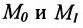

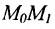
Если ординаты точек 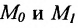
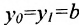
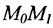
угловой коэффициент прямой.
Уравнение (7.3.6) называется уравнением прямой, проходящей через точку 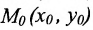
Пример:
Составить уравнение прямой, проходящей через две точки
Решение:
I способ. Воспользуемся уравнением (7.3.5). Подставив известные координаты точек 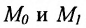
II способ. Зная координаты точек 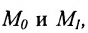
Тогда, воспользовавшись уравнением (7.3.6), найдём искомое уравнение прямой: 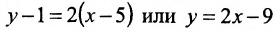
Заметим, что составленное уравнение можно записать как уравнение прямой в отрезках, разделив все члены уравнения
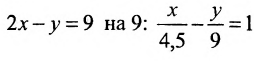
Взаимное расположение двух прямых на плоскости
Пусть на плоскости заданы две прямые общими уравнениями 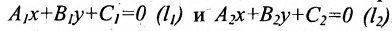
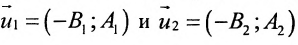
Если прямые параллельны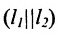
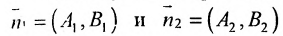
И обратно, если координаты при неизвестных х и у пропорциональны, то прямые параллельны. Следовательно, можно сформулировать следующую теорему:
Теорема 7.4.1. Две прямые 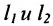
Например, прямые 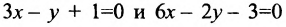
т. к.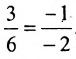
Если прямые перпендикулярны 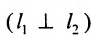
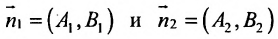
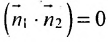
Справедливо и обратное утверждение: если скалярное произведение нормальных векторов равно нулю, то прямые /, и /2 перпендикулярны.
Теорема 7.4.2. Две прямые 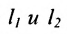
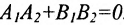
Например, прямые 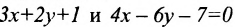
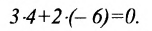
Если прямые заданы уравнениями вида 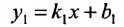
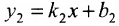
Для того чтобы прямые были параллельны, необходимо и достаточно, чтобы выполнялось равенство
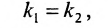
а для их перпендикулярности необходимо и достаточно, чтобы
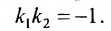
Пример:
Найти проекцию точки Р (2, 3) на прямую, проходящую через точки А (4, 3) и В (6, 5).
Решение:
Проекция точки Р на прямую АВ — это точка пересечения перпендикуляра, проведенного к этой прямой из точки Р.
Вначале составим уравнение прямой АВ. Воспользовавшись уравнением (7.3.5), последовательно получаем:
Для того, чтобы составить уравнение перпендикуляра, проведенного из точки Р на прямую АВ, воспользуемся уравнением (7.3.6). Угловой коэффициент k определим из условия перпендикулярности двух прямых, т. е. из формулы (7.4.6). Поскольку 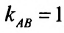
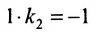
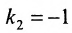
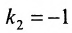
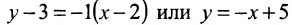
Решая систему уравнений, составленную из уравнений прямой АВ и перпендикуляра
найдём координаты проекции точки Р на прямую АВ: х=3 у=2, т.е.
Пример:
Издержки на производство шести автомобилей составляют 1000 млн. ден. ед., а на производство двадцати автомобилей- 15000 млн. ден. ед. Определить издержки на производство 22 автомобилей при условии, что функция К(х) издержек производства линейна, т.е. имеет вид у = ах + b .
Решение:
Обозначим через х количество автомобилей, а через y- издержки производства. Тогда из условия задачи следует, что заданы координаты двух точек- А(6; 1000) и В(20; 15000), принадлежащих линейной функции у = ах +b. Воспользовавшись уравнением (7.3.6 ), найдём искомое уравнение:
Подставив в найденную функцию х = 22, определим издержки на производство 22 автомобилей:
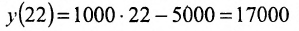
Пример:
Фирма продаёт свои изделия по 10 ден. ед. за единицу. Затраты на изготовление одного изделия составляют 6 ден. ед. Непроизводственные расходы фирмы равны 300 ден. ед. в год. Определить годовой выпуск продукции, необходимой для того, чтобы фирма работала с прибылью.
Решение:
Обозначим через х объём произведенной продукции. Тогда доход фирмы равен D = 10x. Затраты на производство определяются уравнением: 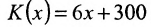
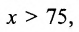
Прямая линия в пространстве
Системы координат в пространстве
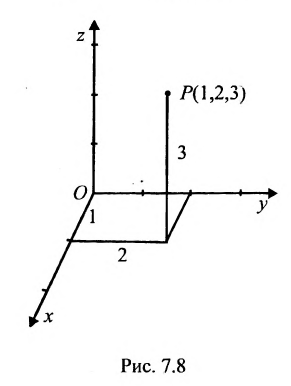
В трехмерном пространстве система координат определяется тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось единицей измерения длин, можно задать тремя упорядоченными числами (называемыми координатами) положение точки в пространстве. Например, точка Р задается упорядоченной тройкой чисел Р( 1,2,3).
Пусть задано пространство
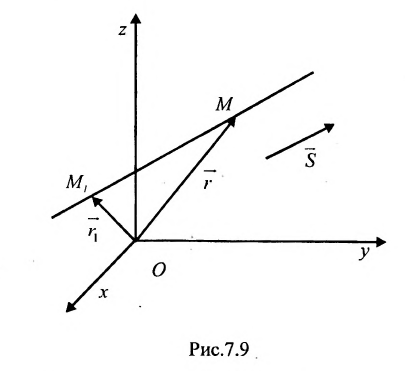
Положение прямой в пространстве вполне определяется заданием какой-либо сё фиксированной точки 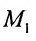
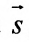
Вектор 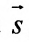
Итак, пусть прямая L проходит через точку 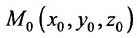
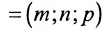
Рассмотрим произвольную точку M(x,y,z) на этой прямой. Из рисунка видно, что вектор 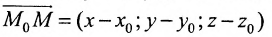
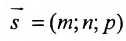
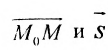
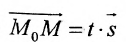
Уравнение 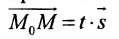
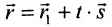
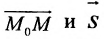
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты х, у и z и точка М перемещается по прямой.
Разрешив уравнения (7.5.2) относительно t
и приравняв найденные значенияt получим канонические уравнения прямой:
Если прямая L в пространстве задается двумя своими точками 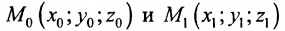
можно взять в качестве направляющего вектора и тогда уравнения (7.5.3) преобразуются в уравнения
где 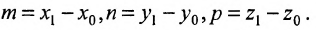
Пример:
Составить параметрические уравнения прямой, проходящей через точку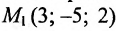
Решение:
В качестве направляющего вектора 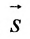
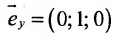
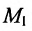
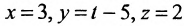
Пример:
Записать уравнения прямой 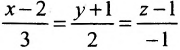
Обозначим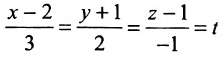
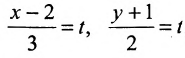
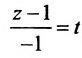
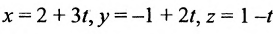
Замечание. Пусть прямая перпендикулярна одной из координатных осей, например, оси Ох. Тогда направляющий вектор
прямой перпендикулярный оси Ох, имеет координаты (о; n; р) и параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае формально можно записывать канонические уравнения прямой в виде 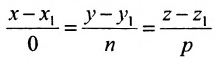
Аналогично, канонические уравнения
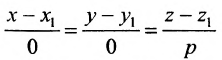
Пример:
Составить канонические и параметрические уравнения прямой, проходящей через точку 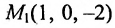
Решение:
Подставив координаты точки 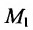
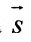
.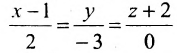
Пример:
Составить канонические уравнения прямой, проходящей через точку М(2, -1,4) параллельно
а) прямой 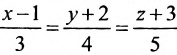
Решение:
а) Поскольку направляющий вектор заданной прямой
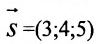
подставив координаты точки М(2; -1; 4) и вектора 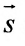
б) Поскольку единичный вектор оси О х: 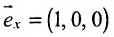
(7.5.3) координаты точки М(2; -1; 4 ) и вектора 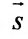
в) В качестве направляющего вектора 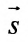
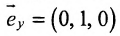
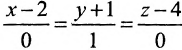
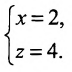
г) Единичный вектор оси Oz : 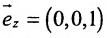
Пример:
Составить уравнение прямой, проходящей через две заданные точки
Решение:
Подставив координаты точек 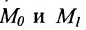
(7.5.4), получим:
Взаимное расположение двух прямых в пространстве
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным. Пусть в пространстве заданы две прямые:
Очевидно, что за угол 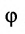
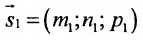
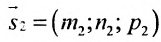
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов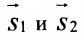
Две прямые параллельны тогда и только тогда, когда пропорциональны соответствующие координаты направляющих векторов:
т.е. 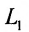
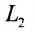
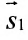
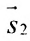
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих координат направляющих векторов равна нулю:
Пример:
Найти угол между прямыми 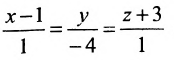
Решение:
Воспользуемся формулой (7.6.1), в которую подставим координаты направляющих векторов 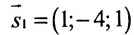
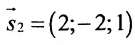
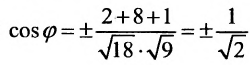
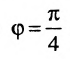
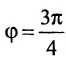
Вычисление уравнения прямой
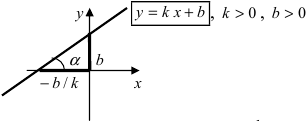
Пусть PQ — некоторая прямая на плоскости Оху (рис. 22). Через произвольную точку М0 (х0, у0) этой прямой (условно называемую «начальной точкой») проведем прямую М0х параллельную оси Ох и имеющую с ней одинаковое направление. Тогда наименьший неотрицательный угол 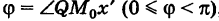
Очевидно, этот угол не зависит от выбора точки М0. Если прямая PQ пересекает ось Ох в некоторой точке А (а, 0), то ф есть обычный угол между направленными прямыми. Если PQ || Ох, то, очевидно, Ф = 0. Начальная точка М0 прямой и угол ф («направление прямой») однозначно определяют положение этой прямой на плоскости.
1) Пусть сначала 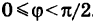
Ордината у = NM текущей точки М (х, у) прямой (рис. 23) состоит из двух частей:
из них первая постоянна, а вторая переменна. Введя угловой коэффициент tg ф = k9 из рис. 23 будем иметь
Нетрудно проверить, что формула (3) остается справедливой также и при х
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Общее уравнение прямой: описание, примеры, решение задач
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат O x y .
Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .
Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.
Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .
Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0
Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
- Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
- Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
- Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
- Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.
Решение
Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:
Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0
Ответ: 7 x — 2 = 0
На чертеже изображена прямая, необходимо записать ее уравнение.
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .
Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .
Ответ: y — 3 = 0 .
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0
Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:
A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0
Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .
Ответ: x — 2 · y + 11 = 0 .
Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
2 3 x 0 — y 0 — 1 2 = 0
Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2
Ответ: — 5 2
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .
Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .
Это равенство возможно записать как пропорцию: x + C A — B = y A .
В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .
Перепишем равенство в виде пропорции: x — B = y + C B A .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .
Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.
Ответ: x — 3 = y — 4 3 0 .
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2
Теперь примем обе части полученного канонического уравнения равными λ , тогда:
x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .
Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x
Ответ: y = — 2 7 x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :
A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1
Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.
Решение
Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .
Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .
Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .
Ответ: x — 1 2 + y 1 14 = 1 .
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0
Каноническое уравнение преобразуется к общему по следующей схеме:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0
Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0
Перейдем от канонического к общему:
x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0
Ответ: y — 4 = 0
Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0
Ответ: 1 3 x + 2 y — 1 = 0 .
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0
Ответ: 2 x — 3 y — 5 = 0 .
Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .
Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0
Глава 1. Уравнение прямой (стр. 1 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
Глава 1. Уравнение прямой
Геометрия развивается по многим направлениям. Возникновение компьютеров привело к появлению такой области математики как вычислительная геометрия. При создании современных приложений часто требуется разработка эффективных алгоритмов для определения взаиморасположения различных объектов на плоскости, вычисления расстояний между ними, вычисления площадей фигур и др.
В данной главе излагается материал, частично известный вам из курса математики. Мы рассмотрим методы решения геометрических задач, которые эффективно реализуются с помощью компьютера, что позволит вам по другому взглянуть на вопросы, изучаемые в рамках школьного курса геометрии. Для этого придется воспользоваться аналитическим представлением геометрических объектов.
1. 1. Формы записи уравнения прямой
В задачах часто приходится задавать на плоскости различные геометрические объекты. Простейшими геометрическими фигурами на плоскости являются точка и прямая. Точка задается указанием своих координат, например A(15; –5), B(x1; y1). Прямую можно задавать с помощью уравнения прямой. Существуют различные формы записи уравнения прямой. Выбор какой-то конкретной зависит от исходных данных, задающих прямую на плоскости. (Могут быть заданы координаты двух точек, через которые проводится прямая, или коэффициенты при неизвестных в линейном уравнении).
В декартовых координатах каждая прямая определяется уравнением первой степени. Уравнение вида
называется общим уравнением прямой.
Если в общем уравнении прямой коэффициент при y не равен нулю, то уравнение можно разрешить относительно y:
Обозначая k = 

получаем уравнение вида y = kx + b. Если же B = 0, то уравнение имеет вид
Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом; k – угловой коэффициент, b – величина отрезка, который отсекает прямая на оси Oy, считая от начала координат (рис. 1).
Уравнение y – y0 = k(x–x0) – это уравнение прямой с угловым коэффициентом k, которая проходит через точку с координатами (x0; y0).
Рассмотрим две точки с координатами (x1; y1) и (x2; y2), лежащие на прямой y = kx + b. Их координаты удовлетворяют уравнению прямой:
Вычитая из второго равенства первое, имеем y2 – y1 = k(x2 – x1), или
k =
Пусть точка с координатами (x; y) – произвольная точка на прямой, проходящей через точки с координатами (x1; y1) и (x2; y2) ( рис. 2 ). Тогда, с учетом того факта, что она имеет тот же коэффициент наклона, получаем
k =




является уравнением прямой, которая проходит через точки с координатами (x1; y1) и (x2; y2). Недостатком этой формулы является ее неопределенность при x1 = x2 и (или) y1 = y2. Поэтому ее лучше использовать в виде
Алгоритм для определения значений коэффициентов A, B, C общего уравнения прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим [1] :
C:= – x1*(y2 – y1)+y1*(x2 – x1)
Рассмотрим пример: x1 = 0, y1 = 0, x2 = 1, y2 = 2. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2) будет следующим:
C = –x1 * (y2 – y1) + y1 * (x2 – x1) = 0 * 2 + 0 * 1 = 0. ЌСледовательно, уравнение прямой будет иметь вид 2х – у = 0.
1. 2. Положение точек относительно прямой
Множество точек прямой, проходящей через две точки с координатами (x1; y1) и (x2; y2), удовлетворяет уравнению
Это значит, что если имеется точка с координатами (x0; y0) и (x0 – x1) * (y2 – y1) – (y0 – y1) * (x2 – x1) = 0, то эта точка лежит на прямой. B дальнейшем, вместо выражения (x – x1) * (y2 – y1) – (y – y1) * (x2 – x1) мы иногда будем использовать для краткости обозначение Ax + By + C или f(x1, y1, x2, y2, x, y).
Прямая Ax + By + C = 0, проходящая через две заданные точки с координатами (x1; y1) и (x2; y2), разбивает плоскость на две полуплоскости. Рассмотрим возможные значения выражения Ax + By + C.
1) Ax + By + C = 0 – определяет геометрическое место точек, лежащих на прямой.
Запишем алгоритм для определения, лежит ли точка с координатами (x3; y3) на прямой, проходящей через точки (x1; y1) и (x2; y2). Переменная P – переменная логического типа, которая имеет значение «истина», если точка лежит на прямой и «ложь» в противном случае.
если (x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)=0
2) Ax + By + C > 0 – определяет геометрическое место точек, лежащих по одну сторону от прямой.
3) Ax + By + C рис. 3 точки (x3; y3) и (x4; y4) лежат по одну сторону от прямой, точки (x3; y3) и (x5; y5) по разные стороны от прямой, а точка (x6; y6) лежит на прямой.
Рассмотрим пример: x1 = 1, y1 = 2, x2 = 5, y2 = 6. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим:
Следовательно, уравнение прямой будет иметь вид 4х – 4у + 4 = 0 или x – y + 1 = 0. Подставим координаты точек (3; 4), (1; 1), (2; 0), (0; 2) в уравнение прямой. Получим:
1 * 3 – 1 * 4 + 1 = 0, 1 * 2 – 1 * 0 + 1 > 0,
1 * 1 – 1 * 1 + 1 > 0, 1 * 0 – 1 * 2 + 1 L:=»по одну»
Z1:=(x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)
Z2:=(x4 – x1)*(y2 – y1) – (y4 – y1)*(x2 – x1)
½ то L:=»по разные» (1. 3)
1.3. Взаимное расположение двух отрезков
Пусть нам необходимо определить взаимное расположение двух отрезков. Отрезки на плоскости заданы координатами своих концевых точек. Предположим, что концевые точки одного из отрезков имеют координаты (x1; y1) и (x2; y2), а концевые точки другого – (x3; y3) и (x4; y4). Пусть общее уравнение первой прямой, проходящей через точки (x1;y1) и (x2;y2), имеет вид A1x + B1y + C1 = 0, а второй прямой, проходящей через точки (x3;y3) и (x4;y4), A2x + B2y + C2 = 0.
Определим расположение точек (x3; y3) и (x4; y4) относительно первой прямой. Если они расположены по одну сторону от прямой, то отрезки не могут пересекаться. Аналогично можно определить положение точек (x1; y1) и (x2; y2) относительно другой прямой.
Таким образом, если значения пары выражений Z1 = A1x3 + B1y3 + C1 и Z2 = A1x4 + B1y4 + C1 имеют разные знаки или Z1*Z2 = 0, а также пары Z3 = A2x1 + B2y1 + C2 и Z4 = A2x2 + B2y2 + C2 имеют разные знаки или Z3*Z4 = 0, то отрезки пересекаются. Если же значения пар выражений Z1 и Z2, или Z3 и Z4, имеют одинаковые знаки, то отрезки не пересекаются.
Различные случаи расположения отрезков показаны на рис. 4 .
На этом рисунке отрезки с концами в точках (x1; y1), (x2; y2) и (x4; y4), (x5; y5) пересекаются, отрезки с концами в точках (x1; y1), (x2; y2) и (x3; y3), (x4; y4) не пересекаются, а отрезки с концами в точках (x3; y3), (x4; y4) и (x4; y4) и (x5; y5) имеют общую вершину, что можно считать частным случаем пересечения.
Алгоритм для определения, пересекаются ли два отрезка с концами в точках (x1; y1), (x2; y2) и (x3; y3), (x4; y4) будет следующим:
Z1:=(x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)
Z2:=(x4 – x1)*(y2 – y1) – (y4 – y1)*(x2 – x1)
Z3:=(x1 – x3)*(y4 – y3) – (y1 – y3)*(x4 – x3)
Z4:=(x2 – x3)*(y4 – y3) – (y2 – y3)*(x4 – x3)
Приведенный фрагмент алгоритма не учитывает крайней ситуации, когда два отрезка лежат на одной прямой. В этом случае (x3 – x1) * (y2 – y1) – (y3 – y1) * (x2 – x1) = 0 и (x4 – x1) * (y2 – y1) – (y4 – y1) * (x2 – x1) = 0.
На рис. 5 отрезки, лежащие на одной прямой не пересекаются, а на рис. 6 – отрезки пересекаются.
Для того, чтобы определить взаимное расположение таких отрезков, поступим следующим образом. Обозначим
Здесь k1 является левой, а k2 – правой точкой проекции первого отрезка (отрезка, заданного координатами (x1; y1), (x2; y2)) на ось Ox. Аналогично k3 является левой, а k4 – правой точкой проекции второго отрезка (отрезка, заданного координатами (x3; y3), (x4; y4)) на ось Ox. Аналогично ищем преокции на ось OY.
Отрезки, лежащие на одной прямой будут пересекаться тогда, когда их проекции на каждую ось пересекаются. (Следует заметить, что если проекции двух произвольных отрезков пересекаются, то это не значит, что и сами отрезки пересекаются, что видно на рис. 7 ).
Для определения взаимного расположения проекций на ось OX воспользуемся следующим фактом (см. рис. 5 и рис. 6 ): координата левой точки пересечения проекций Lx равна max(k1; k3), т. е. максимальной из координат левых точек проекций. Рассуждая аналогично для правых точек проекций, получим, что координата правой точки Rx пересечения равна min(k2; k4). Для того, чтобы отрезки пересекались, необходимо, чтобы левая координата пересечения проекций была не больше правой координаты пересечения отрезков (такой случай имеет место на рис. 5 , когда Lx = х3, а Rx = х2). Поэтому условием пересечения проекций является выполнение неравенства Lx £ Rx. Аналогично можно вычислить величины Lу и Rу, беря соответствующие проекции на ось Оу.
Следует отметить, что длина пересечения проекций в этом случае равна величине Lx– Rx (если Lx– Rx = 0, то проекции имеют только общую точку).
1.4. Точка пересечения отрезков
Для определения места пересечения отрезков (если известно, что они пересекаются), достаточно определить точку пересечения прямых, на которых эти отрезки лежат.
Пусть A1x + B1y + C1 = 0 является уравнением прямой, проходящей через концевые точки первого отрезка, а A2x + B2y + C2 = 0 является уравнением прямой, проходящей через концевые точки второго отрезка.
Тогда для определения точки пересечения отрезков достаточно решить систему уравнений
Домножив первое уравнение на A2, а второе уравнение на A1, получим
Вычитая из первого уравнения второе, можно найти значение y:
y =
Аналогично можно вычислить значение x:
x =
Это справедливо в случае, если выражение A2 * B1 – A1 * B2 ¹ 0. Но мы уже знаем, что отрезки пересекаются и не лежат на одной прямой. А это невозможно, если A2 * B1 – A1 * B2 = 0.
2.1 Расстояния между точками. Расстояние от точки до прямой
Расстояние между точками M1(x1; y1) и M2(x2; y2) на плоскости ( рис. 8 ) определяется по формуле
D = 
Расстояние от точки до прямой на плоскости определяется как длина отрезка перпендикуляра, опущенного из точки на прямую. Уравнение вида

где T = 
Запишем алгоритм для определения расстояния от точки (x3; y3) до прямой, проходящей через точки (x1; y1) и (x2; y2).
C:= – x1*(y2 – y1)+y1*(x2 – x1) (1. 5)
Рассмотрим пример: x1 = 0, y1 = 0, x2 = 3, y2 = 4 x3 = –1, y3 = 7. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим:
Т = 


D = 

2.2. Расстояние между точкой и отрезком
Для определения расстояния между точкой и отрезком необходимо выяснить, пересекает ли перпендикуляр, опущенный из данной точки на прямую, проходящую через концы отрезка, сам отрезок. Если перпендикуляр пересекает отрезок, то расстояние между точкой и отрезком равно расстоянию между точкой и прямой, проходящей через отрезок. (Эту задачу вы уже умеете решать.)
Если перпендикуляр не пересекает отрезок, то расстояние между точкой и отрезком равно минимальному из расстояний между точкой и одним из концов отрезка.
Для определения взаимного расположения отрезка и перпендикуляра поступим следующим образом.
Рассмотрим треугольник, образованный тремя точками, две из которых (x1; y1) и (x2; y2) являются концами данного отрезка, а третья – данная точка с координатами (x3; y3) (см. рис. 10 , б, в). Конечно, может оказаться, что все точки лежат на одной прямой и такого треугольника не существует. В этом случае, однако, мы будем полагать, что треугольник существует, правда он вырожденный (особый). В вырожденном треугольнике длины сторон могут быть равными 0 (см. рис. 10 , а).
Более того, мы будем полагать, что данный отрезок является основанием рассматриваемого треугольника (см. рис. 10 , б, в).
При таких предположениях для решения исходной задачи нам достаточно определить, является ли один из углов при основании тупым или нет. Действительно, если один из углов при основании является тупым, то перпендикуляр, опущенный из вершины, соответствующей исходной точке, не попадает на основание (отрезок). Иначе перпендикуляр, опущенный из вершины, соответствующей исходной точке, попадает на основание (отрезок).
Для решения последней задачи воспользуемся следующим свойством. Пусть a, b, c – длины сторон треугольника, причем с – длина основания. Тогда треугольник является тупоугольным при основании, если
Поэтому, вычислив значения квадратов длин сторон, нетрудно определить, пересекает ли перпендикуляр, опущенный из точки (x3; y3) на прямую, отрезок с концами в точках (x1; y1) и (x2; y2). И если не пересекает, то расстояние от точки до отрезка равно минимуму из величин a, b. Если же пересекает, то необходимо воспользоваться свойством нормального уравнения прямой .
§ 3. Многоугольники
3.1. Виды многоугольников
Ломаной называется фигура, которая состоит из точек A1, A2, . An и соединяющих их отрезков A1A2, A2A3, . An – 1An ( рис. 11 , а). Точки называются вершинами ломаной, а отрезки – звеньями. Наиболее распространенным способом задания ломаной является использование таблицы, элементы которой соответствуют координатам вершин ломаной в порядке ее обхода из одного конца в другой. Длиной ломаной называется сумма длин ее звеньев.
Многоугольником называется замкнутая ломаная линия без самопересечений (рис. 11, б).
Плоским многоугольником называется конечная часть плоскости, ограниченная многоугольником (рис. 11, в).
Обход плоского многоугольника называется положительным, если при обходе область расположена по левую руку, и отрицательным, если область остается по правую руку.
Расстояние между фигурами на плоскости определяется как длина минимального отрезка, один конец которого принадлежит одной фигуре, а второй конец – другой фигуре.
3.2. Выпуклость многоугольников
Многоугольник является выпуклым, если для каждой прямой, проходящей через любую его сторону, все остальные вершины лежат в одной полуплоскости относительно прямой. Проверим для каждой прямой, проходящей через вершины (x1; y1) и (x2; y2), (x2; y2) и (x3; y3), . (xn – 1; yn – 1) и (xn; yn), (xn; yn) и (x1; y1) взаимное расположение вершин многоугольника. Если они каждый раз расположены в одной полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если же найдется прямая, проходящая через одну из сторон, и пара вершин многоугольника, лежащих по разные стороны относительно проведенной прямой, то многоугольник не является выпуклым. Случаи выпуклого и невыпуклого многоугольников изображены на рис. 12.
Можно заметить, что для каждой прямой, проходящей через вершины (x1; y1) и (x2; y2), (x2; y2) и (x3; y3), . (xn – 1; yn – 1) и (xn; yn), (xn; yn) и (x1; y1) достаточно ограничится определением взаимного расположения вершин многоугольника (xn; yn) и (x3; y3), (x1; y1) и (x4; y4), . (xn – 2; yn – 2) и (x1; y1), (xn – 1; yn – 1) и (x2; y2), соответственно. Если они каждый раз расположены в одной полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если же найдется прямая и пара вершин многоугольника, лежащих по разные стороны относительно проведенной прямой, то многоугольник не является выпуклым. Поэтому для определения, является ли многоугольник выпуклым, достаточно воспользоваться алгоритмом
нц для i от 1 до n
½ j:= mod( i, n +1 ) : номер вершины после вершины i
½ k:= mod (j, n +1) : номер вершины после вершины j
½½ то m:=n : номер вершины перед вершиной i
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-prjamoj/
http://pandia.ru/text/79/489/58441.php
Простейшие задачи аналитической геометрии на плоскости
1. Расстояние между двумя точками.
Теорема
1.
Для любых двух точек




(1.1)
Например,
если
даны точки
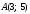
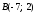
то расстояние между ними:

2. Площадь треугольника.
Теорема
2.
Для любых точек

не лежащих на одной прямой, площадь
треугольника


(1.2)
Например,
найдем площадь треугольника, образованного
точками




Замечание.
Если площадь треугольника равна нулю,
это означает, что точки лежат на одной
прямой.
3. Деление отрезка в заданном отношении.
Пусть
на плоскости дан произвольный отрезок
и
пусть

точка этого отрезка, отличная от точек
концов. Число

определенное равенством
называетсяотношением,
в
котором точка

.
Задача
о делении отрезка в данном отношении
состоит в том, чтобы по данному отношению
и данным координатам точек
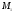


Теорема
3.
Если
точка
делит отрезок
в
отношении
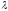
то
координаты этой точки определяются
формулами:





Следствие:
Если
– середина отрезка

где

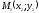
то

Например.
Даны точки
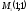

Найти координаты точки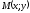
которая в два раза ближе к
чем к
Решение:
Искомая точка
делит
отрезок
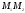
отношении

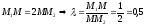
тогда
,
получили

Полярные координаты
Наиболее
важной после прямоугольной системы
координат является полярная система
координат. Она состоит из некоторой
точки
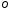
называемойполюсом,
и исходящего из нее луча

оси.
Кроме того, задается единица масштаба
для измерения длин отрезков.
Пусть
задана полярная система координат и
пусть

–
расстояние от точки
точки
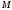

полярную ось для совмещения с лучом
Полярными
координатами точки

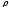

При этом число
радиусом,
число

углом.
Обозначается

Полярный радиус может иметь любое
неотрицательное значение:
Обычно считают, что полярный угол
изменяется в следующих пределах:
Однако в ряде случаев приходится
определять углы, отсчитываемые от
полярной оси по часовой стрелке.
Связь между полярными координатами точки и ее прямоугольными координатами.
Будем
считать, что начало прямоугольной
системы координат находится в полюсе,
а положительная полуось абсцисс совпадает
с полярной осью.
Пусть


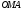

Тогда(1.5).
Эти формулы выражают прямоугольные
координаты через полярные.
С
другой стороны, по теореме Пифагора

(1.6)
– эти формулы, выражают полярные
координаты через прямоугольные.
Заметим,
что формула


так как
Из этих двух значений угла
равенства
Например,
найдем полярные координаты точки




т.к.
четверти
Пример
1:
Найти точку, симметричную точке
относительно
биссектрисы первого координатного
угла.
Решение:
Проведем
через точку А
прямую l1,
перпендикулярную биссектрисе l
первого координатного угла. Пусть

На прямой
l1
отложим отрезок
СА1,
равный
отрезку
АС.
Прямоугольные треугольники
АСО
и
А1СО
равны
между собой (по двум катетам). Отсюда
следует, что |ОА|
= |OA1|.
Треугольники
ADO
и
ОЕА1
также равны между собой (по гипотенузе
и острому углу). Заключаем, что
|AD|
= |ОЕ|
= 4,
|OD| = |EA1|
=
2, т.е. точка имеет координаты х
= 4, у = -2,
т.е. А1(4;-2).
Отметим,
что имеет место общее утверждение: точка
A1,
симметричная точке
относительно биссектрисы первого и
третьего координатных углов, имеет
координаты
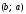
то есть
Пример
2:
Найти точку, в которой прямая, проходящая
через точки

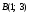
пересечет ось
Ох.
Решение:
Координаты
искомой точки
С
есть (x;
0). А так как точки
А,
В и
С
лежат на одной прямой, то должно
выполняться условие (x2-x1)(y3-y1)-(x3-x1)(y2-y1)=0
(формула (1.2), площадь треугольника ABC
равна
нулю!), где
–
координаты точки А,
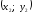
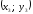
Получаем

т.е.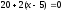


Следовательно, точка
С
имеет координаты


т.е.
Пример
3: В
полярной системе координат заданы точки


Найти:
а)
расстояние между точками
и

б)
площадь треугольника
ОМ1М2
(О
– полюс).
Решение:
а)
Воспользуемся формулами (1.1) и (1.5):

то
есть,
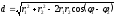
б)
пользуясь формулой для площади
треугольника со сторонами
а
и
b
и углом


находим площадь треугольника
ОМ1М2.