Как найти точку опоры
Рычаг — это простейший механизм, известный нашим предкам с незапамятных времен, он представляет собой твердое тело, вращающееся вокруг неподвижной точки – точки опоры. Рычаг служит для получения выигрыша в силе, для совершения работы или для изменения направления приложения силы. В качестве рычага может выступать обычная палка, лом, доска. Разновидностью рычага являются также ворот и блок. И способы поиска точки опоры в зависимости от этого могут быть различны.

Вам понадобится
- — рычаг;
- — грузы;
- — динамометр;
- — линейка.
Инструкция
Вектор силы F, приложенной к рычагу, лежит на прямой, которая называется линией действия силы. Кратчайшее расстояние от этой линии до точки опоры – плечо силы L. Рычаг находится в равновесии при условии, что отношение приложенных к нему сил обратно пропорционально отношению плеч этих сил: F1/F2=L2/L1 (формула 1). Таким образом, точку опоры можно найти, если известны силы F1 (нагрузка), F2 (прилагаемое усилие) и длина самого рычага L.
При помощи динамометра измерьте величину сил F1 и F2 в ньютонах. Линейкой измерьте длину рычага L и запишите значение в метрах.
Нахождение точки опоры для рычага 1 рода. Такой рычаг еще называют «Коромысло» или «Весы». Линии действия сил находятся по разные стороны от оси вращения рычага. Примером такого рычага будут качели, ножницы, клещи. В этом случае L=L1+L2. Выразите длину одного из плеч рычага через длину другого плеча и длину всего рычага: L2=L-L1 (формула 2).
Подставьте формулу 2 в формулу 1: F1/F2=(L-L1)/L1 (формула 3). Из формулы 3 путем преобразований выразите L1: L1=F2*L/(F1+F2) (формула 4). Подставьте соответствующие значения F1, F2 и L в формулу 4 и вычислите значение L1. От точки приложения силы F1 отложите полученную длину L1 и сделайте засечку. Это и будет искомая точка опоры рычага 1 рода.
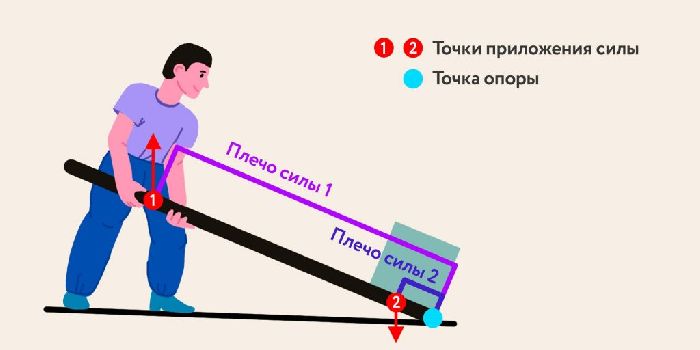
Нахождение точки опоры для рычага 2 рода. Такой рычаг носит название «Тачка». В данном случае силы действуют по одну сторону от точки опоры, причем усилие F2 оказывается на свободный конец рычага. По такому принципу работают щипцы для колки орехов, тачки. В данном случае точкой опоры является тот конец рычага, который ближе к точке приложения нагрузки, силы F1.
Нахождение точки опоры для рычага 3 рода. Такой рычаг называется «Пинцет». Здесь силы тоже действуют по одну сторону от точки опоры, как и в рычаге 2 рода. Но усилие F2 приложено между осью вращения рычага и нагрузкой F1. Такая схема используется при работе человеческого предплечья, пинцета. В данном случае точка опоры – это конец рычага противоположный нагрузке.
Видео по теме
Обратите внимание
Если в качестве рычага выступают ворот или неподвижный блок, то точкой опоры является ось вращения. У подвижного блока точка опоры расположена на противоположной стороне от точки приложения усилия.
Полезный совет
При вычислениях одни и те же физические величины измеряйте в одинаковых единицах: силу – в ньютонах, длину – в метрах.
Источники:
- Физика (для углубленного изучения), Е.И. Бутиков, А.С Кондратьев, В.М. Уздин, 2004
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Простейшие механизмы. Рычаг
Можно ли поднять земной шар?
Выдающийся древнегреческий учёный Архимед более (2000) лет назад ответил примерно так:
Дайте мне точку опоры, и я подниму земной шар.
Простейшим механизмом, при помощи которого можно поднять тяжёлые предметы, является рычаг.
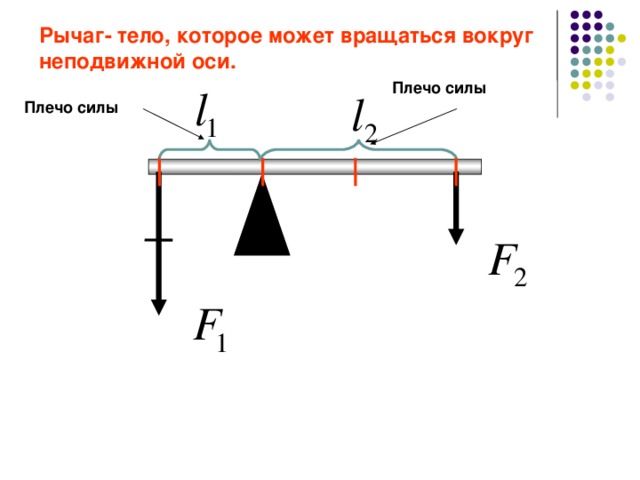
Рычаг состоит из перекладины, рычага и опоры.
Точка опоры перекладину рычага делит на два плеча рычага.
Точка опоры может быть расположена между плечами рычага ((1)) или по одну сторону от плеч рычага ((2)).
Рис. (1). Изображение рычага в двух вариантах расположения точки опоры
Рычаг находится в равновесии, если произведение силы на плечо по обе стороны опоры одинаково:
Из условия равновесия рычага следует, что если рычаг находится в равновесии, тогда приложенные силы обратно пропорциональны длине плеч рычага:
Рис. (2). Изображение рычага в равновесном состоянии
Используя рычаг, можно поднимать тяжёлые предметы, прикладывая небольшое усилие.
Величина экономии силы одинакова с соотношением длин более длинного и более короткого плеча рычага.
В обиходе часто используют рычаги. Например, ножницы, плоскогубцы, лопата, тачка являются примером использования рычагов.
Рис. (3). Изображение плоскогубцев
Источники:
Рис. 1. Изображение рычага в двух вариантах расположения точки опоры. © ЯКласс.
Рис. 2. Изображение рычага в равновесном состоянии. © ЯКласс.
Рис. 3. Изображение плоскогубцев. © ЯКласс.
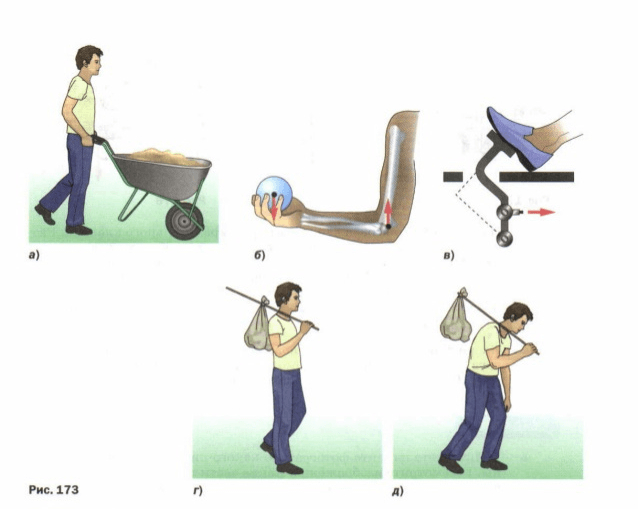
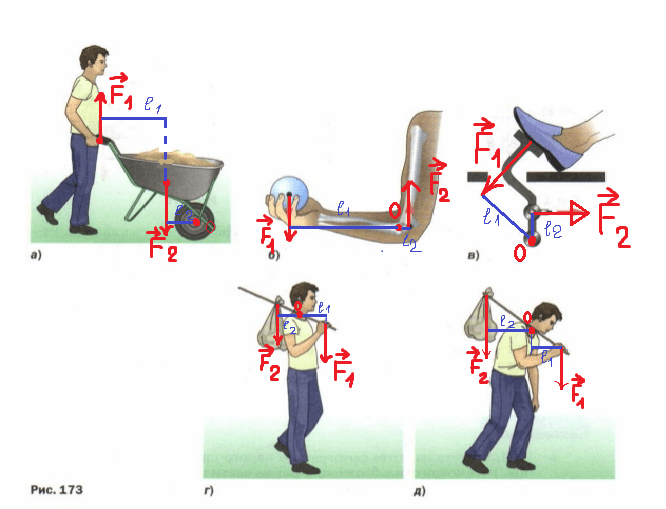
Укажите точку опоры и плечи рычагов, изображённых на рисунке 173.
рис. 173
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. §60. Упражнение 32. Номер №1
Решение
Точку опоры рычага − это единственная неподвижная точка рычага. Она может располагаться в центральной части рычага, у его края и др.
Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.
.Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.
О− точка опоры, F − действующие силы, L − плечо рычага.
Рычаг
4.6
Средняя оценка: 4.6
Всего получено оценок: 138.
Обновлено 14 Июля, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 138.
Обновлено 14 Июля, 2021
Человек всегда стремился увеличить силу своих мускулов и производить работу, требующую значительных усилий. В результате были сделаны важные изобретения, на основе которых позже придумали сложные механизмы и машины. Главным действующим элементом таких механизмов является рычаг. Рассмотрим принципы, на которых он функционирует.
Рычаг и его структура
Практически любому человеку приходилось приподнимать тяжелые грузы с помощью длинной палки, короткий конец которой подкладывался под груз. Это очень древнее приспособление, которое называется рычаг.
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной опоры.
Рычаг может иметь различные виды, но в любом случае он представляет собой твердое тело, имеющее опору, вокруг которой он поворачивается, и на некотором расстоянии от опоры к рычагу прикладываются силы (в простейшем случае — две).
Часть рычага, лежащая между точкой опоры и точкой приложения силы, называется плечом рычага. Силу можно приложить к плечу рычага под разными углами: чтобы учесть это обстоятельство, необходимо определить плечо силы. Из курса физики 7 класса известно, что для нахождения плеча силы необходимо опустить перпендикуляр из точки опоры до линии приложения силы. Длина получившегося перпендикуляра — это и есть плечо силы.
Для приведенного примера, когда палка подкладывается под тяжелый предмет — она является твердым телом, рычагом, а опорой является конец палки, опирающийся в грунт или поверхность пола. К палке приложены две силы — сила тяжести груза и мускульная сила рук. Соответственно, в рычаге два плеча — одно короткое, от точки опоры до точки, упирающейся в груз, и второе — длинное, от точки опоры до точки приложения силы рук. Поскольку силы приложены перпендикулярно палке, плечи обоих сил равны длинам плеч рычага.
Действие рычага
Действие рычага заключается в том, что рычаг поворачивается относительно опоры под действием одной силы и за счет своей твердости создает усилие в другой точке. При этом расстояние от опоры до точек приложения сил может быть различно.
Из опыта известно, что чем длиннее рычаг, тем меньшее усилие требуется для его поворота. Отсюда следует главное свойство рычага, позволяющее решать задачи:
Величина сил, действующих на рычаг, обратно пропорциональна длине плеч этих сил.
То есть, если на рычаг действует сила $F_1$ c плечом $l_1$ и ей противостоит сила $F_2$ c плечом $l_2$, то соотношение сил и плеч рычага можно выразить следующей формулой:
$${F_1 over F_2} = {l_2 over l_1}$$
Это свойство рычага было установлено еще в античности Архимедом.
По преданию, установив это правило, Архимед сказал: «Дайте мне точку опоры, и я сдвину Землю». Однако из приведенной формулы следует, что для того, чтобы Архимед силой своих рук мог бы двигать Землю, длинное плечо рычага должно было бы быть в $10^{23}$ раз длиннее. Всей жизни Архимеду бы не хватило, чтобы с помощью такого длинного плеча сдвинуть Землю даже на толщину волоса.
Что мы узнали?
Рычаг — это простейший механизм, который представляет собой твердое тело, способное поворачиваться вокруг неподвижной опоры. К рычагу на разном расстоянии от опоры приложены силы. Величина сил, действующих на рычаг, обратно пропорциональна длине плеч этих сил.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 138.
А какая ваша оценка?
Простые механизмы. «Золотое правило» механики
- Виды простых механизмов
- Принцип действия рычага
- «Золотое правило» механики
- Блоки и полиспасты
- «Золотое правило» механики для гидравлического пресса
- «Золотое правило» механики для наклонной плоскости
- Задачи
п.1. Виды простых механизмов
Простой механизм – это механическое устройство, изменяющее направление или величину силы.
По традиции, сложившейся ещё со времен Возрождения, к простым механизмам относятся:
- наклонная плоскость и её разновидности – клин и винт;
- рычаг и его разновидности – блок и ворот;
- колесо;
- поршень.
Примеры физических систем в механике
п.2. Принцип действия рычага
Подробно рычаги и условия равновесия были рассмотрены в §26 данного справочника.
Там же было получено правило моментов $$ F_1L_1=F_2L_2. $$
Если (F_2) – это нагрузка, а (F_1) — приложенная сила, то выигрыш в силе: $$ i=frac{F_2}{F_1}=frac{L_1}{L_2} $$
В этом разделе мы рассмотрим принцип работы рычага с точки зрения закона сохранения энергии.
Пусть действие приложенной силы (F_1) приводит к перемещению (h_1) левого плеча вниз.
Работа приложенной силы равна (A_1=F_1h_1).
Тогда правое плечо при этом переместится вверх на расстояние (h_2).
Работа нагрузки (A_2=-F_2h_2). Работа нагрузки отрицательна, т.к. направления вектора нагрузки (F_2) и вектора перемещения (h_2) противоположны. Для замкнутой системы выполняется закон сохранения энергии, а значит, сумма работ должна быть равна нулю: $$ A_1+A_2=F_1h_1-F_2h_2=0 $$
Получаем, что (F_1h_1=F_2h_2).
Равнобедренный треугольник с основанием (h_1) и боковыми сторонами (L_1) слева подобен равнобедренному треугольнику с основанием (h_2) и боковыми сторонами (L_2) справа (по двум пропорциональным сторонам и углу между ними). Следовательно, выигрыш в силе: $$ i=frac{F_2}{F_1}=frac{h_1}{h_2}=frac{L_1}{L_2} $$
Что соответствует результату, полученному ранее.
п.3. «Золотое правило» механики
«Золотое правило» механики
Ни один механизм не дает выигрыша в работе.
Во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии.
Выигрыш в силе для рычага $$ i=frac{F_2}{F_1}=frac{h_1}{h_2} $$ показывает, что перемещение (h_1) левого плеча с приложенной силой (F_1) обязательно должно быть в разы больше перемещения (h_2) правого плеча с нагрузкой.
 |
Архимеду приписывают следующую фразу: «Дайте мне точку опоры, и я переверну Землю». Попробуем для начала хотя бы сдвинуть Землю на 1 микрон с орбиты, (h_2=1 text{мкм}=10^{-6} text{м}). Это послужит хорошей иллюстрацией «золотого ПРАВИЛО» механики. |
Допустим, мы нашли «точку опоры» и можем приложить к рычагу силу, равную собственному весу (F_1=720 text{Н}). Сила, удерживающая Землю на орбите вокруг Солнца равна (F_2=3,6cdot 10^{22} text{Н}). Получаем, что нам нужно со своей стороны переместить рычаг на $$ h_1frac{F_2}{F_1}h_2=frac{3,6cdot 10^{22}}{720}cdot 10^{-6}=5cdot 10^{13} (text{м})=5cdot 10^{10} (text{км}) $$ т.е. 50 миллиардов километров.
Расстояние от Солнца до Земли – 1 астрономическая единица – это «всего лишь» 150 миллионов километров:(1 text{а.е.}approx 1,5cdot 10^{11} text{(м)}).
Радиус всей Солнечной системы – около 100 астрономических единиц, т.е. около (1,5cdot 10^{13} text{м}). Тогда (5cdot 10^{13} text{м}) — это чуть больше полутора диаметров Солнечных систем.
Значит, если на одной стороне рычага мы сдвигаем Землю на 1 микрон, то на другой стороне – прикладывая весь свой вес – должны преодолеть расстояние в полторы Солнечных системы. Вот что такое – «проигрыш в расстоянии».
п.4. Блоки и полиспасты
Блок — это колесо с желобом, по которому пропущена веревка или трос.
В технике используют неподвижные и подвижные блоки.
 |
Неподвижный блок Ось неподвижного блока закреплена и при подъёме грузов неподвижна. Неподвижный блок – равноплечий рычаг с точкой вращения (O). Получаем тождество $$ FR=FR $$ где (R) — радиус блока. Выигрыша в силе нет. Неподвижный блок позволяет менять направление действия силы, но выигрыша в силе не даёт. Зато нет и проигрыша в расстоянии: на какое расстояние опустится веревка справа, на такое же расстояние поднимется груз слева. |
 |
Подвижный блок Ось подвижного блока поднимается или опускается вместе с грузом. По правилу моментов для рычага с точкой вращения (O) получаем тождество: $$ Fcdot OA=frac F2cdot OB Leftrightarrow Fcdot R=frac F2cdot 2R $$ Откуда следует двойной выигрыш в силе. Подвижный блок даёт выигрыш в силе в 2 раза. |
В реальных ситуациях выигрыш в силе при использовании подвижного блока получается меньшим, т.к. часть работы уходит на подъем самой веревки и блока (они тоже имеют вес) и преодоление трения.
На практике используют комбинации из неподвижных и подвижных блоков – полиспасты.
Они позволяют получить выигрыш в силе и менять её направление.
Чем больше в полиспасте подвижных блоков, тем большим будет выигрыш в силе.
Характеристики полиспастов представлены в таблице.
| № | К-во неподвижных блоков | К-во подвижных блоков | Изменение направления силы, раз | Выигрыш в силе, раз | Проигрыш в расстоянии, раз |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 2 | 2 |
| 3 | 1 | 2 | 1 | 3 | 3 |
| 4 | 1 | 3 | 1 | 4 | 4 |
| 5 | 1 | 4 | 1 | 5 | 5 |
| 6 | 1 | 5 | 1 | 6 | 6 |
п.5. «Золотое правило» механики для гидравлического пресса
Подробней о гидравлическом прессе – см. §30 данного справочника.
 |
Когда малый поршень под действием силы (F_1), опускается вниз на расстояние (h_1), он вытесняет некоторый объём жидкости. На столько же увеличивается объём жидкости под большим поршнем, который при этом поднимается на высоту (h_2). При опускании малого поршня слева сила (F_1) совершает работу (A_1=F_1h_1), где (h_1) — длина хода. При этом из левого сосуда в правый вытесняется объем воды $$ V=S_1h_1=S_2h_2 $$ |
В правом сосуде при подъёме поршня совершается работа $$ A_2=F_2h_2. $$
Давление на одном уровне в обоих сообщающихся сосудах равно $$ p=frac{F_1}{S_1}=frac{F_2}{S_2}. $$
Получаем: $$ left. begin{array}{r} p=frac{F_1}{S_1}=frac{F_2}{S_2}Rightarrow frac{S_2}{S_1}=frac{F_2}{F_1}\ V=S_1h_1=S_2h_2Rightarrow frac{S_2}{S_1}=frac{h_1}{h_2} end{array} right} Rightarrow frac{F_2}{F_1}=frac{h_1}{h_2}Rightarrow F_1h_1=F_2h_2Rightarrow A_1=A_2 $$
Работы малого и большого поршня равны.
Таким образом, «золотое правило» для гидравлического пресса также выполняется.
Гидравлический пресс не дает выигрыша в работе.
Выигрыш в силе равен проигрышу в расстоянии: $$ i=frac{F_2}{F_1}=frac{h_1}{h_2} $$
п.6. «Золотое правило» механики для наклонной плоскости
Если груз поднимать равномерно вертикально вверх на высоту (h) (из точки C в точку B), необходимо прикладывать силу, равную весу (P). При этом работа по подъему груза равна произведению веса на высоту: $$ A_{CB}=Ph $$
Если груз поднимать равномерно по наклонной плоскости вверх на высоту (h) (из точки A в точку B), работа по подъему груза равна произведению приложенной силы на длину: $$ A_{AB}=FL $$
В любом случае тело, оказавшись в точке B, приобретает потенциальную энергию begin{gather*} E_p=mgh,\[7pt] Delta E_p=E_p-E_{p0}=mgh-0=mgh end{gather*}
Работа внешних сил при этом $$ A_{CB}=A_{AB}=Delta E_p $$
Получаем begin{gather*} Ph=FL\[7pt] i=frac PF=frac Lh end{gather*}
Наклонная плоскость не дает выигрыша в работе.
Выигрыш в силе компенсируется проигрышем в расстоянии.
Выигрыш в силе равен отношению длины наклонной плоскости к высоте.
Например, из пяти наклонных плоскостей, представленных на рисунке, наибольший выигрыш в силе даст плоскость 5, т.к. у нее отношение (frac Lh) максимально (угол наклона минимален).
В реальности, если учесть силу трения, этот выигрыш уменьшается, т.к. с уменьшением угла наклона сила трения растет.
п.7. Задачи
Задача 1. Груз весом 200 Н равномерно поднимают по наклонной плоскости на высоту 5 м, прикладывая силу 100 Н. Найдите длину наклонной плоскости. Трением можно пренебречь.
Дано:
(P=200 text{Н})
(h=5 text{м})
(F=100 text{Н})
__________________
(L-?)
Работы при подъеме тела вверх и при перемещении вдоль наклонной плоскости равны: (A=Ph=FL). Получаем begin{gather*} L=frac PF h end{gather*} Подставляем begin{gather*} L=frac{200}{100}cdot 5=10 (text{м}) end{gather*} Ответ: 10 м
Задача 2. При штамповке детали больший поршень гидравлического пресса поднялся на 1 см, а меньший поршень опустился на 20 см. Какая сила действовала на деталь, если на малый поршень действовала сила 500 Н.
Дано:
(h_1=20 text{см}=0,2 text{м})
(h_2=1 text{см}=0,01 text{м})
(F_1=500 text{Н})
__________________
(F_2-?)
Работы по перемещению поршней равны: begin{gather*} A=F_1h_1=F_2h_2 end{gather*} Сила, действующая на деталь begin{gather*} F_2=frac{h_1}{h_2}F_1,\[6pt] F_2=frac{0,2}{0,01}cdot 500=10000 (text{Н})=10 (text{кН}) end{gather*} Ответ: 10 кН
Задача 3. К концам рычага длиной 1 м подвешены грузы массой 8 кг и 12 кг. На каком расстоянии от середины рычага должна быть точка опоры, чтобы рычаг находился в равновесии? Ответ запишите в сантиметрах.
Дано:
(m_1=8 text{кг})
(m_2=12 text{кг})
(d=1 text{м})
__________________
(x-?)
Плечо для груза 1: begin{gather*} L_1=frac d2+x end{gather*} Плечо для груза 2: begin{gather*} L_2=frac d2-x end{gather*} Условие равновесия: begin{gather*} F_1L_1=F_2L_2\[6pt] F_1left(frac d2+xright)=F_2left(frac d2-xright)\[6pt] (F_1+F_2)x=(F_2-F_1)frac d2 end{gather*} Учитывая, что (F_1=m_1g) и (F_2=m_2g): begin{gather*} x=left(frac{m_2-m_1}{m_1+m_2}right)frac d2 end{gather*} Получаем begin{gather*} x=left(frac{12-8}{8+12}right)cdot frac 12=frac 15cdot frac 12=0,1 (text{м})=10 (text{см}) end{gather*} Ответ: 10 см
Задача 4. Если груз лежит на левой чашке неравноплечих весов, его уравновешивают гири массой (m_1=2 text{кг}) на правой чашке. Если же груз положить на правую чашку, его уравновесит только одна гиря массой (m_2=0,5 text{кг}) на левой чашке. Какова масса (m) груза? Во сколько раз одно плечо весов длиннее другого?
Пусть длина правого плеча (L_1), левого плеча – (L_2).
По условию задачи begin{gather*} left{ begin{array}{l} mL_1=m_1L_2\ m_2L_1=mL_2 end{array} right. end{gather*} Разделим верхнее равенство на нижнее begin{gather*} frac{mL_1}{m_2L_1}=frac{m_1L_2}{mL_2}Rightarrow frac{m}{m_2}=frac{m_1}{m}Rightarrow m^2=m_1m_2 end{gather*} Масса груза begin{gather*} m=sqrt{m_1m_2}\[7pt] m=sqrt{2cdot 0,5}=1 text{кг} end{gather*} Отношение плечей begin{gather*} frac{L_1}{L_2}=frac{m_1}{m}=frac 21=2 end{gather*} Левое плечо длиннее правого в 2 раза.
Ответ: 1 кг; левое плечо длиннее правого в 2 раза
Задача 5*. Прямолинейный кусок проволоки массой (m=40 text{г}) подвешен за середину. Левую половину куска согнули, как показано на рисунке. Какой массы груз надо подвесить в точке A, чтобы восстановить равновесие.
Пусть длина всей проволоки (L).
Тогда расстояние от центра тяжести проволоки слева до точки подвеса (OK=L/4), а расстояние от центра тяжести проволоки справа до точки подвеса (OE=L/2).
Груз массой (M) подвешен на расстоянии (OA=L/2).
Из ПРАВИЛА моментов получаем: begin{gather*} Mgcdotfrac L2+frac{mg}{2}cdot frac L4=frac{mg}{2}cdot frac L2 end{gather*} Справа в равенстве – моменты, поворачивающие проволоку вокруг точки подвеса O против часовой стрелки, слева – по часовой стрелке.
Сокращаем на (gL) begin{gather*} frac M2+frac m8=frac m4Rightarrow frac m4-frac m8=frac m8Rightarrow M=frac m4\[6pt] M=frac{40}{4}=10 (text{г}) end{gather*} Ответ: 10 г
Задача 6*. Балка массой 1200 кг и длиной 3 м лежит на опорах, равноудаленных от ее концов. Расстояние между опорами 2 м.
Какую силу, перпендикулярную балке и направленную вертикально вверх нужно приложить, чтобы приподнять балку за один из её краёв?
Дано:
(M=1200 text{кг})
(CD=3 text{м})
(AB=2 text{м})
(gapprox 10 text{м/с}^2)
__________________
(F-?)
По условию begin{gather*} AC=BD=frac 12(CD-AB)=frac 12(3-2)=0,5 text{м} end{gather*} Если приподнять балку за левый край с силой (F), то останется только одна опора (B). Балка превращается в рычаг с осью вращения, проходящей через точку (B). Точка (K) — центр тяжести отрезка балки (CB).
Точка (E) — центр тяжести отрезка балки (BD).
По правилу моментов begin{gather*} Fcdot CB+m_2gcdot BE=m_1gcdot KB end{gather*} Слева – моменты, поворачивающие балку вокруг точки (B) по часовой стрелке, справа – против часовой стрелки.
Искомая сила: begin{gather*} F=frac{m_1gcdot KB-m_2gcdot BE}{CB} end{gather*} Плечи сил: begin{gather*} CB=CD-BD=3-0,5=2,5 text{м}\[6pt] KB=frac 12 CB=1,25 text{м}\[6pt] BE=frac 12 BD=0,25 text{м} end{gather*} Распределение масс: begin{gather*} m_1+m_2=M\[6pt] frac{m_1}{m_2}=frac{CB}{BD}=frac{2,5}{0,5}=5Rightarrow 1+5=6 text{частей}\[6pt] m_1=frac 56 M=frac 56cdot 1200=1000 text{кг},\[6pt] m_2=frac 16 M=frac 16cdot 1200=200 text{кг} end{gather*} Подставляем: begin{gather*} F=frac{1000cdot 10cdot 1,25-200cdot 10cdot 0,25}{2,5}=frac{12500-500}{2,5}=4800 (text{Н})=4,8 (text{кН}) end{gather*} Ответ: 4,8 кН