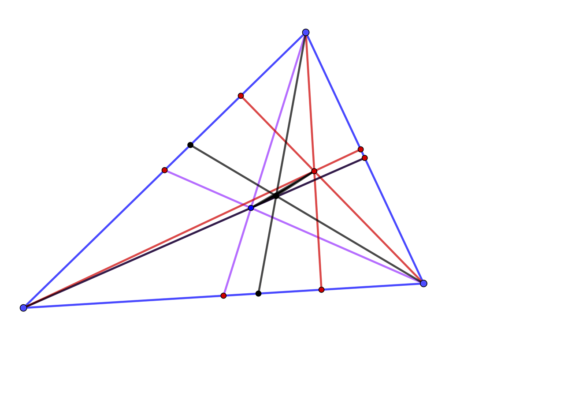
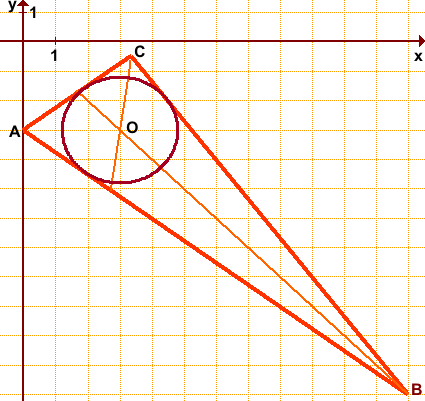Как найти точку пересечения биссектрис треугольника по координатам его вершин?
Как найти радиус вписанной в треугольник окружности по координатам его вершин?
Точка пересечения биссектрис треугольника является центром вписанной в этот треугольник окружности.
Эта точка равноудалена от сторон треугольника. Расстояние от точки пересечения биссектрис до сторон треугольника равно радиусу вписанной окружности.
Следовательно, все три задачи сводятся к нахождению точки пересечения биссектрис треугольника.
Для этого надо сначала составить уравнения биссектрис треугольника и найти точку их пересечения.
Пример.
Дан треугольник ABC с вершинами в точках A(0;-3), B(12;-12) и C(3,36;-0,48).
1) Найти точку пересечения биссектрис треугольника ABC.
2) Найти радиус вписанной в треугольник ABC окружности.
3) Составить уравнение вписанной в треугольник ABC окружности.
Решение:
1) Составим уравнения прямых, содержащих стороны треугольника.
Уравнение прямой, проходящей через две точки можно искать, например, в виде
Для прямой AB
Уравнение прямой AC:
Уравнение прямой BC:
Составим уравнение биссектрисы треугольника ABC, исходящей из угла B. Она образована прямыми AB и BC:
откуда уравнения биссектрис угла B: x-y-24=0 или x+y=0. Чтобы понять, которое из двух уравнений является биссектрисой внутреннего угла треугольника, следует подставить в уравнения координаты точек A и C. Поскольку они лежат по разные стороны от биссектрисы внутреннего угла B, то подстановка их координат в уравнение биссектрисы даёт числа разных знаков.
A(0;-3) и C(3,36;-0,48) в x-y-24=0: 0-(-3)-24<0; 3,36-(-0,48)-24<0. Получили числа одного знака, значит это уравнение не является биссектрисой внутреннего угла треугольника.
A(0;-3) и C(3,36;-0,48) в x+y=0: 0+(-3)<0, 3,36+(-0,48)>0. Получили числа разных знаков, x+y=0 — биссектриса угла B треугольника ABC.
Составим уравнение биссектрисы угла C. Угол C образован прямыми AC и BC, откуда
уравнения биссектрис угла C: 7x-y-24=0 и x+7y=0.
A(0;-3), B(12;-12) в 7x-y-24=0: 7·0-(-3)-24<0, 7·12-(-12)-24>0. Получили числа разных знаков, значит 7x-y-24=0 — уравнение биссектрисы внутреннего угла C.
Поскольку все три биссектрисы треугольника пересекаются в одной точке, третью биссектрису находить не требуется.
Точку пересечения биссектрис углов B и C найдём из системы уравнений
O(3;-3) — точка пересечения биссектрис треугольника ABC. Эта точка является центром вписанной в треугольник окружности.
2) Радиус вписанной в треугольник ABC окружности можно найти как расстояние от точки O до прямой AB, BC или AC. Найдем, например, расстояние от O до AB:
3) Чтобы найти уравнение вписанной в треугольник ABC окружности, в уравнение окружности подставляем координаты центра O(3;-3) и r=9/5:
План урока:
Точка пересечения биссектрис в треугольнике
Серединный перпендикуляр
Точка пересечения высот треугольника
Вписанная окружность
Описанная окружность
Построение вписанной и описанной окружности
Точка пересечения биссектрис в треугольнике
Напомним, что для каждой прямой и точки можно вычислить расстояние между ними. Оно представляет собой длину перпендикуляра, который из точки проведен к этой прямой.
Если есть пара прямых и одна точка, то можно определить расстояние от точки до каждой из прямых. В случае, когда эти расстояния одинаковы, точку называют равноудаленной от обеих прямых.
Например, на этом рисунке длины AВ и ВС одинаковы, а потому точка А – равноудаленная от прямых m и n.
Сформулируем важную теорему.
Для доказательства опустим из произвольно выбранной точки М, принадлежащей биссектрисе ∠AВС, расстояния МК и МL на AВ и ВС:
Сравним ∆ВКМ и ∆ВМL. Это два прямоугольных треуг-ка, у которых общая гипотенуза ВМ, а также одинаковы острые углы ∠МВL и ∠KBM (они одинаковы, ведь биссектриса по определению разбивает угол пополам). Тогда ∆BKM и ∆BLM равны, и отрезки КM и МС также одинаковы, ч. т. д.
Верно и обратное утверждение.
Для доказательства можно использовать тот же рисунок. Пусть точка М находится на одинаковом расстоянии от ВК и ВL. То есть КМ = МL. Тогда ∆ВКМ и ∆ВМL снова оказываются равными, но уже как прямоугольные треуг-ки с одинаковыми катетом и гипотенузой. Из равенства треуг-ков вытекает, что
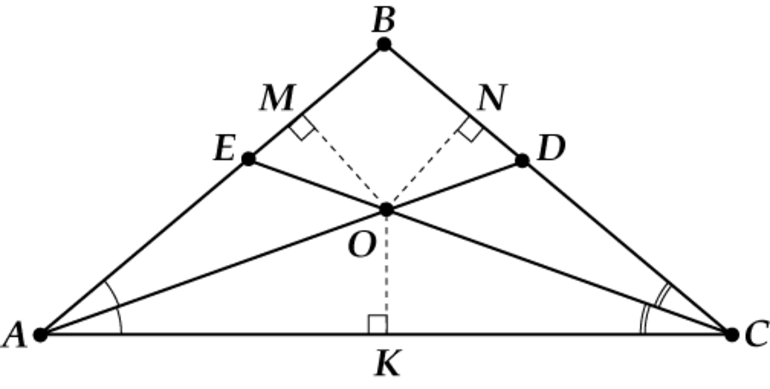
Действительно, если в ∆AВС построить биссектрисы ∠А и ∠В, то они должны будут пересечься в какой-нибудь точке О:
Опустим из О перпендикуляры на все стороны треуг-ка. Так как О принадлежит биссектрисе ∠А, то она находится на одинаковом расстоянии от АС и AВ, то есть
Из него следует, что О также находится на одном расстоянии от АС и ВС и потому принадлежит биссектрисе ∠С. Получается, что О – общая точка для всех трех биссектрис ∆AВС.
Серединный перпендикуляр
Введем новое понятие – серединный перпендикуляр.
На рисунке О – это середина AВ. Через нее проведена прямая m, образующая прямой угол с AВ. Тогда по определению m – это серединный перпендикуляр:
Рассмотрим две теоремы, которые связаны с серединным перпендикуляром и являются обратными друг для друга.
Сначала рассмотрим первое утверждение. Пусть точка М находится на серединном перпендикуляре, проведенному к AВ. Нам надо
Изучим∆АОМ и ∆ВОМ. Они прямоугольные, имеют одинаковые катеты АО и ОВ (ведь О – середина AВ) и общий катетОМ. Получается, что ∆АОМ и ∆ВОМ равны. Значит, одинаковы и отрезки АМ и МВ, ч. т. д.
Во второй теореме уже изначально известно, что
AM = MB
Надо доказать, что М принадлежит серединному перпендикуляру. Изучим∆АМВ, он равнобедренный, ведь АМ = МВ. Теперь из М опустим медиану МО на AВ. ∆АМВ – равнобедренный, поэтому эта медиана окажется также и высотой. Получается, что отрезок ОМ перпендикулярен AВ и одновременно делит его пополам. Значит, ОМ – это серединный перпендикуляр.
Из этих двух теорем вытекает важное утверждение:
Действительно, в ∆AВС проведем серединные перпендикуляры к сторонам треугольника AВ и АС:
Здесь N и K – середины сторон AN и AC, а О – точка пересечения серединных перпендикуляров в треугольнике. Так как О лежит на серединном перпендикуляре, проведенному к AВ, то справедливо равенство
AO = OB
Аналогично О равноудаленная от вершин А и С, ведь она лежит на серединном перпендикуляре, проведенному к АС:
AO = OC
В итоге можно составить двойное равенство:
OC = AO = OB
Оно показывает, что О также расположена на одном расстоянии от В и С. Отсюда вытекает, что она должна принадлежать серединному перпендикуляру, проведенному к ВС, ч. т. д.
Точка пересечения высот треугольника
Следующая теорема касается высот треуг-ка.
Для доказательства выполним такое построение – через вершины ∆AВС проведем прямые, которые будут параллельны сторонам ∆АВС. Они образуют новый ∆А1В1С1:
Из условий AВ||A1В1 и АС||А1С1 вытекает, что четырехуг-к АСА1В – это параллелограмм. Значит, у него одинаковы противоположные стороны:
Аналогично можно показать, что четырехуг-ки AВСВ1 и АСВС1 – также параллелограммы, откуда вытекают равенства:
Теперь обозначим на рисунке все отрезки, равные AВ, одной черточкой, отрезки, равные ВС – двумя чертами, в тремя черточками отметим те отрезки, равные АС:
Получается, что А, В и С являются серединами сторон А1В1, А1С1 и В1С1. Построим в ∆А1В1С1 серединные перпендикуляры. Они по определению будут проходить через середины А, В и С и при этом будут иметь общую точку О:
Заметим, что проведенные перпендикуляры будут также перпендикулярны сторонам исходного ∆AВС. Например, ОВ⊥А1С1 и А1С1|| АС, значит, ОВ⊥АС (прямая, перпендикулярная одной из двух параллельных прямых, будет перпендикулярна и второй прямой). Аналогично можно продемонстрировать, что АО⊥ВС, а СО⊥AВ. Другими словами, прямые АО, ВО и СО оказываются высотами, и при этом они пересеклись точке О. Так как ∆AВС был выбран произвольно, то получается, что в любом треуг-ке высоты пересекутся в одной точке, ч. т. д.
Ранее, изучая подобие треуг-ков, мы уже выяснили, что и медианы треуг-ка будут пересекаться в одной точке. В итоге можно сформулировать следующее утверждение:
Задание. На рисунке ∠MKN = 66°. Вычислите величину ∠FNO.
Решение. Судя по рисунку, в точке О пересекаются высоты MF и KE. Но тогда и прямая ON также должна быть высотой. Достроим рисунок с учетом этого факта:
Теперь на рисунке множество прямоугольных треуг-ков. Напомним, что у каждого из них острые углы в сумме составляют 90°. Например, в ∆MKF
Ответ: 24°.
Задание. В ∆AВС биссектрисы АА1 и ВВ1 пересеклись в точке М, причем ∠АМВ = 128°. Вычислите ∠МСВ1.
Решение. Изучим ∆АМВ. В сумме его углы должны составлять 180°:
Ясно, что МС – это биссектриса ∠АСВ, ведь она проходит через общую точку двух других биссектрис ∆AВС. То есть МС делит ∠АСВ пополам:
Задание. На рисунке RO = 20. Вычислите длину OK:
Решение. На рисунке видно, что OM и ON – это серединные перпендикуляры. Отсюда вытекает, что точка О равноудалена от ОР и OR:
OP = OR = 20
Теперь можно рассмотреть ∆РОК. Он прямоугольный, и в нем есть ∠30°. Напомним, что катет, лежащий против такого угла, вдвое короче гипотенузы:
OK = OP/2 = 20/2 = 10
Ответ: 10.
Вписанная окружность
Иногда в многоугольник можно вписать окруж-ть. Это значит, что возможно построить такую окруж-ть (ее именуют вписанной окружностью), которая будет касаться каждой стороны многоуг-ка (его в таком случае называют описанным около окружности многоуг-ком).
Для того чтобы, построить вписанную в многоуг-к окруж-ть, надо сначала определить, возможно ли вообще это сделать. Оказывается, что в треуг-к окруж-ть можно вписать всегда.
Действительно, построим произвольный ∆AВС и биссектрисы в нем. Они пересекутся в какой-нибудь точке О. Далее из О проведем перпендикуляры на стороны ∆AВС.
Эти перпендикуляры являются, по сути, расстояниями от О до сторон углов ∠А, ∠В и ∠С. По свойству биссектрисы они окажутся одинаковыми. Теперь проведем окруж-ть с центром в О, радиус которой будет равен длине этих перпендикуляров.
r = OK = OL = OM
Ясно, что точки M, L и K будут принадлежать окруж-ти, ведь они находятся на расстоянии R от ее центра. При этом отрезки OK, OM, OL будут радиусами. Заметим, что прямая AВ перпендикулярна радиусу OK, а потому является касательной. По той же причине ВС и АС также окажутся касательными. В итоге окруж-ть оказывается вписанной, ч. т. д.
В данном доказательстве мы не просто доказали, что для каждого треуг-ка существует вписанная окруж-ть, но и показали, как ее построить. Надо сначала провести биссектрисы углов, найти точку их пересечения (это и будет центр вписанной окруж-ти), после чего из этой точки надо опустить перпендикуляр на одну из сторон треуг-ка. Осталось лишь построить окруж-ть, радиус которой будет этот перпендикуляр. Заметим, что так как в треуг-ке есть только одна точка пересечения биссектрис, то и окруж-ть в треуг-к можно вписать лишь одну.
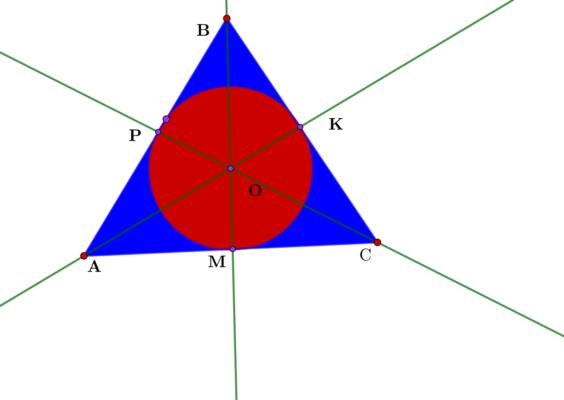
Ещё раз посмотрим на окружность, вписанную в треугольник:
Заметим, что радиусы OK, ОМ и ОL одновременно являются и высотами в ∆AВО, ∆АОС и ∆ВОС. Тогда через радиус можно выразить площади этих треуг-ков:
Сумма сторон AВ, АС и ВС – это периметр ∆AВС (его обозначают буквой Р), а потому можно записать, что
Эту формулу часто используют не для вычисления площади треуг-ка, а для нахождения радиуса вписанной окружности.
Задание. Найдите радиус окруж-ти, вписанной в равнобедренный треуг-к, основание которого имеет длину 20, а боковая сторона – 26.
Теперь надо найти его площадь. Для этого опустим на основание MN высоту KH, которая одновременно будет и медианой:
Отрезок HN будет вдвое короче MN:
Зная в ∆MKN высоту и основание, к которой она проведена, сможем найти его площадь:
Теперь запишем формулу площади, содержащую радиус вписанной окруж-ти, и найдем из нее этот радиус:
Ответ: 20/3.
Задание. В прямоугольный треуг-к, длина гипотенузы которого составляет 52, вписана окруж-ть радиусом 8. Вычислите периметр этого треуг-ка.
Решение. Проведем радиусы ОМ и ОК из центра окруж-ти к катетам:
Буквой N обозначим точку касания окруж-ти и гипотенузы. Сначала изучим четырехуг-к МОКС. В нем∠С – прямой, ведь ∆AВС – прямоугольный, а ∠ОМС и ∠ОКС также составляют 90°, так как образованы радиусом и касательной. Тогда и ∠МОК тоже должен быть прямым. Значит, МОКС – это квадрат, и его стороны одинаковы:
MO = OK = CK = MC
Заметим, что отрезки AN и AM одинаковы, ведь они представляют собой отрезки касательных, которые построены из одной точки:
AN = AM
Аналогично одинаковы ВК и BN:
BK = BN
Тогда периметр можно записать так:
Ответ: 120.
Задание. Вписанная в ∆AВС окруж-ть касается его сторон AВ, ВС и АС в точках Е, М и F. Известно, что АЕ = 4, СF = 6, МВ = 10. Определите периметр ∆AВС.
Решение. Заметим, отрезки касательных, проведенных к окруж-ти из одной точки, одинаковы, поэтому
Это позволяет найти каждую из сторон ∆AВС:
Ответ: 40.
В многоугольники, имеющие 4 и более вершины, вписать окруж-ть можно лишь в отдельных случаях. В частности, четырехуг-к должен для этого обладать особым свойством.
Действительно, пусть в четырехуг-к AВСD вписана окруж-ть. Тогда отрезки касательных, которые построены из точек А, В, С и D, будут одинаковыми.
Обозначим их маленькими буквами a, b, cи d:
Тогда стороны четырехуг-ка будут вычисляться так:
Действительно, пусть есть четырехуг-к AВСD, у которого
AD + BC = CD + AB (1)
Проведем биссектрисы ∠Aи ∠B, они пересекутся в некоторой точке О. Эта точка окажется равноудаленной от сторон AD, AB и ВС, то есть можно построить окруж-ть, которая коснется этих трех прямых. Докажем, что она также коснется и CD. Возможны три варианта:
1) СD вообще не пересекается с окруж-тью;
2) CD – секущая, и пересекается с окруж-тью в 2 точках;
3) CD – касательная.
Сначала рассмотрим первый вариант, когда СD и окруж-ть не имеют общих точек. Тогда можно провести касательную С’D’, параллельную CD:
Мы видим, что существует описанный четырехуг-к AВС’D’, а значит, суммы его противоположных сторон будут одинаковыми:
Мы получили, что в четырехуг-ке С’D’DC сторона CD равна сумме трех других сторон. Это невозможно, то есть мы получили противоречие. Значит, принятое нами предположение о том, что CD не имеет общих точек с окруж-тью, является ошибочным. С помощью аналогичных утверждений можно отбросить и вариант, согласно которому CD – это секущая. Остается один вариант, по которому СD – касательная, ч. т. д.
Задание. В четырехуг-к MCЕА вписана окруж-ть, причем МС = 5, СЕ = 10, АЕ = 8. Какова длина АМ?
Решение. Если в четырехуг-к можно вписать окруж-ть, то суммы его противоположных сторон одинаковы:
Рассмотрим частные случаи четырехуг-ков. Очевидно, что в ромб и квадрат вписать окруж-ть можно, ведь у них одинаковы все стороны, значит, одинаковы и суммы противоположных сторон. С другой стороны, если параллелограмм НЕ является ромбом, то есть его смежные стороны различны, то вписать в него окруж-ть не получится. Также ее нельзя вписать и в прямоугольник, если он НЕ является квадратом:
Ранее мы составили формулу, которая связывала периметр треуг-ка с его площадью и радиусом вписанной окруж-ти. Оказывается, она справедлива и для четырехуг-ка. Действительно, пусть есть произвольный описанный четырехуг-к AВСD. Соединим центр вписанной окруж-ти с вершинами, а также проведем из нее радиусы к точкам касания:
В результате мы разбили AВСD на ∆АОD, ∆DOC, ∆COВ и ∆АОВ, причем высотой для каждого из них являются радиусы длиной r. Тогда площади этих треуг-ков можно вычислить так:
Аналогичным образом эту формулу можно доказать и для пятиугольника, и для шестиугольника, и т. д.
Задание. В четырехуг-к AВСD, у которого стороны AB и CD соответственно составляют 13 и 8, вписана окруж-ть радиусом 5. Какова площадь AВСD?
Решение.
Мы можем найти сумму сторон AВ и CD:
AB + CD = 13 + 8 = 21
Так как в четырехуг-к вписана окруж-ть, то и сумма двух других сторон, AD и BC, будет такой же:
AD + BC = AB + CD = 21
Теперь можно вычислить и периметр AВСD:
P = AB + CD + AD + BC = 21 + 21 = 42
Осталось только применить формулу и рассчитать площадь:
Ответ: 105.
Задание. В квадрат вписана окруж-ть с радиусом 6. Какова площадь квадрата?
Решение. Проведем в окруж-ти радиусы, которые коснутся противоположных сторон квадрата:
В результате получится прямоугольник ВСНК. КН – диаметр окруж-ти, поэтому он вдвое длиннее радиуса:
KH = 6*2 = 12
В прямоугольнике противоположные стороны одинаковы, поэтому
BC = KH = 12
Но ВС – это сторона квадрата, площадь которого и надо найти. Для этого ВС надо возвести в квадрат:
S = BC2 = 122 = 144
Ответ: 144.
Описанная окружность
Возможна и ситуация, при которой не окруж-ть вписана в многоуг-к, а наоборот, многоуг-к в окруж-ть. В таком случае все его вершины будут лежать на окруж-ти.
Есть несколько важных теорем, касающихся описанных окружностей.
Для доказательства построим в произвольном ∆AВС серединные перпендикуляры. Они пересекутся в некоторой точке О:
Каждая точка, лежащая на серединном перпендикуляре, равноудалена от концов отрезка, к которому этот перпендикуляр проведен. Значит, и точка О равноудалена от вершин ∆AВС:
OA = OB = OC
Но тогда из О можно провести окруж-ть, на которой будут лежать точки А, В и С. Она как раз и окажется окружностью, описанной около треугольника. Так как серединные перпендикуляры пересекаются только в одной точке, то и окруж-ть около треуг-ка можно описать лишь одну.
Из теоремы следует важный вывод:
Действительно, три точки, не лежащие на прямой, образуют на плоскости треуг-к.Окруж-ть, проведенная через его вершины, по определению и будет описанной окруж-тью.
Задание. Около равнобедренного треуг-ка с основанием длиной 6 описана окруж-ть радиусом 5. Какова длина боковых сторон этого треуг-ка?
Решение: Проведем радиусы ОА, ОВ и ОС к вершинам вписанного треуг-ка, а на основание ВС опустим перпендикуляр:
Стоит обратить внимание, что точки А, О и Н лежат на одной прямой. Это высота, проведенная к основанию. Она же, по свойству равнобедренного треуг-ка, является медианой, то есть Н – середина ВС. Тогда ОН оказывается серединным перпендикуляром.
Сначала найдем ВН, он равен половине ВС:
BH = BC:2 = 6:2 = 3
Далее изучим ∆ОНВ. Он прямоугольный, то есть для него верна теорема Пифагора:
Задание. Выведите формулу, которая связывает длину стороны равностороннего треуг-ка с радиусом описанной окружности.
Решение. Обозначим буквой a сторону треуг-ка, а буквой R – радиус описанной окруж-ти. Также проведем один серединный перпендикуляр:
Так как ∆AВС – равносторонний, то все его углы, в частности, ∠AВС, составляют 60°.
Заметим, что ∆ВОС и ∆АОВ равны по трем одинаковым сторонам, поэтому
В четырехуг-к окруж-ть удается вписать не всегда. Для этого должно соблюдаться одно условие:
Действительно, пусть около четырехуг-ка ABCD описана окруж-ть:
Тогда вся окруж-ть может быть разбита на две дуги: ⋃ВАD и ⋃ВСD. Их сумма составляет 360°:
Аналогично доказывается утверждение и для другой пары противоположных углов, ∠ADC и ∠ABC.
Обратное утверждение также справедливо:
Докажем эту теорему методом от «противного». Пусть есть четырехуг-к AВСD, у которого сумма противоположных углов составляет 180°, но вокруг него нельзя описать окруж-ть. Тогда проведем окруж-ть через любые три его вершины. Четвертая вершина (пусть это будет D) не может оказаться на окруж-ти. То есть она находится либо внутри окруж-ти, либо вне ее. Сначала рассмотрим случай, когда точка оказывается внутри окруж-ти:
Продолжим прямые AD и CD до пересечения окруж-ти в точках А’ и C’, а потом выберем произвольную точку D’ на окруж-ти между ними.
Теперь сравним ∆АСD и ∆АСD’. У обоих сумма углов одинакова и составляет 180°:
Получается, что ∠D и ∠D’ должны быть равны, но ранее мы показали, что ∠D больше. Это противоречие означает, что точка D не может быть внутри окруж-ти. Аналогичным образом рассматривается второй случай, когда D лежит вне окруж-ти:
Здесь, рассматривая ∆АСD и АСD’, можно показать, что ∠D меньше, чем ∠D’. Однако они должны быть равны друг другу, ведь в сумме с∠В должны давать 180°.
Задание. В окруж-ть вписан четырехуг-к AВСD, причем∠А составляет 110°, а ∠В – 62°. Найдите два других угла четырехуг-ка.
Решение.
Здесь надо просто использовать тот факт, что противоположные углы в AВСD должны давать в сумме 180°:
Задание. Докажите, что если трапеция вписана в окруж-ть, то она равнобедренная.
Решение.
Пусть в окруж-ть вписана трапеция AВСD, причем AD и ВС– ее основания. Тогда∠А и ∠В – это односторонние углы при параллельных прямых ВС и AD и секущей AВ, и в сумме они дают 180°. Но так как AВСD вписана в окруж-ть, то и ее противоположные углы, ∠А и ∠С, также должны составлять в сумме 180°:
∠А + ∠B = 180°
∠А + ∠C = 180°
Естественно, эти равенства могут одновременно справедливыми только в том случае, если∠В и ∠С одинаковы. Они являются углами при основании трапеции. Если они одинаковы, то трапеция – равнобедренная (это признак равнобедренной трапеции).
Построение вписанной и описанной окружности
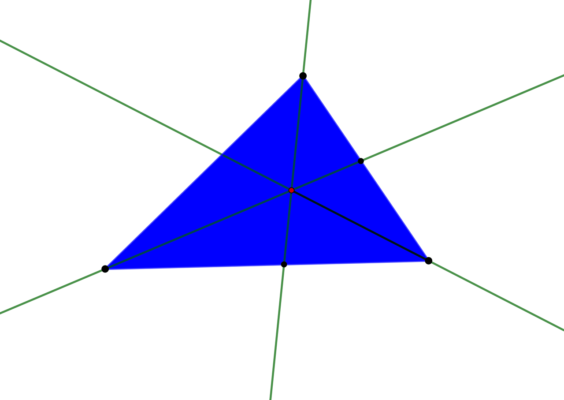
Дополнительно уточним, как выполнить построение вписанной окружности либо описанной окруж-ти. Мы уже говорили, в центр вписанной окружности в треуг-ке – это центр пересечения его биссектрис, ведь он равноудален от сторон. То же самое относится и к многоуг-кам. Вписанная окруж-ть равноудалена от его сторон, поэтому будет лежать на биссектрисе каждого из углов многоуг-ка. При этом строить биссектрисы всех углов не нужно, достаточно выбрать любые два из них. Найдя таким способом центр вписанной окруж-ти, из нее надо опустить перпендикуляр на любую сторону – он и будет радиусом окруж-ти:
При построении описанной окружности нужно помнить, что ее центр описанной окруж-ти находится уже в той точке, где пересекаются серединные перпендикуляры. Снова достаточно провести только два перпендикуляра:
Итак, мы узнали про вписанные и описанные окруж-ти, как определять их центры, и какими свойствами обладают вписанные и описанные многоуг-ки. Это поможет решить ряд задач на экзаменах, в том числе и на ЕГЭ.
Точка пересечения биссектрис — свойства, теорема и соотношения
Общие сведения
Треугольник — геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и отрезков, соединяющих их. Точки имеют другое название — вершины. Обозначается треугольник символом Δ, после которого идут 3 латинских буквы. Например, ΔMNO. Допускается использовать и русские литеры, но злоупотреблять этим не стоит.
В высших учебных заведениях преподаватели требуют от студентов международное обозначение. Кроме того, большинство программных продуктов и онлайн-сервисов воспринимают только латинские символы.
Существует определенная классификация Δ, на основании которой доказываются теоремы, выводятся формулы, свойства и решаются задачи. В последнем случае следует правильно производить идентификацию, чтобы избежать ошибок при расчетах.
Классификация треугольников
Необходимо отметить, что Δ различаются между собой по некоторым критериям.
Они бывают нескольких типов:
- Произвольные.
- Прямоугольные.
- Равнобедренные.
- Равносторонние.
- Тупоугольные.
- Остроугольные.
В первом случае стороны фигуры не равны между собой. Чтобы идентифицировать прямоугольный треугольник, необходимо рассмотреть его углы. Если один из них является прямым (равен 90 градусам), такая фигура называется прямоугольной. В третьем виде основным критерием считается наличие двух, равных между собой сторон.
В равностороннем треугольнике все стороны равны между собой. Математики его называют «правильным». Он обладает важным свойством — вокруг него можно описать окружность. Пятый тип определяет наличие тупого угла, градусная мера которого больше 90. Если фигура является остроугольной, это значит, что все 3 его угла меньше 90, т. е. являются острыми.
Один треугольник может относиться к нескольким типам. Например, прямоугольный Δ может быть равнобедренным на основании свойства геометрии: если Δ является равнобедренным, то углы (∠), образованные боковыми сторонами с основанием, равны между собой. В этом случае их градусные меры эквивалентны 45, поскольку сумма ∠ любого Δ составляет 180. Следовательно, 180 — 90 = 2k, где неизвестная величина «к» соответствует углу при основании.
Решая уравнение, можно получить искомое значение угла: k = 45. Исходя из вычислений, треугольник является прямоугольным и равнобедренным.
Дополнительные элементы
У любого Δ существуют определенные дополнительные элементы, необходимые при построении чертежей или схематических рисунков, доказательства теорем и решения задач по геометрии.
К ним относятся:
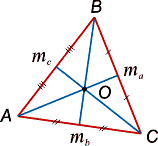
Биссектриса — отрезок (прямая), проходящий через вершину Δ и делящий угол на 2 равные части. Медиана — единственный отрезок для каждой вершины, соединяющий ее с серединой стороны, на которую он опущен.
Высотой является перпендикуляр, опущенный из вершины на противоположную сторону.
В равнобедренном и равностороннем треугольниках биссектриса является медианой и высотой. В последнем случае их можно провести всего 3.
Однако в произвольном Δ — по 3, т. е. 3 высоты, 3 медианы и 3 биссектрисы.
Теорема о биссектрисах
Теорема о биссектрисах треугольника звучит таким образом: в любом Δ биссектрисы пересекаются только в одной точке — инцентре фигуры. Для доказательства нужно построить произвольный ΔКLМ, а затем следовать по такому алгоритму:
- Провести биссектрисы LN (к стороне КМ) и КU (к LM).
- На рисунке видно, что LN и KU пересекаются в одной точке (W).
- Доказывать теорему следует от противного — пусть биссектрисы не пересекаются.
- Если прямые не пересекаются, значит, они параллельны, т. е. LN || KU. Следовательно, KL — секущая.
- Сумма градусных мер односторонних углов эквивалентна 180, т. е. (∠К/2) + (∠L/2) = 180 (свойство параллельных прямых и секущей).
- Из соотношения в 5 пункте следует, что сумма ∠К + ∠L = 360.
- Сумма углов Δ эквивалентна 180. Однако при сложении значений двух ∠ величина их суммы больше 180. Следовательно, биссектрисы треугольника пересекаются в одной точке.
Необходимо доказать, что третья биссектриса (МV), проведенная из вершины М, проходит через точку W. Это делается таким образом:
- Из W следует опустить перпендикуляры на стороны Δ: WG, WF и WE.
- Нужно рассмотреть 2 ΔGBW и ΔBFW, которые являются прямоугольными, поскольку WG и WF — перпендикуляры, а BW — общая сторона. Углы ∠GBW и ∠WВF равны, т. к. их образует биссектриса LN (общий угол будет делиться на 2 равные части). Следовательно, ΔGBW и ΔBFW равны.
- Из равенства ΔGBW и ΔBFW получается отношение WG и WF.
- Аналогично доказывается равенство сторон WG и WЕ.
Далее следует рассмотреть ∠М. Следовательно, что координата точки W равноудалена от вершины М. На основании признака биссектрисы, W лежит на МV, поскольку W — точка пересечения биссектрис треугольника КLМ. Утверждение доказано.
Свойства и соотношения
На основании теоремы о биссектрисах Δ были получены некоторые важные свойства, которые рекомендуется применять при решении задач и доказательства других утверждений:
- Центр вписанной окружности соответствует точке их пересечения.
- Точка при пересечении делит биссектрису по такому соотношению: отношение суммарного значения прилежащих к противолежащей стороне.
- Угол между биссектрисами двух смежных углов является прямым.
- В равнобедренном Δ равны только 2 биссектрисы, а в равностороннем — 3. Кроме того, она является медианой и высотой.
При решении задач нужно находить их длину (L).
Для удобства необходимо обозначить стороны таким образом: КМ = d, КL = e и LМ = f, чтобы воспользоваться следующими формулами через известные параметры треугольника:
- Все стороны: Lm = [2 * (d * e * p * (p — f))^(½)] / (d + e), Lк = [2 * (d * f * p * (p — e))^(½)] / (d + f) и Ll = [2 * (d * f * p * (p — e))^(½)] / (d + f). Параметр «р» — полупериметр, т. е. р = (d + e + f) / 2.
- Стороны и угол: Lm = (2 * d * e * cos (∠M)) / (d + e), Lk = (2 * d * f * cos (∠K)) / (d + f) и Ll = (2 * f * e * cos (∠L)) / (f + e).
Соотношения позволяют найти не только длины Lk, Lm и Ll, но и другие параметры треугольников. Следует отметить, что углы во второй группе формул соответствуют биссектрисам, исходящим из них.
Таким образом, для решения задач на нахождение длины биссектрис необходимо знать теорию, доказательство теоремы, свойства, а также основные соотношения.
Точка пересечения биссектрис
Как найти точку пересечения биссектрис треугольника по координатам его вершин?
Как найти радиус вписанной в треугольник окружности по координатам его вершин?
Точка пересечения биссектрис треугольника является центром вписанной в этот треугольник окружности.
Эта точка равноудалена от сторон треугольника. Расстояние от точки пересечения биссектрис до сторон треугольника равно радиусу вписанной окружности.
Следовательно, все три задачи сводятся к нахождению точки пересечения биссектрис треугольника.
Для этого надо сначала составить уравнения биссектрис треугольника и найти точку их пересечения.
Дан треугольник ABC с вершинами в точках A(0;-3), B(12;-12) и C(3,36;-0,48).
1) Найти точку пересечения биссектрис треугольника ABC.
2) Найти радиус вписанной в треугольник ABC окружности.
3) Составить уравнение вписанной в треугольник ABC окружности.
1) Составим уравнения прямых, содержащих стороны треугольника.
Уравнение прямой AC:
Уравнение прямой BC:
Составим уравнение биссектрисы треугольника ABC, исходящей из угла B. Она образована прямыми AB и BC:
откуда уравнения биссектрис угла B: x-y-24=0 или x+y=0. Чтобы понять, которое из двух уравнений является биссектрисой внутреннего угла треугольника, следует подставить в уравнения координаты точек A и C. Поскольку они лежат по разные стороны от биссектрисы внутреннего угла B, то подстановка их координат в уравнение биссектрисы даёт числа разных знаков.
A(0;-3) и C(3,36;-0,48) в x-y-24=0: 0-(-3)-24 0. Получили числа разных знаков, x+y=0 — биссектриса угла B треугольника ABC.
Составим уравнение биссектрисы угла C. Угол C образован прямыми AC и BC, откуда
уравнения биссектрис угла C: 7x-y-24=0 и x+7y=0.
A(0;-3), B(12;-12) в 7x-y-24=0: 7·0-(-3)-24 0. Получили числа разных знаков, значит 7x-y-24=0 — уравнение биссектрисы внутреннего угла C.
Поскольку все три биссектрисы треугольника пересекаются в одной точке, третью биссектрису находить не требуется.
Точку пересечения биссектрис углов B и C найдём из системы уравнений
O(3;-3) — точка пересечения биссектрис треугольника ABC. Эта точка является центром вписанной в треугольник окружности.
2) Радиус вписанной в треугольник ABC окружности можно найти как расстояние от точки O до прямой AB, BC или AC. Найдем, например, расстояние от O до AB:
3) Чтобы найти уравнение вписанной в треугольник ABC окружности, в уравнение окружности подставляем координаты центра O(3;-3) и r=9/5:
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Пример задачи
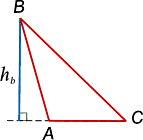
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
Точка пересечения биссектрис треугольника

4.6
Средняя оценка: 4.6
Всего получено оценок: 135.
4.6
Средняя оценка: 4.6
Всего получено оценок: 135.
В треугольнике есть три характерные линии: высоты, медианы и биссектрисы. Для каждой из этих линий есть своя точка пересечения, характеризующая треугольник. Первой всегда изучают точку пересечения биссектрис, потому что именно она дает представление о взаимосвязи величин треугольника и связанных с ним окружностей.
Определение
Точка соединения биссектрис это одна из самых проблемных точек. Она ведет к пониманию вписанных и описанных фигур, восприятие которых очень затруднено. Приходится думать не только о треугольнике, а еще и об окружностях, вписанной и описанной, что затрудняет решение задачи.
Но с другой стороны, значения радиусов вписанной и описанной окружности фигурирует во многих формулах, что позволяет упростить решение многих задач. Но для начала разберемся, что такое вписанная и описанная окружность, а потом узнаем, как это связано с точкой пересечения биссектрис и связано ли вообще.
В произвольном остроугольном треугольнике характерные точки не совпадают, а соединив их можно получить золотое сечение треугольника, для правильного треугольника золотое сечение является точкой. В равнобедренном треугольнике золотое сечение становится линией.
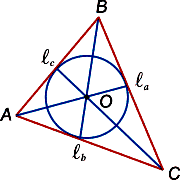
Вписанная окружность, это окружность, которая касается каждой из сторон треугольника.
Центр такой окружности называется инцентром треугольника. При этом, инцетр, или точка пересечения биссектрис тупоугольного треугольника всегда находится внутри треугольника, в отличие от высот.
Расстояние от инцентра до каждой из сторон одинаково и является радиусом вписанной окружности. Треугольник в таком случае будет считаться описанным вокруг окружности.
Описанной окружностью считается окружность, касающаяся каждой из вершин треугольника. То есть, каждая вершина должна входить в границу окружности. Треугольник в этом случае наоборот будет считаться вписанным, а расстояние от вершин треугольника до центра окружности будет всегда одинаковым и равным радиусу описанной окружности.
Теоремы о точке пересечения биссектрис
Теорема, на самом деле, одна, но доказательство разбито на две части. Формулировка звучит так: биссектрисы треугольника пересекаются в одной точке и эта точка является центром вписанной окружности.
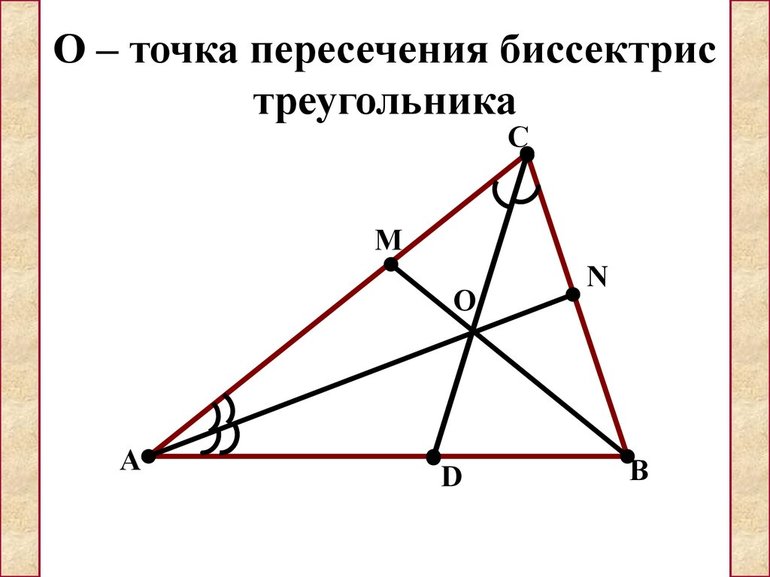
Сначала докажем, что три биссектрисы пересекаются в одной точке. Для этого в треугольнике АВС проведем биссектрисы ВМ, СР и АК. Точку пересечения обозначим О. Тогда рассмотрим каждую биссектрису в отдельности. Для биссектрисы АК расстояния до сторон треугольника а и в, должны быть одинаковы. Для биссектрисы СР расстояния с и а должны быть одинаковы. Для биссектрисы ВМ расстояния в и с должны быть одинаковы. Отрезки а, в и с равны между собой по свойству биссектрисы: любая геометрическая точка на биссектрисе равноудалена от сторон угла.
А точка равноудаленная от каждой из сторон может быть только одна. Достаточно попробовать поставить точку пересечения в другом месте и сразу станет заметно, что условие не соблюдается, что невозможно.
Мы уже сказали, что в треугольнике только одна точка может быть равноудалена от всех сторон. Это означает, что окружность с центром в этой точке будет вписана в треугольник, так как радиус этой окружности будет перпендикулярен стороне треугольника. Теперь докажем, что в треугольнике может быть только одна вписанная окружность. Если точку о переместить в любое другое место треугольника и опустить перпендикуляры на стороны, то станет ясно, что перпендикуляры не равны между собой, а значит в этой точке центр находиться не может. Что и требовалось доказать.
Что мы узнали?
Мы узнали о точке пересечения биссектрис треугольника, выделили и доказали две части теоремы. Доказали, что в треугольнике может быть только одна вписанная окружность и узнали о золотом сечении треугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Emil Marozav
10/10
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 135.
А какая ваша оценка?
Треугольник
– многоугольник с тремя сторонами, или
замкнутая ломаная линия с тремя звеньями,
или фигура, образованная тремя отрезками,
соединяющими три точки, не лежащие на
одной прямой (см.
рис. 1).
Рис. 1.
Вершины
– точки A,
B, и C;
Стороны
– отрезки a = BC, b = AC и c = AB, соединяющие
вершины;
Углы
– α , β, γ образованные тремя парами
сторон. Углы часто обозначают так же,
как и вершины, – буквами A, B и C.
Угол, образованный
сторонами треугольника и лежащий в его
внутренней области, называется внутренним
углом, а смежный к нему является смежным
углом треугольника (2, стр. 534).
Высоты, медианы, биссектрисы и средние линии треугольника
Кроме основных
элементов в треугольнике рассматривают
и другие отрезки, обладающие интересными
свойствами: высоты, медианы, биссектрисы
исредние
линии.
Высота
Высоты треугольника
– это перпендикуляры, опущенные из
вершин треугольника на противоположные
стороны.
Для построения
высоты необходимо выполнить следующие
действия:
1) провести прямую,
содержащую одну из сторон треугольника
(в случае, если проводится высота из
вершины острого угла в тупоугольном
треугольнике);
2) из вершины,
лежащей напротив проведенной прямой,
провести отрезок из точки к этой прямой,
составляющий с ней угол 90 градусов.
Рис. 2.
Точка пересечения
высоты со стороной треугольника называется
основанием
высоты
(см. рис. 2).
Свойства высот треугольника
-
В прямоугольном
треугольнике высота, проведенная из
вершины прямого угла, разбивает его на
два треугольника, подобные исходному
треугольнику. -
В остроугольном
треугольнике две его высоты отсекают
от него подобные треугольники. -
Если треугольник
остроугольный, то все основания высот
принадлежат сторонам треугольника, а
у тупоугольного треугольника две высоты
попадают на продолжение сторон. -
Три высоты в
остроугольном треугольнике пересекаются
в одной точке и эту точку называют
ортоцентром
треугольника.
Медиана
Медианы (от
лат. mediana
– «средняя»)
– это отрезки, соединяющие вершины
треугольника с серединами противолежащих
сторон (см. рис. 3).
Для построения
медианы необходимо выполнить следующие
действия:
1) найти середину
стороны;
2)соединить точку,
являющуюся серединой стороны треугольника,
с противолежащей вершиной отрезком.
Рис. 3.
Свойства
медиан треугольника
-
Медиана
разбивает треугольник на два треугольника
одинаковой площади. -
Медианы
треугольника пересекаются в одной
точке, которая делит каждую из них в
отношении 2:1, считая от вершины. Эта
точка называется
центром
тяжести треугольника.
Весь
треугольник разделяется своими медианами
на шесть равновеликих треугольников.
Биссектриса
Биссектрисами
(от лат. bis
– дважды» и seko
– рассекаю) называют заключенные внутри
треугольника отрезки прямых, которые
делят пополам его углы (см. рис. 4).
Для построения
биссектрисы необходимо выполнить
следующие действия:
1) построить луч,
выходящий из вершины угла и делящий его
на две равные части (биссектрису угла);
2) найти точку
пересечения биссектрисы угла треугольника
с противоположной стороной;
3) выделить отрезок,
соединяющий вершину треугольника с
точкой пересечения на противоположной
стороне.
Рис. 4.
Свойства
биссектрис треугольника
-
Биссектриса угла
треугольника делит противоположную
сторону в отношении, равном отношению
двух прилежащих сторон. -
Биссектрисы
внутренних углов треугольника
пересекаются в одной точке. Это точка
называется центром вписанной окружности. -
Биссектрисы
внутреннего и внешнего углов
перпендикулярны. -
Если биссектриса
внешнего угла треугольника пересекает
продолжение противолежащей стороны,
то ADBD=ACBC. -
Биссектрисы одного
внутреннего и двух внешних углов
треугольника пересекаются в одной
точке. Эта точка — центр одной из трех
вневписанных окружностей этого
треугольника. -
Основания биссектрис
двух внутренних и одного внешнего углов
треугольника лежат на одной прямой,
если биссектриса внешнего угла не
параллельна противоположной стороне
треугольника. -
Если биссектрисы
внешних углов треугольника не параллельны
противоположным сторонам, то их основания
лежат на одной прямой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #