Как найти точку пересечения отрезка с плоскостью - Исправление недочетов и поиск решений вместе с Examum.ru

Определение точки пересечения прямой с плоскостью

Для
определения точки пересечения прямой
с плоскостью пользуемся следующим
алгоритмом: прямую заключаем во
вспомогательную плоскость, находим
линию пересечения этих двух плоскостей
(заданной и вспомогательной), и линия
пересечения плоскостей в пересечении
с заданной прямой даст искомую точку.
Последним этапом в построении является
определение видимости прямой при помощи
конкурирующих точек.

Пример1.
Плоскость задана следами (рис.70)

Рис.70

1.
Для построения точки пересечения прямой
_l
с плоскостью необходимо через прямую
провести вспомогательную плоскость
частного положения, например,
фронтально-проецирующую βπ₂,
_l»f_оβ,
f_оβ
– собирающий след, h_оβх
(рис.71).

Рис.71

2.
Строим линию пересечения MN
заданной и вспомогательной плоскости
М’=h_оα∩
h_оβ,
N»=
f_оβ∩
f_оα
(рис.72).

Рис.72

3.
Определяем точку пересечения К
заданной прямой l
с линией пересечения MN.
К’=М’N’∩l ‘, К»
– в пересечении линии проекционной
связи, проведенной из К’
и l ».

4.
Видимость прямой l
в случае задания плоскости следами не
определяем.

Пример
2. Пересечение прямой с проецирующей
плоскостью (рис.73).

При
построении точки пересечения прямой с
проецирующей плоскостью задача
упрощается, т.к. одна из проекций искомой
точки будет лежать на собирающем следе.
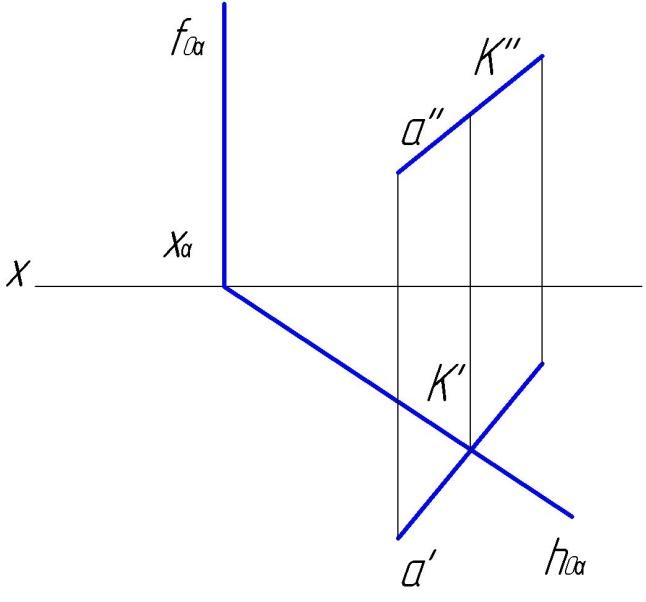
На рис.73 дана горизонтально-проецирующая
плоскость. Искомая точка К
будет одновременно принадлежать
плоскости α и прямой а.

Рис.73

Пример
3.
Плоскость
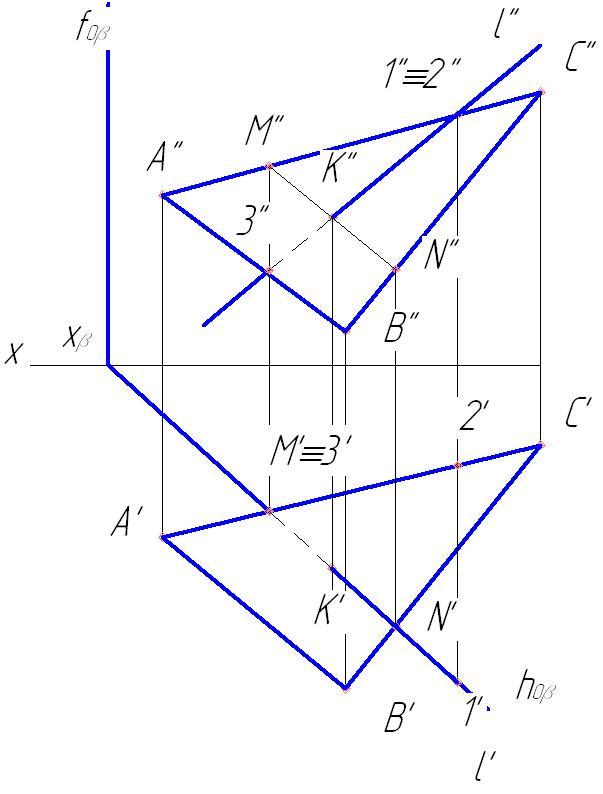
задана плоской фигурой (рис.74).

Рис.74

Через
прямую
l
проводим вспомогательную плоскость
частного положения, например,
горизонтально-проецирующую βπ₁.l‘
h_оβ,
h_оβ
– собирающий след, f_оβх
(рис.75).

Рис.75

2.
Строим линию пересечения MN
заданной и вспомогательной плоскостей.
М’=А’С’∩
hоβ М»А»С»
и N’=В’С’∩ hоβ N»В»С»
(рис. 76).

3.
Строим точку пересечения К
заданной прямой l
с линией пересечения МN.
К»= М»N»∩l». К’
находится в пересечении линии проекционной
связи, проведенной из К»
и М’N’.

4.
Определяем видимость прямой относительно
ΔАВС
с помощью конкурирующих точек.

Определяем
видимость относительно плоскости π₂
.Отметим фронтальную проекцию 1»
совпадающую с 2».
Горизонтальную проекцию 2′
отметим на А’С’,
а 1′
на l’.
Горизонтальная проекция 1′
лежит перед 2′,
следовательно, фронтальная проекция
2»
не видима относительно π₂.
Точка 1
лежит на прямой l, она видима на π₂,
следовательно, фронтальная проекция
l»
от 1″2» до К»
видима, в точке К»
видимость меняется на противоположную.

Определим
видимость прямой l
относительно плоскости π₁.
Отметим горизонтальную проекцию 3′,
совпадающую с горизонтальной проекцией
М’.
М»А»С»
уже отмечена, 3»l’‘.
Фронтальная проекция М»
лежит выше фронтальной проекции 3»,
следовательно, точка М
видима относительно π₁.
Точка 3
лежит на l,
следовательно, от М’≡3′
до
К’,
горизонтальная проекция l’
невидима. В горизонтальной проекции К’
видимость
меняется на противоположную. За границами
ΔАВС
прямая l
везде
видима.

Рис.76

Взаимное расположение прямых линий и плоскостей

Прямые
и плоскости могут быть параллельны или
перпендикулярны друг другу.

Параллельность
прямой и плоскости.

Прямая
параллельна плоскости, если она
параллельна прямой, лежащей в этой
плоскости.

Плоскость
задана ΔАВС.
Через (∙)D
провели прямую l
. Прямая l
|| ВС
(рис.77).

Рис.77

Параллельность
плоскостей

Две
плоскости параллельны между собой, если
две пересекающиеся прямые одной плоскости
параллельны двум пересекающимся прямым
другой плоскости.

Плоскость
задана двумя параллельными прямыми а
и b.
В этой плоскости проведем прямую 12.

Через
(∙)К
проведем две пересекающиеся прямые l
и n.
Прямая а
|| l,
прямая 12
|| n.
Эти две плоскости параллельны (рис.78).

Рис.78

Перпендикулярность
прямой и плоскости.

Прямая
перпендикулярна плоскости, если она
перпендикулярна двум пересекающимся
прямым, лежащим в этой плоскости. А так
как прямой угол, у которого одна из
сторон параллельна плоскости проекций,
проецируется ортогонально на эту
плоскость в прямой угол, то, следовательно,
горизонтальная проекция перпендикуляра
к плоскости перпендикулярна к
горизонтальной проекции горизонтали,
а фронтальная проекция — к фронтальной
проекции фронтали.

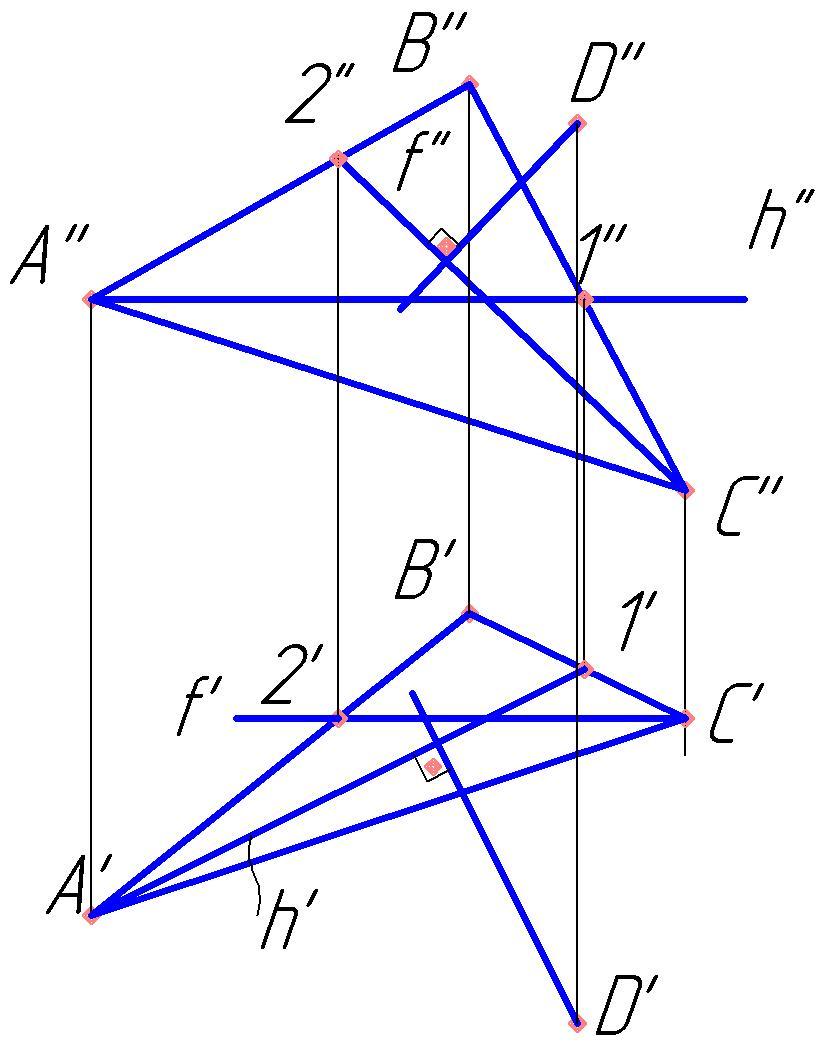
На
рис.79 показано построение прямой,
проведенной из точки D
(D’, D»)
перпендикулярно плоскости ΔАВС.
Прямая l перпендикулярна плоскости α,
если l’
┴ h ‘(h_0α),
l»┴ f» (f_0α).

Рис.79

На
рис.80 показано построение ┴ из (•) D
к плоскости, заданной следами.

Рис.80

Соседние файлы в папке Компьютерная графика

#
#
15.03.20153.99 Mб11Геометрическое черчение учебно-методическое пособие.wbk
#

Источник

3.7. Пересечение прямой и плоскости

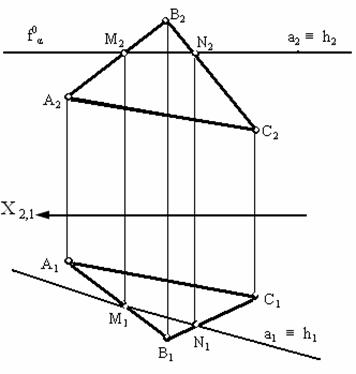
Линия пересечения двух плоскостей – прямая линия. Рассмотрим сначала частный случай (рис. 3.9), когда одна из пересекающихся плоскостей параллельна горизонтальной плоскости проекций (α π₁, f⁰_α Х). В этом случае линия пересечения а, принадлежащая плоскости α, будет также параллельна плоскости π₁, (рис. 3.9. а), т. е. будет совпадать с горизонталью пересекающихся плоскостей (а ≡ h).

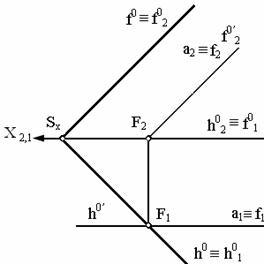
Если одна из плоскостей параллельна фронтальной плоскости проекций (рис. 3.9. б), то линия пересечения а, принадлежащая этой плоскости, будет параллельна плоскости π₂ и будет совпадать с фронталью пересекающихся плоскостей (а ≡ f).

Рис. 3.9. Частный случай пересечения плоскости общего положения с плоскостями: а – горизонтального уровня; б – фронтального уровня

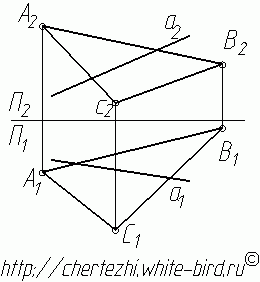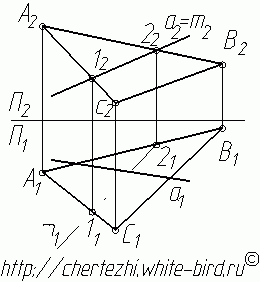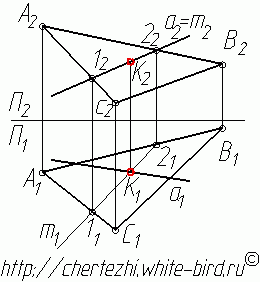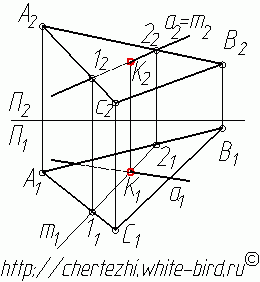
Пример построения точки пересечения (К) прямой а (АВ) с плоскостью α (DEF) показан на рис. 3.10. Для этого прямая а заключена в произвольную плоскость β и определена линия пересечения плоскостей α и β.

В рассматриваемом примере прямые АВ и MN принадлежат одной плоскости β и пересекаются в точке К, а так как прямая MN принадлежит заданной плоскости α (DEF), то точка К является и точкой пересечения прямой а (АВ) с плоскостью α. (рис. 3.11).

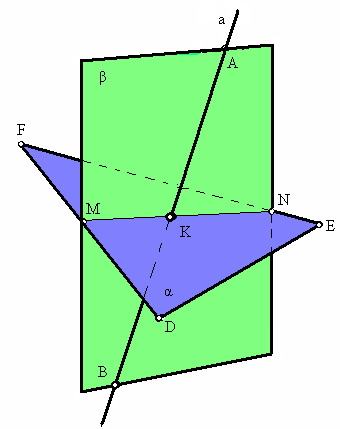
Рис. 3.10. Построение точки пересечения прямой с плоскостью

Для решения подобной задачи на комплексном чертеже необходимо уметь находить точку пересечения прямой общего положения с плоскостью общего положения.

Рассмотрим пример нахождения точки пересечения прямой АВ c плоскостью треугольника DEF представленный на рис. 3.11.

Для нахождения точки пересечения через фронтальную проекцию прямой А₂В₂ проведена фронтально-проецирующая плоскость β которая пересекла треугольник в точках M и N. На фронтальной плоскости проекций (π₂) эти точки представлены проекциями M₂,N₂. Из условия принадлежности прямой плоскости на горизонтальной плоскости проекций (π₁) находятся горизонтальные проекции полученных точек M₁ N₁. В пересечении горизонтальных проекций прямых А₁В₁ и M₁N₁ образуется горизонтальная проекция точки их пересечения (К₁). По линии связи и условиям принадлежности на фронтальной плоскости проекций находится фронтальная проекция точки пересечения (К₂).

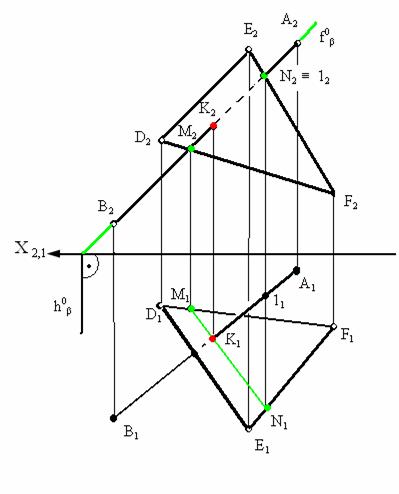
Рис. 3.11. Пример определения точки пересечения прямой и плоскости

Видимость отрезка АВ относительно треугольника DEF определена методом конкурирующих точек.

На плоскости π₂ рассмотрены две точки NEF и 1АВ. По горизонтальным проекциям этих точек можно установить, что точка N расположена ближе к наблюдателю (Y_N>Y₁ ), чем точка 1 (направление луча зрения параллельно S). Следовательно, прямая АВ, т. е. часть прямой АВ (К₁) закрыта плоскостью DEF на плоскости π₂(ее проекция К₂1₂ показана штриховой линии). Аналогично установлена видимость на плоскости π₁.

Вопросы для самоконтроля

1) В чем заключается сущность метода конкурирующих точек?

2) Какие свойства прямой вы знаете?

3) Каков алгоритм определения точки пересечения прямой и плоскости?

4) Какие задачи называются позиционными?

5) Сформулируйте условия принадлежности прямой плоскости.

Источник

Построение точки пересечения прямой и плоскости

Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h_0α, f_0α.

Алгоритм

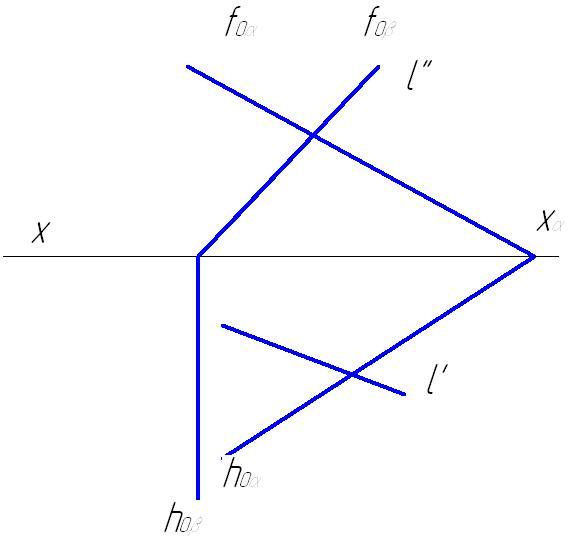
Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h_0γ, f_0γ.
Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B’ = h_0α ∩ h_0γ, A» = f_0α ∩ f_0γ. Точки A’ и B» лежат на оси x, их положение определяется по линиям связи.
Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K’ = a’ ∩ A’B’. Фронтальная проекция K» лежит на прямой a».

Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами.

Видимость прямой a относительно плоскости α. Метод конкурирующих точек

Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A» и С» совпадают, но при этом т. A и С удалены от плоскости проекций П₂на разное расстояние.
Найдем горизонтальные проекции A’ и C’. Как видно на рисунке, точка C’ удалена от плоскости П₂ на большее расстояние, чем т. A’, принадлежащая пл. α. Следовательно, участок прямой а», расположенный левее точки K», будет видимым. Участок a» правее K» является невидимым. Отмечаем его штриховой линией.
Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D’ и E’ совпадают, но при этом т. D и E удалены от плоскости П₁на разное расстояние.
Определим положение фронтальных проекций D» и E». Как видно на рисунке, точка D», находящаяся в пл. α, удалена от плоскости П₁ на большее расстояние, чем т. E», принадлежащая прямой a. Следовательно, участок а’, расположенный правее точки K’, будет невидимым. Отмечаем его штриховой линией. Участок a’ левее K’ является видимым.

Дополнительные материалы:

Построение линии пересечения двух плоскостей
Способы задания плоскости на чертеже

Источник

Пересечение прямой линии с плоскостью. Определение видимости прямой

6 февраля, 2014 Анна Веселова

Здравствуйте друзья! Сегодня разбираем тему из начертательной геометрии – пересечение прямой линии с плоскостью и определение видимости прямой.

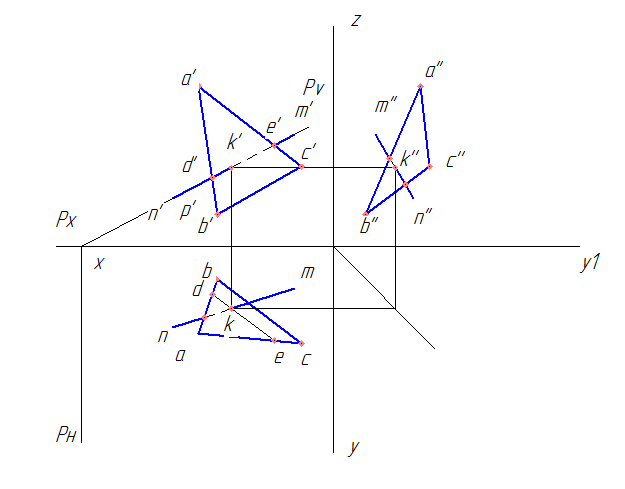
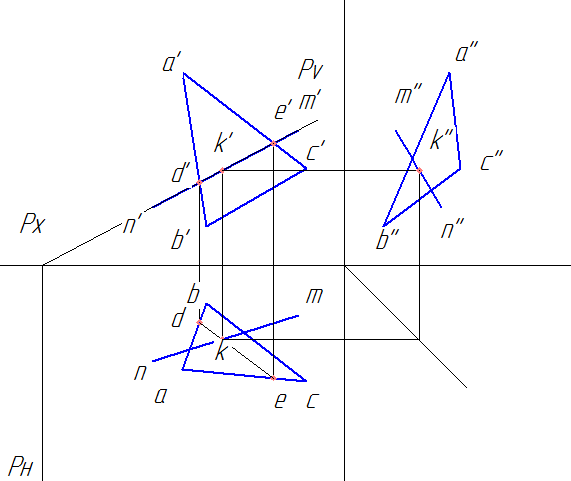
Задание берем из сборника Боголюбова, 1989 год, стр. 63, вар. 1. Нам требуется по заданным координатам построить комплексный чертеж треугольника ABC и прямой MN. Найти точку встречи (пересечения) прямой с непрозрачной плоскостью ABC.Определить видимые участки прямой.

Пересечение прямой линии с плоскостью

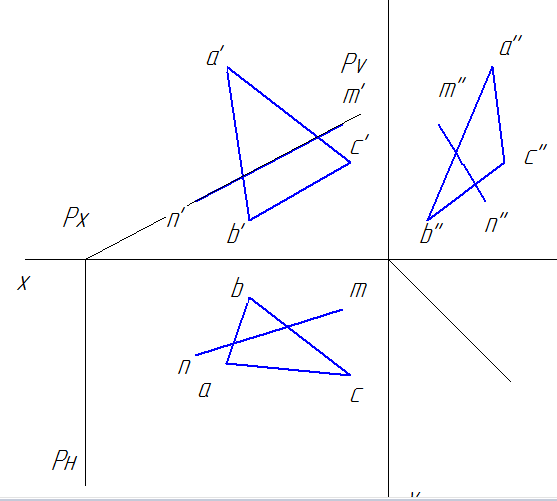
1. По координатам точек A, B и C строим комплексный чертеж треугольника и прямой NM. Начинаем чертить с горизонтальной проекции. Координаты точек проекции находим при помощи вспомогательных прямых.

2. Получаем вот такой комплексный чертеж.

3. Для определения координат точки пересечения прямой и плоскости выполним следующее.

a) Через прямую NM проводим вспомогательную плоскость Р, т.е. на фронтальной проекции проводим след плоскости Pv, на горизонтальную плоскость опускаем перпендикуляр Рн – горизонтальный след плоскости Р.

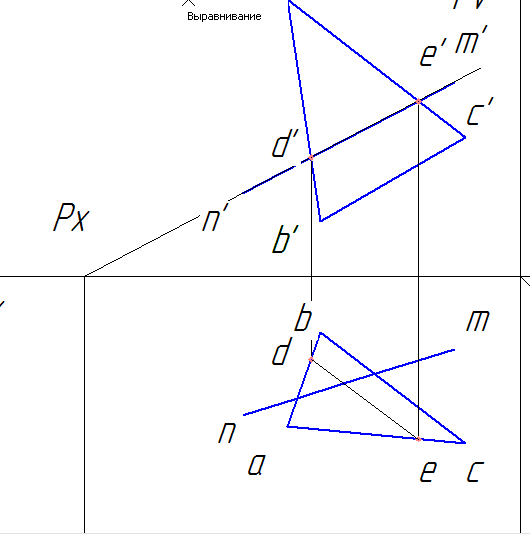
b) Находим фронтальную проекцию линии пересечения следа плоскости Р с треугольником АВС. Это отрезок d’e’. Горизонтальную проекцию находим по линиям связи до пересечения со сторонами ab (т. d) и ac (т. e) треугольника. Точки d и e соединяем.

c) Вместе пересечения de и nm будет находиться горизонтальная проекция искомой точки пересечения прямой линии с плоскостью k.

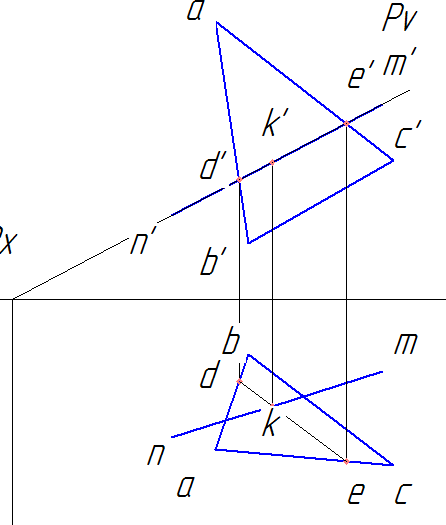
d) Проводим линию связи из k до пересечения с d’e’, получаем фронтальную проекцию точки k’.

e) по линиям связи находим профильную проекцию точки k’’.

Координаты точки пересечения прямой и плоскости К найдены. Эта точка также называется точкой встречи прямой и плоскости.

Определение видимости прямой

Для определения видимости прямой воспользуемся методом конкурирующих точек.

Конкурирующие точки – это точки, расположенные на одной проекционной прямой и имеющие одинаковые одноименные координаты.

Применительно к нашему чертежу конкурирующими будут точки:

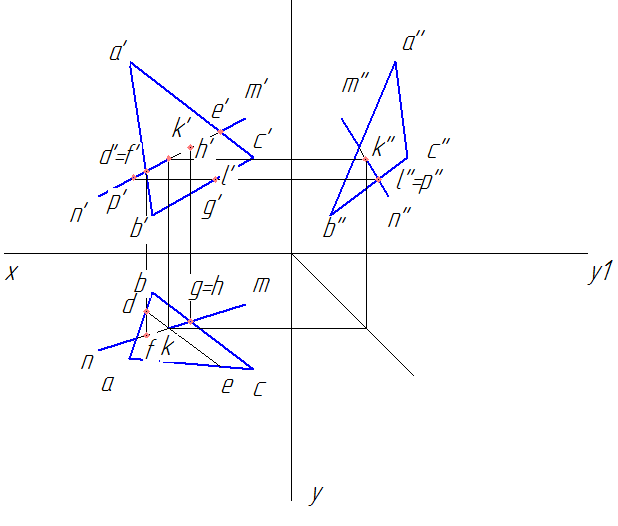
— точки: d’ принадлежащая a’b’ и e’ принадлежащая n’m’ (фронтально конкурирующие),

— точки: g принадлежащая bc и h принадлежащая nm (горизонтально конкурирующие),

— точки: l’’ принадлежащая b’’c’’ и p’’ принадлежащая n’’m’’ (профильно конкурирующие).

Из двух конкурирующих точек видимой будет та, высота которой будет больше. Граница видимости ограничена точкой К.

Для пары точек d’ и e’ видимость определяем так: опускаем перпендикуляр до пересечения с ab и nm на горизонтальной проекции, находим точки d и f. Видим, что координата по y для точки f больше, чем у d → точка f видима → видима прямая nm на участке f’k’, а на участке k’m’ невидима.

Аналогично рассуждаем и для пары точек g и h: на фронтальной проекции координата по z у точки h’ больше, чем у g’ → точка h’ видима, g’ – нет → прямая nm на отрезке hk видима, а на участке kn невидима.

И для пары точек l’’p’’: на фронтальной проекции координата по x больше у точки p’, а значит она закрывает собой точку l’’ на профильной проекции → р’’ видима, l’’ нет → отрезок прямой n’’k’’ видим, k’’m’’ невидим.

Заменяем в нужных местах линию nm на невидимую. На этом определение видимости прямой NM на комплексном чертеже треугольника АВС завершено.

Окончательно чертеж выглядит следующим образом.

Еще полезные материалы по начертательной геометрии

Как построить линию пересечения поверхностей двух взаимно перпендикулярных цилиндров?

Все о построении усеченных цилиндра и призмы, а также разверток этих геометрических тел.

Подробно весь процесс построения и определения видимости прямой описан в видеоуроке.

Скачать чертеж бесплатно можно здесь

Теперь у вас не вызовет затруднений нахождение точки пересечения прямой линии с плоскостью и определение видимости прямой на проекциях чертежа.

The following two tabs change content below.

Bio
Latest Posts

Рада приветствовать Вас в своем блоге! Я создала его с целью помочь всем желающим освоить программу Компас 3d. Мы пройдем весь путь от азов черчения до создания серьезных сборок. Присоединяйтесь!

Понравился материал? Подпишись на обновления!

Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.

Источник

Разделы

Уроки по теме

Точка пересечения прямой и плоскости

Автор: Moroz

Дата: 2010-09-30

Рассмотрим пошаговую инструкцию построения точки пересечения прямой общего положения с плоскостью общего положения.Отметим, что построение точки пересечения прямой и плоскости — это одна из основ решения задач по предмету начертательная геометрия, не освоив которую дальнейшее понимание предмета будет достаточно трудным.

Порядок построения точки пересечения прямой и плоскости

1. Заключим прямую а во вспомогательную фронтально-проецирующую плоскость (плоскость перпендикулярную фронтальной плоскости проекции). На фронтальной проекции она сольется с прямой а. Очевидно, что линия m пересечения этой плоскости с плоскостью треугольника АВС на фронтальной проекции так же будет сливаться с прямой а (а=m).

2. Определим фронтальные проекции двух точек этой линии m: точки 1 и 2.

3. Найдем их горизонтальные проекции.

4. Соединим горизонтальные проекции точек 1 и 2 — получим горизонтальную проекцию прямой m (которая является линией пересечения вспомогательной плоскости с плоскостью треугольника АВС, и соответственно принадлежит обеим плоскостям). Так как прямая а принадлежит вспомогательной плоскости, и прямая m принадлежит ей же, то точка пересечения этих прямых К и есть точка пересечения прямой а с плоскостью треугольника АВС.

5. С помощью линии связи найдем фронтальную проекцию точки пересечения К.

6. Осталось только определить видимость прямой а. Это можно сделать с помощью метода конкурирующих точек.

Обратите внимание, что мы начали поиск точки пересечения прямой с плоскостью с того, что заключили прямую а во вспомогательную фронтально-проецирующую плоскость. Точно таким же образом можно было заключить прямую а в горизонтально-проецирующую плоскость, и тогда бы построения начались как бы «снизу вверх», но смысл остался бы точно таким же, как и конечное решение — точка пересечения прямой с плоскостью.

Внимание! Для этой темы есть видеоурок.

Вы можете сказать «спасибо!» автору статьи:

пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»

или

или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи

или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.

А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны:

Комментарии:

Очень легко и понятно вы описали как найти точку пересечения прямой и плоскости, мегареспект!

Сделайте нормальные чертежи!!! Без анимации пошаговые.
Оставляйте адрес, может вам и будет подарок. Новый год ведь скоро

А вот нечего торопиться. Надо покушать как следует, сесть и всмотреться в гифку. Тогда и познаешь дзен.

Не торопиться, быть сытым и выспавшимся — да, это отличное подспорье. Спасибо за то, что указали на столь важные моменты. Да прибудет с вами сила, Михаил!

Помогите пожалуста!!!!!!у меня плоскость перпендикулярна фронтальной плоскости проекции и задана следами, а прямая горизонтальна горизонтальной плоскости проекций

Это простооо кул,все понятно,мегареспект вам!!

4. Соединим горизонтальные проекции точек 1 и 2 — получим горизонтальную проекцию прямой m (которая является точкой пересечения вспомогательной плоскости с плоскостью треугольника АВС…
Тут надо исправить: прямая не может являться точкой. Также отсутствует закрывающая скобка.

Я всё равно ничего не понял. Хоть на первый взгляд это более толковое объяснение решения, чем пишут в книгах — там ваще мрак.

Высший класс! Ключевое предложение для понимания сути: «Заключим прямую а во вспомогательную фронтально-проецирующую плоскость …»

Эмм… Это сарказм?
Если да, то в свое оправдание могу сказать лишь то, что терминология должна быть вам в некоторой мере знакома. С меня лишь графический порядок решения. Но с другой стороны давать его в абсолютном отрыве от теории тоже нехорошо. Указанная в вашем комментарии фраза пригодится вам на экзамене, или как минимум на защите данной работы. Но для графического решения прямо сейчас она не так важна. Просто выполняйте по шагам.

Спасибо огромное.Всё доходчиво и ясно!

Как быть если прямая на П2 перпендикулярна Ох, а на П1 в точку проэцируется?

Добавьте свой комментарий:

Последние уроки

Как построить диметрию детали?

Построение наклонного сечения, заданного на виде слева

Определение линии пересечения двух плоскостей. Метод вспомогательных секущих плоскостей.

Наша почта:

zakaz@trivida.ru

Наша страница в ВК:

Случайный комментарий

Ирина:

Антон, спасибо за отлично выполненные чертежи!!! У меня единственная пятерка на курсе :))). Всем рекомендую обращаться только сюда! Работы выполнены безупречно! Сама рабатаю в комании, где есть конструкторский отдел и решила показать им чертежи Антона. Собрался целый консилиум, говорили где надо подправить, что-то вообще не так, но я решила сдать ничего не исправляя. И это было правильное решение :))). Еще раз спасибо, Антон!!!

Ирина, я преклоняюсь перед вашим желанием оставить комментарий спустя 3 месяца после нашего сотрудничества. От этого он еще более ценен! И главное — в нем яркий пример того, насколько сильное значение имеет субъективность восприятия чертежа разными людьми. Мы делаем чертежи в соответствии с ГОСТами, но у каждого преподавателя может быть свое видение «более удачного варианта исполнения», и поэтому иногда студентам приходится что-то менять в наших работах.

Источник