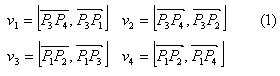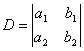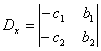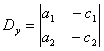Оглавление
- Расположение отрезков на плоскости
- Параметрическое уравнение отрезка
- Найти точку пересечения двух отрезков
- Отрезки не пересекаются
- Метод SegmentSegment(…)
- Исходник приложения с классом Intersections
Расположение отрезков на плоскости
Два отрезка могут иметь различные положения на плоскости относительно друг друга. Поскольку отрезок ограниченная с двух сторон линия, данная геометрическая фигура предлагает больше вариантов расположения в сравнении с прямой и лучом.
Из вариантов пересечения или непересечения можно выделить несколько особых случаев, например: начала и концы отрезков совпадают, отрезки параллельны и не лежат друг на друге, начало или конец одного отрезка лежит на другом отрезке, совпадают только начальные или конечные точки.
Параметрическое уравнение отрезка
Расположение отрезка в координатной системе и его геометрия, также как прямой и луча, может описываться параметрическими уравнениями. Параметрическое уравнение отрезка(прямой, луча) представляет из себя выражение включающее координату начала, вектор направления и параметр задающий множество точек отрезка(прямой, луча).
Параметр может иметь ограничения или не иметь их.
система из параметрических уравнений: | x = x0 + vt | y = y0 + wt где v и w координаты (x, y) вектора направления v = x1 - x0 w = y1 + y0 при 0 ≤ t ≤ 1 - уравнения описывают отрезок, при 0 ≤ t < +∞ - уравнения описывают луч, при -∞ < t < +∞ - уравнения описывают прямую
Найти точку пересечения двух отрезков
Система из 4-х параметрических уравнений позволяет найти точку пересечения двух отрезков. Нахождение точки пересечения отрезков аналогично описанному для двух лучей.
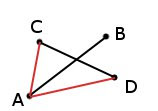
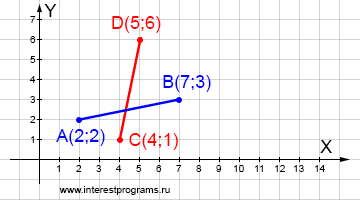
Дано: отрезок AB с координатами начальной и конечной точек — A(2;2) и B(7;3), отрезок CD с координатами — C(4;1) и D(5;6). Найти возможную точку пересечения отрезков AB и CD.
Отрезки имеют точку пересечения если оба параметра отрезков больше или равно нулю и меньше или равно единице.
| x = 2 + (7 - 2)tab | x = 2 + 5tab | y = 2 + (3 - 2)tab => | y = 2 + tab | x = 4 + (5 - 4)tcd | x = 4 + tcd | y = 1 + (6 - 1)tcd | y = 1 + 5tcd
Чтобы узнать есть ли точка пересечения отрезков AB и CD вычислим их параметры:
найдём соотношение параметров через возможно общую координату x 2 + 5tab = 4 + tcd => 5tab = 2 + tcd => tab = (2 + tcd)/5 (у.1) вычислим параметр tcd через возможно общую координату y 2 + tab = 1 + 5tcd => 2 + (2 + tcd)/5 = 1 + 5tcd => 10 + 2 + tcd = 5 + 25cd => tcd = 7/24 ≈ 0.292 вычислим параметр tab использую полученное соотношение (у.1) tab = (2 + 0.292)/5 ≈ 0.458
Оба параметра положительные и меньше единицы — отрезки пересекаются. Найдем точку пересечения используя уравнения из системы для двух отрезков:
x = 2 + 5tab => x = 2 + 5 * 0.458 = 4.29 y = 2 + tab => y = 2 + 0.458 = 2.458
Точка пересечения отрезков AB и CD имеет координаты (4.29; 2.458).
Отрезки не пересекаются
Отсутствие точки пересечения двух отрезков, безусловно, также подтверждается вычислением.
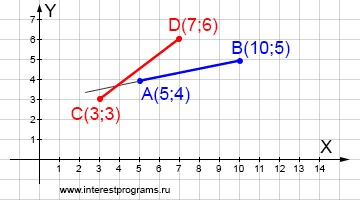
Дано: отрезок AB с координатами начальной и конечной точек — A(5;4) и B(10;5), отрезок CD с координатами — C(3;3) и D(7;6). Определить: отрезки пересекаются или не пересекаются. Если отрезки не пересекаются, найти мнимую точку пересечения.
Отрезки не пересекаются если хотя бы один из параметров отрицательный или больше единицы. Для вычисления используем систему из параметрических уравнений.
| x = 5 + (10 - 5)tab | x = 5 + 5tab | y = 4 + (5 - 4)tab => | y = 4 + tab | x = 3 + (7 - 3)tcd | x = 3 + 4tcd | y = 3 + (6 - 3)tcd | y = 3 + 3tcd
Чтобы узнать пересекаются отрезки или нет вычислим их параметры, вычисление будет происходит аналогично случаю пересечения описанному выше.
3 + 4tcd = 5 + 5tab => 4tcd = 2 + 5tab => tcd = (2 + 5tab)/4 3 + 3tcd = 4 + tab => 3 + 3(2 + 5tab)/4 = 4 + tab => 3 + (6 + 15tab)/4 = 4 + tab => 2 + 11tab = 0 => tab = -2/11 ≈ -0.182 параметр tab меньше нуля, значит отрезки не пересекаются tcd = (2 + 5tab)/4 => tcd = (2 + 5*-0.182)/4 ≈ 0.273 параметр tcd положительный и меньше единицы, значит мнимая точка лежит на отрезке CD
Найдем мнимую точку, расположенную на отрезке CD:
x = 5 + 5 * -0.182 = 4.09 y = 4 - 0.182 = 3.818
Метод SegmentSegment(…)
Метод вычисления точки пересечения отрезков инкапсулирован в классе Intersections. Метод статический, для вычисления точки пересечения не требуется создание экземпляра класса. Методы вычисляющие точки пересечения прямых и лучей описаны на страницах точка пересечения двух прямых на плоскости, пересечение луча и прямой, пересечение двух лучей.
В исходнике приложения, прикрепленного к странице происходит вычисление точки пересечения и создание параметрических уравнений каждого отрезка.
class Intersections
{
// Вычисление точки пересечения отрезков.
public static bool SegmentSegment(Point r1, Point r2, Point p1, Point p2, out Point pCross, out Info info)
{
// Параметрическое уравнение отрезка
// x = x0 + vt
// y = y0 + wt
// где v = x1 - x0
// w = y1 - y0
// при 0 <= t <= 1
// Оповещение о событиях пересечения или не пересечения.
info = new Info();
// Координаты направления вектора синего отрезка
double v = r2.X - r1.X;
double w = r2.Y - r1.Y;
// Координаты направления вектора красного отрезка
double v2 = p2.X - p1.X;
double w2 = p2.Y - p1.Y;
// ===== Частные случаи не пересечения =====
// Отрезки должны быть определены
if (v == 0 && w == 0 && v2 == 0 && w2 == 0)
{
info.Id = 10;
info.Message = "Отрезки неопределённы";
return false;
}
else if (v == 0 && w == 0)
{
info.Id = 11;
info.Message = "Синий отрезка неопределён";
return false;
}
else if (v2 == 0 && w2 == 0)
{
info.Id = 12;
info.Message = "Красный отрезка неопределён";
return false;
}
// Для вычисления параллельности отрезка
// необходимо сравнить направления их векторов.
// Вычисляем длины векторов
double lenBlue = Math.Sqrt(v * v + w * w);
double lenRed = Math.Sqrt(v2 * v2 + w2 * w2);
// Нормализация векторов - создание единичного вектора направления
double x = v / lenBlue;
double y = w / lenBlue;
double x2 = v2 / lenRed;
double y2 = w2 / lenRed;
// Точность совпадения величин double
double epsilon = 0.000001;
// Проверка на совпадение
if (r1.X == p1.X && r1.Y == p1.Y && r2.X == p2.X && r2.Y == p2.Y)
{
info.Id = 20;
info.Message = "Отрезки совпадают";
return false;
}
// Проверка на параллельность с определенной точностью.
if (Math.Abs(x - x2) < epsilon && Math.Abs(y - y2) < epsilon)
{
info.Id = 21;
info.Message = "Отрезки параллельны";
return false;
}
// ===== /Частные случаи не пересечения =====
// ===== Вычисление точки пересечения =====
// Проверка факта пересечения
// x = p1.X + v2t2
// y = p1.Y + w2t2
// r1.X + vt = p1.X + v2t2 => vt = p1.X - r1.X + v2t2 =>
// t = (p1.X - r1.X + v2t2) / v - (у.1) соотношение t-параметров
//
// Вычисление одного параметра с заменой соотношением другого
// r1.Y + wt = p1.Y + w2t2 => wt = p1.Y - r1.Y + w2t2 => t = (p1.Y - r1.Y + w2t2) / w
// (p1.X - r1.X + v2t2) / v = (p1.Y - r1.Y + w2t2) / w =>
// (p1.X - r1.X + v2t2) * w = (p1.Y - r1.Y + w2t2) * v =>
// w * p1.X - w * r1.X + w * v2t2 = v * p1.Y - v * r1.Y + v * w2t2 =>
// w * v2t2 - v * w2t2 = -w * p1.X + w * r1.X + v * p1.Y - v * r1.Y =>
// (w * v2 - v * w2) * t2 = -w * p1.X + w * r1.X + v * p1.Y - v * r1.Y =>
// t2 = (-w * p1.X + w * r1.X + v * p1.Y - v * r1.Y) / (w * v2 - v * w2) - (у.2)
double t2 = (-w * p1.X + w * r1.X + v * p1.Y - v * r1.Y) / (w * v2 - v * w2);
// t = (p1.X - r1.X + v2t2) / v - (у.1)
double t = (p1.X - r1.X + v2 * t2) / v;
// Если один из параметров меньше 0 и больше 1, значит пересечения нет.
if (t < 0 || t > 1 || t2 < 0 || t2 > 1)
{
info.Id = 20;
info.Message = "Пересечения нет";
return false;
}
// Координаты точки пересечения
pCross.X = p1.X + v2 * t2;
pCross.Y = p1.Y + w2 * t2;
info.Id = 0;
info.Message = "Пересечение есть";
return true;
// ===== /Вычисление точки пересечения =====
}
}
public class Info
{
// Для визуального сообщения.
public string Message;
// Для автоматических действий.
public int Id;
}
Исходник приложения с классом Intersections
К странице приложен исходник приложения на языке C#. Приложение демонстрирует вычисление точки пересечения двух отрезков. Графика приложения создает различные положения отрезков на плоскости окна. Управление начальными и конечными точками мышью и служебными клавишами.
Скачать исходник
WpfAppCrossSegmentSegment-vs17.zip
- Размер: 205 Кбайт
- Загрузки: 186
Простой алгоритм определения пересечения двух отрезков
Время на прочтение
4 мин
Количество просмотров 204K
Введение
В былые времена я увлекался компьютерной графикой, как 2х так и 3х мерной, в том числе математическими визуализациями. Что называется just for fun, будучи студентом, написал программу визуализирующую N-мерные фигуры, вращающиеся в любых измерениях, хотя практически меня хватило только на определение точек для 4-D гиперкуба. Но это только присказка. Любовь к геометрии осталась у меня с тех пор и по сей день, и я до сих пор люблю решать интересные задачи интересными способами.
Одна из таких задач попалась мне в 2010 году. Сама задача достаточно тривиальна: необходимо найти, пересекаются ли два 2-D отрезка, и если пересекаются — найти точку их пересечения. Более интересно решение, которое, я считаю, получилось достаточно элегантным, и которое я хочу предложить на суд читателя. На оригинальность алгоритма не претендую (хотя и хотелось бы), но в сети подобных решений я найти не смог.
Задача
Даны два отрезка, каждый из которых задан двумя точками: (v11, v12), (v21, v22). Необходимо определить, пересекаются ли они, и если пересекаются, найти точку их пересечения.
Решение
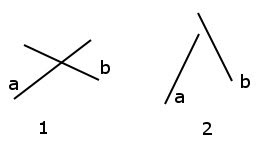
Для начала необходимо определить, пересекаются ли отрезки. Необходимое и достаточное условие пересечения, которое должно быть соблюдено для обоих отрезков следующее: конечные точки одного из отрезков должны лежать в разных полуплоскостях, если разделить плоскость линией, на которой лежит второй из отрезков. Продемонстрируем это рисунком.
На левом рисунке (1) показаны два отрезка, для обоих из которых условие соблюдено, и отрезки пересекаются. На правом (2) рисунке условие соблюдено для отрезка b, но для отрезка a оно не соблюдается, соответственно отрезки не пересекаются.
Может показаться, что определить, с какой стороны от линии лежит точка — нетривиальная задача, но у страха глаза велики, и всё не так сложно. Мы знаем, что векторное умножение двух векторов даёт нам третий вектор, направление которого зависит от того, положительный или отрицательный угол между первым и вторым вектором, соответственно такая операция антикоммутативна. А так как все вектора лежат на плоскости X-Y, то их векторное произведение (которое обязано быть перпендикулярным перемножаемым векторам) будет иметь ненулевой только компоненту Z, соответственно и отличие произведений векторов будет только в этой компоненте. Причем при изменении порядка перемножения векторов (читай: угла между перемножаемыми векторами) состоять оно будет исключительно в изменении знака этой компоненты.
Поэтому мы можем умножить попарно-векторно вектор разделяющего отрезка на векторы направленные от начала разделяющего отрезка к обеим точкам проверяемого отрезка.
Если компоненты Z обоих произведений будет иметь различный знак, значит один из углов меньше 0 но больше -180, а второй больше 0 и меньше 180, соответственно точки лежат по разные стороны от прямой. Если компоненты Z обоих произведений имеют одинаковый знак, следовательно и лежат они по одну сторону от прямой.
Если один из компонент Z является нулём, значит мы имеем пограничный случай, когда точка лежит аккурат на проверяемой прямой. Оставим пользователю определять, хочет ли он считать это пересечением.
Затем нам необходимо повторить операцию для другого отрезка и прямой, и убедиться в том, что расположение его конечных точек также удовлетворяет условию.
Итак, если всё хорошо и оба отрезка удовлетворяют условию, значит пересечение существует. Давайте найдём его, и в этом нам также поможет векторное произведение.
Так как в векторном произведении мы имеем ненулевой лишь компоненту Z, то его модуль (длина вектора) будет численно равен именно этой компоненте. Давайте посмотрим, как найти точку пересечения.
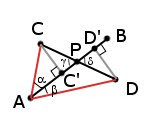
Длина векторного произведения векторов a и b (как мы выяснили, численно равная его компоненте Z) равна произведению модулей этих векторов на синус угла между ними (|a| |b| sin(ab)). Соответственно, для конфигурации на рисунке мы имеем следующее: |AB x AC| = |AB||AC|sin(α), и |AB x AD| = |AB||AD| sin(β). |AC|sin(α) является перпендикуляром, опущенным из точки C на отрезок AB, а |AD|sin(β) является перпендикуляром, опущенным из точки D на отрезок AB (катетом ADD’). Так как углы γ и δ — вертикальные углы, то они равны, а значит треугольники PCC’ и PDD’ подобны, а соответственно и длины всех их сторон пропорциональны в равном отношении.
Имея Z1 (AB x AC, а значит |AB||AC|sin(α) ) и Z2 (AB x AD, а значит |AB||AD|sin(β) ), мы можем рассчитать CC’/DD’ (которая будет равна Z1/Z2), а также зная что CC’/DD’ = CP/DP легко можно высчитать местоположение точки P. Лично я делаю это следующим образом:
Px = Cx + (Dx-Cx)*|Z1|/|Z2-Z1|;
Py = Cy + (Dy-Cy)*|Z1|/|Z2-Z1|;
Вот и все. Мне кажется что это действительно очень просто, и элегантно. В заключение хочу привести код функции, реализующий данный алгоритм. В функции использован самодельный шаблон vector<typename, int>, который является шаблоном вектора размерностью int с компонентами типа typename. Желающие легко могут подогнать функцию к своим типам векторов.
1 template<typename T>
2 bool are_crossing(vector<T, 2> const &v11, vector<T, 2> const &v12, vector<T, 2> const &v21, vector<T, 2> const &v22, vector<T, 2> *crossing)
3 {
4 vector<T, 3> cut1(v12-v11), cut2(v22-v21);
5 vector<T, 3> prod1, prod2;
6
7 prod1 = cross(cut1 * (v21-v11));
8 prod2 = cross(cut1 * (v22-v11));
9
10 if(sign(prod1[Z]) == sign(prod2[Z]) || (prod1[Z] == 0) || (prod2[Z] == 0)) // Отсекаем также и пограничные случаи
11 return false;
12
13 prod1 = cross(cut2 * (v11-v21));
14 prod2 = cross(cut2 * (v12-v21));
15
16 if(sign(prod1[Z]) == sign(prod2[Z]) || (prod1[Z] == 0) || (prod2[Z] == 0)) // Отсекаем также и пограничные случаи
17 return false;
18
19 if(crossing) { // Проверяем, надо ли определять место пересечения
20 (*crossing)[X] = v11[X] + cut1[X]*fabs(prod1[Z])/fabs(prod2[Z]-prod1[Z]);
21 (*crossing)[Y] = v11[Y] + cut1[Y]*fabs(prod1[Z])/fabs(prod2[Z]-prod1[Z]);
22 }
23
24 return true;
25 }
Как найти точку пересечения отрезков
Простейшие геометрические примитивы, такие как точки, прямые, плоскости, фигурируют в большинстве научных и инженерных задач, связанных с проектированием, графическими построениями, визуализацией и машинной графикой. Подобные задачи, как правило, решаются путем применения принципа декомпозиции и сведения их к последовательностям элементарных действий с геометрическими примитивами. Так, сложные трехмерные объекты в машинной графике аппроксимируются полигонами, а те в свою очередь — треугольниками, треугольники задаются отрезками ребер, которые определяются их конечными точками. Именно поэтому понимание того, как решить простейшие геометрические задачи, например того, как найти точки пересечения отрезков, весьма важно для любого технического специалиста.
Вам понадобится
- Лист бумаги, ручка.
Инструкция
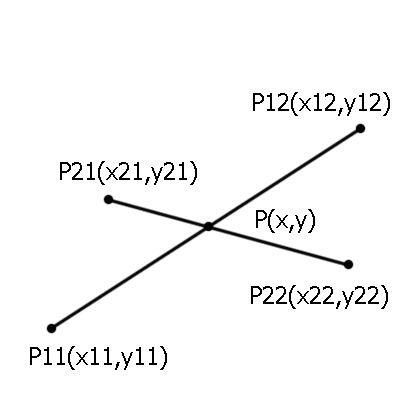
Подготовьте исходные данные. В качестве исходных данных удобно принять отрезки, заданные координатами точек их концов в декартовой системе координат. В данной системе координатные оси ортогональны и имеют одинаковый линейный масштаб. Допустим, имеются отрезки O1 и O2. Отрезок O1 задан точками с координатами P11(x11, y11) и P12(x12, y12), а отрезок O2 задан точками с координатами P21(x21, y21) и P22(x22, y22).
Составьте уравнения прямых, к которым принадлежат отрезки O1 и O2. Уравнение прямой отрезка O1 будет иметь вид: K1*x+d1-y=0. Уравнение прямой отрезка O2 будет иметь вид: K2*x+d2-y=0. Здесь K1=(y12-y11)/(x12-x11), d1=(x12*y11-x11*y12)/(x12-x11), K2=(y22-y21)/(x22-x21), d2=(x22*y21-x21*y22)/(x22-x21).
Решите систему уравнений, состоящую из уравнений прямых, составленных на предыдущем шаге. Вычтя из первого уравнения второе, можно получить: K1*x-K2*x+d1-d2=0. Откуда x=(d2-d1)/(K1-K2). Подставив x в первое уравнение, получим: y=K1*(d2-d1)/(K1-K2)+d1. Значения K1, K2, d1, d2 известны. Точка P(x, y) является пересечением прямых, на которых лежат исходные отрезки.
Проверьте, является ли точка с найденными координатами точкой пересечения именно отрезков, а не прямых, на которых они лежат. Для этого убедитесь, что координата точки x принадлежит одновременно диапазонам значений [x11,x12] и [x21,x22], а координата y принадлежит одновременно диапазонам [y11,y12] и [y21,y22].
Видео по теме
Источники:
- как пересекаются два отрезка
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Не такая тривиальная задача, скажу я вам. Всякий раз, когда возникает необходимость посчитать координату пересечения пары прямых, каждая из которых задана парой точек, снова беру блокнот и вывожу пару формул. И всякий раз – блин, ну это уже когда-то было, опять надо что-то делать с параллельными прямыми, опять появляется пакостная строго вертикальна линия, когда на (x1-x2) никак не разделить и т.д.
Поэтому – в подборку теории и практики, пригодится, сэкономим блокнот, спасем дерево.
Коэффициенты А, B, C
Все помним со школы формулу:
Тоже самое, но с претензией на образование (некоторые индивидуумы утверждают, что существует такая, и только такая, и никакая другая, формулировка):
Те же фаберже, только сбоку.
В теории надо составить и решить систему уравнений для первой и второй линии, где переменными будут X и Y точки пересечения.
Загвоздка в том, что мы не знаем коэффициенты для обеих линий.
В нашем случае известны координаты двух точек, по которым проходит линия. Поэтому мне, как последователю геометрического агностицизма, более привлекательная следующая формула:
Путем несложных операций приходим к следующей записи:
Глядя на вариант в исполнении высшего образования, получаем следующие формулы для нахождения коэффициентов:
Пока все идет отлично, нигде вероятного деления на ноль не встретилось.
Итак, мы можем легко найти два набора коэффициентов для первой и второй прямых. Переходим к системе уравнений.
Система уравнений
Как правило, подобная система уравнений решается путем выражения одной переменной через другую, подстановкой во второе уравнение, получая таким образом уравнение одной переменной. Далее переменная находится, подставляется, решается. Или определяется, что система решения не имеет.
Но нас интересует метод Крамера. Потому что с помощью этого метода можно получить сразу значения для обеих переменных, без дополнительных телодвижений.
Сразу же запишем метод под нашу систему.
Имеем следующую систему:
Определители будут такими:
Исходя из метода, решение выглядит так:
Ага! Вот и возможное деление на ноль, скажете вы. И правильно! В этой, в высшей степени непозволительной ситуации, когда знаменатель равен нулю, решения нет, прямые либо параллельны, либо совпадают (что, впрочем, частный случай параллельности). В коде, естественно, этот момент надо учитывать.
Практика 1
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
//******************************************************* // Нахождение точки пересечения прямых (p1,p2) и (p3,p4) // Результат — факт пересечения //******************************************************* function CrossLines(const p1,p2,p3,p4: TxPoint; var res: TxPoint): Boolean; const Prec = 0.0001; var a1, a2: Extended; b1, b2: Extended; c1, c2: Extended; v: Extended; begin a1 := p2.y — p1.y; a2 := p4.y — p3.y; b1 := p1.x — p2.x; b2 := p3.x — p4.x; v := a1*b2 — a2*b1; Result := (abs(v) > Prec); if Result then begin c1 := p2.x*p1.y — p1.x*p2.y; c2 := p4.x*p3.y — p3.x*p4.y; res.X := —(c1*b2 — c2*b1)/v; res.Y := —(a1*c2 — a2*c1)/v; end; end; |
Частные случаи
- Прямые параллельны: ∆ab = 0
- (A1B2 – B1A2 = 0);
- Прямые совпадают: ∆ab = ∆X = ∆Y = 0
- (A1B2 – B1A2 = 0) И (A1C2 — A2C1 = 0) И (C1B2 -B1C2 = 0);
- Прямые перпендикулярны:
- (A1 A2 + B1 B2 = 0).
Принадлежность точки отрезку
В общем случае, чтобы определить принадлежность точки отрезку, надо установить две вещи:
- Точка принадлежит прямой, проходящей через конечные точки отрезка. Для этого достаточно подставить значение X и Y в уравнение прямой и проверить получившееся равенство. В нашем случае, этот пункт уже выполнен, т.к. точка пересечения априори принадлежит обеим прямым.
- Проверить факт нахождения точки между концами отрезка.
Займемся пунктом 2. Данный факт можно установить двумя способами:
- Логически, т.е. (x1 <= x <= x2) ИЛИ (x1 >= x >= x2). На случай «вертикальности» линии добавить проверку на Y:
- (y1 <= y <= y2) ИЛИ (y1 >= y >= y2).
- Арифметически. Сумма отрезков |x-x1| + |x-x2| должна быть равна длине отрезка |x1-x2|. Аналогично, на случай «вертикальности» , добавить проверку:
- |y-y1| + |y-y2| = |y1-y2|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//***************************************************** // Проверка факта нахождения точки res между // концами отрезка (p1,p2). // Решение с помощью условных операторов и // коэффициентов A=(y2-y1) B=(x1-x2). // Выступают в качестве параметров, чтобы не тратить // время на их подсчет, т.к. в вызывающей стороне // они уже посчитаны //***************************************************** function CheckCrossPoint(const p1, p2, res: TxPoint; const A,B: Extended): Boolean; begin Result := (((B<0) and (p1.X < res.X) and (p2.X > res.X)) or ((B>0) and (p1.X > res.X) and (p2.X < res.X)) or ((A<0) and (p1.y > res.Y) and (p2.Y < res.Y)) or ((A>0) and (p1.y < res.Y) and (p2.Y > res.Y))); end; //***************************************************** // Проверить факт нахождения точки res между // концами отрезка (p1,p2) // Арифметическое решение без коэффициентов //***************************************************** function CheckCrossPoint(const p1, p2, res: TxPoint): Boolean; begin Result := (abs(p2.x—p1.x)>= abs(p2.x—res.x) + abs(p1.x—res.x)) and (abs(p2.y—p1.y)>= abs(p2.y—res.y) + abs(p1.y—res.y)); end; |
Практика показывает, что арифметический способ быстрее примерно в 3 раза. Когда-то я считал, что операции сравнения самые быстрые. Это давно уже не так.
Задача нахождения принадлежности точки P(x,y) отрезку, заданного двумя точками с координатами P1(x1, y1) и P2(x2, y2) подробно рассмотрена в отдельной статье.
Угол пересечения прямых
Угол пересечения прямых — это угол пересечения направляющих векторов. Т.е., взяв уже знакомые ранее точки p1 и p2, получим направляющий вектор V(p1,p2), и аналогично второй вектор M(p3,p4). В теории мы должны вычислить достаточно «затратную» функцию, с корнями, квадратами, дробями и арккосинусом.
Давайте не будем останавливаться на ней, она долгая, нудная и в нашем случае ненужная. Рассмотрим вектор:
α — угол наклона вектора к оси X, который можно найти, как:
α = arctan (A1 / B1)
Где расстояния:
A1 = (y1 — y2)
B1 = (x2 — x1)
Что-то знакомое? Да это ни что иное, как коэффициенты в уравнении прямой от образованных фанатов. Может они и правы в своем испепеляющем фанатизме…
Одним словом, коэффициенты (расстояния) у нас уже есть по обеим прямым.
Судя по рисунку, угол между векторами, это сумма углов наклона векторов к оси X. Ммм… не совсем так, на самом деле это разность.
По рисунку явно видно, что угол между векторам это γ = (β — α).
В предыдущем примере все правильно, просто знаки углов разные, т.к. находятся по разные стороны от оси X, а формула работает та же.
От теории к практике
Теперь в плане практического применения. Мне нужно точно знать, откуда, куда и в каком направлении этот угол. В теории, углом между прямыми считается наименьший из пары γ и (180-γ). Так вот, нам это не надо. Какой угол получится – такой нам и нужен.
Поэтому, под углом между векторами понимаем угол от вектора V(p1,p2) к вектору M(p3,p4). Если знак угла – отрицательный, понимаем, что он против часовой стрелки, иначе – по часовой стрелке.
Следует заметить, что, зная коэффициенты, для нахождения угла пересечения, координаты уже не нужны. Листинг таков:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
//********************************************************** // Посчитать угол пересечения векторов по коэфф-ам А и B //********************************************************** function CalcCrossAngle(const a1,b1: Extended; const a2,b2: Extended): Extended; var c1, c2: Extended; begin c1 := ArcTan2(a1,b1); c2 := ArcTan2(a2,b2); Result := c2—c1; if Result < —pi then Result := 2*pi + Result; if Result > pi then Result := Result — 2*pi; end; |
Тут ситуация с вертикальной прямой, т.е. когда теоретически происходит деление на ноль, явно не обрабатывается. Она корректно обрабатывается функцией ArcTan2, которая вернет в этом случае и знак, и 90 градусов.
Практика 2
В дополнение к функции нахождения точки пересечения, напишем «продвинутую» функцию, которая находит эту точку, определяет нахождение на каждом из отрезков, и определяет угол между направляющими векторами. Или же определяет, что прямые параллельны/совпадают.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
//********************************************************** // Тип пересечения прямых (p1,p2) и (p3,p4) //********************************************************** type TxCrossLineResult = ( xclrEqual = —32// эквивалентны ,xclrParallel = —16// параллельны ,xclrOk = 0 // как минимум пересечение есть ,xclrFirst = 1 // попадает в первый отрезок ,xclrSecond = 2 // попадает во второй отрезок ,xclrBoth = 3 // попадает в оба ,xclrPerpend = 4 // перпендикулярны // можно найти по маске через AND, но для полноты картины ,xclrFirstP = 5 // перпендикулярны и попадает в первый ,xclrSecondP = 6 // перпендикулярны и попадает в второй ,xclrBothP = 7 // перпендикулярны и попадает в оба ); //********************************************************** // Нахождение точки пересечения прямых (p1,p2) и (p3,p4) // Определяет параллельность, совпадение, // перпендикулярность, пересечение. // Определяет, каким отрезкам принадлежит. // Находит угол(рад.) от (p1,p2) к (p3,p4): // отрицательное значение — против часовой // положительное — по часовой //********************************************************** function CrossLines(const p1,p2,p3,p4: TxPoint; var res: TxPoint; var Angle: Extended): TxCrossLineResult; const Prec = 0.0001; var a1, a2: Extended; b1, b2: Extended; c1, c2: Extended; v: Extended; begin Angle := 0; a1 := p2.y — p1.y; a2 := p4.y — p3.y; b1 := p1.x — p2.x; b2 := p3.x — p4.x; c1 := p2.x*p1.y — p1.x*p2.y; c2 := p4.x*p3.y — p3.x*p4.y; v := a1*b2 — a2*b1; if abs(v) > Prec then begin Result := xclrOk; res.X := —(c1*b2 — c2*b1)/v; res.Y := —(a1*c2 — a2*c1)/v; if CheckCrossPoint(p1,p2,res) then Result := TxCrossLineResult(Integer(Result) + Integer(xclrFirst)); if CheckCrossPoint(p3,p4,res) then Result := TxCrossLineResult(Integer(Result) + Integer(xclrSecond)); if (abs(a1*a2 + b1*b2) < Prec) then Result := TxCrossLineResult(Integer(Result) + Integer(xclrPerpend)); Angle := CalcCrossAngle(a1,b1,a2,b2); end else begin Result := xclrParallel; if ((abs(c1*b2 — c2*b1) < Prec) and (abs(a1*c2 — a2*c1) < Prec)) then Result := xclrEqual; end; end; |
Исходники
Небольшие комментарии по интерфейсу.
Скачать (219 Кб): Исходники (Delphi XE 7-10)
Скачать (1.14 Мб): Исполняемый файл
При запуске генерируется случайным образом 4 точки, по две на прямую. Точки и отрезки можно перетаскивать мышкой. Также, слева присутствует панель, на которой можно ввести координаты точек или коэффициенты уравнения прямой. При нажатии «Enter» или когда элемент ввода теряет фокус, происходит перерасчет и перерисовка.
Внизу есть 4 кнопки переключения режимов отображения. Начиная со второй, помимо координат точки пересечений в верхнем левом углу будет отображаться текущий угол пересечения между направляющими векторами.
Если точка пересечений попадает в какой-либо из отрезков, соответствующий заголовок линии отрезка станет жирным. На рисунке это зеленая линия 2.
По умолчанию, рабочее поле системы координат имеет размерность [-10..10], которую можно изменить ползунком в нижнем правом углу.
Пусть даны два отрезка. Первый задан точками P1(x1;y1) и P2(x2;y2). Второй задан точками P3(x3;y3) и P4(x4;y4).
Взаимное расположение отрезков можно проверить с помощью векторных произведений:
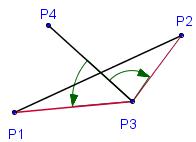
Рассмотрим отрезок P3P4 и точки P1 и P2.
Точка P1 лежит слева от прямой P3P4, для нее векторное произведение v1 > 0, так как векторы положительно ориентированы.
Точка P2 расположена справа от прямой, для нее векторное произведение v2 < 0, так как векторы отрицательно ориентированы.
Для того чтобы точки P1 и P2 лежали по разные стороны от прямой P3P4, достаточно, чтобы выполнялось условие v1v2 < 0 (векторные произведения имели противоположные знаки).
Аналогичные рассуждения можно провести для отрезка P1P2 и точек P3 и P4.
Итак, если v1v2 < 0 и v3v4 < 0, то отрезки пересекаются.
Векторное произведение двух векторов вычисляется по формуле:
где:
ax, ay — координаты первого вектора,
bx, by — координаты второго вектора.
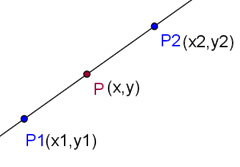
Уравнение прямой, проходящей через две различные точки, заданные своими координатами.
Пусть на прямой заданы две не совпадающие точки:P1 с координатами (x1;y1) и P2 с координатами (x2; y2). Соответственно вектор с началом в точке P1 и концом в точке P2 имеет координаты (x2-x1, y2-y1). Если P(x, y) – произвольная точка на прямой, то координаты вектора P1P равны (x — x1, y – y1).
С помощью векторного произведения условие коллинеарности векторов P1P и P1P2 можно записать так:
|P1P,P1P2|=0, т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1)=0
или
(y2-y1)x + (x1-x2)y + x1(y1-y2) + y1(x2-x1) = 0
Последнее уравнение переписывается следующим образом:
ax + by + c = 0, (1)
где
a = (y2-y1),
b = (x1-x2),
c = x1(y1-y2) + y1(x2-x1)
Итак, прямую можно задать уравнением вида (1).
Как найти точку пересечения прямых?
Очевидное решение состоит в том, чтобы решить систему уравнений прямых:
ax1+by1=-c1
ax2+by2=-c2 (2)
Ввести обозначения:
Здесь D – определитель системы, а Dx,Dy — определители, получающиеся в результате замены столбца коэффициентов при соответствующем неизвестном столбцом свободных членов. Если D ≠ 0, то система (2) является определенной, то есть имеет единственное решение. Это решение можно найти по следующим формулам: x1=Dx/D, y1=Dy/D, которые называются формулами Крамера. Небольшое напоминание, как вычисляется определитель второго порядка. В определителе различают две диагонали: главную и побочную. Главная диагональ состоит из элементов, взятых по направлению от верхнего левого угла определителя в нижний правый угол. Побочная диагональ – из правого верхнего в нижний левый. Определитель второго порядка равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.

 WpfAppCrossSegmentSegment-vs17.zip
WpfAppCrossSegmentSegment-vs17.zip