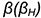Внимание!
Точка пересечения
перпендикуляра с плоскостью определяется
по правилам нахождения точки пересечения
прямой с плоскостью. А именно, искомая
точка К определяется с помощью
вспомогательной прямой, заведомо
принадлежащей плоскости
— проведём через
перпендикуляр вспомогательную
проецирующую плоскость (горизонтально
проецирующую или фронтально проецирующую);
— построим линию
пересечения
(3-4)
данной плоскости ΔАВС
и вспомогательной плоскости, (точка
встречи К
определится при пересечении перпендикуляра
и построенной прямой (3-4));
— на чертеже через
горизонтальную проекцию перпендикуляра
проведём горизонтально проецирующую
плоскость β1
и построим линию пересечения (3-4)
плоскости ΔАВС
с проецирующей плоскостью
β1.
Черт. 4
Фронтальная
проекция точки встречи К2
лежит на пересечении фронтальной
проекции перпендикуляра и фронтальной
проекции линии (32
-42).
Горизонтальная проекция К1
определяется по линии связи.
Видимость
перпендикуляра и плоскости ΔАВС
определяется по конкурирующим точкам.
Видимость горизонтальной проекции А1С1
стороны ΔАВС
и горизонтальной проекции отрезка D1К1
перпендикуляра
относительно горизонтальной плоскости
проекций определяется конкуренцией
точек 42
и 52
(точка
51
принадлежащая
перпендикуляру – видима).
Видимость фронтальной
проекции А2В2
стороны ΔАВС
и фронтальной проекции отрезка D2K2
определяется
конкуренцией точек 61
и 71
(точка
72
принадлежащая перпендикуляру – видима).
3. Определить натуральную величину отрезка от точки d до точки встречи методом прямоугольного треугольника,(черт. 5), для этого:
— на горизонтальной
проекции перпендикуляра D1К1
строим
прямоугольный треугольник D1К1Do,
в котором катет D1Do
равен расстоянию Δ,
а гипотенуза DoК1
будет равна
натуральной величине отрезка
DК.
Черт. 5
Условие задачи
№3:
Построить линию
пересечения двух плоскостей. Определить
их видимость на плоскостях проекций.
Алгоритм
построения линии пересечения плоскостей
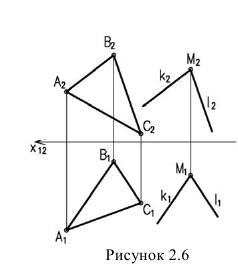
1. Строим точки пересечения прямых, принадлежащих одной плоскости, со второй плоскостью (черт. 6), для этого:
Черт.6
Внимание!
Линия пересечения
двух плоскостей общего положения может
быть построена двумя способами:
— построив точки
пересечения двух прямых одной плоскости
с другой плоскостью, т.е. дважды применив
решение задачи на пересечение прямой
с плоскостью. Этот способ применяют,
как правило, для построения линии
пересечения плоскостей в случае их
совмещенного расположения;
— вводя две
вспомогательные проецирующие плоскости,
построить линии их пересечения с
заданными плоскостями.
Две соответственные
точки пересечения этих линий определят
искомую линию пересечения плоскостей.
Способ введения
двух вспомогательных проецирующих
плоскостей применяют и для построения
линии пересечения разнесенных
плоскостей.
Отметим, что при
решении задачи первым способом, точка
пересечения прямой с плоскостью также
может быть определена с помощью
вспомогательной проецирующей плоскости,
проведенной через рассматриваемую
прямую.
Нахождение точки
пересечения прямой с плоскостью
посредством проведения через данную
прямую вспомогательной проецирующей
плоскости базируются на собирательном
свойстве
проецирующей плоскости. А именно, всё,
что находится в этой плоскости (точки,
прямые и том числе, точка пересечения
этой плоскости с заданной прямой)
располагаются на вырожденной
(в виде
прямой) проекции проецирующей плоскости.
— одну из плоскостей
∆EFD
выбираем в качестве основной плоскости,
а во второй плоскости ∆АВС
возьмем две прямые, ей принадлежащие
АВ
и СВ;
— через прямые
проведём вспомогательные плоскости
(горизонтально или фронтально
проецирующие). В нашем примере через
С2В2
фронтально-проецирующую плоскость α2
,
через А1В1
– горизонтально-проецирующую β1;
— построим линию
пересечения (1-2)
и (3-4)
плоскости ∆EFD
с плоскостями α2
и β1.
Горизонтальная
проекция точки встречи М1
стороны ВС
с плоскостью ∆EFD
будет находиться на пересечении
горизонтальной проекции В1С1
с горизонтальной проекцией линии (11
-21).
Фронтальная
проекция точки встречи N2
стороны АВ
с плоскостью ∆EFD
будет находиться на пересечении
фронтальной проекции А2В2
с горизонтальной проекцией линии (32
-42).
Фронтальная
проекция точек M2
и N1
определится
по линиям проекционной связи.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
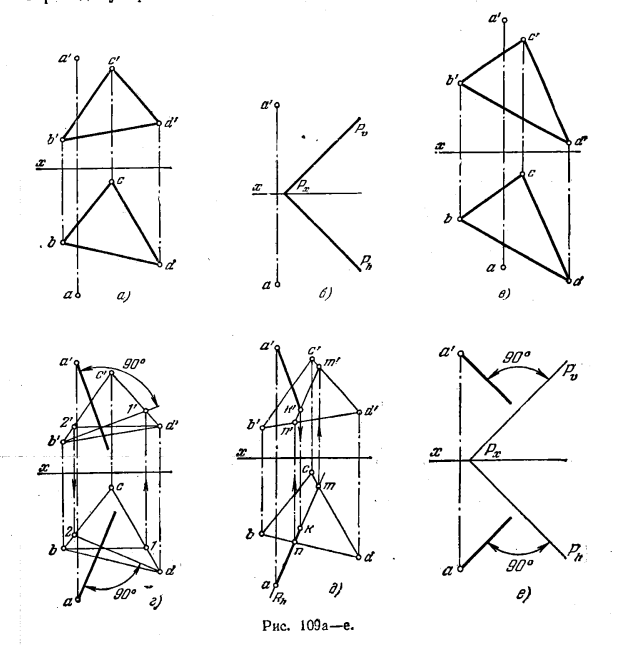
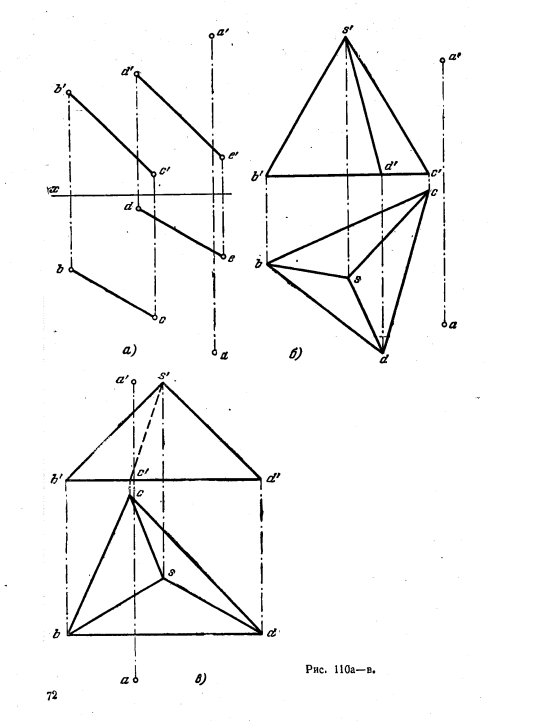
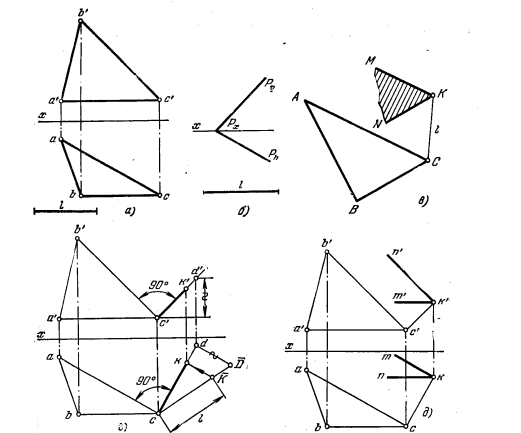
111*. Провести перпендикуляр из точки А к плоскости, заданной: а) треугольником BCD (рис. 109, а); б) следами (рис. 109,6); в) треугольником BCD (рис. 109, в). Во всех случаях построить основание перпендикуляра на заданной плоскости.
Решение, а) Через точку В (рис. 109, г) проводим фронталь В—1 заданной плоскости, а через точку D — горизонталь D—2. фронт. проекция искомого перпендикуляра проходит через а’ перпендикулярно к b’1′ а горизонтальная — через а перпендикулярно к d—2. Основание перпендикуляра (рис. 109, д) определяется как точка пересечения этого перпендикуляра с плоскостью. Заключаем его в гориэонтально-проецирующую плоскость R (задаем ее следом Rh) и находим линию пересе-
чения этой плоскости с плоскостью треугольника — прямую NM. Получаем точку k’ — фронт. проекцию основания перпендикуляра — и по k’ находим k.
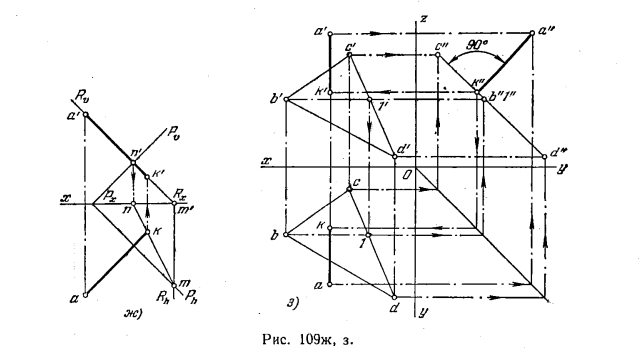
б) На рис. 109, е фронт. проекция перпендикуляра проведена под прямым углом к следу Pϑ, а горизонтальная — под прямым углом к Ph. Для построения основания перпендикуляра заключаем его (рис. 109, ж) во фронтально-проецирующую плоскость R, строим линию пересечения плоскостей R и Р — прямую MN. Получаем точку k — горизонт. проекцию основания перпендикуляра; по ней находим k’.
в) Проведя горизонталь В—1 (рис. 109, а), видим, что эта прямая параллельна оси х. Из этого заключаем, что плоскость треугольника является профильно-проецирующей. Следовательно, перпендикуляр к ней — прямая профильная.
Строим профильные проекции треугольника и точки А. Из a» проводим перпендикуляр на с»d». Точка k» — профильиая проекция основания перпендикуляра. По k» находим k’ и k на одноименных с ними проекциях искомого перпендикуляра.
112. Найти основания перпендикуляров, проведенных из точки А:
а) к плоскости, заданной параллельными прямыми ВС и DE (рис. 110, а);
б) к плоскости грани SCD пирамиды SBCD (рис. 110, б);
в) к плоскости грани SBD пирамиды SBCD (рис. 110, в).
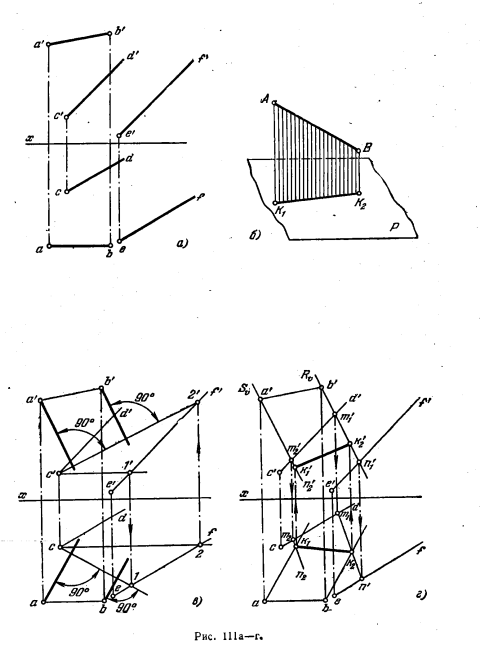
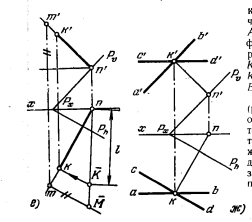
113*. Построить на плоскости, заданной параллельными прямыми CD и EF, геометрическое место оснований перпендикуляров, проведенных из точек прямой АВ к этой плоскости (рис. 111, а)
Решение. Искомым геометрическим местом точек является (рис. 111, б) линия пересечения K1K2 плоскостей, 1) заданной и 2) перпендикулярной к ней, проведенной через прямую АВ.
Проводим (рис. 111, в) в заданной плоскости горизонталь С—1 и фронталь С—2. фронт. проекции перпендикуляров перпендикулярны к с’2′, а горизонтальные — к с—1.
Для построения искомого геометрического места точек находим (рио. 111, г) точки К1 и K2 пересечения проведенных перпендикуляров с заданной плоскостью. Прямая К1К2 и есть искомое геометрическое место.
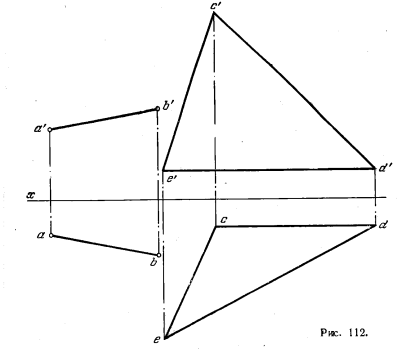
114. Построить на плоскости, заданной треугольником CDE, геометрическое место оснований перпендикуляров, проведенных из точек прямой АВ к этой плоскости (рис. 112).
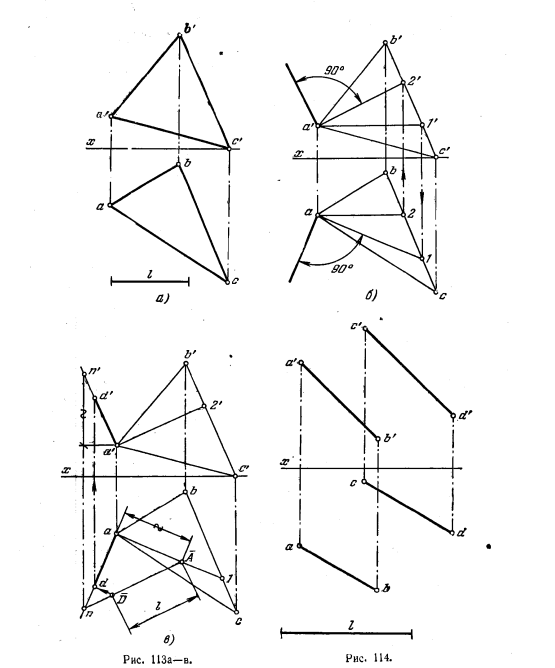
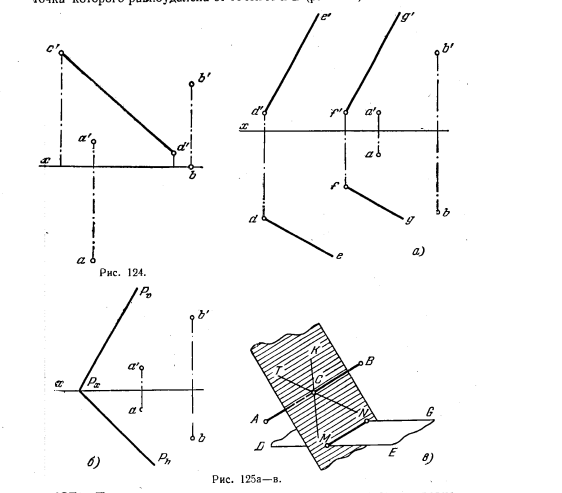
115*. Из вершины А провести перпендикуляр к плоскости треугольника ABC (рис. 113, а) и отложить на нем отрезок длиной l.
Решение. Для построения перпендикуляра проводим (рис. 113, 6) горизонталь А— 1 и фраяталь А—2 плоскости треугольника; фронт. проекция перпендикуляра перпендикулярна к a’2′, а горизонтальная — к а—1.
Дальнейшее построение (рис. 113, в) аналогично выполненному в задаче 20. Прямые a’d’ и ad являются проекциями искомого отрезка.
Эта задача имеет два решения. Во втором случае надо продолжить перпендикуляр в другую сторову от заданной плоскости.
116. Из точки D провести перпендикуляр к плоскости, заданной параллельными прямыми АВ и CD, и отложить на нем отрезок длиной l (рис. 114).
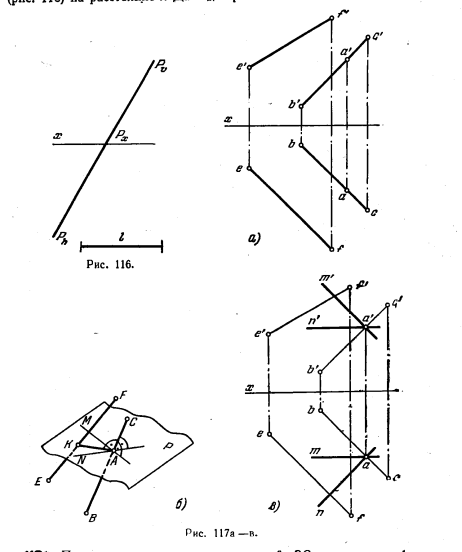
117*. Построить геометрическое место точек, удаленных от некоторой плоскости на расстояние l. Дать решение для случаев, когда плоскость задана треугольником ABC (рис. 115, а) или следами (рис. 115, б).
Решение. Искомым геометрическим местом точек являются две плоскости, параллельные данной и расположенные по обе стороны от нее на расстоянии l.
На рис. 115, в показана одна из таких плоскостей. Для построения этой плоскости (рис. 115, г) проводим из любой точки данной плоскости (например, С) перпендикуляр
к плоскости (обратите внимание на то, что в заданном треугольнике сторона АС является горизонталью, а ВС— фронталью) и откладываем на нем отрезок КС длиной l. Затем через точку К (рис, 115, д) проводим прямые КN и КМ, параллельные хотя бы сторонам ВС и АС треугольника ABC.
Если плоскость задана следами (рис. 115, б), то удобно взять точку на одном из следов. На рис. 115, е взята точка N на следе Pϑ. Проведя из этой точки перпендикуляр к пл. Р и отложив на нем отрезок, равный l, проводим через точку К (рис. 15,ж) горизонталь CD и фронталь АВ искомой плоскости
118. Построить геометрическое место точек, удаленных от пл. Р (рис. 116) на расстояние l. Дать два решения.
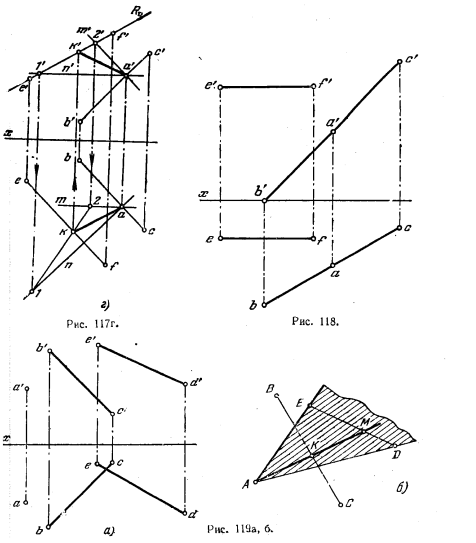
119*. Провести перпендикуляр к прямой ВС из ее точки А до пересечения его с прямой EF (рис. 117, а).
Решение. Геометрическим местом перпендикуляров к прямой ВС, проведенных из точки А, является пл. Р, проходящая через точку А перпендикулярно к прямой ВС (рис. 117, б). Точка К пересечения этой плоскости с прямой EF является точкой пересечения искомого перпендикуляра с прямой EF.
на рис. 117, в задаем плоскость, перепендикулярную к BC, фронталью AM и горизонталью AN. Определяем точку K пересечения прямой EF с этой плоскостью (рис. 117,г), заключая EF во фронтально-проецирующую плоскость R(задаем ее следом Rϑ); k’a’ и ka — проекции искомого перпендикуляра.
120. Из точки A провести перпендикуляр к прямой BC до пересечения его с прямой EF (рис. 118).
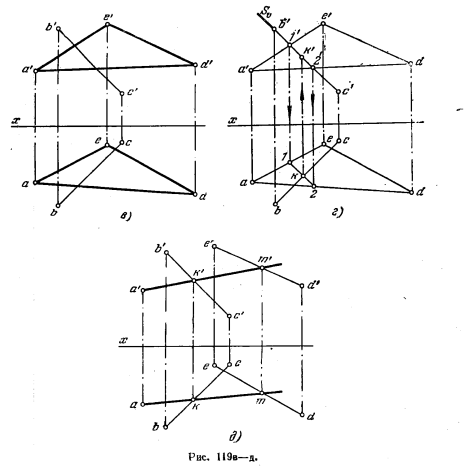
121*. Через точку А провести прямую, пересекающую прямые
ВС и ED (рис. 119, а).
Решение. Геометрическим местом прямых, проходящих через точку А и пересекающих прямую ED, является плоскость, задаваемая этими элементами (рис. 119, б). Если построить такую плоскость и найти точку К ее пересечения со второй прямой (ВС), то искомая прямая пройдет через точки А а К. Такое построение выполнено на рис. 119, в и 119, г, где сначала плоскость, определяемая точкой А и прямой ED, выражена треугольником AED, а затем найдена точка К пересечения второй прямой (ВС) с плоскостью этого треугольника.
Искомая прямая проходит через точки А и К и пересекает прямую ED в точке М (ряс. 119,6). Конечно, при точном построении проекции m и m’ должны оказаться на линии связи m’m, перпендикулярной к оси х.
Данную задачу можно решить и иначе: взять две плоскости — одну, определяемую точкой А и прямой ED (как это сделано на рис. 119, в), а другую — точкой А я прямой ВС. Линия пересечения этих двух плоскостей н будет искомой прямой, проходящей через точку А и пересекающей ВС в ED,
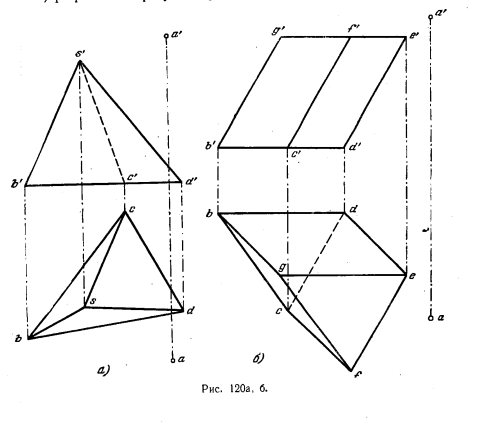
122. Через точку А провести прямую, пересекающую:
а) ребро SD и сторону ВС основания пирамиды SBCD (рис. 120, а),
б) ребро BG и сторону EF верхнего основания призмы (рис. 120,6).
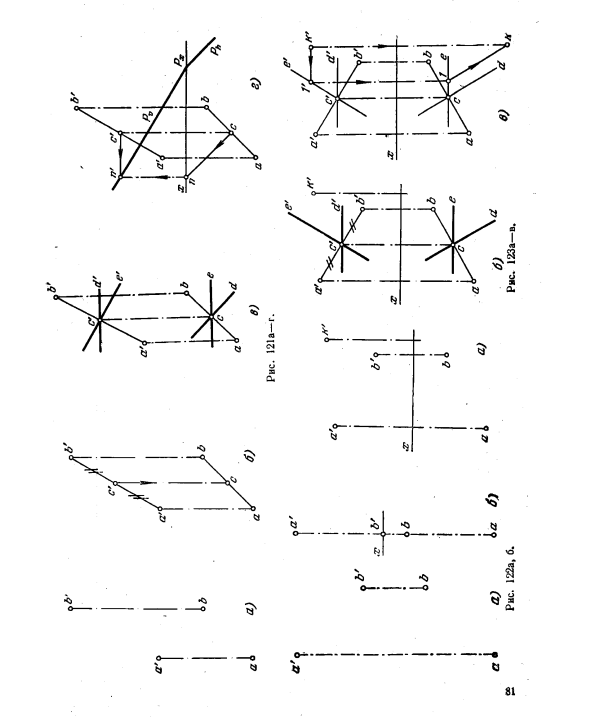
123*. Построить геометрическое место точек, равноудаленных от точек А и В (рис, 121, а).
Решение. Искомым геометрическим местом является плоскость, проходящая через середину отрезка АВ перпендикулярно к нему.
Делим проекции отрезка АВ пополам (рис. 121, б). Через середину (точку С) проводим горизонталь CD ⊥ АВ и фронталь СЕ ⊥ АВ (рис.121, в) искомой плоскости. Чтобы выразить эту плоскость следами, надо задаться осью проекций и построить хотя бы фронт. след горизонтали (точка N, рис. 121,а) и через него провести соответствующий след пл. p. След Рϑ ⊥ a’b’, а след Ph ⊥ ab (или || nс).
124. Построить геометрическое место точек, равноудаленных от точек A и В (рис. 122, а и б). В первом случае ответ дать без следов, А во втором — в следах.
125*. Построить недостающую проекцию точки К, равноудаленной от точек А и В (рис. 123, а).
Решение. Так как геометрическим местом всех точек пространства, равноудаленных от точек А и В, является плоскость, проходящая через середину отрезка АВ перпендикулярно к нему, то точка К должна принадлежать этой плоскости.
На рис. 123, б такая плоскость определена фронталью СЕ и горизонталью CD, проходящими через середину отрезка АВ.
Проводим {рис. 123, в) через k’ фронт. проекцию к’1′ горизонтали плоскости и строим ее горизонт. проекцию, на которой отметим точку k — искомую проекцию точки К-
126. Построить недостающую проекцию отрезка CD, каждая точка которого равноудалена от точек А и В (рис. 124).
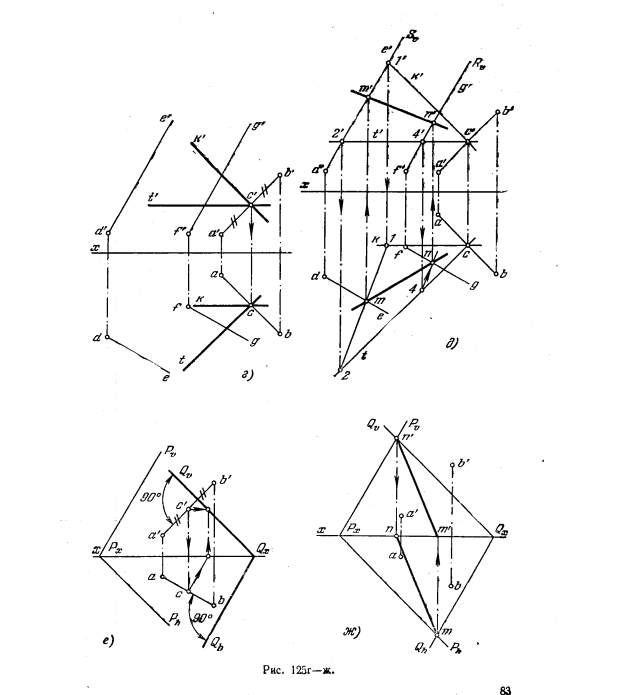
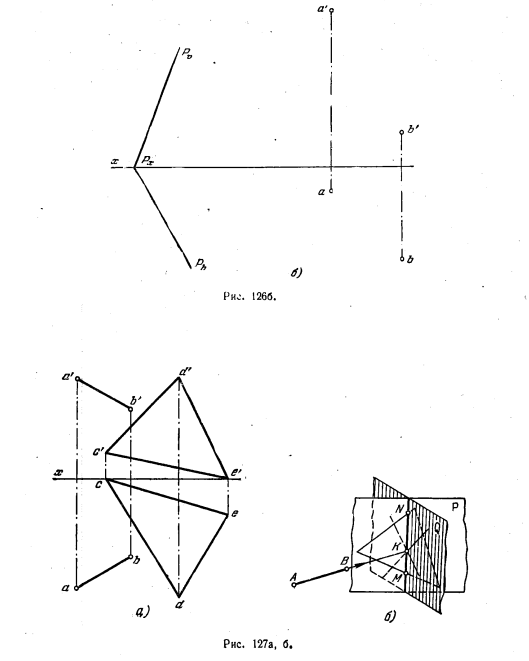
127*. Построить на плоскости геометрическое место точек, равноудалённых от двух данных точек А и В: а) плоскость задана параллельными прямыми (рис. 125, а); б) плоскость задана следами (рис. 125, б).
Решение. Так как геометрическим местом точек, равноудаленных от точек А и В, является плоскость, проходящая через середину отрезка АВ перпендикулярно к нему (рис. 125, в), то искомым геометрическим местом будет линия пересечения этой плоскости с заданной (прямая MN).
На рис. 125, г плоскость, перпендикулярная к отрезку АВ в его середине, выражена фронталью КС и горизонталью ТС.
Теперь надо найти линию пересечения двух плоскостей, что сделано путем нахождения точек пересечения прямых DE и FG (рис. 125, д), определяющих заданную плоскость, с плоскостью, выраженной горизонталью ТС и фронталью КС (см. задачу 86).
На рис. 125, е плоскость Q, перпендикулярная к отрезку АВ в его середине, выражена следами. Находим точки М и N пересечения одноименных следов плоскостей Р и Q и проводим через них искомую прямую MN (рис. 125, ж).
128. Построить геометрическое место точек, равноудаленных от точек A и B:
а) на плоскости, заданной треугольником CDE (рис. 126, а);
б) на пл. Р (рис. 126, б).
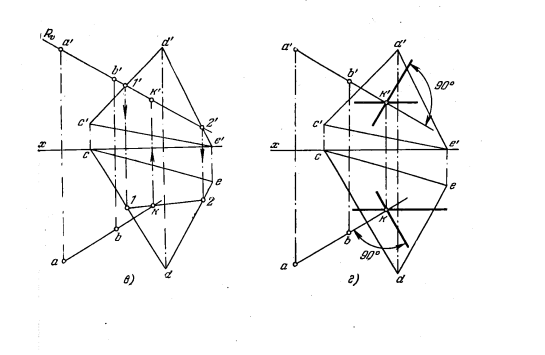
129* Дана плоскость треугольника CDE и прямая АВ (рис. 127, а). Провести в этой плоскости прямую, пересекающую АВ под прямым углом.
Решение. Искомая прямая получится (рис. 127, б) как линия пересечения плоскости треугольника (Р) с пл. Q, перпендикулярной к АВ и проходящей через точку (K) пересечения АВ с заданной плоскостью.
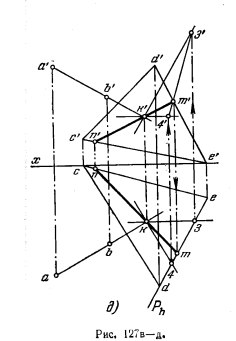
Поэтому находим (рис. 127, в) точку К пересечения прямой АВ с плоскостью треугольника CDE. В качестве вспомогательной плоскости взята фроятально-проецирующая плоскость R, проведенная через прямую АВ. Найдя проекции k и k’, проводим через них проекции горизонтали и фронтали плоскости, перпендикулярной к АВ (рис. 127, г). Для построения искомой линии пересечения плоскостей находим (рис. 127, д) точку (m’; m) пересечения стороны треугольника ED с проведенной через точку К плоскостью. Прямая МК (m’k’; mk) является искомой прямой
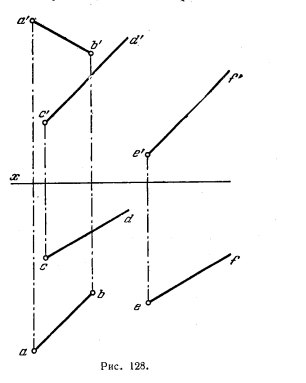
130. Дана прямая АВ и плоскость, заданная параллельными прямыми CD и EF. Провести в этой плоскости прямую, пересекающую прямую АВ под прямым углом (рис. 128).
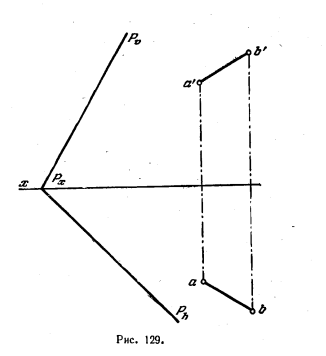
131. Дана прямая АВ и пл. Р. Провести в этой плоскости прямую, пересекающую прямую АВ под прямым углом (рис. 129).
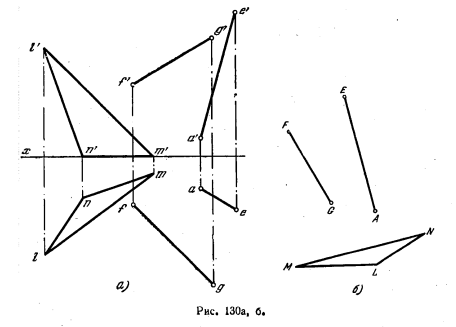
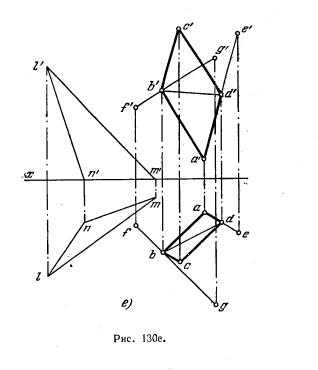
132*. Даны плоскость треугольника LMN и прямые АЕ и FG. Построить параллелограмм, у которого сторона AD лежит на прямой АЕ, сторона АВ параллельна плоскости треугольника, вершина В принадлежит прямой FG, диагональ BD перпендикулярна к стороне AD (рис. 130, а).
Решение. Наметим план решения (рис. 130, б и в).
1. Через точку А пронести плоскость (P), параллельную плоскости треугольника LMN.
2. Найти точку пересечения (В) прямой FG с пл. Р.
3. Через, точку В провести плоскость (Q), перпендикулярную к прямой АЕ.
4. Найти точку пересечения (D) прямой АЕ с пл. Q.
5. Провести отрезок АВ и параллельно ему прямую через точку D, а через В — прямую, параллельную AD.
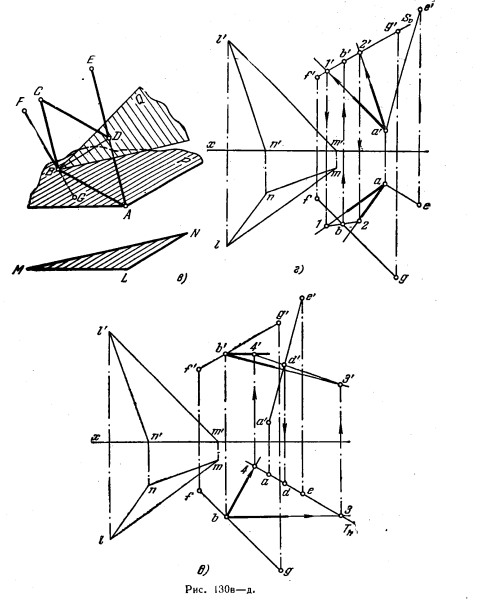
На рис. 130, в и г показано построение пл. P, параллельной плоскости треугольника LMN. Пл. P, проведенная через точку А, задана двумя пересекающимися прямыми А— 1 и А— 2, из которых А—1 параллельна LM, а А—2 параллельнаLN.
На тех же рисунках показано нахождение точки В пересечения прямой FG с пл. Р, для чего через FG проведена фронтально-проецирующая плоскость S, заданная следом Sϑ. горизонт. проекция 1—2 линии пересечения плоскостей Р и S пересекает горизонт. проекцию fg в точке b. По точке b находим проекцию b’ на f’g’.
На рис. 130, д показано построение пл. Q, перпендикулярной к АЕ. Эта плоскость проведена через точку В и выражена горизонталью В—4 и фронталью В—3, перпендикулярными к АЕ. На том же чертеже показано построение точки D, в которой прямая АЕ пересекает пл. Q, выраженную горизонталью В—4 и фронталью В—3.
Через АЕ проведена горизонтально-проецирующая плоскость Т, выраженная ее следом Тh, построены проекции 3—4 и 3’4′ линии пересечения плоскостей Т и Q и проекции d’ и d.
На рис. 130, е показано построение искомого параллелограмма, для чего проведены проекции а’b’ и ab, a’d’ и ad двух сторон параллелограмма, а затем b’с’|| а’d’; bc || ad; d’c’ || а’b и dc || ab. Точки с’ и с должны оказаться на линии связи сс’, перпенди-кулярной к оси x.
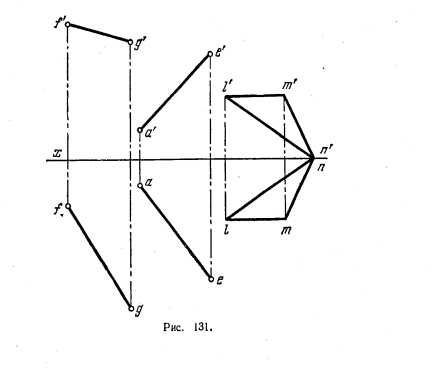
133. Даны треугольник LMN и прямые АЕ и FG. Построить параллелограмм, у которого сторона AD лежит на прямой АЕ, сторона АВ параллельна плоскости треугольника, вершина В принадлежит прямой FG, диагональ BD перпендикулярна к стороне AD (рис. 131).
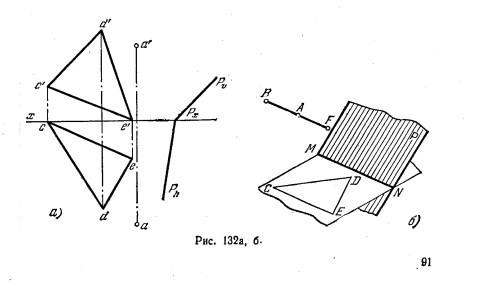
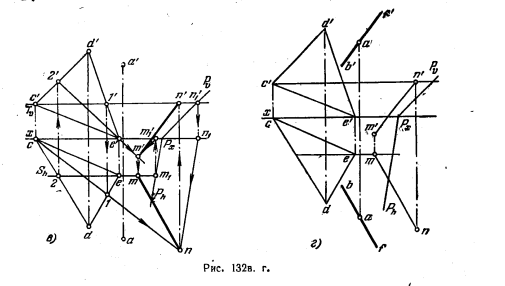
134*. Через точку А провести прямую, параллельную пл. Р и плоскости треугольника CDE (рис. 132, а).
Решение. Если искомая прямая должна быть одновременно параллельна двум плоскостям, то она должна быть параллельна линии пересечения этих плоскостей
(рис, 132, б). Вводя две вспомогательные плоскости Т и S, находим линию пересечения MN плоскостей (рис. 132, в). Проекции искомой прямой b’f’ и bf проходят через а’ и a параллельно одноименным с ними проекциям прямой MN (рис. 132,г).
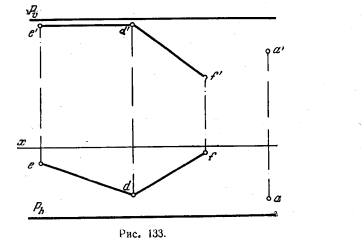
I3S. Через точку А провести прямую, параллельную пл. Р и плоскости, заданной пересекающимися прямыми DE и DF (рис, 133).
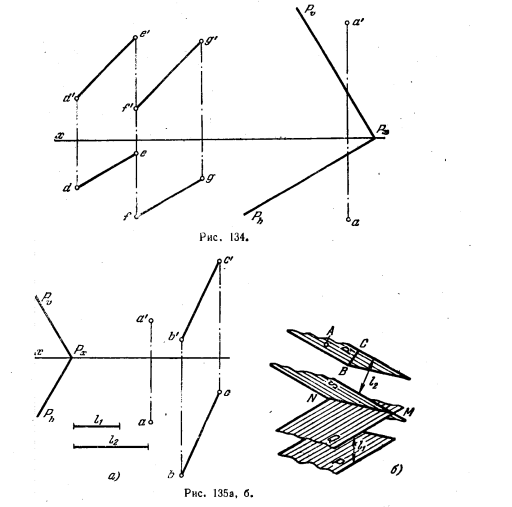
136. Через точку А провести прямую, параллельную пл. Р и плоскости, заданной параллельными прямыми DE и FG (рис. 134).
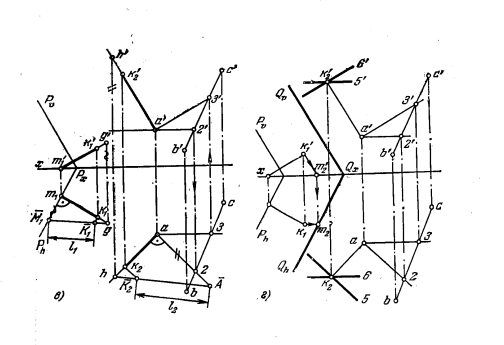
137*. Провести прямые, каждая из которых отстоит от пл. Р на расстояние l1, а от плоскости, заданной прямой ВС и точкой А, на расстояние l2 (рис. 135, а).
Решение. В основе решения лежит представление о геометрическом месте прямых, отстоящих от данной плоскости на определенное расстояние, т. е. от плоскости параллельной данной.
Искомыми прямыми являются линии MN пересечения двух плоскостей Q, параллельных пл. Р и расположенных по обе стороны от нее.на расстоянии l1, с двумя
плоскостями S, параллельными второй из заданных плоскостей и отстоящими от нее на расстояние l2. Всего таких прямых может быть четыре. На рис. 135, б изображена одна из них.
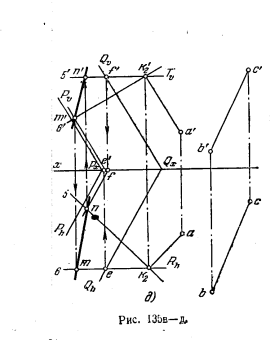
На рис. 135, в показано: 1) проведение перпендикуляра к пл. Р из взятой в ней точки М1 и построение точки К1 на этом перпендикуляре на расстоянии М1K1 = l1; 2) проведение перпендикуляра к плоскости, заданной точкой А и прямой ВС, из точки А (при помощи горизонтали А—2 и фронтали А—3) и построение точки K2 на этом перпендикуляре на расстоянии АК2 = l2
На рис. 135, г показано проведение через точку K1 пл.Q параллельно пл. P и через точку плоскости K2, выраженной горизонталью К25 и фронталью К26, соответственно параллельными горизонтали А—2 и фронтали А—3, принадлежащим плоскости, заданной точкой А и прямой ВС.
На рис. 135, д построена линия пересечения пл. Q и плоскости S, выраженной горизонталью К25 и фронталью К26. Полученная прямая МN параллельна обеим заданным плоскостям.
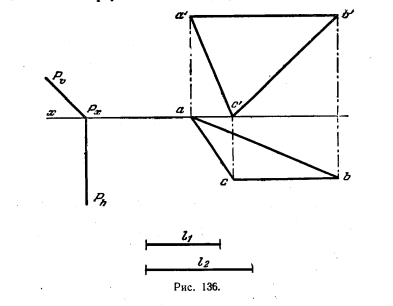
138. Провести одну из прямых, отстоящих от пл. Р на расстояние l1 и от плоскости треугольника ABC на расстояние l2 (Рис. 136).
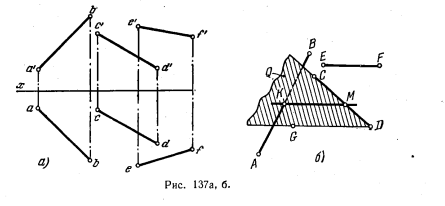
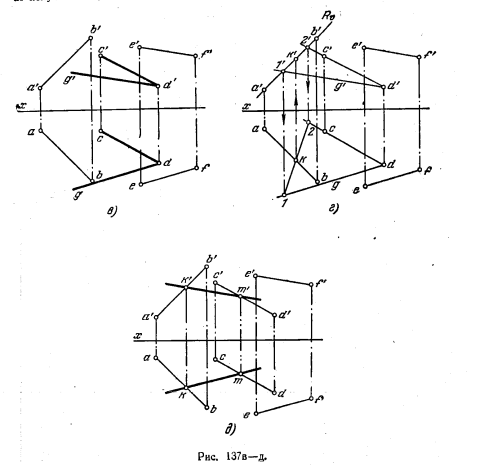
139*. Провести прямую, пересекающую заданные прямые АВ и CD и параллельную прямой EF (рис. 137, а).
Решение. Наметим план решения задачи {рнс. 137, б).
1. Через прямую CD провести плоскость (Q), параллельную прямой ЕF.
2. Найти точку (К), в которой прямая АВ пересечет пл. Q.
3. Через точку К провести прямую (КМ), параллельную заданной прямой ЕF.
На рис. 137, в показано построение пл. Q, проходящей через прямую CD и параллельной прямой EF Пл. Q выражена прямой CD и пересекающей ее прямой DG, проведенной через точку D параллельно EF.
На рис. 137, в показано построение точки К, в которой прямая АВ пересекает пл. Q. Прямая АВ заключена в фронтально-проецирукпцую плоскость R, выраженную ее следом Rϑ. Пл. R пересекает пл. Q по прямой 1—2. В пересечении 1—2 и ab получается проекция k; по точке k находим фронт. проекцию k’.
Наконец, на рис. 137, д показаны проекции km и k’m’ искомой прямой: k’m’ || e’f’ и km || ef. Конечно, проекции m’ и m должны получиться на линии связи m’m, перпендикулярной к оси х.
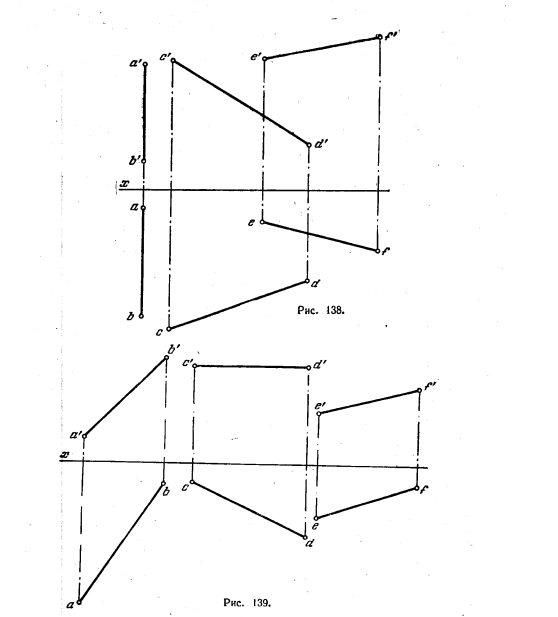
140. Провести прямую, пересекающую заданные прямые АВ и CD и параллельную прямой EF (рис. 138).
141. Провести прямую, пересекающую заданные прямые АВ и CD, параллельно прямой EF (рис. 139).
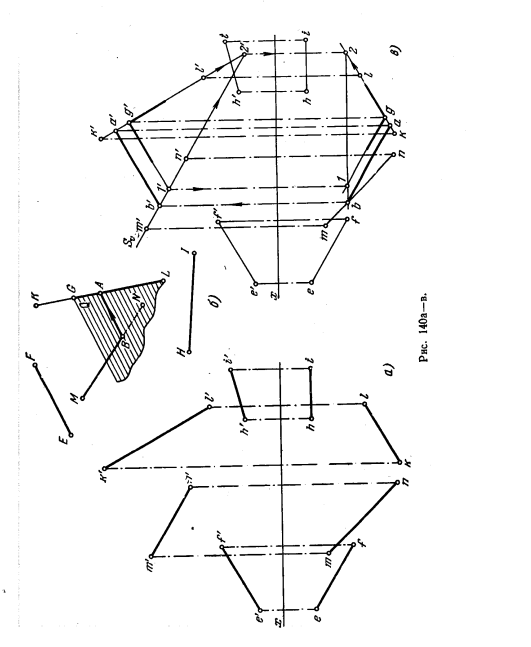
142*. Даны прямые EF, MN, KL и HI. Построить прямоугольник ABCD, у которого сторона АВ параллельна прямой EF, вершина А лежит на прямой KL, вершина В — на прямой MN и вершина С — на прямой HI (рис. 140, а).
Решение. Сторона АВ должна пересечь KL и МN и быть параллельной ЕF (см. задачу 139).
Если (рис. 140,6) провести хотя бы через точку G, лежащую на KL, прямую, параллельную EF, то получим пл. Q, параллельную EF. Далее надо найти точку В пересечения этой плоскости с прямой MN и через точку В провести в пл. Q. Прямую, параллельную EF. Эта прямая АВ пересекает прямые MN и KL и параллельна EF.
Построение показано на рис. 140, в. Так как стороны ВС и АВ должны быть взаимно перпендикулярны, то проводим (рис. 140,гид) через точку В пл. Р, перпендикулярную к стороне АВ, и строим точку С пересечения ее с прямой HI.
Через точки А и С проводим прямые (рис. 140, г и ё), параллельные прямым ВС и АВ, до пересечения их в точке D.
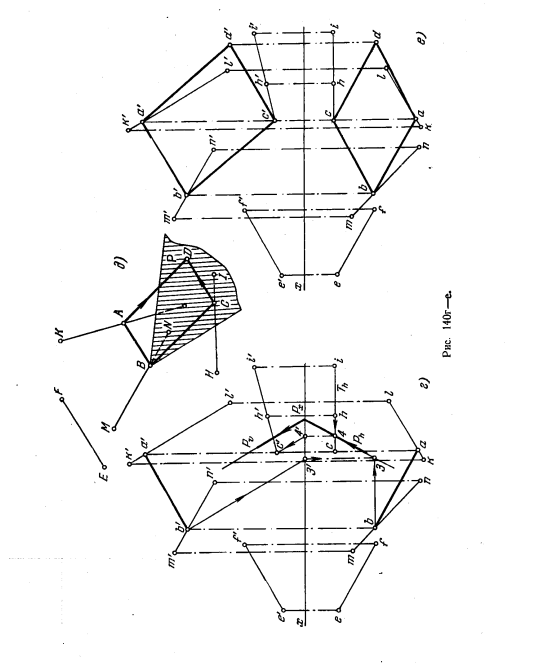
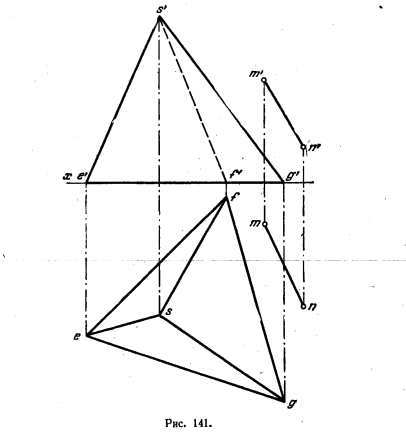
143.. Даны пирамида SEFG и прямая MN (рис. 141). Построить прямоугольник ABCD, у которого сторона АВ параллельна прямой MN, вершина А лежит на ребре SF, вершинАВ — на стороне основания EG, вершина D — на ребре SE.
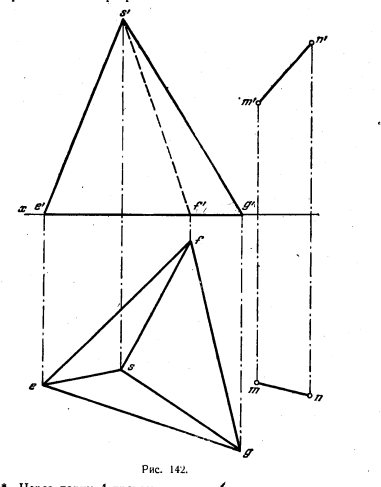
144. Даны пирамида SEFG и прямая MN (рис. 142). Построить прямоугольник ABCD, у которого сторона АВ параллельна прямой MN, вершина А лежит на ребре SG, вершина В — на стороне основании EF и вершина D — на ребре SF.
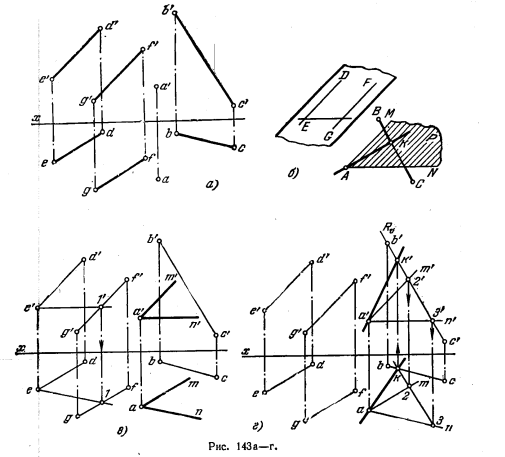
145*. Через точку А провести прямую, параллельную плоскости, заданной параллельными прямыми ED и FG, и пересекающую прямую ВС (рис. 143, а).
Решение. Можно составить следующий план решения задачи (рис. 143, б):
1) через точку А провести плоскость (Р), параллельную заданной плоскости;
2) найти точку (К) пересечения ВС о пл. Р;
3) провести искомую прямую АК.
На рис. 143, в пл. Р, проведенная через точку A, выражена прямой АМ || ED (a’m’ || e’d’, am || ed) и горизонталью AN, для проведения горизонт. проекции которой
взята горизонталь E—1 в плоскости, заданной прямыми ED я FG (an || ef). На рис. 143, г показано построение точки К, в которой заданная прямая ВС пересекает пл. Р: через ВС проведена фронтально-проецирующая плоскость (она выражена
следом Rϑ), построены проекции 2’3′ и 2—3 прямой пересечения плоскостей Р и R, получена точка к в пересечении прямой 2—3 и bс. По проекции k найдена проекция k’. Проекции искомой прямой а’k’и аk.
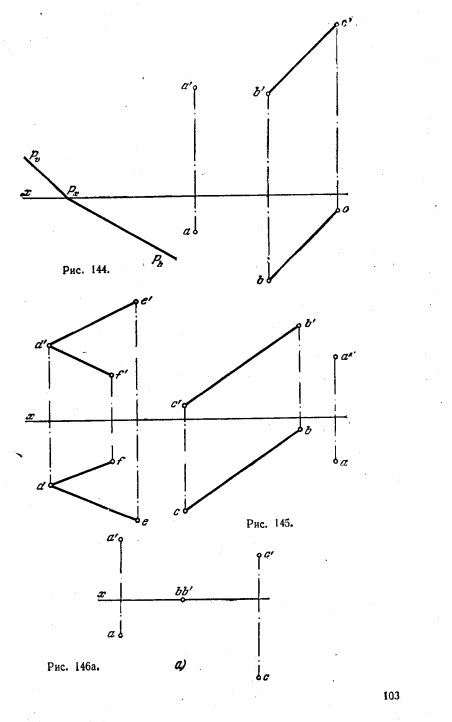
146. Через точку А (рис. 144) провести прямую, параллельную пл. Р и пересекающую прямую ВС.
147. Через точку А (рис. 145) провести прямую, параллельную плоскости, заданной пересекающимися прямыми DE и DF, и пересекающую прямую ВС.
148*. Построить геометрическое место точек, равноудаленных от заданных точек А, В и С (рис. 146, а),
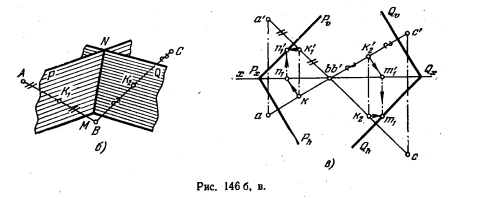
Решение. Искомым геометрическим местом является линия пересечения MN (рис. 146, б) плоскостей Р и Q, соответственно перпендикулярных к отрезкам АВ и ВС и проходящих через точки K1 и K2 в серединах этих отрезков. На рис. 146, в эти
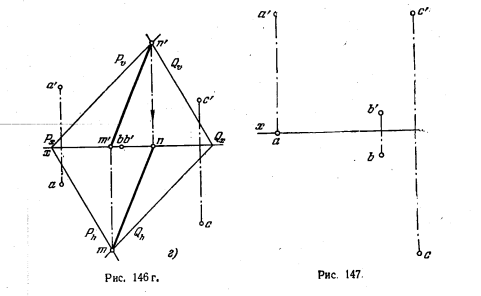
плоскости выражены их следами. Используя (рис. 146, г) точки пересечения одноименных следов плоскостей, строим линию их пересечения MN.
149. Построить геометрическое место точек, равноудаленных от заданных точек А, В и С (рис. 147).
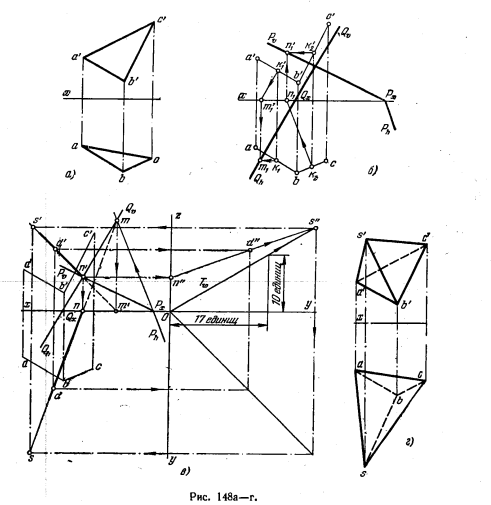
150*. Дан треугольник ABC (рис. 148, а). Построить пирамиду SABC, вершина S которой равноудалена от точек А, В и С. Расстояние от точки S до пл. V в 1,7 раза больше расстояния ее до пл. Н.
Решение. Геометрическим местом точек, равноудаленных от точек А, В и С (см. задачу 148*), является линия пересечения MN плоскостей Q и Р, проведенных через середины (K1 и К2) отрезков АВ и ВС перпендикулярно к ним (риc. 148, б и в). Вершина S должна лежать на этой прямой. Геометрическим местом точек, для которых ордината в 1,7 раза больше апликаты, является осевая плоскость T; ее профильный след Tω проходит (риc. 148, в) через точку О и точку, расстояние которой до
оси у равно 10 единицам, а до оси z — 17 единицам. Точка S принадлежит этой плоскости. Профильная проекция s» вершины пирамиды находится на пересечении m»n» со следом Tω (на рисунке для упрощения чертежа построена профильная проекция точки D, лежащей на прямой MN). По s» находим s’ и s. На рис. 148, г показаны проекции искомой пирамиды.
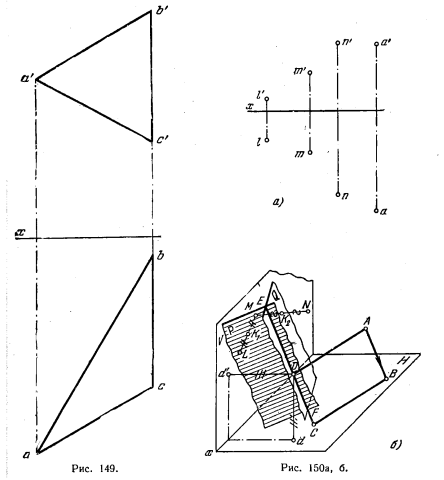
151. Дан треугольник ABC (рис. 149). Построить проекции пирамиды SABC, вершина S которой равноудалена от вершин основания ABC и лежит в пл. V.
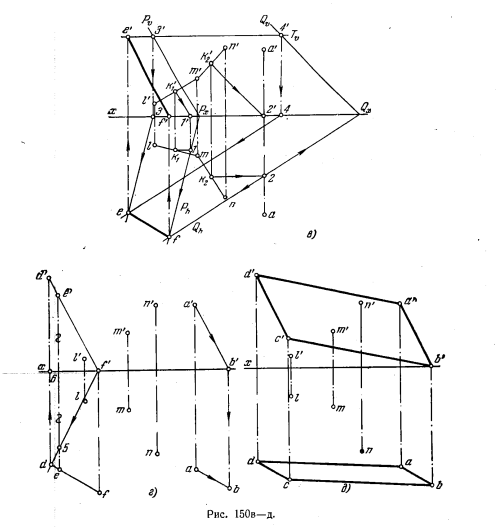
152*. Даны точки A, L, М и N (рис. 150,а). Построить параллелограмм ABCD, у которого вершина В лежит на пл. Н, сторона CD — на прямой, равноудаленной от точек L, М и N, вершина D равноудалена от плоскостей V и Н.
Решение. Так как сторона CD искомого параллелограмма должна лежать на прямой, равноудаленной от трех точек, то начинаем с построения этой прямой. Подобное построение уже встречалось: прямая EF получается как линия пересечен ния двух плоскостей (рис. 150, 6 и в) Р и Q, проведенных перпендикулярно к отрезкам LM и MN через их середины. Точку D на этой прямой находим из условия, что
она равноудалена от пл. V и пл. Н (рис. 150, г): проведем через точку f вспомогательную прямую f’5 под тем же углом к оси х, что и прямая f’e’, получаем на проекции ef точку d, а по ней d», причем d’6 = d—6.
Итак, мы получили одну из вершин искомого параллелограмма (точку D) и направление стороны, проходящей через эту точку (прямая EF). Проведя через заданную
точку А прямую, параллельную EF, получаем сторону АВ, зная, что по условию точка В должна быть в пл. Н.
Остается закончить построение проекций параллелограмма, проведя а’b’ и ab (рис. 150,6), b’с’ || a’d’ и bc || ad. Точки с’ и с должны оказаться на линии связи с’c, перпендикулярной к оси х.
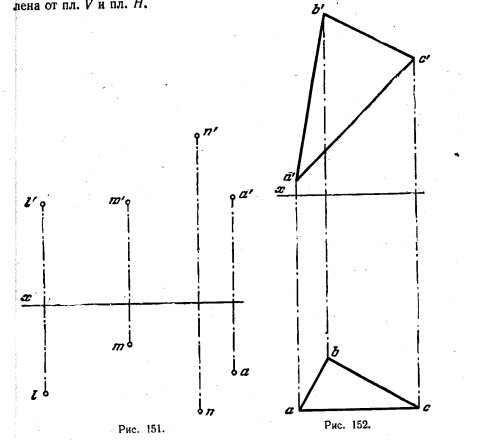
153. Даны точки A, L, М и N (рио. 151). Построить параллелограмм ABCD, у которого вершина В лежит на пл. Н, сторона CD лежит на прямой, равноудаленной от точек L, М и N, вершина D равноудалена от пл. V и пл.H
154. Дан треугольник ABC (рис. 152). Построить проекции пирамиды SABC, вершина S которой равноудалена от точек А, В и С и находится на равных расстояниях от пл. V и пл. H.
Содержание:
Проекции прямого угла:
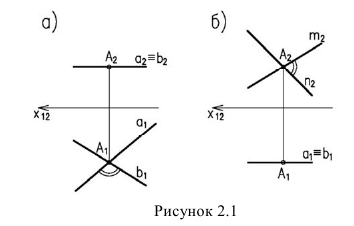
Величина угла между двумя пересекающимися прямыми в общем случае на проекциях искажается. В натуральную величину этот угол будет проецироваться в том случае, если плоскость угла параллельна одной из плоскостей проекций. Тогда другие проекции сторон угла совпадают и параллельны оси проекций (рисунок 2.1).
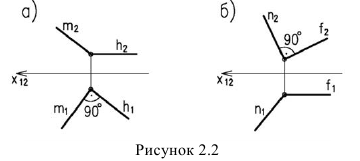
Прямой угол проецируется в натуральную величину, если одна из его сторон параллельна одной из плоскостей проекций (рисунок 2.2).
Взаимное положение примой и плоскости, двух плоскостей
Прямая относительно плоскости может занимать следующие положения: лежать в плоскости (что рассматривалось ранее); быть ей параллельна; пересекать плоскость; быть перпендикулярной плоскости (т.е. пересекать под прямым углом).
Две плоскости могут быть:
- взаимно параллельными,
- пересекающимися;
- взаимно перпендикулярными.
Перпендикулярность примой и плоскости
Условие перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым лежащим в этой плоскости.
Так как прямой угол между прямыми линиями проецируется на плоскость проекций без искажения, если одна из прямых параллельна этой плоскости проекций, то пересекающимися прямыми плоскости, которые нужно взять для построения перпендикуляра, могут быть только ее горизонталь и фронталь.
Следовательно, прямая перпендикулярна плоскости, если ее фронтальная проекция перпендикулярна фронтальной проекции фронгали плоскости, а горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали плоскости.
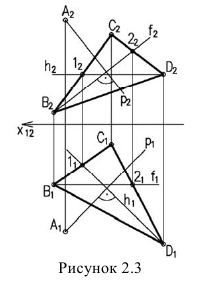
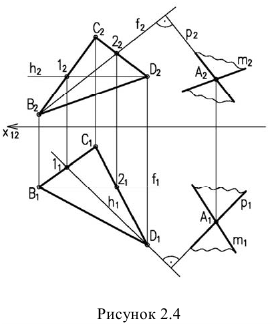
На рисунке 2.3 через точку 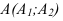
В плоскости 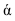
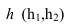
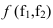
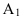
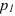
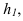
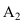
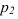
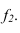
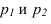
Перпендикулярности двух плоскостей
Две плоскости взаимно перпендикулярны, если одна из них содержи! перпендикуляр к другой.
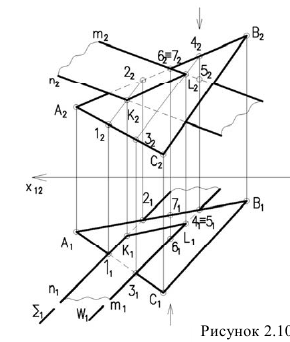
Пусть через данную прямую т необходимо провести плоскость, перпендикулярную плоскости а. заданной треугольником 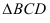
Для решения задачи достаточно на прямой т взять произвольную точку А и провести через нее прямую р, перпендикулярную данной плоскости 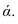
Пересекающиеся прямые m и р образуют плоскость 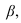
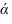
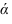
Параллельность прямой и плоскости
Условие параллельности прямой и плоскости:
Прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей этой плоскости.
Рассмотрим пример решения задачи на параллельности прямой и плоскости.
Задача: построить фронтальную проекцию прямой n, проходящей через точку А и параллельной
Для решения задачи:
Проводим горизонтальную проекцию прямой 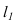
Строим фронтальную проекцию
Через точку 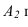
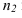
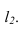
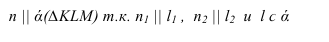
Параллельность двух плоскостей
Условие параллельности двух плоскостей:
- две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
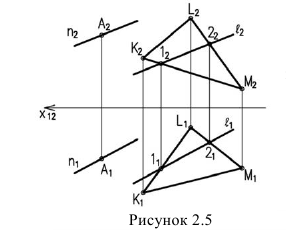
Изображенные на рисунке 2.6 плоскости 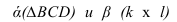
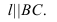
Задача на нахождение точки пересечения прямой линии с плоскостью является первой основной позиционной задачей курса начертательной геометрии.
Алгоритм решения задачи (рисунок 2.7):
1. Прямую 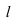
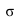
2. Находим линию пересечения (1-2) вспомогательной плоскости с заданной
3. Отмечаем точку пересечения К найденной линии пересечения (1-2) с заданной прямой
4. Определяем видимость прямой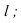
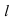
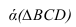
Пересечение двух плоскостей
Две плоскости пересекаются по прямой линии, поэтому для её построения достаточно найти две точки одновременно принадлежащие двум плоскостям.
Рассмотрим несколько случаев построения линии пересечения двух плоскостей.
1-й случай — пластины непрозрачные заданы с нахлёстом (рисунок 2.10).
Задача сводится к нахождению точек пересечения прямых m и n с плоскостью а. 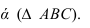
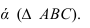
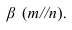
2-й случай — плоскости заданы на некотором расстоянии, что не дает возможность определить линии пересечения двух плоскостей первым способом. В этом случае используется метод плоскостей-посредников.
Алгоритм решения задачи (рисунок 2.11):
- Заданные плоскости
рассекаем вспомогательной плоскостью посредником
- Определяем линию пересечения 1-2 плоскости а с плоскостью а и линию пересечения 3-4 плоскости
с плоскостью
- Определяем точку К — точку пересечения линий 1-2 и 3-4, принадлежащую плоскостям
- Аналогичным образом находим точку L с помощью плоскости посредника
- Соединив две точки К и М, получим линию пересечения двух плоскостей
Видимость при этом не определяется.
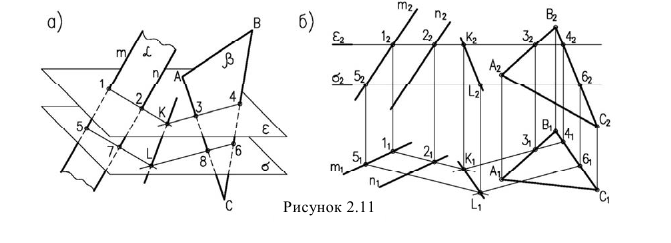
3-й случай — пересекающиеся плоскости общего положения заданы следами пересекающимися в пределах чертежа (рисунок 2.12).
В данном случае в качестве плоскостей-посредников могут быть использованы плоскость проекций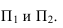
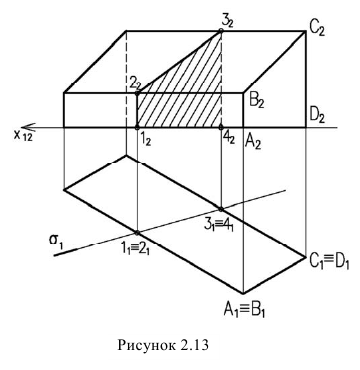
Пересечение многогранника проецирующей плоскостью
Так как секущая плоскость горизонтально-проецирующая, то фронтальную проекцию сечения можно построить, определив точку пересечения каждого ребра с плоскостью о (рисунок 2.13)
Взаимное положение двух плоскостей
Две плоскости могут принадлежать одна другой; быть параллельны или пересекаться.
Пересечение плоскостей. Линия пересечения двух плоскостей -прямая. Положение прямой в пространстве определяют две точки. Чтобы найти линию пересечения плоскостей, достаточно знать две точки, принадлежащие двум плоскостям одновременно.
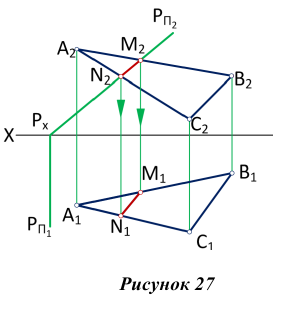
Пересечение плоскости общего положения с плоскостью частного положения
На рис. 27 показано построение линии пересечения фронтально-проецирующей плоскости Р с плоскостью треугольника AВС.
Так как линия пересечения двух плоскостей принадлежит фронтально-проецирующей плоскости Р, то ее фронтальная проекция 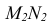
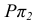
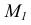
Пересечение двух плоскостей общего положения
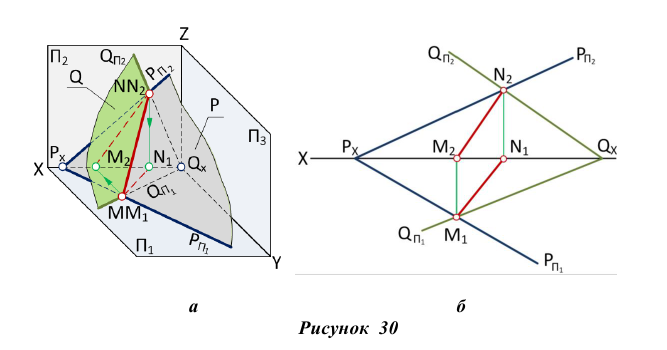
Задача. Построить линию пересечения двух плоскостей общего положения
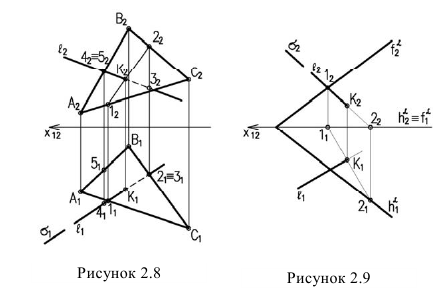
Алгоритм решения задачи (рис. 28)
- Вводим вспомогательную секущую плоскость Q общего положения
- Находим линии пересечения вспомогательной плоскости Q с двумя заданными Р и Т:
- Определяем точку пересечения построенных линий:
Точка М принадлежит одновременно плоскостям Р и Т, следовательно, она принадлежит линии их пересечения.
- Для нахождения второй общей точки вводим еще одну секущую плоскость и повторяем построения (п.2, п.З). Решение этой задачи на эпюре показано на рис. 29:
Согласно алгоритму решения задачи проводим вспомогательные секущие плоскости частного положения 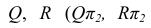
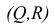
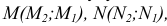
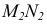
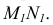
Плоскости параллельны
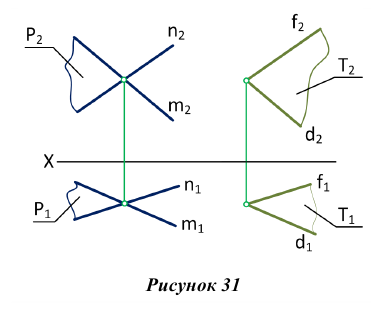
Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.
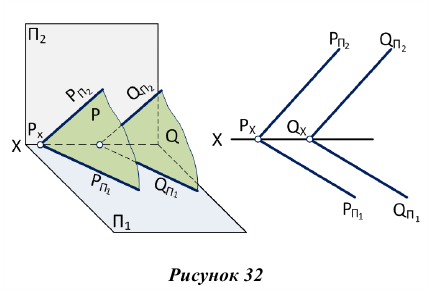
Изображенные на рис. 31 плоскости 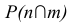
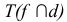
Плоскости общего положения также параллельны, если два любых одноименных следа параллельны между собой.
Изображенные на рис. 32 плоскости Р и Q параллельны, т.к.
Взаимное положение прямой линии и плоскости
Прямая может лежать в плоскости, пересекать плоскость и быть параллельной плоскости.
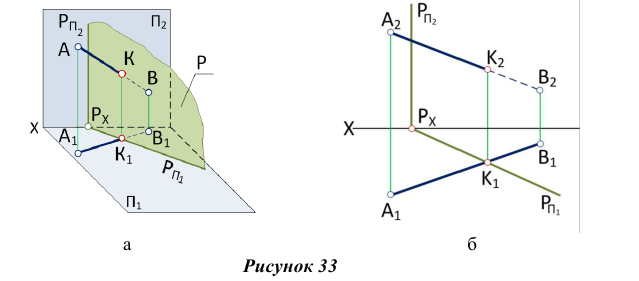
Пересечение прямой линии с плоскостью частного положения
Если заданная плоскость перпендикулярна к какой-либо плоскости проекций (рис.33, а), то она проецируется на эту плоскость проекций в виде прямой линии, на которой обязательно будут находиться соответствующие проекции всех точек, принадлежащих данной плоскости, в том числе и проекции точки пересечения какой-то прямой с заданной плоскостью (точка встречи прямой с плоскостью). Поэтому точка встречи прямой с плоскостью частного положения находится па эпюре без дополнительных построений (рис. 33,6).
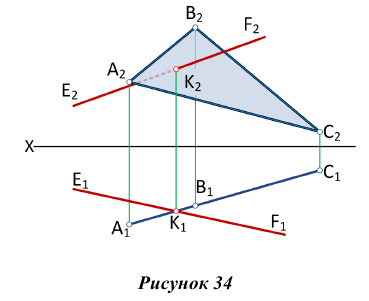
На рис. 34 точка встречи прямой EF с горизонтально-проецирующей плоскостью, заданной треугольником ABC, является точкой пересечения горизонтальных проекций 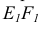
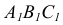
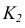
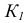
- Заказать чертежи
Определение видимости на эпюрах
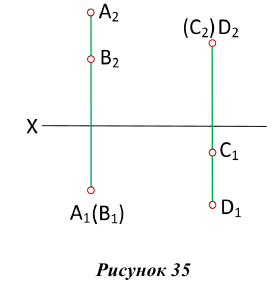
Вопрос о видимости линий или поверхностей всегда может быть сведен к вопросу о видимости точек. Если несколько точек находятся на общей для них линии связи, то видимой будет только одна из них — наиболее удаленная от той плоскости проекций, по отношению к которой определяется видимость.
Точки, расположенные на одной линии связи, называются конкурирующими. Точки А, В и С, D — конкурирующие (рис. 35).
Относительно плоскости проекций 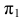
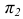
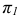
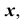
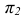
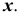
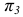
Пересечение прямой линии с плоскостью общего положения
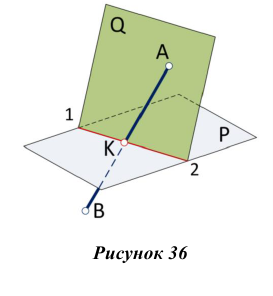
Точку пересечения прямой линии АВ с плоскостью общего положения Р (рис. 36) находят следующим образом:
- а) через заданную прямую АВ проводим некоторую вспомогательную плоскость Q, обычно плоскость частного положения;
- б) строим линию пересечения 1-2 заданной плоскости Р и вспомогательной Q;
- в) находим положение точки пересечения данной прямой АВ и линии пересечения 1-2 плоскостей (точки К).
- г) определяем видимость прямой АВ по отношению к плоскости Р.
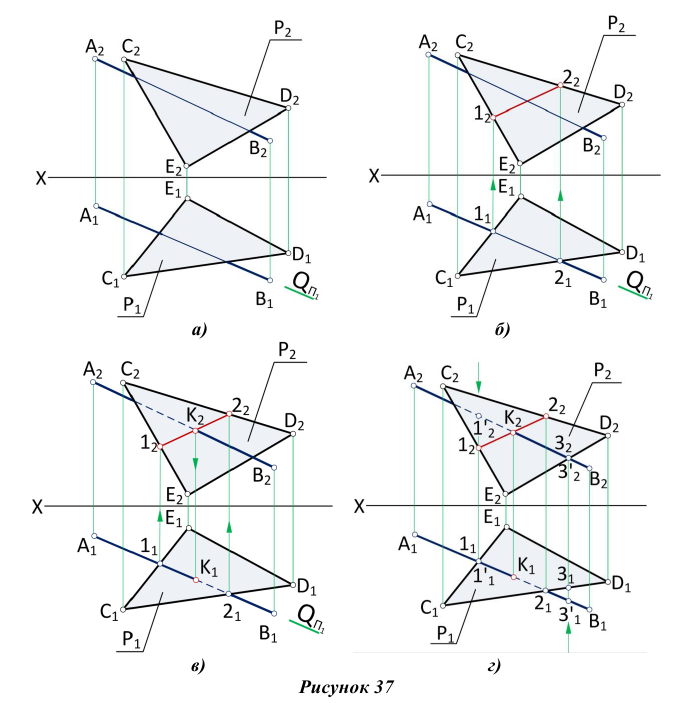
Пошаговые построения по определению точки пересечения прямой АВ с плоскостью треугольника CDE на эпюре приведены на рис. 37 (а-в).
Видимость прямой АВ относительно плоскости Р (рис. 37,г) определяем с помощью двух пар конкурирующих точек 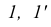
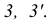
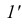
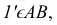
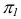
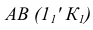
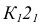
Аналогично, используя конкурирующие точки 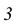
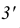
Задачи, на построение линии пересечения плоскостей, заданных пересекающимися прямыми, можно решать подобно задаче на пересечение прямой с плоскостью.
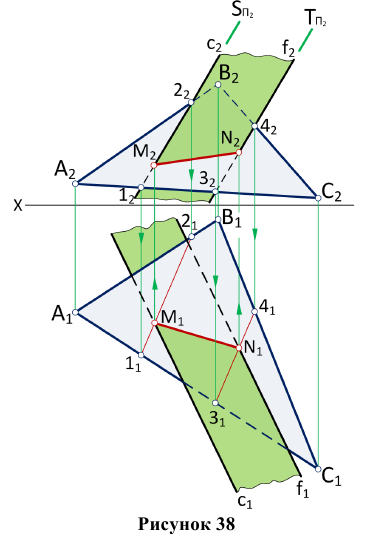
Одна из изображенных на рис. 38 плоскостей задана треугольником AВС, а вторая — двумя параллельными прямыми с и f.
Линия пересечения этих плоскостей (линия MN) определена при помощи построения точек встречи прямых с и f с плоскостью треугольника. Для этого через прямую с проведена фронтально — проецирующая плоскость S. Прямая 1-2 — линия пересечения плоскости треугольника с вспомогательной фронтально-проектирующей плоскостью S. Точка М — точка встречи прямой с с плоскостью треугольника AВС.
Точка N найдена аналогично. Прямая MN — искомая. Видимость на рис. 86 определена из условия, что заданные плоскости ограничены треугольником и двумя параллельными прямыми, определяющими их.
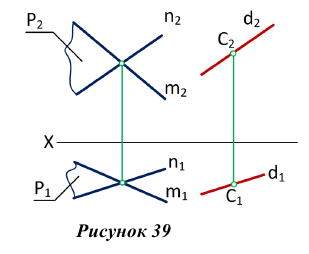
Прямая параллельна плоскости
Если прямая линия параллельна какой-либо прямой, находящейся в плоскости, то она параллельна этой плоскости. Следовательно, для построения прямой, параллельной заданной плоскости, надо взять в этой плоскости какую — либо прямую и построить ей параллельную.
На рис. 39 через точку С проведена прямая d, параллельная плоскости Р, заданной пересекающимися прямыми т и п.
Прямая d параллельна прямой n, принадлежащей плоскости 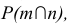
Прямая перпендикулярна плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Чтобы построить перпендикуляр из точки D на плоскость треугольника AВС (рис.40) необходимо предварительно построить
горизонталь 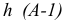
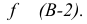
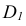
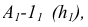
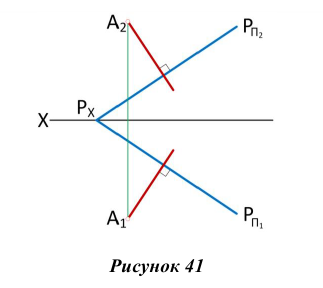
Если же плоскость задана следами, то, учитывая, что фронтальная проекция любой фронтали в этой плоскости всегда параллельна фронтальному следу плоскости, а горизонтальная проекция любой горизонтали параллельна горизонтальному следу плоскости, легко видеть (рис. 41), что проекции перпендикуляра к плоскости должны быть перпендикулярны соответствующим следам плоскости.
Плоскости перпендикулярны
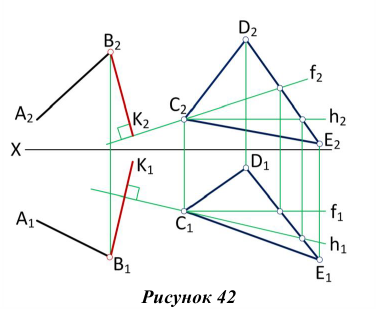
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. На рис. 42 через прямую АВ проведена плоскость, перпендикулярная плоскости треугольника CDE. Для этого из точки В прямой АВ восстановлен перпендикуляр ВК к плоскости треугольника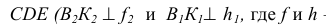
Если возникает необходимость в построении взаимно перпендикулярных прямых общего положения, необходимо построить плоскость, перпендикулярную заданной прямой, и взять в ней любую прямую.
Задача.
Через точку М провести прямую, перпендикулярную прямой
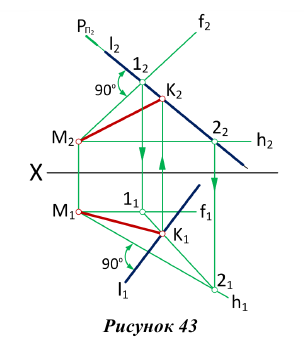
Для построения взаимно перпендикулярных прямых (рис. 43), одна из которых 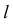
Задача:
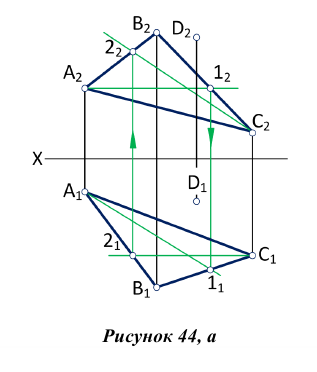
Определить расстояние от точки до плоскости, заданной треугольником ABC (рис.44)
Расстояние от точки до плоскости определяется длиной перпендикуляра, опущенного из точки на плоскость. Поэтому решение этой задачи выполняем в следующей последовательности:
1. Из точки D опускаем перпендикуляр на плоскость треугольника AВС (рис.44, а), для этого в плоскости треугольника проводим горизонталь 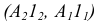
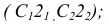
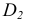
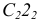
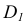
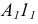
2. Находим точку пересечения перпендикуляра с плоскостью 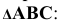
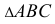
3. Методом прямоугольного треугольника определяем натуральную величину отрезка DK, для чего в плоскости 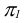
- Решение метрических задач
- Тени в ортогональных проекциях
- Кривые поверхности
- Пересечения криволинейных поверхностей
- Образование и задание поверхности на чертеже
- Пересечение поверхности плоскостью и прямой
- Развертки поверхностей
- Способы преобразования проекций
|
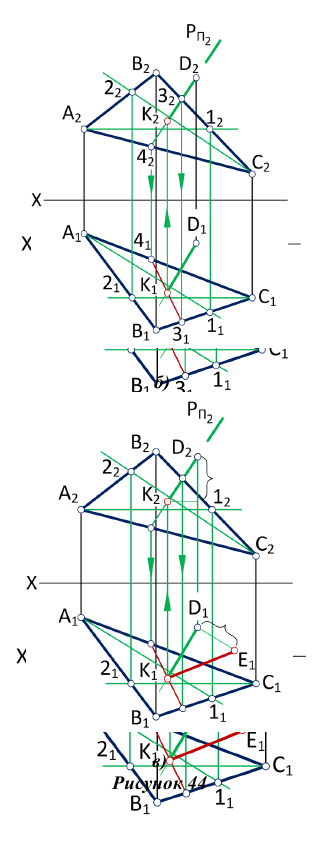
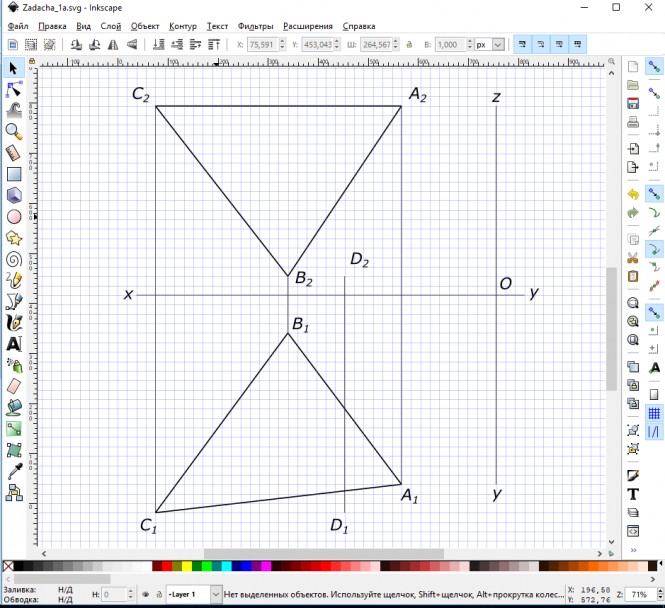
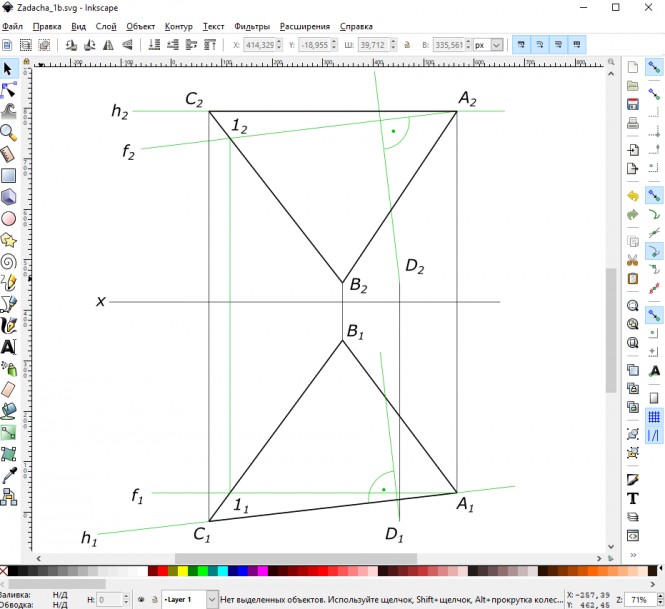
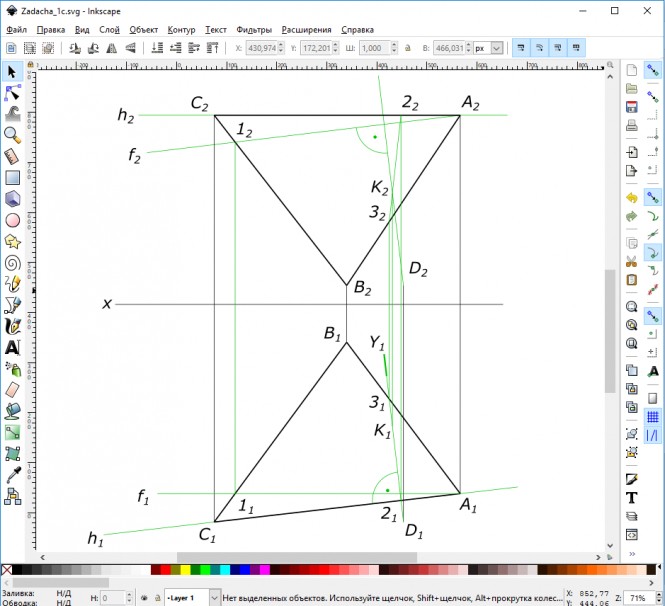
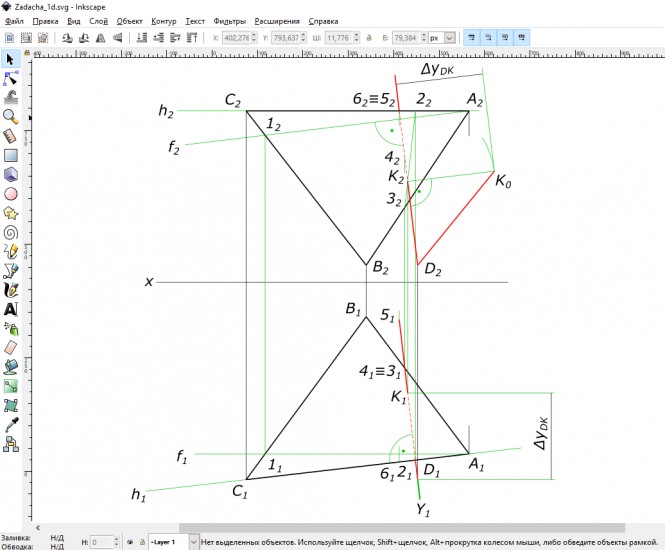
Дано: плоскость треугольника (А, В, С) и точка D. Требуется определить расстояние от точки D до плоскости, заданной треугольником (А, В, С). Определить видимость перпендикуляра, проходящего через точку D, и плоскости треугольника(А, В, С). Данные для выполнения задачи взять из та6л. 3, в соответствии с вариантом. Оцените сложность задачи: 1 голосов, средняя сложность: 5.0000 Решения задачиПо заданным значениям координат, мм: Ха=50, Уа=90, Za=100; Хв=110, Ув=20, Zв=10; Хс=180, Ус=115, Zc=100; Хd=80, Уd=115, Zd=10 строим треугольник ABC и точку D Построение треугольника ABC и точки D Следуя указаниям к задаче, выполняем ее в такой последовательности: 1) из точки D опустить перпендикуляр к плоскости ∆ ABC/ Строим горизонталь h(h1≡A1C1, h2≡A2C2) и фронталь f(f1//Ox, f2≡A2-12) плоскости. Строим перпендикуляр: его горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали h1, а фронтальная перпендикулярна фронтальной проекции фронтали f2; Построение горизонтали и фронтали плоскости и перпендикуляра к ней 2) определить точку пересечения перпендикуляра с плоскостью ∆АВС: — перпендикуляр (прямую) заключаем во вспомогательную, проецирующую, плоскость Y; — находим линию пересечения плоскостей 2-3 и отмечаем точку К, в пересечении этой линии с перпендикуляром; Точка пересечения перпендикуляра с плоскостью 3) определяем натуральную величину (Н.В.) расстояния от точки D до плоскости ∆АВС, применяя способ прямоугольного треугольника; 4) видимость проекций перпендикуляра определяем методом конкурирующих точек. Натуральная величина расстояния от точки D до плоскости ∆АВС, способ прямоугольного треугольника. Видимость проекций перпендикуляра методом конкурирующих точек Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все инженеры |
Перпендикулярность
Решение задач на тему перпендикулярности прямой и плоскости основано на двух теоремах геометрии:
- 1-я теорема: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
- 2-я теорема: о проекции прямого угла (изложена выше — см. рис. 2.14, 2.15 и 2.16) — если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то на эту плоскость проекций угол проецируется прямым.
Из этих двух теорем следует, что на чертеже проекции перпендикуляра к плоскости можно провести только к проекциям фронтали и горизонтали, то есть к двум пересекающимся прямым уровня, которые можно провести в плоскости.
!!! Запомните:
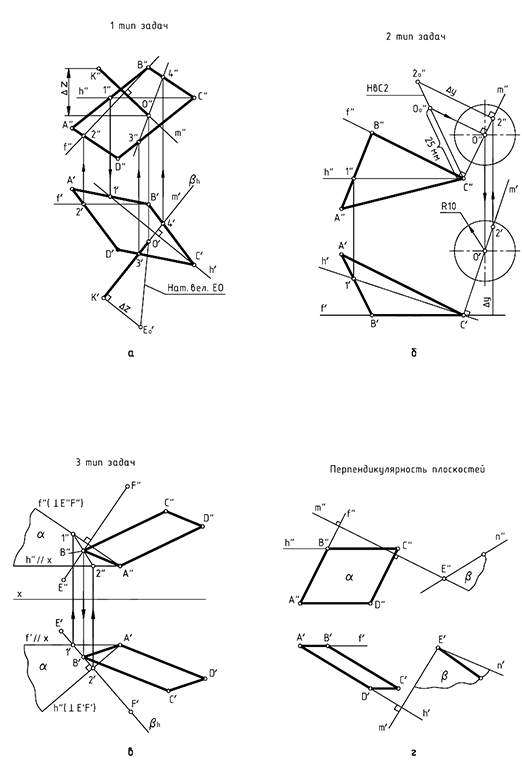
Задачи на тему перпендикулярности прямой и плоскости можно разделить на три группы:
1-я группа. Провести от точки, лежащей в плоскости, перпендикуляр в пространство.
2-я группа. Провести из точки, не лежащей в плоскости, перпендикуляр к этой плоскости.
3-я группа. Построить плоскость, перпендикулярную к прямой общего положения (построить геометрическое место точек — ГМТ).
Первая группа задач требует по условию проведения перпендикуляра от плоскости (восставить перпендикуляр) в пространство (см. рис. 5.1).
В этой группе задач требуется, как правило, построить на проведенном перпендикуляре проекции отрезка заданной величины. Графические действия по построению проекций отрезка заданной величины на проекциях прямой общего положения изложены ранее (см. рис. 2.9).
На рисунке 5.1 показано решение примерной задачи первой группы: построить плоскость 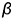
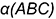
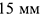
Эта задача относится к первой группе, поскольку для построения параллельной плоскости 
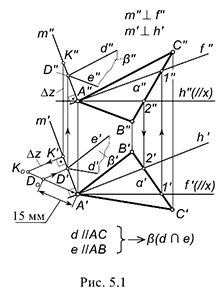
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Провести в заданной плоскости общего положения 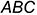
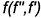
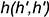
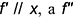
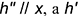
2-е действие. Провести от точки плоскости, например, от вершины 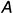
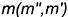
3-е действие. На проекциях перпендикуляра 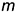
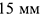
- Ограничить построенную прямую
произвольным отрезком
.
- Построить натуральную величину этого отрезка (см. рис. 5.1) способом прямоугольного треугольника — это гипотенуза
.
- На построенной гипотенузе отложить заданную величину
и построить проекции отрезка
заданной величины (см. построения), то есть проекции точки
, находящейся на расстоянии
от плоскости
.
4-е действие. Построить плоскость 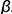
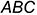
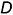
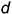
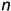
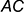

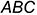
Вторая группа задач требует по условию проведения перпендикуляра из точки в пространстве к плоскости (опустить перпендикуляр). В этой группе задач, как правило, требуется построить точку пересечения построенного перпендикуляра с заданной плоскостью.
Построение точки пересечения прямой общего положения с плоскостью общего положения было рассмотрено выше (см. рис. 4.6).
На рис. 5.2 показано решение примерной задачи второй группы: определить расстояние от точки 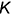
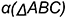
Эта задача относится ко второй группе, так как расстояние от точки 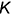
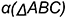
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Провести в плоскости фронталь 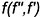
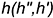
2-е действие. Провести через заданную точку 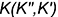
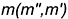
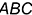
3-е действие. Построить точку пересечения 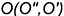
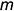
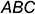
- Заключить прямую
во вспомогательную горизонтально-проецирующую плоскость
- Построить вспомогательную линию пересечения 3-4 заданной плоскости
со вспомогательной плоскостью
:
- Определить проекции искомой точки пересечения
на пересечении проекций построенной вспомогательной линии пересечения 3-4 с проекциями перпендикуляра
.
4-е действие. Построить натуральную величину отрезка 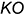
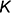
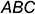
Третья группа задач требует по условию построения некоторой вспомогательной плоскости (геометрического места точек), перпендикулярной к прямой общего положения. Эту перпендикулярную плоскость можно задать двумя пересекающимися прямыми, каждая из которых должна быть перпендикулярна прямой общего положения (теорема о перпендикулярности прямой и плоскости, т. е. признак перпендикулярности прямой и плоскости). На чертеже плоскость, перпендикулярную к прямой общего положения, можно задать только проекциями пересекающихся прямых уровня — фронтальной (параллельной плоскости проекций 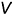
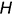
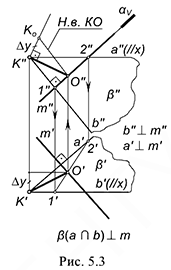
На рис. 5.3 показано решение примерной задачи третьей группы: определить расстояние от точки 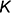
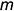
Эта задача относится к третьей группе, поскольку на чертеже провести перпендикуляр к прямой общего положения, по которому определяется расстояние от точки 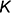
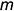
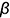
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Построить троим вспомогательную плоскость 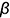
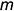
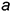
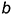
2-е действие. Построить точку 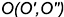
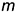

3-е действие. Соединить одноименные проекции точек 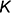

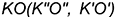
4-е действие. Построить натуральную величину построенного отрезка 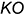
Структуризация материала пятой лекции в рассмотренном объеме схематически представлена на рис. 5.4 (лист 1). На последующем листе 2 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 5.5).
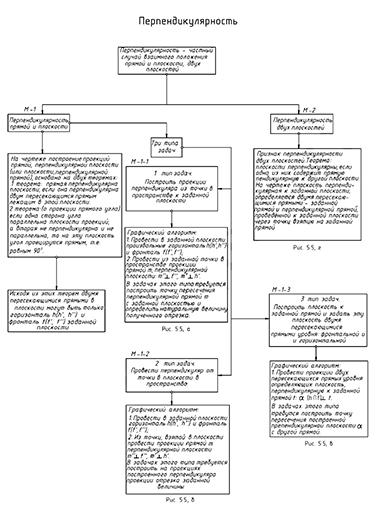
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:




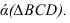
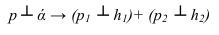
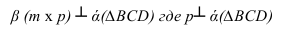
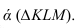
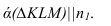
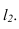
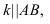
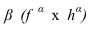
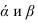 рассекаем вспомогательной плоскостью посредником
рассекаем вспомогательной плоскостью посредником 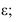
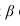 с плоскостью
с плоскостью 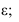
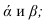
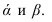
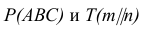
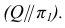
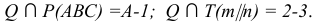
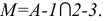 Точка М принадлежит одновременно плоскостям Р и Т, следовательно, она принадлежит линии их пересечения.
Точка М принадлежит одновременно плоскостям Р и Т, следовательно, она принадлежит линии их пересечения.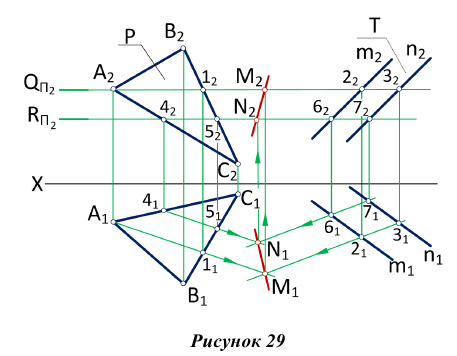
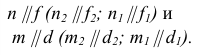
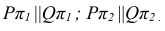
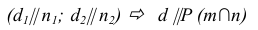
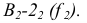
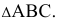

 .
.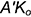 .
.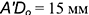 и построить проекции отрезка
и построить проекции отрезка 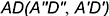 заданной величины (см. построения), то есть проекции точки
заданной величины (см. построения), то есть проекции точки 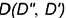 , находящейся на расстоянии
, находящейся на расстоянии