Как найти точку пересечения перпендикуляра с прямой - Исправление недочетов и поиск решений вместе с Examum.ru

найти координаты пересечения прямой и перпендикуляра

	От:	coreduo
Дата:	18.07.07 10:18
	Оценка:

День добрый!

Есть прямая, заданная двумя точками, p1 и p2. Есть третья точка — p3. Из p3 проводим перпендикуляр к прямой p1-p2, как посчитать координаты пересечения перпендикуляра и прямой?
Ткните пожалуйста мордой в алгоритм или в исходники, а то что-то туплю…

С уважением,
Михаил Белов

Re: найти координаты пересечения прямой и перпендикуляра

От:

SergH

Дата:

18.07.07 10:54

Оценка:

Здравствуйте, coreduo, Вы писали:

C>Есть прямая, заданная двумя точками, p1 и p2. Есть третья точка — p3. Из p3 проводим перпендикуляр к прямой p1-p2, как посчитать координаты пересечения перпендикуляра и прямой?
C>Ткните пожалуйста мордой в алгоритм или в исходники, а то что-то туплю…

Находим первую прямую в виде a1x + b1y + c1 = 0
Любой перпендикуляр к ней имеет вид b1x — a1y + c2 = 0
Теперь нужо найти c2 такое, что перпендикуляр проходи через точку p3
А потом найти точку пересечения двух прямых.

Делай что должно, и будь что будет

Re: найти координаты пересечения прямой и перпендикуляра

От:

Socrat

Дата:

18.07.07 11:02

Оценка:

Здравствуйте, coreduo, Вы писали:

C>День добрый!

C>Есть прямая, заданная двумя точками, p1 и p2. Есть третья точка — p3. Из p3 проводим перпендикуляр к прямой p1-p2, как посчитать координаты пересечения перпендикуляра и прямой?
C>Ткните пожалуйста мордой в алгоритм или в исходники, а то что-то туплю…

Сначала найдем скалярное произведение (p2-p1) и (p3-p1). Назовем его P. Длина проекции (p3-p1) на прямую равна L=P/|p2-p1|.

А дальше все просто — искомая точка O=p1+(p2-p1)*L/|p2-p1|=p1+(p2-p1)*P/|p2-p1|^2

Re[2]: найти координаты пересечения прямой и перпендикуляра

	От:	coreduo
Дата:	18.07.07 11:28
	Оценка:

Здравствуйте, Socrat, Вы писали:

спасибо большое, возник вопрос…

S>Сначала найдем скалярное произведение (p2-p1) и (p3-p1). Назовем его P. Длина проекции (p3-p1) на прямую равна L=P/|p2-p1|.

а вот это точно? пытаюсь нарисовать и что-то не то у меня получается…

S>А дальше все просто — искомая точка O=p1+(p2-p1)*L/|p2-p1|=p1+(p2-p1)*P/|p2-p1|^2

С уважением,
Михаил Белов

Re[3]: найти координаты пересечения прямой и перпендикуляра

От:

Socrat

Дата:

18.07.07 11:34

Оценка:

Здравствуйте, coreduo, Вы писали:

C>Здравствуйте, Socrat, Вы писали:

C>спасибо большое, возник вопрос…

S>>Сначала найдем скалярное произведение (p2-p1) и (p3-p1). Назовем его P. Длина проекции (p3-p1) на прямую равна L=P/|p2-p1|.

C>а вот это точно? пытаюсь нарисовать и что-то не то у меня получается…

Вообще-то скалярное произведение равно произведению длин векторов на косинус угла между ними. Длина проекции равна длине |p3-p1|, умноженной на косинус. Что не получается?

S>>А дальше все просто — искомая точка O=p1+(p2-p1)*L/|p2-p1|=p1+(p2-p1)*P/|p2-p1|^2

C>С уважением,
C>Михаил Белов

Re[3]: найти координаты пересечения прямой и перпендикуляра

От:

SergH

Дата:

18.07.07 12:03

Оценка:

Здравствуйте, coreduo, Вы писали:

C>а вот это точно? пытаюсь нарисовать и что-то не то у меня получается…

Точно. Скалярное произведение это произведение длинн векторов и косинуса угла между ними. Если одну длину убрать (разделить на неё), получится вторая длина на косинус, а это и есть длина проекции.

Делай что должно, и будь что будет

Re[4]: найти координаты пересечения прямой и перпендикуляра

	От:	coreduo
Дата:	18.07.07 17:44
	Оценка:

Да-да, вы правы… а как проще всего посчитать угол, без арк-функций это получится?

Здравствуйте, Socrat, Вы писали:

S>Здравствуйте, coreduo, Вы писали:

C>>Здравствуйте, Socrat, Вы писали:

C>>спасибо большое, возник вопрос…

S>>>Сначала найдем скалярное произведение (p2-p1) и (p3-p1). Назовем его P. Длина проекции (p3-p1) на прямую равна L=P/|p2-p1|.

C>>а вот это точно? пытаюсь нарисовать и что-то не то у меня получается…

S>Вообще-то скалярное произведение равно произведению длин векторов на косинус угла между ними. Длина проекции равна длине |p3-p1|, умноженной на косинус. Что не получается?

S>>>А дальше все просто — искомая точка O=p1+(p2-p1)*L/|p2-p1|=p1+(p2-p1)*P/|p2-p1|^2

C>>С уважением,
C>>Михаил Белов

Re[5]: найти координаты пересечения прямой и перпендикуляра

От:

Socrat

Дата:

18.07.07 19:29

Оценка:

Здравствуйте, coreduo, Вы писали:

C>Да-да, вы правы… а как проще всего посчитать угол, без арк-функций это получится?

Это вряд ли… Думаю, длину дуги вычислить сложней, чем арк-функцию.

Re: найти координаты пересечения прямой и перпендикуляра

От:

Пётр Седов

Дата:

18.07.07 19:36

Оценка:

Здравствуйте, coreduo, Вы писали:
C>Есть прямая, заданная двумя точками, p1 и p2. Есть третья точка — p3. Из p3 проводим перпендикуляр к прямой p1-p2, как посчитать координаты пересечения перпендикуляра и прямой?

Здесь

Автор:
Дата: 22.06.07

Пусть есть точка — xc,yc, отрезок x1,y1,x2,y2, как найти точку пересечения прямой, проходящей через отрезок x1,y1,x2,y2 и перпендикуляра опущенного из точки xc,yc на эту прямую

Пётр Седов (ушёл с RSDN)

Wait...

Переместить
Удалить
Выделить ветку

Пока на собственное сообщение не было ответов, его можно удалить.

Источник

Точка пересечения перпендикуляра к двум прямым с первой прямой — это точка, удовлетворяющая уравнению перпендикуляра к двум прямым и уравнению первой прямой.

Содержание

1 Обозначения
2 Формулы:
- 2.1 Пример
3 Другие формулы:
4 Ссылки

Обозначения

Введём обозначения:

— радиус-вектор точки пересечения;

— радиус-вектор точки на первой прямой;

— радиус-вектор точки на второй прямой;

— направляющий вектор первой прямой;

— направляющий вектор второй прямой;

— уравнение первой прямой;

— уравнение второй прямой.

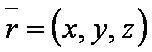
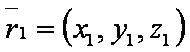
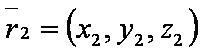
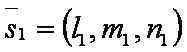
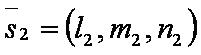
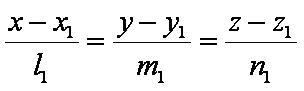
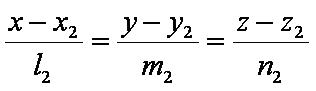
Формулы:

Векторная форма:

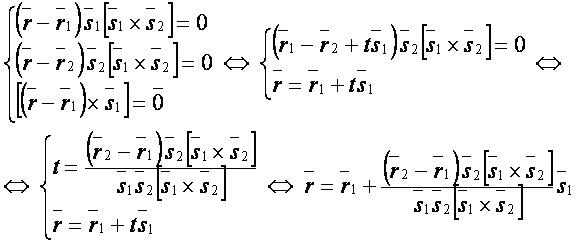
Координатная форма:

Заметим, что формулы верны только для скрещивающихся прямых.

Пример

Даны две скрещивающиеся прямые:

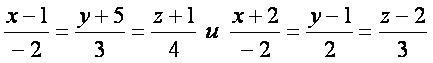
Найти точку пересечения перпендикуляра к двум прямым с первой прямой.

Решение.

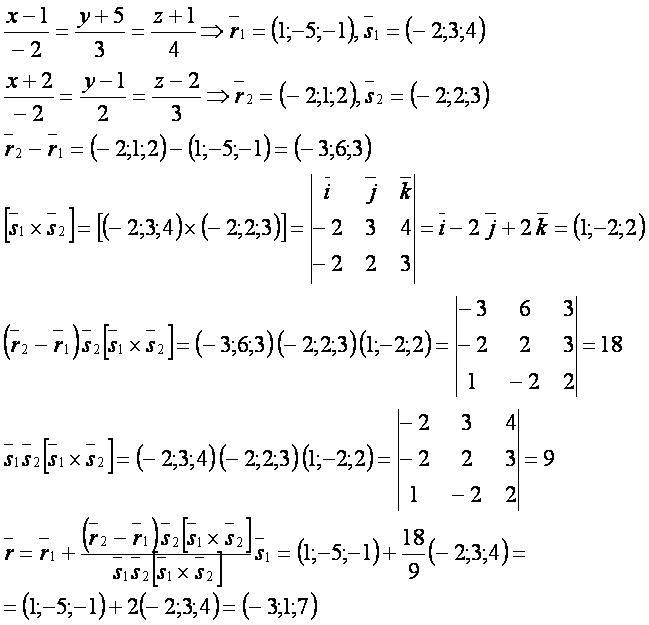
Другие формулы:

Основание перпендикуляра из точки к прямой;
Основание перпендикуляра из точки к плоскости;
Точка пересечения перпендикуляра к двум прямым с первой прямой;
Точка пересечения перпендикуляра к двум прямым со второй прямой;
Точка пересечения прямой и плоскости;
Точка пересечения трёх плоскостей;
Точка, равноудалённая от двух прямых;
Точка, равноудалённая от четырёх точек;
Точка деления отрезка в данном отношении;
Точка прямой, находящаяся от первой точки прямой до второй в данном отношении;
Точка прямой, находящаяся перед первой точкой прямой до второй в данном отношении;
Точка прямой, находящаяся от первой точки прямой за второй в данном отношении.

Ссылки

Участник:Logic-samara

Источник

Содержание

1 Обозначения
2 Формулы
- 2.1 Пример
3 Другие формулы
4 Ссылки

Обозначения[править]

Введём обозначения:

— радиус-вектор точки пересечения;

${displaystyle {bar {r}}_{1}=(x_{1},y_{1},z_{1})}$ — радиус-вектор точки на первой прямой;

${displaystyle {bar {r}}_{2}=(x_{2},y_{2},z_{2})}$ — радиус-вектор точки на второй прямой;

${displaystyle {bar {s}}_{1}=(l_{1},m_{1},n_{1})}$ — направляющий вектор первой прямой;

${displaystyle {bar {s}}_{2}=(l_{2},m_{2},n_{2})}$ — направляющий вектор второй прямой;

${displaystyle {frac {x-x_{1}}{l_{1}}}={frac {y-y_{1}}{m_{1}}}={frac {z-z_{1}}{n_{1}}}}$ — уравнение первой прямой;

${displaystyle {frac {x-x_{2}}{l_{2}}}={frac {y-y_{2}}{m_{2}}}={frac {z-z_{2}}{n_{2}}}}$ — уравнение второй прямой.

Формулы[править]

Векторная форма:

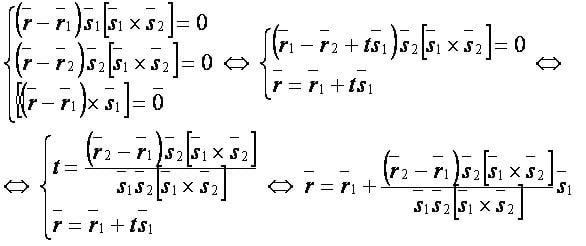
Координатная форма:

Заметим, что формулы верны только для скрещивающихся прямых.

Пример[править]

Даны две скрещивающиеся прямые:
${displaystyle {frac {x-1}{-2}}={frac {y+5}{3}}={frac {z+1}{4}}}$ и
${displaystyle {frac {x+2}{-2}}={frac {y-1}{2}}={frac {z-2}{3}}}$ .

Найти точку пересечения перпендикуляра к двум прямым с первой прямой.

Решение.

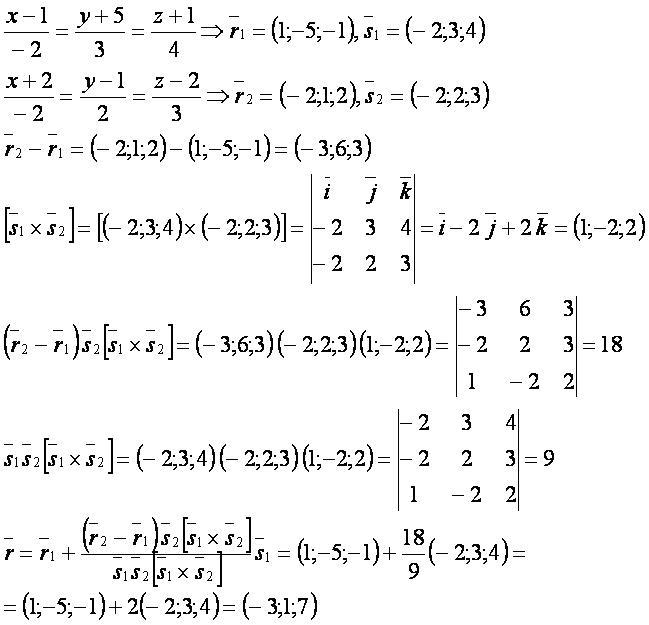
Другие формулы[править]

Основание перпендикуляра из точки к прямой;
Основание перпендикуляра из точки к плоскости;
Точка пересечения перпендикуляра к двум прямым с первой прямой;
Точка пересечения перпендикуляра к двум прямым со второй прямой;
Точка пересечения прямой и плоскости;
Точка пересечения трёх плоскостей;
Точка деления отрезка в данном отношении;
Точка прямой, находящаяся от первой точки прямой до второй в данном отношении;
Точка прямой, находящаяся перед первой точкой прямой до второй в данном отношении;
Точка прямой, находящаяся от первой точки прямой за второй в данном отношении.

Ссылки[править]

Участник:Logic-samara

Источник

~~Butt-Head~~

Заблокирован

Найти точку пересечения отрезка и перпендикуляра, опущенного на отрезок из точки

23.07.2015, 13:33. Показов 15551. Ответов 30

Метки нет (Все метки)

Привет! Помогите двоишнику, я же тупой батхэд !

Есть отрезок, заданный двумя точками P1 и P2. Есть точка P3. Так вот, нужно найти координаты точки пересечения перпендикуляра, опущенного на заданный отрезок и, собственно этого отрезка, причём, если точка не находится на отрезке — как то просигнализировать …

Нужен рабочий код. Можно использовать С++ 11/14 и Qt, в котором есть

C++

1	static float dotProduct(const QVector2D& v1, const QVector2D& v2);

…

Миниатюры

Programming

Эксперт

94731 / 64177 / 26122

Регистрация: 12.04.2006

Сообщений: 116,782

23.07.2015, 13:33

Ответы с готовыми решениями:

Найти точку пересечения отрезка и перпендикуляра, опущенного на отрезок из точки
Привет! Помогите двоишнику, я бивис!

Есть отрезок, заданный двумя точками P1 и P2. Есть точка…

Найти основание перпендикуляра, опущенного из точки на прямую
Необходимо решить 2 задачи,но я не понимаю каким образом это можно сделать.
1.Дан метрический…

Написать уравнение перпендикуляра, опущенного из точки на прямую
Доброго времени суток
Прорешиваю практику по экзамена по алгему,попался вопрос,который звучит так…

Написать уравнение перпендикуляра, опущенного из точки на прямую
написать уравнение перпендикуляра, опущенного из точки А(-1;0;3) на прямую (х+1)/3 = (у-1)/2=z/1

1471 / 826 / 140

Регистрация: 12.10.2013

Сообщений: 5,456

23.07.2015, 13:53

Сообщение было отмечено Butt-Head как решение

Решение

Хлебнете вы от аналитической геометрии…
Может тут?
Подобие math.h для геометрии
Где-то на форуме была точно помню…
Гуглить вроде “ перпендикуляр на прямую, Координаты перпендикуляра на прямую”?.

Добавлено через 6 минут
Вот ответ.
Перпендикуляр из точки на прямую

~~Butt-Head~~

Заблокирован

23.07.2015, 14:05

[ТС]

Сообщение от Excalibur921

Подобие math.h для геометрии

Не… буст в топку

Сообщение от Excalibur921

Гуглить вроде “ перпендикуляр на прямую, Координаты перпендикуляра на прямую”?.

Да гуглил… Найти расстояние (длину этого перпендикуляра) от этой точки до отрезка — нет проблем, а вот координаты — хз как находить.

Мне собственно нужны даже не совсем координаты, а просто смещение от точки P1 до точки P4, то есть расстояние от начальной точки отрезка, до точки пересечения. Конечно же, зная координаты, я это расстояние найду. Но вроде бы как то можно скалярным произведением всё решить …. Помогите, dotProduct использовать можно !

Добавлено через 6 минут
То есть фактический ответом на мой вопрос будет это: (верно? Excalibur921 ? )

C++

//Прямая задана двумя точками (x1,y1) (x2,y2). Есть третья точка (x3,y3). Из точки нужно опустить перпендикуляр и найти координаты его основания на прямой (x4,y4)
float x1, x2, x3, x4;
float y1, y2, y3, y4;
//...
x4=((x2-x1)*(y2-y1)*(y3-y1)+x1*pow(y2-y1, 2)+x3*pow(x2-x1, 2))/(pow(y2-y1, 2)+pow(x2-x1, 2));
y4=(y2-y1)*(x4-x1)/(x2-x1)+y1;

Добавлено через 1 минуту
Ну ок, а как проверить, есть ли вообще решение? Ну то есть если перпендикуляр опускается на отрезок, но не попадает в его границы (попадает по лучу, а не по отрезку) ?

1471 / 826 / 140

Регистрация: 12.10.2013

Сообщений: 5,456

23.07.2015, 14:10

Сообщение от Butt-Head

попадает по лучу, а не по отрезку)

То найдет координаты точки на луче вроде.

~~Butt-Head~~

Заблокирован

23.07.2015, 14:17

[ТС]

Сообщение от Excalibur921

То найдет координаты точки на луче вроде.

чта?
Я нахожу координаты точки пересечения перпендикуляра и отрезка. Как теперь мне определить, принадлежать ли эти координаты этому отрезку?

1471 / 826 / 140

Регистрация: 12.10.2013

Сообщений: 5,456

23.07.2015, 14:27

Сообщение от Butt-Head

чта?

Найдет координаты точки перпендикуляра на луч за границами отрезка.

Может можно и проще если важна скорость, но нужно очень шарить в геометрии. Надобыло в геометрии создавать…и просить решение в символьной форме.

Сообщение от Butt-Head

Как теперь мне определить,

Ну наверно проверить принадлежность точки отрезку… вход точки в интервал между X и Y точек P1 и P2. А как еще?

Добавлено через 1 минуту
Может есть еще решение в что то типа высота треугольника…

~~Butt-Head~~

Заблокирован

23.07.2015, 14:34

[ТС]

Сообщение от Excalibur921

Ну наверно проверить принадлежность точки отрезку… вход точки в интервал между X и Y точек P1 и P2. А как еще?

ну это — то понятно:

C++

1	if((x3 > x1 && x3 < x2) && ... и тд

но дело в том, что у тебя отрезок может быть направлен в отрицательную сторону, тогда у тебя x2 будет меньше x1 и по этому тут нужно сперва всё это перегонять в 1-ю четверть (всего 3 координатные четверти), делать операцию и обратно. Понимаешь? По этому я и спрашиваю готовую формулу, т.к. лень всё делать самому.

В Qt наверняка что — то есть, неужели нет?

1471 / 826 / 140

Регистрация: 12.10.2013

Сообщений: 5,456

23.07.2015, 14:41

А можно узнать угол отрезка P1 P3 даст Альфа 1 и угол отрезка P1 P2 даст Альфа 2. Повернуть отрезок P1 P3 на Альфа 2 будет как треугольник с горизонтальным основанием(без поворота). Тогда P4=(x1,y3).

Добавлено через 3 минуты

Сообщение от Butt-Head

В Qt наверняка что — то есть,

Скорей всего…
Тогда надобыло в теме Qt создавать .Или поискать либы по геометрии в Qt…А чем плоха что я кидал либу? Там и 3д есть.

~~Butt-Head~~

Заблокирован

23.07.2015, 14:49

[ТС]

Сообщение от Excalibur921

Тогда надобыло в теме Qt создавать

Да толку то …, всё равно все сидят только здесь

Сообщение от Excalibur921

А чем плоха что я кидал либу?

Тем что её надо изучать.

Ладно, через жопу на Qt реализовал, скоростью и не пахнет, да мне она и не нужна.
Вообще странно, что нет ничего готового для таких стандартных вещей …

1471 / 826 / 140

Регистрация: 12.10.2013

Сообщений: 5,456

23.07.2015, 14:57

Сообщение от Butt-Head

Вообще странно, что нет ничего готового для таких стандартных вещей

Я в Qt сначала неделю его ставил… Неверные переменные среды QT 4.8.0 Creator 2.4.1
потом не мог вывести синусоиду никто не подсказал 600 чел смотрели тему…
Синусоида OpenGL и слайдер
Потом ели стер этот Qt еще и с ошибками даже на удалении =).А примеры там это вообще жесть… куча мусора. Как не программист делал примеры туда.

2013 / 1342 / 382

Регистрация: 16.05.2013

Сообщений: 3,463

Записей в блоге: 6

23.07.2015, 15:01

Берете три вектора $https://www.cyberforum.ru/cgi-bin/latex.cgi?{vec{r}}_{31}, {vec{r}}_{32}$ и $https://www.cyberforum.ru/cgi-bin/latex.cgi?{vec{r}}_{21}$
Что бы перпендикуляр лежал на отрезке достаточно, что бы скалярные произведения $https://www.cyberforum.ru/cgi-bin/latex.cgi?({vec{r}}_{31}, {vec{r}}_{21})$ и $https://www.cyberforum.ru/cgi-bin/latex.cgi?({vec{r}}_{32}, {vec{r}}_{21})$ были разных знаков.
Точка пересечения перпендикуляра находится как $https://www.cyberforum.ru/cgi-bin/latex.cgi?vec{r} = {vec{r}}_{1} + ({vec{r}}_{31}, {vec{e}}_{21}){vec{e}}_{21}$ , где $https://www.cyberforum.ru/cgi-bin/latex.cgi?{vec{e}}_{21} = frac{{vec{r}}_{21}}{left|{vec{r}}_{21} right|}$

~~Butt-Head~~

Заблокирован

23.07.2015, 15:18

[ТС]

Сообщение от Excalibur921

потом не мог вывести синусоиду никто не подсказал 600 чел смотрели тему…
Синусоида OpenGL и слайдер

Так там есть же ответ в последнем посте На самом деле сейчас большинство современного софта пишется на Qt, т.к. код на Qt собирается на любой современной ОС. Зря ты от него отказался

Сообщение от Ilot

Берете три вектора и

Спасибо. Но я не очень понимаю, что значит берёте три вектора.
У меня есть три пары координат (см рисунок в первом посте), вот как из них получить векторы?

Сообщение от Ilot

Точка пересечения перпендикуляра находится как

А это что, сложение вектора с о скобками, в которых чего? скалярное произведение или что ?

Не могли бы вы в координаты ваши формулы перевести?

2013 / 1342 / 382

Регистрация: 16.05.2013

Сообщений: 3,463

Записей в блоге: 6

23.07.2015, 15:30

Условие того, что точка лежит внутри отрезка:
$https://www.cyberforum.ru/cgi-bin/latex.cgi?left( ({x}_{3} - {x}_{1}) * ({x}_{2} - {x}_{1}) + ({y}_{3} - {y}_{1}) * ({y}_{2} - {y}_{1})right) * left( ({x}_{3} - {x}_{2}) * ({x}_{2} - {x}_{1}) + ({y}_{3} - {y}_{2}) * ({y}_{2} - {y}_{1})right) < 0$
Точка пересечения перепендикулляра и отрезка:
$https://www.cyberforum.ru/cgi-bin/latex.cgi?x = {x}_{1} + frac{ ({x}_{3} - {x}_{1}) * ({x}_{2} - {x}_{1}) + ({y}_{3} - {y}_{1}) * ({y}_{2} - {y}_{1})}{sqrt{({x}_{2} - {x}_{1}) * ({x}_{2} - {x}_{1}) + ({y}_{2} - {y}_{1}) * ({y}_{2} - {y}_{1})}} * frac{ ({x}_{2} - {x}_{1})}{sqrt{({x}_{2} - {x}_{1}) * ({x}_{2} - {x}_{1}) + ({y}_{2} - {y}_{1}) * ({y}_{2} - {y}_{1})}}$
$https://www.cyberforum.ru/cgi-bin/latex.cgi?y = {y}_{1} + frac{ ({x}_{3} - {x}_{1}) * ({x}_{2} - {x}_{1}) + ({y}_{3} - {y}_{1}) * ({y}_{2} - {y}_{1})}{sqrt{({x}_{2} - {x}_{1}) * ({x}_{2} - {x}_{1}) + ({y}_{2} - {y}_{1}) * ({y}_{2} - {y}_{1})}} * frac{ ({y}_{2} - {y}_{1})}{sqrt{({x}_{2} - {x}_{1}) * ({x}_{2} - {x}_{1}) + ({y}_{2} - {y}_{1}) * ({y}_{2} - {y}_{1})}}$
Надеюсь нигде не соврал…
p.s. В последних выражениях корни одинаковые поэтому их можно схлопнуть. Расписал для лучшего понимания.

~~Butt-Head~~

Заблокирован

23.07.2015, 15:48

[ТС]

Сообщение от Ilot

Условие

Хмм… а что это за условие?

Результирующие координаты это x и у ?

Добавлено через 2 минуты
Ааа понял, это что б как бы точка принадлежала именно отрезку, а не лучу…
Ну что ж, спасибо, но в итоге это получается намноОого громоздче, нежели

C++

1 2	x4=((x2-x1)(y2-y1)(y3-y1)+x1pow(y2-y1, 2)+x3pow(x2-x1, 2))/(pow(y2-y1, 2)+pow(x2-x1, 2)); y4=(y2-y1)*(x4-x1)/(x2-x1)+y1;

из 3-го поста …
Всё таки векторная математика — чисто понт, в действительности — то всё идёт через обычные умножения, сложения и тд, но если решать всё с понтом, то решение получится намного сложнее

Ilot

2013 / 1342 / 382

Регистрация: 16.05.2013

Сообщений: 3,463

Записей в блоге: 6

23.07.2015, 16:03

Сообщение было отмечено Ilot как решение

Решение

Сообщение от Butt-Head

Ну что ж, спасибо, но в итоге это получается намноОого громоздче, нежели…

Это еще как посмотреть:

C++

1
2
3

k = ((x3-x1) * (x2-x1) + (y3-y1)*(y2-y1))/ (pow(x2-x1, 2) + pow(y2-y1, 2));
x = x1 + k * (x2-x1);
y = y1 + k * (y2-y1);

~~Butt-Head~~

Заблокирован

23.07.2015, 16:10

[ТС]

Сообщение от Ilot

Это еще как посмотреть:

Ну в принципе да…
Ладно, спасибо тебе о великий Ilot

1471 / 826 / 140

Регистрация: 12.10.2013

Сообщений: 5,456

23.07.2015, 16:53

ТС у вас работает?
Решил попробовать и не работает ваш код.
вершина
отрезок
искомая

1471 / 826 / 140

Регистрация: 12.10.2013

Сообщений: 5,456

23.07.2015, 17:30

Сообщение от Butt-Head

Работает что?

Второй метод который вы просили расписать через вектора… и который быстрей должен быть.

Сообщение от Butt-Head

А ты что за формулы привёл?

Второй метод Ilot.

Добавлено через 24 минуты
Получается Butt-Head, использует метод который я предложил, а модератор отметил неработающую формулу как лучший ответ… забавно… =).

~~Butt-Head~~

Заблокирован

23.07.2015, 17:46

[ТС]

Сообщение от Excalibur921

Получается Butt-Head, использует метод который я предложил, а модератор отметил неработающую формулу как лучший ответ… забавно… =).

Это не модератор отметил, а я Раз так, снимаю с ИЛОТА лучший ответ. Садись — два Илот .
Ставлю лучший ответ чудо мечу. (и не один, я не жадный ехехе)

Источник

Авторское построение. С произвольно взятой точки можно опустить перпендикуляр только на диаметр вспомогательной окружности. Следовательно необходимо построить диаметр этой окружности параллельно прямой ВС (верхний рисунок). Проведем через В и С два диаметра ВЕ и СD. Ясно, что четырех угольник BDEC прямоугольный, а стороны ВD и СЕ параллельны. Разделим одну из этих сторон пополам, воспользовавшись леммой о трапеции: «Прямая, соединяющая точку пересечения диагоналей трапеции с точкой пересечения продолженных ее боковых сторон, делит оба основания трапеции пополам».

Возьмем произвольно точку F вне прямоугольника и проведем прямые DF и ВF. Обозначим точками N и М их пересечения со стороной ЕC. Тогда прямая FG, проходящая через точку Н, пересечения диагоналей трапеции ВDNМ, делит сторону ВD пополам. Следовательно, диаметр КL, проходящий через точку G, параллелен прямой ВС (нижний рисунок).

Проведем хорды КТ и LР через точку А. Пусть прямые КР и LТ пересекаются в точке S. В треугольнике KSL отрезки КТ и LР являются его высотами. В результате прямая SV, проходящая через точку А третья его высота, так как все высоты треугольника проходят через одну точку.

Источник