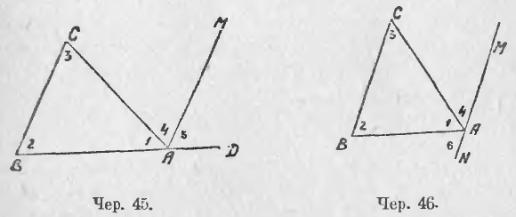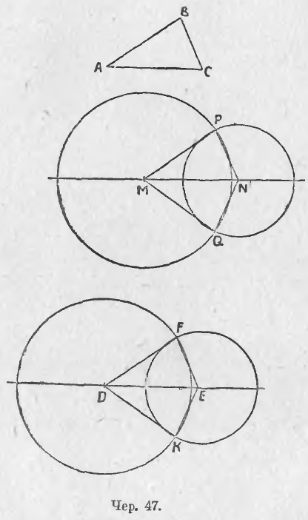Чертежик
Метки
Точки пересечения треугольников пошаговое выполнение
Точки пересечения треугольников определяются в следующем порядке:
1.) Согласно заданию строятся точки по координатам.
2.) Теперь важным шагом является определение плоскости относительно которой будем искать точки пересечения треугольников.
Вы можете сказать: «можно найти точки относительно плоскости АВС», но нет. Почему!? Я объясню, посмотрев на рисунок, расположенный внизу, можно увидеть что треугольник D2E2F2, а точнее две стороны пересекают треугольник А2В2С2 в четырех точках, соответственно используем треугольник D2E2F2,как опорную плоскость.
- Сторона D2E2 пересекает плоскость А2В2С2 в точках 1 2 и 2 2, эти точки переносим на нижнее изображение: на стороны относительно которых они были найдены и обозначаем 1 1 и 2 1.
- Точки 1 1 и 2 1 соединяются.
- Прямая 1 1 2 1 пересекает сторону D1E1 в точке, обозначим Р1 (первая точка найдена).
3.) Сторона E2F2 пересекает стороны B2C2 и A2C2 в точках 4 2 и 3 2. Опускаем их на нижний рисунок и обозначаем 4 1 и 3 1.
4.) Соединяются точки 3 1 и 4 1.
5.) Продливается прямая 3 1 4 1 до пересечения с отрезком E1F1. В месте пересечения ставим точку и обозначаем Н.
6.) Точки P1 и H соединяются. Полученная прямая P1H пересекает отрезок А2С2 в точке K1 (найдена вторая точка).
7.) Переносятся точки P1 и K1, расположенные на отрезках D1E1 и E1F1, на отрезки D2E2 и E2F2. И обозначаются P2 и K2.
8.) Соединяются P2 и K2.
9.) А теперь главный момент: указать видимые и невидимые стороны.
Посмотрите на рисунок снизу. На нем точки D, F, B, C и E находятся в двух проекциях «свободно», но не точка A. Соответственно, относительно ее и необходимо начинать чертить линии.
Пример выполненной работы на эту тему смотрите здесь.
Немного добавлю по этой статье: «Точки пересечения треугольников»
По своему опыту скажу: «чтобы начертить подобный чертеж, необходимо обладать пространственным воображением» и понимать, относительно какой плоскости отталкиваться для решения подобной задачи. Но благодаря этой статьи надеюсь у Вас получится разобраться с темой: пересечение плоских фигур.
Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.
1. Строим проекции треугольника АВС.
2. Строим проекции треугольника EDK.
3. Находим точку пересечения стороны АС с треугольником EDK
4. Находим точку пересечения стороны А B с треугольником EDK и строим линию пересечения MN
5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.
6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.
7. В треугольнике ABC проводим горизонталь CL и плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.
Строим фронтальную проекцию треугольника ABC . Треугольник должен проецироваться в прямую линию.
8. Определяем действительную величину треугольника ABC и строим на нем линию пересечения MN.
Нахождение пересечение двух треугольников
Пошаговое руководство решения задачи №1 — «Нахождение линии пересечения двух плоскостей и определение натуральной величины»
В задаче необходимо найти линию пересечения двух плоскостей и определить натуральную величину одной из них методом плоскопараллельного перемещения.
Для решения такой классической задачи по начертательной геометрии необходимо знать следующий теоретический материал:
— нанесение проекций точек пространства на комплексный чертеж по заданным координатам;
— способы задания плоскости на комплексном чертеже, плоскости общего и частного положения;
— главные линии плоскости;
— определение точки пересечения прямой линии с плоскостью (нахождение «точки встречи»);
— метод плоскопараллельного перемещения для определения натуральной величины плоской фигуры;
— определение видимости на чертеже прямых линий и плоскостей с помощью конкурирующих точек.
Порядок решения Задачи
1. Согласно варианту Задания по координатам точек наносим на комплексный чертеж две плоскости, заданные в виде треугольников ABC (A’, B’, C’; A, B, C) и DKE (D’, K’, E’; D, K, Е) (рис.1.1).
Рис.1.1
2. Для нахождения линии пересечения воспользуемся методом проецирующей плоскости. Суть его в том, что берется одна сторона (линия) первой плоскости (треугольника) и заключается в проецирующую плоскость. Определяется точка пересечения этой линии с плоскостью второго треугольника. Повторив эту задачу еще раз, но для прямой второго треугольника и плоскости первого треугольника, определим вторую точку пересечения. Так как полученные точки одновременно принадлежат обеим плоскостям, они должны находиться на линии пересечения этих плоскостей. Соединив эти точки прямой, будем иметь искомую линию пересечения плоскостей.
3. Задача решается следующим образом:
а) заключаем в проецирующую плоскость Ф(Ф’) сторону AB(A’B’) первого треугольника во фронтальной плоскости проекций V. Отмечаем точки пересечения проецирующей плоскости со сторонами DK и DE второго треугольника, получая точки 1(1’) и 2 (2’). Переносим их по линиям связи на горизонтальную плоскость проекций H на соответствующие стороны треугольника, точка 1(1) на стороне DE и точка 2(2) на стороне DK.
Рис.1.2
б) соединив проекции точек 1 и 2, будем иметь проекцию проецирующей плоскости Ф. Тогда точка пересечения прямой АВ с плоскостью треугольника DKE определится (согласно правилу) вместе пересечения проекции проецирующей плоскости 1-2 и одноименной проекции прямой AB. Таким образом, получили горизонтальную проекцию первой точки пересечения плоскостей – M, по которой определяем (проецируем по линиям связи) её фронтальную проекцию – M’ на прямой A’B’(рис.1.2.а);
в) аналогичным путем находим вторую точку. Заключаем в проецирующую плоскость Г(Г) сторону второго треугольника DK(DK). Отмечаем точки пересечения проецирующей плоскости со сторонами первого треугольника AC и BC во горизонтальной проекции, получая проекции точек 3 и 4. Проецируем их на соответствующие стороны в фронтальной плоскости, получаем 3’ и 4’. Соединив их прямой, имеем проекцию проецирующей плоскости. Тогда вторая точка пересечения плоскостей будет в месте пересечения линии 3’-4’ со стороной треугольника D’K’, которую заключали в проецирующую плоскость. Таким образом, получили фронтальную проекцию второй точки пересечения – N’, по линии связи находим горизонтальную проекцию – N (рис.1.2.б).
г) соединив полученные точки MN(MN) и (M’N’) на горизонтальной и фронтальной плоскостях, имеем искомую линию пересечения заданных плоскостей.
4. С помощью конкурирующих точек определяем видимость плоскостей. Возьмем пару конкурирующих точек, например, 1’=5’ во фронтальной проекции. Спроецируем их на соответствующие стороны в горизонтальную плоскость, получим 1 и 5. Видим, что точка 1, лежащая на стороне DЕ имеет большую координату до оси x, чем точка 5, лежащая на стороне AВ. Следовательно, согласно правилу, большей координаты, точка 1 и сторона треугольника D’Е’ во фронтальной плоскости будут видимые. Таким образом, определяется видимость каждой стороны треугольника в горизонтальной и фронтальной плоскостях. Видимые линии на чертежах проводятся сплошной контурной линией, а не видимые — штриховой линией. Напомним, что в точках пересечения плоскостей (M—N и M’-N’) будет происходить смена видимости.
Рис.1.3
Рис.1.4.
На эпюре дополнительно показано определение видимости в горизонтальной плоскости с использованием конкурирующих точек 3 и 6 на прямых DK и АВ.
5. Методом плоскопараллельного перемещения определяем натуральную величину плоскости треугольника ABC, для чего:
а) в указанной плоскости через точку С(С) проводим фронталь C—F (С-F и C’-F’);
б) на свободном поле чертежа во горизонтальной проекции берем (отмечаем) произвольную точку С1, считая, что это одна из вершин треугольника (конкретно вершина C). Из нее восстанавливаем перпендикуляр к фронтальной плоскости (через ось х);
Рис.1.5
в) плоскопараллельным перемещением переводим горизонтальную проекцию треугольника ABC, в новое положение A1B1C1 таким образом, чтобы в фронтальной проекции он занял проецирующее положение (преобразовался в прямую линию). Для этого: на перпендикуляре от точки С1, откладываем фронтальную проекцию горизонтали C1—F1 (длина lCF) получаем точку F1. Раствором циркуля из точки F1 величиною F-A делаем дуговую засечку, а из точки C1 — засечку величиной CA, тогда в пересечении дуговых линий получаем точку A1 (вторая вершина треугольника);
— аналогично получаем точку B1 (из точки C1 делаем засечку величиной C—B (57мм), а из точки F1 величиной F—B (90мм).Заметим, что при правильном решении три точки A1 F’1 и B’1 должны лежать на одной прямой (сторона треугольника A1—B1)две другие стороны С1—A1 и C1—B1 получаются путем соединения их вершин;
г) из метода вращения следует, что при перемещении или вращении точки в какой-то плоскости проекций — на сопряженной плоскости проекция этой точки должна двигаться по прямой линии, в нашем конкретном случае по прямой параллельной оси х. Тогда проводим из точек A’B’C’ фронтальной проекции эти прямые (их называют плоскостями вращения точек), а из фронтальных проекций перемещенных точек A1 В1 C1 восстановим перпендикуляры (линии связи) (рис.1.6).
Рис.1.6
Пересечения указанных линий с соответствующими перпендикулярами дает новые положения фронтальной проекции треугольника ABC, конкретно A’1В’1C’1 который должен стать проецирующим (прямой линией), поскольку горизонталь h1 мы провели перпендикулярно фронтальной плоскости проекций (рис.1.6);
5) тогда для получения натуральной величины треугольника достаточно его фронтальную проекцию развернуть до параллельности с горизонтальной плоскостью. Разворот осуществляем с помощью циркуля через точку А’1, считая ее как центр вращения, ставим треугольник A’1В’1C’1 параллельно оси х, получаем A’2В’2C’2. Как было сказано выше, при вращении точки, на сопряженной (теперь на горизонтальной) проекции они двигаются по прямым параллельным оси х. Опуская перпендикуляры (линии связи) из фронтальных проекций точек A’2 В’2 C’2 пересечения их с соответствующими линиями находим горизонтальную проекцию треугольника ABC (A2В2C2) в натуральную величину (рис.1.7).
Рис. 1.7
У меня есть все готовые решения задач с такими координатами, купить можно >>здесь
Цена 55 руб, чертежи по начертательной геометрии из книжки Фролова Вы легко можете скачать сразу после оплаты или я вышлю Вам на почту. Они находятся в ZIP архиве в различных форматах:
*.jpg – обычный цветной рисунок чертежа в масштабе 1 к 1 в хорошем разрешении 300 dpi;
*.cdw – формат программы Компас 12 и выше или версии LT;
*.dwg и .dxf — формат программы AUTOCAD, nanoCAD;
http://student-com.ru/%D0%BF%D0%BE%D1%81%D1%82%D1%80%D0%BE%D0%B5%D0%BD%D0%B8%D0%B5-%D0%BB%D0%B8%D0%BD%D0%B8%D0%B8-%D0%BF%D0%B5%D1%80%D0%B5%D1%81%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D1%8F-%D0%B4%D0%B2%D1%83%D1%85-%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%BE%D0%B2.html
http://stud55.ru/peresechenie-treugolnikov-zadacha1/
Построение линии пересечения двух треугольников.
Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.
1. Строим проекции треугольника АВС.
2. Строим проекции треугольника EDK.
3. Находим точку пересечения стороны АС с треугольником EDK
4. Находим точку пересечения стороны АB с треугольником EDKи строим линию пересечения MN
5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.
6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.
7. В треугольнике ABCпроводим горизонталь CLи плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.
Строим фронтальную проекцию треугольника ABC. Треугольник должен проецироваться в прямую линию.
8. Определяем действительную величину треугольника ABCи строим на нем линию пересечения MN.
9. Оформление задачи.
| № вар. | ХА | YА | ZА | ХB | YB | ZB | ХC | YC | ZC | ХD | YD | ZD | ХE | YE | ZE | ХK | YK | ZK | Цена | В корзину | № вар. |
| 1 | 117 | 90 | 9 | 52 | 25 | 79 | 0 | 83 | 48 | 68 | 110 | 85 | 135 | 19 | 36 | 14 | 52 | 0 | 50 руб. | в корзину | 1 |
| 2 | 120 | 90 | 10 | 50 | 25 | 80 | 0 | 85 | 50 | 70 | 110 | 85 | 135 | 20 | 35 | 15 | 50 | 0 | 50 руб. | в корзину | 2 |
| 3 | 115 | 90 | 10 | 52 | 25 | 80 | 0 | 80 | 45 | 64 | 105 | 80 | 130 | 18 | 35 | 12 | 50 | 0 | 50 руб. | в корзину | 3 |
| 4 | 120 | 92 | 10 | 50 | 20 | 75 | 0 | 80 | 46 | 70 | 115 | 85 | 135 | 20 | 32 | 10 | 50 | 0 | 50 руб. | в корзину | 4 |
| 5 | 117 | 9 | 90 | 52 | 79 | 25 | 0 | 48 | 83 | 68 | 85 | 110 | 135 | 36 | 19 | 14 | 0 | 52 | 50 руб. | в корзину | 5 |
| 6 | 115 | 7 | 85 | 50 | 80 | 25 | 0 | 50 | 85 | 70 | 85 | 110 | 135 | 20 | 20 | 15 | 0 | 50 | 50 руб. | в корзину | 6 |
| 7 | 120 | 10 | 90 | 48 | 82 | 20 | 0 | 52 | 82 | 65 | 80 | 110 | 130 | 38 | 20 | 15 | 0 | 52 | 50 руб. | в корзину | 7 |
| 8 | 116 | 8 | 88 | 50 | 78 | 25 | 0 | 46 | 80 | 70 | 85 | 108 | 135 | 36 | 20 | 15 | 0 | 52 | 50 руб. | в корзину | 8 |
| 9 | 115 | 10 | 92 | 50 | 80 | 25 | 0 | 50 | 85 | 70 | 85 | 110 | 135 | 35 | 20 | 15 | 0 | 50 | 50 руб. | в корзину | 9 |
| 10 | 18 | 10 | 90 | 83 | 79 | 25 | 135 | 48 | 82 | 67 | 85 | 110 | 0 | 36 | 19 | 121 | 0 | 52 | 50 руб. | в корзину | 10 |
| 11 | 20 | 12 | 92 | 85 | 89 | 25 | 135 | 50 | 85 | 70 | 85 | 110 | 0 | 35 | 20 | 120 | 0 | 52 | 50 руб. | в корзину | 11 |
| 12 | 15 | 10 | 85 | 80 | 80 | 20 | 130 | 50 | 80 | 70 | 80 | 108 | 0 | 35 | 20 | 120 | 0 | 50 | 50 руб. | в корзину | 12 |
| 13 | 16 | 12 | 88 | 85 | 80 | 25 | 130 | 50 | 80 | 75 | 85 | 110 | 0 | 30 | 15 | 120 | 0 | 50 | 50 руб. | в корзину | 13 |
| 14 | 18 | 12 | 85 | 85 | 80 | 25 | 135 | 50 | 80 | 70 | 85 | 110 | 0 | 35 | 20 | 120 | 0 | 50 | 50 руб. | в корзину | 14 |
| 15 | 18 | 90 | 10 | 83 | 25 | 79 | 135 | 83 | 48 | 67 | 110 | 85 | 0 | 19 | 36 | 121 | 52 | 0 | 50 руб. | в корзину | 15 |
| 16 | 18 | 40 | 75 | 83 | 117 | 6 | 135 | 47 | 38 | 67 | 20 | 0 | 0 | 111 | 48 | 121 | 78 | 86 | 50 руб. | в корзину | 16 |
| 17 | 18 | 75 | 40 | 83 | 6 | 107 | 135 | 38 | 47 | 67 | 0 | 20 | 0 | 48 | 111 | 121 | 86 | 78 | 50 руб. | в корзину | 17 |
| 18 | 117 | 75 | 40 | 52 | 6 | 107 | 0 | 38 | 47 | 135 | 0 | 20 | 86 | 48 | 111 | 15 | 68 | 78 | 50 руб. | в корзину | 18 |
Начертательная геометрия решение задач
Начертательная геометрия 1 курс готовые чертежи по вариантам
Добавить комментарий

Точки пересечения треугольников определяются в следующем порядке:
1.) Согласно заданию строятся точки по координатам.
2.) Теперь важным шагом является определение плоскости относительно которой будем искать точки пересечения треугольников.
Вы можете сказать: «можно найти точки относительно плоскости АВС», но нет. Почему!? Я объясню, посмотрев на рисунок, расположенный внизу, можно увидеть что треугольник D2E2F2, а точнее две стороны пересекают треугольник А2В2С2 в четырех точках, соответственно используем треугольник D2E2F2,как опорную плоскость.
- Сторона D2E2 пересекает плоскость А2В2С2 в точках 12 и 22, эти точки переносим на нижнее изображение: на стороны относительно которых они были найдены и обозначаем 11 и 21.
- Точки 11 и 21 соединяются.
- Прямая 1121 пересекает сторону D1E1 в точке, обозначим Р1 (первая точка найдена).
3.) Сторона E2F2 пересекает стороны B2C2 и A2C2 в точках 42 и 32. Опускаем их на нижний рисунок и обозначаем 41 и 31.
4.) Соединяются точки 31 и 41.
5.) Продливается прямая 3141 до пересечения с отрезком E1F1. В месте пересечения ставим точку и обозначаем Н.
6.) Точки P1 и H соединяются. Полученная прямая P1H пересекает отрезок А2С2 в точке K1 (найдена вторая точка).
7.) Переносятся точки P1 и K1, расположенные на отрезках D1E1 и E1F1, на отрезки D2E2 и E2F2. И обозначаются P2 и K2.
8.) Соединяются P2 и K2.
9.) А теперь главный момент: указать видимые и невидимые стороны.
Посмотрите на рисунок снизу. На нем точки D, F, B, C и E находятся в двух проекциях «свободно», но не точка A. Соответственно, относительно ее и необходимо начинать чертить линии.
Пример выполненной работы на эту тему смотрите здесь.
Немного добавлю по этой статье: «Точки пересечения треугольников»
По своему опыту скажу: «чтобы начертить подобный чертеж, необходимо обладать пространственным воображением» и понимать, относительно какой плоскости отталкиваться для решения подобной задачи. Но благодаря этой статьи надеюсь у Вас получится разобраться с темой: пересечение плоских фигур.
Просмотрели 414
1.
Построение линии пересечения двух
треугольников
Построить линию пересечения треугольников ABC и
EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.
1
2.
1. Строим проекции треугольника АВС
2
3.
2. Строим проекции треугольника EDK
3
4.
3. Находим точку пересечения стороны АС с треугольником EDK
4
5.
4. Находим точку пересечения стороны АB с треугольником EDKи строим
линию пересечения MN
5
6.
5. С помощью конкурирующих точек 4 и 5 определяем видимость
треугольников на фронтальной плоскости проекций
6
7.
6. С помощью конкурирующих точек 6 и 7 определяем видимость
треугольников на горизонтальной плоскости проекций
7
8.
7. В треугольнике ABCпроводим горизонталь CLи плоскопараллельным
перемещением относительно горизонтальной плоскости проекций
располагаем горизонталь перпендикулярно фронтальной плоскости
проекций.
Строим фронтальную проекцию треугольника ABC. Треугольник должен
проецироваться в прямую линию
8
9.
9
10.
8. Определяем действительную величину треугольника ABCи строим на
нем линию пересечения MN
10
11.
Варианты заданий
№
Х
вар. А
YА
ZА
ХB
YB
ZB
ХC
YC
ZC
ХD
YE
ZE
ХK YK ZK
YD
ZD
ХE
1
117 90
9
52
25
79
0
83
48
68 110 85 135 19
36
14
52
0
2
120 90
10
50
25
80
0
85
50
70 110 85 135 20
35
15
50
0
3
115 90
10
52
25
80
0
80
45
64 105 80 130 18
35
12
50
0
4
120 92
10
50
20
75
0
80
46
70 115 85 135 20
32
10
50
0
5
117
9
90
52
79
25
0
48
83
68
85 110 135 36
19
14
0
52
6
115
7
85
50
80
25
0
50
85
70
85 110 135 20
20
15
0
50
7
120 10
90
48
82
20
0
52
82
65
80 110 130 38
20
15
0
52
8
116
8
88
50
78
25
0
46
80
70
85 108 135 36
20
15
0
52
9
115 10
92
50
80
25
0
50
85
70
85 110 135 35
20
15
0
50
10
18
90
83
79
25 135 48
82
67
85 110
19 121
0
52
11
10
0
36
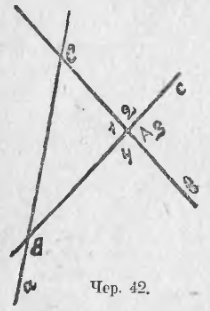
36. Мы уже рассматривали фигуру, состоящую из двух пересекающихся прямых (вертикальные углы, п. 18). Присоединим к ним еще третью прямую, пересекающую каждую из первых двух прямых в отдельно точке. Получим фигуру, данную на чер. 42: прямая a и прямая b пересекаются в точке C, прямые b и c – в точке A и прямые c и a – в точке B (мы называем для сокращения письма и речи каждую прямую одною малою буквою). Построенная фигура называется треугольником. Слово «треугольник» обозначается знаком Δ; обыкновенно треугольник обозначают тремя буквами, которыми названы три точки пересечения прямых. На чер. 42 имеем ΔABC.
Прямые a, b и с называют сторонами треугольника, точки A, B и C – его вершинами. Треугольник разделяет плоскость на 7 областей, из которых 6 бесконечны, а одна конечная. Эта последняя ограниченна сторонами треугольника и называется площадью треугольника. При каждой вершине треугольника образуется по 4 угла меньших выпрямленного, например, ∠1, ∠2, ∠3 и ∠4 при точке A; внутренняя область одного из них, а именно ∠1, захватывает площадь треугольника (или: площадь треугольника лежит внутри ∠1) – этот угол называется внутренним углом треугольника, а остальные три (∠2, ∠3 и ∠4) – внешними. Среди внешних углов рассматривают обыкновенно лишь один при каждой вершине: при точке A ∠2 или ∠4, которые равны между собою как вертикальные, а ∠3 = внутреннему ∠1 на том же основании. Всего имеем в треугольнике 3 внутренних угла, которые часто называются просто углами треугольника.
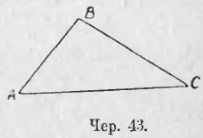
Название «сторона треугольника» употребляется в двух смыслах: 1) этим именем называют, как указано выше, одну из трех прямых, напр., прямую a, неопределенно продолженную, 2) этим же именем называют отрезок этой прямой между двумя вершинами, напр., отрезок BC. Если вопрос таков, что приходится рассматривать только отрезки наших трех прямых, то треугольник изображают так, как на чер. 43.
В треугольнике обыкновенно рассматривают 6 элементов: три стороны (отрезки) AB, BC и CA и 3 внутренних угла – ∠A, ∠B и ∠C.
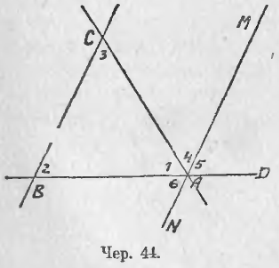
37. Рассматривая ΔABC (чер. 42), мы видим, что здесь является возможным применить построение п. 29. Именно в конце п. 29 мы пришли к заключению, что если дана прямая и вне ее точка, то через эту точку можно построить прямую, параллельную данной. На чер. 42 мы можем, например, счесть прямую a за данную прямую и точку A за данную точку (либо: прямую b и точку B, либо прямую c и точку C). Построим же через точку A прямую, параллельную стороне BC (или прямой a). Получим фигуру, данную на чер. 44, где MN || BC. Назовем внутренние углы ΔABC нумерами 1, 2, 3 и занумеруем еще нумерами 4, 5 и 6 некоторые углы при точке A, полученные после построения прямой MN (см. чер. 44). Мы видим, что при точке A выполнено сложение нескольких углов. Например, мы видим, что
∠1 + ∠4 + ∠5,
причем сумма равна выпрям. углу BAD, т. е.
∠1 + ∠4 + ∠5 = выпрям. углу.
Но ∠4 = ∠3, так как это внутренние накрест-лежащие углы при параллельных BC и MN и секущей AC; также ∠5 = ∠2 как соответственные углы при параллельных BC и AM и секущей BD. Поэтому в предыдущем равенстве мы можем заменить ∠4 и ∠5 углами 3-м и 2-м; тогда получим
∠1 + ∠3 + ∠2 = выпр. углу,
т. е. оказывается, что во всяком треугольнике сумма внутренних углов (если их сложить) равна выпрямленному углу.
К тому же результату мы придем, если обратим внимание, что при точке A выполнено сложение ∠6, ∠1 и ∠4, причем сумма равна выпрям. углу NAM. Здесь, следовательно, мы видим:
∠6 + ∠1 + ∠4 = выпр. углу.
Но мы знаем, что ∠6 = ∠2, как внутр. накр.-леж. при параллельных BC и NM и секущей BD и ∠4 = ∠3, как внутр. накр.-леж. при тех же параллельных и секущей CA. Поэтому заключаем, что
∠2 + ∠1 + ∠3 = выпр. углу.
Обратим еще внимание на ∠CAD, являющийся внешним для ΔABC. Мы видим, что лучом AM он разбит на 2 слагаемых, на ∠4 и ∠5, т. е.
∠CAD = ∠4 + ∠5.
Но, как мы уже выяснили, ∠4 = ∠3 и ∠5 = ∠2; следовательно.,
∠CAD = ∠3 + ∠2.
Эти 2 угла (∠3 и ∠2) являются внутренними углами ΔABC, не смежными с ∠CAD (с ∠CAD смежен ∠1). Поэтому мы заключаем:
Внешний угол треугольника (образованный одною его стороною и продолжением другой) равен сумме двух внутренних углов с ним не смежных.
Мы можем из чертежа 44 выделить только те элементы, которые необходимы для выяснения полученных свойств, и удалить все остальное, не нужное, тогда получим упрощенный чертеж. На чертежах 45 и 46 даны 2 таких упрощенных чертежа. Для чер. 45 имеем:
1) ∠1 + ∠4 + ∠5 = выпр. углу, но ∠4 = ∠3 и ∠5 = ∠2; след., ∠1 + ∠3 + ∠2 = выпр. углу.
2) ∠CAD = ∠4 + ∠5, но ∠4 = ∠3 и ∠5 = ∠2. Следов, ∠CAD = ∠3 + ∠2.
Для чер. 46 имеем: ∠6 + ∠1 + ∠4 = выпр. углу, но ∠6 = ∠2 и ∠4 = ∠3, следов., ∠2 + ∠6 + ∠3 = выпр. углу.
38. Задача. Построить Δ с такими же сторонами, как у данного треугольника. Пусть дан ΔABC (чер. 47). Строим где-либо прямую и на ней при помощи циркуля откладываем отрезок MN = AC. Таким образом мы получили две вершины искомого треугольника M и N. Чтобы найти третью вершину, воспользуемся задачею п. 27: надо найти такую точку, чтобы отрезок, соединяющий ее с точкой M, был равен AB и отрезок, соединяющий ее с точкою N, был = CB. Эти круги пересекутся в двух точках P и Q; соединив эти точки прямыми с M и N, получим два искомых треугольника: один ΔMPN и другой ΔMQN (MN = AC; MP = MQ = AB; NP = NQ = CB). Примем, что два круга не могут пресекаться более, чем в двух точках (впоследствии этот вопрос будет разъяснен в п. 128). Согласно п. 26 точки пересечения наших кругов P и Q расположены симметрично относительно линии центров MN. Поэтому при перегибании всей фигуры по оси симметрии MN точка P должна совместиться с точкою Q, а, следовательно, ΔMPN совместиться с ΔMQN. Согласно п. 2, мы можем назвать эти треугольники равными или конгруэнтными.
Если мы повторим где-либо на ином месте плоскости предыдущее построение, то получим еще 2 треугольника DEF и DEK с такими же сторонами, как у ΔABC (DE = AC; DF = DK = AB, EF = EK = CB). Также в силу того, что прямая DE есть ось симметрии всей фигуры, мы заключим, что эти два треугольника равны или конгруэнтны между собою. Возникает теперь вопрос: можно ли добиться того, чтобы какой-либо из треугольников второй пары (напр., ΔDEF) совпал с каким-либо треугольником первой пары (напр., с ΔMPN)?
Круги позволят решить этот вопрос. Передвинем нижнюю фигуру чертежа 47 так, чтобы точка D совпала с точкой M и точка E с точкой N (этого добиться можно потому, что MN = DE, – каждый из этих отрезков = AC). Тогда круги фигуры DFEK совпадут соотв. с кругами фигуры MPNQ (ибо радиусы этих кругов соотв. равны между собою и центры их совместились). Поэтому и точки пересечения этих двух пар кругов должны совместиться, т. е., напр., точка F совместится с точкою P и точка K с Q. Отсюда заключаем, что и ΔDEF должен совместиться с ΔMNP, что принято записывать в виде ΔDEF = ΔMNP. Мы также могли бы к ΔABC пристроить два круга, принимая точки A и C за центры и отрезки AB и CB за радиусы, и также при помощи этих кругов пришли бы к заключению, что
ΔABC = ΔMPN = ΔMQN = ΔDFE = ΔDKE.
Итак, если построить два треугольника с попарно равными сторонами, то эти треугольники конгруэнтны (или равны).
(Следует помнить, что для геометрических фигур слова «конгруэнтны» или «равны» означают, что эти фигуры совпадают при наложении).
39. В предыдущем п. мы научились строить равные треугольники. Пусть ΔA’B’C’ = ΔABC (чер. 48) и при наложении сторона A’B’ совпадает с AB, B’C’ – с BC и A’C’ – с AC. Тогда и углы этих треугольников совпадают, а именно ∠C’ с ∠C, ∠A’ с ∠A и ∠B с ∠B, т. е. ∠C’ = ∠C, ∠A’ = ∠A и ∠B = ∠B. Ясно, что в равных треугольниках равные углы лежат против равных сторон и обратно: равные стороны против равных углов.
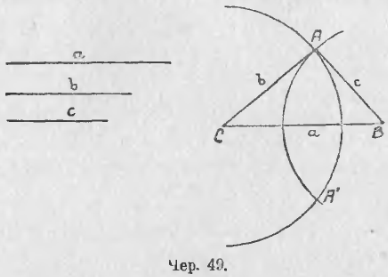
40. Задача. Построить треугольник по трем данным сторонам.
Пусть даны три отрезка a, b и c (чер. 49); требуется построить треугольник так, чтобы его стороны были соответственно равны данным отрезкам.
Строим где-либо один из данных отрезков a; тогда определяется две вершины треугольника B и C. Третья вершина должна расположиться так, чтобы отрезок, соединяющий ее с точкою B, был = с и отрезок, соединяющий ее с точкою C, был = b; поэтому нахождение ее сведется к задаче п. 27: надо, принимая B за центр, построить круг радиусом = c, и принимая C за центр, – круг радиусом = b и точку пересечения этих кругов, напр., точку A, соединить с точками B и C – тогда ΔABC и есть искомый. Соединив другую точку пересечения окружностей A’ с точками B и C, получим другой такой же Δ, расположенный симметрично с первым относительно оси BC.
Для того, чтобы задача была возможна, надо, чтобы: 1) a – b < c или c > a – b и 2) a + b > c или c < a + b, т. е. чтобы один из данных отрезков был больше разности двух других и меньше их суммы.
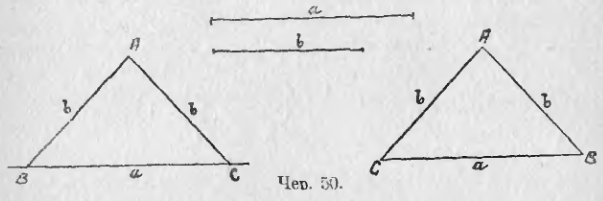
41. Пусть теперь даны 2 отрезка a и b (чер. 50). Требуется построить треугольник так, чтобы его стороны были a, b и b (задача возможна, если a < b + b или a < 2b).
Согласно предыдущему п., построение легко выполняется и получим, напр., ∆ABC, у которого две стороны (AB и AC) равны между собой. Такой ∆ называется равнобедренным; та его сторона, которая не имеет себе равных (в ∆ABC сторона BC = a), называется основанием равнобедренного треугольника, а противоположная вершина A называется «вершиною равнобедренного треугольника», причем этим названием эта вершина A как бы выделяется из остальных вершин.
Вообразим, что ∆ABC повернут другою стороною, то новый ∆ABC (чер. 50 — справа) можно простым передвижением совместить с прежним: сторона BC левого треугольника равна стороне CB правого, сторона AB левого = стороне AC правого и сторона AC левого = стороне AB правого, а мы уже знаем, что если стороны двух треугольников попарно равны, то эти треугольники равны, т. е. при наложении совмещаются (п. 38) и ∠B левого треугольника равен, следовательно, углу C правого, или, что то же самое, углу C тоже левого треугольника. Итак, в равнобедренном ∆ABC, у которого AB = AC, ∠B также = ∠C. Это свойство выразим словами:
В равнобедренном треугольнике углы при основании равны
или
В треугольнике, у которого две стороны равны, против равных сторон лежат равные углы.
42. Построим, наконец, ∆, у которого все 3 стороны равнялись бы данному отрезку a. Построение легко выполнить (чер. 50 bis). Этот ∆ называется равносторонним. Легко видеть, что этот ∆ можно счесть за равнобедренный с основанием CB; тогда ∠C = ∠B. Но его можно принять и за равнобедренный с основанием AB и тогда ∠A = ∠B, откуда приходим к заключению, что в равностороннем треугольнике все 3 угла равны между собою.
43. В п. 38 мы получили признак равенства треугольников: если стороны двух треугольников попарно равны, то и треугольники равны. Теперь мы можем, накладывая один треугольник на другой, получить еще другие признаки.
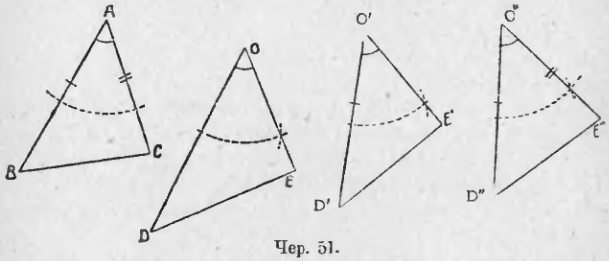
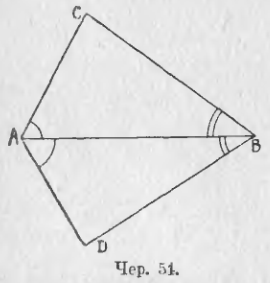
Построим какой угодно ∆ABC (чер. 51); затем построим ∠O = ∠A (п. 28) и на сторонах этого угла отложим отрезки OD > AB и OE < AC). На чер. 51 даны пунктиром те дуги, которые необходимы для построения ∠O = ∠A. Соединив точки D и E, получим ∆ODE. Наложим ∆ODE на ∆ABC так, чтобы ∠O совпал с ∠A (ведь ∠O = ∠A). В силу неравенств OD > AB и OE < AC, ∆ODE при этом наложении не совместится с ∆ABC (следует нарисовать, как именно расположится ∆ODE при этом наложении). Построим еще ∆O’D’E’ так, чтобы 1) ∠O’ = ∠A, 2) ∠O’D’ = ∠AB и 3) O’E’ < AC. Тогда при наложении треугольника O’D’E’ на ∆ABC так, чтобы ∠O’ совместился с ∠A, легко уясним, что и вершина D’ должна также совместиться с точкою B (в силу равенства O’D’ = AB), но точка E’ не совпадет с точкою C, — треугольники опять не совместятся (нарисовать их расположение при указанном наложении!). Теперь легко ответить на вопрос: как надо изменить сторону O’E’ треугольника O’D’E’, чтобы быть убежденным, что этот ∆ совместится с ∆ABC?
Надо, ответим мы, увеличить сторону O’E’ так, чтобы она сделалась равною стороне AC.
Итак, если мы построим ∆O»D»E» так, чтобы 1) ∠O» = ∠A, 2) O»D» = AB и 3) O»E» = AC, то мы можем быть убеждены, что ∆O»D»E» = ∆ABC. Замечая, что ∠O» и ∠A составлены попарно равными сторонами (на чертеже равные стороны и равные углы отмечены одинаковыми значками), мы можем сделать заключение:
Если построены два треугольника так, что у них по две равных стороны и углы, составляемые этими сторонами, также равны, то эти треугольники равны.
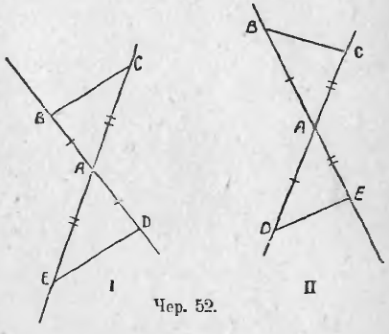
44. Построим два вертикальных угла при точке A – они, мы знаем, равны (чер. 52) и на сторонах этих углов отложим попарно равные отрезки AB = AD и AC = AE (это можно сделать двумя способами, почему на чер. 52 даны две фигуры I и II). Равны ли полученные треугольники? Как надо переместить ∆AED, чтобы он совпал с ∆ABC? Указать, какой угол одного из каждой пары треугольников равен какому-либо углу другого (можно воспользоваться п. 39 или выяснить, как именно расположится ∆AED при совмещении его с ∆ABC).
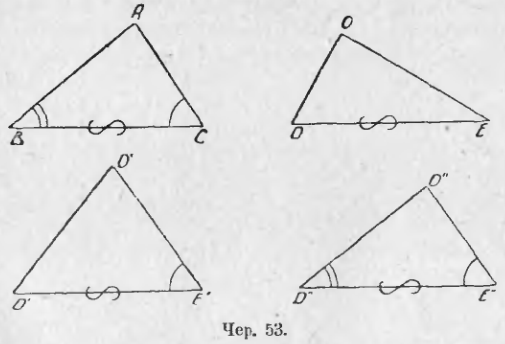
45. Построим какой-либо ∆ABC (чер. 53); затем построим ∆ODE так, чтобы сторона DE = стороне BC, чтобы ∠D был больше ∠B, но ∠E был меньше ∠C. Наложим ∆ODE на ∆ABC так, чтобы DE совпала с BC (точка D с B и точка E с C); этого добиться можно, так как эти стороны равны по построению.
Тогда, в силу того, что ∠D > ∠B и ∠E < ∠C, ∆ODE не совместится ∆ABC (следует нарисовать, как именно при этом наложении расположится ∆ODE). Построим еще ∆O’D’E’ так, чтобы D’E’ = BC, а также ∠E = ∠C, но, по-прежнему, ∠D’ был больше ∠B. Тогда при наложении ∆O’D’E’ на ∆ABC так, чтобы точки D’ и E’ совпали соответственно с точками B и C, увидим, что сторона E’O’ пойдет вне угла B (∠D’ > ∠B) и точка O’ не совпадет с точкою A (следует нарисовать расположение этих треугольников при рассматриваемом наложении). ∆O’D’E’ опять не совместиться с ∆ABC.
Теперь не трудно ответить на вопрос: как надо изменить ∠D’, чтобы добиться совпадения ∠O’D’E’ с ∆ABC? Надо, ответим мы, уменьшить ∠D’ так, чтобы он сделался равен ∠B.
Итак, если мы построим ∆O»D»E» так, чтобы 1) D»E» = BC, 2) ∠E» = ∠C и 3) ∠D» = ∠B, то мы можем быть убеждены, что ∆O»D»E» = ∆ABC. Замечая, что равные стороны D»E» и BC этих треугольников расположены между соответственно равными углами (на чертеже равные стороны и равные углы отмечены одинаковым знаками), мы можем установить еще признак равенства треугольников:
Если построены 2 треугольника так, что они имеют по два равных угла и по равной стороне между этими углами, то такие треугольники равны.
46. Построим какой-либо ∆ABC (чер. 54) и при концах стороны AB построим ∠BAD = ∠CAB и ∠ABD = ∠ABC. Тогда получим ∆ABD.
Равны ли треугольники ACB и ABD? Как можно добиться совмещения этих треугольников? Указать равные стороны в этих треугольниках (можно воспользоваться п. 39).
47. Имея в виду пп. 38, 43 и 45, мы можем теперь свести вместе признаки равенства треугольников:
1) Если три стороны одного треугольника равны соответственно трем сторонам другого, то эти треугольники равны.
2) Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого, то эти треугольники равны.
3) Если два угла и сторона между ними одного треугольника равны соответственно двум углам и стороне между ними другого, то эти треугольники равны.
Прибавим сюда еще заключение п. 39: в равных треугольниках равные углы расположены против равных сторон и равные стороны против равных углов.
Для совмещения равных треугольников иногда бывает необходимо один из них перевернуть другою стороною.
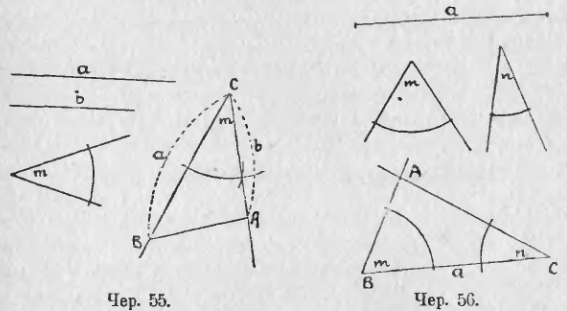
48. Задача. Построить треугольник по двум данным сторонам и углу между ними.
Пусть даны 2 отрезка a и b и угол m (чер. 55). Требуется построить ∆ так, чтобы данные отрезки были его сторонами и угол, ими составленный, был = ∠m.
Строим: 1) при точке C угол, равный ∠m, 2) на сторонах построенного угла откладываем CB = a и CA = b, 3) соединяем точки A и B. Получим искомый ∆ABC.
49. Задача. Построить треугольник по данной стороне и двум прилегающим к ней углам.
Дан отрезок a и 2 угла m и n (чер. 56); требуется построить ∆ так, чтобы одна из его сторон = a и углы, к ней прилегающие, были равны ∠m и ∠n.
Строим: 1) отрезок BC = a, 2) при точке B угол = ∠m и при точке C угол = ∠n так, чтобы одна сторона каждого из этих углов шла по BC; точка пересечения A других сторон построенных углов даст вершину A искомого треугольника.
Может случиться, что стороны построенных углов или вовсе не пересекаются (параллельны между собою – это случится, если ∠m + ∠n = выпр. углу) или пересекутся по другой стороне от BC; в последнем случае получится треугольник, у которого к стороне a прилегают углы не m и не n, а дополняющие их до выпрямленного.
Мы знаем, что сумма всех трех внутренних углов треугольника равна выпрямленному углу, а сумма двух внутренних его углов должна быть, следовательно, меньше выпрямленного. Поэтому для возможности данной задачи необходимо, чтобы было: ∠m + ∠n < выпрямленного угла.
Упражнения
- Построить равнобедренный треугольник по углу при его вершине и по боковой стороне.
- Построить равнобедренный треугольник по основанию и по углу при основании.