Решение
Найдём уравнение прямой BC по двум точкам:

, или y = —
x — 6.
Тогда её угловой коэффициент k1 = — . Если k2 — угловой коэффициент прямой, содержащей высоту AP, то k1 . k2 = — 1. Поэтому
k2 = — = 2.
Уравнение прямой, содержащей высоту AP треугольника ABC, найдём по точке A(5; — 1) и угловому коэффициенту k2 = 2:
y + 1 = 2(x — 5), или y = 2x — 11.
Найдём уравнение прямой AC по двум точкам:

, или y =
x —
.
Тогда её угловой коэффициент k3 = . Если k4 — угловой коэффициент прямой, содержащей высоту BQ, то k4 . k3 = — 1. Поэтому
k4 = — = — 3.
Уравнение прямой, содержащей высоту BQ треугольника ABC, найдём по точке B(4; — 
y + 8 = — 3(x — 4), или y = — 3x + 4.
Координаты точки H пересечения высот треугольника ABC найдём, решив систему уравнений, задающих прямые AP и BQ:
Получим: x = 3, y = — 5.

Ответ
(3; — 5).
Примеры решений по аналитической геометрии на плоскости
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.
Решения задач о треугольнике онлайн
Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.
Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.
Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.
Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.
Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.
Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.
Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.
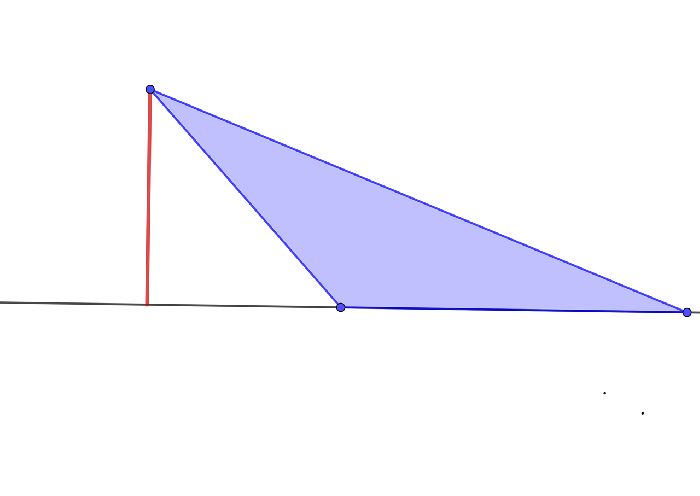
Даны точки A(5; — 1), B(4; — 8), C(- 4; — 4). Найдите координаты точки пересечения высот треугольника ABC.
Найдём уравнение прямой BC по двум точкам:
= , или y = — x — 6.
Тогда её угловой коэффициент k1 = — . Если k2 — угловой коэффициент прямой, содержащей высоту AP, то k1 . k2 = — 1. Поэтому
k2 = — = 2.
Уравнение прямой, содержащей высоту AP треугольника ABC, найдём по точке A(5; — 1) и угловому коэффициенту k2 = 2:
Найдём уравнение прямой AC по двум точкам:
= , или y = x — .
Тогда её угловой коэффициент k3 = . Если k4 — угловой коэффициент прямой, содержащей высоту BQ, то k4 . k3 = — 1. Поэтому
k4 = — = — 3.
Уравнение прямой, содержащей высоту BQ треугольника ABC, найдём по точке B(4; — 
Координаты точки H пересечения высот треугольника ABC найдём, решив систему уравнений, задающих прямые AP и BQ:
Ответ
Точка пересечения высот треугольника

Средняя оценка: 4.2
Всего получено оценок: 316.
Средняя оценка: 4.2
Всего получено оценок: 316.
Точка пересечения высот треугольника относится к одной из трех замечательных точек треугольника. Замечательными эти точки зовутся не за красоту, а за отношение к золотому сечению треугольника, которое характеризует данную фигуру.
Высота
Что такое высота? Высота это перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону треугольника (может получиться, что высота будет падать на продолжение стороны, как это бывает с тупоугольными треугольниками).

Точка пересечения высот
У любого треугольника есть три высоты, и они всегда пересекаются в одной точке. Эта точка является одним из 3 центров треугольника и зовется ортоцентром.
Еще со времен Древней Греции приставкой «орто» обозначали перпендикуляр. Ортогоналями звались перпендикулярные прямые.
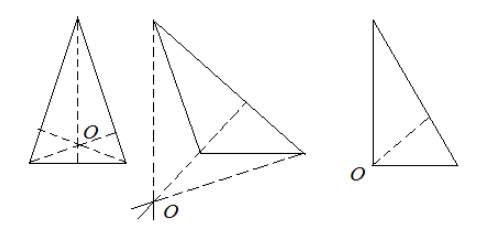
Ортоцентр имеет три варианта расположения в зависимости от вида треугольника:
- Внутри фигуры. В остроугольных треугольниках точка пересечения высот всегда находится внутри фигуры. Это обусловлено тем, что все высоты в таком треугольнике внутренние.
- Совпадает с вершиной. Этот случай характерен для прямоугольных треугольников. В таких треугольниках две из трех высот будут совпадать со сторонами. Если быть точнее, то совпадающие стороны это катеты. Остается одна высота, которая будет опускаться из вершины при остром угле. Именно эта вершина и будет ортоцентром треугольника.
- Вне фигуры. Внешнее расположение ортоцентра возможно только в тупоугольном треугольнике. Для того, чтобы получить ортоцентр такого треугольника, иногда потребуется продлить высоты до пересечения с внешней высотой. Почему?
Золотое сечение треугольника
Золотое сечение треугольника это маленький треугольник внутри фигуры, который определяется как пересечение трех центров треугольника.
Три центра треугольника это:
- Точка пересечения биссектрис
- Точка пересечения высот
- Точка пересечения медиан.
Золотое сечение иногда может вырождаться в прямую или даже точку. В равнобедренном треугольнике точка пересечения высот и медиан совпадает, в результате для построения золотого сечения понадобится только 2 точки и золотое сечение выродится в отрезок.
О центрах треугольника существует целая онлайн энциклопедия. Список центров треугольника и свойств каждого из них был начат Карлом Кемберлингом в 1994 году. Онлайн ресурс пополняется все новыми и новыми данными по мере их открытия в высшей математике. В школьном курсе рассматривается только 3 центра треугольника.
В правильном треугольнике и вовсе каждая высота будет совпадать с соответствующей медианой, биссектрисой и высотой. Значит, все три центра треугольника совпадут, и золотым сечением треугольника будет – точка.
Обратите внимание, что нельзя составить уравнение точки пересечения высот треугольника. Можно составить только уравнение прямой. Например, составить два уравнения высот, затем приравнять их и найти координату точки пересечения.
Что мы узнали?
Мы узнали, в каких построениях участвует точка пересечения высот треугольника. Поговорили о случаях, когда эта точка совпадает с другими центрами треугольника, выяснили особенности расположения ортоцентра в разных видах треугольников.
http://gitun.com/q/18151
http://obrazovaka.ru/geometriya/tochka-peresecheniya-vysot-treugolnika.html
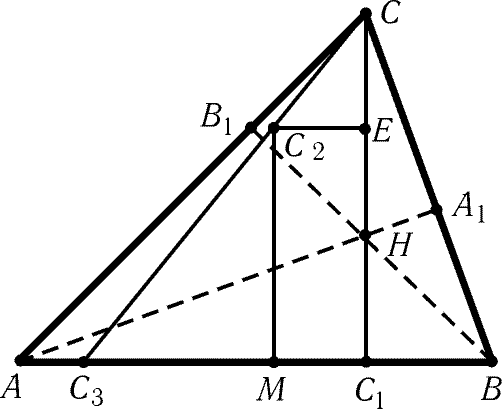
Как найти точку пересечения высот треугольника
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение. Точка пересечения трех высот носит название «ортоцентр». Понятие и свойства ортоцентра бывают полезны при решении задач на геометрические построения.
Вам понадобится
- треугольник, линейка, ручка, карандаш координаты вершин треугольника
Инструкция
Определитесь с видом имеющегося треугольника. Самый простой случай — прямоугольный треугольник, поскольку его катеты одновременно служат и двумя высотами. Третья высота такого треугольника располагается на гипотенузе. При этом ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.
В случае остроугольного треугольника точка пересечения высот будет находиться внутри фигуры. Проведите из каждой вершины треугольника линию, перпендикулярную стороне, находящейся напротив данной вершины. Все эти линии пересекутся в одной точке. Это и будет искомый ортоцентр.
Точка пересечения высот тупоугольного треугольника будет находиться вне фигуры. Прежде чем проводить перпендикуляры-высоты из вершин, вам необходимо сначала продолжить линии, образующие тупой угол треугольника. Перпендикуляр в данном случае опускается не на сторону треугольника, а на линию, содержащую данную сторону. Далее опускаются высоты и находится их точка пересечения, как описано выше.
Если известны координаты вершин треугольника на плоскости или в пространстве, нетрудно найти координаты точки пересечения высот. Если А, B, C — обозначения углов, O — ортоцентра, то отрезок AО перпендикулярен отрезку BС, а BО перпендикулярен AC, таким образом, получаете уравнения AО-BC=0, BО-AC=0. Этой системы линейных уравнений достаточно для нахождения координат точки О на плоскости. Вычислите координаты векторов BC и AC, вычитая из координат второй точки соответствующие координаты первой точки. Принимаете, что точка О имеет координаты x и y (О(x,y)), далее решите систему из двух уравнений с двумя неизвестными. Если задача дана в пространстве, то в систему следует добавить уравнения AО-a=0, где вектор a=AB*AC.
Видео по теме
Обратите внимание
Не перепутайте точку пересечения высот (ортоцентр) с точкой пересечения медиан (центроидом), биссектрис или серединных перпендикуляров (проведенных через середину каждой стороны треугольника).
Полезный совет
Для определения ортоцентра достаточно найти точку пересечения двух высот из трех, поскольку высоты любого треугольника всегда пересекаются в одной точке.
Источники:
- Интерактивный справочник формул.
- пересечение высот
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Точка пересечения высот треугольника

4.2
Средняя оценка: 4.2
Всего получено оценок: 418.
4.2
Средняя оценка: 4.2
Всего получено оценок: 418.
Точка пересечения высот треугольника относится к одной из трех замечательных точек треугольника. Замечательными эти точки зовутся не за красоту, а за отношение к золотому сечению треугольника, которое характеризует данную фигуру.
Опыт работы учителем математики — более 33 лет.
Высота
Что такое высота? Высота это перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону треугольника (может получиться, что высота будет падать на продолжение стороны, как это бывает с тупоугольными треугольниками).
Точка пересечения высот
У любого треугольника есть три высоты, и они всегда пересекаются в одной точке. Эта точка является одним из 3 центров треугольника и зовется ортоцентром.
Еще со времен Древней Греции приставкой «орто» обозначали перпендикуляр. Ортогоналями звались перпендикулярные прямые.
Ортоцентр имеет три варианта расположения в зависимости от вида треугольника:
- Внутри фигуры. В остроугольных треугольниках точка пересечения высот всегда находится внутри фигуры. Это обусловлено тем, что все высоты в таком треугольнике внутренние.
- Совпадает с вершиной. Этот случай характерен для прямоугольных треугольников. В таких треугольниках две из трех высот будут совпадать со сторонами. Если быть точнее, то совпадающие стороны это катеты. Остается одна высота, которая будет опускаться из вершины при остром угле. Именно эта вершина и будет ортоцентром треугольника.
- Вне фигуры. Внешнее расположение ортоцентра возможно только в тупоугольном треугольнике. Для того, чтобы получить ортоцентр такого треугольника, иногда потребуется продлить высоты до пересечения с внешней высотой. Почему? Потому что внешняя высота проходит за пределами треугольника и опускается на продолжение одной из сторон, а две внутренние стороны всегда ограничены треугольником. Поэтому без дополнительных построений ортоцентр тупоугольного треугольника не найти.
Золотое сечение треугольника
Золотое сечение треугольника это маленький треугольник внутри фигуры, который определяется как пересечение трех центров треугольника.
Три центра треугольника это:
- Точка пересечения биссектрис
- Точка пересечения высот
- Точка пересечения медиан.
Золотое сечение иногда может вырождаться в прямую или даже точку. В равнобедренном треугольнике точка пересечения высот и медиан совпадает, в результате для построения золотого сечения понадобится только 2 точки и золотое сечение выродится в отрезок.
О центрах треугольника существует целая онлайн энциклопедия. Список центров треугольника и свойств каждого из них был начат Карлом Кемберлингом в 1994 году. Онлайн ресурс пополняется все новыми и новыми данными по мере их открытия в высшей математике. В школьном курсе рассматривается только 3 центра треугольника.
В правильном треугольнике и вовсе каждая высота будет совпадать с соответствующей медианой, биссектрисой и высотой. Значит, все три центра треугольника совпадут, и золотым сечением треугольника будет – точка.
Обратите внимание, что нельзя составить уравнение точки пересечения высот треугольника. Можно составить только уравнение прямой. Например, составить два уравнения высот, затем приравнять их и найти координату точки пересечения.
Что мы узнали?
Мы узнали, в каких построениях участвует точка пересечения высот треугольника. Поговорили о случаях, когда эта точка совпадает с другими центрами треугольника, выяснили особенности расположения ортоцентра в разных видах треугольников.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 418.
А какая ваша оценка?
Треугольник
– многоугольник с тремя сторонами, или
замкнутая ломаная линия с тремя звеньями,
или фигура, образованная тремя отрезками,
соединяющими три точки, не лежащие на
одной прямой (см.
рис. 1).
Рис. 1.
Вершины
– точки A,
B, и C;
Стороны
– отрезки a = BC, b = AC и c = AB, соединяющие
вершины;
Углы
– α , β, γ образованные тремя парами
сторон. Углы часто обозначают так же,
как и вершины, – буквами A, B и C.
Угол, образованный
сторонами треугольника и лежащий в его
внутренней области, называется внутренним
углом, а смежный к нему является смежным
углом треугольника (2, стр. 534).
Высоты, медианы, биссектрисы и средние линии треугольника
Кроме основных
элементов в треугольнике рассматривают
и другие отрезки, обладающие интересными
свойствами: высоты, медианы, биссектрисы
исредние
линии.
Высота
Высоты треугольника
– это перпендикуляры, опущенные из
вершин треугольника на противоположные
стороны.
Для построения
высоты необходимо выполнить следующие
действия:
1) провести прямую,
содержащую одну из сторон треугольника
(в случае, если проводится высота из
вершины острого угла в тупоугольном
треугольнике);
2) из вершины,
лежащей напротив проведенной прямой,
провести отрезок из точки к этой прямой,
составляющий с ней угол 90 градусов.
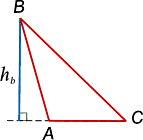
Рис. 2.
Точка пересечения
высоты со стороной треугольника называется
основанием
высоты
(см. рис. 2).
Свойства высот треугольника
-
В прямоугольном
треугольнике высота, проведенная из
вершины прямого угла, разбивает его на
два треугольника, подобные исходному
треугольнику. -
В остроугольном
треугольнике две его высоты отсекают
от него подобные треугольники. -
Если треугольник
остроугольный, то все основания высот
принадлежат сторонам треугольника, а
у тупоугольного треугольника две высоты
попадают на продолжение сторон. -
Три высоты в
остроугольном треугольнике пересекаются
в одной точке и эту точку называют
ортоцентром
треугольника.
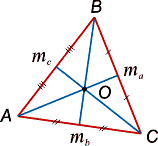
Медиана
Медианы (от
лат. mediana
– «средняя»)
– это отрезки, соединяющие вершины
треугольника с серединами противолежащих
сторон (см. рис. 3).
Для построения
медианы необходимо выполнить следующие
действия:
1) найти середину
стороны;
2)соединить точку,
являющуюся серединой стороны треугольника,
с противолежащей вершиной отрезком.
Рис. 3.
Свойства
медиан треугольника
-
Медиана
разбивает треугольник на два треугольника
одинаковой площади. -
Медианы
треугольника пересекаются в одной
точке, которая делит каждую из них в
отношении 2:1, считая от вершины. Эта
точка называется
центром
тяжести треугольника.
Весь
треугольник разделяется своими медианами
на шесть равновеликих треугольников.
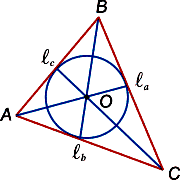
Биссектриса
Биссектрисами
(от лат. bis
– дважды» и seko
– рассекаю) называют заключенные внутри
треугольника отрезки прямых, которые
делят пополам его углы (см. рис. 4).
Для построения
биссектрисы необходимо выполнить
следующие действия:
1) построить луч,
выходящий из вершины угла и делящий его
на две равные части (биссектрису угла);
2) найти точку
пересечения биссектрисы угла треугольника
с противоположной стороной;
3) выделить отрезок,
соединяющий вершину треугольника с
точкой пересечения на противоположной
стороне.
Рис. 4.
Свойства
биссектрис треугольника
-
Биссектриса угла
треугольника делит противоположную
сторону в отношении, равном отношению
двух прилежащих сторон. -
Биссектрисы
внутренних углов треугольника
пересекаются в одной точке. Это точка
называется центром вписанной окружности. -
Биссектрисы
внутреннего и внешнего углов
перпендикулярны. -
Если биссектриса
внешнего угла треугольника пересекает
продолжение противолежащей стороны,
то ADBD=ACBC. -
Биссектрисы одного
внутреннего и двух внешних углов
треугольника пересекаются в одной
точке. Эта точка — центр одной из трех
вневписанных окружностей этого
треугольника. -
Основания биссектрис
двух внутренних и одного внешнего углов
треугольника лежат на одной прямой,
если биссектриса внешнего угла не
параллельна противоположной стороне
треугольника. -
Если биссектрисы
внешних углов треугольника не параллельны
противоположным сторонам, то их основания
лежат на одной прямой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #