Как найти точку приложения веса

Определение

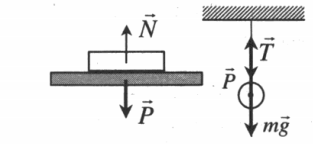
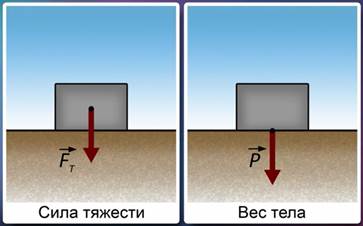
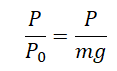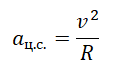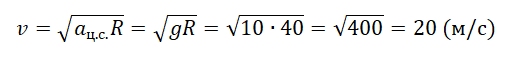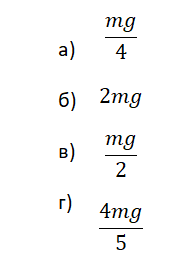Вес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.

Вес тела имеет электромагнитную природу (не путать с силой тяжести – она возникает между двумя телами и имеет гравитационную природу!). Обозначается P. Измеряется динамометром. Единица измерения — Н (Ньютон).

Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P↑↓N или P↑↓T.

Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:

P = T; P = N; P = F_упр.

Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:

P₀ = F_тяж = mg

Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.

Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.

Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:

P = mg = 16,38∙10 = 163,8 (Н)

Перегрузка

Перегрузка — отношение абсолютной величины линейного ускорения, вызванного негравитационными силами, к стандартному ускорению свободного падения на поверхности.

Перегрузка определяется отношением:

Перегрузка возникает, когда система, в которой находится тело, движется с ускорением.

Вес тела в движущейся равноускоренно системе

Вес тела в движущейся системе может быть больше или меньше веса того же тела в системе, которая находится в состоянии покоя:

1. Если система движется равноускоренно в направлении ускорения свободного падения, вес тела меньше веса тела в неподвижной системе: при a↑↑g — P < P₀.
2. Если система движется равноускоренно в направлении, противоположном ускорению свободного падения, вес тела больше веса тела в неподвижной системе: при a↑↓g — P > P₀.
3. Если система движется с равномерной скоростью (ускорение равно нулю) в любом направлении по отношению к ускорению свободного падения, вес тела равен весу тела в неподвижной системе: при a = 0 — P = P₀.

Применение законов Ньютона для определения веса тела

Опора или подвес неподвижны
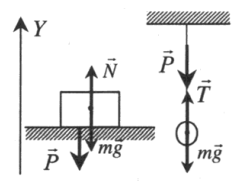	Второй закон Ньютона в векторной форме: N + mg = ma или T + mg = ma Проекция на ось ОУ: N – mg = 0 или T — mg = 0
Ускорение опоры направлено вверх
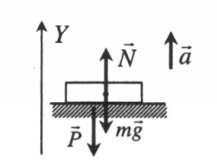	Второй закон Ньютона в векторной форме: N + mg = ma Проекция на ось ОУ: N – mg = ma Вес тела: P = N = ma + mg = m(a + g)
Ускорение опоры направлено вниз
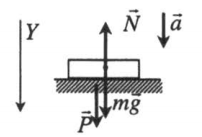	Второй закон Ньютона в векторной форме: N + mg = ma Проекция на ось ОУ: mg – N = ma Вес тела: P = N = mg – ma = m(g – a)
Вершина выпуклого моста
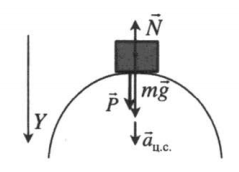	Второй закон Ньютона в векторной форме: N + mg = maц.с. Проекция на ось ОУ: mg – N = m aц.с. Вес тела: P = N = mg – m aц.с. = m(g – aц.с.)
Нижняя точка вогнутого моста
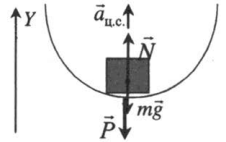	Второй закон Ньютона в векторной форме: N + mg = maц.с. Проекция на ось ОУ: N – mg = maц.с. Вес тела: P = N = maц.с. + mg = m(aц.с. + g)
Полный оборот на подвесе
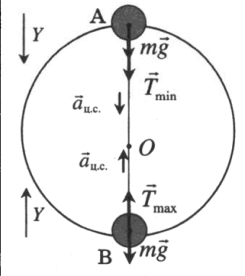	Второй закон Ньютона в векторной форме: T + mg = ma Проекция на ось ОУ в точке А: T + mg = maц.с. Вес тела в точке А: P = T = maц.с. – mg = m (aц.с. – g) Проекция на ось ОУ в точке В: T – mg = maц.с. Вес тела в точке В: P = T = maц.с. + mg = m (aц.с. + g) Важно! Центростремительное ускорение всегда направлено к центру окружности.

Пример №2. Автомобиль массой 1000 кг едет по выпуклому мосту с радиусом кривизны 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали невесомость?

Вес тела в верхней точке выпуклого моста равен:

P = m(g – a_ц.с.)

Чтобы пассажиры почувствовали состояние невесомости, вес тела должен быть равен 0:

m(g – a_ц.с.) = 0

Масса не может быть нулевой, поэтому:

g – a_ц.с. = 0

g = a_ц.с

Значит, пассажиры в верхней точке моста почувствуют невесомость, если центростремительное ускорение будет равно ускорению свободного падения. Центростремительное ускорение определяется формулой:

Отсюда скорость автомобиля в верхней точке моста должна быть равна:

Задание EF18133

Четыре одинаковых кирпича массой m каждый сложены в стопку (см. рисунок). Если убрать два верхних кирпича, то модуль силы N, действующей со стороны горизонтальной опоры на первый кирпич, уменьшится на…

---

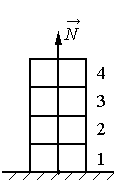
Алгоритм решения

1.Вычислить силу, с которой оставшиеся кирпичи давят на опору.

2.Применить третий закон Ньютона.

3.Определить силу, с которой действует горизонтальная опора на первый кирпич.

Решение

Так как кирпичи покоятся, вес каждого равен:

P = mg

Вес двух кирпичей равен:

2P = 2mg

Опора действует на первый кирпич с такой же силой, с какой на него действует два кирпича, оставшихся после того, как два верхних кирпича убрали.

Следовательно:

N = 2P = 2mg

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17624

Подъёмный кран поднимает груз с постоянным ускорением. На груз со стороны каната действует сила, равная по величине 8⋅10³ H. На канат со стороны груза действует сила, которая:

а) 8∙10³ Н

б) меньше 8∙10³ Н

в) больше 8∙10³ Н

г) равна силе тяжести, действующей на груз

---

Алгоритм решения

1.Сформулировать третий закон Ньютона.

2.Применить закон Ньютона к канату и грузу.

3.На основании закона сделать вывод и определить силу, которая действует на канат со стороны груза.

Решение

Третий закон Ньютона формулируется так:

«Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны».

Математически он записывается так:

F_A = –F_B

Если на груз со стороны каната действует некоторая сила, то и груз действует на канат с этой силой, которая называется весом этого груза, или силой натяжения нити. Следовательно, груз действует на канат с силой 8∙10³ Н.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22586

Мальчик медленно поднимает гирю, действуя на неё с силой 100 Н. Гиря действует на руку мальчика с силой:

а) больше 100 Н, направленной вниз

б) меньше 100 Н, направленной вверх

в) 100 Н, направленной вниз

г) 100 Н, направленной вверх

 

---

Алгоритм решения

1.Записать исходные данные.

2.Сделать чертеж, иллюстрирующий ситуацию.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в виде проекций.

5.Вычислить силу, с которой гиря действует на руку мальчика.

Решение

Запишем исходные данные: мальчик поднимает гирю вверх с силой F = 100 Н.

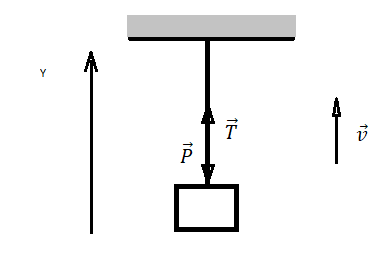
Сделаем рисунок. В данном случае рука мальчика выступает в роли подвеса. Так как мальчик поднимает гирю медленно, можно считать, что он поднимает ее равномерно (равнодействующая всех сил равна нулю). Выберем систему координат, направление оси которой совпадает с направлением движения руки и гири.

На руку (подвес) действуют только две силы. Поэтому второй закон Ньютона выглядит следующим образом:

P + T = 0

Запишем этот же закон в проекции на ось ОУ:

–P + T = 0

Отсюда:

P = T

Следовательно, на руку мальчика действует вес гири, который по модулю равен силе, с которой мальчик действует на эту гирю.

Внимание! Существует второй способ решения задачи через третий закон Ньютона. Согласно ему, тела действуют друг на друга с силами, равными по модулю, но противоположными по направлению.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 6.6k

1. Что такое вес тела

Пре­жде всего, вспом­ним, что такое сила тя­же­сти. Это сила, с ко­то­рой все тела при­тя­ги­ва­ют­ся к Земле. Сила тя­же­сти опи­сы­ва­ет вза­и­мо­дей­ствие тела с Зем­ным шаром.

По­ста­вим один груз на непо­движ­ную опору, а дру­гой по­ме­стим на под­вес. Оба груза непо­движ­ны. Зна­чит, сила тя­же­сти, дей­ству­ю­щая на них, урав­но­ве­ше­на силой упру­го­сти, воз­ни­ка­ю­щей в опоре и под­ве­се.

Рис. 1. Тело на опоре и тело на под­ве­се

Но по­сколь­ку в при­ро­де су­ще­ству­ет толь­ко вза­и­модей­ствие тел, то с такой же по ве­ли­чине силой, на­прав­лен­ной в про­ти­во­по­лож­ную сто­ро­ну, тела дей­ству­ют на опору и под­вес.

Сила, с ко­то­рой тело дей­ству­ет на опору или рас­тя­ги­ва­ет под­вес, на­зы­ва­ет­ся весом тела.

2. Направление и точка приложения веса

Сила тя­же­сти и вес тела – это ве­ли­чи­ны, ко­то­рые, как и ско­рость, имеют на­прав­ле­ние. Как вы пом­ни­те, такие ве­ли­чи­ны на­зы­ва­ют­ся век­тор­ны­ми. Их удоб­но пред­став­лять на ри­сун­ках в виде стре­лок. Кроме того, у силы есть еще одна ха­рак­те­ри­сти­ка – точка при­ло­же­ния. Стрел­ка, изоб­ра­жа­ю­щая силу, на­чи­на­ет­ся в точке при­ло­же­ния силы.

Изоб­ра­зим на одном ри­сун­ке силу тя­же­сти тела, а на дру­гом его вес.

Пре­жде всего, сила тя­же­сти при­ло­же­на к са­мо­му телу. Точка при­ло­же­ния силы тя­же­сти на­зы­ва­ет­ся цен­тром тя­же­сти тела. На­прав­ле­на сила тя­же­сти вер­ти­каль­но вниз.

Вес тела при­ло­жен не к телу, а к опоре. Его точка при­ло­же­ния рас­по­ло­же­на на опоре в точке со­при­кос­но­ве­ния с телом. А ка­ко­во на­прав­ле­ние веса?

Вспом­ним, что вес тела на­прав­лен про­ти­во­по­лож­но силе упру­го­сти опоры. Если тело непо­движ­но, то сила упру­го­сти опоры ком­пен­си­ру­ет силу тя­же­сти, то есть на­прав­ле­на вер­ти­каль­но вверх. Сле­до­ва­тель­но, если тело непо­движ­но (или дви­жет­ся рав­но­мер­но и пря­мо­ли­ней­но), то вес тела также на­прав­лен вер­ти­каль­но вниз и чис­лен­но равен силе тя­же­сти.

На­ко­нец, обо­зна­чим силу тя­же­сти бук­вой  , а вес бук­вой .

Рис. 2. Изоб­ра­же­ние век­то­ров силы тя­же­сти и веса тела

Еще раз об­ра­ти­те вни­ма­ние: сила тя­же­сти дей­ству­ет на тело, а вес – на опору или под­вес.

На сле­ду­ю­щих уро­ках мы по­зна­ко­мим­ся с тем, как вы­чис­лить чис­лен­ное зна­че­ние силы тя­же­сти и веса тела.

3. Вес — разновидность силы упругости

Тела, на­хо­дя­щи­е­ся на опоре или под­ве­се, де­фор­ми­ру­ют опору и под­вес. Эта де­фор­ма­ция не видна нево­ору­жен­ным гла­зом, но она су­ще­ству­ет. Ведь без де­фор­ма­ции не по­яви­лась бы сила упру­го­сти, ко­то­рая пре­пят­ству­ет дви­же­нию тела к цен­тру Земли. Точно так же под дей­стви­ем опоры и под­ве­са де­фор­ми­ру­ет­ся тело (опора сжи­ма­ет ниж­нюю часть тела, а под­вес, на­о­бо­рот, рас­тя­ги­ва­ет его верх­нюю часть). Эта де­фор­ма­ция тела и вы­зы­ва­ет по­яв­ле­ние в теле силы упру­го­сти, ко­то­рую мы и на­зы­ва­ем весом.

§ 6. Закон всемирного тяготения. Вес тела

Анализируя законы Кеплера, описывающие движение планет, И. Ньютон в 1667 году пришёл к открытию закона всемирного тяготения:

В такой форме закон справедлив только для двух тел, которые можно считать материальными точками. Однако можно доказать, что для двух однородных тел шарообразной формы эта форма записи закона тоже справедлива.

Измерить величину гравитационной постоянной удалось английскому физику Г. Кавендишу в 1798 году.

С помощью крутильных весов и свинцовых шаров ему удалось получить значение гравитационной постоянной:

Второй закон Ньютона позволяет записать для силы, с которой тело притягивается к Земле: `F=G(Mm)/(R^2)=mg`, тогда `g=GM/R^2` — ускорение свободного падения на поверхности Земли (измерено Галилеем и Ньютоном), на расстоянии, большем радиуса на величину `h`, ускорение свободного падения находится по формуле:

Рассмотрим твёрдое тело, расположенное на горизонтальной неподвижной опоре: под действием силы тяжести тело деформируется. Если тело находится на опоре, то на нижний слой действуют все верхние слои, и, как следствие,  этот  слой деформируется наибольшим образом. На предпоследний слой действует меньшее количество слоёв, и он деформируется  меньше. Таким образом, тело, бывшее прямоугольным, примет вид трапеции. Нижний слой приблизился при такой деформации к центру тела, а значит, возникла сила упругости, направленная в сторону, противоположную направлению смещения частиц при деформации. Сила упругости, возникшая внутри данного тела, направлена перпендикулярно опоре. Эту силу, созданную деформированным телом и приложенную к опоре, называют весом тела. Опора под действием веса деформируется. Противоположная весу сила упругости действует на данное тело со стороны деформированной опоры и тоже направлена перпендикулярно опоре, но называется силой реакции опоры `N` (от слова normal — перпендикуляр).

На рисунке 9 тело не касается опоры для того, чтобы показать, что вес приложен к опоре, а сила реакции опоры к телу. В действительности площадь реального соприкосновения твёрдых тел невелика. Большей частью между телами находится тонкий слой воздуха.

Вполне очевидно, что если опоры нет, то и веса тело иметь не будет. Такое случится в том случае, если тело движется под действием только одной силы — силы тяготения.

Также легко понять, что если на тело действует две силы (сила тяжести и сила реакции опоры), то эти силы не обязательно равны друг другу. Одна из них может быть больше другой.

Рассмотрим движение тела, помещённого в лифт. Пусть сам лифт движется с ускорением `veca`. 

Такое ускорение будет в двух случаях:

1) лифт поднимается равноускорено,

2) лифт опускается равнозамедленно.

Второй закон Ньютона для данного тела примет вид:

`vecN+mvecg=mveca`.

При рассмотрении данного движения из лабораторной неподвижной системы отсчёта `Oy` увидим, что в проекции на вертикальную ось `Oy` второй закон запишется следующим образом:

`N-mg=ma`, 

откуда   

`N=ma+mg=m(g+a)`.

Но по третьему закону Ньютона знаем, что сила реакции опоры и вес тела равны и противоположны, следовательно:

`N=P`, 

тогда:

Не трудно проследить за тем, что мы получим, если ускорение тела будет направлено вниз.

В проекции на ось `Oy` ускорение проецируется со знаком «`-`», что даст окончательную формулу для веса:

Или в общем случае:

Подобным образом можно получить выражение для веса тела, движущегося равномерно по выпуклому участку дороги.

Важное дополнение:

Для рассматриваемой силы, называемой весом, важно понимать и уметь правильно изображать точку приложения этой силы.

На рисунке 11а показан лифт, у которого нет ускорения. Тогда сила тяжести равна силе реакции опоры. А по третьему закону Ньютона, сила реакции опоры равна весу тела. Точка приложения силы тяжести расположена в геометрическом центре тела, если тело однородно и правильной формы. Точка приложения силы реакции опоры должна быть изображена внутри тела вблизи с нижней поверхностью тела на линии действия силы тяжести. Последнее свойство на рисунке не выдержано для удобства изображения (иначе силы на рисунке будут накладываться друг на друга). Точка приложения веса тела находится внутри опоры (пола лифта) вблизи поверхности на линии действия силы реакции опоры.

   

На рисунке 11б ускорение лифта направлено вниз. Тогда сила реакции опоры меньше силы тяжести. А вес снова равен силе реакции опоры.

На рисунке 11в ускорение лифта направлено верх. Тогда сила реакции опоры больше силы тяжести. А вес снова равен силе реакции опоры.

ДИНАМИКА
(ПРОДОЛЖЕНИЕ).

Теперь, когда
мы знаем, что такое масса, самое время разобраться с понятием силы.

Сила — это векторная физическая
величина, являющаяся мерой взаимодействия тел.

Из данного
определения можно сделать вывод, что сила — это характеристика моего
воздействия на другие тела. И эта величина имеет направление. В механике
несколько базовых сил, то есть сил которые обязан знать каждый учащийся.

-И что это
за силы?

Сейчас мы
рассмотрим их по порядку. Для начала давайте определимся какие характеристики
мы должны будем давать каждой силе, вот они:

—
определение силы;

—
обозначение силы;

— точка
приложения силы;

—
направление действия силы;

— численное
значение силы.

То есть
начиная разбирать ту или иную силу мы будем обязаны давать ей эти
характеристики. Ну начнём!

Сила
тяжести.

Сила
тяжести —
это сила, действующая на все тела, находящиеся у поверхности Земли, со стороны
Земли.

Обозначать силу
тяжести принято следующим образом: F_т.

Точка
приложения силы тяжести находится в центре масс тела. Если тело однородно, то
его центр масс совпадает с геометрическим центром, если же тело не однородно
(то есть состоит из частей с разной плотностью), то центр масс смещён в сторону
части с большей плотностью.

Сила тяжести
всегда направлена вертикально вниз. Например

Ну и
численное значение силы тяжести мы будем определять по следующему уравнению

F_т=mg

Где F_т-сила тяжести, m— масса тела, g— ускорение свободного падения.
Принято считать, что g=10 м/с².

Для силы
тяжести надо помнить следующее:

— если тело
предоставлено самому себе, то под действием силы тяжести оно принимает наиболее
устойчивое положение, когда центр масс тела находится в максимально низкой
точке.

-Так вот
почему бутерброд с маслом всегда падает маслом вниз!

Совершенно
верно, именно по этой причине. В свободном падении под действием силы тяжести
цент масс бутерброда занимает наинизшее положение, а так как масло более
плотное чем хлеб, то центр масс смещён к маслу, вот бутерброд и поворачивается
в полёте маслом вниз.

Так же надо
учитывать, что сила тяжести есть возле любого небесного объекта, а это значит,
что в нашей вселенной нет такого места где бы отсутствовала сила тяжести.

-Подождите,
но я же своими глазами видел репортаж с космической станции и там космонавты
плавали, не падая вниз!

И опять
Ростик ты совершил грубую физическую ошибку спутав вес тела с силой тяжести.

-Да что же
это такое! Что ж это за вес такой, с массой его путать нельзя, с силой тяжести
снова нельзя!

Ну что же
Ростик давай разберёмся, что же такое вес тела.

Вес
тела.

Вес тела — это сила, действующая со
стороны тела на опору или подвес.

Вес тела
принято обозначать буквой латинского алфавита P.

Точка
приложения веса тела находится в точке подвеса или в центре площади опоры тела.

Вес тела
всегда направлен вдоль подвеса или перпендикулярно плоскости опоры. Например

Из рисунка
видно, что направление веса тела зависит от расположения подвеса или плоскости
опоры тела.

Сложнее дело
обстоит с нахождением численного значения веса тела. В седьмом классе мы будем
находить вес тела только в двух случаях это когда тело находится на
вертикальном подвесе или горизонтальной опоре.

В этих
случаях вес тела численно равен силе тяжести

P=mg

В других
случаях вес тела может быть меньше, может быть больше mg, но как его находить мы поговорим
позже, потому что сейчас у нас не хватает математических знаний и навыков. Но
уже сейчас видно, что вес и масса разные вещи.

-Да
действительно что бы найти вес необходимо массу тела умножить на ускорение
свободного падения.

Поэтому
заменять одно на другое категорически нельзя! Да и измеряются они в разных
единицах, масса измеряется в килограммах, а вес измеряется в ньютонах. Что же
касается космонавтов на орбите, то они находятся в невесомости, в состоянии
отсутствия веса. Если вы вспомните определение веса, там сказано, что это сила,
действующая на опору или подвес, значит если у тела нет опоры или подвеса, то у
него нет и веса.

-Но, если у
тела нет опоры оно же падает.

Вот именно,
отсюда следует что вес у тела отсутствует при его свободном падении. Обращаю
ваше внимание сила тяжести на тело действует, именно под действием силы тяжести
тело падает, а вес у тела отсутствует. Полёт космического корабля это ни что
иное как падения корабля на Землю. Но ввиду того что Земля имеет закруглённую
форму, а скорость космического корабля направлена под прямым углом к радиусу
Земли, корабль не может упасть на Землю, так как она постоянно из-под корабля
уходит.

Скорость, которая
позволяет телу быть спутником небесного тела, то есть вращаться вокруг
небесного тела, не падая на его поверхность, называется первой космической
скоростью. Для Земли первая космическая скорость составляется 7,8 км/с.

-А для
других космических тел эта скорость другая?

Да Ростик,
чем массивнее небесное тело, тем большее значение имеет первая космическая
скорость.

Задачи
для самостоятельного решения.

Задача
14. Масса
спускаемой части корабля «Восток» составляла 4,73 т. Определите вес данной
части на старте.

Задача
15. На
самолёт Як-42 находящийся на взлётной полосе действует сила тяжести равная
145000 Н. Определите массу самолёта.

Задача
16. Масса
комара 1,5 мг, определите действующую на него силу тяжести.

Задача
17.
Латунный цилиндр высотой 20 см имеет вес 8,3 Н. Какова площадь основания
цилиндра, если плотность латуни 8300 кг/м³?

Ответы: 14. 47,3 кН; 15.
14,5 т; 16. 15 мН; 17. 0,005 м².

4-я лекция.

4. ГИДРОСТАТИКА-2

4.1. Сила давления жидкости па плоскую стенку.

4.2. Точка приложения силы давления.

4.3 Сила давления жидкости на криволинейную стенку.

4.4.Плавание тел.

4.5. Прямолинейное равноускоренное движение сосуда с жидкостью.

4.6. Равномерное вращение сосуда с жидкостью.

4.1. Сила давления жидкости па плоскую стенку

Рекомендуемые материалы

Давление жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом  α, определяется по  основному уравнению гидростатики

Р=Р₀+hρg

Определим силу давления F, действующую со стороны жидкости, на участок рассматриваемой стенки, ограниченный произвольным контуром, имеющим площадь S.

Ось Ох направим перпендикулярно плоскости стенки от точки ее пересечения со свободной поверхностью жидкости, а ось Оу — перпендикулярно оси Ох в  плоскости стенки.

Выразим элементарную силу давления, приложенную к бесконечно малой площадке δS , для остальных площадок силы будут определяться таким же образом

δFж = P*δS =(P₀ + ρhg) δS = P₀*δS + ρhg*δS,

где Р₀ — давление на свободной поверхности, h — глубина расположения площадки  δS. 

Переходя к пределу при  стремлении  площадки δS→0, получим выражение для дифференциала силы давления:

dFж = P₀*dS + ρhg*dS,

Проинтегрировав этот дифференциал по площади S,  получим выражение для определения полной силы Fж

,

где у — координата площадки dS, h = у*Sinα .

Интеграл  представляет собой статический момент площади S относительно оси Ох , который  равен произведению  площади S на координату у_с ее центра тяжести — точки С:

Усилие давления жидкости на плоскую, наклоненную стенку равно

Fж = P₀S+ρg(y_c Sinα) S = P₀S+ρgh_cS,    (4.1)

здесь h_c = (y_c Sinα)— глубина расположения центра тяжести площади S.

Fж = ρg (H₀ +h_c)S = P_cS,                     (4. 2)

Сила давления жидкости Fж  = ρgh_cS – это вес объема V = h_cS жидкости.

Полная сила давления жидкости Fж на плоскую стенку равна произведению площади стенки S  на гидростатическое давление Р_с в центре тяжести этой площади.

1.В частном случае, когда давление Р₀ является атмосферным и действует также с другой стороны стенки, сила избыточного давления жидкости F_{изб ж}  на плоскую стенку равна лишь силе Fж давления от веса столба жидкости, т. е.

F_{изб ж} = P_cS= ρgh_cS.

2. В общем случае давление Р₀ может существенно отличаться от атмосферного, поэтому полную силу F давления жидкости на стенку можно  рассматривать как сумму двух сил: F₀ от внешнего давления Р₀ и силы Fж   от веса столба жидкости, т. е.

F= F₀ + Fж = (P₀+Pс)S.        (4.3.)

4.2. Точка приложения силы давления.

Внешнее давление Р₀ передается всем точкам площади S одинаково, и его равнодействующая сил внешнего давления F₀ будет приложена в центре тяжести площади S  с координатой  —  у_с.

Для нахождения точки D приложения силы давления Fж от веса жидкости применим теорему механики, согласно которой момент равнодействующей силы относительно оси Ох равен сумме моментов составляющих сил, в данном случае элементарных сил.

где у_D — координата точки приложения силы, h=y*Sinα.

Используя выражение для:

 F_ж = ρgh_c*S = ρg(y_cSinα)*S  — силы жидкости, действующей на плоскую стенку,

и для:

dF_ж= ρgh*dS= ρg(ySinα)*dS —  силы жидкости, действующей на элементарную площадку, получим 

        (4.4)

где  — момент инерции площади S относительно оси Оx.

Подставляя в формулу (4.4) значение:

 момента инерции и площади S — Jx  относительно оси х,  через момент инерции той же площади  — Jx₁  относительно центрально оси х₁ параллельной оси Ох, находим

Jx = Jx₁+y_C²S,                    (4.5)

у_D = у_C+ J_x1/(у_сS),              (4.6.)

Точка D  приложения силы F_ж расположена ниже центра тяжести площади стенки; расстояние между ними

Δу_D= у_D -Δу_C = J_x0/( у_сS),                 (4.7) .

Если давление Р₀ равно атмосферному, то точка D  будет центром давления.

При Р₀ > Pат  центр давления находят по правилам механики, как точку приложения равнодействующей двух сил F₀ и F_ж ,  чем больше первая сила по сравнению со второй  тем, очевидно, центр давления ближе к центру тяжести площади S.

Если стенка имеет форму прямоугольника размерами а × b (рис. 4.2) и с одной стороны  — атмосферное давление, центр давления D находится па расстоянии b/3 от нижней стороны.

4.3 Сила давления жидкости на криволинейную стенку.

Нахождение силы давления жидкости на поверхности произвольной формы в общем случае приводится к определению трех составляющих суммарной силы и трех моментов.

Рассмотрим действие жидкости на цилиндрические или сферические поверхности, имеющие вертикальную плоскость симметрии. Сила давления жидкости в этом случае сводится к равнодействующей силе, лежащей в плоскости симметрии.

Возьмем криволинейную поверхность АВ,  образующая которой  перпендикулярна к плоскости чертежа (рис.4.3а), определим силу давления жидкости на эту поверхность.

Выделим объем жидкости, ограниченный поверхностью АВ, вертикальными плоскостями, проведенными через границы этого участка ВС и AD,  свободной поверхностью жидкости. Рассмотрим  условия равновесия объема АВСD  в вертикальном и горизонтальном направлениях.

Сила давления  жидкости P действует на стенку АВ, стенка АВ удерживает действие  жидкости силой реакции стенки Rс = P, направленной в противоположную сторону. На рис. 4.3 сила реакции стенки и сила давления жидкости  разложены на горизонтальные и вертикальные составляющие.

Условие равновесия объема АВСD в вертикальном направлении имеет вид

Rс_в =Pжв= Р₀F_г + G = Р₀F_г + ρgV₀,                (4.8)

где Р₀  — давление на свободной поверхности жидкости; F_г — площадь горизонтальной проекции поверхности АВ; G — вес выделенного объема жидкостиV_0. Объем V₀  называют – объем тела давления..

Условие равновесия того же объема в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности ЕС и АD взаимно уравновешиваются и остается лишь сила давления на площадь ВЕ т. е. на вертикальную проекцию поверхности S_в = L_EB*B. Тогда

Rсг=Pжг= F_вρgh_c+ F_в Р₀ = F_в(ρgh_c+ Р₀).            (4.9)

Определив по формулам (4.8) и (4.9) вертикальную и горизонтальную составляющие полной силы Рж, найдем

 ,              (4.10).

Сила давления жидкости на криволинейную стенку будет равна сила реакции стенки Rж =  P и направлена в противоположную сторону.

Когда жидкость расположена снаружи (рис.4.3б), сила гидростатического давления на криволинейную поверхность АВ определяется также, но направление ее будет противоположным.

При этом под величиной G следует понимать так же, как и в первом случае вес жидкости в объеме АВСD, хотя этот объем и не заполнен жидкостью.

Положение центра давления на  цилиндрической стенке можно найти, если известны силы Fв и Fг и определены центр давления на вертикальной проекции h_D стенки и центр тяжести выделенного объема АВСD.

Задача значительно облегчается в том случае, когда рассматриваемая криволинейная  поверхность является круговой. Равнодействующая сила при этом пересекает ось поверхности, так как любая элементарная сила давления нормальна к поверхности, т. е. направлена по радиусу.

Изложенный способ определения силы давления на цилиндрические поверхности применим и к сферическим поверхностям, причем равнодействующая сила в этом случае также проходит через центр поверхности и лежит в вертикальной плоскости симметрии.

4.4. Плавание тел.

Описанный выше прием нахождения вертикальной составляющей силы давления жидкости па криволинейную стенку используют для доказательства закона Архимеда.

Пусть в жидкость погружено тело произвольной формы объемом V (рис.4.4).

Спроектируем его на свободную поверхность жидкости и проведем проек-тирующую цилиндрическую поверхность W, которая касается поверхности тела по замкнутой кривой. Эта кривая отделяет верхнюю часть поверхности тела АСВ от нижней ее части ADB.  Вертикальная составляющая F_в1 силы избыточного давления жидкости на верхнюю часть поверхности тела направлена вниз и равна весу жидкости в объеме АА’BВ’CA. Вертикальная составляющая F_в2 силы давления жидкости на нижнюю часть поверхности тела направлена вверх и равна весу жидкости в объеме АА’В’BDA. Отсюда следует, что вертикальная равнодействующая сил давления жидкости на тело будет направлена вверх и равна весу жидкости в объеме, равном разности указанных двух объемов, т. е.

F_А = F_в2  — F_в1  = G_ACBD =Vρg.                     (4.11)

Закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила направленная вертикально вверх, численно равная весу жидкости вытесненной телом и приложенная в центре тяжести объема погруженной части тел.

Сила F_А называется архимедовой силой,  а точка ее приложения, т. е. центр тяжести объема V — центром водоизмещения.

В зависимости от соотношения веса G тела и архимедовой силы возможны три случая:

 1) G> F_А — отрицательная  плавучесть, тело тонет;

2) G<F_А — положительная плавучесть, тело всплывает и плавает на поверхности жидкости;

3) G = F_А нулевая плавучесть, тело плавает погруженным в жидкость полностью.

Для равновесия плавающего тела, кроме равенства G = F_А  должен быть равен нулю суммарный момент. Последнее условие соблюдается тогда, когда центр тяжести тела лежит на одной вертикали с центром водоизмещения. Условие устойчивого равновесия тела, плавающего в полностью погруженном состоянии,  заключается в следующем: центр тяжести тела должен находиться ниже центра водоизмещения.

4.5. Прямолинейное равноускоренное движение

сосуда с жидкостью.

Если при движении сосуда на частицы жидкости, кроме сил тяжести действуют еще силы инерции,  под действием этих сил жидкость принимает новое положение равновесия — положение  относительного покоя.

Относительным покоем называется равновесие жидкости, находящейся под действием сил тяжести и инерции в  движущемся сосуде.

При относительном покое положение свободной поверхности и поверхностей уровня,  отличается от их положения для жидкости в неподвижном сосуде.

При определении формы и положения этих поверхности учитывается основное свойство поверхности уровня. 

Основное свойство поверхностей уровня  —  равнодействующая массовых сил всегда нормальна  к этим поверхностям.

В полном дифференциале давления

dP=ρ(X*dх+У*dy+Z*dz),          (4.12)

Х,У,Z – алгебраическая сумма проекций на оси координат ускорений силы тяжести и сил инерции переносного движения.

Вдоль поверхности уровня  dР=0 , так как поверхности уровня  — это поверхности равного давления. Дифференциальное уравнение поверхности равного давления:

X*dх+У*dy+Z*dz = 0          (4.13),

Этот трехчлен (4.13) определяет элементарную работу массовых сил X,У,Z на перемещениях dх, dy, dz. В данном случае перемещение взято по поверхности равного давления, dР=0.

Из этого выражения следует, что  работа массовых сил вдоль поверхности равного давления равна нулю. Это значит, что в состоянии относительного покоя результирующее ускорение перпендикулярно к  соответствующему элементу поверхности равного давления.

Рассмотрим два случая относительного покоя.

Первый случай:   сосуд, движущийся прямолинейно и равноускоренно.

Второй случай: сосуд, вращающийся вокруг вертикальной оси с постоянной угловой скоростью.

На рис.4.5 изображен сосуд, движущийся вниз с ускорением а по плоскости наклонённой под углом  α   к горизонту. Оси координат оси координат связаны с движущимся телом. 

1. Пусть на жидкость действует  суммарная массовая сила F, проекции которой F_x, Fy, Fz , поделенные на  массу: Fx/m  являются проекциями единичной массовой силы на оси Ох, Оу, Oz:  Х, У и Z.

F = Fx+Fy+Fz = mа,  F/m = Fx/m +Fy/m +Fz/m = X +Y + Z = а.

Все выделенные составляющие являются векторными величинами.

 Проекции массовых сил, действующие на выделенный объем в направлении координатных осей, будут равны произведениям проекций единичных сил, умноженным на массу выделенного объема.

Fx = mX,               Fy = mY,                     Fz = mZ.

Результирующую единичную массовую силу, действующую на жидкость,  найдем как сумму единичных векторов силы инерции j  и силы тяжести g. Единичная сила инерции Fи = j = — a направлена в сторону  противоположную ускорению а (рис.4.5).

Проекции сумм массовых сил на оси:

          Ox: X = j — gSinα,   

         Oz : Z = —gCosα,

Оx: Y = 0.

При подстановке этих проекций в дифференциал давления, получим

(1/ρ)dp = [(j — gSinα)dx – (gCosα)dz].

Проинтегрировав дифференциал в проекциях, получим выражение для давления на поверхностях уровня

Р = ρ [(j — gSinα) x – (gCosα)z] + С.  (4.14)

На произвольной поверхности уровня давление постоянно Р = const и,  обозначив новую постоянную  С₁ — Р = const, где Р получим уравнение  изобарических поверхностей

ρ [(j — gSina) x – ρgCosa* z] +С₁ = 0                (4.15)

Это уравнение дает семейство плоскостей, параллельных оси Оу. Одной из них является свободная поверхность.

Обозначим через z₀ координату пересечения свободной поверхности с осью z. Подставив в формулу (4.15) х₀ = 0, z = z₀, находим С₁=ρg z₀Cosα для свободной поверхности. Уравнение этой поверхности имеет вид

ρ [(j — gSina) x – ρgCosa* z] + ρg z₀Cosα = 0

 (j — gSina) x –gCosa*( z + z₀) = 0

  

 где коэффициент в линейном уравнении равен тангенсу угла β .

Для определения положения свободной поверхности жидкости в сосуде, движущемся прямолинейно   и   равноускоренно к уравнению (4.16) нужно добавить уравнение объемов, т. е. нужно знать первоначальный объем жидкости в сосуде и выразить его через размеры сосуда В и Н и первоначальный уровень h.

Если сосуд движется только под действием силы тяжести, то j= gSinα β = 0, то свободная поверхность параллельна  плоскости движения.

 При нулевых условиях: х = 0, z = z₀, P = P₀  в  формуле (4.14),   получим C = P₀+ (ρgCosa)z₀:  

Р = ρ [(j — gSinα) x – (gCosα)z + С

Р = P₀+ρ(j-gSina)x+ρgCosa(z₀ – z).   (4.19)

Эта формула используется для определения давления в любой точке жидкости, находящейся в относительном покое при прямолинейном движении

Можно также использовать суммарную массовую единичную силу q для определения давления в любой точке.

Возьмем на рис.4.5 около точки М площадку dS, параллельную свободной поверхности, и на этой площадке построим цилиндрический  объем с осью, нормальной к  свободной поверхности. Условие равновесия указанного объема жидкости в направлении нормали к свободной поверхности будет иметь вид

РdS = P₀dS + q(ρldS),

где последний член представляет собой полную массовую силу,  q – суммарная единичная массовая сила, М = ρldS —   масса выделенного объема жидкости,  l — расстояние от точки М до свободной поверхности.

После сокращения на dS получим давление в точке

Р = P₀ + qρl,                          (4.20)

4.6. Равномерное вращение сосуда с жидкостью

Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему вращение с постоянной угловой скоростью ω  вокруг его вертикальной оси. Силы трения о стенки вращающегося сосуда будут увлекать за собой жидкость. Она постепенно приобретет ту же угловую скорость, что и сосуд, находясь по отношению к  сосуду в покое. Свободная поверхность жидкости  изменится.

В центральной части уровень жидкости опустится, у стенок  она поднимется, и вся свободная поверхность жидкости станет поверхностью вращения (рис.4.6).

На жидкость будут действовать силы давления, силы тяжести и силы инерции переносного движения. Частица жидкости будет находиться под действием ускорения силы тяжести и центростремительного ускорения, а  равное ему ускорение силы инерции будет центробежным. Единичная массовая сила тяжести F_g = g и единичная массовая центробежная сила F_цб = ω²r.

Проекции этих сил на оси координат дадут следующие выражения

X = (V²/r) Cos(r^x) = ω²r Cos(r^x)= ω²X

Y = (V²/r) Cos(r^y) = ω²r Cos(r^у)= ω²Y,  

                                      Z = -g

Подставляя эти проекции в дифференциальное уравнение поверхности   равного давления и интегрируя :                 

X*dх+У*dy+Z*dz = 0,

получим                                 ρ(ω²/2) (X²  + Y²) – ρgz + С = 0.

Уравнение  свободной поверхности, например, получим, при нулевых условиях:    Р₀ = const, х = у = 0, z= z₀,  где  координата вершины параболоида свободной поверхности. Тогда   С = ρgz₀.  

ρ(ω²/2) (X²  + Y²) – ρgz + ρgz₀  = 0,

(ω²/2) (X²  + Y²) =g(z — z₀)

и после деления на g   уравнение свободной поверхности получит вид

                      (4.22)

Таким образом, поверхности равного давления, в том числе и свободная поверхность, образуют семейство параболоидов, сдвинутых вдоль вертикальной оси. Каждому значению р соответствует свой параболоид, положение которого определяет константа С.

Эти поверхности  будут конгруэнтными параболоидами вращения  с осью Oz. Один из этих параболоидов – свободная поверхность жидкости, где Р₀= Ратм.

Две геометрические фигуры называются конгруэнтными, если их можно совместить одну с другой, изменив их положение в пространстве.

Подставляя проекции массовых сил в дифференциал давления

dp  = ρ(Xdx  +  Ydy + Zdz), 

получим                                  dp  = ρω² (Xdx  + Ydy) –ρ gdz,

вынесем знак дифференциала за скобки,

dp  = ρ d[(ω²/2) (X²  + Y²)] –ρ gdz,

и проинтегрировав,  получим выражение для определения давления в любой точке

 p  = ρ(ω²/2) (X²  + Y²) –ρ gz + С₁,    (4.21)

Значение константы для свободной поверхности Р = Р₀, x=y=0, z = z₀: С₁ = Р₀ + ρgz_0.

Получим уравнение для определения давления в любой точке:

             (4.22)

Пользуясь этими уравнениями  можно определить положение свободной поверхности и давление в сосуде.

Максимальная высота Н подъема жидкости в параболоиде со свободной поверхностью может быть определена, следующим образом.

 На практике часто рассматривается вращение сосуда с жидкостью, когда угловая скорость ω столь велика, что силой тяжести можно пренебречь по сравнению с центробежными силами. При этом закон изменения давления в жидкости легко получить из формулы (4.22),  в которой следует принять g(z₀ — z) = 0.

Поверхности уровня примут вид цилиндров с общей осью  —   осью вращения сосуда. Если сосуд не был заполнен перед началом вращения,  давление Р₀ будет действовать не в центре, а при r = r₀,  вместо выражения (4.22) будем иметь

Р = Р₀ + ρ ω² (r —r₀²)/2g,                          (4.23)

Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к оси вращения (или на кольцевую часть этой стенки).

Для этого необходимо выразить сначала силу давления, приходящуюся на элементарную кольцевую площадку dS = 2πrdr радиусом r и шириной dr;

 

Уравнение, выражающее величину давления имеет вид

Ещё посмотрите лекцию «Лекция 11.1» по этой теме.

При определении давления на верхнюю крышку где Z=0,  Z₀ может быть больше нуля Z0>0, равно нулюи меньше нуля

В первом случае

а затем выполнить интегрирование в требуемых пределах.

При большой угловой скорости жидкости можно получить весьма значительную суммарную силу давления на стенку. Этот эффект используется в некоторых фрикционных муфтах, где для осуществления сцепления двух валов требуется создание больших сил нормального давления. Способ, указанный выше,  применяют для определения силы осевого давления жидкости на рабочие колеса центробежных насосов, а также на крышки центрифуг.