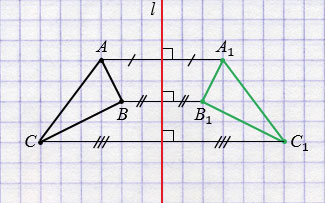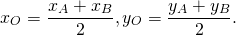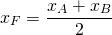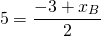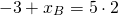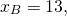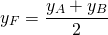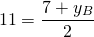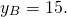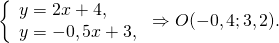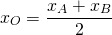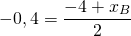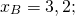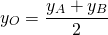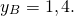Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
Примеры.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Решение:
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
Ответ: (13;15).
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Решение:
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
Ответ: (-9;4).
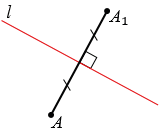
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
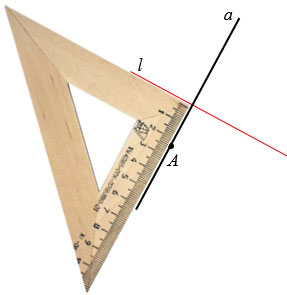
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
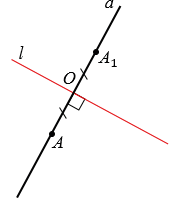
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Пример
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Решение:
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
5=-0,5·(-4)+b, откуда b=3.
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Найдём координаты точки пересечения прямых:
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Ответ: (3,2;1,4).
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
| для точки A(x;y) | |
| симметрия относительно: | |
| оси Ox | A1(x;-y) |
| оси Oy | A2(-x;y) |
|
биссектрисы I и II координатных четвертей (прямой y=x) |
A3(y;x) |
|
биссектрисы I b II координатных четвертей (прямой y= -x) |
A4(-y;-x) |
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Осевая и центральная симметрии
Осевая симметрия
Рассмотрим построение точки, симметричной данной точке А относительно данной прямой 
Пусть дана точка А и прямая 
Точку симметричную точке А относительно прямой 



Пусть прямые 


Получаем точки А и А1, которые симметричны относительно прямой 
Также можно построить фигуры, симметричные относительно прямой.
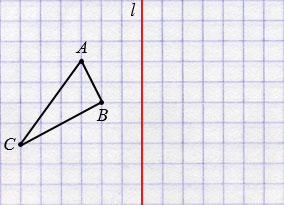
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой 
Пусть дан треугольник АВС и прямая 
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно прямой 

Обратите внимание, любые две фигуры, симметричные относительно прямой, равны.
Если фигура имеет ось симметрии (прямая 
Центральная симметрия
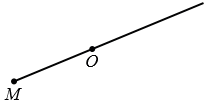
Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1 (смотри рисунок ниже).
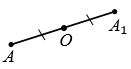
Рассмотрим построение точки, симметричной данной точке М относительно данной точки О.
Пусть даны точки М и О. Точку, симметричную точке М относительно точки О, можно построит так. Проведем луч МО.
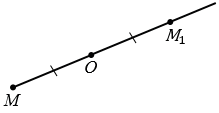
На луче МО отложим отрезок ОN , равный отрезку ОМ.
Точки М и М1, которые симметричны относительно точки О.
Также можно построить фигуры, симметричные относительно точки.
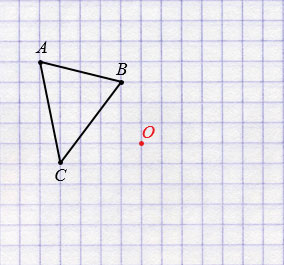
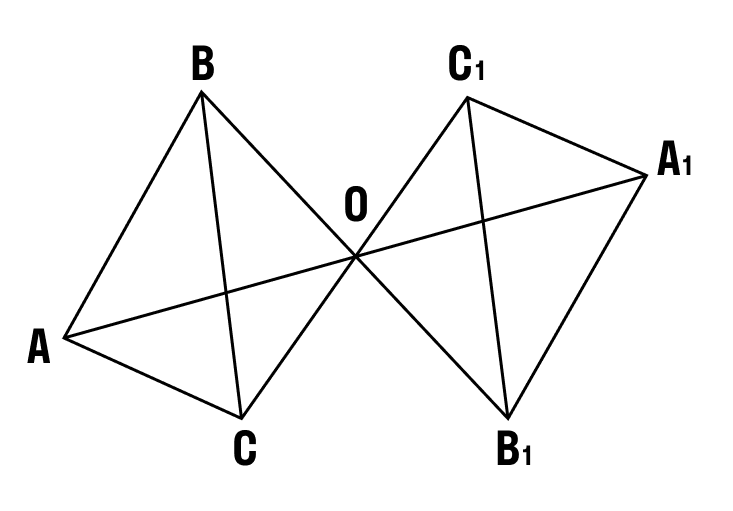
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
Пусть дан треугольник АВС и точки О.
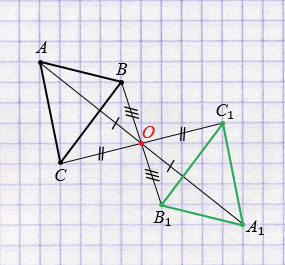
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно точки О (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
Обратите внимание, любые две фигуры, симметричные относительно точки, равны.
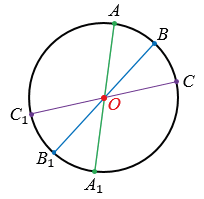
Рассмотрим окружность с центром в точке О. Все точки окружности можно разбить на пары точек, симметричных относительно точки О.
В таком случае говорят, что окружность имеет центр симметрии — точку О.
Также центр симметрии имеют такие фигуры, как отрезок, прямоугольник, эллипс.
Советуем посмотреть:
Перпендикулярные прямые
Параллельные прямые
Координатная плоскость
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1252,
Мерзляк, Полонский, Якир, Учебник
Номер 1262,
Мерзляк, Полонский, Якир, Учебник
Номер 1264,
Мерзляк, Полонский, Якир, Учебник
Номер 1270,
Мерзляк, Полонский, Якир, Учебник
Номер 1272,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 5,
Мерзляк, Полонский, Якир, Учебник
Номер 9,
Мерзляк, Полонский, Якир, Учебник
Номер 10,
Мерзляк, Полонский, Якир, Учебник
Точка
пересечения прямой и плоскости
Постановка
задачи.
Найти точку пересечения прямой
и
плоскости
.
План
решения.
1.
Находим параметрические уравнения
прямой. Для этого полагаем
.
откуда
получаем

2.
Подставляя эти выражения для
в
уравнение плоскости и решая его
относительно t,
находим значение параметра
,
при котором происходит пересечение
прямой и плоскости.
3.
Найденное значение
подставляем
в параметрические уравнения прямой и
получаем искомые координаты точки
пересечения:

Замечание.
Если в результате решения уравнения
относительно параметра
получим
противоречие, то прямая и плоскость
параллельны (это эквивалентно условию
).
Задача
13.
Найти точку пересечения прямой и
плоскости.

Запишем
параметрические уравнения прямой.

Подставляем
в уравнение плоскости:
Откуда
координаты точки пересечения прямой и
плоскости будут
Задача 14
Симметрия
относительно прямой или плоскости
Симметрия относительно прямой
Постановка
задачи.
Найти координаты точки
,
симметричной точке
относительно
прямой
.
План
решения.
1.
Находим уравнение плоскости, которая
перпендикулярна данной прямой и проходит
через точку
.
Так плоскость перпендикулярна заданной
прямой, то в качестве ее вектора нормали
можно взять направляющий вектор прямой,
т.е.
Поэтому
уравнение плоскости будет
2.
Находим точку
пересечения
прямой
и
плоскости
(см.
задачу 13).
3.
Точка
является
серединой отрезка
,
где точка
является
точкой симметричной точке
,
поэтому
Задача
14.
Найти точку
,
симметричную точке
относительно
прямой.
.
Уравнение
плоскости, которая проходит через точку
перпендикулярно
заданной прямой будет:
Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.
является
серединой отрезка
,
поэтому



Т.е.
.
Симметрия относительно плоскости
Постановка
задачи.
Найти координаты точки
,
симметричной точке
относительно
плоскости
.
План
решения.
1.
Находим уравнение прямой, которая
перпендикулярна данной плоскости и
проходит через точку
.
Так прямая перпендикулярна заданной
плоскости, то в качестве ее направляющего
вектора можно взять вектор нормали
плоскости, т.е.
.
Поэтому
уравнение прямой будет
.
2.
Находим точку
пересечения
прямой
и
плоскости
(см.
задачу 13).
3.
Точка
является
серединой отрезка
,
где точка
является
точкой симметричной точке
,
поэтому
Задача
14.
Найти точку
,
симметричную точке
относительно
плоскости.
Уравнение
прямой, которая проходит через точку
перпендикулярно
заданной плоскости будет:

Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.
является
серединой отрезка
,
поэтому



Т.е.
.
Литература
-
Ван дер Варден
Б.Л. Алгебра. — СПб. : Лань, 2004. — 624 с. -
Кузнецов Л.А.
Сборник заданий по высшей математике
(типовые расчеты). — СПб: «Лань»,
2008.- 240 c. -
Привалов И.И.
Аналитическая геометрия. — СПб. ; М. ;
Краснодар: Лань, 2007. — 304 с. -
Цубербиллер О.Н.
Задачи и упражнения по аналитической
геометрии. — СПб.: Лань, 2003. — 336 с. -
Фаддеев Д.К.,
Соминский И.С. Задачи по высшей алгебре.
— СПб.; М. ; Краснодар : Лань, 2007. — 288 с. -
Курош А.Г. Курс
высшей алгебры. — СПб. ; М. ; Краснодар :
Лань, физматкнига, 2007. — 432 с. -
Окунев Л.Я. Высшая
алгебра.- СПб.: Лань, 2009. — 336 с.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти точку, симметричную относительно прямой
Пусть даны некоторая прямая, заданная линейным уравнением, и точка, заданная своими координатами (x0, y0) и не лежащая на этой прямой. Требуется найти точку, которая была бы симметрична данной точке относительно данной прямой, то есть совпадала бы с ней, если плоскость мысленно согнуть пополам вдоль этой прямой.
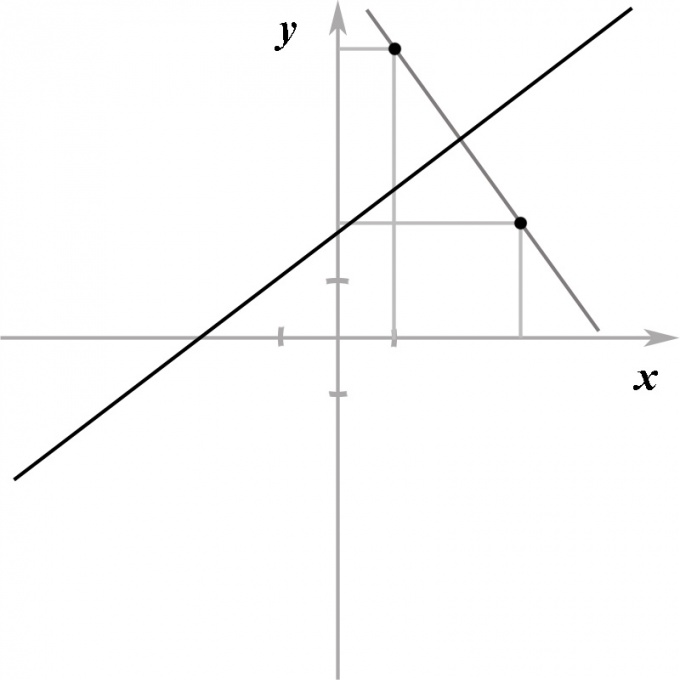
Инструкция
Ясно, что обе точки — заданная и искомая — должны лежать на одной прямой, причем эта прямая должна быть перпендикулярна данной. Таким образом, первая часть задачи заключается в том, чтобы найти уравнение прямой, которая была бы перпендикулярна некоторой данной прямой и при этом проходила бы через данную точку.
Прямая может быть задана двумя способами. Каноническое уравнение прямой выглядит так: Ax + By + C = 0, где A, B, и C — константы. Также прямую можно определить при помощи линейной функции: y = kx + b, где k — угловой коэффициент, b — смещение.
Эти два способа взаимозаменяемы, и от любого можно перейти к другому. Если Ax + By + C = 0, то y = — (Ax + C)/B. Иными словами, в линейной функции y = kx + b угловой коэффициент k = -A/B, а смещение b = -C/B. Для поставленной задачи удобнее рассуждать, исходя из канонического уравнения прямой.
Если две прямые перпендикулярны друг другу, и уравнение первой прямой Ax + By + C = 0, то уравнение второй прямой должно выглядеть Bx — Ay + D = 0, где D — константа. Чтобы найти конкретное значение D, нужно дополнительно знать, через какую точку проходит перпендикулярная прямая. В данном случае это точка (x0, y0).
Следовательно, D должно удовлетворять равенству: Bx0 — Ay0 + D = 0, то есть D = Ay0 — Bx0.
После того как перпендикулярная прямая найдена, нужно вычислить координаты точки ее пересечения с данной. Для этого требуется решить систему линейных уравнений:
Ax + By + C = 0,
Bx — Ay + Ay0 — Bx0 = 0.
Ее решение даст числа (x1, y1), служащие координатами точки пересечения прямых.
Искомая точка должна лежать на найденной прямой, причем ее расстояние до точки пересечения должно быть равно расстоянию от точки пересечения до точки (x0, y0). Координаты точки, симметричной точке (x0, y0), можно, таким образом, найти, решив систему уравнений:
Bx — Ay + Ay0 — Bx0 = 0,
√((x1 — x0)^2 + (y1 — y0)^2 = √((x — x1)^2 + (y — y1)^2).
Но можно поступить проще. Если точки (x0, y0) и (x, y) находятся на равных расстояниях от точки (x1, y1), и все три точки лежат на одной прямой, то:
x — x1 = x1 — x0,
y — y1 = y1 — y0.
Следовательно, x = 2×1 — x0, y = 2y1 — y0. Подставив эти значения во второе уравнение первой системы и упростив выражения, легко убедиться, что правая его часть становится идентична левой. Дополнительно учитывать первое уравнение уже нет смысла, поскольку известно, что точки (x0, y0) и (x1, y1) ему удовлетворяют, а точка (x, y) заведомо лежит на той же прямой.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание
- Осевая и центральная симметрия
- Что такое симметрия
- Осевая симметрия
- Центральная симметрия
- Задачи на самопроверку
- Координаты симметричных точек
- ВИДЫ СИММЕТРИИ
- СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ (ОСЕВАЯ СИММЕТРИЯ)
- зеркальная симметрия
- центральная симметрия
- поворотная симметрия (симметрия вращения)
- симметрия подобия
- переносная (трансляционная симметрия)
- примеры симметрии геометрических фигур
Осевая и центральная симметрия
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
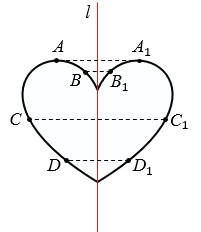
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равнобедренного треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу квадрат, треугольник (если его сложить пополам) и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
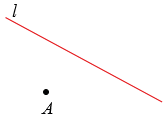
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Измеряем расстояние от точки B до прямой l и от точки A до прямой l.
- Проводим прямую от точки А через прямую l под прямым углом к прямой l, выводя за ось симметрии.
- Проводим прямую от точки B через прямую l под прямым углом к прямой l, выводя за ось симметрии.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Постройте треугольник A1B1C1, симметричный треугольнику ABC, относительно центра (точки О).
- По аналогии с предыдущим примером сначала соединяем точки ABC с точкой O.
- Выводим прямые за точку О.
- Измеряем отрезки AO, BO, CO и отмеряем такие же на противоположной стороне.
- Получаем два центрально-симметричных треугольника.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки равные отрезкам АО и OB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Источник
Координаты симметричных точек
Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
Источник
ВИДЫ СИММЕТРИИ
СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ (ОСЕВАЯ СИММЕТРИЯ)
Одна точка называются симметричной другой относительно прямой, если данная прямая проходит через середину отрезка, соединяющего эти точки, и перпендикулярна к этому отрезку. Каждая точка прямой а считается симметричной самой себе. Прямая называется осью симметрии фигуры если каждая точка фигуры симметрична относительно некоторой точки той же фигуры.
зеркальная симметрия
Геометрическая фигура называется симметричной относительно плоскости S, если для каждой точки этой фигуры может быть найдена другая точка этой же фигуры, так что отрезок, соединяющий эти точки, перпендикулярен плоскости S и делится этой плоскостью пополам. Плоскость S называется плоскостью симметрии.
Симметричные фигуры, предметы и тела не равны друг другу в узком смысле слова (например, левая перчатка или ботинок не подходит для правой руки или ноги и наоборот). Они называются зеркально равными.
центральная симметрия
Две точки называются симметричными относительно центра симметрии О, если О — середина отрезка, соединяющего эти точки. Точка О считается симметричной самой себе.
Геометрическая фигура (или тело) называется симметричной относительно центра О, если для каждой точки этой фигуры может быть найдена другая точка этой же фигуры, так что отрезок, соединяющий эти точки, проходит через центр О и делится в этой точке пополам. Точка О называется центром симметрии.
поворотная симметрия (симметрия вращения)
При поворотной симметрии переход частей фигуры в новое положение или преобразование исходной фигуры происходит при повороте фигуры на определенный угол вокруг точки, которая называется центром поворота. Поворотная симметрия может рассматриваться на плоскости и в пространстве.
Тело (фигура) обладает симметрией вращения, если при повороте на угол 360°/n (n – целое число, например, 2, 3, 4 и т.д. до бесконечности) вокруг некоторой прямой (оси симметрии) оно полностью совпадает со своим начальным положением. При n = 2 мы имеем осевую симметрию.
симметрия подобия
Представляет собой своеобразный аналог предыдущих симметрий с той лишь разницей, что она связана с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки.
переносная (трансляционная симметрия)
О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние, либо расстояние, кратное этой величине, она совмещается сама с собой. Прямая, вдоль которой производится перенос, называется осью переноса.
примеры симметрии геометрических фигур
Разными видами симметрии могут обладать и плоские и объемные фигуры. Например, квадрат, прямоугольник, ромб имеют и центр симметрии и оси симметрии.
Окружность и круг имеют центр симметрии и бесконечно много осей симметрии. Объемные фигуры могут иметь центр симметрии, оси симметрии и обладать зеркальной симметрией.
Правильные многогранники своей симметрией с древних времён привлекали к себе внимание учёных, архитекторов, художников. Их по праву называют самыми симметричными из всех многогранников.
Подробно описал свойства правильных многогранников древнегреческий учёный Платон. Поэтому их называют телами Платона. Правильным многогранникам посвящена 13 книга “Начал” Евклида.
Очень симметричной фигурой является, например, куб. Центром симметрии куба является точка пересечения его диагоналей. Через центр симметрии проходят 9 осей симметрии. Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра (6), либо через середины противоположных ребер (3).
Через центр симметрии проходят 9 осей симметрии. Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра (6), либо через середины противоположных ребер (3).
Источник