Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
Примеры.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Решение:
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
Ответ: (13;15).
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Решение:
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
Ответ: (-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Пример
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Решение:
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
5=-0,5·(-4)+b, откуда b=3.
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Найдём координаты точки пересечения прямых:
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Ответ: (3,2;1,4).
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
| для точки A(x;y) | |
| симметрия относительно: | |
| оси Ox | A1(x;-y) |
| оси Oy | A2(-x;y) |
|
биссектрисы I и II координатных четвертей (прямой y=x) |
A3(y;x) |
|
биссектрисы I b II координатных четвертей (прямой y= -x) |
A4(-y;-x) |
Точка
пересечения прямой и плоскости
Постановка
задачи.
Найти точку пересечения прямой
и
плоскости
.
План
решения.
1.
Находим параметрические уравнения
прямой. Для этого полагаем
.
откуда
получаем

2.
Подставляя эти выражения для
в
уравнение плоскости и решая его
относительно t,
находим значение параметра
,
при котором происходит пересечение
прямой и плоскости.
3.
Найденное значение
подставляем
в параметрические уравнения прямой и
получаем искомые координаты точки
пересечения:

Замечание.
Если в результате решения уравнения
относительно параметра
получим
противоречие, то прямая и плоскость
параллельны (это эквивалентно условию
).
Задача
13.
Найти точку пересечения прямой и
плоскости.

Запишем
параметрические уравнения прямой.

Подставляем
в уравнение плоскости:
Откуда
координаты точки пересечения прямой и
плоскости будут
Задача 14
Симметрия
относительно прямой или плоскости
Симметрия относительно прямой
Постановка
задачи.
Найти координаты точки
,
симметричной точке
относительно
прямой
.
План
решения.
1.
Находим уравнение плоскости, которая
перпендикулярна данной прямой и проходит
через точку
.
Так плоскость перпендикулярна заданной
прямой, то в качестве ее вектора нормали
можно взять направляющий вектор прямой,
т.е.
Поэтому
уравнение плоскости будет
2.
Находим точку
пересечения
прямой
и
плоскости
(см.
задачу 13).
3.
Точка
является
серединой отрезка
,
где точка
является
точкой симметричной точке
,
поэтому
Задача
14.
Найти точку
,
симметричную точке
относительно
прямой.
.
Уравнение
плоскости, которая проходит через точку
перпендикулярно
заданной прямой будет:
Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.
является
серединой отрезка
,
поэтому



Т.е.
.
Симметрия относительно плоскости
Постановка
задачи.
Найти координаты точки
,
симметричной точке
относительно
плоскости
.
План
решения.
1.
Находим уравнение прямой, которая
перпендикулярна данной плоскости и
проходит через точку
.
Так прямая перпендикулярна заданной
плоскости, то в качестве ее направляющего
вектора можно взять вектор нормали
плоскости, т.е.
.
Поэтому
уравнение прямой будет
.
2.
Находим точку
пересечения
прямой
и
плоскости
(см.
задачу 13).
3.
Точка
является
серединой отрезка
,
где точка
является
точкой симметричной точке
,
поэтому
Задача
14.
Найти точку
,
симметричную точке
относительно
плоскости.
Уравнение
прямой, которая проходит через точку
перпендикулярно
заданной плоскости будет:

Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.
является
серединой отрезка
,
поэтому



Т.е.
.
Литература
-
Ван дер Варден
Б.Л. Алгебра. — СПб. : Лань, 2004. — 624 с. -
Кузнецов Л.А.
Сборник заданий по высшей математике
(типовые расчеты). — СПб: «Лань»,
2008.- 240 c. -
Привалов И.И.
Аналитическая геометрия. — СПб. ; М. ;
Краснодар: Лань, 2007. — 304 с. -
Цубербиллер О.Н.
Задачи и упражнения по аналитической
геометрии. — СПб.: Лань, 2003. — 336 с. -
Фаддеев Д.К.,
Соминский И.С. Задачи по высшей алгебре.
— СПб.; М. ; Краснодар : Лань, 2007. — 288 с. -
Курош А.Г. Курс
высшей алгебры. — СПб. ; М. ; Краснодар :
Лань, физматкнига, 2007. — 432 с. -
Окунев Л.Я. Высшая
алгебра.- СПб.: Лань, 2009. — 336 с.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как построить симметричную точку
Строить симметричные точки учат на уроках геометрии в средней школе. Это умение может в дальнейшем пригодиться на уроках черчения, а также на занятиях в высших учебных заведениях.

Инструкция
Прочитайте условие задачи и определите, относительно чего должна быть симметрична точка. Например, может потребоваться построение точки, симметричной относительно другой точки, оси симметрии, начала координат, оси Ох или Оу и т.п.
Если вам нужно построить точку А1, симметричную А относительно начала координат, сначала определите координаты точки А. А1 будет иметь те же координаты, но с противоположным знаком. Например, А1 (3; -5) будет симметрична А (-3; 5). Найдите и постройте на графике точку А1 с полученными координатами.
Чтобы построить точку А1, симметричную А относительно оси Ох, нужно найти точку с такой же абсциссой, но при этом с ординатой, противоположной по знаку. Это значит, что точке А (х; у) будет симметрична А1 (х; -у). Например, если А имеет координаты 6 по оси Ох и 2 по оси Оу, то вам нужно будет найти и построить точку А1 (6; -2).
Если требуется построить А1, симметричную А относительно оси Оу, найдите А1, ордината которой будет равна А, а абсцисса противоположна абсциссе А по знаку. Это означает, что А1 (-х; у) будет симметрична А (х; у). Например, если дана А (4; 8), то нужно найти и построить А1 (-4; 8).
Если необходимо построить точку А1, симметричную А относительно точки В, то нужно сначала начертить луч из А, проходящий через В. Измерьте расстояние от А до В и постройте точку А1 на таком же расстоянии от В, но в противоположной стороне луча. В результате у вас получится отрезок АА1, центром которого является точка В.
Чтобы построить точку А1, симметричную А относительно прямой, постройте луч с начальной точкой А, пересекающийся с прямой и перпендикулярный ей. Измерьте расстояние от А до точки пересечения прямой и луча, а затем постройте точку А1 на том же расстоянии от прямой, но в противоположной стороне. У вас должен получиться отрезок АА1, который разделен прямой ровно пополам.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Симметрия относительно точки
Симметрия относительно точки
Пусть О — фиксированная точка и X — произвольная точка плоскости (рис. 187). Отложим на продолжении отрезка ОХ за точку О отрезок ОХ’, равный ОХ.
Точка X’ называется симметричной точке X относительно точки О. Точка, симметричная точке О, есть сама точка О. Очевидно, что точка, симметричная точке X’, есть точка X.
Преобразование фигуры F в фигуру F’, при котором каждая ее точка X переходит в точку X’, симметричную относительно данной точки О, называется преобразованием симметрии относительно точки О. При этом фигуры F и F’ называются симметричными относительно точки О (рис. 188).
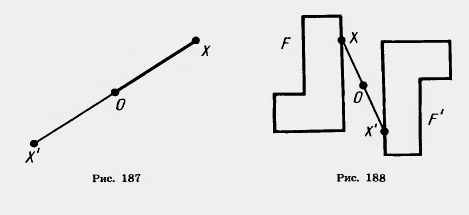
Если преобразование симметрии относительно точки О переводит фигуру F в себя, то она называется центрально-симметричной, а точка О называется центром симметрии.
Например, параллелограмм является центрально-симметричной фигурой. Его центром симметрии является точка пересечения диагоналей (рис. 189).
Теорема 9.2. Преобразование симметрии относительно точки является движением.
Доказательство. Пусть X и Y — две произвольные точки фигуры F (рис. 190). Преобразование симметрии относительно точки О переводит их в точки X’ и У.
Рассмотрим треугольники XOY и X’OY’. Эти треугольники равны по первому признаку равенства треугольников. У них углы при вершине О равны как вертикальные, а ОХ=ОХ’, OY=OY’ по определению симметрии относительно точки О. Из равенства треугольников следует равенство сторон: XY=X’Y’. А это значит, что симметрия относительно точки О есть движение. Теорема доказана.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Математика скачать, задача школьнику 8 класса, материалы по математике для 8 класса онлайн
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: