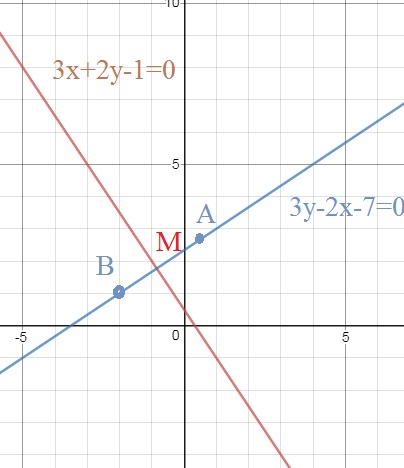Как найти точку, симметричную относительно прямой
Пусть даны некоторая прямая, заданная линейным уравнением, и точка, заданная своими координатами (x0, y0) и не лежащая на этой прямой. Требуется найти точку, которая была бы симметрична данной точке относительно данной прямой, то есть совпадала бы с ней, если плоскость мысленно согнуть пополам вдоль этой прямой.
Инструкция
Ясно, что обе точки — заданная и искомая — должны лежать на одной прямой, причем эта прямая должна быть перпендикулярна данной. Таким образом, первая часть задачи заключается в том, чтобы найти уравнение прямой, которая была бы перпендикулярна некоторой данной прямой и при этом проходила бы через данную точку.
Прямая может быть задана двумя способами. Каноническое уравнение прямой выглядит так: Ax + By + C = 0, где A, B, и C — константы. Также прямую можно определить при помощи линейной функции: y = kx + b, где k — угловой коэффициент, b — смещение.
Эти два способа взаимозаменяемы, и от любого можно перейти к другому. Если Ax + By + C = 0, то y = — (Ax + C)/B. Иными словами, в линейной функции y = kx + b угловой коэффициент k = -A/B, а смещение b = -C/B. Для поставленной задачи удобнее рассуждать, исходя из канонического уравнения прямой.
Если две прямые перпендикулярны друг другу, и уравнение первой прямой Ax + By + C = 0, то уравнение второй прямой должно выглядеть Bx — Ay + D = 0, где D — константа. Чтобы найти конкретное значение D, нужно дополнительно знать, через какую точку проходит перпендикулярная прямая. В данном случае это точка (x0, y0).
Следовательно, D должно удовлетворять равенству: Bx0 — Ay0 + D = 0, то есть D = Ay0 — Bx0.
После того как перпендикулярная прямая найдена, нужно вычислить координаты точки ее пересечения с данной. Для этого требуется решить систему линейных уравнений:
Ax + By + C = 0,
Bx — Ay + Ay0 — Bx0 = 0.
Ее решение даст числа (x1, y1), служащие координатами точки пересечения прямых.
Искомая точка должна лежать на найденной прямой, причем ее расстояние до точки пересечения должно быть равно расстоянию от точки пересечения до точки (x0, y0). Координаты точки, симметричной точке (x0, y0), можно, таким образом, найти, решив систему уравнений:
Bx — Ay + Ay0 — Bx0 = 0,
√((x1 — x0)^2 + (y1 — y0)^2 = √((x — x1)^2 + (y — y1)^2).
Но можно поступить проще. Если точки (x0, y0) и (x, y) находятся на равных расстояниях от точки (x1, y1), и все три точки лежат на одной прямой, то:
x — x1 = x1 — x0,
y — y1 = y1 — y0.
Следовательно, x = 2×1 — x0, y = 2y1 — y0. Подставив эти значения во второе уравнение первой системы и упростив выражения, легко убедиться, что правая его часть становится идентична левой. Дополнительно учитывать первое уравнение уже нет смысла, поскольку известно, что точки (x0, y0) и (x1, y1) ему удовлетворяют, а точка (x, y) заведомо лежит на той же прямой.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
Примеры.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Решение:
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
Ответ: (13;15).
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Решение:
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
Ответ: (-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Пример
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Решение:
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
5=-0,5·(-4)+b, откуда b=3.
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Найдём координаты точки пересечения прямых:
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Ответ: (3,2;1,4).
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
| для точки A(x;y) | |
| симметрия относительно: | |
| оси Ox | A1(x;-y) |
| оси Oy | A2(-x;y) |
|
биссектрисы I и II координатных четвертей (прямой y=x) |
A3(y;x) |
|
биссектрисы I b II координатных четвертей (прямой y= -x) |
A4(-y;-x) |
Точка
пересечения прямой и плоскости
Постановка
задачи.
Найти точку пересечения прямой
и
плоскости
.
План
решения.
1.
Находим параметрические уравнения
прямой. Для этого полагаем
.
откуда
получаем

2.
Подставляя эти выражения для
в
уравнение плоскости и решая его
относительно t,
находим значение параметра
,
при котором происходит пересечение
прямой и плоскости.
3.
Найденное значение
подставляем
в параметрические уравнения прямой и
получаем искомые координаты точки
пересечения:

Замечание.
Если в результате решения уравнения
относительно параметра
получим
противоречие, то прямая и плоскость
параллельны (это эквивалентно условию
).
Задача
13.
Найти точку пересечения прямой и
плоскости.

Запишем
параметрические уравнения прямой.

Подставляем
в уравнение плоскости:
Откуда
координаты точки пересечения прямой и
плоскости будут
Задача 14
Симметрия
относительно прямой или плоскости
Симметрия относительно прямой
Постановка
задачи.
Найти координаты точки
,
симметричной точке
относительно
прямой
.
План
решения.
1.
Находим уравнение плоскости, которая
перпендикулярна данной прямой и проходит
через точку
.
Так плоскость перпендикулярна заданной
прямой, то в качестве ее вектора нормали
можно взять направляющий вектор прямой,
т.е.
Поэтому
уравнение плоскости будет
2.
Находим точку
пересечения
прямой
и
плоскости
(см.
задачу 13).
3.
Точка
является
серединой отрезка
,
где точка
является
точкой симметричной точке
,
поэтому
Задача
14.
Найти точку
,
симметричную точке
относительно
прямой.
.
Уравнение
плоскости, которая проходит через точку
перпендикулярно
заданной прямой будет:
Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.
является
серединой отрезка
,
поэтому



Т.е.
.
Симметрия относительно плоскости
Постановка
задачи.
Найти координаты точки
,
симметричной точке
относительно
плоскости
.
План
решения.
1.
Находим уравнение прямой, которая
перпендикулярна данной плоскости и
проходит через точку
.
Так прямая перпендикулярна заданной
плоскости, то в качестве ее направляющего
вектора можно взять вектор нормали
плоскости, т.е.
.
Поэтому
уравнение прямой будет
.
2.
Находим точку
пересечения
прямой
и
плоскости
(см.
задачу 13).
3.
Точка
является
серединой отрезка
,
где точка
является
точкой симметричной точке
,
поэтому
Задача
14.
Найти точку
,
симметричную точке
относительно
плоскости.
Уравнение
прямой, которая проходит через точку
перпендикулярно
заданной плоскости будет:

Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.
является
серединой отрезка
,
поэтому



Т.е.
.
Литература
-
Ван дер Варден
Б.Л. Алгебра. — СПб. : Лань, 2004. — 624 с. -
Кузнецов Л.А.
Сборник заданий по высшей математике
(типовые расчеты). — СПб: «Лань»,
2008.- 240 c. -
Привалов И.И.
Аналитическая геометрия. — СПб. ; М. ;
Краснодар: Лань, 2007. — 304 с. -
Цубербиллер О.Н.
Задачи и упражнения по аналитической
геометрии. — СПб.: Лань, 2003. — 336 с. -
Фаддеев Д.К.,
Соминский И.С. Задачи по высшей алгебре.
— СПб.; М. ; Краснодар : Лань, 2007. — 288 с. -
Курош А.Г. Курс
высшей алгебры. — СПб. ; М. ; Краснодар :
Лань, физматкнига, 2007. — 432 с. -
Окунев Л.Я. Высшая
алгебра.- СПб.: Лань, 2009. — 336 с.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Координаты симметричных точек
Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
Задача 32579 Найти точку A, симметричную точке B(-2.
Условие
Найти точку A, симметричную точке B(-2, 1) относительно прямой 3x+2y-1=0
Решение
Составляем уравнение прямой, перпендикулярной данной прямой и проходящей через точку B
3х+2у-1=0 ⇒ у=-(3/2)х+(1/2)
угловой коэффициент k=(-3/2)
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
k=2/3 — угловой коэффициент искомой прямой
y=(2/3)x+b — множество прямых, перпендикулярных данной.
чтобы выделить прямую, проходящую через точку B
подставим координаты точки В
Найдем координаты точки М — точки пересечения двух прямых
<3x+2y-1=0
По свойству симметричных точек
ВМ=МА
x_(M)=(x_(B)+x_(A))/2 ⇒
x_(A)=2x_(M)-x_(B)=(-22/13)-(-2)=4/13
О т в е т. (4/13; 33/13)
http://reshimvse.com/zadacha.php?id=32579
Задача 32136 Найти координаты точки, симметричной…
Условие

Найти координаты точки, симметричной точке А=(-6,-6,10) относительно плоскости ,заданной уравнением 2*x+3*y-3*z-6=0.
математика ВУЗ
18959
Решение
★
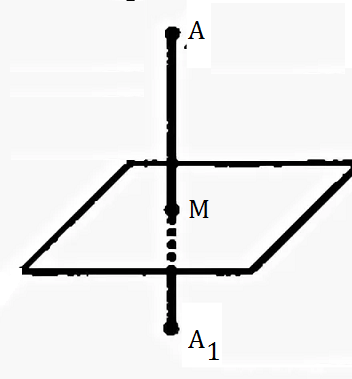
Составим уравнение прямой, проходящей через точку А и перпендикулярной плоскости
При этом нормальный вектор плоскости vector{n}=(2;3 ;-3) является направляющим вектором прямой.
(х + 6)/(2)=(y + 6)/(3)=(z — 10)/(-3)
Перейдем от этого уравнения к параметрическому:
(х + 6)/(2)=(y + 6)/(3)=(z -10)/(-3) = t ⇒
x=2t-6
y=3t -6
z=-3t+10
Найдем координаты точки пересечения прямой и плоскости.
Подставим параметрические уравнения прямой в уравнение плоскости
2*(2t-6)+3*(3t-6)-3*(-3t+10)-6=0
4t-12+9t-18+9t-30-6=0
22t=66
t=3
При t=3
x=0; y=3; z=1
M(0;3;1) — проекция точки А на плоскость.
По свойству симметричных точек,
АМ=МА_(1)
Поэтому
х_(M)=(x_(A)+x_(A_(1)))/2 ⇒(-6+ x_(A_(1)))/2=0 ⇒ x_(A_(1))=6
y_(M)=(y_(A)+y_(A_(1)))/2 ⇒ y_(A_(1))=12
z_(M)=(z_(A)+z_(A_(1)))/2 ⇒ z_(A_(1))=-8
О т в е т. (6;12;-8)