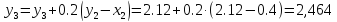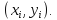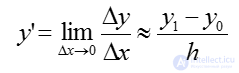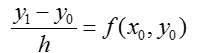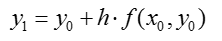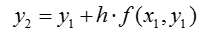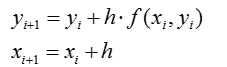Как найти точное решение в методе эйлера - Исправление недочетов и поиск решений вместе с Examum.ru

Метод Эйлера

Содержание:

Примеры с решением

Пусть требуется решить задачу Коши: найти решение дифференциального уравнения удовлетворяющее начальному условию

При численном решении уравнения (14.1) задача ставится так: в точках найти приближения для значений точного решения . Разность во многих случаях принимают постоянной h и называют шагом сетки, тогда

Метод Эйлера для решения указанной задачи Коши основан на непосредственной замене производной разностным отношением по приближенной формуле

Приближенные значения в точках вычисляются по формуле

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Примеры с решением

Пример 1.

С помощью метода Эйлера найти значения решения уравнения удовлетворяющего условию , в первых пяти точках отрезка [0; 0,5] при .

Решение:

По формуле (14.2) находим точки

Значения искомой функции удовлетворяющей условиям данной задачи Коши, находим в соответствии с формулой (14.3). Результаты вычислений отражены в таблице 14.1. Замечание.

Точное решение уравнения удовлетворяющее условию , выражается формулой Следовательно, Таблица 14.1

Возможно вам будут полезны данные страницы:

Пример 2.

Методом Эйлера найти значения решения дифференциального уравнения , для которого , в пяти точках отрезка [1; 1,5], приняв

Решение:

На основании формулы (14.2) определяем точки Значения искомой функции , удовлетворяющей условию дайной задачи Коши, вычисляем по формуле (14.3). Результаты вычислений занесены в таблицу 14.2.

Таблица 14,2

Лекции:

Производная функции
Иррациональные выражения
Метод вариации произвольных постоянных
Сходимость ряда
Как найти область определения функции: решение
Уравнение сферы
Пределы: примеры решения
Площадь поверхности конуса
Целые рациональные выражения
Числовые ряды. Числовой ряд. Сумма ряда

Источник

Простейшим
численным методом решения задачи Коши
для обыкновенного дифференциального
уравнения является метод Эйлера, который
еще называют методом ломанных Эйлера.

По
оси
введем равномерную сетку с шагом,
т.е рассмотрим систему точек.
Обозначим черезточное решение задачиа через— приближенные значения функцийв заданной системе точек.

Заменяя
в уравнении
производную в окрестности каждогого
узла сетки разностным отношением
приходим к уравнению:

Определение
.Алгебраические
соотношения между компонентами сеточной
функции заменяемые исходными
дифференциальными уравнениями в
окрестности каждого узла сетки, называются
разностными
уравнениями.

Поэтому
уравнение
– разностное уравнение.

В
окончательной форме
можно определить по явной формуле

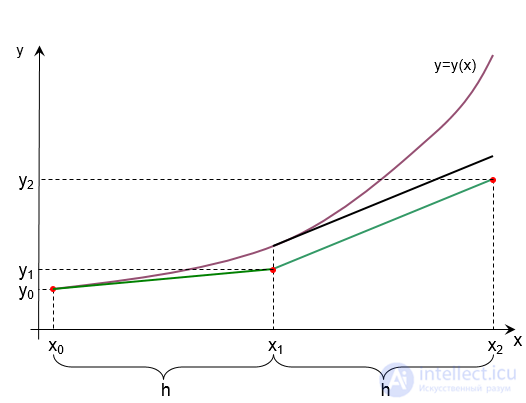
Геометрическая
интерпретация метода Эйлера: интегральная
кривая

на
отрезкеприближается
к ломанной, наклон которой определяется
наклоном интегральной кривой уравнения
в точке [].
Рис.

Метод
Эйлера относится к явным одношаговым
методам. Вследствие систематического
накопления ошибок метод используется
редко или используется только для оценки
вида интегральной кривой. Метод Эйлера
называют методом Рунге-Кутта первого
порядка точности.

Пример
7.1. Применяя
метод Эйлера, найти решение задачи Коши
в трех последовательных точках,,.
Найти точное решение задачи и найти
величину абсолютной погрешности в
указанных точках.

Решение.

Возьмем
шаг
Используя расчетную формулу Эйлера,
найдем приближенное решение задачи
Коши:

Таким
образом, получили численное решение
задачи:

	0	0.2	0.4	0.6
	1.5	1.8	2.12	2.464

Графиком
приближенного решения является ломанная,
последовательно соединяющая точки

В
этой задаче легко находится точное
решение, например, методом вариации
постоянной:
0.5.
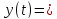
Вычислим значения точного решения в
указанных точках.

	0	0.2	0.4	0.6
	1.5	1.811	2.146	2.511

Абсолютную
погрешность вычислим так:
.
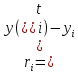
Тогда,,.
Таким образом, максимальная величина
погрешности равна

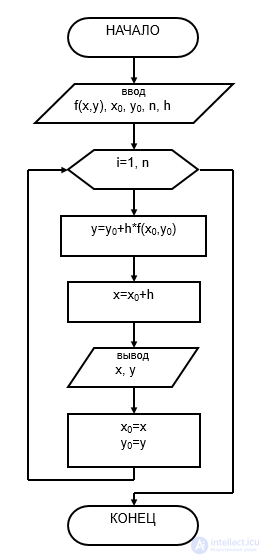
Реализация
метода Эйлера с помощью системы Maxima

Зададим
концы отрезка, на котором будем искать
решение, и шаг:

Найдем
количество точек разбиения отрезка с
шагом

Сформируем
два пустых одномерных массива размера

для хра-

нения
значения координат точек
искомого решения:

Зададим
начальное условие:

Заполним
массив
значениями, начиная сдос шагом.
Для этого используем цикл с параметром.

Используя
расчетную формулу Эйлера, заполним
массив

Выведем
полученное решение на экран:

Выполним
построение ломаной Эйлера средствами
пакета

Для
нахождения точного решения задачи Коши
воспользуемся встроенной командой
Дифференциальное уравнение запомним
под именем

Зададим
начальное условие

Находим
точное решение задачи Коши
:

Вычислим
значения функции в точках отрезка
с шагом.

Найдем
величину абсолютной погрешности:

§8.Метод Эйлера-Коши

Отличительная
особенность метода Эйлера-Коши от метода
Эйлера заключается в том, что значение
в правой части уравнения вычисляется
не только в точках сетки (шаг
),
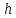
но и также в середине отрезков (шаг)
(промежуточных точках).

Предположим,
что промежуточное значениерешения задачи в точке

,
уже известно,вычисляются по следующим формулам:

,
=

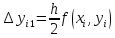
Отсюда
вычисляют

Геометрическая
интерпретация метода Эйлера-Коши:
определяется направление интегральной
кривой в исходной точке
и во вспомогательной точке,,
а в качестве окончательного выбирается
среднее из этих направлений. Метод
Эйлера-Коши называют методом Рунге-Кутта
второй точности.

Пример
8.1. Применяя
метод Эйлера-Коши, найти решение задачи
Коши
в
трех последовательных точках,,.

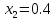
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
25.11.2019128.51 Кб51а.doc
#

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Given a differential equation dy/dx = f(x, y) with initial condition y(x0) = y0. Find its approximate solution using Euler method.

Euler Method :
In mathematics and computational science, the Euler method (also called forward
Euler method) is a first-order numerical procedure for solving ordinary differential
equations (ODEs) with a given initial value.
Consider a differential equation dy/dx = f(x, y) with initial condition y(x0)=y0
then a successive approximation of this equation can be given by:

y(n+1) = y(n) + h * f(x(n), y(n))
where h = (x(n) – x(0)) / n
h indicates step size. Choosing smaller
values of h leads to more accurate results
and more computation time.

Example :

    Consider below differential equation
            dy/dx = (x + y + xy)
    with initial condition y(0) = 1 
    and step size h = 0.025.
    Find y(0.1).
   
    Solution:
    f(x, y) = (x + y + xy)
    x0 = 0, y0 = 1, h = 0.025
    Now we can calculate y1 using Euler formula
    y1 = y0 + h * f(x0, y0)
    y1 = 1 + 0.025 *(0 + 1 + 0 * 1)
    y1 = 1.025
    y(0.025) = 1.025.
    Similarly we can calculate y(0.050), y(0.075), ....y(0.1).
    y(0.1) = 1.11167

Below is the implementation:

C++

#include <iostream>

using namespace std;

float func(float x, float y)

{

return (x + y + x * y);

}

void euler(float x0, float y, float h, float x)

{

float temp = -0;

while (x0 < x) {

temp = y;

y = y + h * func(x0, y);

x0 = x0 + h;

}

cout << "Approximate solution at x = "

<< x << " is " << y << endl;

}

int main()

{

float x0 = 0;

float y0 = 1;

float h = 0.025;

float x = 0.1;

euler(x0, y0, h, x);

return 0;

}

Java

import java.io.*;

class Euler {

float func(float x, float y)

{

return (x + y + x * y);

}

void euler(float x0, float y, float h, float x)

{

float temp = -0;

while (x0 < x) {

temp = y;

y = y + h * func(x0, y);

x0 = x0 + h;

}

System.out.println("Approximate solution at x = "

+ x + " is " + y);

}

public static void main(String args[]) throws IOException

{

Euler obj = new Euler();

float x0 = 0;

float y0 = 1;

float h = 0.025f;

float x = 0.1f;

obj.euler(x0, y0, h, x);

}

Python3

def func( x, y ):

return (x + y + x * y)

def euler( x0, y, h, x ):

temp = -0

while x0 < x:

temp = y

y = y + h * func(x0, y)

x0 = x0 + h

print("Approximate solution at x = ", x, " is ", "%.6f"% y)

x0 = 0

y0 = 1

h = 0.025

x = 0.1

euler(x0, y0, h, x)

C#

using System;

class GFG {

static float func(float x, float y)

{

return (x + y + x * y);

}

static void euler(float x0, float y, float h, float x)

{

while (x0 < x) {

y = y + h * func(x0, y);

x0 = x0 + h;

}

Console.WriteLine("Approximate solution at x = "

+ x + " is " + y);

}

public static void Main()

{

float x0 = 0;

float y0 = 1;

float h = 0.025f;

float x = 0.1f;

euler(x0, y0, h, x);

}

PHP

<?php

function func($x, $y)

{

return ($x + $y + $x * $y);

}

function euler( $x0, $y, $h, $x)

{

$temp = -0;

while($x0 < $x)

{

$temp = $y;

$y = $y + $h * func($x0, $y);

$x0 = $x0 + $h;

}

echo "Approximate solution at x = ",

$x, " is ", $y, "n";

}

$x0 = 0;

$y0 = 1;

$h = 0.025;

$x = 0.1;

euler($x0, $y0, $h, $x);

?>

Javascript

<script>

function func(x, y)

{

return (x + y + x * y);

}

function euler(x0, y, h, x)

{

let temp = -0;

while (x0 < x) {

temp = y;

y = y + h * func(x0, y);

x0 = x0 + h;

}

document.write("Approximate solution at x = "

+ x + " is " + y);

}

let x0 = 0;

let y0 = 1;

let h = 0.025;

let x = 0.1;

euler(x0, y0, h, x);

</script>

Output

Approximate solution at x = 0.1  is  1.11167

Time complexity: O(x/h)
Auxiliary space: O(1)

Last Updated :
23 Nov, 2022

Like Article

Save Article

Источник

Привет, сегодня поговорим про метод эйлера, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
метод эйлера, уточненный метод эйлера , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.

метод эйлера — простейший численный метод решения систем обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление». Метод Эйлера является явным, одношаговым методом первого порядка точности. Он основан на аппроксимации интегральной кривой кусочно-линейной функцией, так называемой ломаной Эйлера.

Описание метода

Ломаная Эйлера (красная линия) — приближенное решение в пяти узлах задачи Коши и точное решение этой задачи (выделено синим цветом)

Пусть дана задача Коши для уравнения первого порядка:

где функция определена на некоторой области . Решение ищется на интервале . На этом интервале введем узлы:

Приближенное решение в узлах , которое обозначим через , определяется по формуле:

Эти формулы непосредственно обобщаются на случай систем обыкновенных дифференциальных уравнений.

Оценка погрешности метода на шаге и в целом

Погрешность на шаге или локальная погрешность — это разность между численным решением после одного шага вычисления и точным решением в точке . Численное решение задается формулой

Точное решение можно разложить в ряд Тейлора:

Локальную ошибку получаем, вычитая из второго равенства первое:

Это справедливо, если {displaystyle y} имеет непрерывную вторую производную . Другим достаточным условием справедливости этой оценки, из которого вытекает предыдущее и которое обычно может быть легко проверено, является непрерывная дифференцируемость по обоим аргументам .

Погрешность в целом, глобальная или накопленная погрешность — это погрешность в последней точке произвольного конечного отрезка интегрирования уравнения. Для вычисления решения в этой точке требуется шагов, где длина отрезка. Поэтому глобальная погрешность метода .

Таким образом, метод Эйлера является методом первого порядка — имеет погрешность на шаге и погрешность в целом .

Значение метода Эйлера

Метод Эйлера являлся исторически первым методом численного решения задачи Коши . Об этом говорит сайт https://intellect.icu . О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

Характеристика метода Эйлера

Метод Эйлера является одношаговым методом, то есть для расчета последующей точки необходимо знать только координаты предыдущей.
Данный метод использует явную схему. В правой части формулы Эйлера стоят все известные величины.
Метод Эйлера не является устойчивым методом, поэтому он применяется только для ОДУ, решением которых являются достаточно гладкие функции.
Этот метод характеризуется первым порядком точности (точность низкая).

Модификации и обобщения

Модифицированный метод Эйлера с пересчетом

Повысить точность и устойчивость вычисления решения можно с помощью неявного метода Эйлера следующего вида.

Прогноз:

Коррекция:

Для повышения точности корректирующую итерацию можно повторить, подставляя .

Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо как минимум дважды вычислять . Метод Эйлера с пересчетом представляет собой разновидность методов Рунге-Кутты (предиктор-корректор).

Двухшаговый метод Адамса — Башфорта

Другой способ повысить точность метода заключается в использовании не одного, а нескольких вычисленных ранее значений функции:

Это линейный многошаговый метод.

Реализации на языках программирования

Реализация на языке Си для функции .

#include 

double func(double x, double y)
{
	return 6*x*x+5*x*y; // функция первой производной
}

int main(int argc, char** argv)
{
    int i, n; 
    double x, y, h;

    h = 0.01; // шаг
    n = 10; // количество итераций
    x = 1; // x0
    y = 1; // y0

    for (i = 0; i < n; i++)
    {
        y += h * func(x, y); // вычисление yi
        x += h;
    }

    return EXIT_SUCCESS;
}

Реализация на языке Python 3.7:

# n - количество итераций, h - шаг, (x, y) - начальная точка
def Euler(n = 10, h = 0.01, x = 1, y = 1):
    for i in range(n):
        y += h * function(x, y)
        x += h
    return x, y # решение

def function(x, y):
    return 6 * x**2 + 5 * x * y # функция первой производной

print(Euler())

Улучшенный метод Эйлера

Метод Эйлера для расчета дифференциальных уравнений имеет небольшую точность расчета. Как было показано ранее (см. Лекцию 10. Численные методы интегрирования дифференциальных уравнений. Метод Эйлера), точность расчета у него зависит от размера шага линейно, зависимость точности от шага — первой степени. То есть, чтобы увеличить точность в 10 раз, надо уменьшить шаг в 10 раз. На практике интересуются более совершенными методами. Вопрос стоит так: можно ли увеличить точность на порядок, но при этом сэкономить на количестве вычислений? Да, такие методы есть. Модифицированный метод Эйлера имеет точность второго порядка. В методе Эйлера производная берется в начале шага и по ней прогнозируется движение системы на конец шага, считая, что во время шага производная неизменна. То есть в течение всего шага производная считается той, какой она была в самом начале шага. Это основной источник неточности.

Улучшение метода состоит в том, что берется производная не в начале шага, а как промежуточное или среднее на разных участках одного шага. В разных вариантах метода вычисляют несколько производных в разных частях шага и усредняют их. Конечно, в этом случае число вычислений увеличивается, — но не в десятки раз, — а вот точность возрастает на порядок, в этом и состоит выигрыш.

Пусть, как и прежде (см. Лекцию 10. Численные методы интегрирования дифференциальных уравнений. Метод Эйлера), требуется решить уравнение y‘ = f(x, y, t). Идея уточненного метода Эйлера состоит в том, что производную вычисляют не в i-ой точке, а между двумя соседними точками: i иi + 1. Данная процедура состоит из следующих шагов:

в точке i вычисляют значение производной:
f(xi, yi, t);
делают пол-шага и вычисляют значение функции на середине отрезка:
yi + 1/2 = yi + f(xi, yi, t) · Δt/2;
в точке i + 1/2 вычисляют производную:
f(xi + 1/2, yi + 1/2, t + Δt/2);
делается полный шаг из точки i в точку i + 1 по значению уточненной производной:
yi + 1 =yi + f(xi + 1/2, yi + 1/2, t + Δt/2) · Δt;
значение t увеличивается: t := t + Δt. Вся процедура повторяется сначала.

Данный метод обладает точностью Ο2(h), то есть на порядок выше, чем метод Эйлера, при увеличении числа вычислений всего в 2 раза.

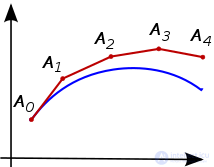
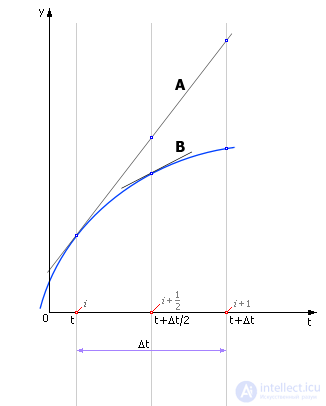
На рис. 14.1 показано, какой будет ошибка ε (расхождение между реальным и вычисленным теоретическим значением), если шаг делается по значению производной, вычисленной в точке i, как это делается в методе Эйлера. Эта ошибка может быть достаточно велика!

Рис. 14.1. Движение реальной и расчетной системы по методу Эйлера и расхождение между ними (ошибка)

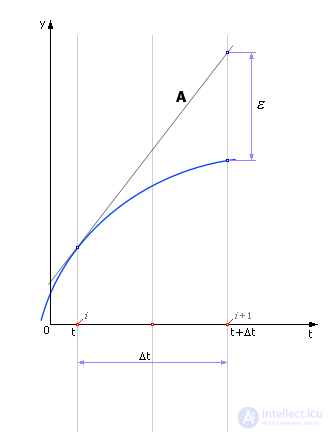
На рис. 14.2 показано, как по значению производной, вычисленной в точке i, делается полшага до точки t + Δt/2 (направление производной показано линией A). И в точке t + Δt/2 вычисляют новую производную. Касательная в точке t + Δt/2 будет другой — линия B. Ее наклон равен производной в точке t + Δt/2.

Рис. 14.2. Уточнение значения производной внутри шага расчета

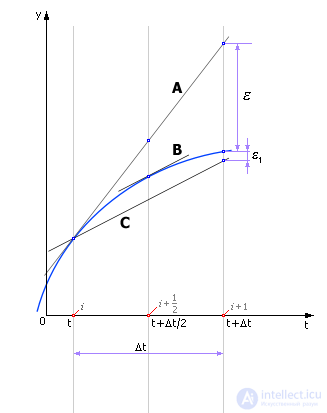
Далее переносят линию B обратно в точку t. Это соответствует тому, что из точки t снова делается, — но уже полный, — шаг Δt до точки t + Δt по направлению, соответствующему линии C(рис. 14.3). Линия C параллельна B. То есть значение производной в точке t берется искусственно равным производной в точке t + Δt/2. Ошибка расчета (см. ε1) во многих случаях при этом уменьшается.

Рис. 14.3. Движение реальной системы и системы, рассчитанной модифицированным методом Эйлера, и расхождение между ними (ошибка). На рисунке для сравнения показан результат, вычисленный по методу Эйлера

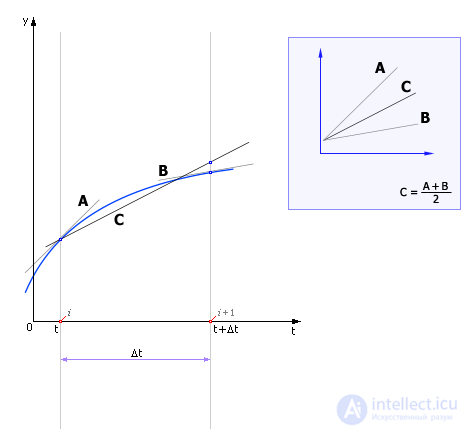
Существует другой вариант модифицированного метода Эйлера, когда производную для того, чтобы сделать шаг из точки i, берут не в i-ой точке и не в i + 1/2, а как среднее арифметическое двух производных: производной в точке i (направление производной показано на рис. 14.4 линией A) и производной в точке i + 1 (направление производной показано линией B). Направление «средней» производной показано линией C.

Рис. 14.4. Расчет движения системы по среднему значению производной на шаге

Блок схема и алгоритм метода Эйлера

Решение ОДУ 1-го порядка

Общий вид ОДУ 1-го порядка:

F(x, y, y’)=0

Уравнение разрешаем относительно старшей производной:

y’=f(x, y)

Начальная точка: x0, y0.

Количество точек на интегральной кривой решения n

Шаг h, с которым будет изменяться значение аргумента.

Метод Эйлера

y’=f(x, y)

Представляем производную функции y’ в виде конечной разности.

За величину приращения аргумента Dx принимается величина шага h:

Тогда:

Аналогично:

В общем виде: — формула Эйлера

Графическая интерпретация метода Эйлера

Предположим, что мы имеем истинное решение ОДУ: y=y(x).

От начальной точки (x0, y0) проводим касательную к графику до пересечения с линией x=x1. Получаем новую точку (x1, y1).

Из графика видно, что с увеличением количества шагов погрешность возрастает.

Если величину шага h уменьшить, то результат получится более точным.

Блок-схема метода Эйлера

См. также

Метод Рунге — Кутты метод рунге-кутты ,
задача Коши общие понятия дифференциальных уравнений первого порядка , задача коши , дифференциальные уравнения первого порядка , ду первого порядка ,
метод Адамса
метод Хенричи
аппроксимация функций , интерполяция , интерполяция функций , аппроксимация ,

Я что-то не договорил про метод эйлера, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое метод эйлера, уточненный метод эйлера
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Моделирование и Моделирование систем

Источник

Variant 19 (Sukach Maxim, BS17-03)

Содержание:

Уравнение
Решение
Метод Эйлера
Усовершенствованный метод Эйлера
Классический метод Рунге-Кутты
Сравнение методов для заданной задачи
Заключение
Запуск
Ссылки

Уравнение

№19:

Решение

$frac{dy}{dx} = 2y^{1/2}+2y newline newline frac{dy}{2(y^{1/2}+y)}=dx newline newline int frac{dy}{2(y^{1/2}+y)}=int dx newline newline ln (sqrt y + 1) = x + C_{1} newline newline sqrt y + 1 = e^{x + C_{1}} newline newline y = (e^{x+C_{1}} - 1)^{2}$

Найдем

В итоге, наше решение принимает вид:

Метод Эйлера

Метод Эйлера дает возможность приближенно выразить функцию теоретически с любой наперед заданной точностью. Суть метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0).
Метод Эйлера является методом 1-го порядка точности и называется методом ломаных.

Для вычисления используются следующие формулы:

В Python:

def next_y(xi, yi):
    return yi + self.h * self.f(xi, yi)

ys = []
xs = np.arange(x0 + h, xf + h, h)  # вектор всех значений x
for x in xs:
    ys.append(y)
    y = next_y(x, y) # В результате ys будет содержать все значения метода Эйлера

Метод Эйлера и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1

Метод Эйлера и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1

Метод Эйлера и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1

Усовершенствованный метод Эйлера

Суть усовершенствованного метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0).
Усовершенствованный метод Эйлера является методом 2-го порядка точности и называется модифицированным методом Эйлера.

Разница между данным методом и методом Эйлера минимальна и заключается в использовании следующих формул:

В Python:

# Заменяем next_y функцию на эту:
	
def next_y(xi, yi):
   h2 = h / 2
   delta_y = h * f(xi + h2, yi + h2 * f(xi, yi))
   return yi + delta_y

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 9, y0 = 1, h = 0.1

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 3, y0 = 1, h = 0.1

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 1, y0 = 1, h = 0.1

Классический метод Рунге-Кутты

Суть метода Рунге-Кутты в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0).
Классический метод Рунге-Кутты является методом 4-го порядка точности и называется методом Рунге-Кутты 4-го порядка точности.

Ну и как обычно, формулы:

В Python:

# Заменяем next_y функцию на эту:
	
def next_y(xi, yi):
    h2 = h / 2
    k1 = f(xi, yi)
    k2 = f(xi + h2, yi + h2 * k1)
    k3 = f(xi + h2, yi + h2 * k2)
    k4 = f(xi + h, yi + h * k3)
    return yi + (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4)

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1

Сравнение методов для заданной задачи

Размер ошибки всех методов на промежутке [0, 9] с шагом 0.1

Размер ошибки всех методов на промежутке [0, 3] с шагом 0.1

Размер ошибки всех методов на промежутке [0, 1] с шагом 0.1

Заключение

Очевидно что, классический метод Рунге-Кутты справляется с задачей аппроксимации в случае данного уравнения намного лучше чем Метод Эйлера и Усовершенствованный метод Эйлера.

График глобальной средней ошибки

Глобальная ошибка в зависимости от размера шага H на промежутке от 0.01 до 0.91 для x0 = 1, xf = 9

Запуск

Установить Python3
Все пакеты необходимые для работы находятся в requirements.txt

matplotlib
numpy
Запустить run.py в корневой директории проекта.

Все настройки находятся в run.py в виде констант (строки 12-16). configparser очень не хотелось подключать. После запуска скрипт покажет 6 графиков (в диком разрешении, там ничего не видно толком) и сохранит их нормальные версии (dpi=300) в папке results.

Ссылки

Latex Редактор: https://www.codecogs.com/latex/eqneditor.php
Метод Эйлера: Wikipedia

Усовершенствованный метод Эйлера: Mathprofi (кык)

Метод Рунге — Кутты: Wikipedia

Источник