Как найти точное значение функции в точке

Ответ.
Приближенные вычисления с помощью
дифференциала функции одной
переменной.
В первом параграфе рулит функция одной
переменной. Как все знают, она обозначается
через

или
через

.
Пример.
Вычислить приближенно

,
заменяя приращения функции ее
дифференциалом. Решение: формула:

.
На первом этапе необходимо составить
функцию

.
По условию предложено вычислить
кубический корень из числа:

,
поэтому соответствующая функция имеет
вид:

.
Нам нужно с помощью формулы найти
приближенное значение

.
Число 67 необходимо представить в виде

.
Алгоритм: вычислим данное значение на
калькуляторе:

.
В качестве

подбираем значение, чтобы корень
извлекался нацело. Естественно, это
значение должно быть как можно ближе к
67. В данном случае:

.
Действительно:

.
Если

,
то приращение аргумента:

.
Итак, число 67 представлено в виде суммы

.
Далее работаем с правой частью формулы

.
Сначала вычислим значение функции в
точке

.
Собственно, это уже сделано ранее:

.
Дифференциал в точке находится по
формуле:

.
Из формулы следует, что нужно взять
первую производную:

.
И найти её значение в точке

:

.
Таким образом:

.
Согласно формуле :

.
Абсолютная
погрешность
вычислений находится по формуле:

.
Знак модуля показывает, что нам без
разницы, какое значение больше, а какое
меньше. Важно, насколько далеко
приближенный результат отклонился от
точного значения в ту или иную сторону.
Относительная
погрешность
вычислений находится по формуле:

.
Относительная погрешность показывает,
на сколько процентов приближенный
результат отклонился от точного значения.
Приближенные вычисления с помощью
полного дифференциала функции двух
переменных.
Пример.
Вычислить приближенное значение функции

в точке

с помощью полного дифференциала, оценить
абсолютную и относительную погрешность.
Рабочая формула:

.
Число 3,04 представим в виде

—

,

.
Число 3,95 представим в виде

—

,

.
Вычислим значение функции в точке

:

.
Дифференциал функции в точке

найдём по формуле:

.
Из формулы следует, что нужно найти
частные производные первого порядка и
вычислить их значения в точке

.
Вычислим частные производные первого
порядка в точке

:

Полный
дифференциал в точке

:

.
Таким образом, по формуле

приближенное значение функции в точке
М:

.
Вычислим точное значение функции в
точке М:

.
Вот это значение является абсолютно
точным. Погрешности рассчитываются по
стандартным формулам.

Соседние файлы в предмете Высшая математика

• #

  21.09.202221.15 Mб27Romanova MA Vysshaia matematika EUMK.pdf

• #
• #
• #
• #

План урока:

Исследование функций на монотонность

Экстремумы функции

Выпуклость и вогнутость функций

Исследование функций и построение их графиков

Исследование функций на монотонность

Говоря о смысле производной, мы замечали, что у возрастающих функций она принимает положительные значения, а у убывающих – отрицательные. Убедиться в этом можно с помощью графиков. Действительно, если провести касательную к возрастающей ф-кции, то она образует с осью Ох острый угол, а потому тангенс этого угла (а он как раз равен произ-ной) окажется положительным числом:

Если же ф-кция убывает, то касательная образует с осью Ох тупой угол, чей тангенс будет отрицательным:

Рассмотрим более сложный случай, когда ф-кция на каких-то промежутках убывает, а на каких-то возрастает. В качестве примера приведем зависимость у = х². Она является убывающей на промежутке (– ∞; 0] и возрастающей на промежутке [0; + ∞). Можно заметить, что любая касательная, проведенная на первом из этих промежутков, будет образовывать тупой угол с Ох. И наоборот, любая касательная на втором промежутке имеет острый угол:

Это означает, что произ-ная ф-кции на первом промежутке должна быть отрицательной, а на втором – положительной (сразу отметим, что граничная точка х = 0 стоит особняком, так как входит в оба промежутка). Попробуем найти произ-ную аналитически. Мы рассматриваем ф-кцию у = х², её произ-ная равна

Действительно, произ-ная у′ = 2х принимает отрицательные значения при х∈ (– ∞;0) и оказывается положительной при х∈(0; + ∞). Заметим, что в граничной точке произ-ная равна нулю.

Это наблюдение подсказывает нам, что по знаку произ-ной можно определить, возрастает или убывает ф-кция. Однако сначала надо разобраться с тем случаем, когда произ-ная оказывается равной нулю. Рассмотрим ф-кцию у = х³. Очевидно, что она возрастает на всей числовой прямой. Значит ли это, что её произ-ная на этой прямой строго положительна? Нет, не значит. Запишем у′:

Произ-ная положительна во всех точках, кроме х = 0. При х = 0 у′ также оказывается равной нулю. Однако мы можем сказать, что у′ неотрицательна на всей числовой прямой.

Можно привести пример ф-кции

ее произ-ная равна

Сама ф-кция убывает на всей числовой прямой, а её произ-ная неположительна на ней.

Рассмотрим особый случай, когда у ф-кции произ-ная одновременно и неположительна, и неотрицательна на отрезке. Как ни сложно догадаться, это означает, что производная равна нулю. Мы помним, что нулю равна произ-ная константы:

В качестве примера приведем ф-кцию у = 2. Её произ-ная на всей числовой прямой равна нулю:

При этом ф-кция и не убывает, и не возрастает на числовой прямой:

Рассматривая все эти примеры, можно сделать вывод, что для возрастания ф-кции на промежутке достаточно, чтобы её произ-ная принимала на этом отрезке только положительные отрезки:

Аналогично можно сформулировать и достаточный признак убывания ф-кции:

Сформулированные признаки не охватывают тех ситуаций, когда произ-ная в отдельных точках промежутка обращается в ноль. Если произ-ная равна нулю на всём промежутке, то ф-кция на нем остается неизменной (как в случае с функцией у = 2). Если же производная обращается в ноль только в отдельных точках (случай у = х³ и у = х²), то эти точки оказываются граничными для промежутков возрастания и промежутков убывания функции. В этих случаях эти граничные точки добавляют в соответствующие промежутки.

Задание. Докажите, что функция

возрастает при любом значении аргумента.

Решение. Найдем произ-ную у′:

Найдем, при каких значениях х произ-ная у′ оказывается положительной. Для этого запишем неравенство:

Множитель (5х² + 6) при любом х положителен, а потому мы можем поделить обе части неравенства на него и преобразовать его к виду

Его решениями являются промежутки (– ∞; 0) и (0; + ∞), а при х = 0 произ-ная оказывается равной нулю, то есть это граничная точка. Значит, промежутками возрастания функции являются (– ∞; 0] и [0; + ∞). Обратите внимание, что мы добавили в каждый из промежутков граничную точку х = 0. Но объединением этих промежутков является вся числовая прямая:

Получается, что ф-кция возрастает при любом х.

Теперь попытаемся найти промежутки возрастания и убывания функции

Для их нахождения определим, где произ-ная положительна, а где отрицательна. Для этого сначала найдем произ-ную:

Решим неравенство у′ > 0, при этом мы используем метод интервалов:

Отмечаем нули на координатной прямой и расставляем знаки промежутков:

Напомним, что для определения знаков промежутков можно просто выбрать на каждом из них одну точку и подставить её в неравенство. Например, на интервале х∈(– ∞; – 1) возьмем число – 2:

Итак, произ-ная положительна на промежутках (– ∞; – 1) и (0; + ∞). При х = 0 и х = 1 произ-ная обращается в ноль – это граничные точки, которые надо добавить в промежутки возрастания. То есть ф-кция возрастает на промежутках (– ∞; – 1] и [0; + ∞).

Рассматривая аналогичное неравенство у′ < 0, получаем, что произ-ная отрицательна при х∈(– 1; 0). Тогда промежутком убывания ф-кции является [– 1; 0].

Для наглядности построим график рассматриваемой нами ф-кции:

Проведенное нами действие (поиск промежутков возрастания и убывания ф-кции) называется исследованием функции на монотонность. Для его проведения необходимо вычислить производную ф-кцию у′, а потом найти, на каких промежутках она положительна или отрицательна. Если в граничных точках полученных промежутков произво-дная обращается в ноль, то эти точки следует включить в промежутки.

Экстремумы функции

Еще раз посмотрим на график рассмотренной нами ф-кции

На нем есть две особые точки: (– 1; 0) и (0; – 1). Они являются границами для промежутков возрастания и убывания. При этом значение произ-ной в этих точках оказалось равным нулю. Если мы проведем касательные к графику в этих точках, то окажется, что они являются горизонтальными линиями, то есть их угол наклона равен нулю:

Действительно, если произ-ная в точке равна нулю, то тангенс угла наклона должен быть также равен нулю. А это значит, что и сам угол равен нулю, ведь tg 0 = 0. Геометрически это означает, что касательная будет выглядеть как горизонтальная линия, которая либо параллельна оси Ох, либо совпадает с ней.

Ещё одна особенность точек (– 1; 0) и (0; – 1). Первая из них в некоторой, достаточно малой локальной области является точкой максимума функции. Действительно, если взять промежуток [– 1,5; – 0,5], то на нем именно в точке х = –1 ф-кция принимает наибольшее значение:

Аналогичную окрестность можно указать и для точки х = 0, только на ней точка (0; – 1) окажется точкой минимума функции, а не максимума:

Ни для какой другой точки на графике такую окрестность указать не удастся. Дадим более точное определение таким понятиям, как точка минимума и точка максимума функции:

Ещё раз заметим, что в таких точках ф-кция достигает наибольшего или наименьшего значения только в определенной локальной области. Поэтому часто их называют локальными максимумами или минимумами. Пусть ф-кция задана следующим графиком:

На графике можно отметить 5 минимумов функции и 5 максимумов, причем только один максимум и минимум будут соответствовать наибольшему или наименьшему значению на всей области определения (их ещё называют глобальными максимумами и минимумами):

Грубо говоря, точки максимума соответствуют вершинам графика, а точки минимума – впадинам графика.

Для обозначения этих точек используют специальный термин – точки экстремума функции.

Довольно очевидно, что точки экстремума находятся на границе промежутков возрастания и убывания ф-кции, то есть в тех самых граничных точках. Напомним, что в этих точках произ-ная равна нулю. Однако возможен ещё один случай появления экстремума. Он связан с так называемыми негладкими ф-кциями, пример одной из которых приведен на рисунке:

На графике явно видно два экстремума функции. Однако в этих точках ф-кция меняет свое поведение резко, а не плавно. Из-за этого график кажется «зазубренным». Обратите внимание, что построить единственную касательную к графику в экстремумах не получается:

С точки зрения математического анализа это означает, что произ-ная в таких точках не существует. Заметим, что все элементарные ф-кции, а также сложные ф-кции, получаемые из нескольких элементарных, являются гладкими. Поэтому на практике в школьном курсе такие случаи почти не встречаются.

Итак, можно сформулировать признак существования экстремума:

Задание. Докажите, что у функции вида

где a, b, c, d – постоянные числа, есть не более двух экстремумов.

Решение. Чтобы найти экстремумы функции, сначала просто продифференцируем её:

Заметим, что производная является квадратичной функцией

Эта ф-кция определена при любом значении х. Это значит, что не существует таких экстремумов, в которых произ-ная не существует. Если приравнять произ-ную к нулю, то получим квадратное уравнение:

Напомним, что квадратное уравнение может иметь не более 2 различных корней. То есть у ф-кции есть не более 2 точек, в которых произ-ная обращается в ноль. Следовательно, и экстремумов у ф-кции не более двух.

Точки, в которых произ-ная обращается в ноль или не существует, называют критическими точками функции.

Заметим, что не каждая критическая точка обязательно оказывается экстремумом. Можно снова привести пример ф-кции у = х³. Она возрастает на всей области числовой прямой, то есть не имеет экстремумов. Однако ее произ-ная имеет вид у′ = 3х², и она обращается в ноль при х = 0. В связи с этим встает вопрос – есть ли какой-то метод, позволяющий достоверно определить наличие экстремума у ф-кции? Оказывается, есть. Надо лишь проанализировать поведение производной вблизи критической точки. Если произ-ная в точке меняет знак, то она является экстремумом, а если не меняет – то не является.

Более того, можно определить, является ли экстремум точкой минимума или точкой максимума. Если произ-ная меняет знак с плюса на минус, то это точка максимума, а если с минуса на плюс – то это точка минимума.

Для примера рассмотрим ф-кцию

Попытаемся найти ее экстремумы. Для этого вычислим производную:

Найдем нули произ-ной:

Теперь отметим на координатной прямой нули ф-кции. Они разобьют числовую прямую на три промежутка. Расставим знаки производной на этих промежутках:

Знаки на промежутках можно определить, просто подставив в произ-ную одно из чисел из промежутка:

Получается, что в точке х = 0 произ-ная меняет знак с «+» на (–), а в точке х = 2 знак произ-ной не меняется. Это значит, что точка х = 0 является точкой минимума, а х = 2 – это вообще не экстремум ф-кции:

В общем случае для определения экстремумов ф-кции можно руководствоваться следующей схемой:

До этого мы рассматривали случаи, когда ф-кция была определена при любом значении аргумента. Теперь изучим ф-кцию

Ее особенностью является то, что она не определена при х = 0, так как при таком значении аргумента получается деление на ноль. Вычислим у′:

Теперь найдем нули произ-ной:

Выражение х² + 4 при любом х не равно нулю, а потому на него можно поделить уравнение:

Теперь на числовой прямой мы должны отметить две найденные критические точки. Но также на ней следует отметить число х = 0, так как в этой точке ф-кция не определена:

Обратите внимание, что точка х = 0 НЕ является экстремумом, хотя кажется, что в ней ф-кция меняет свой знак. Дело в том, ф-кция не существует при таком значении аргумента. Это значит, что х = 0 – это асимптота графика. График ф-кции будет выглядеть примерно так:

Выпуклость и вогнутость функций

Нарисуем две немного отличающиеся друг от друга возрастающие ф-кции:

Видно, что эти графики будто выгнуты в разные стороны. Оказывается, в математике есть специальное свойство ф-кций, которое указывает на направление, в котором выгнуты их графики. Левая ф-кция является вогнутой функцией, а правая – выпуклой функцией.

Определить, выпукла или вогнута ф-кция, очень просто. Достаточно провести к графику касательную. Если она проходит выше графика, то это указывает на вогнутость функции, а если ниже, то она выпукла:

Естественно, встречаются ф-кции, которые на одном промежутке выпуклые, а на другом – вогнутые. Классическим примером является кубическая парабола у = х³. На промежутке (– ∞; 0] она вогнутая, а на промежутке [0; + ∞) она становится выпуклой. При этом в точке х = 0 она меняет свой характер. Такая точка называется точкой перегиба функции:

Ранее мы уже заметили, что точка х = 0 для ф-кции у = х³ – этой пример критической точки, которая не является экстремумом. Действительно, произ-ная ф-кции у = х³ имеет вид

и она обращается в ноль при х = 0, однако в этой точке ф-кция возрастает. Это подсказывает нам, что критические точки, в которых ф-кция НЕ меняет своего знака, являются точками перегиба. И это действительно так.

Заметим, однако, что в общем случае точка перегиба может и вовсе не являться критической точкой ф-кции. В рамках школьного курса мы не будем детально изучать выпуклость функций и точки перегиба. Отметим лишь, что для их поиска необходимо вычислять уже не только первую, но и вторую произ-ную функции.

Исследование функций и построение их графиков

Ранее мы строили графики ф-кций в основном «по точкам». То есть мы просто вычисляли значение ф-кции при различных значениях х, отмечали получившиеся точки на координатной плоскости, а потом соединяли их плавной кривой. Однако при этом можно упустить некоторые важные особенности ф-кций – наличие у них минимумов и максимумов, точки их пересечения с осями координат и т.п. Поэтому в математике используют особый алгоритм для построения графиков ф-кции, который называют «исследованием функции».

Последовательность алгоритма следующая:

1. Находят область определения ф-кции. Здесь нужно учесть такие простые правила, согласно которым нельзя делить на ноль, под знаком квадратного корня не может стоять отрицательное число и т.п.
2. Выясняют, является ли ф-кция четной или нечетной, периодической или непериодической.
3. Находят производную ф-кции.
4. Приравнивая произ-ную к нулю, находят критические точки ф-кции, промежутки ее возрастания и убывания (то есть проводят исследование на монотонность).
5. Находят точку пересечения графика с осью Оу, для чего подставляют в ф-кцию х = 0. Конечно, это действие совершается только в том случае, если точка х = 0 входит в область определения ф-кции.
6. Находят точку пересечения графика с горизонтальной осью Ох. Для этого надо составить уравнение у(х) = 0 и решить его. Возможна ситуация, когда решить уравнение точно не получается, тогда этот этап можно пропустить.
7. Находят промежутки знакопостоянства ф-кции.
8. Изучают поведение ф-кции вблизи ее особых точек. Обычно это подразумевает поиск пределов ф-кции на бесконечности или в точках, где она не определена.
9. Определяют область значений ф-кции.
10. С учетом всех особенностей ф-кции строят ее график.

Заметим, что у ф-кции можно также найти точки перегиба ф-кции, исследовать ее на выпуклость и вогнутость, однако в рамках программы 11 класса это не делается.

Сразу скажем, что исследование ф-кции – это трудоемкая задача. Она не очень сложная, но требует больших затрат времени и бумаги.

Для начала рассмотрим относительно простой пример ф-кции

Область ее определения – это вся числовая прямая. Ф-кция не является ни четной, ни нечетной. Доказать это на примере конкретной точки. Возьмем х = 1:

Однако у нас это условие явно не выполняется, ведь 0 ≠ 4. Если бы ф-кция была нечетной, то выполнялось бы условие

Оно также не выполняется, так как 0 ≠ – 4.

Вычислим произ-ную ф-кции:

Произ-ная также определена на всей числовой прямой. Для поиска критических точек приравняем ее к нулю:

Получили две критические точки. Отметим их на прямой и расставим знаки:

Итак, мы смогли найти точку максимума функции, равно как и ее точку минимума.

Сразу же вычислим значение ф-кции в ее экстремумах:

Для расстановки знаков возьмем по одному значению из каждого промежутка. Например, можно взять числа (– 2), 0 и 2:

Далее находим, где прямая пересекается с осью Оу, для чего подставляем в ф-кцию значение х = 0:

Получили точку (0; 2). Для нахождения точек пересечения графика с горизонтальной остью Ох надо приравнять всю ф-кцию к нулю:

Это кубическое уравнение. Решить его можно методом подбора корней и последующим делением многочлена на многочлен. Не останавливаясь на подробностях решения, укажем, что его корнями являются числа (– 2) и 1, а других корней. Убедиться в этом можно, просто подставив в уравнение эти числа.

Следующий шаг – определение промежутков знакопостоянства. Для этого надо решить неравенство у(х) > 0:

Это неравенство решается методом интервалов. Он сводится к тому, что находятся нули левой части, которые мы уже нашли – это числа (– 2) и 1. Далее они отмечаются на прямой, после чего на образовавшихся промежутках проставляются знаки:

Знаки определяем, выбирая по одной точке из каждого промежутка:

Достаточно очевидно, что при х→∞ сама ф-кция также стремится к бесконечности. Если же х→ – ∞, то и у→ – ∞.

Представим найденную нами информацию в виде таблицы. В верхней строке будем записывать промежутки и отдельные точки, а ниже – особенности ф-кции на этих промежутках (возрастает ф-кция или убывает, положительна она или отрицательна и т.п.):

В итоге график ф-кции будет иметь следующий вид:

Теперь исследуем более сложную ф-кцию

Начнем с области определения. Знаменатель дроби не может равняться нулю, а потому

Итак, аргумент ф-кции может принимать любые значение, кроме 1 и (– 1). Поэтому её область определения (она обычно обозначается как D (x)) можно записать так:

Далее проверяем ф-кцию на четность или нечетность. Напомним, что для этого надо подставить в нее вместо аргумента х аргумент (– х):

Мы получили у(х). Это означает, что ф-кция четная, а ее график симметричен относительно оси Оу.

Следующий шаг – находим произ-ную ф-кции:

Заметим, что область определения произ-ной полностью совпадает с областью определения самой ф-кции. Поэтому у ф-кции нет таких критических точек, в которых произ-ная не существует.

Теперь произ-ную можно приравнять к нулю:

Мы нашли всего одну критическую точку. Отметив ее на координатной прямой, можно выяснить, что она является точкой максимума. При этом стоит также отметить точки х = 1 и х = – 1, в которых ф-кция не определена (их ещё называют точками разрывов):

Для определения знаков произ-ной достаточно вычислить её значение в одной точке на каждом получившемся промежутке. Возьмем значения (– 2), (– 0,5), 0,5 и 2

Найдем точку пересечения графика с осью Оу, для чего подставим в ф-кцию значение х = 0:

Получили точку (0; – 1).

Далее находим точку пересечения графика с осью Ох. Для этого подставим в ф-кцию значение у = 0 и решим получившееся уравнение:

Числитель дроби в правой части при любом значении х положителен, то есть не равен нулю. Это значит, что уравнение не имеет решения. Отсюда вывод – график НЕ пересекается с осью Ох.

Следующий шаг – это определение промежутков знакопостоянства функции. Чтобы найти, при каких значениях аргумента ф-кция положительная, составим неравенство:

Это дробно-рациональное неравенство. Для его решения надо отметить на координатной прямой те значения х, при которых либо знаменатель, либо числитель обращается в ноль. Числитель при любом аргументе положителен, а нулями знаменателя являются точки х = – 1 и х = 1:

Знаки на промежутках определяем, подставляя точки из промежутков в ф-кцию:

Далее следует исследовать поведение ф-кции вблизи при х →∞ и х→ –∞. Для этого преобразуем ф-кцию, выделив целую часть:

При х→∞ число (х² – 1) также стремится к бесконечности, а дробь

будет стремиться к единице. Аналогично можно убедиться, что при х→ – ∞ ф-кция также стремится к единице.

Все полученные данные можно удобно представить в табличном виде:

На основании этих результатов строим график:

Из рисунка видно, что область значений ф-кции имеет вид

Итак, мы узнали, что с помощью производной можно определять промежутки, на которых функция возрастает и убывает, а также находить ее минимумы и максимумы. Эти навыки помогают при решении многих практических задач, когда требуется найти такое значение некоторых параметров, при которых какая-то величина принимает максимальное или минимальное значение. Например, продавцы товара могут назначать такую цену на свою продукцию, которая принесет им максимальный доход (просто назначить как можно большую цену нельзя, так как слишком дорогой товар никто не купит). Более подробно такие задачи мы рассмотрим подобные задачи в следующих уроках.

Непрерывность функции в точке

30 декабря 2021

В этом уроке мы выясним, что такое непрерывность функции в точке, непрерывность на множестве; познакомимся с основными свойствами таких функций; научимся искать точки разрыва и решим множество интересных задач.

Содержание:

1. Интуитивное определение непрерывности
2. Непрерывность функции в точке
3. Непрерывность функции на множестве
4. Точки разрыва

Поначалу теория будет совсем простой, но затем выкладки и задачи начнут быстро усложняться. И чем глубже вы хотите разобраться в математике, тем больше пользы получите от этого урока.

1. Интуитивное определение непрерывности

Большинство студентов, когда слышат термин «непрерывная функция», представляют себе линию, которую можно начертить, не отрывая карандаша от бумаги. Например, обычную параболу:

Или просто какую-нибудь плавную кривую:

Главное, чтобы у этих линий не было никаких особенностей. Они не «разваливаются» на куски, не «улетают» в бесконечность рядом с какой-то точкой, и вообще для любого $x$ мы прямо по графику можем определить, чему будет равен $y$.

Другое дело — функции с нарушением непрерывности. Или, как говорят, с точками разрыва. Обычно студенты сразу называют функцию $y={1}/{{{x}^{2}}};$ — классическую гиперболу, которая не определена в точке $x=0$, а график «улетает» в бесконечность в окрестности этой точки:

Впрочем, для возникновения разрыва функции вовсе не обязательно уходить куда-то в бесконечность. Достаточно просто иметь выколотую точку. Взгляните:

Перед нами всё та же парабола $y={{x}^{2}}$, но с выколотой точкой $x=-2$. Как такое возможно? Очень просто. Например, именно так выглядит график функции

[y=frac{{{x}^{2}}left( x+2 right)}{x+2}]

Значение этой функции не определено при $x=-2$, поскольку знаменатель дроби обращается в ноль. Но во всех остальных точках знаменатель $x+2ne 0$, и можно выполнить сокращение:

[y=frac{{{x}^{2}}left( x+2 right)}{x+2}={{x}^{2}}quad left( xne -2 right)]

И это не какая-то «искусственная» задача — такие функции регулярно встречаются на ОГЭ и ЕГЭ по математике, особенно в задачах с параметром.

Но и это ещё не всё. Функция может быть определена на всей числовой прямой — и всё равно иметь точку разрыва:

Это график кусочно-заданной функции

[fleft( x right)=left{ begin{align} & 1, & x gt 0 \ & 0, & x=0 \ & -1, & x lt 0 \ end{align} right.]

Она определена для всех $xin mathbb{R}$, в т.ч. при $x=0$. Однако именно в точке $x=0$ происходит скачкообразное изменение: $fleft( 0 right)=0$, но малейший шаг влево — и вот уже $fleft( x right)=-1$. А малейший шаг вправо — и $fleft( x right)=1$.

Итого проблемы возникают там, где функция «улетает» в бесконечность, либо меняется скачкообразно, либо вообще не определена. И тут мы переходим к строгому определению непрерывности.

2. Непрерывность функции в точке

Определение 1. Функция $fleft( x right)$ называется непрерывной в точке ${{x}_{0}}$, если она определена в этой точке и имеет предел, равный значению функции в этой точке:

[limlimits_{xto {{x}_{0}}} fleft( x right)=fleft( {{x}_{0}} right)]

На практике удобно считать, что функция непрерывна в точке ${{x}_{0}}$, если выполнены сразу три условия:

1. Функция определена в этой точке, т.е. существует $fleft( {{x}_{0}} right)$;
2. Существует конечный предел функции $limlimits_{xto {{x}_{0}}} fleft( x right)$;
3. Этот предел равен значению функции в точке: $limlimits_{xto {{x}_{0}}} fleft( x right)=fleft( {{x}_{0}} right)$.

Если хотя бы одно из этих условий не выполнено, функция перестаёт быть непрерывной. Так, в приведённых выше примерах гипербола $y={1}/{x};$ не определена и не имеет предела в точке $x=0$. Парабола с выколотой точкой просто не определена при $x=-2$. А кусочно-заданная функция определена в точке $x=0$, но имеет разные левые и правые пределы, отличные от $fleft( 0 right)$.

2.1. Непрерывность по Коши и по Гейне

Среди трёх условий непрерывности особый интерес представляет второй пункт — существование предела $limlimits_{xto {{x}_{0}}} fleft( x right)$. Именно на вычислении предела функции в точке спотыкается большинство учеников.

Если вы чувствуете себя неуверенно в вычислении таких пределов, рекомендую повторить тему «Что такое предел функции в точке». А сейчас мы адаптируем два ключевых определения из того урока — предел функции по Коши (в нотации «$varepsilon $—$delta $») и по Гейне (через последовательности) — для проверки непрерывности.

Определение 2. (непрерывность по Коши) Функция $fleft( x right)$ непрерывна в точке ${{x}_{0}}$, если

[begin{align} & forall left( varepsilon gt 0 right)quad exists left( delta =delta left( varepsilon right) gt 0 right): \ & xin {{overset{circ }{mathop{U}},}_{delta }}left( {{x}_{0}} right)Rightarrow left| fleft( x right)-fleft( {{x}_{0}} right) right| lt varepsilon\ end{align}]

Когда «посвящённый» человек слышит фразу «предел функции в точке», он чаще всего вспоминает именно такое определение (по Коши, т.е. в нотации «$varepsilon $—$delta $»). Но есть ещё одно определение:

Определение 3. (непрерывность по Гейне) Функция $fleft( x right)$ непрерывна в точке ${{x}_{0}}$, если для любой числовой последовательности $left{ {{x}_{n}} right}$ такой, что

[limlimits_{nto infty } {{x}_{n}}={{x}_{0}}]

выполняется условие

[limlimits_{nto infty } fleft( {{x}_{n}} right)=fleft( {{x}_{0}} right)]

Все три определения непрерывности эквивалентны. Это следует из эквивалентности определения предела по Коши и по Гейне (доказательство такой эквивалентности — в уроке про пределы функции в точке).

Нас сейчас интересует другое: а как вообще проверить, что все эти пределы существуют? Тут нам на помощь приходят односторонние пределы.

2.2. Критерий существования предела в точке

Теорема 1. Предел функции в точке $limlimits_{xto a} fleft( x right)$ существует и равен числу $Ain mathbb{R}$ тогда и только тогда, когда существуют конечные односторонние пределы $limlimits_{xto a+} fleft( x right)$ и $limlimits_{xto a-} fleft( x right)$, причём эти пределы должны быть равны числу $A$:

[limlimits_{xto a} fleft( x right)=limlimits_{xto a+} fleft( x right)=limlimits_{xto a-} fleft( x right)=A]

Эта теорема прекрасно подходит и для проверки непрерывности, и для классификации точек разрыва (об этом позже). Давайте рассмотрим пару примеров, а затем сформулируем общий алгоритм.

Пример 1. Непрерывная функция.

Рассмотрим график функции $y={{x}^{2}}$ и найдём односторонние пределы в точке ${{x}_{0}}=2$.

Вот график с интересующей нас точкой:

Если встать в начало координат, а затем приближаться к точке ${{x}_{0}}=2$ слева, значения функции будут постепенно расти, становясь всё ближе к $y=4$:

А если двигаться из бесконечности влево, приближаясь к ${{x}_{0}}=2$, значения функции будут убывать, становясь всё ближе к тому же $y=4$:

Получается, что односторонние пределы существуют и равны одному и тому же числу:

[limlimits_{xto 2-} {{x}^{2}}=limlimits_{xto 2+} {{x}^{2}}=4]

Это значит, что и стандартный предел функции в точке ${{x}_{0}}=2$ тоже существует и равен

[limlimits_{xto 2} {{x}^{2}}=4]

Значение функции $y={{x}^{2}}$ в точке ${{x}_{0}}=2$ тем более определено и равно тому же самому числу:

[fleft( 2 right)={{2}^{2}}=4]

Вот и получается, что (1) функция равна 4, (2) предел существует (мы доказали это через односторонние пределы) и равен 4, (3) значения функции и предела в точке совпадают. Следовательно, функция $y={{x}^{2}}$ непрерывна в точке ${{x}_{0}}=2$.

Возможно, прочитав всё это, вы скажете: «Спасибо, кэп. А разве бывает иначе?» Ещё как бывает! Взгляните на следующий пример.

Пример 2. Функция с разрывом в точке ${{x}_{0}}=0$.

Рассмотрим график функции $y={left| x right|}/{x};$ и найдём односторонние пределы в точке ${{x}_{0}}=0$.

Этот график весьма схож с тем, что мы рассматривали в самом начале урока. Для удобства обозначим точки $left( 0;1 right)$ и $left( 0;-1 right)$, не принадлежащие графику, выколотыми точками (а не стрелками, как было раньше):

Функция не определена в нуле — одно из условий непрерывности уже не выполняется, и на этом можно было бы закончить. Но нас сейчас интересуют односторонние пределы.

Начнём движение по левой ветке графика — из минус бесконечности влево к $x=0$:

При этом значение функции будет оставаться неизменным: $y=-1$. Следовательно,

[limlimits_{xto 0-} frac{left| x right|}{x}=-1]

Теперь пройдёмся по правой ветке — из плюс бесконечности к $x=0$:

Как бы близко к нулю мы ни приближались, значения функции всё равно равны $y=1$. Поэтому

[limlimits_{xto 0+} frac{left| x right|}{x}=1]

Получается, что односторонние пределы существуют, но не равны:

[limlimits_{xto 0-} frac{left| x right|}{x}ne limlimits_{xto 0+} frac{left| x right|}{x}]

Следовательно, общего предела функции в точке $x=0$ не существует.

2.3. Алгоритм исследования функции на непрерывность

Сформулируем универсальный алгоритм, по которому доказывается непрерывность функции $fleft( x right)$ в точке ${{x}_{0}}$. Или наоборот — опровергается. Алгоритм состоит из трёх шагов:

1. Проверить, определена ли функция $fleft( x right)$ в точке $x={{x}_{0}}$. Другими словами, можно ли найти значение $fleft( {{x}_{0}} right)$. Если посчитать $fleft( {{x}_{0}} right)$ нельзя — функция не является непрерывной, исследование закончено. Если можно, переходим к пункту 2;
2. Найти односторонние пределы и проверить: выполняется ли критерий существования предела функции в точке. Если односторонние пределы существуют и равны — переходим к пункту 3. Если хотя бы один односторонний предел не существует, либо они не равны — функция не является непрерывной, исследование закончено.
3. Сравнить значения $fleft( {{x}_{0}} right)$ и $limlimits_{xto {{x}_{0}}} fleft( x right)$. Если они равны, функция непрерывна. Если нет — значит, функция не является непрерывной.

Может показаться, что действий слишком много. И что проверка слишком сложная. На самом деле это не так. Взгляните:

Пример 3. Доопределите функцию $fleft( x right)$ в точке ${{x}_{0}}$ так, чтобы она стала непрерывной:

[fleft( x right)=frac{sin x}{x},quad {{x}_{0}}=0]

Это одна из любимейших задач всех преподавателей по матанализу. Очевидно, функция не проходит уже первый пункт проверки: $fleft( 0 right)$ не существует, поскольку деление на ноль не определено.

Однако нам предлагают доопределить функцию, т.е. найти такое $Ain mathbb{R}$, чтобы полученная функция

[fleft( x right)=left{ begin{align} & frac{sin x}{x}, & xne 0 \ & A, & x=0 \ end{align} right.]

была непрерывна в точке ${{x}_{0}}=0$.

Поэтому проверим пункт 2. Посчитаем левосторонний и правосторонний пределы:

[begin{align} & limlimits_{xto 0+} frac{sin x}{x}=1; \ & limlimits_{xto 0-} frac{sin x}{x}=limlimits_{xto 0-} frac{sin left( -x right)}{-x}=limlimits_{tto 0+} frac{sin t}{t}=1 \ end{align}]

[begin{align} limlimits_{xto 0+} frac{sin x}{x}&=1; \ limlimits_{xto 0-} frac{sin x}{x}&=limlimits_{xto 0-} frac{sin left( -x right)}{-x} \ &=limlimits_{tto 0+} frac{sin t}{t}=1 \ end{align}]

Односторонние пределы легко сводятся к первому замечательному пределу и равны $A=1$. Следовательно, если мы доопределим $fleft( x right)$ так, чтобы $fleft( 0 right)=1$, мы получим функцию, непрерывную в ${{x}_{0}}=0$:

[fleft( x right)=left{ begin{align} & frac{sin x}{x}, & xne 0 \ & 1, & x=0 \ end{align} right.]

Вот и всё. Задача решена.

Обратите внимание на график функции $y=fleft( x right)$. Вот так он выглядит изначально (очевидно нарушение непрерывности в ${{x}_{0}}=0$):

А вот так — после того, как мы доопределим $fleft( 0 right)=1$:

Получили функцию, которая непрерывна в любой точке. И это видно на графике. Из чего сразу сделаем два замечания:

Замечание 1. Если в задании требуется исследовать функцию на непрерывность, обязательно постройте хотя бы примерный график этой функции. Так вы сразу поймёте: где могут быть проблемы, как ведёт себя функция в окрестности «проблемных» точек и что с этим можно сделать.

Замечание 2. Исследование на непрерывность всегда проводится в конкретных точках. Но график функции — это чаще всего бесконечное множество точек, большинство из которых ничем не примечательны. Поэтому нужно научиться определять непрерывность на бесконечных множествах.

Вот вторым пунктом — непрерывностью на бесконечных множествах — мы сейчас и займёмся.

3. Непрерывность функции на множестве

До сих пор мы говорили о непрерывности лишь в одной конкретной точке — некой ${{x}_{0}}in mathbb{R}$. Но большинство функций определено на огромных множествах — вплоть до всей числовой прямой. Как быть в этом случае? Здесь нам помогут следующие определения.

3.1. Непрерывность на интервале

Определение 4. Функция $fleft( x right)$ непрерывна на интервале $left( a;b right)$, если она непрерывна в каждой точке ${{x}_{0}}in left( a;b right)$.

Пример. Функция $y={1}/{x};$ непрерывна на интервале $left( -infty ;0 right)$ и на интервале $left( 0;+infty right)$.

Почему именно интервал? Почему не отрезок? Потому что интервал — это открытое множество, т.е. каждая точка ${{x}_{0}}in left( a;b right)$ входит в этот интервал с некоторой своей $delta $-окрестностью. На языке кванторов записывается это так:

[begin{align} {{x}_{0}}in left( a;b right) & Rightarrow exists left( delta gt 0 right): \ xin {{U}_{delta }}left( {{x}_{0}} right) & Rightarrow xin left( a;b right) \ end{align}]

А на числовой прямой всё это безобразие выглядит так:

На интервале мы никогда достигаем границ — точек $a$ и $b$. Поэтому не имеет значения, как близко к этим границам располагается точка ${{x}_{0}}$. Всегда можно взять расстояние до ближайшей границы (например, $left| {{x}_{0}}-a right|$), поделить пополам — вот вам и отступ $delta gt 0$.

3.2. Непрерывность на отрезке

Отрезок $left[ a;b right]$ принципиально отличается от интервала $left( a;b right)$ тем, что мы можем зайти, например, в левый конец отрезка — точку $a$ — и ничего левее этой точки принадлежать отрезку уже не будет.

Никакие отступы, никакие $delta $-окрестности тут не помогут. Поэтому нам нужны два новых определения.

Определение 5. Функция $fleft( x right)$ называется непрерывной справа в точке ${{x}_{0}}$, если

[limlimits_{xto {{x}_{0}}+} fleft( x right)=fleft( {{x}_{0}} right)]

непрерывной слева в точке ${{x}_{0}}$, если

[limlimits_{xto {{x}_{0}}-} fleft( x right)=fleft( {{x}_{0}} right)]

Теперь мы можем рассматривать непрерывность на любых привычных нам множествах — интервалах и отрезках. Чуть позже в этом уроке мы сформулируем замечательную теорему о непрерывности элементарных функций, но пока давайте рассмотрим пару примеров.

Пример 4. Функция $fleft( x right)=sqrt{4-{{x}^{2}}}$ непрерывна на всей своей области определения.

Проверить это и построить график.

Для начала найдём область определения $fleft( x right)$. Поскольку арифметический квадратный корень определён только из неотрицательного числа, имеем:

[begin{align} 4-{{x}^{2}} & ge 0 \ {{x}^{2}} & le 4 \ left| x right| & le 2 \ x& in left[ -2;2 right] \ end{align}]

Для лучшего понимания ситуации начертим график $y=sqrt{4-{{x}^{2}}}$. Заметим, что

[begin{align} {{y}^{2}} & =4-{{x}^{2}} \ {{x}^{2}}+{{y}^{2}} & ={{2}^{2}} \ end{align}]

это уравнение окружности с центром в начале координат и радиусом $r=2$. Графиком функции будет лишь та часть этой окружности, для которой $yge 0$:

Очевидно, что функция непрерывна для всех $xin left[ -2;2 right]$, причём в $x=-2$ непрерывна справа, в $x=2$ непрерывна слева.

Пример 5. Функция $fleft( x right)=sqrt{x}$ непрерывна на всей своей области определения.

Проверить это и построить график.

Область определения функции $fleft( x right)=sqrt{x}$:

[xin left[ 0;+infty right)]

График — стандартная «уложенная набок» ветвь параболы:

Видим, что функция $fleft( x right)$непрерывна во всех точках $xin left[ 0;+infty right)$, причём в $x=0$ непрерывна справа. Задача решена.

Возможно, вы уже заметили, что все функции, которые мы сегодня изучали, были непрерывны на всей своей области определения. Проблемы возникали лишь во всяких конструкциях вида ${1}/{x};$, где возможно деление на ноль. Но даже гипербола $y={1}/{x};$ не определена лишь в точке $x=0$, а во всех остальных точках она определена и непрерывна.

И это не случайно. Существует целый класс функций, которые непрерывны на всей своей области определения. Настала пора познакомиться с ними.

3.3. Непрерывность элементарных функций

В математическом анализе существует особый класс функций, которые называются элементарными.

Определение 6. Элементарные функции — это любые функции из списка:

1. Любой многочлен $Pleft( x right)={{a}_{n}}{{x}^{n}}+…+{{a}_{1}}x+{{a}_{0}}$;
2. Рациональная функция $fleft( x right)={Pleft( x right)}/{Qleft( x right)};$, где $Pleft( x right)$ и $Qleft( x right)$ — многочлены;
3. Степенная функция $fleft( x right)={{x}^{a}}$, где $ain mathbb{R}$;
4. Логарифмическая функция $fleft( x right)={{log }_{a}}x$, где $a gt 0$, $ane 1$;
5. Показательная функция $fleft( x right)={{a}^{x}}$, где $a gt 0$, $ane 1$;
6. Все тригонометрические функции: $sin x$, $cos x$, $operatorname{tg}x$, $operatorname{ctg}x$;
7. Все обратные тригонометрические функции: $arcsin x$, $arccos x$, $operatorname{arctg}x$, $operatorname{arcctg}x$;
8. Любые функции, которые можно составить из предыдущих с помощью конечного числа арифметических операций и композиций.

Кстати, модуль тоже является элементарной функцией:

[left| x right|=sqrt{{{x}^{2}}}]

Для всех таких функций выполняется замечательная теорема:

Теорема 2. Все элементарные функции непрерывны на всей своей области определения.

Если область определения представляет собой отрезок или иное замкнутое множество, то на концах таких отрезков выполняется односторонняя непрерывность.

Универсального доказательства этой теоремы сразу для всех элементарных функций не существует. Сначала доказывают непрерывность степенной и показательной функции. Затем показывают непрерывность арифметических операций (тот ещё квест, особенно для многочленов).

Кроме того, есть целая группа теорем, которые верны для всех непрерывных функций:

• 1.Теорема о нуле непрерывной функции и о промежуточном значении на отрезке.
• 2.Теоремы Вейерштрасса об ограниченности непрерывной функции на отрезке и о достижении точной верхней и нижней грани.
• 3.Теоремы о непрерывности обратной функции и композиции функций.

Каждой из этих теорем посвящён отдельный урок — с точной формулировкой, доказательством и примерами (см. содержание раздела). Сейчас нас интересуют более приземлённые вопросы.

Например, может возникнуть вопрос: а что, разве есть какие-то другие функции, помимо элементарных? Конечно есть.

Пример 6. Функция Дирихле:

[Dleft( x right)=left{ begin{align} & 1, & xin mathbb{Q} \ & 0, & xnotin mathbb{Q} \ end{align} right.]

Функция Дирихле определена для всех $xin mathbb{R}$. Она равна единице в том случае, если $x={p}/{q};$ — рациональное число, и равна нулю во всех остальных случаях.

Очевидно, что в любой $delta $-окрестности точки ${{x}_{0}}in mathbb{Q}$ и слева, и справа найдутся иррациональные числа. И наоборот: в любой $delta $-окрестности иррационального числа $ain mathbb{R}backslash mathbb{Q}$ найдутся его рациональные приближения с избытком и недостатком. Следовательно, односторонние пределы

[limlimits_{xto {{x}_{0}}-} Dleft( x right)quad limlimits_{xto {{x}_{0}}+} Dleft( x right)]

не существуют ни в одной точке графика. И функция Дирихле терпит разрыв в каждой точке числовой прямой.:)

Кстати, сам график выглядит примерно так:

Линия $y=1$ проведена пунктиром из тех соображений, что множество рациональных чисел счётно, а множество всех действительных чисел — нет. Но это всё условности.:)

Пример 7. Исследовать на непрерывность функцию

[fleft( x right)=sin left( {1}/{x}; right)]

Эта функция представляет собой композицию двух элементарных функций: $sin x$ и ${1}/{x};$. Следовательно, перед нами элементарная функция, которая определена и непрерывна везде, кроме $x=0$.

Посчитаем левосторонний и правосторонний предел в точке $x=0$. Для этого заметим, что при $xto 0$ величина ${1}/{x};to infty $. Следовательно, в любой $delta $-окрестности точки $x=0$ найдутся и точки вида $t=pi n$, $nin mathbb{Z}$, в которых $sin t=0$; и точки вида $t={pi }/{2};+pi n$, в которых $sin t=pm 1$.

Следовательно, ни левосторонний, ни правосторонний пределы не определены:

[limlimits_{xto 0+} sin frac{1}{x}quad limlimits_{xto 0-} sin frac{1}{x}]

А это значит, что общий предел в точке $x=0$ тоже не определён. Следовательно, $x=0$ — не просто точка разрыва (это и так понятно, поскольку в нуле функция не определена). Принципиально невозможно доопределить $fleft( x right)$ в нуле так, чтобы получилась непрерывная функция.

График $y=sin left( {1}/{x}; right)$ выглядит так (единичный отрезок — две клетки):

Чем ближе $xto 0$, тем быстрее график «бегает» между $y=-1$ и $y=1$. В какой-то момент из-за конечной толщины линий на чертеже строить график становится невозможно. Даже если мы возьмём за единичный отрезок тысячу клеток. Даже если будем чертить на огромных листах. Никакие листы и отрезки не могут сравниться с бесконечностью.:)

Ну и перед тем как переходить к практике, давайте разберёмся, что же произойдёт, если хотя бы одно условие непрерывности не выполняется.

4. Точки разрыва

Урок о непрерывности функции в точке будет неполным, если мы не поговорим про точки разрыва.

Напомню, что функция $fleft( x right)$ является непрерывной в точке ${{x}_{0}}$, когда выполнены три условия:

1. Функция $fleft( x right)$ определена в этой точке, т.е. мы можем посчитать $fleft( {{x}_{0}} right)$.
2. Существует конечный предел $limlimits_{xto {{x}_{0}}} fleft( x right)$.
3. Должно выполняться равенство $limlimits_{xto {{x}_{0}}} fleft( x right)=fleft( {{x}_{0}} right)$.

А что, если хотя бы одно условие не выполнено? Перед нами точка разрыва.

Определение 7. Если функция $fleft( x right)$ не является непрерывной в точке ${{x}_{0}}$, то она называется разрывной в точке ${{x}_{0}}$. Сама точка ${{x}_{0}}$ при этом называется точкой разрыва функции $fleft( x right)$.

Определение 8. Точка разрыва ${{x}_{0}}$ называется точкой разрыва первого рода функции $fleft( x right)$, если существуют конечные односторонние пределы $limlimits_{xto {{x}_{0}}+} fleft( x right)$ и $limlimits_{xto {{x}_{0}}-} fleft( x right)$.

В противном случае ${{x}_{0}}$ называется точкой разрыва второго рода.

Классический пример точки разрыва второго рода:

[y=frac{1}{x},quad {{x}_{0}}=0]

Ветви гиперболы «улетают» в бесконечность рядом с точкой ${{x}_{0}}=0$.

Ещё один пример:

[y=sin frac{1}{x},quad {{x}_{0}}=0]

Мы уже рассматривали график этой функции и знаем, что односторонних пределов в ${{x}_{0}}=0$ не существует. Поэтому функция терпит разрыв второго рода.

Да даже обычный $y=operatorname{tg}x$ терпит разрыв второго рода в точках вида ${{x}_{n}}={pi }/{2};+pi n$, $nin mathbb{Z}$.

Определение 9. Разрыв первого рода в точке ${{x}_{0}}$ называется устранимым, если существует конечный предел $limlimits_{xto {{x}_{0}}} fleft( x right)=A$, но $Ane fleft( {{x}_{0}} right)$.

То же самое, если существует конечный предел $limlimits_{xto {{x}_{0}}} fleft( x right)=A$, но $fleft( {{x}_{0}} right)$ не определена.

Из определения очевидно, что устранимыми могут быть только разрывы первого рода. Вот несколько примеров:

• $y=frac{sin x}{x}$, ${{x}_{0}}=0$ (устранимый: $yleft( 0 right)=1$)
• $y=frac{left| x-1 right|}{x-1}$, ${{x}_{0}}=1$ (неустранимый)
• $y=frac{{{x}^{2}}left( x+2 right)}{x+2}$, ${{x}_{0}}=-2$ (устранимый: $yleft( -2 right)=4$)

Рассмотрим более сложный пример

Пример 8. Исследуйте точки разрыва функции

[y=xcdot {{e}^{{1}/{x};}}]

Это элементарная функция, поэтому единственная точка разрыва: $x=0$ — в ней не определена дробь ${1}/{x};$.

Выясним, какого рода этот разрыв. Посчитаем предел слева:

[begin{align} limlimits_{xto 0-} xcdot {{text{e}}^{{1}/{x};}} & =limlimits_{xto 0-} frac{x}{{{text{e}}^{-{1}/{x};}}}=frac{limlimits_{xto 0-} x}{limlimits_{xto 0-} {{text{e}}^{-{1}/{x};}}}= \ & =frac{0}{limlimits_{xto 0+} {{text{e}}^{{1}/{x};}}}=left[ frac{0}{infty } right]=0 end{align}]

[begin{align}limlimits_{xto 0-}xcdot {{text{e}}^{{1}/{x};}}&=limlimits_{xto 0-}frac{x}{{{text{e}}^{-{1}/{x};}}}= \ &=frac{limlimits_{xto 0-}x}{underset{xto 0-}{{text{e}}^{-{1}/{x};}}}= \ &=frac{0}{limlimits_{xto 0+}{{text{e}}^{{1}/{x};}}}= \ &=left[ frac{0}{infty } right]=0 end{align}]

И предел справа:

[begin{align} limlimits_{xto 0+} xcdot {{text{e}}^{{1}/{x};}} & =limlimits_{xto 0+} frac{{{text{e}}^{{1}/{x};}}}{{1}/{x};}=left[ {x=1}/{t}; right]= \ & =limlimits_{tto +infty } frac{{{text{e}}^{t}}}{t}=+infty\ end{align}]

[begin{align}limlimits_{xto 0+}xcdot {{text{e}}^{{1}/{x};}}&=limlimits_{xto 0+}frac{{{text{e}}^{{1}/{x};}}}{{1}/{x};}= \ &=left[ {x=1}/{t}; right]= \ &=limlimits_{tto +infty }frac{{{text{e}}^{t}}}{t}=+infty end{align}]

Понятно, что показательная функция $y={{text{e}}^{t}}$ растёт быстрее линейной $y=t$ при $tto +infty $. Поэтому конечного предела нет.

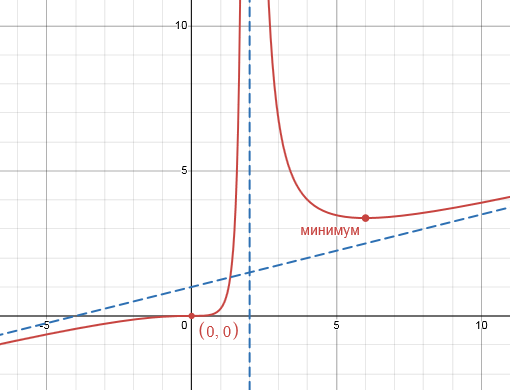
Итого функция терпит разрыв второго рода в точке $x=0$. Этот разрыв хорошо виден на графике:

Обратите внимание: точка $x=1$ является точкой локального минимума, а прямая $y=x+1$ — наклонная асимптота нашего графика. Чтобы находить такие точки, нужно разобраться с производными.

О производных и дифференциалах мы поговорим в отдельных уроках. А пока лишь одна заключительная рекомендация:

При исследовании функции на непрерывность обязательно чертите её график. Хотя бы в виде эскиза. Даже если задание кажется вам «очевидным».

Так вы защитите себя от глупых ошибок. И намного быстрее поймёте, как ведёт себя функция в окрестностях точек разрыва.

На этом всё. Приступайте к практике.:)

Смотрите также:

1. Теоремы Вейерштрасса о непрерывной функции
2. Критерий Коши сходимости последовательности
3. Тест к уроку «Что такое логарифм» (средний)
4. Не пишите единицы измерения в задаче B12
5. Однородные тригонометрические уравнения: общая схема решения
6. Задача B4: тарифы на сотовую связь

Как найти значение функции

Под понятием функции в математике понимают связь между элементами множеств. Если говорить более точно, это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Вам понадобится

• Знания в области алгебры и математического анализа.

Инструкция

Значения функции это некая область, значения из которой может принимать функция. Например область значения функции f(x)=|x| от 0 до бесконечности. Чтобы найти значение функции в конкретной точке необходимо подставить вместо аргумента функции его числовой эквивалент, полученное число и будет значением функции. Пусть дана функция f(x)=|x| — 10 + 4x. Найдем значение функции в точке x=-2. Подставим вместо x число -2: f(-2)=|-2| — 10 + 4*(-2) = 2 — 10 — 8 = -16. То есть значение функции в точке -2 равно -16.

Обратите внимание

Прежде чем искать значение функции в точке — убедитесь, что она входит в область определения функции.

Полезный совет

Аналогичным способом можно найти значение функции нескольких аргументов. Отличие в том, что вместо одного числа необходимо будет подставить несколько — по числу аргументов функции.

Исследование функции и построение графика

На этой странице мы постарались собрать для вас наиболее полную информацию об исследовании функции. Больше не надо гуглить! Просто читайте, изучайте, скачивайте, переходите по отобранным ссылкам.

Что будет дальше?

Общая схема исследования

Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены «горбы» выпуклости, где не определены значения и т.п.

А уже на основании этих «особенностей» и строится макет графика — картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).

Начнем, конечно же, с плана. Исследование функции — объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.

Алгоритм

1. Найти область определения. Выделить особые точки (точки разрыва).
2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
3. Найти точки пересечения с осями координат.
4. Установить, является ли функция чётной или нечётной.
5. Определить, является ли функция периодической или нет (только для тригонометрических функций).
6. Найти точки экстремума и интервалы монотонности.
7. Найти точки перегиба и интервалы выпуклости-вогнутости.
8. Найти наклонные асимптоты. Исследовать поведение на бесконечности.
9. Выбрать дополнительные точки и вычислить их координаты.
10. Построить график и асимптоты.

В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте требования/предпочтения вашего учителя при оформлении решения.

Схема исследования в формате pdf: скачать.

Полный пример решения онлайн

Провести полное исследование и построить график функции
$$
y(x)=frac{x^2+8}{1-x}.
$$

1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
$$1-x=0, quad Rightarrow quad x=1.$$
Исключаем единственную точку $x=1$ из области определения функции и получаем:
$$
D(y)=(-infty; 1) cup (1;+infty).
$$

2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:

Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ — вертикальная асимптота.

3) Определим точки пересечения графика функции с осями координат.

Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:

Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.

Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:

Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.

Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x in (-infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x in (1; +infty)$ функция $ylt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).

4) Функция не является ни четной, ни нечетной, так как:

5) Исследуем функцию на периодичность. Функция не
является периодической, так как представляет собой дробно-рациональную функцию.

6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:

Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):

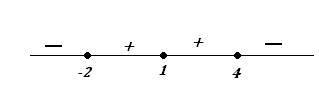
Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:

При $x in (-infty; -2), (4;+infty)$ производная $y’ lt 0$, поэтому функция убывает на данных промежутках.

При $x in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.

При этом $x=-2$ — точка локального минимума (функция убывает, а потом возрастает), $x=4$ — точка локального максимума (функция возрастает, а потом убывает).

Найдем значения функции в этих точках:

Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.

7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:

Приравняем вторую производную к нулю:

Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x in (-infty; 1)$ выполняется $y» gt 0$, то есть функция вогнутая, когда $x in (1;+infty)$ выполняется $y» lt 0$, то есть функция выпуклая.

Исследуем поведение функции на бесконечности, то есть при .

Так как пределы бесконечны, горизонтальных асимптот нет.

Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:

Получили, у что функции есть одна наклонная асимптота $y=-x-1$.

9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.

$$
y(-5)=5.5; quad y(2)=-12; quad y(7)=-9.5.
$$

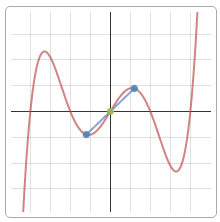
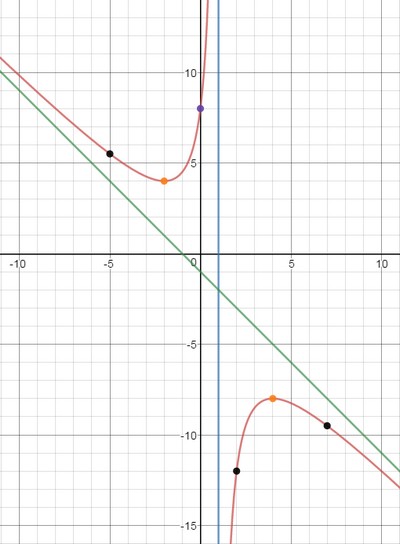
10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):

Примеры решений по исследованию функции

Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении!

Задача 1. Исследовать функцию методами дифференциального исчисления и построить график.

$$y=frac{e^x}{x}.$$

Задача 2. Исследовать функцию и построить ее график.

$$y=-frac{1}{4}(x^3-3x^2+4).$$

Задача 3. Исследовать функцию с помощью производной и построить график.

$$y=ln frac{x+1}{x+2}.$$

Задача 4. Провести полное исследование функции и построить график.

$$y=frac{x}{sqrt{x^2+x}}.$$

Задача 5. Исследовать функцию методом дифференциального исчисления и построить график.

$$y=frac{x^3-1}{4x^2}.$$

Задача 6. Исследовать функцию на экстремумы, монотонность, выпуклость и построить график.

$$y=frac{x^3}{x^2-1}.$$

Задача 7. Проведите исследование функции с построением графика.

$$y=frac{x^3}{2(x+5)^2}.$$

Задача 8. Построить график функции $y=y(x)$, заданной параметрически

$$x=frac{t^2}{t+1}, y=frac{1}{t}-frac{t^3}{3}.$$

Задача 9. Исследовать функцию и построить ее график $r=1+tg phi$.

Задача 10. Исследовать функцию и построить ее график $(x^2+y^2)^3=4x^2y^2$.

Задача 11. Провести полное исследование периодической функции
$y = cos 3x – 2 sin 6x$ и построить её график.

Задача 12. Провести полное исследование и построить график функции $y=f(x)$ с помощью Excel. Найти наибольшее и наименьшее значения функции на отрезке $[-3; -1]$.

$$y=frac{4-x^3}{x^2}.$$

Задача 13. Провести полное исследование и построить график функции.

$$f(x)=frac{x}{2}-arccosfrac{2x}{1+x^2}.$$

Еще примеры исследования функции (контрольные работы)

Как построить график онлайн?

Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).

Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?

Графический калькулятор Desmos

Desmos.com

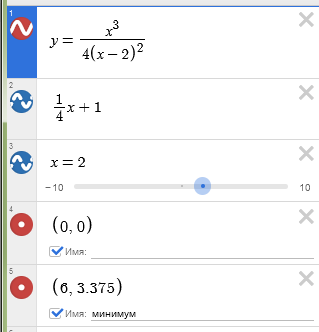
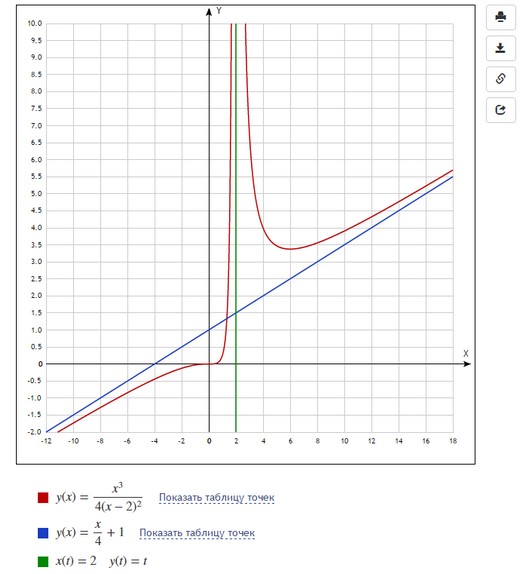
Невероятно гибкий и функциональный графический калькулятор. Интутивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=frac{x^3}{4(x-2)^2}$ буквально за минуту построены основной график и асимптоты, вот что получилось:

При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.

Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!

Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):

Сайт для построения графиков y(x).ru

y(x).ru

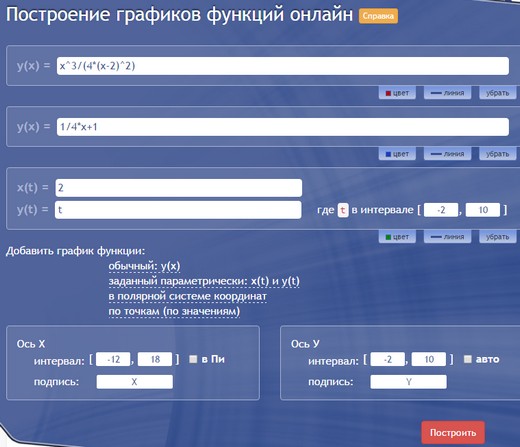
Это уже наш продукт, возможно, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:

И такой график получается в итоге:

Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).

Другие сайты

Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:

• ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
• mathsolution.ru Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл.
• easyto.me При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа.
• grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет

Больше знаний: теория и практика

Еще немного ссылок для тех, кто хочет углубиться в тему. Первая ссылка на теоретический материал, где вы найдете и подробные примеры, и отсылки к предыдущим разделам теории (а исследовать функцию не зная пределов, производных, понятия непрерывности и т.п. нельзя) с не менее подробным объяснением. Все это сдобрено порцией юмора, отчего очень «съедобно» даже для полного чайника в математике: Исследование функций от Александра Емелина.

Вторая ссылка практическая, для тех, кто хочет научиться строить красивые графики в Desmos.com (см. выше описание): Полная инструкция по работе с Desmos. Эта инструкция довольно старая, с тех пор интерфейс сайта поменялся в лучшую сторону, но основы остались неизменными и помогут быстро разобраться с важными функциями сервиса.

Официальные инструкции, примеры и видео-инструкции на английском можно найти тут: Learn Desmos.

Решебник

Срочно нужна готовая задача? Более сотни разных функций с полным исследованием уже ждут вас. Подробное решение, быстрая оплата по SMS и низкая цена — около 50 рублей. Может, и ваша задача уже готова? Проверьте!

Полезные видео-ролики

Вебинар по работе с Desmos.com. Это уже полноценный обзор функций сайта, на целых 36 минут. К сожалению, он на английском языке, но базовых знаний языка и внимательности достаточно, чтобы понять большую часть.

Классный старый научно-популярный фильм «Математика. Функции и графики». Объяснения на пальцах в прямом смысле слова самых основ.