Определение точности опыта
В
практике биометрического анализа
используется относительная ошибка
измерений – «показатель точности опыта»
– отношение ошибки средней к самой
средней арифметической, выраженное в
процентах:
.
Чем точнее определена средняя, тем
меньше будет ε,
и наоборот. Точность считается хорошей,
если ε
меньше 3%, и удовлетворительной при
3 < ε < 5%.
Иначе приходится собирать дополнительный
материал. В примере показатель точности
составил ε = (0.11 / 9.3) ∙ 100
= 1.2%, что говорит о достаточной надежности
выборочной оценки.
Оптимальный объем выборки
В
биологических исследованиях часто
заранее требуется установить число
наблюдений, достаточное для получения
репрезентативных оценок генеральной
совокупности.
Для
непрерывных признаков метод состоит в
том, чтобы, используя известные соотношения
между средней, стандартным отклонением,
ошибкой средней, плотностью вероятности
распределения Стьюдента, найти число
степеней свободы, соответствующее
доверительному интервалу для средней
при уровне значимости α = 0.05.
Объем выборки, достаточной для получения
результата заданной точности, находят
по формуле:
,
где п
– объем
выборки,
t – граничное
значение из таблицы распределения
Стьюдента (табл. 6П),
соответствующее принятому уровню
значимости при планируемом объеме
выборки,
CV
– приблизительное значение коэффициента
вариации (%),
ε
– планируемая точность оценки
(погрешности) (%).
Рассчитаем
необходимый объем условной выборки,
обеспечивающий хорошую точность ε = 3%,
для уровня значимости α = 0.05
(t = 1.98,
для df ≈ 100)
и для коэффициента вариации CV
=
12% (такова относительная изменчивость
многих размерно-весовых признаков
животных):
≈63 экз.
Если
исследуется фенотипическое (видовое)
разнообразие (дискретный признак), может
возникнуть задача определения минимального
объема выборки, в которой будет
присутствовать хотя бы один экземпляр
с определенным фенотипом (Животовский,
1991). С позиций теории вероятности задача
ставится так: определить объем выборки,
в которой с вероятностью P
можно ожидать присутствие особи с
признаком, частота которого в генеральной
совокупности составляет π.
Предлагается следующая формула:
.
В
первом приближении значение π можно
определить приблизительно по имеющимся
данным. Что же касается вероятности P,
то ее уровень довольно сильно влияет
на величину необходимого объема выборки.
Для большей надежности следует брать
P = 0.99,
но тогда возрастет объем работ; не столь
высокие требования (P = 0.95)
могут и не позволить найти искомый
фенотип. В частности, при уровне
вероятности P = 0.95
и предположительной частоте фенотипа
в популяции π = 0.05
потребуется
=
58.4 ≈ 59 экз.,
чтобы
отловить хотя бы одну особь с этим
дискретным признаком.
Оценка принадлежности варианты к выборке
Иногда
встречается ситуация, когда одна из
полученных вариант сильно отличается
от остальных. Можно ли такие резко
выделяющиеся значения использовать
при дальнейших расчетах? В терминах
математической статистики поставленный
вопрос звучит так: относится
ли данная варианта вместе с другими
вариантами изучаемой выборки к одной
и той же генеральной совокупности или
– к разным?
Его можно сформулировать и по-другому:
сформировано ли данное значение варианты
под действием тех же доминирующих и
случайных факторов, что и все остальные
варианты данной выборки, или это были
иные факторы? Здесь возможны два ответа.
1.
Факторы те же, т. е. все варианты взяты
из одной и той же генеральной совокупности.
2.
Факторы иные, т. е. особенная варианта
и выборка порознь взяты из разных
генеральных совокупностей.
Ответ
на этот вопрос можно получить с
использованием рассмотренных выше
свойств нормального распределения.
Так, если все варианты были взяты из
одной генеральной совокупности, значит,
они должны отличаться друг от друга
только в силу случайных причин и (с
вероятностью P = 0.95)
находиться в диапазоне M ± 2 ∙ S.
Иными словами, по случайным причинам
варианты достаточно большой выборки
будут отклоняться влево или вправо от
средней арифметической не более чем на
2 ∙ S:
x−M
< 2 ∙ S
или (x−M)/S
< 2.
Эта
величина, нормированное
отклонение,
и служит безразмерной характеристикой
отклонения отдельной варианты от средней
арифметической:
~
tтабл.,
где
t – критерий
выпада (исключения),
x – выделяющееся
значение признака,
М – средняя
величина для группы вариант,
tтабл. – стандартные
значения критерия выпадов, определяемые
свойствами нормального распределения,
их можно найти по табл. 5П
для трех уровней вероятности (для больших
выборок обычно пользуются значением
tтабл.
=
2 при P = 0.95,
или α = 0.05).
Для
вариант, принадлежащих изучаемой
достаточно большой выборке, нормированное
отклонение меньше двух (с вероятностью
P = 0.95):
t < 2.
В случае действия на варианту некоего
необычного фактора, она окажется за
пределами указанного диапазона M ± 2S,
и ее нормированное отклонение будет
равно или больше двух: t 2.
Нормированное
отклонение есть простейший статистический
критерий,
который помогает определять так
называемые «выскакивающие» варианты
и решать вопрос о возможности их
отбрасывания как артефактов (исключать
из дальнейшей обработки). После такой
«чистки» параметры выборки должны быть
рассчитаны заново. К оценке чужеродности
вариант, как и к другим методам статистики,
нельзя подходить формально; цель
биометрического исследования всегда
состоит в том, чтобы понять специфику
явления. В частности, «отскакивающая»
варианта может быть следствием того,
что признак имеет иное, не-нормальное
распределение.
Рассмотрим
работу критерия на примере. При измерении
длины черепа взрослых самцов обыкновенной
землеройки-бурозубки получены выборки
с такими параметрами: М = 18.8,
S = 0.3 мм.
Общее число животных n = 85.
Среди прочих вариант два больших значения
(19.2 и 21.0) вызывали сомнения. Определим
для них критерии выпада:
,
.
Согласно
таблице 5П,
критическое значение нормированного
отклонения для уровня значимости
α = 0.05
и n = 85
равно t = 2.0.
Поскольку первое полученное значение
(1.3) меньше табличного (2), первый из
сомнительных результатов исключать не
следует, а второй должен быть отброшен
– критерий выпада (7.3) превышает табличное
значение (2).
Понятие
нормированного отклонения позволяет
ввести важнейшее понятие статистики.
Статистика
–
безразмерная
случайная величина, которая имеет
известный закон распределения и
используется в качестве критерия для
проверки статистических гипотез.
В этом
смысле нормированное отклонение есть
статистика. Во-первых, это безразмерная
величина, поскольку единицы измерения
числителя (xi−M)
и знаменателя (S)
взаимно уничтожаются. Во-вторых,
нормированное отклонение имеет вполне
определенное распределение (в случае
непрерывных признаков – нормальное)
со своими параметрами (рис. 9). Его средняя
равна нулю Mt
=
tM
=
(M − M) / S = 0,
а стандартное отклонение равно единице
St = tS = (S − M) / S
=
(S − 0) / S
=
S / S
=
1.
Рис.
9.
Переход от реального признака x
к нормированному отклонению t
Нормированное
отклонение – универсальная величина.
Какой бы признак (имеющий нормальное
распределение) мы ни брали, его значения
можно выразить в виде расстояния от
центра в единицах стандартного отклонения,
т. е. на сколько S
данное значение x
отклонилось от M.
При этом, как следует из свойств
нормального распределения, крайние
значения в 95% случаев не будут принимать
значения меньше −2 и больше 2.
С
помощью нормированного отклонения
можно, например, оценивать отличия
разнокачественных объектов (пород и
сортов, видов, популяций, генераций
и пр.), причем даже по разным признакам.
Нормированное
отклонение можно использовать и для
сравнительной оценки разных индивидов
по одному и тому же признаку. Например,
если сопоставляемые по относительному
весу сердца молодая и взрослая
землеройки-бурозубки демонстрируют
одинаковые показатели (10.5 мг%), то
это, тем не менее, не означает их
сходства по изучаемому признаку.
Используя известную информацию (у
молодых средний индекс сердца равен
M = 10.0
при стандартном отклонении S = 1.3,
у взрослых – M = 11.8,
S = 1.1),
рассчитаем нормированное отклонение
для молодого зверька
и для взрослого
.
Налицо существенное различие: взрослый
зверек имеет относительно низкий
показатель сердечного индекса, а
молодой близок по этому признаку к
видовой норме.
Наибольшее
развитие такой подход получает в
процедурах обработки многомерных
данных, при исследовании объектов,
охарактеризованных по многим признакам,
методом корреляций, главных компонент,
при их кластеризации и т. п. Во многих
случаях обработка многомерного массива
начинается с нормирования
данных по формуле нормированного
отклонения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2.3. Объем выборки и объединение данных разных опытов
Вопрос объема выборки возникает в любом эксперименте. Но в селекции он ключевой и, вероятно, самый сложный. Физические возможности исследователя ограничены, и приходится выбирать – либо малые выборки и много вариантов, либо точное значение показателя и меньшее число вариантов. Ввиду сложности освоение данного вопроса для бакалавров мы ограничиваем только первым способом планирования объема выборки.
Для оценки точности полученного среднего значения используют так называемую «точность опыта» (точность определения среднего значения). Ее обозначают буквой «р» или «Р» и определяют по формуле:
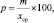
|
где р – |
точность опыта, %; |
|
m – |
статистическая ошибка выборочной величины; |
|
хср – |
среднее значение признака в выборке. |
При планировании выборки в несложных опытах чаще всего применяют следующую простую формулу:
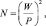
|
где N – |
объем выборки (число наблюдений); |
|
Р – |
точность опыта, %; |
|
W – |
коэффициент вариации, определяемый по формуле: |
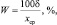
|
где δ – |
стандартное отклонение; |
|
хср – |
среднее значение признака в выборке. |
Обычно принимают Р = ±5,0 %. Так, если вариация W = ±20 %, то получаем выборку 16 шт., а если вариация будет ±30 %, то выборка увеличится до 36 шт.
Однако данная формула учитывает выполнение указанной точности лишь для 68 % выборок, т.е. в пределах плюс-минус одно стандартное отклонение в ряде распределения этих средних. Напомним, что для множества средних выборочных значений совершенно также, как и для единичных измерений, можно построить частотный ряд, который будет в виде округлого холма и будет подчиняться закону нормального распределения. Поэтому, чтобы охватить указанной точностью опыта не 68 %, а 95 % выборок, в числитель формулы (2.4) вводят критерий Стьюдента t0,95 = 2,0, а для охвата 99 % выборок это значение t увеличивают до 2,6. Тогда расчеты для Р = ±5 % при t0,95 = 2,0 дают объем выборки уже 64 шт. Заметим, что в лесную селекцию (вероятно, из лесной таксации) перекочевало убеждение, что для надежных оценок высоты и диаметра нужна точность в ±2–3 %. Тогда для точности ±3,0 % при t0,95 = 2,0 нужна выборка уже из 178 растений. Как видим, даже эта простая формула дает разные решения касательно объема выборки.
Какая же точность опыта нужна, и почему ее часто принимают в ±3–5 %? Ответ на этот вопрос лежит в доказательстве достоверности превышения роста лучшего потомства, например, на 10 %. При вариации W = ±20 % и объеме выборки 64 шт. для такого превышения критерий Стьюдента составит t = 2,83 > t0,99 = 2,63. Различие оказалось высоко достоверно. Если же снизить выборку до 33 шт., то различие будет доказано на среднем уровне при t = 2,03 > t0,95 = 2,0 и этот уровень обычно считают достаточным.
При испытаниях на быстроту роста превышение на 10 % часто принимают как критерий отбора, и выборка из 33 растений его доказывает при вариации W = ±20 % и при t0,95 = 2,0. Однако тут сразу возникают вопросы:
– мы доказываем наличие некоего превышения вообще, а каким будет это превышение в точном его значении, остается неизвестным;
– можно ли снизить критерий до t0,90 = 1,65?
И это далеко не все вопросы. Например, проводится сложный опыт с испытаниями семенами нескольких урожаев для расчета общей комбинационной способности (ОКС), причем в тест-культурах в разных условиях. Как обобщать такие сложные опыты?
С этой целью данные переводят в относительные величины, для чего в каждом испытании нужен контрольный вариант, принимаемый за 100 %. В результате разнородные опыты объединяют и получают общую среднюю оценку роста потомства в % от контроля. Если контроля нет, то рассчитывают среднюю величину в одном опыте или в его блоке, и уже ее принимают за 100 % (однако тогда эффект селекции будет совершенно неясен). Наиболее точным является «парный» контроль, когда рядом с опытной делянкой высаживают контроль. Применяют его редко и обычно контроль сокращают до 8–10 % от числа и объемов выборок всех вариантов опыта.
Минимизация выборки крайне важна, так как позволяет резко увеличить число вариантов. Для лучших потомств обычно принимают их высоту 110 % от высоты контроля. Но чтобы доказать это превышение на 10 %, выборка должна иметь почти нулевую ошибку, что практически недостижимо, так как нужны тысячи растений. Поэтому высоту для лучших потомств берут заведомо больше 110 %, например 113–115 %, и это превышение на 3–5 % называют «наименьшая существенная разность» (НСР).
Первый способ планирования выборки как раз и основан на подборе ее объемов для доказательства выбранной НСР при условии tф ≥ t0,95 = 1,96.
Возьмем реальный пример – испытания 246 семей ели в 21–23-летнем возрасте, где средняя вариация высот внутри семей составила в среднем 28 %. С возрастом эта вариация может быть разной, поэтому рассмотрим два сценария планирования, при вариации 25 и 30 %. Поясним, что в этом опыте семей с высотой от 115 % оказалось 9,3 %, с высотой от 114 % – в 1,1, а семей с высотой от 113 % было уже в 1,3 раза больше. Все они – лучшие, но чтобы правильно их отобрать, нужны разные выборки. Так, при вариации 25 % и снижении высоты их отбора от 115 к 113 % общее число растений для 100 опытных семей возрастает в 3,8 раза (табл. 2.2).
Это увеличение в 3,8 раза было бы оправдано, если бы сильно возрастала и доля лучших семей, но она выросла лишь в 1,3 раза. Поэтому при планировании лучше увеличить число семей в те же 1,3 раза, но отбирать их по большей высоте в 115 %, а выборку оставить минимальной (110 шт.). В результате будет отобрано точно такое же число лучших потомств, но объем работ увеличится лишь в 1,3, а не в 3,8 раза. Еще большее увеличение объема работ – в 4,3 раза – получаем в неблагоприятном сценарии.
Если поделить полученный минимальный объем выборки на 4 испытания, то получим в каждом ≈ 30 шт. при вариации 25 % и 56 шт. – при вариации 30 %. Но следует учесть, что можно селекционировать и устойчивые потомства, с вариацией высот около 20 %. Поэтому выборки вполне можно снизить в каждом из 4-х испытаний даже меньше 20 шт.
Таблица 2.2
Планирование испытательных культур 100 потомствами с целью отбора семей, достоверно превышающих контроль на 10 % и более
|
Высота лучших семей, % |
Число растений во всех опытах* |
Ошибка среднего, % |
Доля лучших |
Общее число |
|||
|
шт. |
% |
% |
увеличение доли, раз |
тыс. шт. |
увеличение, раз |
||
|
Благоприятный сценарий, коэффициент вариации высот 25 % |
|||||||
|
115 |
110 |
100 |
2,4 |
9,3 |
1 |
11,8 |
1 |
|
114 |
200 |
182 |
1,8 |
10 |
1,1 |
20,8 |
1,8 |
|
113 |
435 |
395 |
1,2 |
12 |
1,3 |
44,3 |
3,8 |
|
Неблагоприятный сценарий, коэффициент вариации высот 30 % |
|||||||
|
115 |
167 |
152 |
2,3 |
9,3 |
1 |
17,5 |
1 |
|
114 |
296 |
269 |
1,7 |
10 |
1,1 |
30,4 |
1,7 |
|
113 |
740 |
673 |
1,1 |
12 |
1,3 |
74,8 |
4,3 |
Примечания:
* – желательны два типа условий и минимально два урожая семян (всего 4 испытания);
** – добавляются растения в контроле (800 шт.).
Второй и третий способы планирования выборки более сложные; их рекомендуется прочитать магистрантам, а также селекционерам при разработке своих конкретных программ селекции на быстроту роста.
Второй способ планирования выборки совершенно иной. В нем снижают выборку на основе генератора случайных чисел, далее сравнивают различия между семьями в дисперсионном анализе и подбором объемов выборок выполняют условие достоверности различий для 95 % случаев. Его применили в республике Коми для сосны (Туркин, Федорков, 2007) и в Ленинградской и Псковской обл. для ели (Бондаренко, Жигунов, 2016). В результате рекомендована численность 200 растений на потомство. С учетом сохранности 50–60 % к 20 годам как раз и получается выборка из 100–110 измеряемых деревьев, или 25–30 растений в каждом опыте (см. табл. 2.2).
Подобных расчетов в лесной селекции ранее не было, так как ее задачу рассматривали с приматом высокой ценности плюс-деревьев, и выборку на потомство доводили до максимума. Вышеприведенный пример показывает, насколько не оправданы такие затраты. Но при сокращении выборки на семью в каждом из четырех испытаний до ≈ 30 шт. растений общее их число составит всего 110 шт. Для 100 семей с учетом контроля число измеряемых растений достигнет 11,8 тыс. (см. табл. 2.2). С учетом их сохранности 50 % в культуры следует высаживать примерно 24 тыс. саженцев. Наш опыт работы показал, что бригада из 4 человек весной в течение 22 календарных дней осуществила выкопку и посадку 50 тыс. саженцев с картированием 560 вариантов опыта на одном, и 400 вариантов – на втором участке, с высадкой от каждой семьи по 40–60 растений в 3–6 повторностей (Рогозин, Разин, 2012), а это уже заявка на высокую интенсивность селекции.
Третий способ еще более сложен, и разобраться в нем можно, только детально планируя весь процесс работы. Он рассматривает общую статистическую ошибку, получаемую как итог в серии опытов и разлагает (разделяет) ее далее на ряд ошибок, вызываемых следующими факторами:
– экологическими различиями (экологическая ошибка);
– генетическими отличиями семян (репродуктивная ошибка);
– вариацией высот внутри семей, округлением данных при измерениях и прочими случайными факторами (прочие ошибки).
Ниже будут приведены только итоговые результаты, а сами расчеты можно представить, если рассматривать всю массу измерений, где бывали случаи, когда семьи в одних условиях имели высоты 120 % и более, а в других условиях их высоты оказывались на уровне лишь 80–90 %. Это будет экологическая ошибка. Репродуктивная ошибка появляется в результате генетической неоднородности семян, где корреляция высот семей от урожаев разных лет оказалась очень слабой (r = 0,16 ± 0,05), и высоты семей имели различия, близкие к различиям в разных почвенных условиях (далее эти корреляции будут рассмотрены в разделах 5.1 и 5.2). Ошибка эта получается из-за различий в генетическом пуле семян, который меняется год от года в зависимости от пыльцевой продуктивности, сроков цветения, вызревания пыльцы и т.д. Снизить ее невозможно. Но экологическую ошибку, т.е. вариацию из-за разных условий, можно снижать, выравнивая эти условия.
Величину статистических ошибок моделировали при разных сценариях – при 200, 50 и 20 растениях в одном потомстве (табл. 2.3).
Таблица 2.3
Статистические ошибки средней высоты в потомствах сосны в возрасте 3–5 лет, вызванные репродуктивной, экологической и случайной изменчивостью при разных сценариях планирования объема выборки, %
|
Показатели |
Число испытаний |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Виды ошибок: |
|||||
|
экологическая |
3,40 |
2,40 |
1,96 |
1,70 |
1,08 |
|
репродуктивная |
5,29 |
3,74 |
3,05 |
2,64 |
1,67 |
|
прочие |
1,13 |
0,80 |
0,65 |
0,50 |
0,32 |
|
в контроле при n = 400 |
1,00 |
0,71 |
0,58 |
0,55 |
0,32 |
|
в потомстве при n = 200 |
1,41 |
1,00 |
0,81 |
0,70 |
0,45 |
|
в потомстве при n = 50 |
2,83 |
2,00 |
1,63 |
1,41 |
0,89 |
|
в потомстве при n = 20 |
4,47 |
3,16 |
2,58 |
2,24 |
1,41 |
|
Статистическая сумма ошибок при числе растений в потомстве, шт: |
|||||
|
n = 200 |
6,6 |
4,7 |
3,8 |
3,3 |
2,1 |
|
n = 50 |
7,1 |
5,0 |
4,1 |
3,5 |
2,2 |
|
n = 20 |
7,9 |
5,6 |
4,5 |
3,9 |
2,5 |
|
Отношение к общей ошибке при n = 200: |
|||||
|
n = 200 |
100 |
100 |
100 |
100 |
100 |
|
n = 50 |
107 |
107 |
107 |
107 |
107 |
|
n = 20 |
119 |
119 |
119 |
119 |
119 |
|
Вклад ошибок при n = 200 шт. (отношение квадратов ошибок к общей ошибке), % |
|||||
|
экологическая |
26 |
26 |
26 |
26 |
27 |
|
репродуктивная |
64 |
64 |
64 |
64 |
64 |
|
прочие |
3 |
3 |
3 |
3 |
3 |
|
в контроле при n = 400 |
2 |
2 |
2 |
3 |
2 |
|
в потомстве при n = 200 |
5 |
5 |
5 |
4 |
5 |
|
Всего ошибок |
100 |
100 |
100 |
100 |
100 |
|
Вклад ошибок при n = 20 шт. (отношение квадратов ошибок к общей ошибке), % |
|||||
|
экологическая |
19 |
19 |
19 |
19 |
19 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
репродуктивная |
45 |
45 |
45 |
45 |
45 |
|
прочие |
2 |
2 |
2 |
2 |
2 |
|
в контроле при n = 400 |
2 |
2 |
2 |
2 |
2 |
|
в потомстве при n = 20 |
32 |
32 |
32 |
32 |
32 |
|
Всего ошибок |
100 |
100 |
100 |
100 |
100 |
Для лучшего понимания структуры ошибок, данные в ней представлены в сокращенном виде, без знаков ± и с округлением. Главным итогом расчетов оказалось то, что общая ошибка зависит не столько от объема выборки, сколько от числа испытаний. Так, при одном испытании и при числе растений n = 200 шт. статистическая сумма ошибок составит 6,6 %, а при n = 20 шт. она увеличивается всего лишь до 7,9 %.
Расчеты кажутся непонятными для одного испытания, где можно рассчитать только вариацию внутри семьи, далее вариацию между средними значениями у семей, и затем общую вариацию по всем растениям. И в одном опыте, конечно же, невозможно рассчитать вклад ошибок экологической и репродуктивной. Но как только мы проводим второе испытание, то эти ошибки появляются. А если они становятся известны, то можно рассчитать их долю и в одном, и в 3–5 испытаниях по известной формуле (2.1), по зависимости ошибки выборочного среднего от стандартного отклонения и числа наблюдений.
Особенно ценным в этих расчетах оказалось разделение ошибок экологической и репродуктивной. Их общий вклад при выборке 200 шт. составляет 26 + 64 = 90 %, и сокращается до 54 % при выборке 20 шт. растений. При этом вклад ошибки, зависимой только от объема выборки на семью, увеличивается с 5 до 32 % и становится уже сопоставим с экологической и репродуктивной ошибками (см. табл. 2.3).
По итогам этих расчетов можно выбрать в целом приемлемый объем выборки из 20–30 растений в одном испытании при условии, что будет еще 3–4 испытания. Средние высоты будут оценены в итоге по 80–110 растениям с ошибкой, обеспечивающей достоверное превышение на 10 % для потомств со средними высотами 115 % и более. При отборе потомств с меньшими высотами, например, от 114 и 113 %, объемы выборок увеличиваются до 200 и 435 измеряемых растений. В целом в этом примере для потомства сосны в возрасте 3–5 лет наиболее значительной оказывается репродуктивная ошибка, и она в 2,5 раза превышает ошибку экологическую.
Таким образом, как бы мы ни старались повысить точность большими выборками в одном испытании, эти усилия, по сути, напрасны, так как в следующих испытаниях на 90 % будут доминировать ошибки, вызываемые экологией и генетической неоднородностью семян. Для их снижения необходимы испытания несколькими урожаями семян и в разных условиях.
Оценка статистических параметров по выборочным данным
Оценка в статистике – это правило вычисления оцениваемого параметра. Она указывает приближенное значение показателей выборки относительно этих параметров генеральной совокупности. По мере увеличения числа наблюдений выборочные средние и другие параметры все больше приближаются к этим значениям генеральной совокупности. Степень соответствия показателей оценивается ошибкой (m). Ее запись производится вместе с оцениваемым параметром, например, M ± mM, σ ± mσ , V ± mV . Ошибка указывает интервал, в пределах которого находится этот показатель в генеральной совокупности. Чем меньше ошибка, тем ближе значение выборочного показателя к этому показателю генеральной совокупности. Чем больше число наблюдений и чем однороднее выборка, тем меньшая ошибка среднего и других показателей. Расчеты ошибок параметров в дальнейшем будут приводиться после характеристик самих параметров. Здесь покажем расчеты ошибок важнейших статистических параметров.
Представление средней арифметической выборки приводится обязательно с ее ошибкой.
Ошибка дисперсии вычисляется путем возведения в квадрат ошибки среднеквадратической.
Поскольку параметр m характеризует ошибку утверждения (прогноза) о том, что выборочное среднее равно генеральному среднему, то чем выше требование к вероятности этого вывода, тем шире должен быть обеспечивающий точность такого прогноза интервал, называемый доверительным интервалом. Его величина задается вероятностью безошибочного прогноза, которую принято называть доверительной вероятностью (уровень вероятности, надежность опыта, вероятность безошибочного прогноза). В исследованиях допускается доверительная вероятность (Р) не менее 95 % (0,95 частей от 1). В этих случаях Р для средних арифметических при достаточно большом числе наблюдений (N > 30) равен ± 2 m. Предельная ошибка выборки Δ = М ± 2 m. При доверительной вероятности 99 % (0,99) доверительный интервал составит ± 3 m, Δ = М ± 3 m. По иному, в отношении доверительного интервала можно сказать так: он показывает какой процент вариант выборки (выборок) подтверждает искомую статистическую закономерность.
Каждому значению доверительной вероятности соответствует свой уровень значимости (α). Он выражает вероятность нулевой гипотезы: вероятность того, что выборочная и генеральная средние не отличаются друг от друга. Иначе говоря, чем выше уровень значимости, тем меньше можно доверять утверждению, что различия существуют, т. е., он показывает, какой процент вариант совокупности (выборок) отвергают искомую статистическую закономерность. Уровень значимости 5 % (0,05) дополняет доверительную вероятность 95 % (0,95). В сумме они составляют 100 % (1). Если доказано подобие между выборками при α = 5 % (0,05), то из этого следует, что до 5 % вариант выборки подобие не подтверждают. В таблицах приложения приводятся численные значения для Р или α соответственно 0,95 и 0,99; 0,05 и 0,01. В этих случаях при интерпретации мы можем утверждать нулевую гипотезу (Н0). При более высоких уровне вероятности 0,99 и уровне значимости 0,01 мы получаем сильный довод для утверждения нулевой гипотезы.
Проверка статистических гипотез. Методологической основой любого исследования является формулировка рабочей гипотезы. В ходе исследования рабочая гипотеза либо принимается, либо отвергается. Статистической называют гипотезу о виде неизвестного распределения или о параметре распределения. Примеры гипотез:
· генеральная совокупность распределяется по закону Пуассона;
· средние арифметические двух совокупностей не равны между собой;
· дисперсии двух совокупностей равны между собой.
Выдвинутую гипотезу называют основной или нулевой (Н0). Гипотезу, которая противоречит нулевой, называют конкурирующей или альтернативной (Н1). Если нулевая гипотеза предполагает, что М = 20, то логическим отрицанием будет М ≠ 15. Простая гипотеза содержит одно предположение, сложная – состоит из конечного или бесконечного множества простых гипотез. Выдвинутую гипотезу проверяют на правильность ее статистическими методами, т. е. проводят статистическую проверку. При проверке могут быть допущены ошибки двух родов.
Ошибка первого рода – отвергается правильная гипотеза. Вероятность совершить ошибку первого рода называют уровнем значимости (α). Это значит, что в 5 случаях из 100 мы рискуем допустить ошибку первого рода.
Ошибка второго рода – принимается неправильная гипотеза, значимость ошибки которой допускается 0,95 и обозначается символом Р. Это значит, что в 95 случаях из 100 мы рискуем допустить ошибку второго рода.
Для проверки нулевых гипотез используют статистические критерии. При сравнении дисперсий используют критерий Фишера. В большинстве исследований для статистической проверки гипотез существенности различий средних арифметических используют параметрический критерий Стьюдента. Если нулевая гипотеза принимается, это не означает ее доказательство. Доказать на основании однократной или косвенной проверки гипотезу нельзя, а опровергнуть можно. Для повышения точности статистических данных необходимо уменьшить вероятности ошибок первого и второго рода, увеличить объем выборок. Область применения того или иного критерия задается законом его распределения.
Оценка точности опыта. При исследованиях методического характера необходимо приводить их оценку по показателю точность опыта (р). Его смысл состоит в установлении величины ошибки среднего арифметического (mM) в процентах от величины среднего арифметического (М).
Опыт считается достаточно точным, если р < 3 %, удовлетворительным – при его величине 3–5 % . Если величина точности опыта более 5 %, к полученным выводам следует относиться осторожно и увеличить число повторностей в опыте. Эти градации обязательны для полевых опытов с растениями. Некоторые приборы для анализа могут давать значительно большую погрешность (р до 15 %).
Пример. Среднее арифметическое общей биомассы многолетних трав в луговом ландшафте прирусловой поймы М = 235 ц/г, ошибка средней арифметической mM = ± 4 ц/га, N = 20. Используя формулу (1.15), выполним расчет показателей:
р = (4 / 235) · 100 = 1,7 %.
Полученная величина точности опыта достаточно точная.
Показатель точности опыта
Предмет
Теория вероятностей
Разместил
🤓 nina.nikolayeva.1970
👍 Проверено Автор24
выражает величину ошибки среднего значения в процентах от самого среднего.
Научные статьи на тему «Показатель точности опыта»
Основные направления совершенствования прогнозирования
От точности государственных прогнозов зависит адекватность прогнозируемых показателей, их соответствие…
государственных прогнозов необходимо учитывать содержание муниципальных и региональных прогнозов, требуя их точности…
социально-экономического развития муниципальных образований, формирующих развитие региона;
во-вторых, повышение точности…
Необходимо осуществлять анализ и адаптацию мирового опыта, проводить собственные исследования процесса…
работать хорошо даже без определенных согласований, однако в условиях проблемного рынка она нуждается в точности

Статья от экспертов
Влияние объема выборки растений на точность сравнения гибридных форм яровой пшеницы
биометрический метод оценки влияния размера выборки растений (m), измеряемых на каждой делянке полевого опыта на относительную точность сравнения средних значений количественного признака, был разработан ранее [2]. Проведена модификация метода для сравнения дисперсий признака на разных делянках опыта как показателя генетической изменчивости популяций. При анализе 7 признаков у гибридов F1 и в популяциях F2, F3 яровой пшеницы установлена степень влияния числа измеряемых растений на относительную точность сравнения как средних значений, так и дисперсий.
Показатели машиностроения
К показателям технического уровня можно отнести мощность, КПД, точность работы, производительность, расход…
Так же в эти показатели включается такой показатель как точность….
За точность принимают величину отклонений отдельных показателей от заранее установленных значений….
исследований с учетом опыта использования прототипов….
Требования к показателям точности с каждым годом становятся все строже.

Статья от экспертов
Анализ лечения деформаций длинных трубчатых костей у подростков с использованием интрамедуллярного остеосинтеза стержнями с блокированием: предварительное сообщение
Цель работы: провести ретроспективный анализ первичного опыта (26 пациентов) оперативного лечения деформаций длинных костей нижних конечностей у подростков различной этиологии с использованием остеотомий в сочетании с остеосинтезом интрамедуллярным стержнем с блокированием. Материалы и методы. Выполнена оценка точности коррекции деформаций по показателям референтных линий и углов после операции, сроков консолидации, количества осложнений и функционального результата. Результаты. Выявлено, что точность коррекции деформаций бедра в зависимости от степени сложности деформации по разным показателям составила от 77,8 до 91,7 %. Лучшие показатели были выявлены при лечении простых деформаций и деформаций средней степени тяжести. Худшие результаты выявлены в группе сложных многоплоскостных деформаций бедренной кости: 5 случаев остаточной деформации, при этом в трех из них остаточный угол деформации составил менее 10°. При лечении деформаций голени точность коррекции составила 90 %. Оценка ф…
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек

