Как найти точность приближенного равенства

Содержание:

1. Приближённые вычисления
2. Абсолютная и относительная погрешности
3. Выполнение действий над приближёнными числами
4. Выполнение действий без точного учёта погрешности

Приближённые вычисления

Приближённые вычисления — вычисления, в которых данные и результат (или только результат) являются числами, приближенно представляющими истинные значения соответствующих величин. Числовые данные, полученные измерением реальных объектов, редко бывают точными значениями соответствующей величины, а обычно имеют некоторую погрешность

Абсолютная и относительная погрешности

При решении практических задач часто приходится иметь дело с приближёнными значениями разных числовых величин. К ним относятся: результаты измерения разных величин с помощью приборов; значения полученные при считывании на графиках, диаграммах, номограммах; проектные данные; результаты округления чисел; результаты действий над приближёнными числами; табличные значения некоторых величин; результаты вычислений значений функции. Приближённые значения (приближение, приближённые числа) могут значительно отличаться от точных, либо быть близкими к ним.

Для оценки отклонения приближённых чисел от точных используют такие понятия как абсолютная и относительная погрешности.

Абсолютной погрешностью  приближённой называется модуль разности между точным значением величины  и её приближённым значением х, то есть

Пример.

Абсолютная погрешность приближённого числа  числом 0,44 составляет

Если точное число неизвестно, то найти абсолютную погрешность  невозможно. На практике вводят оценку допустимой при данных измерениях или вычислениях абсолютной погрешности, которую называют пределом абсолютной погрешности и обозначают буквой h. Считают, что h. Как правило, предел абсолютной погрешности устанавливают из практических соображений, например, при измерениях  пределом абсолютной погрешности считают наименьшее деление прибора.

При записи приближённых чисел часто используют понятия верной и сомнительной цифры.

Цифра  называется верной, если предел абсолютной погрешности данного приближения не превышает единицы того разряда, в котором записана эта цифра. В другом случае цифра называется  сомнительной.

Например: в числе две цифры верны, поскольку погрешность 0,04 не превышает единицу разряда десятых. Цифры 9 и 7 верны, поскольку  а цифры 4 и 6 являются сомнительными, поскольку 

В конечной записи приближённого числа сохраняют только верные цифры. Так число  можно записать в виде  , число  в виде  Если в десятичной дроби последние верные цифры — нули, то их оставляют в записи числа.

Например: если , то правильной записью числа будет 0,260.

Если в целом числе последние нули являются сомнительными, их исключают из записи числа.

Именно поэтому при работе с приближёнными числами широко используют стандартную форму записи числа.

Например: в числе  верными являются три первые цифры, а два последних нуля — сомнительные цифры. Запись числа возможна только в виде: 

Следовательно, в десятичной записи приближённого числа последняя цифра указывает на точность приближённости, то есть предел абсолютной погрешности не превышает единицу последнего разряда.

Например:

1. Запись  означает, что , то есть предел абсолютной погрешности h=0,01.

2. Запись 

3. Если 

В десятичной записи числа значимыми цифрами называются все его верные цифры начиная с первой слева, отличной от нуля.

Например: в числе 1,13 — три значимых цифры, в числе 0,017 — две, в числе 0,303 — три, в числе 5,200 — четыре, в числе 25_*10³ — две значимых цифры.

При таком подходе к записи приближенного числа необходимо уметь округлять числа.

Правила округления чисел:

— Если первая цифра, которую отбрасываем является меньше пяти, то в основном разряде, который сохраняется цифра не меняется. Например: 879,673≈879,67.

— Если первая цифра, которую отбрасываем больше пяти, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 456,87≈456,9.

— Если первая цифра, которая отбрасывается пять и за ней есть ещё отличны от нуля, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 1246,5002≈1247.

— Если первая цифра, которая отбрасывается — пять и за ней нет больше никаких цифра, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 0,275≈0,28; 1,865≈1,86.

Абсолютная погрешность не полностью характеризует точность приближения. Например,  будет грубой ошибкой при измерении жука, и незначительной при измерении кита. Тоже самое можно сказать и про предел абсолютной погрешности. Качество (точность) приближённости лучше характеризуется относительной погрешностью.

Относительной погрешностью  (омега) приближённости х величины  называется отношением абсолютной погрешности  этого приближения к модулю приближённого значения х, то есть 

Поскольку абсолютная погрешность  обычно бывает неизвестна, то на практике оценивают модуль относительной погрешности некоторым числом, которое не меньше чем этот модуль: 

Число  называется пределом относительной погрешности.

Предел относительной погрешности можно вычислить по формуле: 

Конечно относительная погрешность выражается в процентах.

С помощью относительной погрешности легко установить точность приближённости.

Пример 1. Найти относительную погрешность числа 

Решение: Имеем 

Следовательно 

Пример 2. Сравнить точность измерения толщины книги d (см) и высоты стола H (см), если известно, что  .

Решение: 

Как видим, точность измерения высоты стола значительно выше.

Выполнение действий над приближёнными числами

Результат арифметических действий над приближёнными числами является также приближённым числом.

Необходимо уметь устанавливать погрешности результатов вычислений. Их находят с точным и без точного учёта погрешностей исходных данных. Правила нахождения погрешностей результатов действий с точным учётом погрешности приведены в таблице (обозначения —  исходные данные;  пределы абсолютных погрешностей относительно чисел; пределы относительных погрешностей).

Пример 3. Вычислить приближение значения выражения  и найти предел погрешностей результата.

Решение: находим значение квадрата числа 5,62 и квадратного корня из числа 18,50.

Найдём границу относительной погрешности результата:

Граница абсолютной погрешности результата:

Ответ: 

Пример 4. Вычислить приближение значения выражения   и найти предел погрешностей результата.

Решение: находим значение квадратного корня из числа 6,24 и , имеем:

Граница относительной погрешности результата:

Граница абсолютной погрешности результата: 

Ответ: 

Выполнение действий без точного учёта погрешности

Точный учёт погрешности усложняет вычисление. Поэтому, если не надо учитывать погрешность промежуточных результатов, можно использовать более простые правила. 

Сложение и вычитание приближённых вычислений рекомендуется выполнять так:

а) выделить слагаемое с наименьшим числом верных десятичных знаков;

б) округлить другие слагаемые так, чтобы каждое из них содержало на один десятичный знак больше чем выделенное;

в) выполнить действия, учитывая все сохранённые десятичные знаки;

г) результаты округлить и сохранить столько десятичных знаков, сколько их есть в приближённом числе с наименьшим числом десятичных знаков.

Умножение и деление приближённых вычислений рекомендуется выполнять так:

а) выделить среди данных чисел, число с наименьшим количеством верных значимых цифр;

б) округлить оставшиеся данные так, чтобы каждое из них содержало на одну значащую цифру больше, чем в выделенном;

в) выполнить действия — сохранить все значимые цифры;

г) сохранять в результате столько значащих цифр, сколько их имеет выделенное число с наименьшим количеством верных значимых цифр.

При возведении в степень приближённого числа в результате сохраняют столько значимых цифр, сколько верных значимых цифр имеет основа степени.

При извлечении корня из приближённого числа в результате сохраняют столько верных цифр, сколько имеет подкоренное число.

В математике используют приближённые значения действительных чисел  для графического решения уравнений и для выполнения  практических вычислений с действительными числами.

Действительные числа — бесконечные десятичные дроби. 

Решение:

найдём площадь круга по формуле S=πR2=4⋅3,14159265359…=12,5663706144….

В ответ мы можем написать приближённое значение:

1) S≈ (12,56) — приближённое значение этого числа  с недостатком с точностью до сотых,

или

2)  S≈(12,57) — приближённое значение этого числа  с избытком с точностью до сотых.

Таким образом, используют округление с недостатком и округление с избытком.

Вычисление
значений функции. Пусть дан степенной
ряд функции.
Задача вычисления значения этой функции
заключается в отыскании суммы ряда при
заданном значении аргумента. Ограничиваясь
определенным числом членов ряда, находим
значение функции с точностью, которую
можно установить путем оценивания
остатка числового ряда либо остаточного
члена

формул Тейлора или Маклорена. Если
данный ряд знакопостоянный, то ряд,
составленный из отброшенных членов,
сравнивают с бесконечно убывающей
геометрической прогрессией. В случае
знакочередующегося ряда используется
оценка,
где
—
первый из отброшенных членов ряда.

Пример
1. Вычислить с точностью до 0,0001 значение
ln1,1.

Решение.

Для
вычисления приближённых значений
функции с заданной точностью удобно
пользоваться рядами в том случае, когда
соответствующий ряд является
знакочередующимся; для знакочередующегося
сходящегося ряда легко оценить погрешность
приближённого значения суммы – она
меньше абсолютного значения первого
из отброшенных членов.

1. Возьмём
   ряд для функции ln(1+x):

,

Который
сходится к ln(1+x)
в интервале (-1,1], и, полагая, x=0,1
, получим ряд для вычисления ln1,1
с любой точностью.

Абсолютное
значение четвёртого члена этого ряда
меньше 0,0001. Поэтому, согласно свойству
знакочередующегося сходящегося ряда,
для вычисления приближённого значения
ln1,1
с точностью до 0,0001 достаточно взять
сумму трёх первых членов ряда

.

Точность: 0,001.

В прикладных
задачах важна оценка погрешности
приближения.

Определение:
Точность вычисления не превышает первого
из отброшенных элементов ряда.

1.Оценить
погрешность приближенного равенства

Решение.
Погрешность этого приближенного
равенства определяется суммой членов,
следующих после

в разложении
:

,

или

Заменив каждый
из сомножителей
,…
меньшей величиной
,
получим неравенство

Просуммируем
бесконечно убывающую геометрическую
прогрессию, получим:

,
т.е.

2.Вычислить

с точностью до 0,00001.

Решение. Используя
разложение

в ряд, получаем

.

Определим число

так, чтобы погрешность приближенного
равенства

не превышала
0,00001. Воспользуемся оценкой погрешности,
данной в предыдущем примере. Полагаем
,
тогда:

т.е.
.

Путем подбора
определим, при каком значении

будет выполняться неравенство
.
Пусть
,
тогда
,
т.е.
.
Пусть
,
тогда
,
т.е.
.
Принимаем
.

.

Вычисляем каждое
слагаемое с точностью до 0,000001, для того
чтобы при суммировании не получить
погрешность, превышающую 0,00001. Окончательно
получаем
.

3. Вычислить

с точностью до 0,00001.

Решение. Имеем

.

Получен
знакочередующийся ряд, удовлетворяющий
условиям сходимости признака Лейбница,
поэтому допускаемая погрешность по
абсолютной величине должна быть меньше
первого из отброшенных членов ряда.
Нетрудно видеть, что
,
поэтому первый из отброшенных членов
равен

и
.
Вычисляем сумму и получаем
.

4. Пользуясь
разложением

в ряд, вычислить

с точностью до 0,0001 .

Решение.
.

Достаточно взять
три члена ряда, так как

Тогда

5. Вычислить

с точностью до 0,0001.

Решение.
Воспользуемся разложением

в ряд, полагая
.
Имеем

.

Четвертый и
следующие за ним члены отбрасываем, так
как четвертый член меньше 0,0001. Итак

6. Вычислить

с точностью до 0,001.

Решение. Так
как

является ближайшим к числу 130 кубом
целого числа, то целесообразно число
130 представить в виде суммы двух слагаемых:
.
Тогда

Четвертый член
меньше
,
поэтому его и следующие за ним члены
можно отбросить. Итак,
,
т.е.
.

7. Вычислить
с
точностью до 0,0001.

Решение.
Воспользуемся разложением

в ряд:

,

или
,
откуда

Вычислить
указанную величину приближенно с
заданной степенью точности
,
воспользовавшись разложением в степенной
ряд соответствующим образом подобранной
функции.

8..
Ответ: 3,017.

9.
Ответ: 0,340.

10..
Ответ: 0,84147.

11.
.
Ответ: 1,3956.

12.
,
.
Ответ: 1,140.

13.

Ответ: 0,302.

14.

Ответ: 0,464.

15.

Ответ: 1,0986.

16.,

Ответ: 0,999.

17.

Ответ: 0,3679.

Вычисление
интегралов. Так как степенные ряды
сходятся равномерно на любом отрезке,
лежащем внутри их интервала сходимости,
то с помощью разложений функций в
степенные ряды можно находить
неопределенные интегралы в виде степенных
рядов и приближенно вычислять
соответствующие определенные интегралы.

18. Вычислить
с
точностью

Решение.
Воспользуемся разложением
.
Заменив в нем

на
,
получим ряд
.

Данный ряд
сходится на всей числовой прямой, поэтому
его можно всюду почленно интегрировать.
Следовательно,

,

поскольку уже
третий член полученного знакочередующегося
ряда меньше

19. Найти интеграл
в
виде степенного ряда и указать область
его сходимости.

Решение.
Воспользуемся разложением
,
получим ряд для подынтегральной функции

.

Он сходится на
всей числовой прямой, и, следовательно,
его можно почленно интегрировать:

.

Поскольку при
интегрировании степенного ряда его
интервал сходимости не изменяется, то
полученный ряд сходится также на всей
числовой прямой.

Используя
разложение подынтегральной функции в
степенной ряд, вычислить указанный
определенный интеграл с точностью до
.

20.
.
Ответ: 0,070.

21.
.
Ответ: 0,223.

22.
.
Ответ: 0,162.

23.
.
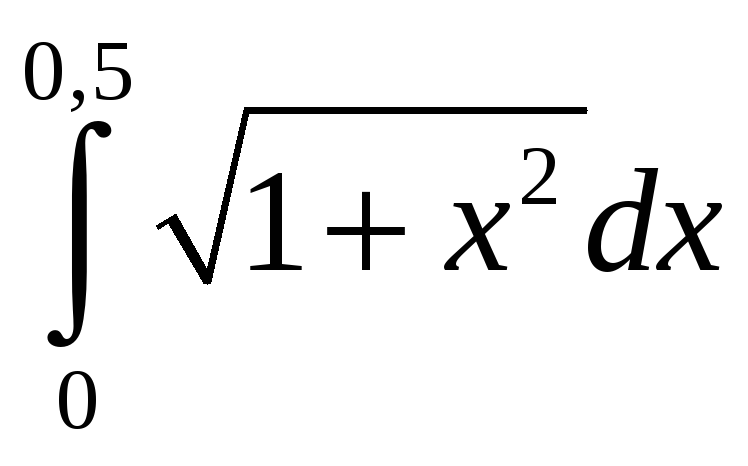
Ответ: 0,480.

24.
.
Ответ: 0,054.

25.
.
Ответ: 0,484.

26.
.
Ответ: 0,487.

27.
.
Ответ: 0,156.

28.
.
Ответ: 0,059.

29.

Ответ: 0,103.

Приближенное
решение дифференциальных уравнений.

В случае, когда
точно проинтегрировать дифференциальное
уравнение с помощью элементарных функций
не удается, его решение удобно искать
в виде степенного ряда, например ряда
Тейлора или Маклорена.

При решении
задачи Коши
,
используется ряд Тейлора
,
где,
а остальные производные
находятся
путем последовательного дифференцирования
уравнения

и подстановки начальных данных в
выражения для этих производных.

Решение задачи
Коши
для
дифференциального уравнения можно
также искать в виде разложения в степенной
ряд

с неопределенными
коэффициентами.

30. Найти пять
первых членов разложения в степенной
ряд решения,
если
.

Решение. Из
данного уравнения находим, что.
Дифференцируем исходное уравнение:

и т.д. Подставляя
найденные значения производных в ряд
Тейлора, получаем

.

31.Найти шесть
первых членов разложения в степенной
ряд решения дифференциального уравнения,
удовлетворяющего начальным условиям
.

Решение. Подставим
в уравнение начальные условия, получим:

Дифференцируя
исходное уравнение, последовательно
находим:

Подставляя найденные
значения производных в ряд Маклорена,
получаем

.

32.Используя ряд

,

записать четыре
первых ненулевых члена разложения в
степенной ряд решения задачи Коши

Решение. В ряде

полагаем
,
с учетом начального условия находим,
что
.
Продифференцируем ряд

и
подставим полученную производную,
а также
в
виде ряда в данное дифференциальное
уравнение. Тогда

+

Теперь в правой и
левой частях последнего равенства
приравняем коэффициенты при одинаковых
степенях разности

(т.е. при
.
Получаем уравнения:

из которых, учитывая,
что
,
находим:

Следовательно,
искомое разложение решения имеет вид

.

Найти разложение
в степенной ряд по степеням

решения дифференциального уравнения
(записать три первых, отличных от нуля,
члена этого разложения

33.

Ответ:
.

34.

Ответ:
.

35.

Ответ:
.

36.

Ответ:
.

37.

Ответ:
.

Методом
последовательного дифференцирования
найти первые

членов разложения в степенной ряд
решения дифференциального уравнения
при указанных начальных условиях.

38.
Ответ:
.

39.

Ответ:
.

40.

Ответ:
.

41.
Ответ:
.

42.

Ответ:
.

Соседние файлы в папке Матан 3 семестр.

• #
• #
• #
• #
• #
• #
• #
• #

Как найти точность приближенного значения

Количественного понятия «точность» в науке не существует. Это качественное понятие. При защите диссертаций говорят только о погрешности (например, измерений). И даже если прозвучало слово «точность», то следует иметь в виду весьма расплывчатую меру величины, обратной погрешности.

Инструкция

Небольшой анализ понятия «приблизительное значение». Возможно, что имеется в виду приблизительный результат вычисления. Погрешность (точность) здесь задает сам исполнитель работы. В таблицах эта погрешность указывается, например «до 10 в минус четвертой степени». Если же погрешность относительная – то в процентах или долях процента. Если вычисления велись на основе числового ряда (чаще всего Тейлора) – на основе модуля остаточного члена ряда.

О приблизительных значениях величин часто говорят как об оценочных их значениях. Результаты измерений случайны. Поэтому это те же случайные величины, обладающие своими характеристиками разброса значений, как та же дисперсия или с.к.о. (среднее квадратичное отклонение). В математической статистике вопросам оценок параметров посвящены целые разделы. При этом различают точечные и интервальные оценки. Последние здесь не рассматриваются. Точечную оценку некоторого параметра λ, подлежащего определению договоримся обозначать λ*. Оценки параметров просто вычисляются по каким-то формулам (статистикам), удовлетворяющим своим требованиям, называемыми критериями качества оценки.

Первый критерий называется несмещенность. Имеется в виду то, что среднее значение (математическое ожидание) оценки λ* равно ее истинному значению, то есть M[λ*]=λ. Об остальных критерия качества говорить пока не стоит. Ими иногда и пренебрегают, обосновывая вопрос тем, что самое главное, чтобы оценка достаточно «слабо» отличалась от истины. Поэтому берется основная характеристика разброса – дисперсия оценки и просто вычисляется. Если исследователь принимает самостоятельное решение, что она достаточно мала, то этим и ограничиваются.

Наиболее часто оценивается среднее значение (математическое ожидание). Это среднее выборочное, вычисляемое, как среднее арифметическое имеющихся результатов наблюдений mx*=(1/n)(x1+x2+ … +xn). Легко показать, что М[mx*]=mx, то есть mx* оценка несмещенная. Дисперсию оценки математического ожидания найдите следуя выкладкам, приведенным на рисунке 1а. Так как истинное значение Dх недоступно, взамен возьмите среднюю выборочную дисперсию (см. рис.1b).

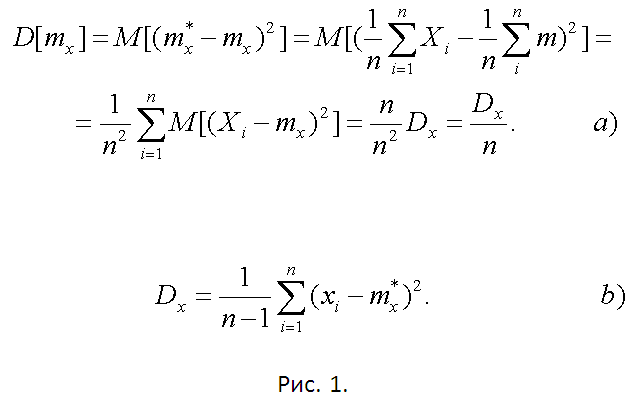
Источники:

• Тихонов В.И. Статистическая радиотехника. – М.: Радио и связь, 1982. – 624 с.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Автор: Софронова Наталия Андреевна,

учитель математики МОУ «Упшинская ООШ»

Оршанского района Республики Марий Эл

( К учебнику Ю.А.Макарычева Алгебра

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

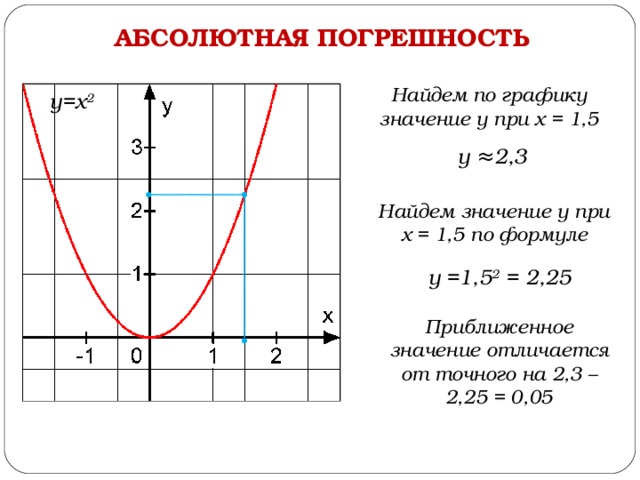
Найдем по графику значение у при х = 1,5

у=х 2

у ≈2,3

Найдем значение у при х = 1,5 по формуле

у =1,5 2 = 2,25

Приближенное значение отличается от точного на 2,3 – 2,25 = 0,05

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

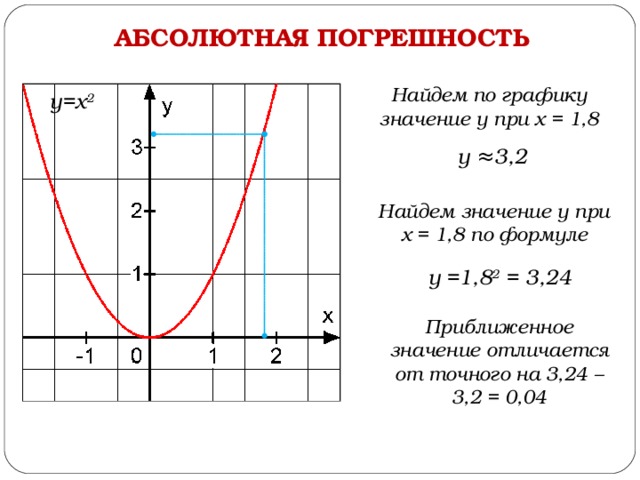
Найдем по графику значение у при х = 1,8

у=х 2

у ≈3,2

Найдем значение у при х = 1,8 по формуле

у =1,8 2 = 3,24

Приближенное значение отличается от точного на 3,24 – 3,2 = 0,04

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

х

1,5

Точное значение у

(по формуле)

1,8

2,25

Приближенное значение у (по графику)

3,24

2,3

3,2

у=х 2

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

у = 2,3 А.П. = |2,25 – 2,3| = |- 0,0 5| = 0,05

у = 3,2 А.П. = |3,24 – 3,2| = | 0,0 4| = 0,04

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

Пример 1 . Старинная русская мера массы пуд равна 16,38. Округлите это значение до целых и найдите абсолютную погрешность приближенного значения.

Решение. 1 6 ,38 ≈ 16

16,38 – точное значение;

16 – приближенное значение.

А.П. = | 16,38 – 16 | = |0 ,38 | = 0, 38

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

Пример 2 . Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков и найдите абсолютную погрешность приближенного значения.

Решение. 10 6 7 ≈ 1070

1067 – точное значение;

1070 – приближенное значение.

А.П. = | 1067 – 1070 | = |-3| = 3

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

Пример 3 . Старинная русская мера длины сажень равна 2,13 м. Округлите это значение до десятых и найдите абсолютную погрешность приближенного значения.

Решение. 2, 1 3 ≈ 2,1

2,13 – точное значение;

2,1 – приближенное значение.

А.П. = | 2,13 – 2,1 | = | 0,03 | = 0,03

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Пример 4 . Представьте дробь в виде бесконечной периодической дроби. Округлите результат до сотых и найдите абсолютную погрешность приближенного значения.

Решение.

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

Всегда ли можно найти абсолютную погрешность ?

АВ ≈ 5,3 см

Найдем длину отрезка АВ

А

В

Точного значения длины отрезка АВ мы определить не можем, поэтому и абсолютную погрешность приближенного значения найти невозможно.

В подобных случаях в качестве погрешности указывают такое число, больше которого абсолютная погрешность быть не может.

В нашем примере в качестве такого числа можно взять число 0,1.

ПОЧЕМУ? Цена деления линейки равна 0,1 см и поэтому абсолютная погрешность приближенного значения 5,3 не больше 0,1.

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

А

В

Говорят, что число 5,3 есть приближенное значение длины отрезка АВ (в санти-метрах) с точностью до 0,1

АВ ≈ 5,3 см

t ≈ 28 0 с точностью до 1

t ≈ 14 0 с точностью до 2

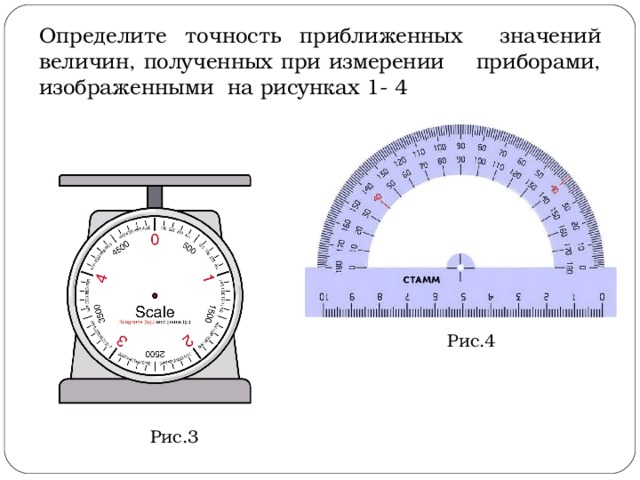
Определите точность приближенных значений величин, полученных при измерении приборами, изображенными на рисунках 1- 4

Рис.2

Рис.1

Определите точность приближенных значений величин, полученных при измерении приборами, изображенными на рисунках 1- 4

Рис.4

Рис.3

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

Говорят, что число 5,3 есть приближенное значение длины отрезка АВ (в сантиметрах) с точностью до 0,1

АВ ≈ 5,3 см

Если х ≈ а и абсолютная погрешность приближенного значения не превосходит некоторого числа h , то число а называют приближенным значением х с точностью до h

х ≈ а с точностью до h

х = а ± h

Длина рулона 10,5 ± 0,5

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

А

В

АВ ≈ 5,3 см

с точностью до 0,1

t ≈ 28 0 с точностью до 1

t ≈ 14 0

с точностью до 2

Определение . Относительной погрешностью (точностью) приближенного значения называется отношение абсолютной погрешности (точности) к модулю приближенного значения

Для оценки качества измерения можно использовать определения относительной погрешности и относительной точности

l = 100,0 ± 0,1

b = 0,4 ± 0,1

ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ

Определение . Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения

Пример 5 . Старинная русская мера массы пуд равна 16,38. Округлите это значение до целых и найдите относительную погрешность приближенного значения.

Решение. 1 6 ,38 ≈ 16

16,38 – точное значение;

16 – приближенное значение.

А.П. = | 16,38 – 16 | = |0 ,38 | = 0, 38

ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ

Определение . Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения

Пример 6 . Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков и найдите относительную погрешность приближенного значения.

Решение. 10 6 7 ≈ 1070

1067 – точное значение;

1070 – приближенное значение.

А.П. = | 1067 – 1070 | = |-3| = 3

ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ

Пример 7 . Представьте дробь в виде бесконечной периодической дроби. Округлите результат до сотых и найдите относительную погрешность приближенного значения.

Решение.