-
Общие сведения о точности размеров
Долговечность
и надежность работы деталей узлов машин
в значительной степени зависит от их
точности.
Точность
детали – это степень приближения формы
детали к геометрически правильному ее
прототипу.
За
меру точности принимают значения
допусков и отклонений от теоретических
значений показателей точности, которыми
она характеризуется.
Стандартами
установлены следующие показатели
точности:
-
точность
размеров, т.е. расстояний между различными
элементами детали и сборочных единиц; -
отклонение
формы, т.е. отклонение формы реальной
поверхности от номинальной поверхности; -
отклонения
от правильного взаимного расположения
поверхностей деталей и их осей.
-
Понятие о допуске
Точность
размеров обработанной детали
характеризуется допуском Т, который
представляет собою разность между
наибольшим и наименьшим предельно
допустимыми размерами:
Т=Нб –
Нм
Различают
номинальный, действительный и предельно
допустимые наибольший и наименьший
размеры.
Номинальный
размер (Нр) указывают на чертежах. Его
находят расчетом детали на прочность
и жесткость, а затем округляют в большую
сторону в соответствии со стандартными
значениями. Номинальный размер служит
началом отсчета отклонений. Относительно
номинального размера определяются
предельно допустимые размеры.
Предельно
допустимые размеры детали, наибольший
(Нб) и наименьший (Нм). Между ними находится
действительный размер годной детали.
Действительный
размер (Др) устанавливается измерением
с допускаемом погрешностью.
Предельные
отклонения от номинального размера:
Верхнее
отклонение (ВО) – алгебраическая разность
между наибольшим предельным размером
и номинальным размером.
Нижнее
отклонение (НО) – алгебраическая разность
между наименьшим предельным размером
и номинальным размером.
Действительное
отклонение – это алгебраическая разность
между действительным и номинальным
размерами.
Формулы
для расчета:
Нб=НрВО
– наибольший предельно допустимый
размер
Нм=НрНО
– наименьший предельно допустимый
размер
Допуск
– всегда величина положительная. Чем
меньше допуск, тем выше точность размера.
С увеличением допуска Т качество изделий
ухудшается, но стоимость изготовления
уменьшается.
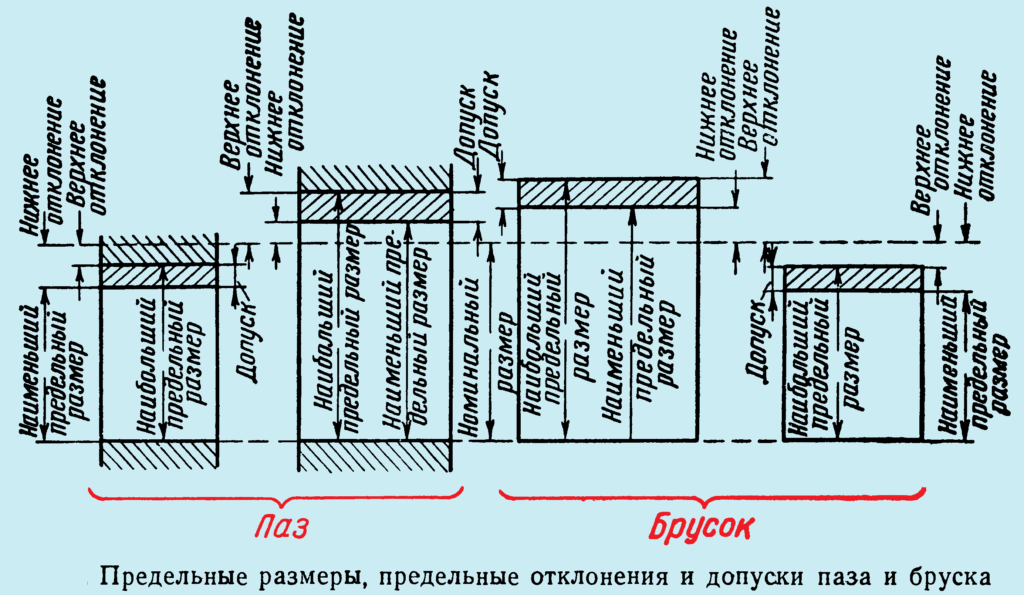
Допуски
можно изображать графически в виде
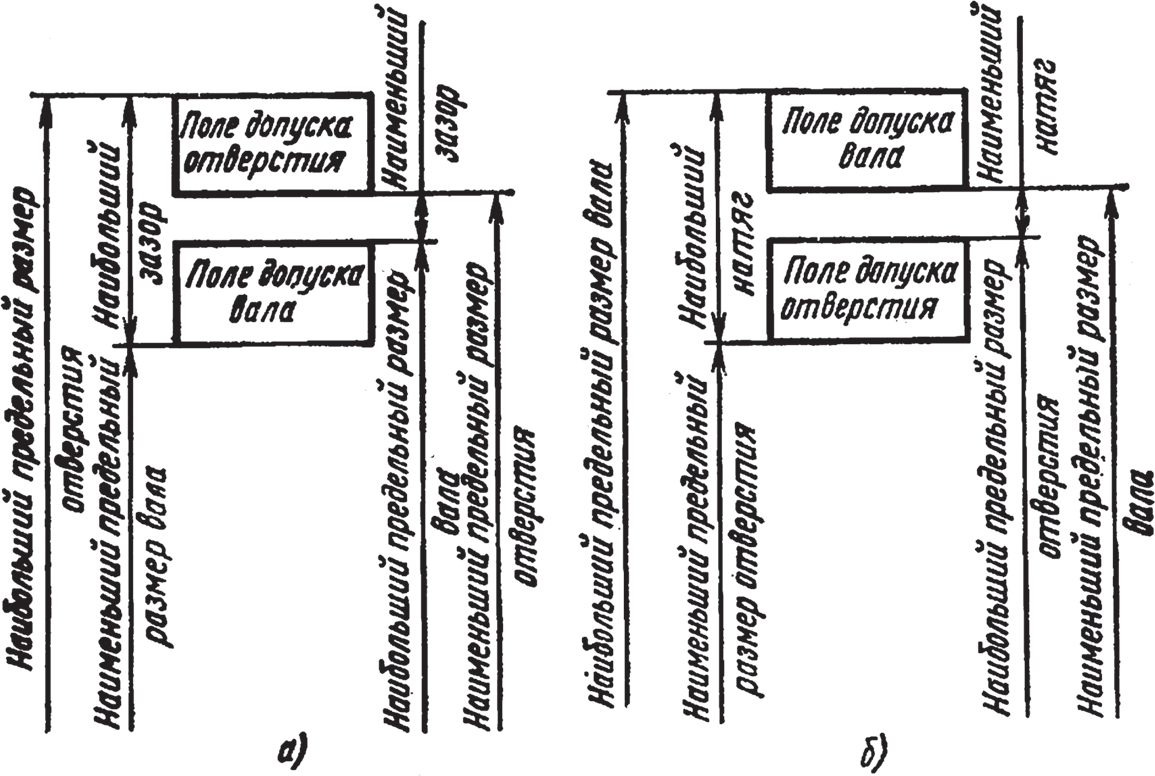
полей допусков, как указано на рис. 17.
Поле
допуска – это поле, ограниченное верхним
и нижним отклонениями.
Допуск
определяет допускаемое поле рассеяния
действительных размеров годных деталей,
т.е. заданную точность изготовления.
+BO
отверстие
г)
+HO
+BO
+BO
б)
0
0
HO=0
BO=0
в)
-HO
-BO
-HO
д)
-HO
вал
-
Расположение
полей допусков относительно номинального
размера.
Пояснения к
рис.17:
00
– нулевая линия, соответствующая
номинальному размеру (Нр); выше нулевой
линии отклонения положительные, ниже
– отрицательные.
Ось изделия не
показана, она всегда располагается под
схемой.
Рисунок
поясняет расположение полей допусков
как для отдельно взятых деталей типа
вал и типа втулка, так и при образовании
ими соединения, когда вал входит в
отверстие втулки.
Для
деталей, составляющих соединение,
номинальный размер является общим.
В
соединении деталей, входящих одна в
другую, различают охватывающие и
охватываемые поверхности.
Вал
– термин для наружных(охватываемых)
поверхностей деталей.
Отверстие – термин
для внутренних (охватывающих) поверхностей
деталей.
Понятие – основной
вал, для которого ВО=0 (рис.1,в)
Понятие – основное
отверстие, для которого НО=0 (рис.1,б)
Допуск
вала – Тd,
Допуск отверстия
–TD.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Download Article
Download Article
Precision means that a measurement using a particular tool or implement produces similar results every single time it is used. For example, if you step on a scale five times in a row, a precise scale would give you the same weight each time. In math and science, calculating precision is essential to determine if your tools and measurements work well enough to get good data. You can report precision of any data set using the range of values, the average deviation, or the standard deviation.
-
1
Determine the highest measured value. It helps to begin by sorting your data in numerical order, from lowest to highest. This will ensure that you do not miss any values. Then select the value at the end of the list.[1]
- For example, suppose you are testing the precision of a scale, and you observe five measurements: 11, 13, 12, 14, 12. After sorting, these values are listed as 11, 12, 12, 13, 14. The highest measurement is 14.
-
2
Find the lowest measured value. Once your data has been sorted, finding the lowest value is as simple as looking at the beginning of the list.[2]
- For the scale measurement data, the lowest value is 11.
Advertisement
-
3
Subtract the lowest value from the highest. The range of a set of data is the difference between the highest and lowest measurements. Just subtract one from the other. Algebraically, the range can be expressed as:
-
4
Report the range as the precision. When reporting data, it is important to let the readers know what you have measured. Because there are different measures of precision, you should specify what you are reporting. For this data, you would report Mean=12.4, Range=3, or simply that the Mean=12.4±3.[3]
- The mean is not actually part of calculating the range or precision, but it is generally the primary calculation for reporting the measured value. The mean is found by adding up the sum of the measured values and then dividing by the number of items in the group. For this set of data, the mean is (11+13+12+14+12)/5=12.4.
Advertisement
-
1
Find the mean of the data. The average deviation is a more detailed measure of the precision of a group of measurements or experiment values. The first step in finding the average deviation is to calculate the mean of the measured values. The mean is the sum of the values, divided by the number of measurements taken.[4]
- For this example, use the same sample data as before. Assume that five measurements have been taken, 11, 13, 12, 14, and 12. The mean of these values is (11+13+12+14+12)/5=12.4.
-
2
Calculate the absolute deviation of each value from the mean. For this calculation of precision, you need to determine how close each value is to the mean. To do this, subtract the mean from each number. For this measurement, it does not matter whether the value is above or below the mean. Subtract the numbers and just use the positive value of the result. This is also called the absolute value.[5]
- Algebraically, the absolute value is shown by placing two vertical bars around the calculation, as follows:
- For the values of this sample data set, the absolute deviations are:
-
3
Find the average deviation. Use the absolute deviations and find their mean. As you did with the original data set, you will add them together and divide by the number of values. This is represented algebraically as:[6]
- For this sample data, the calculation is:
-
4
Report the precision result. This result may be reported as the mean, plus or minus the average deviation. For this sample data set, this result would look like 12.4±0.88. Note that reporting precision as the average deviation makes the measurement appear much more precise than with the range.[7]
Advertisement
-
1
Use the correct formula for standard deviation. For any size data set, the standard deviation is a reliable statistic for reporting precision. There are two formulas for calculating standard deviation, with a very slight difference between them. You will use one formula if your measured data represents an entire population. You will use the second formula if your measured data is from only a sample of the population.[8]
-
2
Find the mean of the data values. As with calculating the average deviation, you will begin by finding the mean of the data values.[9]
- Using the same set of measurements as above, the mean is 12.4.
-
3
Find the square of each variation. For each data point, subtract the data value from the mean, and square that result. Because you are squaring these variations, whether the difference is positive or negative does not matter. The square of the difference will always be positive.[10]
- For the five data values in this sample, these calculations are as follows:
-
4
Calculate the sum of the squared differences. The numerator of the standard deviation fraction is the sum of the squared differences between each value and the mean. To find this sum, add together the figures from the previous calculation.[11]
- For the sample data set, these are:
- For the sample data set, these are:
-
5
-
6
Find the square root of the result. At this point, the calculation represents what is called the variance of the data set. The standard deviation is the square root of the variance. Use a calculator to find the square root, and the result is the standard deviation.[13]
-
7
Report your result. Using this calculation, the precision of the scale can be represented by giving the mean, plus or minus the standard deviation. For this data, this will be 12.4±1.14.
- The standard deviation is perhaps the most common measurement of precision. Nevertheless, for clarity, it is still a good idea to use a footnote or parentheses to note that the precision value represents the standard deviation.
Advertisement
-
1
Use the word precision correctly. Precision is a term that describes the level of repeatability of measurements. When collecting a group of data, either by measurement or through an experiment of some kind, the precision describes how close together the results of each measurement or experiment are going to be.[14]
- Precision is not the same as accuracy. Accuracy measures how close experimental values come to the true or theoretical value, while precision measures how close the measured values are to each other.
- It is possible for data to be accurate but not precise or to be precise but not accurate. Accurate measurements are close to the target value but may not be close to each other. Precise measurements are close to each other, whether or not they are close to the target.
-
2
Choose the best measure of precision. The word “precision” does not have a single meaning. You can represent precision using several different measurements. You need to decide the best one.
- Range. For small data sets with about ten or fewer measurements, the range of values is a good measure of precision. This is particularly true if the values appear reasonably closely grouped. If you see one or two values that appear far from the others, you may wish to use a different calculation.
- Average deviation. The average deviation is a more accurate measure of precision for a small set of data values.[15]
- Standard deviation. The standard deviation is perhaps the most recognized measure of precision. Standard deviation may be used to calculate the precision of measurements for an entire population or a sample of the population.
-
3
Report your results clearly. Very often, investigators will report data by giving the mean of the measured value, followed by a statement of the precision. The precision is shown with a “±” symbol. This provides an indication of precision, but it does not clearly explain to the reader if the number following the “±” symbol is a range, standard deviation, or some other measurement. To be very clear, you should define what measure of precision you are using, either in a footnote or parenthetical note.
- For example, for one series of data, the result could be reported as 12.4±3. However, a more explanatory way to report the same data would be to say “Mean=12.4, Range=3.”
Advertisement
Add New Question
-
Question
How do you measure accuracy?
Accuracy is a measure of how close you are to the known, expected value of what you are measuring. If you have a known weight of 10 kg, for example, and you put it on a scale and the scale says «9.2,» then your scale is accurate within 0.8 kg.
-
Question
How do I calculate the level of precision of an equipment? It’s an electrolyte analyser
Use it to take several measurements and then follow the directions in this article.
-
Question
How do you know if a measurement is precise?
When the mean absolute deviation or the standard range is as close to zero as possible.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If one of your trial values is much higher or lower than the rest of your values, do not exclude this number from your calculations. Even if it was a mistake, it is data and should be utilized for a proper calculation.
-
In this article, only five values were used for mathematical simplicity. In an actual experiment, you should perform more than five trials to achieve a more accurate calculation. The more trials you run, the closer you will get to a clear precision value.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate precision using a range of values, start by sorting the data in numerical order so you can determine the highest and lowest measured values. Next, subtract the lowest measured value from the highest measured value, then report that answer as the precision. When reporting precision data, be sure to specify what you measured and what you’re reporting, such as the range or mean! For tips on calculating average and standard deviation, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 545,505 times.
Reader Success Stories
-
«Thanks a lot. Before I read this article, all my work was without organization. From now on I’ll apply your…» more
Did this article help you?
Содержание страницы
- 1. Общие сведения о единой системе допусков и посадок
- 2. Указание на чертежах допусков размеров
- 3. Допуски формы и расположения поверхностей деталей
- 4. Отклонения и допуски расположения
- 5. Указание на чертежах допусков точности деталей
1. Общие сведения о единой системе допусков и посадок
При изготовлении деталей из заготовок необходимо выдерживать определенные геометрические параметры поверхностей — их размеры, форму и относительное расположение. Степень приближения истинного значения рассматриваемого параметра к его теоретическому значению называется точностью.
Размер – это числовое значение линейной величины (диаметра, длины и т.д.), который в машиностроении измеряют в миллиметрах. Размеры подразделяют на номинальные, действительные и предельные.
Номинальный – это размер, относительно которого определяются предельные размеры и который служит также началом отсчета отклонений. Номинальный размер — это основной размер, полученный на основе кинематических, динамических и прочностных расчетов или выбранный из конструктивных, технологических, эксплуатационных, эстетических и других соображений. Номинальные размеры можно классифицировать по назначению на определяющие величину и форму детали, координирующие и сборочные (монтажные). Кроме того, из соображений удобства и точности обработки иногда вводятся технологические размеры. Это тот теоретический размер, к которому как можно ближе должен соответствовать размер готовой детали.
Действительный – это размер, установленный измерением с допустимой погрешностью.
Чтобы изделие считалось годным, т.е. отвечало своему целевому назначению, его действительный размер должен быть выдержан между двумя теоретически допустимыми предельными размерами, разность которых образует допуск. Наибольший предельный размер — это больший из двух предельных, наименьший — это меньший из двух предельных размеров.
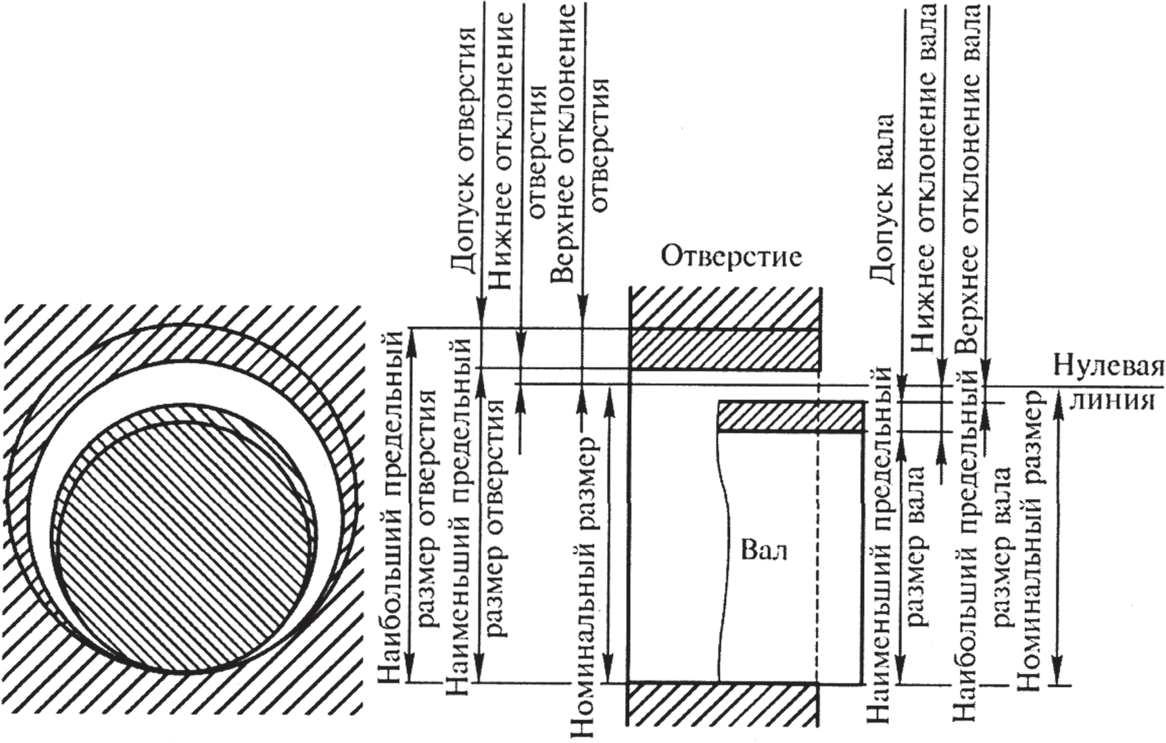
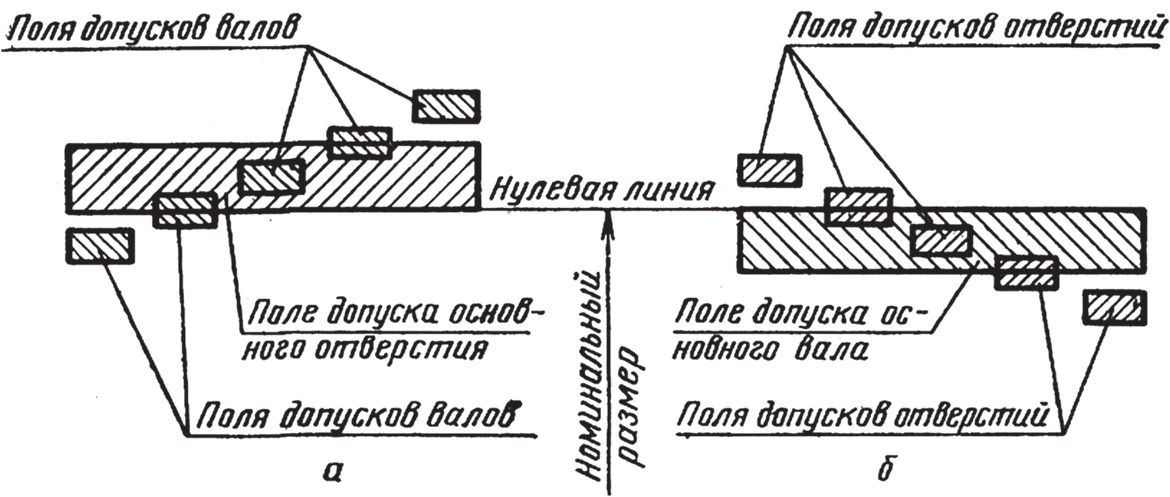
Для удобства указывают номинальный размер детали, а каждый из двух предельных размеров определяют по его отклонению от этого номинального размера (рис. 1). Абсолютную величину и знак отклонения получают вычитанием номинального размера из соответствующего предельного размера.
Рис. 1. Формирование отклонений для вала и отверстия относительно нулевой линии номинального размера
Отклонение – это алгебраическая разность между размером (действительным, предельным и т. д.) и соответствующим номинальным размером.
Действительное отклонение — это алгебраическая разность между действительным и номинальным размерами.
Предельное отклонение – это алгебраическая разность между предельным и номинальным размерами. Предельные отклонения подразделяют на верхнее и нижнее.
Верхнее отклонение – это алгебраическая разность между наибольшим предельным и номинальным размерами; нижнее отклонение – это алгебраическая разность между наименьшим предельным и номинальным размерами. Верхнее и нижнее отклонения приводятся в справочных таблицах и измеряются в микрометрах (мкм), а на чертежах указываются в миллиметрах (мм).
Классификацию отклонений по геометрическим параметрам целесообразно рассмотреть на примере соединения вала и отверстия. Термин «вал» применяют для обозначения наружных (охватываемых) элементов деталей, термин «отверстие» — для обозначения внутренних (охватывающих) элементов деталей. Термины «вал» и «отверстие» относят не только к цилиндрическим деталям круглого сечения, но и к элементам деталей другой охватываемой и охватывающей формы (например, ограниченным двумя параллельными плоскостями — шпоночное соединение).
Допуск — это разность между наибольшим и наименьшим предельными размерами или абсолютная величина алгебраической разности между верхним и нижним отклонениями.
Квалитет (степень точности) — совокупность допусков, соответствующих одинаковой степени точности для всех номинальных размеров.
Нулевая линия — это линия, соответствующая номинальному размеру, от которой откладываются отклонения размеров при графическом изображении допусков и посадок. При горизонтальном расположении нулевой линии положительные отклонения откладываются вверх от нее, а отрицательные — вниз.
Поле допуска — это поле, ограниченное верхним и нижним отклонениями. Поле допуска определяется величиной допуска и его положением относительно номинального размера. При графическом изображении поле допуска заключено между двумя линиями, соответствующими верхнему и нижнему отклонениям относительно нулевой линии.
Основное отклонение – одно из двух отклонений (верхнее или нижнее), ближайшее к нулевой линии, используемое для определения положения поля допуска относительно нулевой линии. Основное отверстие — это отверстие, нижнее отклонение которого равно нулю. Основной вал — это вал, верхнее отклонение которого равно нулю.
В зависимости от взаимного расположения полей допусков отверстия и вала различают посадки с зазором, с натягом и переходные, когда возможно получение как зазора, так и натяга (рис. 2).
Рис. 2. Типы посадок: а — с зазором; б — с натягом
Номинальным размером посадки называется номинальный размер, общий для отверстия и вала, составляющих соединение. Зазором называется разность размеров отверстия и вала, если размер отверстия больше размера вала.
Посадка с зазором — это посадка, при которой обеспечивается зазор в соединении (поле допуска отверстия расположено над полем допуска вала). К посадкам с зазором относятся также посадки, в которых нижняя граница поля допуска отверстия совпадает с верхней границей поля допуска вала. Поскольку идеально точное изготовление деталей невозможно, то невозможно получить в соединении один и тот же по величине зазор. В связи с этим назначаются два предельных значения — наименьший и наибольший зазоры, между которыми должен находиться зазор в соединении по выбранной посадке.
Натягом называется разность размеров вала и отверстия до сборки, если размер вала больше размера отверстия.
Посадка с натягом — это посадка, при которой обеспечивается натяг в соединении. Поле допуска отверстия расположено под полем допуска вала.
Если после назначения экономически целесообразных допусков на обработку вала и отверстия оказывается, что их поля допусков перекрываются частично или полностью, то такие соединения относят к переходным посадкам.
Переходная посадка — это посадка, при которой возможно получение как зазора, так и натяга.
Для оценки точности соединений (посадок) пользуются понятием «допуск посадки», под которым понимают сумму допусков отверстия и вала, составляющих соединение.
При соединении двух деталей (отверстие и вал) образуется посадка, определяемая разностью их размеров до сборки, т.е. величиной получающихся зазоров или натягов в соединении. Посадка характеризует свободу относительного перемещения соединяемых деталей или степень сопротивления их взаимному смещению.
Различают две равноценные системы образования посадок — система отверстия и система вала (рис. 3).
Рис. 3. Примеры посадок в системах: а — отверстия; б — вала
Посадки в системе отверстия – это посадки, у которых различные зазоры и натяги получаются соединением различных валов с основным отверстием. У основного отверстия нижнее отклонение равно нулю или наименьший предельный размер его совпадает с номинальным размером соединения, а верхнее зависит от квалитета.
Посадки в системе вала – это посадки, у которых различные зазоры и натяги получаются соединением различных отверстий с основным валом. У основного вала верхнее отклонение равно нулю или наибольший предельный размер совпадает с номинальным размером соединения, а нижнее зависит от квалитета.
2. Указание на чертежах допусков размеров
Прежде чем назначить предельные отклонения размерам на чертежах определяют характер соединения, возможности ремонта, условия эксплуатации и др.
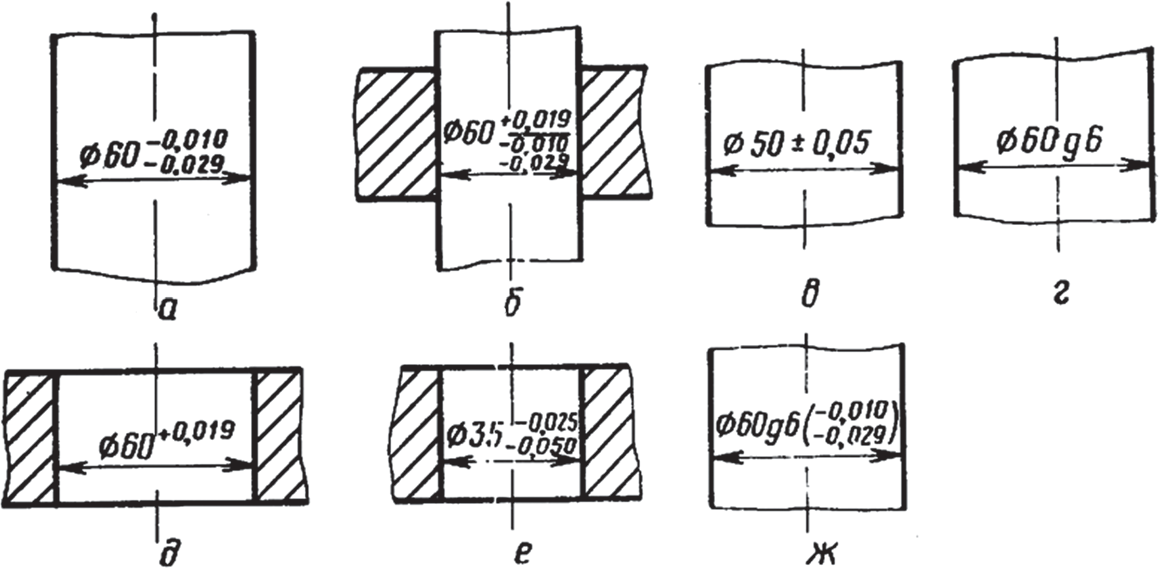
Предельные размеры с помощью предельных отклонений указывают на чертежах с помощью таблиц несколькими способами:
- числовыми величинами (рис. 4, а), причем отклонение, равное нулю, опускается (рис. 4, д), а одинаковые по абсолютной величине, но противоположные по знаку отклонения указывают один раз со знаками ± (рис. 4, e);
- условными (символическими) обозначениями полей допусков и посадок согласно стандартам (рис. 4, г);
- символическими условными обозначениями полей допусков с указанием справа в скобках их числовых величин (рис. 4, ж).
Рис. 4. Нанесение предельных (верхнего и нижнего) отклонений на чертежах
Предельные отклонения размеров деталей, изображенных на чертеже в сборе, указывают также одним из трех перечисленных способов в виде дроби: в числителе представляют предельные отклонения отверстия, в знаменателе — вала (рис. 4, б). На рис. 4, г символ g6 обозначает поле допуска, т.е. два отклонения: верхнее отклонение — 0,010 и нижнее — 0,029 мм. В обозначениях положительных предельных отклонений знак «+» опускать нельзя. Предельные отклонения записывают до последней значащей цифры включительно, выравнивая количество знаков в верхнем и нижнем отклонении добавлением нулей (рис. 4; а,б,е,ж).
Буквенный способ обозначения полей допуска предпочтителен в случае применения предельных калибров для измерения размеров на производстве, так как на калибрах, как правило, маркируются буквенные обозначения полей допусков контролируемых деталей.
Числовые обозначения удобнее при работе на универсальных металлообрабатывающих станках и при контроле изделий универсальными средствами измерений. Смешанные обозначения применяют при неопределенности вопроса о средствах контроля, которые будут использованы на производстве.
3. Допуски формы и расположения поверхностей деталей
В процессе механической обработки деталей под действием сил резания, а также в процессе эксплуатации машины под нагрузкой происходит деформация деталей. В результате нежесткости центров токарного станка или самой заготовки и других причин после обработки деталь может иметь бочкообразный, седлообразный или конусный профиль, т.е. иметь погрешность формы, или иметь радиальное биение наружной поверхности относительно линии центров, т.е. иметь погрешность расположения наружной поверхности относительно осевой линии.
В основу нормирования и систему отсчета отклонений формы и расположения поверхностей положен принцип прилегающих поверхностей и профилей, элементов, деталей, сборочных единиц (узлов).
Под элементом понимается поверхность (часть поверхности, плоскость симметрии нескольких поверхностей), профиль поверхности, линия пересечения двух поверхностей, ось поверхности или сечения (точка пересечения линии, линии и поверхности, центр окружности или сфера).
Различают следующие основные виды прилегающих поверхностей, плоскостей и профилей: номинальная (идеальная) поверхность, номинальная форма, которая задана чертежом или другой технической документацией, и реальная поверхность, ограничивающая деталь и отделяющая ее от окружающей среды.
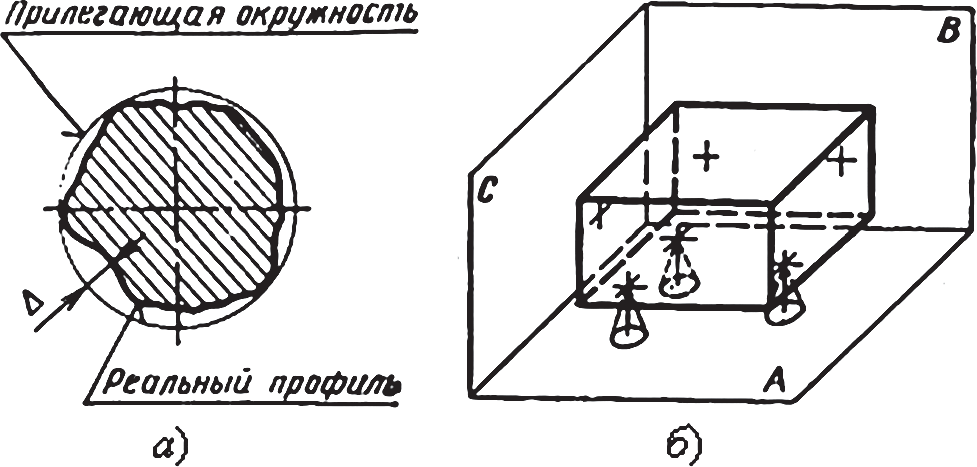
Профиль — это линия пересечения поверхности с плоскостью или заданной поверхностью. Различают профили номинальной и реальной поверхностей. Прилегающая плоскость и прилегающая прямая — плоскость или прямая, соприкасающаяся с реальной поверхностью или профилем и расположенная вне материала детали так, чтобы отклонение от ее наиболее удаленной точки соответственно реальной поверхности или профиля в пределах нормируемого участка имело минимальное значение (рис. 5, а).
Рис. 5. Номинальные профиль и поверхности: а — прилегающая окружность; б — комплект баз
Нормируемый участок — это участок поверхности или линии, к которому относится допуск или отклонение формы или расположение элемента. Нормируемый участок должен задаваться размерами, определяющими его площадь, длину или угол сектора (в полярных координатах). Если нормируемый участок не задан, то допуск или отклонение формы или расположения должен относиться ко всей поверхности или длине рассматриваемого элемента.
Прилегающая окружность — это окружность минимального диаметра, описания вокруг реального профиля наружной поверхности вращения, или минимального диаметра, вписанная в реальный профиль внутренней поверхности вращения (рис. 5, а).
База — элемент детали (или выполняющее ту же функцию сочетание элементов), определяющий одну из плоскостей или осей системы координат, по отношению к которой задается допуск расположения или определяется отклонение расположения рассматриваемого элемента. Базами могут быть, например, базовая плоскость, базовая ось, базовая плоскость симметрии.
Комплект баз — совокупность двух или трех баз, образующих систему координат, по отношению к которой задается допуск расположения или определяется отклонение расположения рассматриваемого элемента. Базы, образующие комплект баз, различают в порядке убывания числа степеней свободы, лишаемых ими (например, на рис. 5, б база А лишает деталь трех степеней свободы, база В – двух, а база С – одной степени свободы).
Отклонение формы определяется как сумма абсолютных значений наибольших отклонений точки от реальной поверхности, расположенных по обе стороны от средней поверхности. Такой способ оценки получил применение в ряде современных измерительных средств. Разница между отклонениями формы, определенными относительно прилегающей и средней поверхности, практически незначительна.
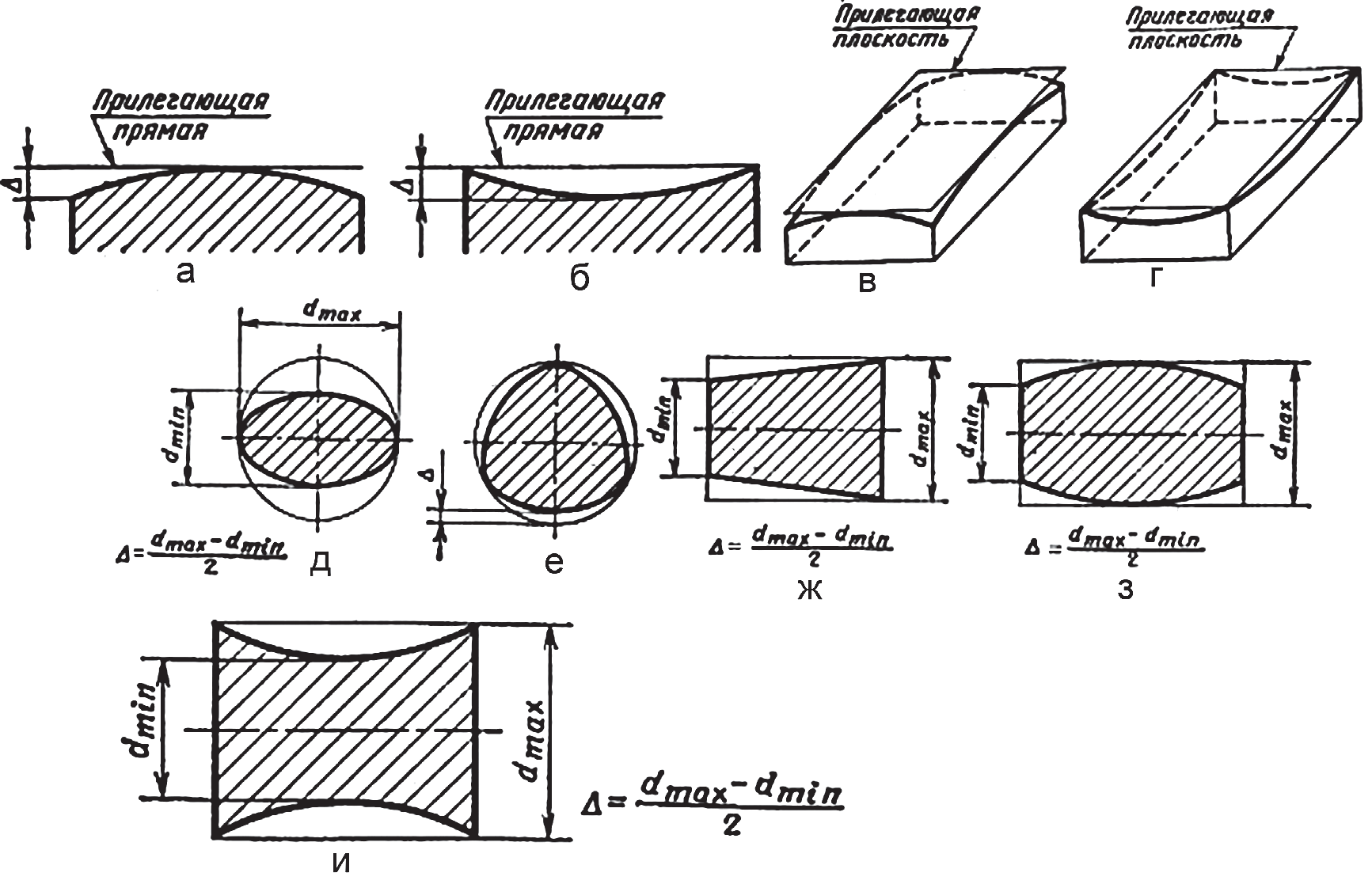
К отклонениям и допускам формы относятся (рис. 6):
- отклонение от прямолинейности в плоскости и допуск. Частными видами отклонения от прямолинейности являются выпуклость и вогнутость;
- отклонение от прямолинейности оси (или линии) в пространстве и допуск (рис. 6; а, б);
- отклонение от плоскостности и допуск. Частными видами отклонений от плоскостности являются выпуклость и вогнутость (рис. 6; в, г);
- отклонение от круглости и допуск. Частными видами отклонений от круглости являются овальность и огранка (рис. 6; д, е);
- отклонение от цилиндричности и допуск;
- отклонение и допуск профиля продольного сечения цилиндрической поверхности. Частными видами отклонения профиля продольного сечения являются конусообразность, бочкообразность и седлообразность (рис. 6; ж, з, и).
Рис. 6. Отклонения и допуски формы поверхностей изделия
Применять частные виды отклонений — выпуклость, вогнутость, огранку, овальность, конусообразность, бочкообразность, седлообразность для их нормирования следует лишь в обоснованных случаях, когда для обеспечения правильного функционирования изделия важно учитывать и характер отклонения формы.
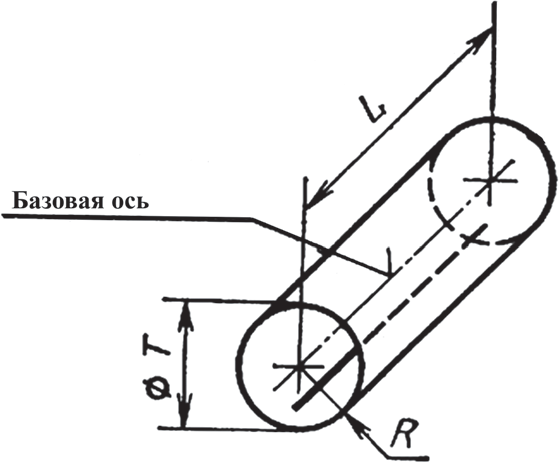
Рис. 7. Поле допуска на соосность
4. Отклонения и допуски расположения
В реальных поверхностях отклонения формы и расположения всегда сочетаются. В работе и при измерениях эти отклонения могут проявляться или раздельно, или совместно. Поэтому установлены собственно отклонения и допуски расположения, предполагающие исключение из рассмотрения отклонений формы путем замены реальных поверхностей прилегающими, и суммарные отклонения и допуски формы и расположения.
Отклонения расположения и допуски определяются относительно баз. Отклонения формы и расположения отдельных баз комплекта могут вызвать неоднозначную оценку геометрических отклонений других поверхностей. Поэтому при назначении комплекта баз важно задать последовательность их выбора, которая должна устанавливаться в порядке убывания числа степеней свободы детали, отнимаемых базами.
Введенный допуск на наклон позволяет нормировать отклонения от любого номинального угла (кроме 0 и 90°) методом, аналогичным методу нормирования допусков на параллельность и перпендикулярность, т.е. в линейной мере.
Допуски на соосность, симметричность, пересечение осей, позиционный допуск можно задавать либо предельным значением отклонения в радиусном выражении, либо диаметром (шириной) поля допуска, что соответствует удвоенному предельному отклонению (допуски в диаметральном выражении). Оба способа выражения допуска показаны на рис. 7 на примере поля допуска на соосность (Т — допуск в диаметральном, R = T/2 — допуск в радиальном выражении).
5. Указание на чертежах допусков точности деталей
На чертежах изделий, как правило, предпочтение отдается условным обозначениям допусков, а не текстовым записям (табл. 1). Записи рекомендуется в основном применять для текстовой документации или в случаях, когда вид допуска или базирования не может быть выражен условным обозначением.
Таблица 1. Условные обозначения допусков
| Группа допусков | Вид допуска | Знак |
| Допуск формы | Допуск прямолинейности | |
| Допуск плоскостности | ||
| Допуск круглости | ||
| Допуск цилиндричности |  |
|
| Допуск профиля продольного сечения | ||
| Допуск расположения | Допуск параллельности | |
| Допуск перпендикулярности | ||
| Допуск наклона | ||
| Допуск соосности |  |
|
| Допуск симметричности | ||
| Позиционный допуск | ||
| Допуск пересечения осей | ||
| Суммарные допуски формы и расположения | Допуск радиального биения Допуск торцового биения
Допуск биения в заданном направлении |
 |
| Допуск полного радиального биения
Допуск полного торцового биения |
 |
|
| Допуск формы заданного профиля | ||
| Допуск формы заданной поверхности |
Опыт применения условных обозначений показал, что они удобны, наглядны, упрощают оформление документации, позволяют избежать разнобоя в текстовых формулировках.
При условном обозначении данные о допусках формы и расположении поверхностей указывают в прямоугольной рамке, разделенной на две части и более (рис. 8), в которых помещают (слева направо): в первой — знак допуска по табл. 1, во второй — числовое значение допуска в миллиметрах, в третьей и последующих — буквенное обозначение базы (баз).
Рис. 8. Указание допусков
Перед числовым значением допуска, который можно задать в радиусном или диаметральном выражениях, должен проставляться символ, указывающий способ выражения. Для допусков в диаметральном выражении применяют символ ø при указании допусков соосности и прецизионных (если поле позиционного допуска круговое или цилиндрическое) — рис. 8, а или символ Т при указании допусков симметричности, пересечения осей, формы заданного профиля и заданной поверхности, позиционного допуска (если поле позиционного допуска ограничено двумя параллельными прямыми или плоскостями) — рис. 8, в. Символ ø применяют также при указании цилиндрических полей допусков прямолинейности, параллельности, перпендикулярности и наклона осей. Для допусков в радиусном выражении используют соответственно символы R или Т/2 (рис. 8; б, г).
Если поле допуска сферическое, пишется слово «сфера» и соответственно символы 0 или Р (рис. 8, д).
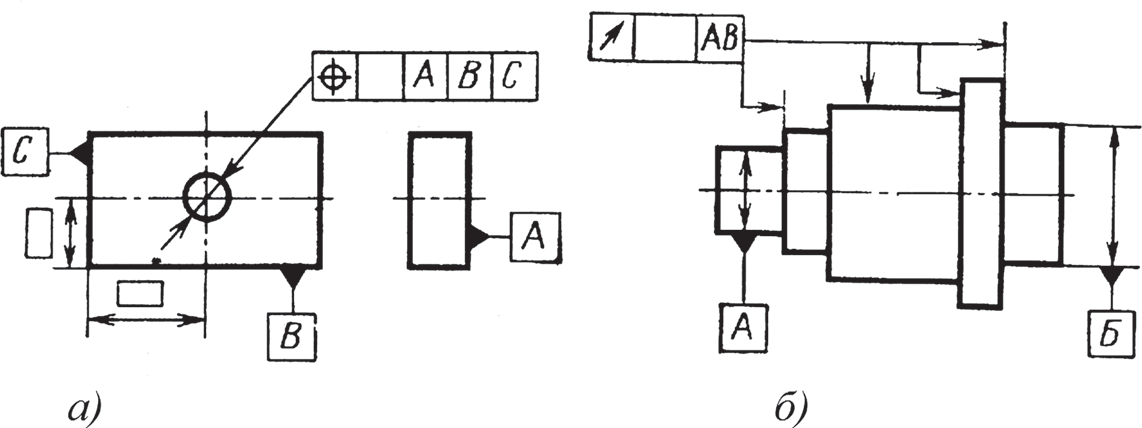
Существует правило базирования и указания баз в машиностроении. Буквенные обозначения каждого базового элемента вносятся слева направо в отдельное поле рамки (третье, четвертое и т.д.) в порядке убывания числа степеней свободы детали (например, на рис. 9, а база А лишает деталь трех, база В — двух, а база С — одной степени свободы).
Рис. 9. Обозначение баз: а — буквенное; б — объединенных баз
Если же два или несколько элементов образуют объединенную базу и их последовательность не имеет значения (например, они образуют общую ось), то их буквенные обозначения вписывают вместе в третье поле рамки (рис. 9, б).
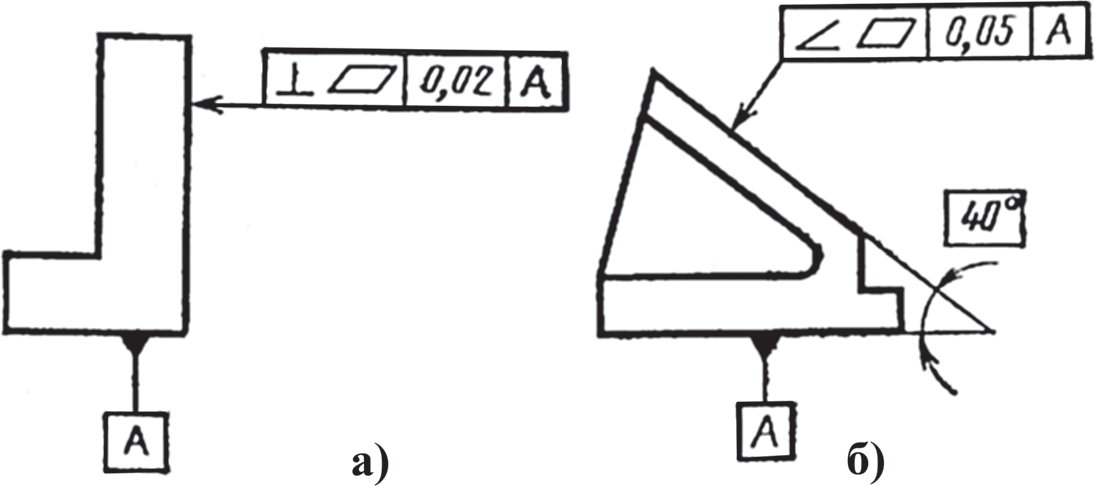
Суммарные допуски формы и расположения поверхностей, для которых не установлены отдельные графические знаки, обозначают знаками составных допусков в такой последовательности: знак допуска расположения, знак допуска формы. Например, рис. 10, а — знак суммарного допуска перпендикулярности и плоскостности поверхности относительно основания 0,02 мм, рис. 10, б — знак суммарного допуска наклона и плоскостности поверхности относительно основания 0,05 мм.
Рис. 10. Суммарные допуски
Отклонения размеров и других параметров готовой детали от указанных в чертеже определяют погрешность обработки, величина которой должна находиться в пределах допуска.
Погрешности подразделяют на систематические и случайные. К систематическим относятся погрешности, которые при обработке партии деталей повторяются на каждой детали. Систематические погрешности по величине больше случайных и определяют точность обрабатываемой детали.
Основными причинами систематических погрешностей обработки являются:
- неточность станка (например, непрямолинейность направляющих станины или неперпендикулярность направляющих оси шпинделя, неточность изготовления шпинделя и его опор и т.д.);
- деформация сборочных единиц (узлов) и деталей станка под действием сил резания и нагрева в процессе работы;
- неточность изготовления режущих инструментов, приспособлений и их износ;
- деформация инструментов и приспособлений под действием сил резания и нагрева в процессе обработки;
- погрешности установки и базирования заготовки на станке;
- деформация обрабатываемой заготовки под действием сил резания и зажима, а также из-за нагрева в процессе обработки;
- погрешности, возникающие при установке инструментов и их настройке на размер;
- погрешности в процессе измерения, вызываемые неточностью измерительных инструментов и приборов, их износом и деформациями, а также ошибкой рабочего при оценке показаний измерительных устройств.
Причины, вызывающие систематические погрешности, можно установить и устранить.
К случайным, непредвиденным относятся погрешности, возникающие вследствие случайных упругих деформаций заготовки, станка, приспособления и режущего инструмента (например, из-за неоднородности обрабатываемого материала).
Точность размеров деталей, производимых литьем под давлением, должна рассматриваться в нескольких аспектах. В первую очередь, с позиции требований, которые гарантируют нормальное функционирование механизмов пресс-формы, а во вторую – с точки зрения технологической возможности достижения наименьших колебаний параметров отливки.
Максимальный экономический эффект литья изделий удается достичь в том случае, если извлеченная из пресс-формы отливка практически не подвергалась мехобработке. Одновременно с этим решение вопроса о потребности в механической обработке возможно только в том случае, когда известна точность размеров, которая получается во время литья под давлением. Количественный критерий в данном случае – максимальная величина отклонений действительных габаритов отливаемого изделия от значения, заданного конструктором.
Что такое точность размера детали?
В процессе производства (отливки) деталей требуется выдержка определенных геометрических параметров поверхностей, а именно должно быть определенное соответствие:
- размера;
- формы;
- относительного расположения.
Степень приближения истинного значения к теоретическому является точностью.
Размером считают числовое значение линейных величин (диаметр, длина и др.), которые в машиностроении измеряются в миллиметрах. Он подразделяется на:
- номинальный – параметр, по которому определяют предельный размер, служащий началом отсчёта отклонений. Он является основным и получается на основании кинематического, динамического и прочностного расчета. Также, номинальные габариты можно выбрать по конструктивным, технологическим, эксплуатационным, эстетическим и другим соображениям. Данный габарит классифицируется по назначению на определяющую величину и форму изделия, монтажные и координирующие. Помимо этого, с позиции удобства и точности обработки нередко вводятся технологические габариты, то есть те, которые по соответствию близки к изготовленной детали;
- действительный – параметр, который устанавливают путем измерения с учётом допустимой погрешности.
Точность размера – это оценивание соответствия реально отлитой детали номинальным параметрам, которые указаны на чертеже.
Как рассчитывается точность размеров деталей?
Чтобы готовое изделие можно было реализовать, оно должно соответствовать своему целевому назначению. То есть, необходимо, чтобы его действительные параметры были выдержаны между теоретически допустимыми и предельными, в результате разницы которых образуется допуск.
Наибольшим предельным параметром считается тот, который больше из двух предельных, а наименьшим – соответственно меньший из 2-х. Для более удобных расчетов указываются номинальные габариты изделия. При этом, каждый предельный размер вычисляют по отклонению от номинального показателя. Абсолютное значение и знак, указывающий на отклонение, получают путем вычитания номинальных параметров из соответствующих предельных.
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: 

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:
и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.
На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше 


Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.
Решение:
1) Цена деления нижней шкалы:
Цена деления средней шкалы:
Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10° 

- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения