Докажем существование верхней точной грани. По условию множество X не пусто, то есть содержит хотя бы один элемент. Возможны два случая:
- множество X содержит хотя бы одно неотрицательное число;
- все элементы множества X отрицательны.
Первый случай. Предположим, что все элементы множества X неотрицательны. По условию множество X ограничено сверху, а значит выполняется условие eqref{ref1}. Пусть C=c0,c1c2…cn…; тогда c0 — неотрицательное целое число, причем C < c0+1, где c0+1 = n0 ∈ (mathbb{N}). Следовательно, $$forall xin X rightarrow x < C < n_0.label{ref5}$$
Если x=a0,a1a2…=a0,{an} — произвольный элемент множества X, то из eqref{ref5} следует, что 0 ≤ a0 < n0. Рассмотрим множество E целых частей элемента множества X. Так как E — конечное непустое множество целых неотрицательных чисел, то в этом множестве есть наибольший элемент ({overline a}_0). Обозначим,$$X_0=left{xin X: x={overline a}_0,left{a_nright}right}.nonumber$$
Множество X0 состоит из всех тех элементов множества X, у которых целая часть равна ({overline a}_0); множество X0 непустое и X ⊃ X0.
Пусть E1 — множество первых десятичных знаков элементов множества X0. Так как множество E1 конечно (его элементы могут быть числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и непусто, то существует ({overline a}_1=underset{xin X_0}{max} a_1) — наибольший из первых десятичных знаков элементов множества X0.
Пусть (X_1=left{xin X: x={overline a}_0,{overline a}_1a_2…right}); тогда X ⊃ X0 ⊃ X1. Обозначим ({overline a}_2=underset{xin X_1}{max} a_2) наибольший из вторых десятичных знаков элементов множества X1,$$X_2=left{xin X_1: a_2={overline a}_2right}=left{xin X: x={overline a}_0,{overline a}_1{overline a}_2a_3…right}.nonumber$$
Продолжая эти рассуждения, построим последовательность {Xk} непустых множеств и последовательность десятичных знаков ({overline a}_k) таких, что X ⊃ X0 ⊃ X1 ⊃ … X ⊃ X0 ⊃ …,$${overline a}_k=underset{xin X_{k-1}}{max} a_k,nonumber$$
$$X_k=left{xin X_{k-1}: a_k={overline a}_kright}=left{xin X: x={overline a}_0,{overline a}_1…{overline a}_ka_{k+1}…right}nonumber$$
Рассмотрим десятичную дробь (overline x={overline a}_0,{overline a}_1{overline a}_2…={overline a}_0,left{{overline a}_nright}). Покажем, что x = sup X, то есть что
$$forall xin X rightarrow x leq overline x,label{ref6}$$
$$forall x’ < overline x existswidetilde xin X: widetilde x > x’.label{ref7}$$
Возьмем произвольное число x ∈ X и пусть x = a0,{an}. Чтобы проверить выполнение условия eqref{ref6}, рассмотрим три произвольных случая:
$$xnotin X_k при k=0,1,2,…,label{ref8}$$
$$xin X_k при k=0,1,2,…,label{ref9}$$
$$exists m: xin X_{m-1}, xnotin X_{m.}label{ref10}$$
Из eqref{ref8} следует, что (a_0 < {overline a}_0) и поэтому (x < overline x). Если выполнено условие eqref{ref9}, то (a_k={overline a}_k) при k = 0, 1, 2,…, откуда, по определению числа (overline x), справедливо равенство (x=overline x). Наконец из eqref{ref10}, согласно определению множества Xm и числа (x=overline x), следует, что
$$x = {overline a}_0,{overline a}_1…{overline a}_{m-1}a_m… <{overline a}_0,{overline a}_1…{overline a}_{m-1}{overline a}_m(0) leq overline x,nonumber$$
и поэтому (x < overline x). Таким образом, неравенство eqref{ref6} доказано.
Проверим условие eqref{ref7}. Если x’ < 0, то eqref{ref7} имеет место при любом (widetilde xin X), т.к. все элементы множества X неотрицательны.
Пусть (0 leq x’ leq overline x) и (x’=a’_0,left{a’_nright}). Тогда либо (a’_0 < {overline a}_0), либо (a’_k=a_k при k=overline{0, m-1},a’_m < {overline a}_m). В первом случае в качестве (widetilde x) можно взять любой элемент множества X0, так как из условий (a’_0 < {overline a}_0) и (widetilde xin X_0) следует, что
$$x’ < widetilde x={overline a}_0,a_1…a_n… leq overline x, то есть x’ < widetilde x leq overline x и xin X_0subset X.nonumber$$
Во втором случае условию eqref{ref7} удовлетворяет произвольный элемент (widetilde xin X_m), так как
$$x’={overline a}_0,{overline a}_1…{overline a}_{m-1}a’_m… < {overline a}_0,{overline a}_1…{overline a}_{m-1}{overline a}_ma_{m+1}…=widetilde x leq overline x.nonumber$$
Таким образом, (x’ < widetilde x leq overline x), где (widetilde xin X_msubset X). Условие eqref{ref7} проверено.
Итак, условия eqref{ref6} и eqref{ref7} выполняются, то есть x = sup X. То есть мы доказали предположение, что существует точная верхняя грань при предположении, что все элементы множества X неотрицательны.
Если множество X содержит хотя бы один неотрицательный элемент x0 ≥ 0, то множество (left{widetilde X=xin X: x geq x_0right}) состоит из неотрицательных чисел, причем (sup X=sup widetilde X). Поэтому непустое ограниченное сверху числовое множество X имеет точную верхнюю грань.
Второй случай. Если все элементы множества X отрицательны, то произвольный элемент x ∈ X записываются в виде
$$x=-a_0,a_1a_2…a_n…label{ref11}$$
Пусть (a_0^ast) — наименьшее из чисел a0 в записи eqref{ref11} для всех x ∈ X, (a_1^ast) — наименьший из первых десятичных знаков тех элементов множества X, у которых (a_0=a_0^ast); (a_2^ast) — наименьший из вторых десятичных знаков тех элементов множества X, у которых (a_0=a_0^ast, a_1=a_1^ast) и т.д. Указанным способом определяется число (x^ast=-a_0^ast,a_1^ast…a_n^ast…=-a_0^ast,left{a_n^astright}). По аналогии с первым случаем доказывается, что число x* является точной верхней гранью множества.
Точная верхняя и нижняя грань — обобщение понятий максимума и минимума множества.
Содержание
- 1 Определения
- 2 Замечание
- 3 Примеры
- 4 Свойства
Определения
Пусть дано частично упорядоченное множество 




Аналогично элемент 


Пишут:
Замечание
Эти определения ничего не говорят о том, принадлежат ли 








Примеры
- На множестве всех действительных чисел больших пяти, не существует минимума, однако существует инфимум.
такого множества равен пяти. Инфимум не является минимумом, так как пять не принадлежит этому множеству. Если же определить множество всех натуральных чисел, больших пяти, то у такого множества есть минимум и он равен шести. Вообще говоря, у любого подмножества натуральных чисел существует минимум.
- Для множества
;
.
- Множество положительных действительных чисел
не имеет точной верхней грани в
, точная нижняя грань
.
- Множество
рациональных чисел, квадрат которых меньше двух, не имеет точных верхней и нижней граней в
, но если его рассматривать как подмножество множества действительных чисел, то
и
.
Свойства
- Для любого ограниченного сверху подмножества
, существует
.
- Для любого ограниченного снизу подмножества
, существует
.
- Вешественное число
, является
тогда и только тогда, когда
есть верхняя грань
т.е. для всех элементов
,
.
- для любого
найдётся
, такой, что
(т.е. к
можно сколь угодно «близко подобраться» из множества
)
- Аналогичное утверждение верно для точной нижней грани.
Точная верхняя и нижняя грани
- Точная верхняя и нижняя грани
-
Точная верхняя и нижняя грани
Точная верхняя грань и точная нижняя грань — обобщение понятий максимума и минимума множества соответственно.
Содержание
- 1 Определения
- 1.1 Замечание
- 2 Примеры
- 3 Свойства
- 4 Вариации и обобщения
- 5 Примечания
Определения
Точной верхней гранью, или супре́мумом (лат. supremum — самый высокий) подмножества X упорядоченного множества M, называется наименьший элемент M, который равен или больше всех элементов множества X. Другими словами, супремум — это наименьшая из всех верхних границ. Обозначается
.
Более формально:
— множество верхних граней X, то есть элементов M, равных или больших всех элементов X
Точной нижней гранью, или и́нфимумом (лат. infimum — самый низкий) подмножества X упорядоченного множества M, называется наибольший элемент M, который равен или меньше всех элементов множества X. Другими словами, инфимум — это наибольшая из всех нижних граней. Обозначается
.
Замечание
Эти определения ничего не говорят о том, принадлежит ли
и
множеству X или нет. В случае
, говорят, что s является максимумом X. В случае
, говорят, что i является минимумом X.
Примеры
;
.
и
.
Свойства
Вариации и обобщения
- Существенный супремум
Примечания
- ↑ Строго говоря, у любого подмножества вполне упорядоченного множества существует в силу принципа фундированности минимум.
- 1 Определения
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Точная верхняя и нижняя грани» в других словарях:
-
Точная верхняя и нижняя границы множеств — Точная верхняя граница (верхняя грань) и точная нижняя граница (нижняя грань) обобщение понятий максимума и минимума множества соответственно. Содержание 1 Используемые определения 2 Определения 2.1 … Википедия
-
Верхняя грань — Точная верхняя грань и точная нижняя грань обобщение понятий максимума и минимума множества соответственно. Содержание 1 Определения 1.1 Замечание 2 Примеры 3 Свойства … Википедия
-
Нижняя грань — Точная верхняя грань и точная нижняя грань обобщение понятий максимума и минимума множества соответственно. Содержание 1 Определения 1.1 Замечание 2 Примеры 3 Свойства … Википедия
-
Ограниченное множество — В математическом анализе, и прилегающих разделах математики, ограниченное множество множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай… … Википедия
-
Ограниченное числовое множество — В математическом анализе, и прилегающих разделах математики, ограниченное множество множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай… … Википедия
-
Грань числового множества — Точная верхняя грань и точная нижняя грань обобщение понятий максимума и минимума множества соответственно. Содержание 1 Определения 1.1 Замечание 2 Примеры 3 Свойства … Википедия
-
Инфимум — Точная верхняя грань и точная нижняя грань обобщение понятий максимума и минимума множества соответственно. Содержание 1 Определения 1.1 Замечание 2 Примеры 3 Свойства … Википедия
-
ЛЕГКИЕ — ЛЕГКИЕ. Легкие (лат. pulmones, греч. pleumon, pneumon), орган воздушного наземного дыхания (см.) позвоночных. I. Сравнительная анатомия. Легкие позвоночных имеются в качестве добавочных органов воздушного дыхания уже у нек рых рыб (у двудышащих,… … Большая медицинская энциклопедия
-
ВЫПУКЛАЯ ПОВЕРХНОСТЬ — область (связное открытое множество) на границе выпуклого тела в евклидовом пространстве Е 3. Вся граница выпуклого тела наз. полной В. п. Если тело конечно, то полная В. п. наз. замкнутой. Если тело бесконечно, то полная В. п. наз. бесконечной.… … Математическая энциклопедия
-
Частично упорядоченное множество — У этого термина существуют и другие значения, см. Упорядоченное множество. Подмножества {x, y, z}, упо … Википедия
Определение. Если для подмножества 







Множество 







Определение. Множество, не являющееся ограниченным сверху множеством, называется неограниченным сверху множеством.
Множество 

Определение. Если для подмножества 



Множество 

Определение. Множество, не являющееся ограниченным снизу множеством, называется неограниченным снизу множеством.
Множество 

Определение. Множество, ограниченное и сверху и снизу, называется ограниченным множеством.
Определение. Множество, не являющееся ограниченным, называется не ограниченным множеством.
Определение. Наименьшее среди всех чисел, ограничивающих сверху множество 





Определение. Наибольшее среди всех чисел, ограничивающих снизу множество 





Пример. 

Теорема. 
Доказательство. Пусть 














Выполнение неравенства 









Если теперь 


Аналогично рассмотренному случаю верхней грани, легко убеждаемся, что, в силу свойства непрерывности действительных чисел, 


Это означает, что 
Точная верхняя граница (верхняя грань) и точная нижняя граница (нижняя грань) — обобщение понятий максимума и минимума множества соответственно.
Содержание
- 1 Используемые определения
- 2 Определения
- 2.1 Замечание
- 3 Примеры
- 4 Теорема о гранях
- 4.1 Формулировка
- 4.2 Доказательство
- 5 Свойства
- 6 Вариации и обобщения
- 7 Литература
- 8 Примечания
Используемые определения[править | править исходный текст]
Мажоранта или верхняя грань (граница) множества 


Миноранта или нижняя грань (граница) множества 

Определения[править | править исходный текст]
Точной (наименьшей) верхней гранью (границей), или супре́мумом (лат. supremum — самый высокий) подмножества 




Более формально:
— множество верхних граней
, то есть элементов
, равных или больших всех элементов
Точной (наибольшей) нижней гранью (границей), или и́нфимумом (лат. infimum — самый низкий) подмножества 




Замечание[править | править исходный текст]
Эти определения ничего не говорят о том, принадлежит ли 


В случае 



В случае 



Примеры[править | править исходный текст]
;
.
и
.
Теорема о гранях[править | править исходный текст]
Формулировка[править | править исходный текст]
Непустое множество, ограниченное сверху, имеет верхнюю грань, ограниченное снизу — нижнюю грань. То есть существуют 

Доказательство[править | править исходный текст]
Для множества ограниченного сверху. Пусть 




.
Множество 


Множество 




Допустим, что для некоторого номера 

- существует элемент
, представление которого в виде бесконечной десятичной дроби начинается с выражения
- если x — элемент
с представлением
, то
-
.
Обозначим 








На основании принципа индукции для любого 

Возьмем произвольное число 





Для множества 
Свойства[править | править исходный текст]
Вариации и обобщения[править | править исходный текст]
- Существенный супремум
Литература[править | править исходный текст]
- Богданов Ю. С., Кастрица О. А., Сыроид Ю. Б. Математический анализ: Учебное пособие для вузов. — М.: ЮНИТИ-ДАНА, 2003.- С. 11-14. ISBN 5-238-00500-8
- Богданов Ю. С. Лекции по математическому анализу. Ч. 1. — Мн.: Издательство БГУ, 1974. — С. 3—8.

























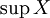 .
.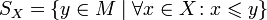 — множество верхних граней
— множество верхних граней 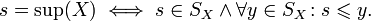
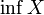 .
.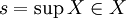 , говорят, что
, говорят, что 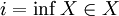 , говорят, что
, говорят, что 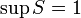 ;
; 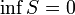 .
.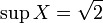 и
и 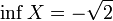 .
.
 — множество верхних граней
— множество верхних граней 
 ;
;  .
. и
и  .
.

 .
. , представление которого в виде бесконечной десятичной дроби начинается с выражения
, представление которого в виде бесконечной десятичной дроби начинается с выражения  , то
, то .
.