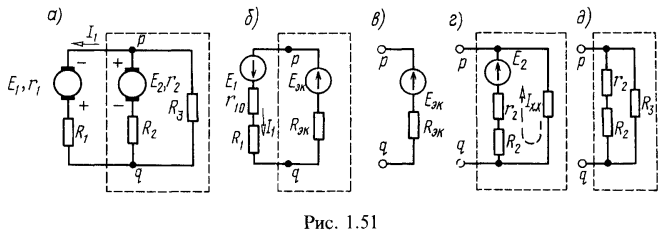
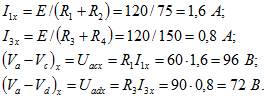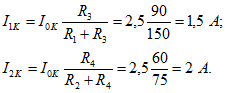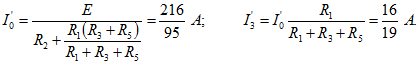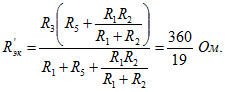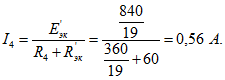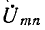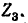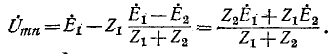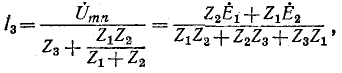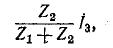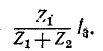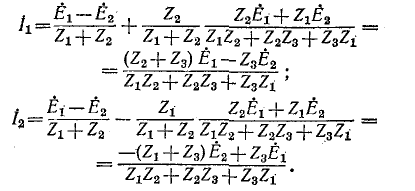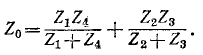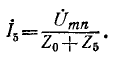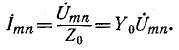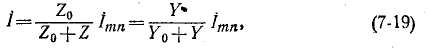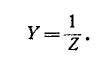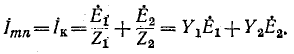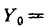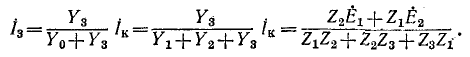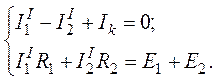1. Для схемы цепи рис. 1.51, а методом эквивалентного источника ЭДС найти ток в ветви резистора, сопротивление которого , если
Решение:
Обозначим положительное направление искомого тока на исходной схеме (рис. 1.51, а). Рассмотрим часть схемы, подключенную к исследуемой первой ветви (обведенную штриховой линией), в качестве эквивалентного источника ЭДС и сопротивлением
. Нарисуем эквивалентную электрическую схему с эквивалентным источником напряжения (рис. 1.51, б).
На схеме выбрано произвольно положительное направление ЭДС эквивалентного источника к точке р. Это позволяет записать, для режима холостого хода эквивалентного источника с отключенной первой ветвью (рис. 1.51, в):
Развернутая схема эквивалентного источника в режиме холостого хода показана на рис. 1.51, г. Во внутренних ветвях источника ток
Напряжение холостого хода определяет ЭДС источника:
Найдем сопротивление эквивалентного источника.
Для подсчета сопротивления источника преобразуем его схему (см. рис. 1.51, г), заменив источник напряжения короткозамкнутым участком (рис. 1.51, д). Входное сопротивление последней схемы является сопротивлением эквивалентного источника
Возвращаясь к схеме рис. 1.51, б, найдем искомый ток по закону Ома:
2. Методами эквивалентного источника ЭДС и эквивалентного источника тока найти ток в ветви , если
(рис. 1.52, а).
Решение:
1. Рассчитаем методом эквивалентного источника ЭДС. Отключим ветвь с (рис. 1.52, б) и найдем его параметры с ЭДС
(т. е. напряжение
холостого хода между точками а и b) и
— сопротивление схемы рис. 1.52, в между точками а и b в режиме холостого хода при закороченных ЭДС
. Схема эквивалентного источника ЭДС приведена на рис. 1.52, г. ЭДС эквивалентного источника и его сопротивление равны:
Искомый ток согласно формуле (0.1.24)
2. При расчете методом эквивалентного источника тока ветвь закорачиваем (рис. 1.52, д). Ток
, проходящий но закороченной ветви ab, является током эквивалентного источника тока
. Найдем его. Это можно сделать, рассчитав двухузловую схему (рис. 1.52, д) методом узловых напряжений. Приняв потенциал точек а и b равным нулю
, найдем
Для определения тока вычисляем
и по первому закону Кирхгофа вычисляем
Сопротивление эквивалентного источника тока равно сопротивлению эквивалентного источника напряжения; однако его можно найти по (0.1.25):
.
Из схемы эквивалентного источника тока (рис. 1.52, е) по формуле (0.1.26) находим искомый ток
Получили тот же результат, что и по методу эквивалентного источника ЭДС.
В заключение рассмотрим вопрос о мощностях, доставляемых источниками при их преобразовании. Из теории известно, что при преобразованиях источников токи в ветвях, не подвергшихся преобразованию, остаются неизменными, а мощности, доставляемые источниками, изменяются. Так, для схем (рис. 1.52, г и е) ток в ветви , не подвергшейся преобразованию, в обоих случаях одинаков:
. Мощности же в цепях схем (рис. 1.52, г, е) различны:
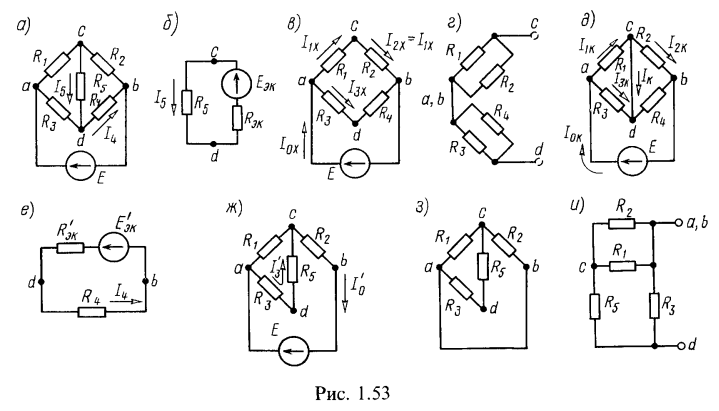
3. Методом эквивалентного источника ЭДС найти ток (рис. 1.53, а), проходящий через резистор, сопротивление которого
, если
.
Тем же методом определить ток в сопротивлении .
Решение:
На схеме рис. 1.53, а обозначим произвольное положительное направление искомого тока . Часть схемы (внешнюю к исследуемой ветви
) рассмотрим в виде некоторого источника ЭДС
. Стрелку ЭДС
произвольно направим к точке с (рис. 1.53, б). Таким образом, ЭДС источника определился напряжением холостого хода:
.
На развернутой схеме источника в режиме холостого хода (рис. 1.53, в) обозначим токи в ветвях .
По закону Ома,
Таким образом, ЭДС эквивалентного источника напряжения:
Найдем сопротивление эквивалентного источника ЭДС двумя методами:
1) путем непосредственного расчета по схеме: для этого в схеме рис. 1.53, в источник напряжения заменим короткозамкнутым участком; после этого схему рис. 1.53, в нарисуем в виде рис. 1.53, г.
Сопротивление источника равно сопротивлению цепи между точками с и d:
2) путем вычисления отношения ЭДС эквивалентного источника к току короткого замыкания; для этого в схеме рис. 1.53, в надо замкнуть точки с и d накоротко, вычислить ток , протекающий через короткозамкнутый участок (рис. 1.53. д), и найти сопротивление короткого замыкания по формуле (0.1.25). Источник ЭДС Е в короткозамкиутой схеме рис. 1.53, д нагружаем на эквивалентное сопротивление
Ток источника напряжения
Токи в ветвях
Отсюда
Сопротивление источника
Значения сопротивления источника, полученные этими методами одинаковы.
Возвращаясь к рис. 1.53, б, по закону Ома находим искомый ток
Таким образом, ток в сопротивлении направлен от точки d к точке с и равен 0,4 А.
Расчет тока резистора, сопротивление которого , метолом эквивалентного источника ЭДС проводится аналогично. Заменяем часть схемы, подключенную к точкам d и b ветви с сопротивлением
, эквивалентным источником
(рис. 1.53, е). ЭДС источника совпадает с напряжением в режиме холостого хода:
.
Для определения этого напряжения рассчитаем вначале токи в развернутой схеме источника в режиме холостого хода (рис. 1.53, ж):
Отсюда находим ЭДС источника
Для определения сопротивления источника ЭДС рассмотрим соответствующую пассивную схему (в схеме источник ЭДС заменен короткозамкнутым отрезком), показанную на рис. 1.53, з. Для ясности эта схема показана в виде рис. 1.53, и.
Сопротивление источника, равное входному сопротивлению последней схемы, относительно зажимов d и b:
Находим искомый ток по схеме эквивалентного источника ЭДС (рис. 1.53, е):
-
Метод эквивалентного источника напряжения (генератора)
При расчете тока в одной из
ветвей разветвленной цепи, содержащей
произвольное число источников и
потребителей, удобно рассматривать
цепь, состоящую из двух частей: искомой
ветви и остальной части. По отношению
к рассматриваемой ветви вся остальная
часть цепи является активным двухполюсником
(рис. 2.9.), и задача заключается в определении
тока или напряжения на зажимах активного
двухполюсника при подключении к нему
потребителя с сопротивлением R..
Согласно II
закону Кирхгофа ток не изменится, если
в цепь, образованную активным двухполюсником
и потребителем, включить последовательно
два идеализированных встречно направленных
источника с одинаковыми ЭДС (рис. 2.10).
Величину
каждой из них выбираем совпадающей с
напряжением UХХ
на зажимах активного двухполюсника в
режиме холостого хода, который имеет
место при отключенном потребителе.
(2.16)
Ток I
в цепи с
двумя источниками определим методом
наложения. С этой целью источники
разбиваем на две группы (рис. 211 и 2.12):
1. Источники
активного двухполюсника и Е1,
которые
сохраняются в подсхеме рис. 2.11.
Согласно II
закону Кирхгофа:
поскольку
.
2. все потребители
активного двухполюсника и Е2,
сохраняются в подсхеме на рис. 2.12.
Поскольку I
= 0, полный ток I
=I.
Если эквивалентное
сопротивление пассивного двухполюсника,
образованного коротким замыканием
источников ЭДС и обрывом ветвей,
содержащих источники тока, обозначить
через Rвх,
получим простую одноконтурную схему
(рис. 2.13), которую можно рассчитать по
закону Ома:
(2.17)
Эта формула отражает
теорему об
активном двухполюснике или
об эквивалентном источнике напряжения:
относительно любой ветви разветвленной
электрической цепи вся остальная часть
схемы может быть представлена как
источник напряжения, ЭДС которого равна
UXX,
а внутренне сопротивление равно Rэкв.
При коротком
замыкании ветви с нагрузкой R
= 0ток
превращается в ток короткого замыкания:
(2.18)
Параметры активного
двухполюсника можно определить опытным
путем. Для этого необходимо разомкнуть
i-ую
ветвь и измерить
,
затем замкнуть накороткоRi
и измерить
IКЗ
:

Rвх
можно найти расчетным путем, если
известна конфигурация цепи и величины
сопротивлений.
Методика расчета
линейной электрической цепи методом
эквивалентного генератора:
-
Отключается
потребитель в ветви с искомым током и
на зажимах обозначается UXX
по направлению тока. -
В образовавшейся
более простой цепи находится Uõõ
с помощью II закона Кирхгофа, записанного
для любого контура, содержащего Uхх.
Токи в ветвях упрощенной схемы
определяются любым известным методом. -
Определяется Rвх
на зажимах разомкнутой ветви при условии
E=0
и
J=0.
В полученной пассивной цепи пользуются
правилами эквивалентных преобразований
для потребителей. -
По найденным Uõõ
и Rвх
определяется ток в искомой ветви,
значение которого может быть и
отрицательным.
Замечание 1:
Rвх
можно найти по формуле
IКЗ
при условии
Ri=0
любым
известным методом.
Замечание 2:
если ветвь, в которой определяется ток,
содержит источник ЭДС, следует данный
источник отнести к активному двухполюснику,
отключив только сопротивление Ri.
Тогда величина E
войдет в расчет UXX
.
Пример.
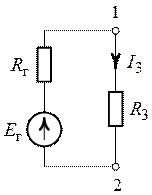
Определить ток I2
в цепи, изображенной на рис. 2.14., а.
Запишем II
закон
Кирхгофа для цепи, в которой отключен
потребитель R2
(рис. 2.14.,б):
Следовательно,
.
Rвх
определим
по цепи (рис. 2.14., в), из которой
исключены все источники, как
.
Тогда искомый ток
Соседние файлы в папке Электротехника
- #
- #
- #
- #
- #
Теорема об эквивалентном источнике:
Теорема об эквивалентном источнике часто применяется в расчетах электрических цепей. С помощью этой важной теоремы сложная электрическая схема с произвольным числом источников электрической энергии приводится к схеме с одним источником, благодаря чему расчет электрической цепи упрощается.
Существуют два варианта теоремы об эквивалентном источнике: вариант с источником э. д. с. и вариант с Источником тока.
Теорема об эквивалентном источнике э. д. с.
Ток в любой ветви тп линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником э. д. с., которая должна быть равна напряжению на выводах разомкнутой цепи тп, а внутреннее сопротивление источника
должно равняться входному сопротивлению пассивной электрической цепи со стороны выводов т и п при разомкнутой ветви mn.
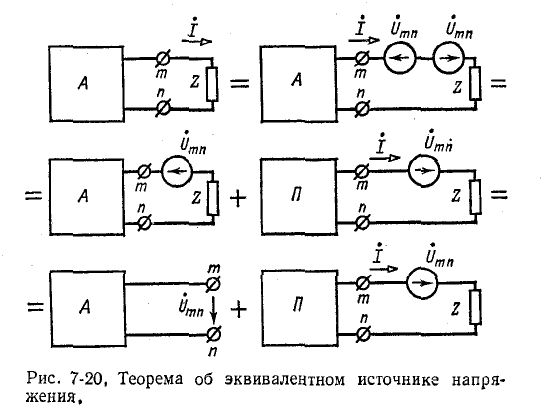
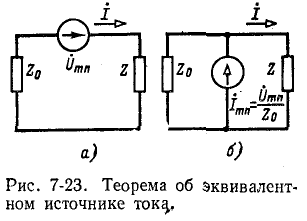
Данная теорема доказывается следующим образом: в ветвь тп вводятся две равные и противоположно направленные э. д. с.
Применение метода наложения в соответствии с рис. 7-20 приводит к выводу, что ток в ветви Z равен:
где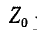
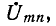
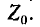
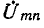
токов при включенной ветви находится весьма легко наложением на предыдущий режим тех токов, которые обусловливаются воздействием на пассивную цепь э. д. с. 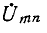
Как уже указывалось выше, метод наложения применим. не только к токам, но и к напряжениям. Поэтому, пользуясь описанным приемом, можно находить также и распределение напряжений.
При наличии в электрической цепи нескольких источников э. д. с. и тока одинаковой частоты напряжение холостого хода является линейной функцией заданных э. д. с. и токов источников.
Для доказательства теоремы, об эквивалентном источнике в ветвь вводились две противоположно направленные
э. д. с., равные напряжению холостого хода в этой ветви. Такой же прием может быть применен одновременно и к двум ветвям любой сложной активной цепи. Тогда действительное токораспределение в цепи получится как сумма токораспределений в двух схемах:
- в активной схеме — при разомкнутых двух ветвях;
- в пассивной схеме — при питании ее из двух ветвей источниками э. д. с., равными напряжениям холостого хода на этих ветвях и направленными по токам, т. е. так же, как напряжения холостого хода.
Указанный прием представляет удобство в том случае, когда известно токораспределенне при режиме холостого хода для обеих ветвей. Тогда при замыкании этих ветвей достаточно лишь наложить токи, полученные из второй схемы с двумя э. д. с.
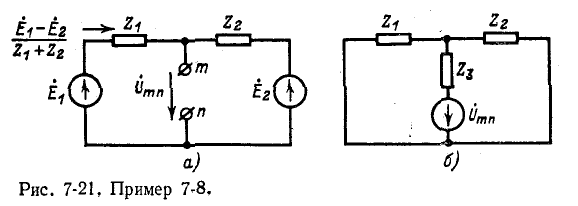
Пример 7-8.
Пользуясь теоремой об -эквивалентном источнике э,д. с., определить токи в ветвях схемы рис. 7-4.
Размыкание ветви и соответственно нахождение напряжения холостого хода могут быть произведены в любой из трех ветвей заданной электрической цепи. Рисунок 7-21 показан для случая размыкания ветви
Напряжение холостого хода 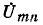
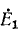
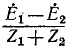
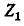
Под воздействием э. д. с. (]тп в схеме рис. 7-21,6 через комплексное. сопротивление 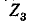
который разветвляется в 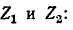
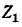
а через 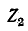
Искомые токи в ветвях 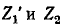
Данный пример иллюстрирует применение теоремы об эквивалентном источнике э. д. с. для вычисления токов в разных ветвях, причем не ставится цель получить решение кратчайшим путем.
Пример 7-9.
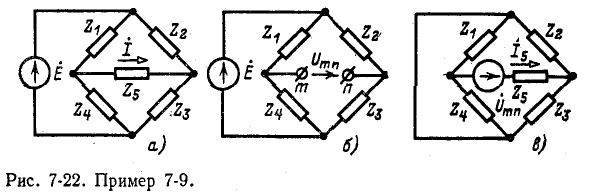
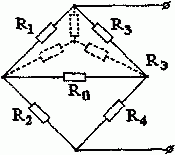
Пользуясь теоремой об эквивалентном источнике Э. Д. с., определить ток в диагональной ветви мостовой схемы рис. 7-22, а.
Разомкнув ветвь 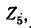
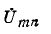
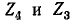
Сопротивление между тип при Е = 0 и разомкнутой ветви 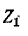
На основании (7-18)
Теорема об эквивалентном источнике тока:
Ток в любой ветви тп линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником тока; ток этого источника должен быть
равен току, проходящему между выводами m и n, замкнутыми накоротко, а внутренняя проводимость источника должна равняться входной проводимости пассивной электрической цепи со стороны выводов тип при разомкнутой ветви тп.
Данное положение вытекает из условия эквивалентности источников напряжения и тока, а именно: источник
э. д. с., которая равна напряжению холостого хода 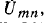
Последнее выражение есть не что иное, как ток, проходящий между выводами тип, замкнутыми накоротко (ток короткого замыкания). Искомый ток в цепи равен:
где
Если известно распределение токов в электрической цепи при закороченных выводах m и n, то распределение токов в цепи при включенной ветви Z может быть найдено посредством наложения на предыдуг щий режим тех токов, которые получаются в результате присоединения источника тока 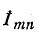
При наличии в электрической цепи нескольких источников э. д. с. и тока одинаковой частоты ток короткого замыкания является линейной функцией заданных э. д. с. и токов источников.
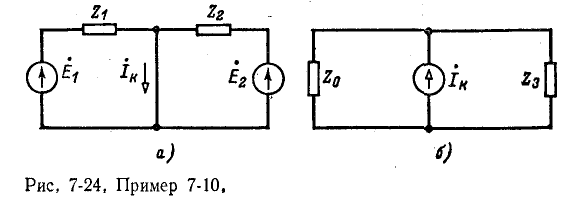
Пример 7-10.
Пользуясь теоремой об эквивалентном источнике тока, определить ток 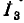
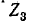
Ток эквивалентного источника равен току короткого замыкания 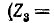
Комплексная проводимость эквивалентного источника равна 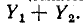
- Применение матриц к расчету электрических цепей
- Дуальные цепи
- Электромеханические аналогии
- Индуктивно связанные электрические цепи
- Теоремы теории цепей
- Теорема обратимости (или взаимности)
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
→
1.5 Метод эквивалентного генератора (метод эквивалентного источника ЭДС)
1.5 Метод эквивалентного генератора (метод эквивалентного источника ЭДС)
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
1.5 Метод эквивалентного генератора (метод эквивалентного источника ЭДС)
Метод эквивалентного генератора основан на теореме об эквивалентном источнике (теорема Тевенена) — активном двухполюснике.
Теорема Тевенена для линейных электрических цепей утверждает, что любая электрическая цепь, имеющая два вывода и состоящая из комбинации источников напряжения, источников тока и резисторов (сопротивлений), с электрической точки зрения эквивалентна цепи с одним источником напряжения E и одним резистором R, соединенными последовательно.
В методе эквивалентного генератора (метод эквивалентного источника ЭДС) сложную разветвленную схему рассматривают как активный двухполюсник по отношению к ветви R с искомым током I, который определяют по выражению
I = EЭГ/ (RЭГ + R),
где
EЭГ = Uхх — ЭДС эквивалентного генератора равная напряжению холостого хода между зажимами подключенного пассивного элемента R в ветви с искомым током;
RЭГ = Rвх — сопротивление эквивалентного генератора равное входному сопротивлению пассивного двухполюсника относительно разомкнутых зажимов.
Алгоритм метода эквивалентного генератора (метод эквивалентного источника ЭДС)
1. Определяют напряжение холостого хода Uхх. Для этого ветвь с искомым током разрывают, удаляя сопротивление, и оставляют ЭДС в этой ветви, если она имеется.
2. Задаются направлением токов в ветвях оставшейся схемы после размыкания ветви. Записывают выражение для напряжения Uхх между разомкнутыми зажимами по второму закону Кирхгофа. В это уравнение войдет ЭДС разомкнутой ветви.
3. Рациональным методом рассчитываются токи в схеме, вошедшие в выражение напряжения Uхх.
4. Определяют входное сопротивление двухполюсника относительно разомкнутых зажимов.
Индивидуалка Вика (24 лет) т.8 985 260-71-05 Москва, метро Ясенево. платно терапевт самара.
5. В соответствии с методом эквивалентного генератора (метод эквивалентного источника ЭДС), определяют искомый ток ветви.
Решение задач методом эквивалентного генератора (методом эквивалентного источника ЭДС)
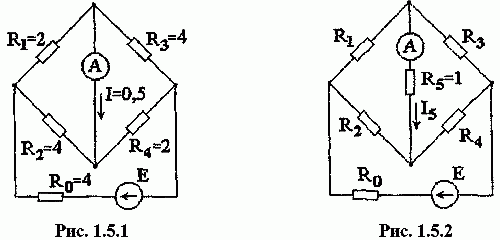
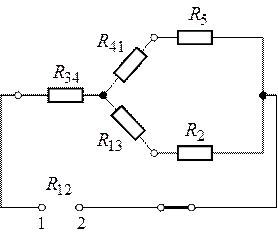
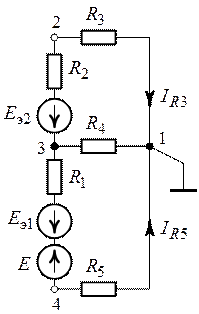
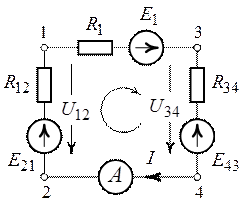
Задача 1.5.1 В схеме рис. 1.5.1 амперметр показывает 0,5 А. Определить его показания в схеме рис. 1.5.2.
Решение. Можно считать, что в схеме рис. 1.5.2 резистор R5 подключен к зажимам эквивалентного генератора, который в схеме рис. 1.5.1 работает в режиме короткого замыкания.
Рис. 1.5.3
Определим внутреннее сопротивление эквивалентного генератора по схеме рис. 1.5.3, где заменим треугольник сопротивлений R1R3R0 эквивалентным соединением звездой
R 13 = R 1 ⋅ R 3 R 1 + R 3 + R 0 = 2⋅4 2+4+4 =0,8 Ом; R 01 = R 1 ⋅ R 0 R 1 + R 3 + R 0 = 4⋅2 2+4+4 =0,8 Ом; R 03 = R 0 ⋅ R 3 R 1 + R 3 + R 0 = 4⋅4 2+4+4 =1,6 Ом; R Э = R 13 + ( R 01 + R 2 )⋅ ( R 03 + R 4 ) ( R 01 + R 2 )+ ( R 03 + R 4 ) = =0,8+ ( 0,8+4 )⋅ ( 1,6+2 ) ( 0,8+4 )+ ( 1,6+2 ) =2,86 Ом.
ЭДС эквивалентного генератора определим из формулы I = EЭГ/ (RЭГ + R) метода эквивалентного генератора. При коротком замыкании I = EЭГ/RЭГ. Откуда ЭДС эквивалентного генератора
E Э =I⋅ R Э =0,5⋅2,86=1,43 В.
Ток I5 в схеме рис. 1.5.2 по методу эквивалентного генератора (методу эквивалентного источника ЭДС)
I 5 = E Э R Э + R 5 = 1,43 2,86+1 =0,371 А.
Метод эквивалентного источника напряжения, метод эквивалентного источника тока, метод активного двухполюсника в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи

теорема об эквивалентном источнике,
метод эквивалентного источника ЭДС,
метод эквивалентного генератора
Страницы работы
Содержание работы
6.
МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА
(ЭКВИВАЛЕНТНОГО
ИСТОЧНИКА)
Целесообразность использования данного метода
становится очевидной, в случае если расчет электрической цепи ограничен в определении
тока только одной ветви. В этом случае вся цепь относительно ветви с
интересующим током заменяется эквивалентной схемой. Таким образом, основной
расчет сводится к определению двух параметров эквивалентной схемы – ЭДС и
сопротивления эквивалентного генератора.
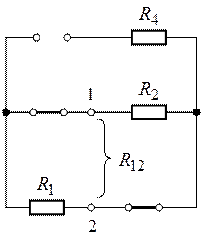
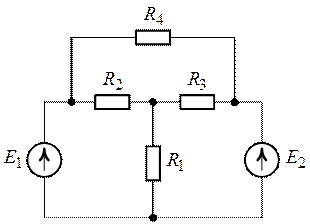
Задача 6.1.
Для схемы цепи (рис. 6.1) методом эквивалентного
генератора найти ток ветви с сопротивлением ,
если ,
,
,
,
,
,
.
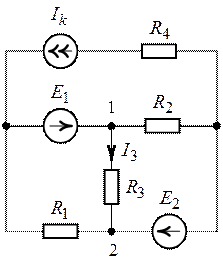
Рис. 6.1. Рис.
6.2.
Решение.
1. Выделим ветвь с сопротивлением и обозначим
ток (рис.6.1) .
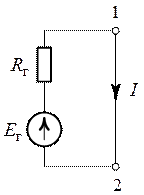
2. Всю цепь, рис. 6.1, относительно ветви с
сопротивлением , представим эквивалентным
генератором с источником ЭДС равным и сопротивлением
(рис. 6.2).
Согласно схеме (рис. 6.2) интересующий ток в ветви
определиться как
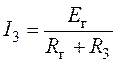
т.е.
решение задачи сводится к определению двух параметров эквивалентного генератора
и
.
3. Найдем ЭДС генератора. По определению равно напряжению
между узловыми точками 1 и 2
разомкнутой ветви с сопротивлением (рис. 6.3).
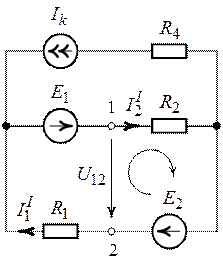
Рис. 6.3.
Рис. 6.4.
Для этого в схеме (рис. 6.3) определим токи и
. На
основании законов Кирхгофа получим систему:
Из системы найдем
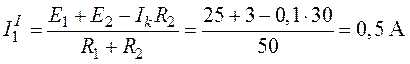
.
На основании второго закона Кирхгофа для указанного в
схеме (рис. 6.3) направления обхода контура получим
.
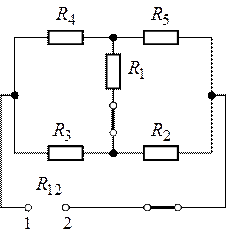
4. Найдем сопротивление генератора. По определению равно входному сопротивлению
между узловыми точками 1 и 2 разомкнутой
ветви с (рис. 6.3). Расчет сопротивления
производим при закороченных источниках
ЭДС ,
и
разомкнутом источнике тока , рис. 6.4.
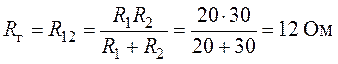
5. Окончательно определяем ток :
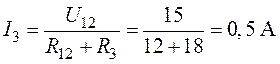
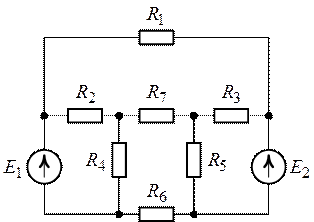
Задача 6.2.
Определить методом эквивалентного генератора ток в
ветви с источником ЭДС (рис. 6.5). Дано:
,
,
,
,
,
,
.
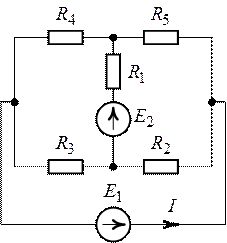
Рис. 6.5. Рис.
6.6.
Решение
1. Обозначим ток в
ветви с источником ЭДС (рис. 6.5).
2. Применив теорему об эквивалентном генераторе, ток в
ветви, имеющей нулевое сопротивление согласно схеме (рис. 6.6):
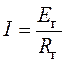
3. Найдем ЭДС генератора. Разомкнем ветвь с источником
(рис.6.7) и найдем напряжение
между точками 1 и 2.
Предварительно выполним расчет токов и
в
схеме (рис. 6.7).
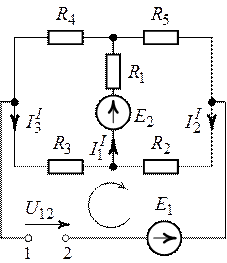
Рис. 6.7.
Рис. 6.8.
Ток в
неразветвленной части схемы
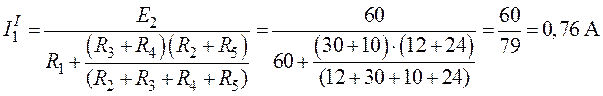
Токи и
в разветвленной части схемы:
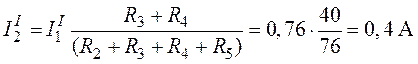
.
На основании второго закона Кирхгофа для обозначенного
на схеме (рис. 6.7) контура запишем:
,
откуда
.
4. Найдем сопротивление генератора , которое равно входному
сопротивлению между точками 1 и 2 (рис.
6.8) (при замкнутых источниках ЭДС ,
).
Преобразуем треугольник сопротивлений ,
и
(рис.6.8) в эквивалентную звезду
(рис. 6.9).
Рис. 6.9.
Величины сопротивлений эквивалентной звезды (рис. 6.9):
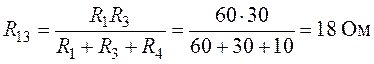
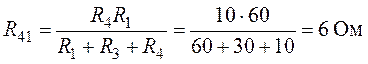
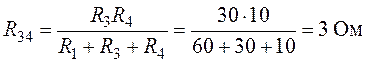
Согласно выполненным преобразованиям окончательно
получим (рис. 6.9):
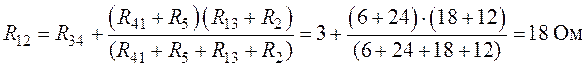
5. Ток в ветви с источником определится
как
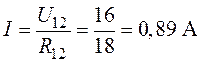
Задачи для самостоятельного решения
Задача 6.3. Методом
эквивалентного генератора для схемы (рис. 6.10) определить ток в ветви с
сопротивлением . Дано
,
,
,
,
,
.
О т в е т: (
,
).
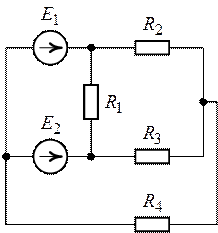
Рис. 6.10.
Рис. 6.11.
Задача 6.4. Для
цепи (рис. 6.11) методом эквивалентного генератора определить ток в ветви с
сопротивление , если
,
,
,
,
.
О т в е т: (
,
)
Задача 6.5. Определить
обозначенный в схеме (рис. 6.12) ток по методу эквивалентного генератора, если ,
,
,
,
,
,
,
.
О т в е т: (
,
)
Задача 6.6. Для
схемы (рис. 6.13) методом эквивалентного генератора определить обозначенный в
ветви ток, если ,
,
,
,
,
.
О т в е т: (
,
)
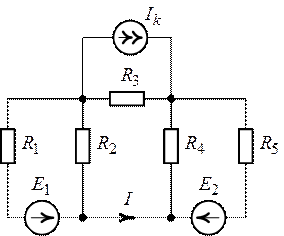
Рис. 6.12.
Рис. 6.13.
Задача 6.6. Рассчитать
обозначенный в схеме (рис. 6.14) ток, используя метод эквивалентного
генератора, если ,
,
,
,
,
.
О т в е т: (
,
)
Задача 6.4. Для
цепи (рис. 6.15) методом эквивалентного генератора определить ток в ветви с
сопротивление , если
,
,
,
,
,
,
,
,
.
О т в е т: (
,
)
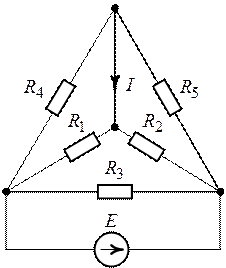
Рис. 6.14.
Рис. 6.15.
7. ПРИМЕНЕНИЕ ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ ПРИ
РАСЧЕТАХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Расчет сложных электрических цепей можно упростить
путем различных эквивалентных преобразований активных участков схем содержащих
ветви с идеальными источниками ЭДС и тока. В частях схемы не затронутых
преобразованиями должно выполняться условие неизменности напряжений и токов
ветвей. Упрощение расчета сводится, как правило, к уменьшению числа ветвей или
узлов схемы и, в конечном счете, к сокращению расчетных уравнений.
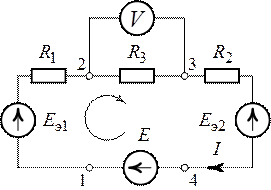
Задача 7.1.
Для цепи (рис.7.1) требуется определить показание
вольтметра, если ,
,
,
,
.
Внутреннее сопротивление вольтметра принять .
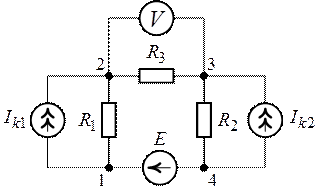
Рис. 7.1. Рис.
7.2.
Решение.
1. Преобразуем источники тока и
(рис. 7.1) в эквивалентные источники
ЭДС ,
(рис.
7.2).
2. Значения ЭДС эквивалентных источников:
;
.
3. Ток, протекающий в контуре (рис. 7.2) найдем на
основании второго закона Кирхгофа
,
откуда
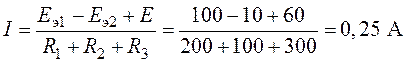
4. Показание вольтметра установленного
в схеме будет соответствовать напряжению на
сопротивлении :
.
Задача 7.2.
Методом узловых потенциалов определить токи в ветвях с
сопротивлениями и
схемы
(рис. 7.3) , если ,
,
,
,
,
,
.
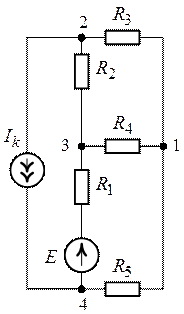
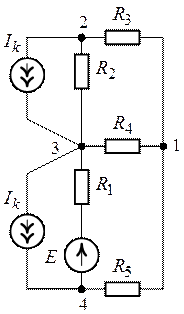
Рис. 7.3. Рис. 7.4. Рис.
7.5.
Решение.
1. Чтобы уменьшить число узлов расчетной схемы и
упростить расчет преобразуем источник тока в
эквивалентные источники ЭДС.
Включая в узле 3 два равных и противоположно
направленных источника тока , получим
эквивалентную схему (рис. 7.4).
После преобразования источников тока в эквивалентные
источники ЭДС получим эквивалентную схеме (рис.7.3) схему представленную на
рис. 7.5.
2. Значения ЭДС эквивалентных источников:
;
.
3. Расчет токов преобразованной схемы (рис. 7.5)
выполним методом двух узлов. Потенциал узловой точки 1 принимаем равным нулю (). Напряжение между узлами 3 и 1
найдем как
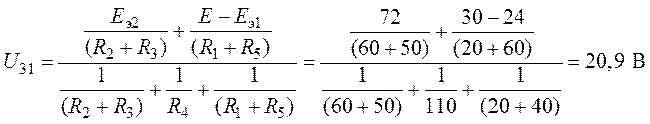
4. Интересующие в схеме токи
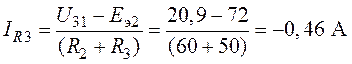
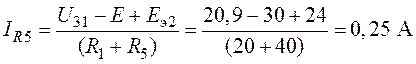
Задача 7.3.
Определить показание амперметра для схемы рис. 7.6, если
,
,
,
,
,
,
,
,
,
.
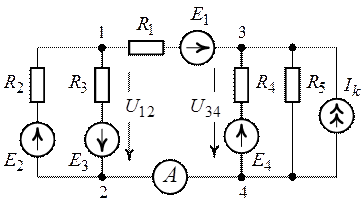
Рис. 7.6. Рис.
7.7.
Решение.
1. Для упрощения расчета воспользуемся
преобразованиями активных участков схем с параллельными ветвями одной
эквивалентной.
2. Эквивалентная ЭДС и
эквивалентное сопротивление двух параллельных
ветвей левой части схемы (рис. 7.6):
Похожие материалы
- Вопросы для защиты отчета по лабораторной работы № 1
- Применение метода наложения к расчету электрических цепей с двумя и более источниками энергии. Метод узловых потенциалов (узловых напряжений) (главы 3-5 учебного пособия «Теоретические основы электротехники в примерах и задачах»)
- Расчет простых цепей при постоянных токах и напряжениях. Расчет сложных цепей с помощью прямого применения законов Кирхгофа (главы 1-2 учебного пособия «Теоретические основы электротехники в примерах и задачах»)