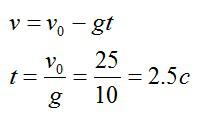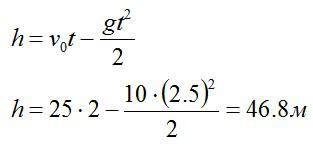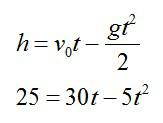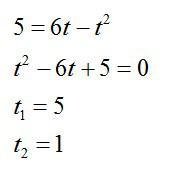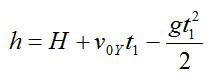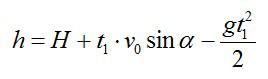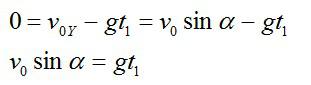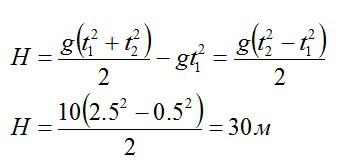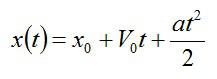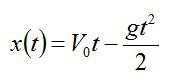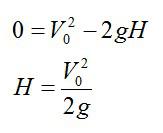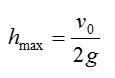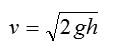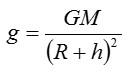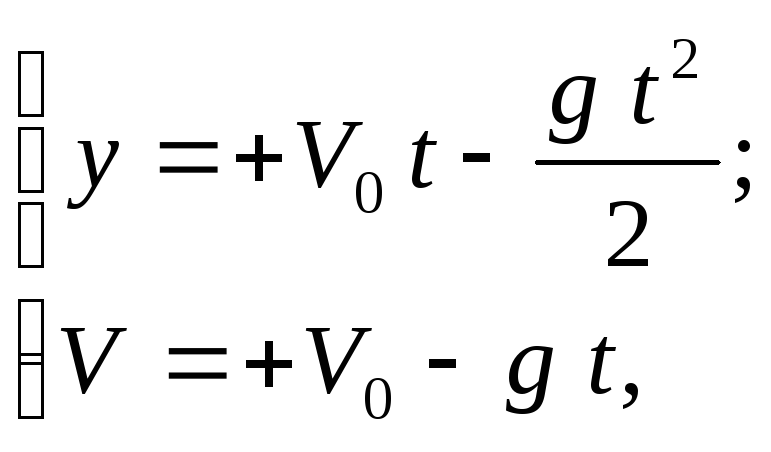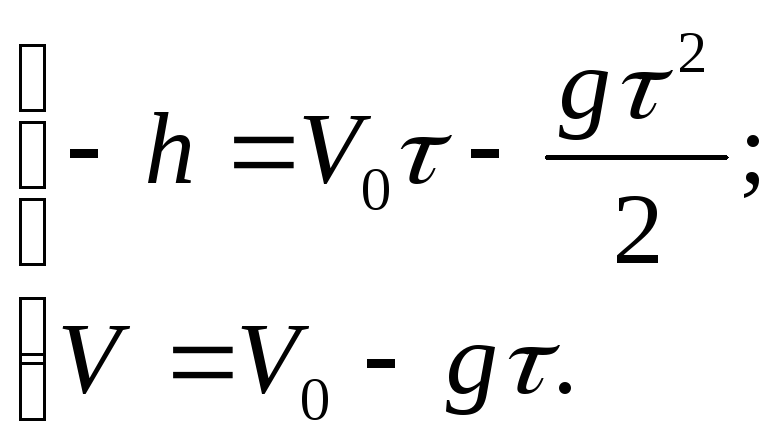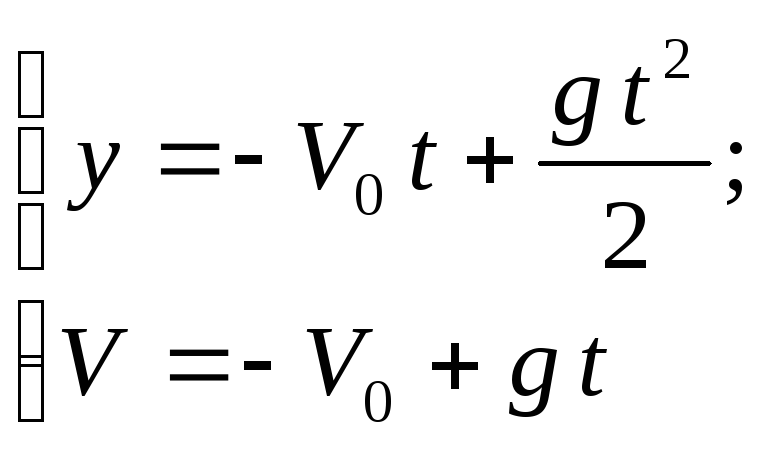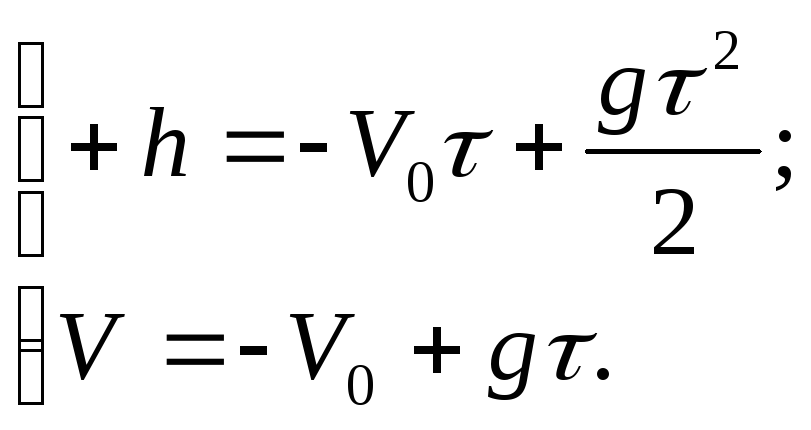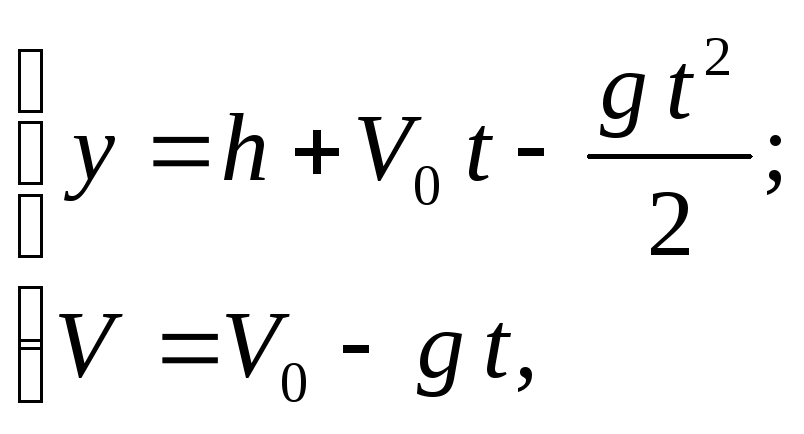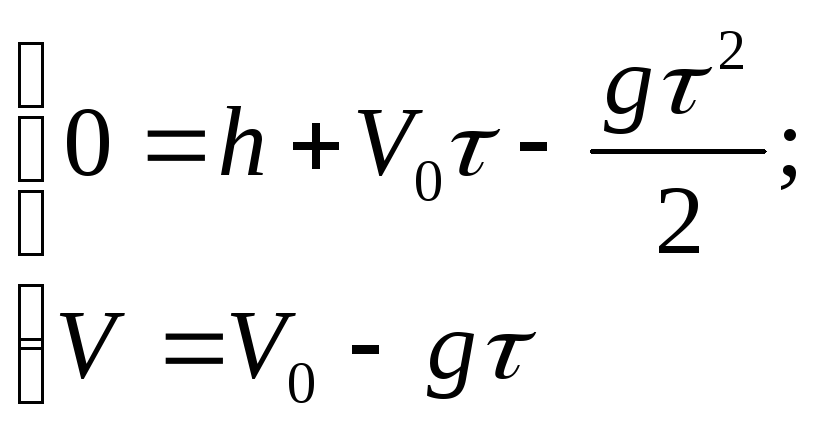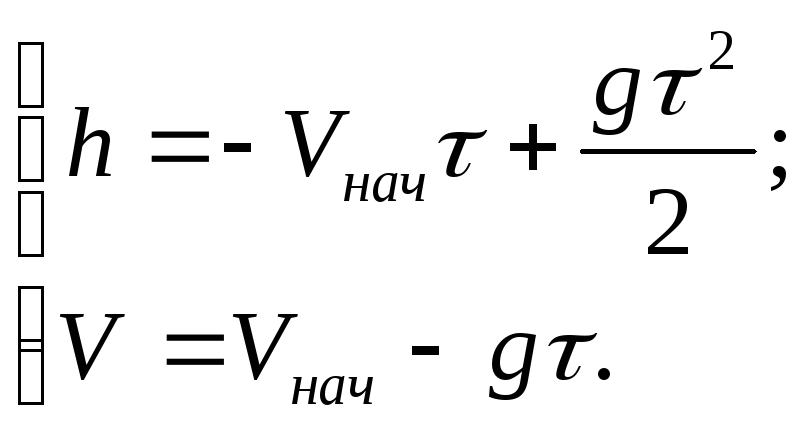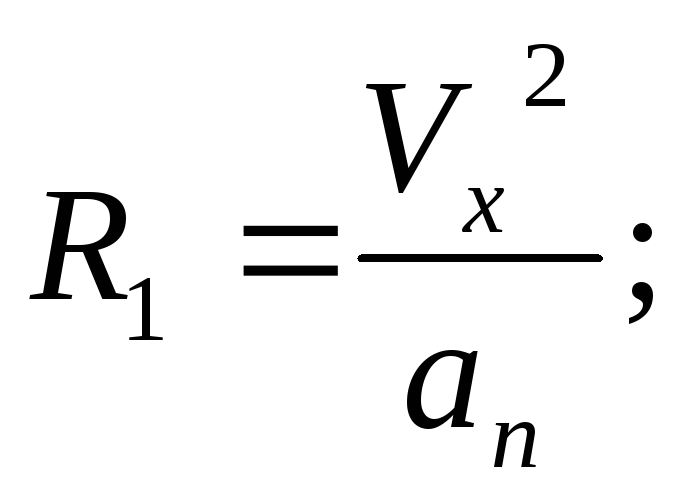Нашел более простое решение задачи. Смотри рисунок.
Камень падает по параболе (жирная кривая линия) и падает на склон в точке А. Х и У – координаты точки А. То есть Х – пройденный камнем путь по оси х, и У – путь по оси У. По оси Х (по горизонтали) камень движется с постоянной скоростью Vх = 8 м/c. По оси У камень падает на землю (то есть по вертикали) за счет силы гравитации Земли со скоростью Vу = gt, где g = 9,81 м/с – ускорение свободного падения и t – время. Пройденный путь по оси х определяется по формуле
х = Vх*t (1)
Пройденный путь по оси У равен (равноускоренное движение)
у = -g(t^2)/2 (2)
Найдем уравнение траектории, по которой камень движется (жирная линия на рисунке). Для этого надо в уравнениях (1) и (2) исключить время t. Из уравнения (1) находим t = х/Vх. Подставляем в уравнение (2), получим
у = -(g/2)(х/Vх)^2 (3)
То есть у зависит от х в квадрате. А это есть уравнение параболы. Теперь надо найти координаты точки А (Х и У), где камень падает на склон. Для этого надо знать еще и уравнение склона (наклонной плоскости или линии 0А на рисунке). Уравнение этой наклонной прямой линии (y = kx) такое
у = tg(-60°)*x = -sgrt3*х = -1,732х, (4)
так как тангенс -60° = -sgrt3 = -1,732. -60° — это угол Х0А (отрицательный), равный по абсолютной величине углу 0АУ = 60°. sgrt – обозначение квадратного корня. Из уравнений (3) и (4) находим (g/2)(х/Vх)^2 = 1,732х. Отсюда находим
Х = 2*1,732*(Vх^2)/g = 22,60 м (5)
так как у нас скорость Vх = 8 м/с. Подставим это Х в уравнение (4), получим
У = -39,14 м. Число отрицательное, так как отсчитываем расстояние вниз от оси х. Х и У – это катеты нашего треугольника. Гипотенузу 0А = S находим по теореме Пифагора
S^2 = X^2 + Y^2 (6)
Из (4) находим Y = -sgrt3*Х, тогда Y^2 = 3Х^2. Из (6) находим S^2 = X^2 + Y^2 = 4Х^2. Отсюда имеем S = 2Х. Используя (5), получим S = 45,2 м. Ответ 45,2 м.
Вторник, а это значит, что сегодня мы снова решаем задачи. На это раз, на тему «свободное падение тел».
Присоединяйтесь к нам в телеграм и получайте актуальную рассылку каждый день!
Задачи на свободное падение тел с решением
Задача №1. Нахождение скорости при свободном падении
Условие
Тело падает с высоты 20 метров. Какую скорость оно разовьет перед столкновением с Землей?
Решение
Высота нам известна по условию. Для решения применим формулу для скорости тела в момент падения и вычислим:
Ответ: примерно 20 метров в секунду.
Задача №2. Нахождение высоты и времени движения тела, брошенного вертикально.
Условие
Индеец выпускает стрелу из лука вертикально вверх с начальной скоростью 25 метров в секунду. За какое время стрела окажется в наивысшей точке и какой максимальной высоты она достигнет стрела?
Решение
Сначала запишем формулу из кинематики для скорости. Как известно, в наивысшей точке траектории скорость стрелы равна нулю:
Теперь запишем закон движения для вертикальной оси, направленной вертикально вверх.
Ответ: 2,5 секунды, 46 метров.
Задача №3. Нахождение времени движения тела, брошенного вертикально вверх
Условие
Мячик бросили вертикально вверх с начальной скоростью 30 метров в секунду. Через какое время мяч окажется на высоте 25 метров?
Решение
Запишем уравнение для движения мячика:
Мы получили квадратное уравнение. Упростим его и найдем корни:
Как видим, уравнение имеет два решения. Первый раз мячик побывал на высоте через 1 секунду (когда поднимался), а второй раз через 5 секунд (когда падал обратно).
Ответ: 1с, 5с.
Задача №4. Нахождение высоты при движении тела под углом к горизонту
Условие
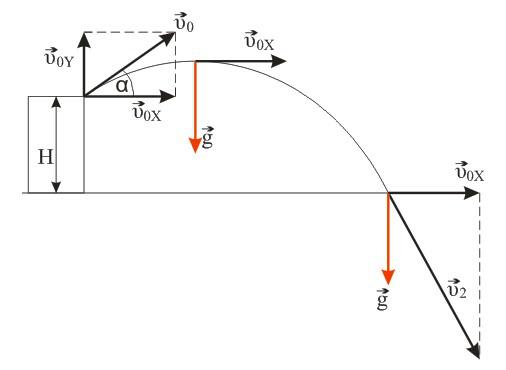
Камень, брошенный с крыши дома под углом альфа к горизонту, через время t1=0,5c достиг максимальной высоты, а еще через время t2=2,5c упал на землю. Определите высоту Н дома. Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/с2.
Решение
Камень брошен со скоростью v0 под углом α к горизонту с дома высотой Н. Эту скорость можно разложить на две составляющие: v0X (горизонтальная) и v0Y (вертикальная). В горизонтальном направлении на камень не действует никаких сил (сопротивлением воздуха пренебрегаем), поэтому горизонтальная составляющая скорости неизменна на протяжении всего времени полета камня (равномерное движение). Максимальная точка траектории камня над уровнем земли (исходя из кинематических соотношений):
Здесь t1 – время подъема камня с высоты Н на высоту h; g – ускорение свободного падения.
Вертикальную составляющую скорости можно вычислить исходя из геометрических соображений:
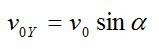
Подставив выражение для скорости в первое уравнение, получим:
Также высоту h можно выразить через время t2 падения камня с высоты h на землю (исходя из кинематических соотношений и учитывая, что с вертикальная составляющая скорости в наивысшей точке равна нулю):
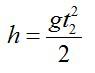
Для высоты дома можно записать:
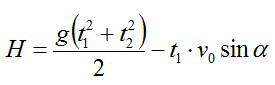
Так как вертикальная составляющая скорости камня в максимальной точке траектории равна нулю:
Подставляем в формулу для высоты H и вычисляем:
Ответ: H = 30 м.
Задача №5. Нахождение закона движения тела
Условие
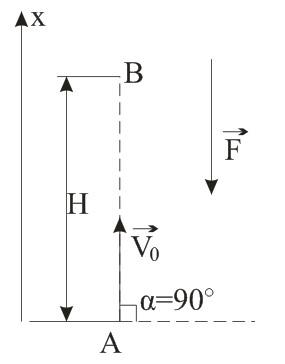
Найти закон движения тела против силы тяжести, при начальной скорости V0. И на какую максимальную высоту поднимется тело? Тело бросили под углом 90 градусов.
Решение
Тело брошено под углом α=90° к горизонту. Другими словами, тело брошено вертикально вверх с начальной скоростью V0. Направим координатную ось х вертикально вверх, так ее направление совпадает с вектором начальной скорости. F – сила тяжести, направленная вниз. В начальный момент тело находится в точке А.
В задаче нужно найти закон движения тела, то есть зависимость координаты тела от времени. В общем случае этот закон задается кинематическим соотношением:
где х0 – начальная координата тела; a – ускорение.
Так как мы поместили начало координат в точку А, х0=0. Тело движется с ускорением свободного падения g, при этом сила тяжести направлена против начальной скорости, поэтому в проекции на вертикальную ось a=-g. Таким образом, искомый закон движения перепишется в виде:
Далее будем использовать еще одно общее кинематическое соотношение:
где V – конечная скорость.
Максимальная высота подъема тела указана на рисунке точной B, в этот момент конечная скорость V равна нулю, а координата х равна максимальной высоте Н подъема тела. Отсюда можно найти выражение для этой величины:
Полезные формулы для решения задач на свободное падение
Свободное падение описывается формулами кинематики. Мы не будем приводить их вывод, но запишем самые полезные.
Формула для максимальной высоты подъема тела, брошенного вертикально вверх c некоторой начальной скоростью:
Кстати, как выводится именно эта формула можно посмотреть в последней задаче.
Формула для времени подъема и падения тела, брошенного вертикально вверх:
Скорость тела в момент падения с высоты h:
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Вопросы с ответами на свободное падение тел
Вопрос 1. Как направлен вектор ускорения свободного падения?
Ответ: можно просто сказать, что ускорение g направлено вниз. На самом деле, если говорить точнее, ускорение свободного падения направлено к центру Земли.
Вопрос 2. От чего зависит ускорение свободного падения?
Ответ: на Земле ускорение свободного падения зависит от географической широты, а также от высоты h подъема тела над поверхностью. На других планетах эта величина зависит от массы M и радиус R небесного тела. Общая формула для ускорения свободного падения:
Вопрос 3. Тело бросают вертикально вверх. Как можно охарактеризовать это движение?
Ответ: В этом случае тело движется равноускоренно. Причем время подъема и время падения тела с максимальной высоты равны.
Вопрос 4. А если тело бросают не вверх, а горизонтально или под углом к горизонту. Какое это движение?
Ответ: можно сказать, что это тоже свободное падение. В данном случае движение нужно рассматривать относительно двух осей: вертикальной и горизонтальной. Относительно горизонтальной оси тело движется равномерно, а относительно вертикальной – равноускоренно с ускорением g.
Баллистика – наука, изучающая особенности и законы движения тел, брошенных под углом к горизонту.
Вопрос 5. Что значит «свободное» падение.
Ответ: в данном контексте понимается, что тело при падении свободно от сопротивления воздуха.
Свободное падение тел: определения, примеры
Свободное падение – равноускоренное движение, происходящее под действием силы тяжести.
Первые попытки систематизированно и количественно описать свободное падение тел относятся к средневековью. Правда, тогда было широко распространено заблуждение, что тела разной массы падают с разной скоростью. На самом деле, в этом есть доля правды, ведь в реальном мире на скорость падения сильно влияет сопротивление воздуха.
Однако, если им можно пренебречь, то скорость падающих тел разной массы будет одинакова. Кстати, скорость при свободном падении возрастает пропорционально времени падения.
Ускорение свободно падающих тел не зависит от их массы.
Рекорд свободного падения для человека на данный момент принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который в 2012 году прыгнул с высоты 39 километров и находился в свободном падении 36 402,6 метра.
Примеры свободного падения тел:
- яблоко летит на голову Ньютона;
- парашютист выпрыгивает из самолета;
- перышко падает в герметичной трубке, из которой откачан воздух.
При свободном падении тела возникает состояние невесомости. Например, в таком же состоянии находятся предметы на космической станции, движущейся по орбите вокруг Земли. Можно сказать, что станция медленно, очень медленно падает на планету.
Конечно, свободное падение возможно не только не Земле, но и вблизи любого тела, обладающего достаточной массой. На других комических телах падения также будет равноускоренным, но величина ускорения свободного падения будет отличаться от земной. Кстати, раньше у нас уже выходил материал про гравитацию.
При решении задач ускорение g принято считать равным 9,81 м/с^2. В реальности его величина варьируется от 9,832 (на полюсах) до 9,78 (на экваторе). Такая разница обусловлена вращением Земли вокруг своей оси.
Нужна помощь в решении задач по физике? Обращайтесь в профессиональный студенческий сервис в любое время.
Решение
В
течение всего времени, пока камень
движется, его движение совершается по
одному и тому же закону. Действительно,
ускорение камня равное ускорению
свободного падения, если пренебречь
сопротивлением воздуха, все время
остается неизменным, следовательно,
движение камня является равнопеременным
движением с отличной от нуля начальной
скоростью. Закон движения не меняется
в тот момент, когда скорость изменяет
свое направление на противоположное
первоначальному.
Движение камня проходит по закону
(1)
его скорость
(2)
Знаки
начальной скорости и ускорения и
численное значение определяются выбором
положительного направления оси и начала
отсчета.
Рассмотрим
эту задачу в трех случаях.
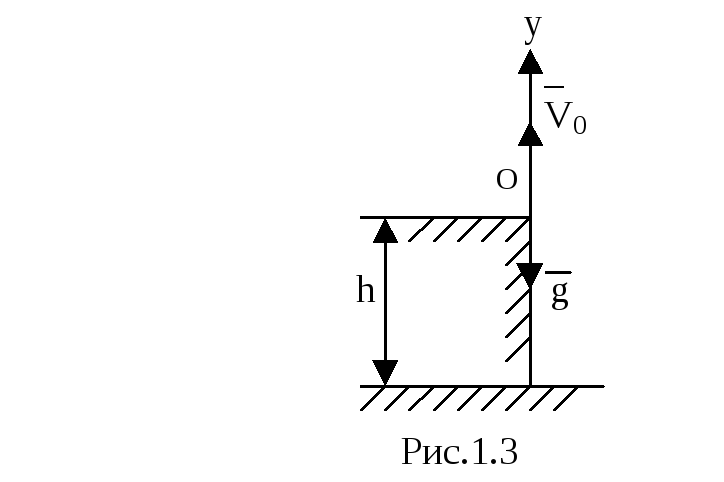
1) Ось OY
направлена
вверх, начало отсчета помещается на
уровне земли (рис.1.3) Тогда при
.
Уравнения (1) и (2)
примут вид
при t
= τ,
y
= —h
2) Ось OY
направлена вниз, начало отсчета на
уровне земли (рис 1.4). Тогда при
.
У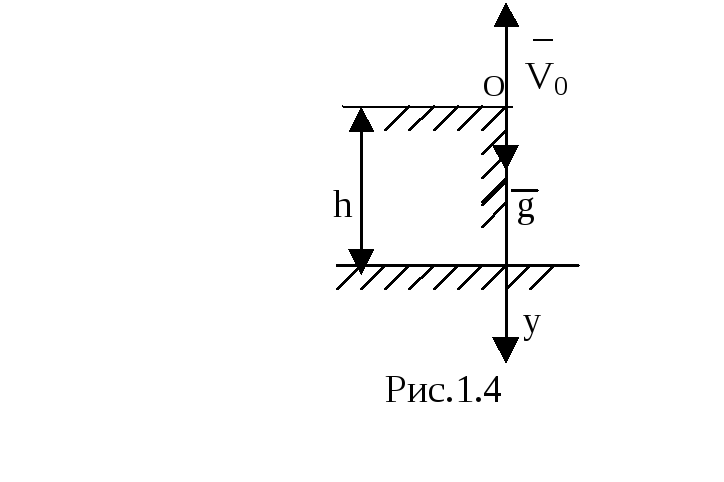
имеют вид
при t
= τ
y
= + h
3) Ось OY
направлена вверх, начало отсчета на
уровне дна колодца (рис.1.5). Тогда при
У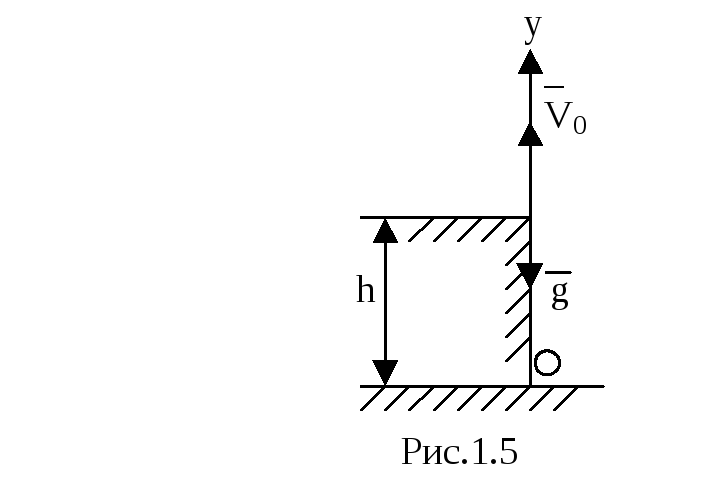
движения имеет вид
при t
= τ,
y
= 0, тогда
Все три варианта
дают одинаковые уравнения движения при
t
= τ
Для определения
решим
квадратное уравнение
Корень
его не учитываем, так как он не имеет
физического смысла.
а) Можно найти
максимальную высоту подъема камня,
исходя из того, что дискриминант
Тогда
а максимальное значение
м;
б)
Найти время, по истечении которого
камень находится в любой промежуточной
точке своего пути.
При
,
имеет два значения, так как в каждой
точке камень бывает дважды за время
движения.
Задача 5.
Камень брошен с высоты h=2,1
м под углом
= 45˚ к горизонту и падает на землю на
расстоянии S
= 42 м (по
горизонтали) от места бросания. Найти
начальную скорость V0
камня,
время полета τ и максимальную высоту
подъема над уровнем земли. Определить
также радиусы кривизны траектории в
верхней точке и в точке падения камня
на землю.
Д
h
= 2,1 м
= 45˚
S
= 42 м
V0
— ? τ
— ? H
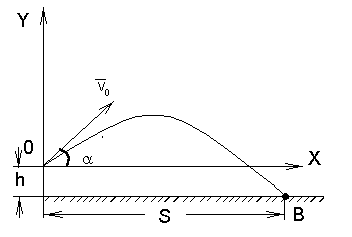
— ?
R1
и R2
— ?
Рис.1.6
Движение камня,
происходящее по параболе, можно
рассматривать как сумму двух независимых
движений: равномерного движения по
горизонтали (по оси Х)
и равнопеременного по вертикали (по оси
Y).
Начало отсчета удобно выбрать в точке
бросания. Ось Y
направлена вертикально вверх.
Для движения камня
по оси Х
получаем
;при
t
= τ x
= S
.
Следовательно,
(1)
Для движения по
оси OY
(2)
.
(3)
При t
= τ,
y
=
h,
поэтому
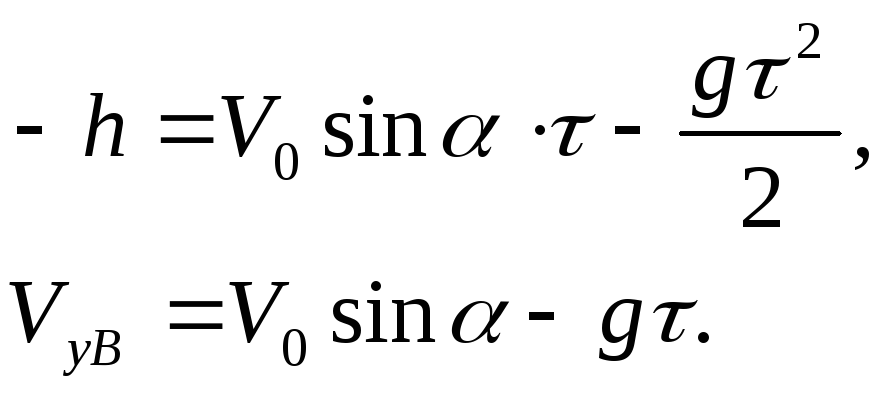
(5)
Решая совместно
уравнения (1) и (4), находим τ и V0:
1) τ
=
с,
2)
3) Высоту подъёма
камня можно найти из условия H
= h
+ ymax
.
При
отсюда
(
– время подъёма камня).
Подставив
в уравнение (4), получим
тогда
м.
4) Для определения
радиуса кривизны траектории в данной
точке нужно определить по величине и
направлению вектор полного ускорения.
В верхней точке траектории
,следовательно,
векторы ускорения и скорости взаимно
перпендикулярны. Это значит, чтоaτ
= 0,
an
= g.
Зная ускорение
и скорость, найдём радиус кривизны
траектории в верхней точке.
;
и
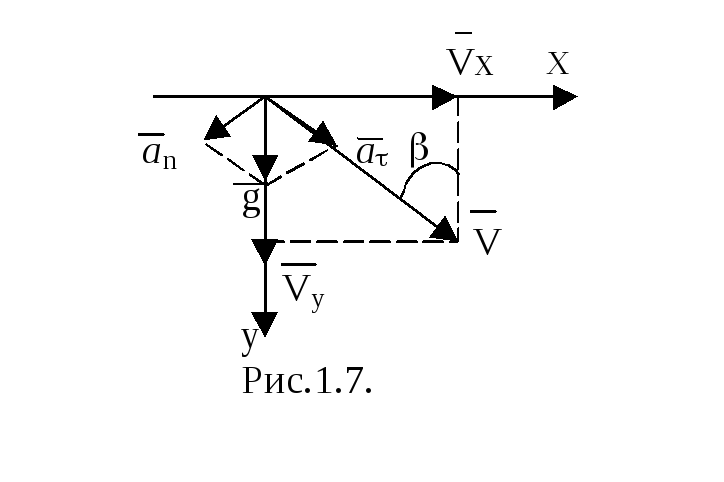
В
конечной точке траектории синус угла
βмежду векторами
скорости и ускорения может быть выражен
как показано на рис.1.7.
Разложим вектор
полного ускорения на нормальное и
тангенциальное, получим
Радиус траектории
в этой точке находится из соотношения
т.е.
Тогда R2
= 63 м.
Ответ:
З
6. Тело
вращается вокруг неподвижной оси по
закону φ
= 10 + 20 t
– 2 t2
рад. Найти: 1) Угловую скорость, угловое
ускорение и полное ускорение точки,
находящейся на расстоянии R
= 0,1 м от оси вращения, для момента времени
= 4 с (рис.
1.8). 2) Через сколько времени тело
остановится? 3)Сколько оборотов сделает
до остановки?
Д
φ
= 10
+ 20 t
–2 t2
рад
R
= 0,1 м
= 4 c
= 0
— ?
ε
— ?
a
—?
t
— ?
N
— ?
Рис.
1.8
Соседние файлы в папке Часть 1
- #
- #
- #
- #
- #
- #
McLosos — 14 октября, 2008 — 21:54
Камень брошен со скоростью V1 = 20 м/с под углом α = π/6 к горизонту.
- Напишите закон движения камня: x(t) и y(t).
- Найдите уравнение траектории камня и начертите ее в координатах OXY.
- Определите дальность полета камня и максимальную высоту подъема.
- При каком условии при заданной начальной скорости дальность полета будет максимальна?
- Определите нормальное и тангенциальное ускорение в верхней точке траектории.
Сопротивлением воздуха можно пренебречь.
Задачу дал на дом преподаватель на курсах при Московском Горном Государственном Институте. Она была взята из методического пособия Хайрнасова А.З.
Теги:
- кинематика
- механика
- формулы и графики
- свободное падение
- криволинейное движение
- неравномерное движение
- задачи с подсказками
- версия для печати
14
Научно-практическая конференция учащихся
МО «Эхирит-Булагатский район»
« Шаг в будущее»
25 апреля 2014 года,п Усть-Ордынский
Изучение траектории движения плоского камня
Работу выполнил:
Класс Максим,
МОУ Усть-Ордынская СОШ №4,
8 класс
Руководитель:
Айхаева Тамара Александровна,
учитель физики
МОУ Усть-Ордынская СОШ №4
П.Усть-Ордынский
2014год
Содержание
Введение …………………………………………………………………………… 3
Глава I. Теоретическое изучение движения плоского камня по воде .……………5
-
Из истории игры «Блинчики» на воде»…………………………………… 5
-
Изучение особенностей механического движения плоского камня,
подпрыгивающего на воде ……………………………………………..………….. 7
Глава II. Опытно-экспериментальная работа по изучению траектории
полёта плоского камня ……………………………….………………………..14
-
Практическое применение эффекта «блинчиков на воде» ……………………14
-
Исследование движения плоского камня на водной поверхности
……………………………………………………………………. 19
Заключение…………………………………………………………………………21
Список использованных источников ….…………………………………….22
Введение
Актуальность проекта. Отдыхая на реке, нам не раз приходилось наблюдать, или самим участвовать в пляжной забаве «Блинчики» на воде». Игра заключается в бросании плоских камешек по гладкой поверхности воды, которые должны подпрыгнуть несколько раз. Все, кто знаком с этой забавой, знают, что добиться даже двух-трех подпрыгиваний не просто: придется потренироваться, выискивая в песке подходящую плоскую гальку. Правильно подобрать и бросить камешек — целое искусство. Поэтому мы решили подойти к делу с научных позиций: определить, почему подпрыгивает плоский камень и где это может найти практическое применение?
Исходя из вышеизложенного, мы сформулировали цель проекта: изучение физических условий, при которых плоский камень многократно отскакивает от поверхности воды.
Объектом нашего исследования является механическое движение плоского камня.
Предмет: зависимость числа подпрыгиваний камня от физических условий броска.
Гипотеза: Проектная работа опирается на предположение о том, что плоский камень многократно будет отскакивать от поверхности воды, если будут соблюдены определённые условия механического движения, а именно:
-
выбран камень необходимой формы;
-
задана наиболее возможная начальная скорость;
-
создано вращательное движение;
-
определён оптимальный угол броска.
В соответствии с целью, объектом, предметом нами определены задачи проекта:
1. Проанализировать научную литературу по теме проекта.
2. Изучить теоретические особенности полёта плоского камня.
3. Провести опытно-экспериментальную работу по изучению траектории полёта плоского камня.
4. Рассмотреть возможности практического применения изучаемого механического процесса.
В работе над проектом применялись следующие методы исследования:
-
теоретический анализ;
-
эксперимент;
-
наблюдение;
4. сравнение физических свойств.
Глава I. Теоретическое изучение движения плоского камня по воде.
-
Из истории игры «Блинчики» на воде»
Проанализировав статью А.Зайцевой «Блинчики» на воде по-научному» [3], мы установили, что искусство пускания «блинчиков» известно с античных времен. Древние греки нередко развлекались, запуская в море найденные на берегу ракушки, камни и глиняные черепки. О состязаниях по бросанию ракушек, называвшихся «эпистокистос» (от греч.- ракушка), упоминает греческий лексикограф Юлий Поллукс (II век н. э.). Победителем считался тот, чья ракушка подпрыгнет наибольшее число раз. Римский христианский писатель Марк Минуций Феликс (II-III века н. э.) в своем «Октавии» оставил подробное описание аналогичных состязаний, где вместо ракушек использовали плоскую гальку округлой формы.
В Средние века традиция бросать камешки, судя по всему, не прерывалась. Так, в Англии с XII века стала популярной игра «утки и селезни», суть которой заключалась в бросании вдоль поверхности воды камней или устричных раковин. Когда раковина подпрыгивала первый раз, говорили «утка», второй раз — «селезень» и т.д. Подобная игра упоминалась в первоначальной версии шекспировской пьесы «ГенрихV» в XVI веке. По легенде, сам король Англии запустил однажды в Темзу соверен (золотую монету). С тех пор выражение «to make ducks and drakes with one’s money» означает «пускать деньги на ветер».
В Америке игру в «блинчики», называемую стоунскиппинг (stone skipping — подпрыгивание камешков), популяризировал Джордж Вашингтон, согласно легенде бросивший серебряный доллар в речку Потомак.
В XVI веке «блинчиками» заинтересовались военные — на этот раз в чисто практических целях. В 1578 году офицер британского флота Уильям Бурн впервые описал явление рикошета при стрельбе из артиллерийских орудий вдоль поверхности воды. Впоследствии этот способ стрельбы, позволявший увеличить дальность полета снаряда в два-три раза, широко использовали военные моряки, а во время Второй мировой войны он послужил основой для создания «прыгающей бомбы».
Американец Джердон Колеман-Мак Ги, всемирно признанный авторитет в пускании «блинчиков», написал книгу «Секреты стоунскиппинга», в которой обобщил свой многолетний опыт. Джердон считает стоунскиппинг не только увлекательным видом спорта, но и одним из лучших способов отдыха и расслабления.
В настоящее время пускание «блинчиков» — вполне серьезный вид спорта. Существует даже Североамериканская ассоциация стоунскиппинга, основанная в 1989 году с целью проведения ежегодных всемирных чемпионатов по бросанию камешков. К участию в состязании приглашаются все желающие независимо от возраста и уровня подготовки. Кстати, первым чемпионом мира, стала двадцатидвухлетняя девушка, заставившая свой камешек подпрыгнуть 23 раза, а в 1992 году Колеман-МакГи (основатель и руководитель ассоциации) добился 38 подпрыгиваний и попал в Книгу рекордов Гиннесса. Его рекорд оставался непревзойденным до 2003 года, когда камешек Курта Стайнера подскочил 40 раз. В 2007 году американец Рассэл Биарз поставил новый рекорд — 51 «блинчик».
1.2.Изучение особенностей механического движения плоского камня, подпрыгивающего на воде
Интуитивно понятно, что камень для пускания «блинчиков» должен быть плоским, не слишком маленьким, но и не очень тяжелым, бросать его нужно довольно сильно и почти горизонтально вдоль поверхности воды под небольшим углом к ней. Люди, которые имеют опыт бросания плоских камней, знают также, что для лучшего результата желательно при броске слегка закрутить камень. Остальное — дело тренировок. И все же, что заставляет камень прыгать, подобно лягушке, по поверхности воды вместо того, чтобы сразу пойти ко дну? Этот вопрос поставили перед собой авторы проекта и изучили статьи, в которых рассматривается этот вопрос с позиций современной гидродинамики, механики и других разделов физики [1, 2, 3, 11].
Нами было установлено, что французский физик Лидерик Боке попытался дать точный ответ на этот вопрос, почему плоские камни, при определённых условиях способны подпрыгивать на воде? В 2002 году он опубликовал статью «Физика стоунскиппинга», описывающую основные закономерности процесса.
Согласно Боке, брошенный камень оказывается во власти двух основных сил. Одна из них — сила тяжести — пропорциональна массе камня и направлена вниз; она заставляет камень падать на поверхность воды и погружаться. Другая — назовем ее «силой отталкивания», — напротив, не дает камню погрузиться в воду, как бы, выталкивая его наружу. Сила отталкивания направлена вверх, перпендикулярно площади контакта камня с водой. Если плоскость камня наклонена по отношению к поверхности воды, то силу отталкивания можно разложить на две составляющие — вертикальную и горизонтальную. Если сила тяжести преобладает над вертикальной составляющей, камень тонет, если наоборот — подпрыгивает, затем снова падает, вновь подпрыгивает, и так несколько раз. Величина силы тяжести не зависит от того, как именно брошен камень, она задается массой камня и потому не меняется в ходе подпрыгиваний. Значение силы отталкивания, напротив, определяется в первую очередь условиями броска, зависит от многих параметров и меняется от прыжка к прыжку.
Любители пускания «блинчиков» знают: при броске нужно закрутить камень, заставив вращаться вокруг оси, перпендикулярной его плоскости. Вращение придает телу большую стабильность, оно стремится сохранить направление оси своего вращения в силу «гироскопического эффекта» [8]. Например, волчок не падает, только когда быстро крутится.
Джердон Колеман-Мак Ги дает следующий практический совет по закручиванию камешков при броске: «Зажмите плоский камень между большим и средним пальцами руки, обхватив его ребро указательным пальцем. Частая ошибка — класть на ребро также и большой палец. Не делайте этого, пусть он лежит сверху. Приготовьтесь к броску, отведя запястье назад и немного вверх и прицелившись так, чтобы камень полетел практически параллельно поверхности воды. Затем резко выбросьте запястье вперед и запустите камень, закрутив его как можно сильнее».
Так держат камень для пускания «блинчиков»: слева — правильно; справа — неправильно.
Теория Лидерика Боке не дает конкретных советов, как держать камень, зато однозначно свидетельствует: чем с большей скоростью вы запускаете «блинчик», тем сильнее надо его закручивать. Кроме того, теория позволяет вычислить оптимальную скорость вращения камешка заданных размеров и скорости его поступательного движения, а также число «испеченных блинчиков» при различных значениях этих параметров. К примеру, расчеты Боке показали, что для получения 38 подпрыгиваний диска радиусом 5 см и массой 100 г Колеман-МакГи должен был бросить его со скоростью 12 м/с, закрутив до 14 оборотов в секунду.
И все же, с какой бы скоростью вы ни бросали и ни закручивали камень, и сколь идеальной ни была бы его форма, он не будет «танцевать» бесконечно, а, в конце концов, утонет. Причин этому, по крайней мере, две. Во-первых, в ходе подпрыгиваний камень постепенно теряет энергию вследствие трения о воду и сопротивления воздуха, что приводит к уменьшению его скорости и, следовательно, к уменьшению силы отталкивания воды. Во-вторых, не- смотря на гироскопический эффект, многочисленные удары о воду понемногу смещают ось вращения камня, что в конечном итоге приводит к полной потере его стабильности. Вопрос в том, что произойдет раньше: уменьшение скорости ниже критического значения или дестабилизация блинчика?
Оказывается, истинную причину потопления можно определить визуально, если внимательно наблюдать за процессом сбоку. Если плоскость камня сохраняет пространственную ориентацию, то с каждым ударом о воду камень теряет примерно одинаковую энергию. В результате расстояние между прыжками постепенно сокращается (оно пропорционально скорости камня). Перед тем как утонуть, камень как бы топчется на месте. В данном случае главная причина затопления — недостаток скорости. Если же перед затоплением этого не наблюдался — причина в преждевременной дестабилизации камня, то есть при выбранной скорости броска он был закручен недостаточно.
Итак, форма камня, скорость его полета и скорость вращения — вот три слагаемых успеха. Однако это еще не все. Как уже говорилось, бросать камень нужно почти горизонтально, вдоль поверхности воды. Но как лучше сориентировать саму плоскость камня, каков оптимальный угол ее наклона по отношению к поверхности воды?
Поначалу Боке пренебрег точными значениями угла наклона плоскости камня, а так же угла между траекторией его полета и поверхностью воды (назовем их углом наклона и углом падения соответственно), положив их в первом приближении просто малыми. Однако затем он вновь задумался о роли углов, поскольку их значения могут существенно влиять на величину силы отталкивания воды (они входят в коэффициент пропорциональности между силой отталкивания и квадратом скорости, умноженной на площадь контакта).
Поскольку описать это влияние теоретически оказалось довольно сложно, Боке решил обратиться к эксперименту, соорудив катапульту, которая метала бы «камешки» в бассейн с водой с определенной скоростью движения и вращения, а также с разными углами наклона и полета. Для проведения точных измерений достаточно было снабдить катапульту камерой скоростной съемки. Такая установка позволила бы проверить на практике предсказания теории, а также устранить некоторые ее неясности.
В качестве моделей камешков использовались алюминиевые диски диаметром несколько сантиметров и толщиной около трех миллиметров.
Камера с частотой съемки 2250 кадров в секунду регистрировала только первый отскок диска от воды. Но при этом можно было измерить время отскока диска от воды и изучить траекторию его полета, плавно меняя по очереди все ключевые параметры (поступательную и вращательную скорости, углы наклона самого диска и его траектории к поверхности воды).
Как ожидалось, эксперименты подтвердили правильность основных выводов теории. Но исследователей ждал и сюрприз: оказалось, что существует значение угла наклона плоскости диска к поверхности воды, при котором он отскакивает лучше всего (то есть время отскока минимально). Эффект наблюдался при любых значениях остальных параметров. Измерения показали, что «магический» угол равен 20 градусам.
Невольно напрашивался вывод: для достижения максимального числа подскоков необходимо запустить «блинчик» под этим «магическим» углом. В предвкушении нового мирового рекорда французские физики приступили к экспериментам в большом бассейне. Однако обнаружилось, что катапульта, как ни старается, не может заставить диск подпрыгнуть более двадцати раз. По мнению Клане, установка оказалась недостаточно устойчивой и при больших скоростях запуска диска начинала сильно вибрировать. Кроме того, выяснилось, что зависимость числа подскоков от угла наклона диска достигает максимума не при «магическом» угле 20 градусов, как ожидалось, а
в интервале от 10 до 20 градусов (причем явно ближе к 10)…
Таким образом, праздновать победу еще рано: ученым предстоят новые исследования. «Наука о блинчиках» — это вам далеко не детская забава.
Помогут ли изыскания французских исследователей рядовым гражданам достичь успехов в пускании «блинчиков»? В отличие от катапульты человек все равно не сможет с ходу запустить камень под строго определенным углом с точно заданной скоростью полета и вращения. Да и как измерить их в момент броска? Так что, даже пройдя «курс теоретической подготовки», все равно придется долго тренироваться, отрабатывая технику броска, как это и делали испокон века миллионы любителей «блинчиков», не обремененные знанием физики. Зато теперь, отправляясь к берегу водоема с плоским камешком в руке, вы будете чувствовать себя гораздо увереннее — как человек, вооруженный последними научными достижениями. И, может быть, удача вам улыбнется.
Оценим минимальную скорость броска, необходимую для того, чтобы камень подпрыгнул хотя бы один раз. Если камень массой m брошен со скоростью v, то в момент удара о поверхность воды на него действуют сила тяжести Р = m·g и сила реакции опоры Fp = kSv2, где S — площадь контакта камня с поверхностью воды, k — коэффициент, имеющий размерность плотности. Его величина зависит от формы камня, угла наклона плоскости камня к поверхности воды и угла между траекторией полета и поверхностью воды (угол падения α). Если считать углы малыми, то для круглого камня радиусом r можно приближенно записать Fp = kπr2v2, где k~ 500 кг/м3. Камень подскочит, если сила реакции опоры больше силы тяжести: Fp Р. Отсюда получаем условие подпрыгивания камня: vmin= √mg/кπr2, где vmin — минимальная скорость броска. Таким образом, чем тяжелее камень и чем меньше его радиус, тем с большей скоростью надо его бросать. Вот почему лучше брать довольно большие, но легкие камни. 
Например, чтобы камень радиусом 5 см и массой 100 г подпрыгнул хотя бы раз, его нужно бросить со скоростью больше 0,5 м/с (2 км/ч), камень радиусом 2,5 см и той же массой — больше 1 м/с (4 км/ч). А если взять камень радиусом 2,5 см и массой 50 г, его начальная скорость должна быть больше 0,7 м/с
(2,8 км/ч).
На камень, скользящий по воде, действуют сила тяжести Р, сила трения Fтр и сила нормального давления N. Она раскладывается на силу сопротивления Fс и силу реакции опоры Fр, которая компенсирует вес камня и не дает ему утонуть.
Теперь оценим максимально возможное число подпрыгиваний камня при заданной скорости броска. При каждом ударе о воду камень теряет энергию ∆Е (в основном за счет трения о воду), величину которой можно считать постоянной для каждого удара, так как она не зависит от скорости полета камня и определяется только его массой (по типу сухого трения). Не будет большой ошибкой предположить, что после последнего N-го удара кинетическая энергия камня станет равна 0 (хотя в действительности это не совсем так), то есть: отсюда получаем формулу для оценки максимального числа подскоков камня: N = mv2/2·∆Е. Из этой формулы следует, что, бросив камень вдвое быстрее, можно учетверить количество подскоков. Расчеты, выполненные Л.Боке, показали, что для камня радиусом 5 см и массой 100 г, брошенного так, что угол наклона его плоскости к поверхности воды а = 10°, потеря энергии при каждом ударе ∆Е = 0,2 Дж. Тогда, если начальная скорость v = 6,3 м/с, максимальное число подскоков N = 10. Чтобы повторить мировой рекорд (N = 40) с помощью такого камня, надо запустить его со скоростью примерно 12,6 м/с с углом наклона 10°.
Оценим теперь, как влияет скорость вращения камня на максимальное число подскоков. Несмотря на стабилизирующее действие гироскопического эффекта, каждый удар о воду смещает положение оси вращения камня на угол β, приближенно равный g/r·ω2, где г — радиус камня, ω — скорость его вращения.
Для многократного подпрыгивания необходимо, чтобы угол β был очень малым, то есть ω√g/r .Поэтому следует брать камень большого радиуса и закручивать его как можно сильнее. После N-го удара ось оказывается смещена на угол N·β. Если в качестве условия полной дестабилизации положить угол смещения оси 90° — α (камень повернулся ребром к поверхности воды), то N·β = π/2-α, то максимальное число подскоков N = (π/2-α)·β. Как показали эксперименты Боке, для оценки числа подскоков достаточно положить N·β = 1. Отсюда N = 1/β = r·ω2/g, ω= √g·N/r
Согласно полученной оценке, для достижения мирового рекорда камень радиусом 5 см нужно закрутить со скоростью не меньше 14 оборотов в секунду (полный оборот равен 2π радиан).
Глава II. Опытно-экспериментальная работа по изучению траектории
полёта плоского камня.
2.1. Практическое применение эффекта «блинчиков на воде».
Изучив ряд научных статей [2, 5, 8], мы узнали, что идея бомбы, прыгающей по воде, подобно камешку, пришла в голову английскому инженеру и авиаконструктору сэру Барнсу Уоллису в годы Второй мировой войны, в 1942-1943 годах. Чтобы сокрушить военную мощь Германии, союзникам требовалось разрушить ее тяжелую промышленность, работавшую в основном на армию.
Главной оружейной мастерской нацистов был Рурский индустриальный район. Военные заводы снабжались водой и электроэнергией из нескольких водохранилищ. И если разрушить их плотины, заводы встанут, поскольку, например, для выплавки тонны стали необходимо затратить семь тонн воды. Кроме того, наводнения, вызванные прорывом плотин, затопят населенные пункты вниз по течению, размоют дороги и мосты, повредят линии связи и нанесут заметный ущерб сельскому хозяйству.
Плотины представляли собой укрепленные бетоном земляные насыпи толщиной более 10 метров. Чтобы разрушить такое сооружение, необходимо затратить 30 тонн взрывчатки. Ни один бомбардировщик того времени не мог поднять бомбу такого веса.
Однако расчеты показали: если поместить заряд с напорной стороны дамбы на определенной глубине, его величину можно уменьшить до 5 тонн (ударная волна в воде усилит эффект от взрыва в несколько раз). Но как доставить заряд в нужное место? Обычные бомбы не годились из-за малой точности бомбометания, а от торпед дамбы надежно защищены противоторпедными сетями.
Уоллиса «заставил» бомбу добираться до нужной точки дамбы по поверхности воды своим ходом, то есть за счет рикошета. Проект Уоллиса состоял в следующем: подвесить бомбу цилиндрической формы под самолетом поперек фюзеляжа, раскрутить цилиндр вокруг его оси до определенной скорости, а затем сбросить бомбу с малой высоты на некотором расстоянии от цели — так, чтобы бомба самостоятельно до нее «до- прыгала». Ударившись о плотину, бомба должна была скатиться вдоль ее стенки под воду до требуемой глубины, где сработает гидростатический взрыватель.

Бомба Dam Buster висела под корпусом тяжелого бомбардировщика на V-образных стойках и раскручивалась до необходимой скорости электромотором.
Вращение бомбы обеспечивало ей стабильность после сброса за счет гироскопического эффекта. Направление вращения выбиралось так, чтобы, во-первых, уменьшить трение бомбы о воду, а во-вторых, чтобы в случае вылета бом- бы на парапет дамбы она скатилась назад, на ее напорную сторону.
Поначалу проект Уоллиса не вызвал энтузиазма у британского руководства, но после серии опытов отношение к нему резко изменилось, и к весне 1943 года ротационная бомба поступила на вооружение 617-й специальной эскадрильи. Она представляла собой цилиндр диаметром 124 сантиметра, длиной около полутора метров и общим весом 4200 килограммов (взрывчатка весила около 3 тонн). Цилиндр раскручивался примерно до 500 оборотов в минуту.
Попадания двух таких бомб должно было хватить для прорыва дамбы.
Предварительные расчеты показали, что бомбу необходимо сбросить при скорости 345 км/ч с высоты 18,5 метра на расстоянии 390 метров до цели. Соблюсти такие жесткие условия казалось почти невозможно.
Обычные средства — барометрические или радиовысотомеры, а также бомбовые прицелы — не годились: слишком мала высота полета. Однако решение все же нашлось, причем, простое и остроумное. Для контроля высоты на самолете установили два прожектора. Первый прожектор, укрепленный на носу самолета, светил вертикально вниз, второй, на его хвосте, — под углом к вертикали.
Лучи прожекторов пересекались на расстоянии 18,5 метра. Пилот должен был вести самолет так, чтобы пятна от прожекторов на поверхности воды сливались. Расстояние до дамбы определяли с помощью простейшего дальномера, а в качестве ориентира использовали две башенки, расположенные на гребне дамбы как раз посередине (расстояние между ними измерили по аэрофотоснимкам). Дальномер представлял собой фанерный треугольник, в одной из вершин которого установлен глазок, а в двух других вбиты гвоздики с таким расчетом, чтобы при взгляде через глазок башенки и гвоздики совпадали как раз в месте, где надо сбросить бомбу.
Атаку провели ночью 16 мая 1943 года. В результате бомбардировки удалось прорвать две крупные плотины, еще две получили серьезные повреждения. В результате опустошения водохранилищ и разрушительных наводнений промышленное производство в Руре на несколько месяцев упало на треть, было введено нормированное потребление воды. Экономика Германии понесла серьезный урон, что отразилось на результатах боевых действий вермахта.
Атака на плотину с использованием бомбы Ват Buster. Прыгая по поверхности воды верхнего бьефа плотины, бомба преодолевала противоторпедные сети, ударялась о стенку плотины и катилась по ней вниз. На глубине 9 метров бомба взрывалась, разрушая плотину.
Правда, и потери британцев в ходе бомбардировки оказались огромными: из 19 самолетов не вернулись 9, а из 133 членов экипажей погибли 56 летчиков. Но в целом операцию признали успешной.
Прыгающую бомбу создали для решения конкретной задачи — разрушения плотин, ни для чего другого она просто не годилась. Вот почему в литературе ее чаще всего называют Dam Buster (разрушитель плотин). Кроме того, Уоллис фактически создал «одноразовое» оружие, повторное применение которого было весьма проблематичным: зная об угрозе, противник мог простейшими мерами свести его эффективность к нулю (например, поставить аэростаты заграждения или добавить зенитных пулеметов). Тем не менее разрушение дамб с помощью прыгающих бомб вошло в историю как одна из наиболее оригинальных и остроумных операций, проведенных британской армией в ходе Второй мировой войны.
Возможно, в будущем гиперзвуковые самолеты (скорость которых в 5—12 раз превышает скорость звука) будут перемещаться по принципу «блинчика» — но только не по воде, а вдоль верхних слоев атмосферы. Специалисты американской национальной лаборатории Поуренса Ливермора предложили проект летательного аппарата, который позволит совершить перелет между любыми двумя точка ми земного шара менее чем за два часа.
Разработчики назвали свое детище HyperSoar («сверхвысокий полет»). Это, по сути, гибрид самолета и ракеты, оснащенный комбинированным ракетным и воздушно-реактивным двигателем. 
Схема полета высотного самолета HyperSoar. Опускаясь с высоты 60 километров до 35 и отражаясь от плотных слоев атмосферы, он совершает прыжки длиной по 450 километров.
Взлетев с аэродрома и развив скорость порядка 10 скоростей звука (3000 м/с), HyperSoar достигнет верхнего края атмосферы (примерно 40 км). Затем двигатель выключают, а самолет по инерции поднимется вверх до высоты 60 км, после чего начнет падать.
Падение будет продолжаться до тех пор, пока самолет не «столкнется» с плотными слоями атмосферы примерно на высоте 35 км и не отскочит вверх как «блин чик». Правда, в момент отскока двигатели вновь кратковременно включатся (примерно на 20 секунд), чтобы скомпенсировать потерю энергии в процессе удара. За один прыжок длительностью 2-3 минуты HyperSoar преодолеет 450 км, и рейс, скажем, из Чикаго в Токио потребует примерно 18 «прыжков» и займет 72 минуты. При этом две трети времени полета он станет находиться в безвоздушном пространстве, что существенно снизит перегрев самолета, неизбежный при движении в атмосфере. HyperSoar привлекателен не только высокой скоростью и грузоподъемностью, но и низким уровнем потребления горючего — вдвое меньшим по сравнению с обычными коммерческими самолетами.
Планируется также использовать его для доставки грузов в космос: при достижении максимальной высоты с его борта будут запускать небольшой носитель, который выведет на низкие орбиты коммерческие и военные грузы. А вот понравится ли HyperSoar пассажирам — еще вопрос. Ведь полет будет представлять собой чередование состояния невесомости и перегрузок до 1,5·g. Тут уж не до прохладительных напитков!
Любопытно, что проект подобного самолета, предназначенного для бомбардировки Америки, предложил еще в 1943 году германский инженер Зенгер. Самолет должен был стартовать с территории Германии и, сбросив мощную бомбу на один из городов США, приземлиться в союзнической Японии или, полностью обогнув земной шар, вернуться на свой аэродром. Немецкие конструкторы намеревались создать самолет уже к 1948 году, но, к счастью, война закончилась и этим планам не суждено было сбыться. Остается надеяться, что, если проект осуществится, применение HyperSoar станет мирным.
2.2.Исследование движения плоского камня на Кударейском озере
Опытно-экспериментальная работа проводилась на Кударейском озере летом 2013 г.
Цель эксперимента – установить зависимость числа подскоков плоских камней от скорости их бросания, вращения и угла наклона при падении.
Задачи опытно-экспериментальной работы:
-
разработка плана исследования;
-
проведение диагностических замеров;
-
анализ полученных результатов.
Основные закономерности силы отталкивания воды можно выяснить в ходе простого опыта. Если медленно опускать ладонь в воду параллельно ее поверхности, то практически никакого сопротивления не почувствуется. Вода, как и положено жидкости, плавно расступится, пропуская руку вглубь. А если резко опустить ладонь в воду, почувствуется удар о ее поверхность; при этом сама вода «разобьется» на брызги. Если ударить по воде ребром ладони — сила толчка заметно уменьшится. Таким образом, сила отталкивания тем больше, чем быстрее взаимодействует предмет с водой (то есть чем больше скорость полета камня или опускания руки) и чем больше площадь поверхности предмета, контактирующая с ней. А именно, отталкивание прямо пропорционально квадрату скорости, умноженной на площадь контакта. Все дело в том, что при быстром ударе молекулы жидкости не успевают «расступиться» и пропустить предмет, и чем он больше, тем труднее им это сделать.
В результате жидкость как бы «твердеет», приобретая свойства твердого тела — упругость, хрупкость и способность создавать реакцию опоры, которая здесь выступает в роли силы отталкивания. Все это хорошо известно любителям водных лыж и прыжков в воду. Встать на лыжи и опереться о воду не удается, пока катер, тянущий лыжника, движется медленно. Но стоит ему набрать скорость, и вода под ногами обретает упругость и твердость. Лыжи увеличивают площадь контакта с поверхностью воды, а при очень большой скорости можно обойтись и без них: для скольжения достаточно площади ступни, а то и пятки. Таким образом, чем выше скорость спортсмена на водных лыжах, тем лучше его держит вода.
Те же закономерности наблюдаются и при прыжках в воду: если плюхнуться всем телом в воду с большой высоты, можно получить не только синяки, но и серьезные травмы. Таким образом, чем больше начальная скорость камня, тем лучше он станет отскакивать от поверхности воды. Чтобы «блинчик» подпрыгнул хотя бы раз, его скорость должна превышать некоторое критическое значение, необходимое для преодоления силы тяжести. Оно определяется из равенства силы тяжести и вертикальной составляющей силы отталкивания. vmin= √mg/кπr2
|
R, м радиус камня |
m, кг масса камня |
v0, м/с начальная скорость |
N число подскоков |
|
0,05 |
0,1 |
0,5 |
1 |
|
0,025 |
0,1 |
1 |
|
|
0,025 |
0,05 |
0,7 |
Далее мы оценили максимально возможное число подпрыгиваний камня при заданной скорости броска.
При каждом ударе о воду камень теряет энергию ∆Е = 0,2 Дж. По формуле N = mv2/2·∆Е вычислим число подскоков камня. Проводя эксперимент, нам удалось добиться 8 подскоков. Рассчитав скорость броска, мы получили значение 5,6 м/с.
|
R, м радиус камня |
m, кг масса камня |
α, угол наклона плоскости плоского камня к поверхности воды |
ΔЕ, Дж энергия, теряемая камнем при каждом ударе |
v0, м/с начальная скорость |
N число подскоков |
|
0,05 |
0,1 |
100 |
0,2 |
6,3 |
10 |
|
12,6 |
40 |
||||
|
5,6 |
8 |
Теперь оценим, как влияет скорость вращения камня на максимальное число подскоков. Для оценки числа подскоков воспользуемся формулой
ω= 1/2 π√g·N/r (об/с). Вычислив скорость вращении камня, мы получили значение 9 об/с.
|
R, м радиус камня |
N число подскоков |
ω, об/с скорость вращения камня |
|
0,05 |
40 |
14 |
|
0, 025 |
8 |
9 |
Таким образом, расчёты подтверждают теоретический факт, что камень должен быть плоским и крупным, но достаточно легким. Невольно напрашивается мысль, что лучше всего взять круглый камень. Однако Колеман-МакГи с этим не согласен: «Одна из лучших форм — правильный треугольник или пятиугольник размером с ладонь». Он даже разработал и запатентовал «фирменную» пятиугольную модель камня, названную им Эко-Камнем. Камень изготовлен из экологически чистых сортов глины — чтобы занятия стоунскиппингом не привели к загрязнению водоемов.
Подобрав подходящий камень и запустив его с достаточно большой скоростью, мы не сразу добились впечатляющих результатов, даже после многочисленных тренировок. Дело в том, что после первого же удара о поверхность воды камешек изменяет ориентацию в пространстве и в следующий
раз ударится уже не плоской частью, а, скажем, ребром. Это резко изменит баланс сил в пользу силы тяжести, и камень скоропостижно утонет, не оправдав возложенных на него надежд. Увеличив скорость камня, мы лишь усилили вероятность его быстрой дестабилизации.
Заключение
Сначала «блинчики на воде» были просто развлечением, дающим прекрасный пример того, как физика помогает лучше понимать явления повседневной жизни.
В ходе выполнения проекта выяснилось, что искусство пускания «блинчиков» известно, по крайней мере, с античных времен. В настоящее время пускание «блинчиков» – вполне серьезный вид спорта.
Работая над проектом, мы опирались на теоретические исследования французского физика Лидерика Боке, благодаря которому наука о «блинчиках» впервые стала достоянием широкой общественности, согласно которому для многократного подскакивания камня необходимо выполнить следующие условия:
1. Камень для пускания «блинчиков» должен быть плоским, не слишком маленьким, но и не очень тяжелым, бросать его нужно довольно сильно под небольшим углом к ней (от 100 до 200).
2. Для лучшего результата необходимо при броске закрутить камень. Число подскоков зависит от скорости вращения камня: N = r·ω2/g,
3. Брошенный камень оказывается под действием двух основных сил. Одна из них — сила тяжести m·g. Другая — «сила отталкивания» Fp = kSv2.
4. Для того, чтобы камень подпрыгивал, его необходимо бросить со скоростью, большей минимальной: vmin= √mg/кπr2.
Проведённая нами опытно-экспериментальная работа на Кударейском озере, полностью подтверждает выдвинутую гипотезу.
Таким образом, теория «блинчиков» вполне актуальна и с научно-технической точки зрения. Ее, например, необходимо учитывать при расчете траектории спуска космических аппаратов, поскольку при входе в плотную атмосферу Земли под слишком малым углом они могут подпрыгивать, подобно камешкам на воде.
Список использованных источников
- Африна Е.И. Движение тела, брошенного под углом к горизонту http://www.home-edu.ru
-
Бросание плоских камней. http://www.krasrab.com/archive
-
Зайцева А. «Блинчики» на воде по-научному//Наука и жизнь. — 2006. — №6. – С.82-89.
-
Камни в воду: ученые высчитали волшебный угол. http://www.ccm.kz
- Карелов К. «Толлбой» — бомба-землетрясение//Тайны ХХ века.- 2007, №18
- Keyword: подпрыгивание камня на воде. Новости из мира математики. http://www.vmj.ru/news
- Павлов В.А. Гироскопический эффект. Его проявление и использование. — Л., Судостроение, 1972. — 284 с.
- Прыгающая бомба. http://dic.academic.ru
- Пускание «лягушек». http://www.dvorsportinfo.ru
-
Сверхзвуковая бомба //Око планеты.- 12.10.2011
- Скольжение камня по воде. http://www.energy-source.ru
-
Транковский С. Космонавтика без космодрома//Наука и жизнь. — 1994.- №9.- С. 12-15