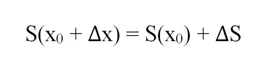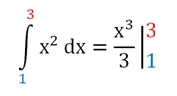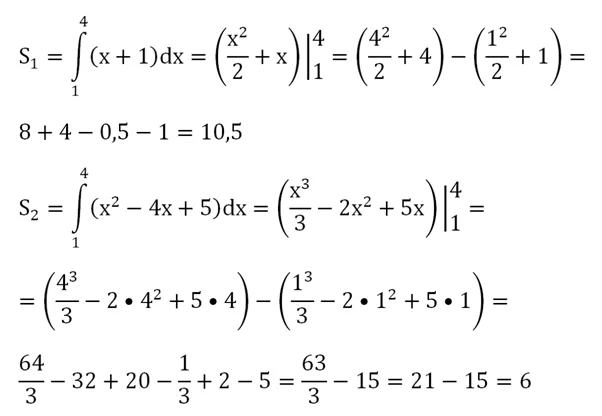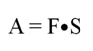План урока:
Криволинейная трапеция и понятие определенного интеграла
Формула Ньютона-Лейбница
Задачи, связанные с определенным интегралом
Криволинейная трапеция и понятие определенного интеграла
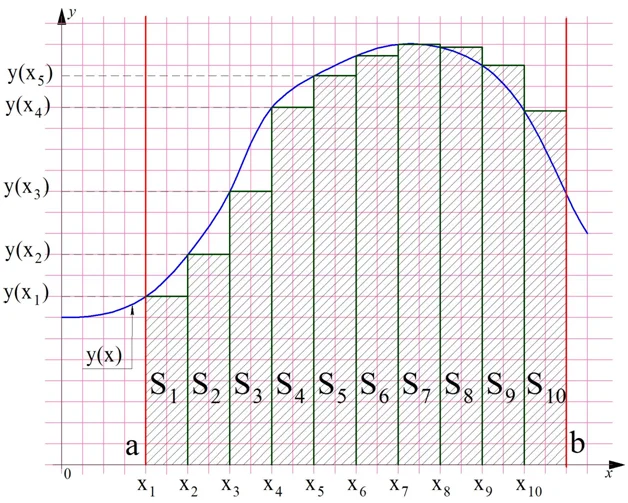
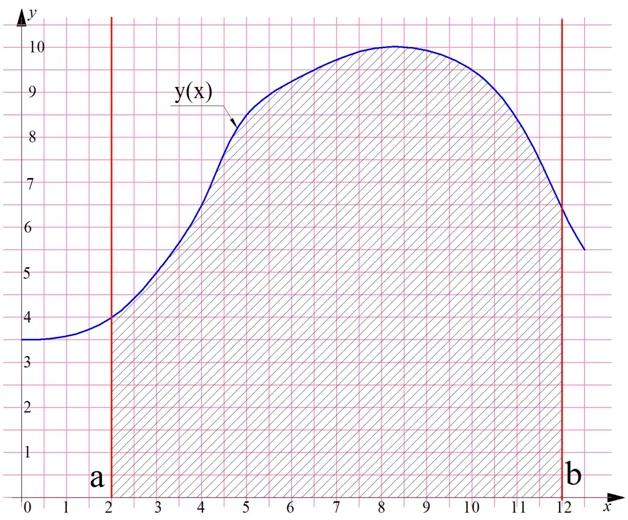
Построим на плоскости график произвольной функции у(х), который полностью располагается выше горизонтальной оси Ох. Далее проведем две вертикальные линии, пересекающие ось Ох в некоторых точках a и b. В результате мы получим интересную фигуру, которая на рисунке показана штриховкой:
Особенностью этой фигуры является то, что одна из ее сторон (верхняя) – это не прямая линия, а какая-то произвольная кривая. Условно будем считать эту фигуру четырехугольником, ведь у нее действительно четыре угла и четыре стороны. Две из них (вертикальные красные линии), очевидно, параллельны друг другу. Две другие стороны (кривую линию и участок оси Ох) параллельными назвать никак нельзя.
Напомним, что в геометрии четырехугольник, у которого две стороны параллельны друг другу, а две другие не параллельны, называют трапецией. Поэтому полученную нами фигуру мы также назовем трапецией. Но так как одна из ее сторон кривая, то мы будем использовать термин «криволинейная трапеция», чтобы отличать ее от трапеции «настоящей».
У каждой плоской фигуры есть площадь, и криволинейная трапеция – не исключение. Но как ее подсчитать? Есть приближенный способ подсчета. Разобьем отрезок [a; b] на несколько более мелких отрезков, и построим на каждом из них прямоугольник:
Обозначим площадь первого прямоугольника как S1, площадь второго прямоугольника – как S2 и т. д. Мы строим прямоугольники таким образом, что их левая сторона в точности равна значению функции в соответствующей точке. Обозначим те точки, на которых стоят стороны прямоугольника, как х1, х2, х3 и т. д. Тогда значения функции в этих точках будут соответственно равны у(х1), у(х2) и т. д.:
Площадь каждого полученного прямоугольника подсчитать несложно – она равна произведению его высоты на ширину. Мы организовали разбиение на прямоугольники таким образом, что ширина у них одинакова. Обозначим ее как ∆х. Тогда площадь каждого отдельного прямоугольника равна
Тогда общая площадь криволинейной трапеции приближенно будет равна сумме площадей всех треугольников:
где n – это количество прямоугольников (на рисунках мы выбрали n = 10).
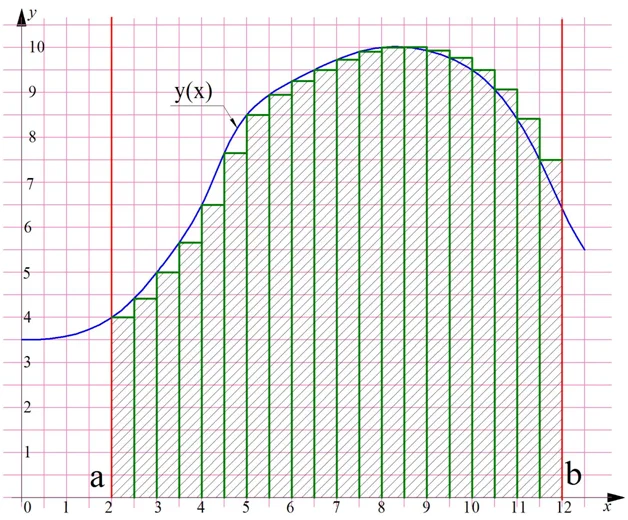
Ясно, что чем больше число n, тем более точное приближение мы получим. Например, если разбить трапецию уже не на 10, а на 20 прямоугольников, то получим такую картинку:
Обратите внимание, что ширина каждого прямоугольника, то есть величина ∆х, уменьшилась.
При росте числа n ошибка при оценке площади трапеции будет уменьшаться и стремится к нулю. Поэтому в предельном случае, когда n стремится к бесконечности, в формуле (1) вместо знака приближенного равенства «≈» можно поставить знак «=». При этом величина ∆х также будет стремится к нулю, то есть становится бесконечно малой. В математике для таких величин вместо символа ∆ принято использовать букву d, то есть вместо ∆х мы напишем dx. С учетом всего этого формула (1) примет вид:
В правой части стоит сумма бесконечного числа слагаемых. У нее есть специальное название – определенный интеграл. Ясно, что величина этой суммы, то есть площадь трапеции, зависят от чисел а и b (боковых границ трапеции). Поэтому обозначение интеграла выглядит так:
Обозначение очень похоже на неопределенный интеграл. Единственное отличие – это появление чисел а и b, которые определяют боковые границы трапеции. Число b называют верхним пределом интегрирования, а число a– нижним пределом интегрирования. Дадим более строгое определение понятию определенного интеграла.
Геометрический смысл определенного интеграла заключается в том, что он равен площади криволинейной трапеции, ограниченной графиком функции у(х) и вертикальными прямыми, проходящими через точки а и b.
Формула Ньютона-Лейбница
Изначально мы хотели научиться вычислять площадь криволинейной трапеции, однако пока что мы лишь придумали, как ее обозначать – через определенный интеграл. Но как вычислить значение его значение? Оказывается, определенный интеграл очень тесно связан с неопределенным интегралом, и эта связь описывается формулой Ньютона-Лейбница.
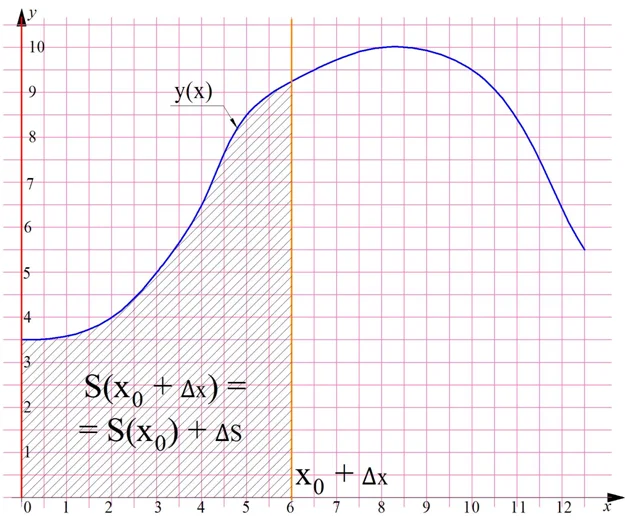
Ещё раз построим криволинейную трапецию, а ее площадь обозначим как S. Пусть ее левая граница совпадает с осью Оу, а правая будет равна некоторому значению х0. Дело в том, что нас будет интересовать зависимость площади трапеции от значения ее правой границы, то есть некоторая функция S(x). Обозначим площадь получившейся трапеции как S(x0):
Теперь сдвинем правую границу вправо на величину ∆х. В итоге получим новую трапецию, площадь которой можно записать как S(x0 + ∆x). При этом ее площадь увеличилась на некоторую величину ∆S:
Получается, что мы дали некоторое приращение аргумента ∆х, и получили приращение функции ∆S. Мы уже выполняли похожие действия в рамках предыдущих уроков, изучая понятие производной.
Итак, мы можем записать, что
Оценим величину ∆S. Если заменить соответствующую площадь прямоугольником, то его площадь окажется равной произведению ширины прямоугольника (она равна ∆x) на высоту, которая равна у(х0):
Поделим обе части равенства (2) на величину ∆х и получим:
А теперь устремим величину ∆х к нулю. В результате в равенство (2), а значит, и (3) будет становиться все более точным. В итоге мы можем написать, что
Хорошо подумайте, что мы получили. Вспомните определение производной. Оказывается, в левой части равенства (4) стоит не что иное, как производная функции S! То есть мы можем написать, что
Получается, что производная функции S на равна значению функции у(х). А это значит, что она является ее первообразной:
Здесь F(x) – первообразная функции у(х), а F(x0) – конкретное значение этой первообразной в точке х0.
Теперь рассмотрим более привычную криволинейную трапецию, у которой правой и левой границей являются числа а и b:
Как найти ее площадь? С помощью формулы (5) мы можем найти две площади:
Из рисунков очевидно, что площадь интересующей нас трапеции равна разности величин S(b) и S(a):
Эту площадь мы и обозначаем определенным интегралом. То есть можно записать, что
Таким образом, чтобы найти площадь криволинейной трапеции, необходимо проинтегрировать функцию у(х), а потом в полученную первообразную подставить числа а и b вычесть один результат из другого.
Для примера вычислим площадь криволинейной трапеции, ограниченной линией у = х2 и вертикальными прямыми х = 1 и х = 3.
Сначала находим первообразную функции у = х2, взяв от нее интеграл (неопределенный):
Отметим, что в обоих случаях речь идет об одной и той же первообразной, поэтому значения констант С у них одинаковы. Теперь вычитаем из F(3) величину F(1):
Константы интегрирования сократились. Для простоты решение записывают в несколько более короткой форме. Сначала сразу после определенного интеграла пишут первообразную (то есть находят неопределенный интеграл), причем без константы интегрирования
Далее ставят вертикальную черту и пишут пределы интегрирования, которые надо подставить в первообразную:
Потом ставят знак равно и подставляют в первообразную верхнее и нижнее число, после чего выполняют оставшиеся арифметические действия:
Задание. Вычислите
Задание. Найдите площадь фигуры, ограниченной полуволной синусоиды и осью Ох.
Решение. Сначала построим схематичный график у = sinx, чтобы понять, что именно нам надо вычислить:
Теперь ясно, что надо произвести вычисление определенного интеграла синуса на отрезке [0; π]:
Итак, мы теперь знаем и про определенный, и про неопределенный интеграл. Хотя они и очень похожи, между ними есть большая разница, и ее важно понимать. Определенный интеграл – это число, а именно величина площади криволинейной трапеции. Неопределенный интеграл – это функция (точнее, семейство функций), которая является первообразной для интегрируемой функции. Формула Ньютона-Лейбница как раз и показывает ту связь, которая есть между двумя этими различными понятиями.
Может ли определенный интеграл быть отрицательным числом? Кажется, что нет, ведь площадь фигур не бывает отрицательной. Но не всё так просто. Рассмотрим случай, когда график функции является не верхней, а нижней границей трапеции. Например, пусть трапеция образована функцией
Просто надо найти определенный интеграл:
Получили отрицательное значение. Дело в том, что фигура располагается под осью Ох. Из-за этого ее площадь получается со знаком минус.
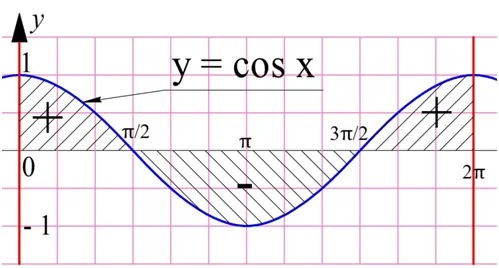
Рассмотрим ещё один пример. Найдем интеграл косинуса на промежутке от 0 до 2π:
Получился ноль. Посмотрим на графике, какую же площадь мы посчитали:
Оказывается, график на отрезке дважды пересекает ось Ох. В результате получается сразу три криволинейных трапеции. Две из них расположены выше оси Ох, а потому из площади считаются со знаком «+». Третья трапеция лежит ниже оси Ох, а потому ее площадь считается со знаком «–». То, что интеграл оказался равным нулю, означает, что площадь нижней трапеции в точности равна сумме площадей двух верхних фигур, поэтому в сумме они и дали ноль.
Отметим важное свойство определенного интеграла:
Проиллюстрируем это правило графически. Каждый из этих интегралов равен площади соответствующих криволинейных трапеций:
Задачи, связанные с определенным интегралом
Определенный интеграл помогает находить и площади более сложных фигур, которые получаются при пересечении нескольких различных графиков.
Рассмотрим задачу на интеграл. Пусть требуется найти площадь фигуры, полученной при пересечении параболы
Сначала найдем точки пересечения графиков. Для этого приравняем функции:
Корнями этого квадратного уравнения являются числа 1 и 4. Именно в этих точках и пересекаются графики (это и так видно из графика). Площадь интересующей нас фигуры можно получить вычитанием из одной криволинейной трапеции другой:
Величины S1и S2 можно вычислить через определенный интеграл. Обратите внимание, что найденные нами корни являются пределами интегрирования:
Тогда искомая нами площадь составит
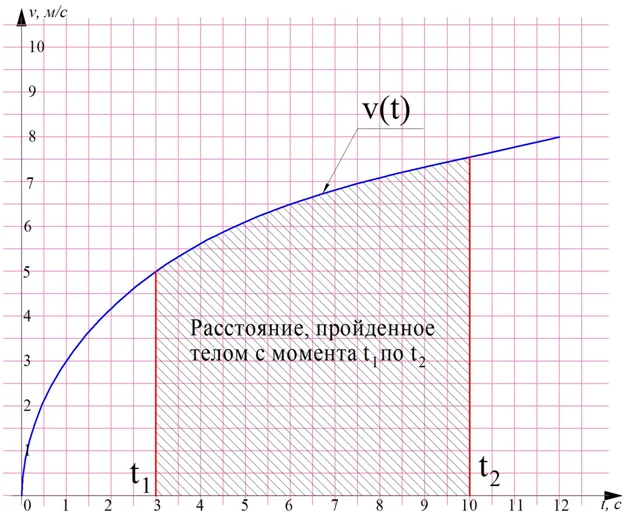
Ошибочно думать, что определенные интегралы нужны только для расчета площадей. С их помощью можно и решать ряд физических задач. Пусть известен закон изменения скорости тела v(t). Можно доказать, что путь, пройденный этим телом за период времени с t1по t2, будет равен интегралу
Задание. Самолет разгоняется, однако из-за сопротивления воздуха он набирает скорость не равномерно. Скорость самолета в момент времени t может быть вычислена по формуле
Определите, какое расстояние пролетит самолет в период времени между 16-ой и 25-ой секундой разгона.
Решение. Задача сводится к простому вычислению интеграла:
Ответ: 610 метров.
Этот пример показывает важную зависимость между скоростью тела и путем, который она преодолевает. Если есть график изменения скорости тела, то площадь под этим графиком равна тому пути, которое проходит тело:
Действительно, если тело двигается равномерно (то есть с постоянной скоростью), то путь, пройденный им, может быть вычислен по известной формуле
Но если построить для такого случая график v(t), то он будет выглядеть как горизонтальная прямая линия. Тогдафигура под графиком окажется прямоугольником, чья площадь равна произведению длины и ширины:
Заметим, что зависимость между путем, скоростью временем носит линейный характер, и именно поэтому здесь может быть использован неопределенный интеграл. Но ведь в физике очень много линейных зависимостей! И во всех этих случаях интегралы играют огромную роль!
Рассмотрим задачу. Есть пружина, которая изначально находится в нерастянутом состоянии. Потом человек начинает медленно и с постоянной скоростью, растягивать пружину, увеличивая ее длину на 0,5 метра. Жесткость пружины (ее коэффициент упругости) равна 100 Н/м. Какую работу совершил человек при растягивании пружины?
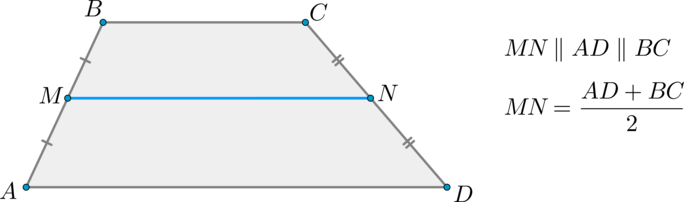
Из средней школы известна следующая формула для вычисления работы:
где F– сама сила, а S– путь, пройденный телом под действием этой силы. Легко заметить, что эта формула похожа на ранее рассмотренную зависимость пути от скорости и времени (они обе являются линейными). Сначала рассмотрим простой случай, когда сила остается неизменной. Тогда можно построить график F(S). Окажется, что площадь под графиком как раз равна работе, совершенной силой:
Случай с пружиной сложнее, ведь сила при растяжении пружины не остается неизменной. Чем сильнее растянута пружина, с тем большей силой ее приходится тянуть. Известен закон Гука, связывающий удлинение пружины с силой ее натяжения:
где k – коэффициент жесткости пружины, а x– ее удлинение. По смыслу задачи максимальное удлинение известно и равно 0,5 м. Можно нарисовать такой график зависимости силы натяжения пружины от ее удлинения (он будет выглядеть как прямая линия, так как эта зависимость является прямой пропорциональностью):
И в данном случае работа также будет равна площади под графиком функции, то есть ее можно посчитать с помощью определенного интеграла! В качестве пределов интегрирования надо взять крайние значения удлинения пружины (это 0 и 0,5 м), а качестве интегрируемой функции – F(t), которая равна
Существует и много других примеров приложений определенного интеграла. С его помощью можно находить объемы сложных фигур (конуса, пирамиды, тел вращения), определять центр масс тел сложной формы. Следует отметить и использование интегралов в механике при решении задач, в которых сила действует не на конкретную точку, а на площадь (задачи на распределенную нагрузку). В качестве примера можно привести расчет прочности крыши, на которой лежит слой снега.Но для их рассмотрения необходим более высокий уровень математических и физических знаний, который можно получить уже в рамках не среднего, а высшего образования.
[{Large{text{Произвольная трапеция}}}]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна (180^circ).
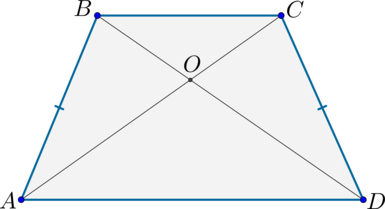
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
Доказательство
1) Т.к. (ADparallel BC), то углы (angle BAD) и (angle ABC) – односторонние при этих прямых и секущей (AB), следовательно, (angle
BAD
+angle ABC=180^circ).
2) Т.к. (ADparallel BC) и (BD) – секущая, то (angle DBC=angle
BDA) как накрест лежащие.
Также (angle BOC=angle AOD) как вертикальные.
Следовательно, по двум углам (triangle BOC sim triangle AOD).
Докажем, что (S_{triangle AOB}=S_{triangle COD}). Пусть (h) – высота трапеции. Тогда (S_{triangle ABD}=frac12cdot hcdot
AD=S_{triangle ACD}). Тогда: [S_{triangle AOB}=S_{triangle ABD}-S_{triangle AOD}=S_{triangle ACD}-S_{triangle AOD}=S_{triangle
COD}]
Определение
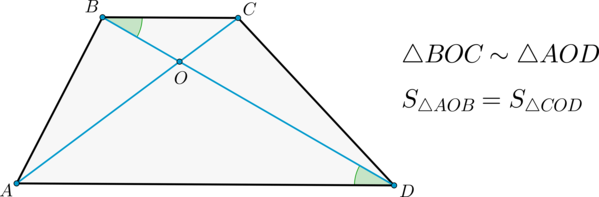
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
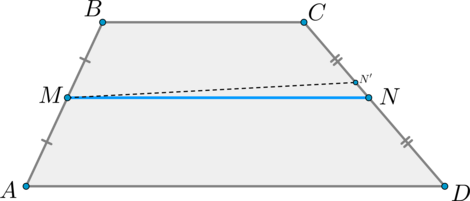
1) Докажем параллельность.
Проведем через точку (M) прямую (MN’parallel AD) ((N’in CD)). Тогда по теореме Фалеса (т.к. (MN’parallel ADparallel BC, AM=MB)) точка (N’) — середина отрезка (CD). Значит, точки (N) и (N’) совпадут.
2) Докажем формулу.
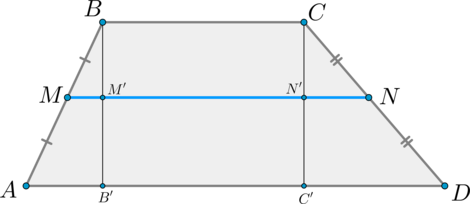
Проведем (BB’perp AD, CC’perp AD). Пусть (BB’cap MN=M’, CC’cap
MN=N’).
Тогда по теореме Фалеса (M’) и (N’) — середины отрезков (BB’) и (CC’) соответственно. Значит, (MM’) – средняя линия (triangle
ABB’), (NN’) — средняя линия (triangle DCC’). Поэтому: [MM’=dfrac12 AB’, quad NN’=dfrac12 DC’]
Т.к. (MNparallel ADparallel BC) и (BB’, CC’perp AD), то (B’M’N’C’) и (BM’N’C) – прямоугольники. По теореме Фалеса из (MNparallel AD) и (AM=MB) следует, что (B’M’=M’B). Значит, (B’M’N’C’) и (BM’N’C) – равные прямоугольники, следовательно, (M’N’=B’C’=BC).
Таким образом:
[MN=MM’+M’N’+N’N=dfrac12 AB’+B’C’+dfrac12 C’D=] [=dfrac12 left(AB’+B’C’+BC+C’Dright)=dfrac12left(AD+BCright)]
Теорема: свойство произвольной трапеции
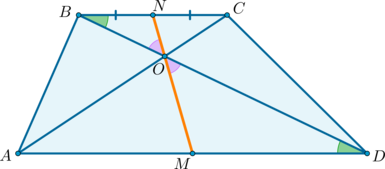
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
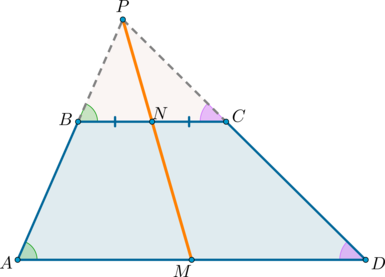
1) Докажем, что точки (P), (N) и (M) лежат на одной прямой.
Проведем прямую (PN) ((P) – точка пересечения продолжений боковых сторон, (N) – середина (BC)). Пусть она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
Рассмотрим (triangle BPN) и (triangle APM). Они подобны по двум углам ((angle APM) – общий, (angle PAM=angle PBN) как соответственные при (ADparallel BC) и (AB) секущей). Значит: [dfrac{BN}{AM}=dfrac{PN}{PM}]
Рассмотрим (triangle CPN) и (triangle DPM). Они подобны по двум углам ((angle DPM) – общий, (angle PDM=angle PCN) как соответственные при (ADparallel BC) и (CD) секущей). Значит: [dfrac{CN}{DM}=dfrac{PN}{PM}]
Отсюда (dfrac{BN}{AM}=dfrac{CN}{DM}). Но (BN=NC), следовательно, (AM=DM).
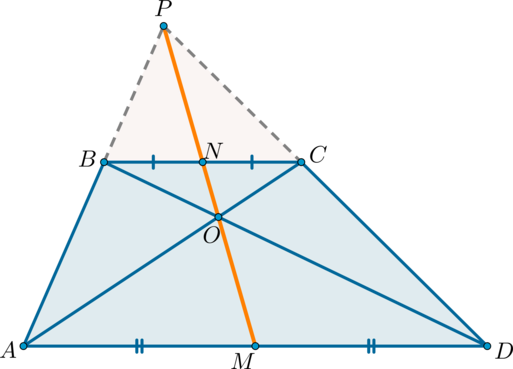
2) Докажем, что точки (N, O, M) лежат на одной прямой.
Пусть (N) – середина (BC), (O) – точка пересечения диагоналей. Проведем прямую (NO), она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
(triangle BNOsim triangle DMO) по двум углам ((angle OBN=angle
ODM) как накрест лежащие при (BCparallel AD) и (BD) секущей; (angle BON=angle DOM) как вертикальные). Значит: [dfrac{BN}{MD}=dfrac{ON}{OM}]
Аналогично (triangle CONsim triangle AOM). Значит: [dfrac{CN}{MA}=dfrac{ON}{OM}]
Отсюда (dfrac{BN}{MD}=dfrac{CN}{MA}). Но (BN=CN), следовательно, (AM=MD).
[{Large{text{Равнобедренная трапеция}}}]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
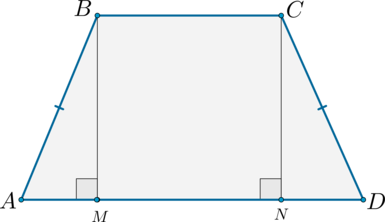
1) Рассмотрим равнобедренную трапецию (ABCD).
Из вершин (B) и (C) опустим на сторону (AD) перпендикуляры (BM) и (CN) соответственно. Так как (BMperp AD) и (CNperp AD), то (BMparallel CN); (ADparallel BC), тогда (MBCN) – параллелограмм, следовательно, (BM = CN).
Рассмотрим прямоугольные треугольники (ABM) и (CDN). Так как у них равны гипотенузы и катет (BM) равен катету (CN), то эти треугольники равны, следовательно, (angle DAB = angle CDA).
2)
Т.к. (AB=CD, angle A=angle D, AD) – общая, то по первому признаку (triangle ABD=triangle ACD). Следовательно, (AC=BD).
3) Т.к. (triangle ABD=triangle ACD), то (angle BDA=angle CAD). Следовательно, треугольник (triangle AOD) – равнобедренный. Аналогично доказывается, что и (triangle BOC) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
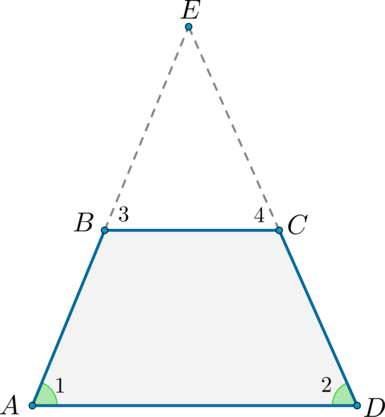
Рассмотрим трапецию (ABCD), такую что (angle A = angle D).
Достроим трапецию до треугольника (AED) как показано на рисунке. Так как (angle 1 = angle 2), то треугольник (AED) равнобедренный и (AE
= ED). Углы (1) и (3) равны как соответственные при параллельных прямых (AD) и (BC) и секущей (AB). Аналогично равны углы (2) и (4), но (angle 1 = angle 2), тогда (angle 3 = angle 1 = angle 2 =
angle 4), следовательно, треугольник (BEC) тоже равнобедренный и (BE = EC).
В итоге (AB = AE — BE = DE — CE = CD), то есть (AB = CD), что и требовалось доказать.
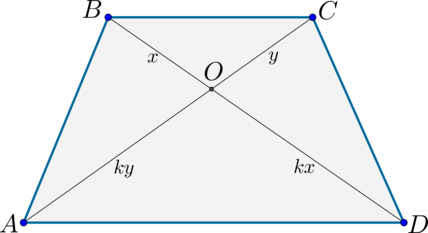
2) Пусть (AC=BD). Т.к. (triangle AODsim triangle BOC), то обозначим их коэффициент подобия за (k). Тогда если (BO=x), то (OD=kx). Аналогично (CO=y Rightarrow AO=ky).
Т.к. (AC=BD), то (x+kx=y+ky Rightarrow x=y). Значит (triangle AOD) – равнобедренный и (angle OAD=angle ODA).
Таким образом, по первому признаку (triangle ABD=triangle ACD) ((AC=BD, angle OAD=angle ODA, AD) – общая). Значит, (AB=CD), чтд.
Немного истории
Для начала вспомним, что такое трапеция.
Трапеция – это фигура, у которой две стороны параллельны, а две другие не параллельны.
Трапеция – одна из самых «загадочных» фигур школьной планиметрии. Она обладает некоторыми признаками параллелограмма, но сильно отличается от него разнообразием форм. Различают трапеции прямоугольные, равнобедренные, общего вида. Одно это разнообразие форм уже подозрительно.
На практике форма трапеции встречается более часто, чем прямоугольники, квадраты или параллелограммы. Поэтому нахождение площади для трапеции – более актуальная задача, чем для других фигур.
Покажем вам несколько формул, как найти площадь трапеции. Каждая формула площади трапеции подходит для решения соответствующего круга задач.
Основные формулы
- Площадь трапеции через её основания и высоту:
- Площадь трапеции через ее высоту и среднюю линию:
- Площадь трапеции через ее диагонали и угол между ними:
Давайте разберем задачу, иллюстрирующую применение одной из этих формул:
Задача
Основания трапеции общего вида равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
Решение
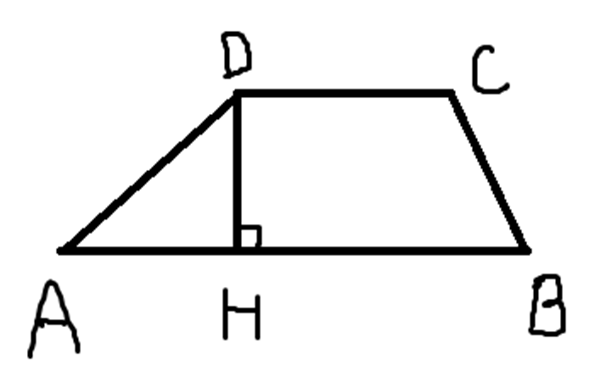
Изобразим трапецию общего вида и введём обозначения, как показано на рисунке ниже.
По условию задачи, один из углов трапеции равен 150°. Этим углом может быть угол ADC. По свойству трапеции, также как и параллелограмма, сумма углов, прилежащих к боковой стороне, равна 180°. Отсюда несложно вычислить, что второй угол, DAН, прилежащий к этой боковой стороне, будет равен 30°.
Отрезком DH на рисунке является высота трапеции. Найдем эту высоту из прямоугольного треугольника AHD, где DH является противолежащим катетом, AD является гипотенузой:
Воспользуемся формулой (1) площади трапеции через ее основания и высоту. По этой формуле площадь трапеции равна произведению полусуммы оснований на ее высоту:
Ответ: 42
Итак, зная длины двух оснований трапеции и ее высоту, вычислить ее площадь достаточно просто. Сложности могут быть, если нам не известны один из требуемых элементов, например, высота трапеции. Но здесь на помощь приходят знания свойств трапеций и соотношений в прямоугольном треугольнике.
Часто задаваемые вопросы
✅ Что такое трапеция?
↪ Трапеция — это четырехугольник, у которого две противоположные стороны параллельны, а две другие стороны непараллельны.
✅ Как найти площадь трапеции?
↪ Площадь трапеции можно найти по формуле: S = (a + b) * h / 2, где a и b — длины оснований трапеции, а h — высота трапеции, опущенная на основание.
✅ Что происходит с площадью трапеции, если увеличить одно из оснований?
↪ Если увеличить одно из оснований трапеции, то ее площадь увеличится, при этом высота трапеции останется неизменной. Если увеличить оба основания на одинаковую величину, то площадь трапеции увеличится в два раза.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Выбирайте формулу в зависимости от известных величин.
1. Как найти площадь трапеции через основания и высоту
Посчитайте сумму оснований трапеции.
Умножьте результат на высоту и поделите на два.
- S – искомая площадь трапеции.
- a и b – основания трапеции (её параллельные стороны).
- h – высота трапеции.
2. Как вычислить площадь трапеции через высоту и среднюю линию
Просто умножьте высоту трапеции на среднюю линию.
- S – искомая площадь трапеции.
- m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
- h – высота трапеции.
3. Как найти площадь трапеции через диагонали и угол между ними
Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.
Поделите результат на два.
- S – искомая площадь трапеции.
- x и y – диагонали трапеции.
- α – любой угол между диагоналями.
4. Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
- S – искомая площадь трапеции.
- a, b – основания трапеции.
- c, d – боковые стороны.
5. Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
- S — искомая площадь трапеции.
- a, b — основания трапеции.
- c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).
6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол
Найдите квадрат радиуса и умножьте его на четыре.
Поделите результат на синус известного угла.
- r — радиус вписанной окружности.
- α — любой угол трапеции.
Читайте также 📐✏️🎓
- 8 способов найти длину окружности
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Трапеция. Формулы, признаки и свойства трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
Виды трапеций:
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m — b
b = 2m — a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a — h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a — c·cos α — d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Определение.
Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 — 2ad·cos β
d2 = √a2 + c2 — 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab — | a(d 2 — c2) |
| a — b |
| d2 = | √ | c2 + ab — | a(c2 — d 2) |
| a — b |
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a — h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a — h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab — d22
d2 = √c2 + d 2 + 2ab — d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 — | ( | (a — b)2 + c2 — d 2 | ) | 2 |
| 2 | 2(a — b) |
5. Формула Герона для трапеции
| S = | a + b | √(p — a)(p — b)(p — a — c)(p — a — d) |
| |a — b| |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p — a)(p — c)(p — d1) |
где
a — большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |