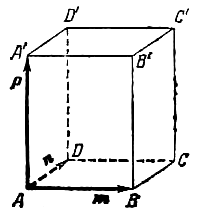
Как найти третий вектор треугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Сложение векторов

Сумма векторов

Свойства сложения векторов:

Для любых векторов

3) свойство прибавления нулевого вектора:

4) сумма противоположных векторов равна нулевому вектору:

Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:

Так как соответствующие координаты равны, то эти векторы равны.

(О сложении векторов)

Каковы бы ни были точки A, B, C, имеет место векторное равенство:

Что и требовалось доказать.

Правило треугольника построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.

Например,

(то есть это правило следует из теоремы о сложении векторов).

Правило параллелограмма построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.

Например,

Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.

При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.

Построить сумму векторов

1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора

Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).

2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы

от общего начала.

Достроим на этих векторах параллелограмм.

Сумма

равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.

1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.

2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.

Фактически в обоих случаях мы используем правило треугольника сложения векторов:

от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.

Из неравенства треугольника следует ещё два свойства сложения векторов:

Сложение и вычитание векторов

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec <0>)

Длина нулевого вектора равна нулю:
( left| vec <0>right| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:

Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;

Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )

Обозначение: ( overrightarrow=koverrightarrow ) .

Правила, по которым происходит сложение векторов

Как происходит сложение векторов, не всегда понятно ученикам. Дети не представляют того, что за ними скрывается. Приходится просто запоминать правила, а не вдумываться в суть. Поэтому именно о принципах сложения и вычитания векторных величин требуется много знаний.

В результате сложения двух и более векторов всегда получается еще один. Причем он всегда обязательно будет одинаковым, независимо от приема его нахождения.

Чаще всего в школьном курсе геометрии рассматривается сложение двух векторов. Оно может быть выполнено по правилу треугольника или параллелограмма. Эти рисунки выглядят по-разному, но результат от действия один.

Как происходит сложение по правилу треугольника?

Оно применяется тогда, когда векторы неколлинеарные. То есть не лежат на одной прямой или на параллельных.

В этом случае от некоторой произвольной точки нужно отложить первый вектор. Из его конца требуется провести параллельный и равный второму. Результатом станет вектор, исходящий из начала первого и завершающийся в конце второго. Рисунок напоминает треугольник. Отсюда и название правила.

Если векторы коллинеарные, то это правило тоже можно применять. Только рисунок будет расположен вдоль одной линии.

Как выполняется сложение по правилу параллелограмма?

Опять же? применяется только для неколлинеарных векторов. Построение выполняется по другому принципу. Хотя начало такое же. Нужно отложить первый вектор. И от его начала — второй. На их основе достроить параллелограмм и провести диагональ из начала обоих векторов. Она и будет результатом. Так выполняется сложение векторов по правилу параллелограмма.

До сих пор их было два. А как быть, если их 3 или 10? Использовать следующий прием.

Как и когда применяется правило многоугольника?

Если требуется выполнить сложение векторов, число которых — больше двух, пугаться не стоит. Достаточно последовательно отложить их все и соединить начало цепочки с ее концом. Этот вектор и будет искомой суммой.

Какие свойства действительны для действий с векторами?

О нулевом векторе. Которое утверждает, что при сложении с ним получается исходный.

О противоположном векторе. То есть о таком, который имеет противоположное направление и равное по модулю значение. Их сумма будет равна нулю.

О коммутативности сложения. То, что известно еще с начальной школы. Смена мест слагаемых не приводит к изменению результата. Другими словами, неважно какой вектор откладывать сначала. Ответ все равно будет верным и единственным.

Об ассоциативности сложения. Этот закон позволяет складывать попарно любые векторы из тройки и к ним прибавлять третий. Если записать это с помощью знаков, то получится следующее:

первый + (второй + третий) = второй + (первый + третий) = третий + (первый + второй).

Что известно о разности векторов?

Отдельной операции вычитания не существует. Это связано с тем, что оно, по сути, является сложением. Только второму из них задается противоположное направление. А потом все выполняется так, как если бы рассматривалось сложение векторов. Поэтому об их разности практически не говорят.

Для того чтобы упростить работу с их вычитанием, видоизменено правило треугольника. Теперь (при вычитании) второй вектор нужно отложить из начала первого. Ответом будет тот, что соединяет конечную точку уменьшаемого с ней же вычитаемого. Хотя можно и откладывать так, как было описано ранее, просто изменив направление второго.

Как найти сумму и разность векторов в координатах?

В задаче даны координаты векторов и требуется узнать их значения для итогового. При этом построений выполнять не нужно. То есть можно воспользоваться несложными формулами, которые описывают правило сложения векторов. Они выглядят так:

а (х, у, z) + в (k, l, m) = с (х+k, y+l, z+m);

а (х, у, z) -в (k, l, m) = с (х-k, y-l, z-m).

Легко заметить, что координаты нужно просто сложить или вычесть в зависимости от конкретного задания.

Первый пример с решением

Условие. Дан прямоугольник АВСД. Его стороны равны 6 и 8 см. Точка пересечения диагоналей обозначена буквой О. Требуется вычислить разность векторов АО и ВО.

Решение. Сначала нужно изобразить эти векторы. Они направлены от вершин прямоугольника к точке пересечения диагоналей.

Если внимательно посмотреть на чертеж, то можно увидеть, что векторы уже совмещены так, чтобы второй из них соприкасался с концом первого. Вот только его направление неверное. Он должен из этой точки начинаться. Это если векторы складываются, а в задаче — вычитание. Стоп. Это действие означает, что нужно прибавить противоположно направленный вектор. Значит, ВО нужно заменить на ОВ. И получится, что два вектора уже образовали пару сторон из правила треугольника. Поэтому результат от их сложения, то есть искомая разность, — вектор АВ.

А он совпадает со стороной прямоугольника. Для того чтобы записать числовой ответ, потребуется следующее. Начертить прямоугольник вдоль так, чтобы большая сторона шла горизонтально. Нумерацию вершин начинать с левой нижней и идти против часовой стрелки. Тогда длина вектора АВ будет равна 8 см.

Ответ. Разность АО и ВО равна 8 см.

Второй пример и его подробное решение

Условие. У ромба АВСД диагонали равны 12 и 16 см. Точка их пересечения обозначена буквой О. Вычислите длину вектора, образованного разностью векторов АО и ВО.

Решение. Пусть обозначение вершин ромба будет таким же, как в предыдущей задаче. Аналогично решению первого примера получается, что искомая разность равна вектору АВ. А его длина неизвестна. Решение задачи свелось к тому, чтобы вычислить одну из сторон ромба.

Для этой цели потребуется рассмотреть треугольник АВО. Он прямоугольный, потому что диагонали ромба пересекаются под углом в 90 градусов. А его катеты равны половинам диагоналей. То есть 6 и 8 см. Искомая в задаче сторона совпадает с гипотенузой в этом треугольнике.

Для ее нахождения потребуется теорема Пифагора. Квадрат гипотенузы будет равен сумме чисел 6 2 и 8 2 . После возведения в квадрат получатся значения: 36 и 64. Их сумма — 100. Отсюда следует, что гипотенуза равна 10 см.

Ответ. Разность векторов АО и ВО составляет 10 см.

Третий пример с детальным решением

Условие. Вычислить разность и сумму двух векторов. Известны их координаты: у первого — 1 и 2, у второго — 4 и 8.

Решение. Для нахождения суммы потребуется сложить попарно первые и вторые координаты. Результатом будут числа 5 и 10. Ответом будет вектор с координатами (5; 10).

Для разности нужно выполнить вычитание координат. После выполнения этого действия получатся числа -3 и -6. Они и будут координатами искомого вектора.

Ответ. Сумма векторов — (5; 10), их разность — (-3; -6).

Четвертый пример

Условие. Длина вектора АВ равна 6 см, ВС — 8 см. Второй отложен от конца первого под углом в 90 градусов. Вычислить: а) разность модулей векторов ВА и ВС и модуль разности ВА и ВС; б) сумму этих же модулей и модуль суммы.

Решение: а) Длины векторов уже даны в задаче. Поэтому вычислить их разность не составит труда. 6 — 8 = -2. Несколько сложнее обстоит дело с модулем разности. Сначала нужно узнать, какой вектор будет являться результатом вычитания. Для этой цели следует отложить вектор ВА, который направлен в противоположную сторону АВ. Потом от его конца провести вектор ВС, направив его в сторону, противоположную исходному. Результатом вычитания получится вектор СА. Его модуль можно вычислить по теореме Пифагора. Несложные вычисления приводят к значению 10 см.

б) Сумма модулей векторов получается равной 14 см. Для поиска второго ответа потребуется некоторое преобразование. Вектор ВА противоположно направлен тому, который дан — АВ. Оба вектора направлены из одной точки. В этой ситуации можно использовать правило параллелограмма. Результатом сложения будет диагональ, причем не просто параллелограмма, а прямоугольника. Его диагонали равны, значит, модуль суммы такой же, как в предыдущем пункте.

источники:

http://calcsbox.com/post/slozenie-i-vycitanie-vektorov.html

http://www.syl.ru/article/191003/mod_pravila-po-kotoryim-proishodit-slojenie-vektorov

Источник

Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий
определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом или . Вектор называется противоположным
вектору и может быть
обозначен .

Сформулируем ряд базовых определений.

Длиной
или модулем
вектора  называется
длина отрезка и обозначается . Вектор нулевой длины (его суть — точка) называется нулевым  и направления
не имеет. Вектор единичной длины, называется единичным. Единичный вектор,
направление которого совпадает с направлением вектора , называется ортом вектора  .

Векторы
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых, записывают. Коллинеарные векторы могут иметь совпадающие или
противоположные направления. Нулевой вектор считают коллинеарным любому
вектору.

Векторы
называются равными , если они коллинеарны, одинаково направлены и имеют
одинаковые длины.

Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или на параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы
компланарны.

Рассмотрим в
пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и
обозначим их через соответственно.
Выберем произвольный вектор

пространства и совместим его начало с началом
координат. Спроектируем вектор
на координатные
оси и обозначим проекции через a_x, a_y, a_z
соответственно. Тогда нетрудно показать, что

. (2.25)

Эта
формула является основной в векторном исчислении и называется разложением
вектора по ортам координатных осей. Числа a_x, a_y, a_z называются координатами вектора . Таким образом, координаты вектора являются его
проекциями на оси координат. Векторное равенство (2.25) часто записывают в
виде

. Мы будем использовать обозначение вектора в фигурных
скобках, чтобы визуально легче различать координаты вектора и координаты точки.
С использованием формулы длины отрезка, известной из школьной геометрии, можно
найти выражение для вычисления модуля вектора

:

, (2.26)

то
есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором
и осями
координат через α, β, γ соответственно. Косинусы этих углов называются
для вектора направляющими, и для них выполняется соотношение:Верность данного равенства можно показать с помощью
свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем
пункте 4.

Пусть в трехмерном пространстве заданы векторы своими
координатами. Имеют место следующие
операции над ними: линейные (сложение, вычитание, умножение на число и
проектирование вектора на ось или другой вектор); не линейные – различные
произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то
есть если

Данная
формула имеет место для произвольного конечного числа слагаемых.

Геометрически
два вектора складываются по двум правилам:

а) правило треугольника –
результирующий вектор суммы двух векторов соединяет начало первого из них с
концом второго при условии, что начало второго совпадает с концом первого
вектора; для суммы векторов –
результирующий вектор суммы соединяет начало первого из них с концом последнего
вектора-слагаемого при условии, что начало последующего слагаемого совпадает с
концом предыдущего;

б)
правило
параллелограмма (для двух
векторов) – параллелограмм строится на векторах-слагаемых как на сторонах,
приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой
векторов.

2. Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если , то

Геометрически два
вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов
является диагональ, соединяющая концы векторов, причем результирующий вектор
направлен из конца вычитаемого в конец уменьшаемого вектора.

Важным следствием
вычитания векторов является тот факт, что если известны координаты начала и
конца вектора, то для вычисления координат вектора необходимо из координат его конца
вычесть координаты его начала. Действительно, любой вектор пространства может быть
представлен в виде разности двух векторов, исходящих из начала координат: . Координаты векторов и совпадают с
координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу
вычитания векторов следует произвести вычитание координат точки А из координат точки В.

3. Умножение вектора на число λ покоординатно:.

При λ>0
– вектор сонаправлен ; λ<0 – вектор противоположно направлен ; |λ|>1 – длина вектора увеличивается в λ раз; |λ|<1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана
направленная прямая (ось l), вектор задан
координатами конца и начала. Обозначим проекции точек A и B на ось l
соответственно через A’ и B’.

Проекцией вектора на ось l называется длина вектора , взятая со
знаком «+», если вектор и ось l сонаправлены, и со
знаком «–», если и l противоположно направлены.

Если
в качестве оси l взять некоторый другой вектор , то получим проекцию вектора на вектор .

Рассмотрим некоторые
основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля
вектора на косинус угла
между вектором и осью, то есть ;

2.) проекция вектора на ось
положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и
равна нулю, если этот угол – прямой;

3) проекция суммы нескольких
векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и
теоремы о произведениях векторов, представляющих нелинейные операции над
векторами.

5. Скалярным произведением векторов и называется
число (скаляр), равное произведению длин этих векторов на косинус угла φ между
ними, то есть

. (2.27)

Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол , поэтому его косинус (в 2.27) равен 1.

Теорема 2.2. Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Теорема 2.3. Скалярное произведение двух векторов ,
заданных своими координатами, равно сумме произведений их одноименных координат, то есть

(2.28)

С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора
своими координатами , то косинус угла φ между ними:

(2.29)

Отсюда
следует условие перпендикулярности ненулевых векторов
и :

(2.30)

Нахождение проекции вектора на направление,
заданное вектором , может осуществляться по формуле

(2.31)

С помощью скалярного произведения векторов находят
работу постоянной силы на
прямолинейном участке пути.

Предположим, что под действием постоянной силы материальная точка перемещается прямолинейно из
положения А в положение B. Вектор силы образует угол φ с вектором перемещения (рис. 2.14). Физика утверждает, что работа силы при перемещении
равна .

Следовательно, работа постоянной силы
при прямолинейном перемещении точки ее приложения равна скалярному произведению
вектора силы на вектор перемещения.

Пример
2.9. С
помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах

Решение. Вычислим модули векторов и их скалярное произведение
по теореме (2.3):

Отсюда согласно формуле (2.29) получим косинус
искомого угла

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых
на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной
тонны творога?

Таблица 2.2

Решение. Введем в рассмотрение два вектора: вектор затрат
ресурсов на тонну продукции и вектор цены единицы
соответствующего ресурса .

Тогда . Общая цена
ресурсов , что представляет собой скалярное произведение
векторов . Вычислим его по формуле (2.28) согласно теореме 2.3:

Таким образом, общая цена затрат на производство одной
тонны творога составляет 279 541,5 рублей

Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix

Пример 2.11. Вычислить работу, произведенную силой , если точка ее приложения перемещается прямолинейно
из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила ?

Решение. Находим вектор перемещения, вычитая из координат его конца координаты
начала

. По формуле (2.28) (единиц работы).

Угол φ между и
находим по
формуле (2.29), то есть

6. Три некомпланарных вектора , взятые в указанном порядке, образуют правую
тройку, если при наблюдении из конца третьего вектора кратчайший
поворот от первого вектора ко второму
вектору совершается против часовой стрелки, и левую,
если по часовой стрелке.

Векторным
произведением вектора на вектор называется
вектор , удовлетворяющий следующим условиям:

– перпендикулярен векторам и ;

– имеет длину, равную , где φ – угол, образованный векторами
и ;

– векторы образуют правую
тройку (рис. 2.15).

Теорема 2.4. Необходимым и достаточным
условием коллинеарности двух векторов является равенство нулю их векторного
произведения

Теорема 2.5. Векторное произведение векторов , заданных своими координатами, равно определителю
третьего порядка вида

(2.32)

Примечание. Определитель (2.25)
раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух
векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Геометрическая
интерпретация векторного произведения состоит в том, что длина результирующего
вектора численно равна площади S
параллелограмма, построенного на векторах–сомножителях как на сторонах,
приведенных к одному началу. Действительно, согласно определению, модуль
векторного произведения векторов равен . С другой стороны, площадь параллелограмма,
построенного на векторах и , также равна

. Следовательно,

. (2.33)

Также с помощью векторного произведения можно
определить момент силы относительно точки и линейную скорость вращения.

Пусть в точке A приложена
сила  и пусть O –
некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом
силы  относительно
точки O называется вектор , который проходит через точку O и удовлетворяет следующим условиям:

— перпендикулярен плоскости, проходящей через точки O, A, B;

— его модуль численно равен произведению силы на плечо .

— образует правую тройку с векторами и .

Следовательно,
момент силы относительно
точки O представляет собой векторное произведение

. (2.34)

Линейная скорость точки М твердого тела, вращающегося с
угловой скоростью вокруг
неподвижной оси, определяется формулой Эйлера , O – некоторая неподвижная

точка оси (рис. 2.17).

Пример 2.12. С помощью
векторного произведения найти площадь треугольника ABC, построенного на векторах
, приведенных к одному началу.

Решение. Найдем векторное произведение заданных векторов по
формуле (2.32).

. Согласно формуле (2.33) модуль векторного
произведения двух неколлинеарных векторов численно равен площади
параллелограмма, построенного на данных векторах как на сторонах, приведенных к
общему началу, то есть . Тогда площадь треугольника
. Следовательно, искомая площадь равна (единиц
площади)

7. Рассмотрим произведение трех векторов , составленное следующим образом: . Здесь первые два вектора перемножаются векторно, а
результирующий вектор – скалярно на третий. Такое произведение называется смешанным
произведением трех векторов
(векторно–скалярным произведением).

Теорема 2.6. Необходимым и достаточным условием компланарности
трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное
произведение представляет собой определитель третьего порядка, составленный из
координат векторов- сомножителей соответственно, то есть

(2.35)

Нетрудно показать, что объем параллелепипеда,
построенного на векторах как на
сторонах, приведенных к общему началу, численно равен модулю смешенного
произведения этих векторов .

Объем треугольной пирамиды, построенной на этих же
векторах, равен

(2.36)

Пример 2.13. Вершинами пирамиды служат точки . Вычислить объем пирамиды.

Решение. Найдем
координаты векторов

. Вычислим смешанное произведение этих векторов:

По формуле (2.36) объем пирамиды, построенной на
векторах равен
(единиц объема)

Рассмотрим очень важный вопрос о
разложении вектора по базису. Приведем
следующие определения.

Система векторов называется
линейно зависимой, если существуют такие числа , хотя бы одно из которых отлично от нуля, что имеет
место равенство

(2.37)

Отсюда всегда можно один из линейно
зависимых векторов выразить через линейную комбинацию остальных. Действительно,
допустим для определенности, что . Тогда на это число разделим равенство (2.37), имеем:

получим выражение вектора через
остальные векторы

Линейно независимыми называют векторы, если равенство
(2.37) выполняется только тогда, когда
все

В системе векторов число линейно
независимых векторов равняется рангу матрицы, которая составлена из координат
этих векторов (смотри раздел I.5).

Базисом n – мерного
пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n
– мерного пространства можно представить
в виде линейной комбинации векторов базиса

таким образом:

Числа
называются координатами
вектора в базисе
векторов .

Линейное пространство называется
конечномерным и имеет размерность n, если в этом
пространстве существует система из n линейно независимых векторов (базис) такая,
что каждое ее расширение приводит к линейной зависимости системы.

Например, в трехмерном пространстве
существует базис единичных орт  такой, что любое расширение этой системы
линейно независимых векторов, то есть каждый вектор  трехмерного
пространства, приводит к линейной зависимости векторов (является линейной
комбинацией орт ): Коэффициенты {x₁, x₂, x₃} такого разложения вектора
по ортам  являются координатами вектора  в трехмерном
пространстве.

Вопросы для самопроверки

Источник

761 По данным векторам

построить
каждый из следующих векторов: 1).

, 2).

, 3).

, 4).

. 762 Даны

=13,

=19 и

=24. Вычислить

. 763 Даны

=11,

=23 и

=30. Определить

. 764 Векторы

взаимно
перпендикулярны, причем

=5,

=12. Определить

. 765 Векторы

образуют
угол

=60⁰, причем

=5 и

=8. Определить

. 766 Векторы

образуют
угол

=120⁰, причем

=3 и

=5. Определить

. 767 Какому условию
должны удовлетворять векторы

, чтобы
имели место следующие соотношения: 767.1

; 767.2

; 767.3

. 768 Какому условию
должны удовлетворять векторы

, чтобы
вектор

делил пополам угол между векторами

. 769 По данным векторам

построить каждый из следующих
векторов: 769.1

; 769.2

; 769.3

; 769.4

. 770 В треугольнике АВС
вектор

и вектор

. Построить каждый из
следующих векторов. Принимая в качестве
масштабной единицы

, построить также векторы: 770.1

; 770.2

; 770.3

; 770.4

; 770.5

; 770.6

. 771 Точка О является
центром масс треугольника АВС. Доказать, что

. 772 В правильном
пятиугольнике ABCDE заданы векторы, совпадающие с
его ребрами:

. Построить векторы: 772.1

; 772.2

; 772.3

. 773 В параллелепипеде
ABCDA’B’C’D’ (рис.) заданы векторы, совпадающие с
его ребрами:

. Построить
каждый из следующих векторов:

773.1

; 773.2

;

773.3

; 773.4

; 773.5

. 774 Три силы

, приложенные к одной
точке, имеют взаимно перпендикулярные
направления. Определить величину их
равнодействующей

, если известно, что

=2Н,

=10Н,

=11Н. 775 Даны два вектора

={3; -2; 6},

={-2; 1; 0}. Определить проекции на координатные
оси следующих векторов: 775.1

; 775.2

; 775.3

; 775.4

; 775.5

; 775.6

. 776 Проверить
коллинеарность векторов

={2; -1; 3} и

={-6;
3; -9}. Установить, какой из них
длиннее другого и во сколько раз, как они
направлены – в одну или в противоположные
стороны. 777 Определить, при
каких значениях

векторы

коллинеарны. 778 Проверить, что
четыре точки A(3; -1; 2), B(1; 2; -1), C(2; 2; -7), D(3; -5; 3) служат
вершинами трапеции. 779 Даны точки A(-1; 5; -10},
B(5; -7; 8), C(2; 2; -7), D(5; -4; 2). Проверить, что векторы

коллинеарны, установить, какой из
них длиннее другого и во сколько раз, как они
направлены – в одну или в противоположные
стороны. 780 Найти орт вектора

={6; -2; -3}. 781 Найти орт вектора

={3; 4; -12}. 782 Определить модули
суммы и разности векторов

={3; -5; 8} и

={-1;
1; -4}. 783 Дано разложение
вектора

по базису

. Определить
разложение по этому же базису вектора

, параллельного
вектору

и противоположного с ним
направления, при условии, что

=75. 784 Два вектора

={2; -3; 6} и

={-1;
2; -2} приложены к одной точке.
Определить координаты вектора

направленного
по биссектрисе угла между векторами

, при
условии, что

. 785 Векторы

={2; 6; -4} и

={4;
2; -2} совпадают со сторонами
теругольника АВС. Определить координаты
векторов, приложенных к вершинам треугольника и
совпадающими с его медианами AM, BN, CP. 786 Доказать, что если

— какие угодно неколлинеарные
векторы, то всякий вектор, лежащих в их плоскости,
может быть представлен в виде

. Доказать,
что числа

однозначно определяются векторами

. 787 На плоскостиданы
два вектора

={2; -3},

={1; 2}. Найи разложение вектора

={9; 4} по
базису

. 788 На плоскости даны
три вектора

={3; -2},

={-2; 1},

={7; -4}. Определить
разложение каждого из этих трех векторов,
принимая в качестве базиса два других. 789 Даны три вектора

={3; -1},

={1; -2},

={-1; 7}. Определить
разложение вектора

по базису

. 790 Принимая в качестве
базиса векторы

, совпадающие
со сторонами треугольника АВС, опреедлить
разложение векторов, приложенных в вершинах
треугольника и совпадающие с его медианами. 791 На плоскости даны
етыре точки A(1; -2), B(2; 1), C(3; 2), D(-2; 3). Определить
разложение векторов

,
принимая в качестве базиса
векторы

. 792 Доказать, что если

— какие угодно
некомпланарные векторы, то всякий вектор

пространства
может быть представлен в виде

. Доказать,
что числа

однознчно
определяются векторами

. (Представление
вектора

в виде

называется разложением
его по базису

. Числа

называются коэффициентами этого
разложения. 793 Даны три вектора

={3; -2; 1},

={-1; 1; -2},

={2; 1; -3}. Найти разложение вектора

={11; -6; 5} по базису

. 794 Даны четыре вектора

={2; 1; 0},

={1; -2; 2},

={2; 2; -1},

={3; 7; -7}. Определить разложение каждого из
этих четырех векторов, принимая в качестве
базиса три остальных.

Источник

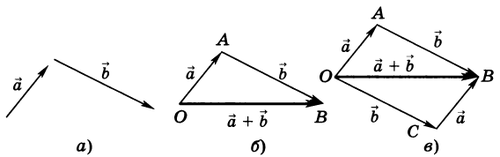
Пусть $overrightarrow{a}$ и $overrightarrow{b}$ — два вектора (рис.1, а).

Сложение двух векторов

Рис.1

Возьмем произвольную точку О и построим вектор $overrightarrow{ОА} = overrightarrow{a}$ . Затем от точки А отложим вектор $overrightarrow{AB} = overrightarrow{b}$. Вектор $overrightarrow{OB}$, соединяющий начало первого слагаемого вектора с концом второго (рис.1, б), называется суммой этих векторов и обозначается $overrightarrow{a} + overrightarrow{b}$$ (правило треугольника).

Ту же самую сумму векторов можно получить иным способом. Отложим от точки О векторы $overrightarrow{ОА} = overrightarrow{a} ,и, overrightarrow{ОС} = overrightarrow{b} $ (рис.1, в). Построим на этих векторах как на сторонах параллелограмм ОABC. Вектор $overrightarrow{ОВ}$, служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов $overrightarrow{a} + overrightarrow{b}$ {правило параллелограмма). Из рисунка 1, в непосредственно следует, что сумма двух векторов обладает переместительным свойством: $overrightarrow{a} + overrightarrow{b} = overrightarrow{b} + overrightarrow{a}$

Действительно, каждый из векторов $overrightarrow{a} + overrightarrow{b} ,и, = overrightarrow{b} + overrightarrow{a}$ равен одному и тому же вектору $overrightarrow{OB}$ .

Пример 1. В треугольнике ABC АВ = 3, ВС = 4, ∠ В = 90°. Найти: $а), overrightarrow{|АВ|} + overrightarrow{|ВС|};,, б), |overrightarrow{АВ} + overrightarrow{ВС}|$ .

Решение

а) Имеем: $|overrightarrow{АВ}| = АВ,,, |overrightarrow{ВС}| = ВС$ и, значит, $|overrightarrow{АВ}| + |overrightarrow{BC}| = 7$ .

б) Так как $overrightarrow{AB} + overrightarrow{ВС} = overrightarrow{АС} ,,,,, то,, |overrightarrow{АВ} + overrightarrow{ВС}| = |overrightarrow{АС}| = АС$ .

Теперь, применяя теорему Пифагора, находим
$$ AC = sqrt{AB^2 + BC^2} = sqrt{9 + 16} = 5
\ т.е., |overrightarrow{АВ} + overrightarrow{ВС}| = 5.
$$

Понятие суммы векторов можно обобщить на случай любого конечного числа слагаемых векторов.

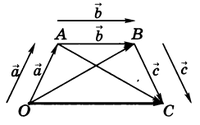
Пусть, например, даны три вектора $overrightarrow{a}, overrightarrow{b} ,и, overrightarrow{c}$ (рис.2).

Сложение трех векторов

Рис.2

Построив сначала сумму векторов $overrightarrow{a} + overrightarrow{b}$ , а затем прибавив к этой сумме вектор $overrightarrow{c}$, получим вектор $(overrightarrow{a} + overrightarrow{b}) + overrightarrow{c}$ . На рисунке 2
$$ overrightarrow{ОА} = overrightarrow{a},; overrightarrow{АВ} = b,; overrightarrow{ОВ} = overrightarrow{a} + overrightarrow{b},; overrightarrow{BC} = overrightarrow{c}
\ и
\ overrightarrow{ОС} = overrightarrow{ОВ} + overrightarrow{ВС} = (overrightarrow{a} + overrightarrow{b}) + overrightarrow{c}
$$
Из рисунка 2 видно, что тот же вектор $overrightarrow{ОС}$ мы получим, если к вектору $overrightarrow{ОА} = overrightarrow{a}$ прибавим вектор
$overrightarrow{АВ} = overrightarrow{b} + overrightarrow{c}$ . Таким образом, $(overrightarrow{a} + overrightarrow{b}) + overrightarrow{c} = overrightarrow{a} + (overrightarrow{b} + overrightarrow{c})$ , т. е. сумма векторов обладает сочетательным свойством.
Поэтому сумму трех векторов $overrightarrow{a},,,overrightarrow{b},,,overrightarrow{c}$ записывают просто $overrightarrow{a} + overrightarrow{b} + overrightarrow{c}$ .

Разностью двух векторов $overrightarrow{a} ,и, overrightarrow{b}$ называется третий вектор $overrightarrow{c} = overrightarrow{a} — overrightarrow{b}$ , сумма которого с вычитаемым вектором $overrightarrow{b}$ дает вектор $overrightarrow{a}$. Таким образом, если $overrightarrow{c} = overrightarrow{a} — overrightarrow{b},,, то, overrightarrow{c} + overrightarrow{b} = overrightarrow{a}$ .

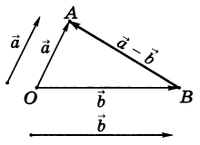
Из определения суммы двух векторов вытекает правило построения вектора-разности (рис.3).

Вычитание векторов

Рис.3

Откладываем векторы $overrightarrow{ОА} = overrightarrow{a} ,и, overrightarrow{OB} = overrightarrow{b}$ из общей точки О. Вектор $overrightarrow{BA}$ , соединяющий концы уменьшаемого вектора $overrightarrow{a}$ и вычитаемого вектора $overrightarrow{b}$ и направленный от вычитаемого к уменьшаемому, является разностью $overrightarrow{c} = overrightarrow{a} — overrightarrow{b}$ . Действительно, по правилу
сложения векторов $overrightarrow{ОВ} + overrightarrow{ВА} = overrightarrow{ОА} text{ , или } overrightarrow{b} + overrightarrow{c} = overrightarrow{a}$ .

Пример 2. Сторона равностороннего треугольника ABC равна а. Найти: $а) |overrightarrow{ВА} — overrightarrow{ВС}|,;, б),, |overrightarrow{АВ} — overrightarrow{АС}|$ .

Решение
а) Так как $overrightarrow{ВА} — overrightarrow{ВС} = overrightarrow{СА}text{ , а }|overrightarrow{СА}| = аtext{ , то }|overrightarrow{ВА} — overrightarrow{ВС}| = а$ .

б) Так как $overrightarrow{АВ} — overrightarrow{АС} = overrightarrow{СВ}text{ , а }|overrightarrow{СВ}| = аtext{ , то }|overrightarrow{АВ} — overrightarrow{АС}| = а$ .

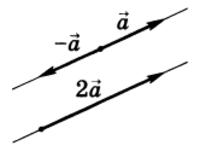
Произведением вектора $overrightarrow{a}$(обозначается $=lambdaoverrightarrow{a}$ или $overrightarrow{a}lambda$) на действительное число $lambda$ называется вектор $overrightarrow{b}$, коллинеарный вектору $overrightarrow{a}$, имеющий длину, равную $|lambda||overrightarrow{a}|$, и то же направление, что и вектор $overrightarrow{a}$, если $lambda > 0$ , и направление, противоположное направлению вектора $overrightarrow{a}$, если $lambda < 0$ . Так, например, $2overrightarrow{a}$ есть вектор, имеющий то же направление, что и вектор $overrightarrow{a}$ , а длину, вдвое большую, чем вектор $overrightarrow{a}$ (рис.4).

Умножение вектора на число

Рис.4

В случае, когда $lambda = 0$ или $overrightarrow{a} = 0$ , произведение $lambdaoverrightarrow{a}$ представляет
собой нулевой вектор. Противоположный вектор $-overrightarrow{a}$ можно рассматривать как результат умножения вектора $overrightarrow{a}$ на $lambda = -1$ (см. рис.4):
$$ -overrightarrow{a} = (-1)overrightarrow{a} $$
Очевидно, что $overrightarrow{a} + (-overrightarrow{a}) = overrightarrow{0}$ .

Пример 3. Доказать, что если О, А, В и С — произвольные точки, то $overrightarrow{ОА} + overrightarrow{АВ} + overrightarrow{ВС} + overrightarrow{СО} = 0$ .

Решение. Сумма векторов $overrightarrow{ОА} + overrightarrow{АВ} + overrightarrow{СВ} = overrightarrow{ОС}$ , вектор $overrightarrow{CO}$ — противоположный вектору $overrightarrow{ОС}$ . Поэтому $overrightarrow{ОС} + overrightarrow{СО} = overrightarrow{0}$ .

Пусть дан вектор $overrightarrow{a}$. Рассмотрим единичный вектор $overrightarrow{a_0}$ , коллинеарный вектору $overrightarrow{a}$ и одинаково с ним направленный. Из определения умножения вектора на число следует, что
$$ overrightarrow{a} = |overrightarrow{a}|, overrightarrow{a_0} $$
, т.е. каждый вектор равен произведению его модуля на единичный вектор того же направления. Далее из того же определения следует, что если $overrightarrow{b} = lambdaoverrightarrow{a}$ , где $overrightarrow{a}$ — ненулевой вектор, то векторы $overrightarrow{a} ,и, overrightarrow{b}$ коллинеарны. Очевидно, что и обратно, из коллинеарности векторов $overrightarrow{a} ,и, overrightarrow{b}$ следует, что $overrightarrow{b} = lambdaoverrightarrow{a}$.

Таким образом, получаем следующую теорему.

Пример 4. Длина вектора AB равна 3, длина вектора AC равна 5.
Косинус угла между этими векторами равен 1/15. Найдите длину вектора AB + AC.

Видео-решение.

Длина вектора

Источник