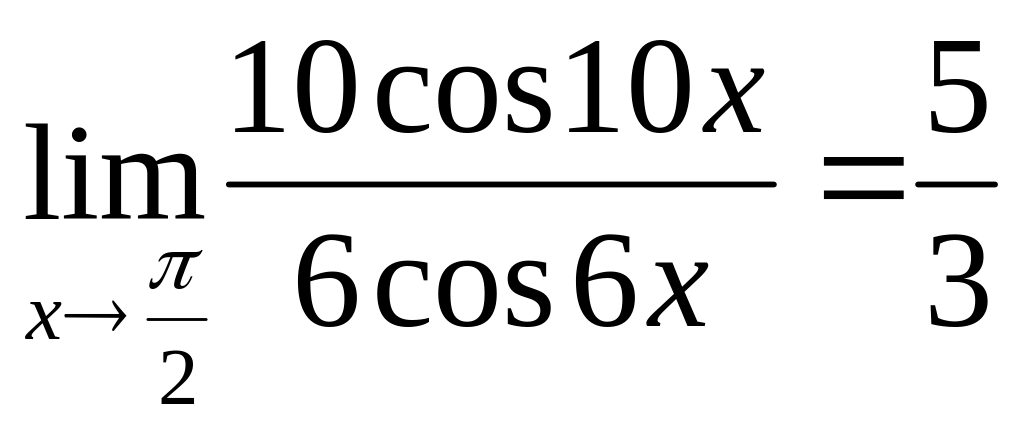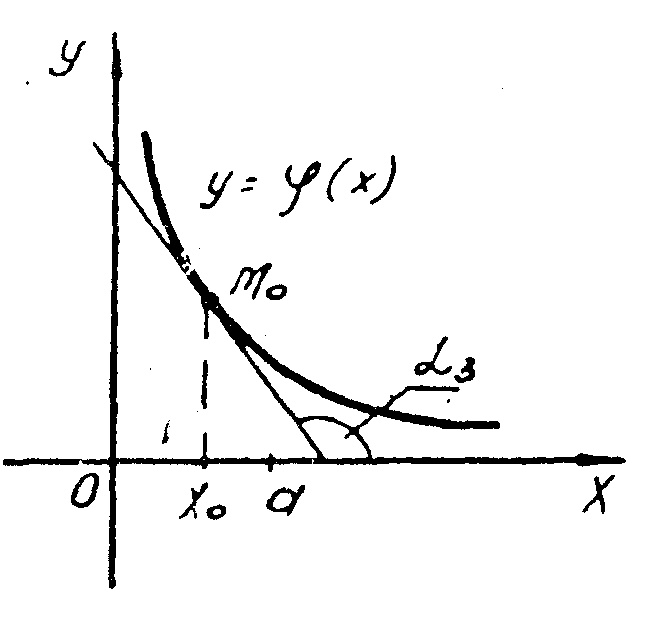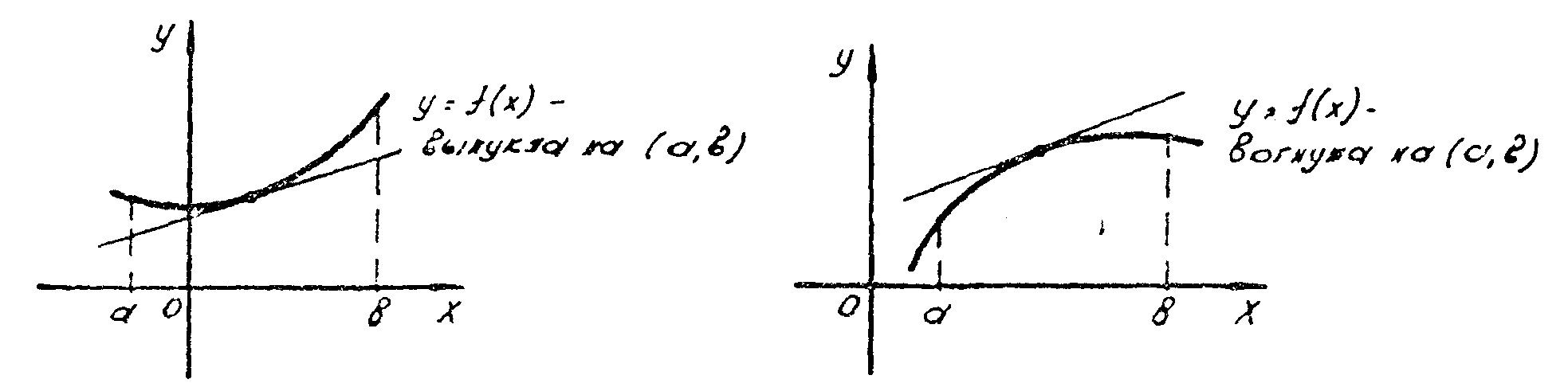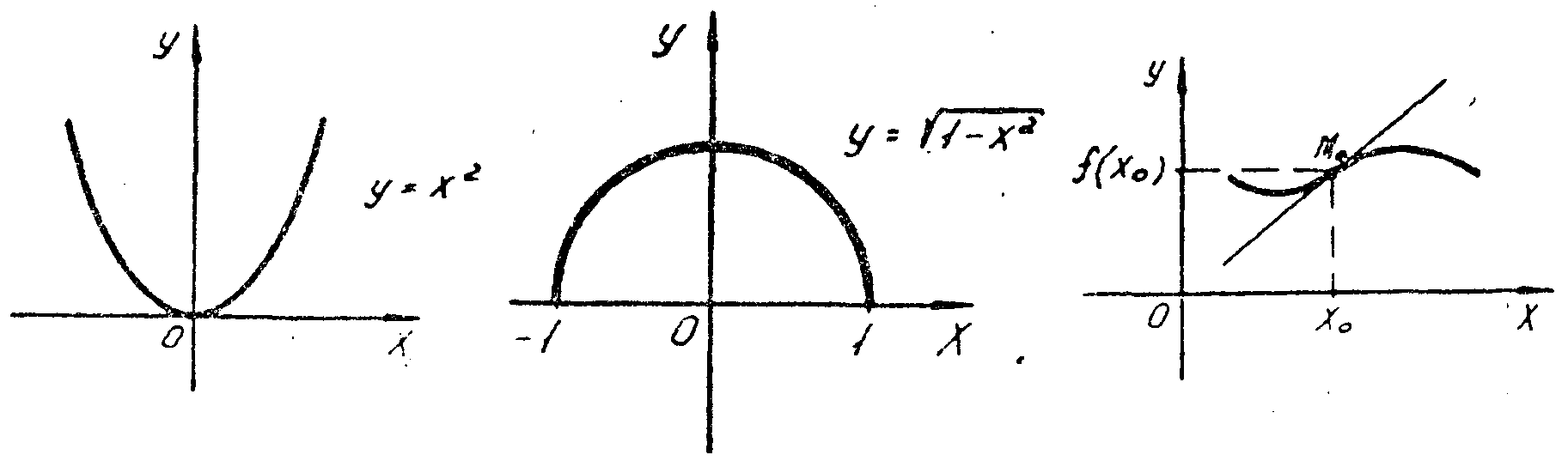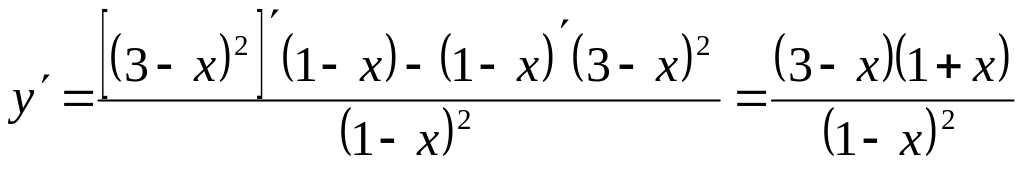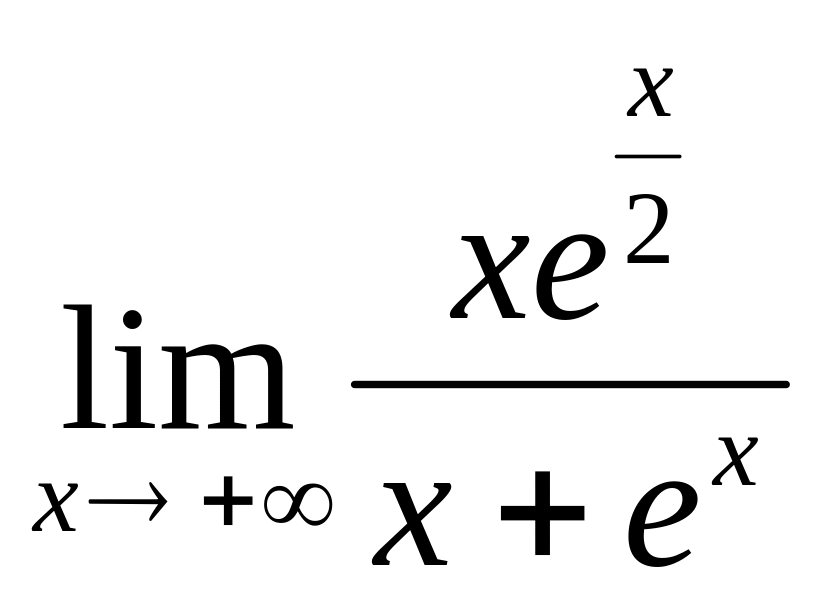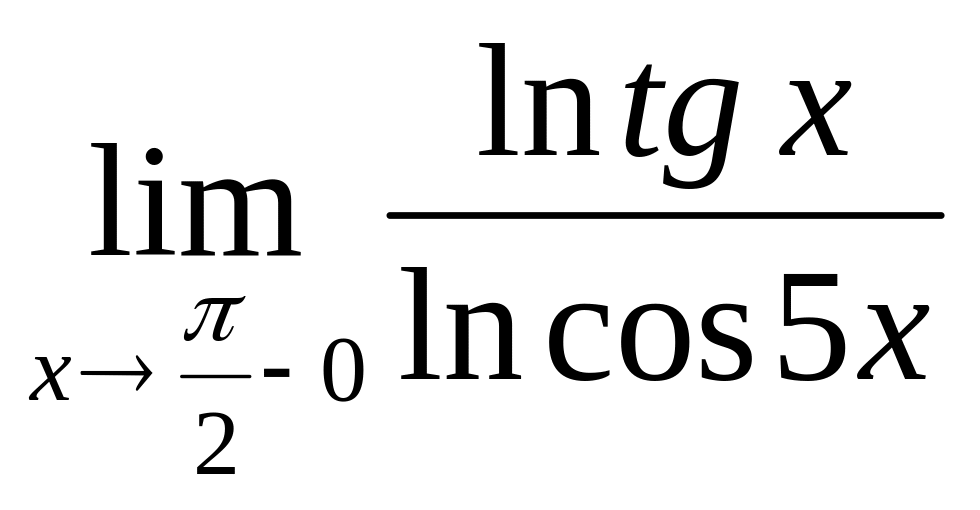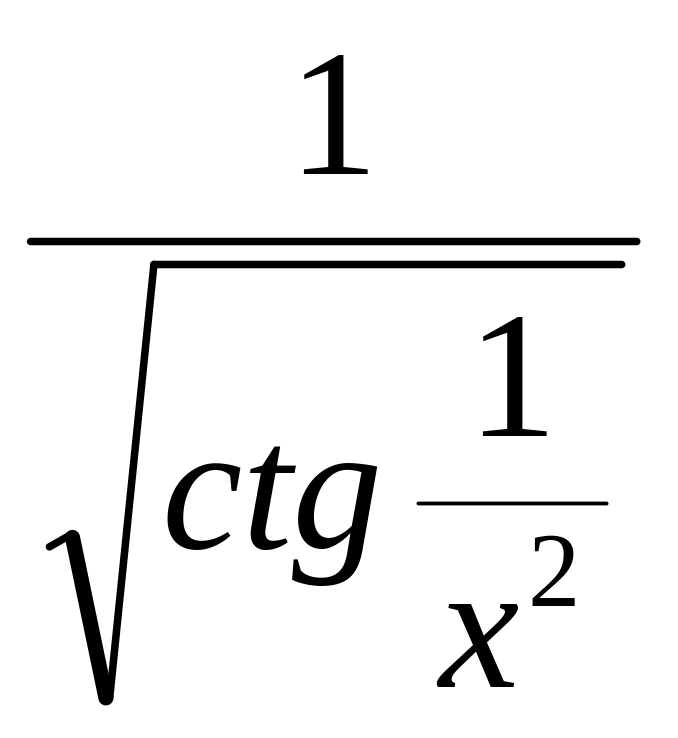Как найти третью производную в точке

Для исследования функции важно уметь определять угловой коэффициент касательной к ее графику.

Этот угловой коэффициент касательной называют производной.

Понятие производной часто используют и при решении многих других задач. Поэтому рассмотрим его подробнее.

Графический смысл производной

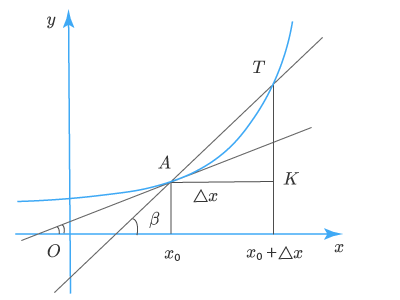
Пусть дан график функции y=f(x)y = f(x) и на нем точка АА, в которой существует касательная к графику:

Если абсцисса точки АА равна x0x_0, то ее ордината f(x0)f(x_0). Предоставим значению аргумента x0x_0 прирост ΔxΔx. Увеличенное значение аргумента х0+Δxх_0 + Δx на графике функции соответствует точка ТТ с абсциссой x0+Δxx_0 + Δx и ординатой f(x0+Δx)f(x_0 + Δx).

Через точки АА и ТТ проведем прямые АКАК и ТКТК, параллельные осям абсцисс и ординат; они пересекутся в некоторой точке КК. Тогда АК−ΔхАК — Δх – приращение аргумента, а ТК=ΔуТК = Δу – прирост функции на [x0;x0+Δx][x_0; x_0 + Δx].

Угловой коэффициент секущей ATAT равен тангенсу угла ββ, то есть отношению ΔуΔу к ΔxΔx:

tgβ=ΔyΔx=f(x0+Δx)−f(x0)Δxtgbeta =frac{Delta y}{Delta x}=frac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x}

Если ΔxΔx бесконечно мало и стремится к нулю, то секущая АТАТ, поворачиваясь вокруг точки АА, приближается к касательной, проведенной в точке АА с графиком данной функции. То есть если kk – угловой коэффициент этой касательной и ΔxΔx стремится к нулю, то

f(x0+Δx)−f(x0)Δx→kfrac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x}to k

Это число kk – производная функции f(x)f(x) в точке x0x_0.

Производной функции f(x)f(x) в точке x0x_0 называется число kk, которому соответствует дробь f(x0+Δx)−f(x0)Δxfrac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x} при Δх→0.

Производную функции f(x)f(x) в точке x0x_0 обозначают f′(x0)f'(x_0). Ее определение записывают также в виде равенства:

f′(x0)=lim⁡Δx→0 f(x0+Δx)−f(x0)Δx{f}'({{x}_{0}})=underset{Delta xto 0}{mathop{lim }},frac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x}

или

f′(x0)=lim⁡Δx→0 ΔyΔx{f}'({{x}_{0}})=underset{Delta xto 0}{mathop{lim }},frac{Delta y}{Delta x}

Задача 1

Найдите производную функции f(x)=x2f(x) = x^2 в точке x=3x = 3.

Решение

Предоставим аргументу x=3x = 3 прирост ΔxΔx. Соответствующий прирост функции Δу=(3+Δx)2−33=6Δx+Δx2Δу = (3 + Δx)^2 — 33 = 6Δx+Δx^2.

Поэтому

ΔyΔx=6Δ+Δ2Δfrac{Delta y}{Delta x}=frac{6Delta +Delta {{}^{2}}}{Delta }

Если Δx→0Δx→0, то Δy/Δx→6Δy/Δx → 6.

Ответ: f′(3)=6f ‘(3) = 6.

Так решают задачу, пользуясь определением производной функции в точке.

Задача 2

Используя формулу (1/x)′=−1/x2(1/x)’ = — 1/x^2, запишите уравнение к графику функции у=1/xу = 1/x в точке с абсциссой x0=1/2x_0 = 1/2.

Уравнение касательной к графику функции у=f(x)у = f (x) в точке с абсциссой x0x^0 в общем виде записывается так:

y=f(x0)+f′(x0)(x−x0)y=f({{x}_{0}})+{f}'({{x}_{0}})(x-{{x}_{0}})

Чтобы записать это уравнение для заданной функции, нужно найти значение f(x0)f(x_0), производную f′(x)f'(x) и значение f′(x0)f'(x_0). Для выполнения соответствующих вычислений удобно обозначить заданную функцию через f(x)f(x) и использовать табличное значение производной: (1/x)′=−1/x2.(1/x)’ = — 1/x^2.

Таким образом, если f(x)=1/xf(x) = 1/x, то f(x0)=f(1/2)=2f(x_0) = f(1/2) = 2.

Тогда f′(x0)=f′(1/2)=−4.f'(x_0) = f'(1/2) = -4.

Подставляя эти значения в уравнение касательной y=f(x0)+f′(x0)(x−x0)y=f({{x}_{0}})+{f}'({{x}_{0}})(x-{{x}_{0}}) получаем

y=2−4(x−12).y=2-4left( x-frac{1}{2} right).

То есть у=−4x+4у = -4x + 4 – искомое уравнение касательной.

Тест на тему “Производная функции в точке”

Производные. Приложения производных. Комплексные числа

Учебно-методическое пособие

для студентов
инженерно-технических специальностей

дистанционной
формы обучения

Тольятти 2005

УДК 517.2

ББК 22.161.1

Ч 49

Производные.
Приложения производных. Комплексные
числа. Учебно-методическое пособие /
Сост. Чернова Ю.К., Крылова С.А. Тольятти:
ТГУ, 2005г. – 170 с.

Рассмотрена
сущность производной для инженерных
задач технической направленности.
Содержание пособия соответствует
Государственному стандарту Министерства
образования и науки Российской Федерации.
Учебное пособие включает два модуля:
производные, приложения производных
и комплексные числа. Для них приведены
примеры практического характера.

Пособие предназначено
для студентов технических специальностей
дистанционной формы обучения.

Рецензент к.ф-м.н.,
доцент Ю.В. Клышевич

Научный редактор:
д.т.н., профессор П.Ф. Зибров

Утверждено
научно-методическим советом факультета
математики и информатики Тольяттинского
государственного университета

 ТГУ

 ФМиИ

Оглавление

ВВЕДЕНИЕ 5

1.
Производная функции 6

1. Определение
   производной, её геометрический

и
механический смысл 6

1. Основные
   правила дифференцирования 11

2. Дифференцирование
   функций, заданных неявно 13

3. Дифференцирование
   функций, заданных

параметрически 14

1. Логарифмическое
   дифференцирование 16

2. Производные
   высших порядков 17

3. Механический
   смысл производной второго порядка 19

4. Производные
   высших порядков неявно заданной

функции 20

1. Производные
   высших порядков от функций,

заданных
параметрически 21

1.10.
Понятие дифференциала функции 22

1.11.
Геометрический смысл дифференциала
функции 23

1.12.
Основные теоремы о дифференциалах 24

1.13.
Таблица дифференциалов 25

1.14.
Применение дифференциала

к
приближённым вычислениям 27

1.15.
Дифференциалы высших порядков 28

1.16.
Правила Лопиталя 29

1. Исследование
   функций при помощи производных 34

   1. Возрастание
      и убывание функций 34

   2. Экстремумы
      функций, наибольшее и

наименьшее
значения функции на отрезке 38

1. Выпуклость
   и вогнутость графика функции.

Точки
перегиба 44

1. Асимптоты
   графика функции 45

2. Общая
   схема исследования функции 47

3.
Векторная функция скалярного аргумента 53

4.
Комплексные числа 60

4.1.
Понятие и представление комплексных
чисел 60

4.2.
Действия над комплексными числами 63

ТЕОРЕТИЧЕСКИЙ
ТЕСТ 71

ПРАКТИЧЕСКИЙ
ТЕСТ по теме «Производная» 72

ПРАКТИЧЕСКИЙ
ТЕСТ по теме «Приложения

производных.
Комплексные числа» 132

ЛИТЕРАТУРА 162

ПРИЛОЖЕНИЕ
1 164

ПРИЛОЖЕНИЕ
2 167

ПРИЛОЖЕНИЕ
3 168

Введение

В настоящем методическом пособии
излагается материал высшей математики
— производные, приложения производных
и комплексные числа, — ориентированный
на студентов инженерно-технических
специальностей. Производная, как одно
из наиболее важных, специфических
понятий математического анализа,
связана с решением многих задач физики,
механики, техники и т.п. Ознакомившись
с дифференциальным исчислением, можно
изучать поведение функции в некотором
промежутке, строить её график наиболее
рациональным способом, устанавливая
наиболее интересные моменты в поведении
функции. Комплексные числа широко
применяются в современной математике
и её приложениях в силу удобства
получения многих соотношений между
вещественными величинами с помощью
комплексных чисел и комплексных функций.

Изложение сопровождается решёнными
примерами, детальный разбор которых
помогает студенту в самостоятельной
работе над усвоением материала.

Каждый модуль имеет теоретическую
часть, представленную в опорных схемах,
которые являются средством обобщения
пройденного материала, быстрого
запоминания и длительного хранения
полученной информации.

1. Производная функции

1.1. Определение производной, её геометрический и механический смысл

Рассмотрим две
задачи, приводящие к понятию производной
функции.

Задача
1. Пусть
материальная точка движется по прямой
в одном направлении. Обозначим S
– путь, пройденный точкой, а t
– время. Путь, пройденный точкой за
время t
зависит от t
и изменяется по некоторому закону S
= S
(t).
Отметим некоторый момент времени t₀
и поставим задачу определить скорость
материальной точки V₀
в момент времени t₀.
Для этого рассмотрим другой момент
времени по прошествии отрезка t,
т.е. момент t₀
+ t.
К моменту t₀
путь, пройденный точкой, составит S
(t₀),
в момент t₀
+ t
будем иметь путь

.
За промежуток времени t
точка прошла путь

.
Средняя скорость движения за время t
составит отношение

.
Эта средняя скорость отличается от
мгновенной скорости в момент t₀,
и тем ближе величина Vср
к скорости V₀,
чем меньше промежуток t.
Устремим t
к нулю (пишут

),
тогда предел, к которому стремится
средняя скорость, и является скоростью
нашей точки V₀
момент t₀.

В
последней формуле рассматривается
предел отношения приращения пути S
к приращению времени t.

Задача
2. Рассмотрим
график непрерывной функции

.
Возьмём на этом графике точку

и поставим задачу написать уравнение
касательной прямой к графику

,
проведённой в точке M₀
(рис. 1).

Рис. 1.

Точка
M₀
имеет координаты

;
дадим переменной x
приращение x
и переместимся по графику из точки M₀
в точку M
(в нашем случае x>0
и мы переместились вправо от точки M₀).

Координаты
M
можно вычислить. Абсцисса M
равна x₀+x,
а ордината y
= f
(x₀
+ x).
На сколько изменилось значение функции

при перемещении из точки M₀
в точку M?
Это изменение функции называется
приращением
функции,
обозначается y
и вычисляется так:

.

В
случае нашей функции (возрастающая)
y>0.
Прямая M₀M
называется секущей и её наклон к оси
Oх
определяется тангенсом угла .
Угловой коэффициент секущей

.

Если
теперь неограниченно уменьшать
приращение x,

,
то приращение функции

(наша функция непрерывна). При этом
секущая M₀M
неограниченно приближается к положению
M₀K.
Это предельное положение секущей и
есть прямая, которая является касательной
к графику

в точке M₀.
Угол 
наклона секущей к положительному
направлению оси OX
превратится в угол наклона касательной
.
Тогда угловой коэффициент касательной
прямой K
получим так:

,

,
т.е. угловой
коэффициент касательной
есть предел отношения приращения
функции y
к приращению аргумента x
при стремлении x
к нулю.

Производной
функции

в точке x₀
называется предел отношения приращения
функции y
= f
(x₀
+ x)
– f (x₀)
к приращению аргумента x
при произвольном стремлении x
к нулю, если такой предел существует.
Обозначается производная функции f
(x)
в точке x₀
символом

.

Итак,
. (1.1)

Из
рассмотренных ранее задач получаем,
что скорость прямолинейного движения
материальной точки в момент времени
t₀
есть производная от пути по времени

.

В
этом состоит механический смысл
производной. Вторая задача приводит
нас к геометрическому смыслу производной.
Мы получили, что угловой коэффициент
касательной к кривой проведённой в
точке M₀
(x₀,
y₀),
есть

.
Поэтому уравнение касательной к графику
в точке M₀
имеет вид:

,
или

(1.2)

Для
производной в точке x₀
можно использовать и другие обозначения,
например:

,

,

,

.

Мы
дали определение производной функции
y =
f (x)
в точке x₀.
Такую производную можно вычислять в
различных значениях x,
величина её зависит от этого значения.
Поэтому можно говорить о производной
функции, определённой на некотором
множестве значений x.
Производную функции обозначают

.

Вернёмся
к рис. 1. Мы показали, что при движении
из точки х₀
в точку х₀
+ х
по графику функции y
= f
(x)
ордината точки получает приращение у
=
f (x₀
+ х)-
f (x₀).
На рисунке это приращение у
равно отрезку NM.
Если же двигаться из точки х₀
в точку х₀
+ х
по касательной, проведённой в точке
М₀,
то ордината получит приращение, равное
отрезку KN.
Вычислим величину этого приращения.
Из треугольника M₀KN
следует: катет KN
= M₀Ntg.
Так как tg
= f
(x₀),
а M₀N
= х,
то NK =
f
(x₀)х.

Произведение
производной f
(x₀)
на приращение х
называется дифференциалом
функции y =
f (x)
в точке x₀.
Обозначают дифференциал dy(x)
или df(x).
Поэтому можно написать dy
= df(x)
= f
(x)х.
Для приращения независимой переменной
имеем х
= dx, и поэтому
дифференциал записывается в виде df
= f
(x)
dx.

Заметим,
что приращение функции у
при малом приращении х
= dx по величине
«очень мало» отличается от приращения
по касательной, т.е. от дифференциала
dy.
Так как касательная в точке М₀
«почти совпадает» с кривой в малой
окрестности точки х₀,
то разность (у

dy) стремится
к нулю «быстрее», чем х,
при х

0. Это обстоятельство используется в
приближённых вычислениях.

1.2. Основные правила дифференцирования

Если
функции u
=
u
(x)
и v
= v (x)
дифференцируемы в точке x,
тогда справедливы следующие правила
дифференцирования:

1.
(cu)
=
cu,
где с
– постоянная;

2.
(u
± v)’
= u‘
± v‘;

3.
(u
v)’
= u
‘
v
–
v
‘
u;

4.

.

Пусть
функция у
= f
(u),
где u
= u (х).
Тогда у
есть сложная функция от х:
у
= f (u
(х)),
а u
– промежуточный аргумент. Чтобы найти
производную этой сложной функции,
применяют следующее правило:

,

.

Например,
если у
=
cos
³ х,
то (см. таблицу основных формул
дифференцирования), обозначив u
=
соs х,
получим у
= u
³.

Тогда
у_x
=
3u
²u_x;
у_x
=
3соs
²
х
(-sin
х).

Таблица
основных формул дифференцирования.

На
практике чаще всего приходится находить
производные от сложных функций. Поэтому
в приведённой ниже таблице формул
дифференцирования используется
промежуточный аргумент «и».

1. (c)
   =
   0, с
   –
   постоянная.

2. (u
   ⁿ)
   = пu
   ^п1,

;

1. (а
   ^u)
   = а
   ^u ln
   a
   
   u,

y
= e
^u,
y
= e
^u;

1. (log_a
   x)
   =
   
   ,

(ln
u)
=

;

1. (sin
   u)
   = cos
   u
   u;

2. (cos
   u)=
   sin
   u
   u;

3. (tg
   u)=
   ;

4. (ctg
   u)=
   .

5. (arcsin
   u)
   =
   ;

6. (arccos
   u)
   =
   ;

7. (arctg
   u)
   =
   ;

8. (arcctg
   u)
   =
   ;

9. (sh
   u)
   = ch
   u
   
   u;

10. (ch
    u)
    = sh
    u
    
    u;

11. (th
    u)
    =
    ;

12. (cth
    u)
    =
    .

Пример
1.

.

=

=

.

1.3 Дифференцирование функций, заданных неявно

Если
функция задана уравнением у
= f (x),
разрешённым относительно y,
то функция задана
в явном виде
(явная
функция).

Под
неявным
заданием
функции
понимают задание функции в виде уравнения
F
(х;
у)
=
0, не разрешённого относительно у.

Всякую
явно заданную функцию у
= f (x)
можно
записать как неявно заданную уравнением
f
(x)
— у = 0,
но не наоборот.

Не
всегда легко, а иногда и невозможно
разрешить уравнение относительно у
(например,
у
+ 2х
+
соs у
— 1
= 0
или 2
^y
—
х
+ у = 0).

Если
неявная функция задана уравнением F
(х;
у)
=
0, то для нахождения производной от у
по
х
нет
необходимости разрешать уравнение
относительно у:
достаточно продиффиринцировать это
уравнение по х,
рассматривая при этом у
как функцию от х
и полученное затем уравнение разрешить
относительно у.

Производная
неявной функции выражается через
аргумент х
и
функцию у.

Пример
2. Найти
производную функции у,
заданную
уравнением х³
+ у³
– 3ху
= 0.

Решение:
функция у
задана
неявно. Дифференцируем по х
равенство
х
³
+ у
³
– 3 х
у
= 0. Из полученного соотношения 3х
²
+ 3у
²у
— 3
(1у
+ ху)
= 0 следует, что у²
у
— ху
= у — х
²,
т.е.

.

1.4 Дифференцирование функций, заданных параметрически

Пусть
зависимость между аргументом х
и
функцией у
задана
параметрически в виде двух уравнений

(1.3)

где
t
– вспомогательная переменная, называемая
параметром.

Найдём
производную у’_х,
считая,
что функции (1.3) имеют производные и что
функция х
= х (t)
имеет
обратную t
=

(x).
По
правилу дифференцирования обратной
функции

. (1.4)

Функцию
у
=
f
(х),
определяемую
параметрическими уравнениями (1.3), можно
рассматривать как сложную функцию у
= y (t),
где t
=

(x).
По
правилу дифференцирования сложной
функции имеем: у’_х
= у_t

t_x.
С учётом равенства (1.4) получаем

,

т.е.

.

Полученная
формула позволяет находить производную
у’_х
от
функции заданной параметрически, не
находя непосредственной зависимости
у
от
х.

Пример
3. Пусть


Найти
у’_х.

Решение:
имеем х’_t
=
3 t
²,
у_t
=
2
t.
Следовательно,

,
т. е.

.

1.5 Логарифмическое дифференцирование

В
ряде случаев для нахождения производной
целесообразно заданную функцию сначала
прологарифмировать.
А
затем результат продифференцировать.
Такую операцию называют логарифмическим
дифференцированием.

Пример
4. Найти
производную функции

у
=

.

Решение:
Можно найти у’
с
помощью правил и формул дифференцирования.
Однако такой способ слишком громоздкий.
Применим логарифмическое дифференцирование.
Логарифмируем функцию:

ln
y
= ln (x
² +
2) +

ln (x
— 1)
+ x
– 3
ln (x
+
5).

Дифференцируем
это равенство по х:

.

Выражаем
у’:

,

т.е.


.

Существуют
функции, производные которых находят
лишь логарифмическим дифференцированием.
К их числу относится так называемая
степенно-показательная функция у
= и
^v,
где
и
= и (х)
и
v
=
v (x)
– заданные дифференцируемые функции
от х.
Найдём
производную этой функции:

ln
y
= v

ln u




 y
= y(v
ln
u + v
u),
т.е. y=
и
^v
(v
ln
u + v
u),

или
(u
^v)
= u
^v
ln
uv+v
u
^v-1
u.
(1.5)

Сформулируем
правило запоминания формулы (1.5):
производная степенно-показательной
функции равна сумме производной
показательной функции, при условии и
= const
и производной степенной функции, при
условии v=
const.

Пример
5. Найти
производную функции

.

Решение:
Пользуясь формулой (1.5), получаем:

.

Отметим, что
запоминать формулу (1.5) необязательно,
легче запомнить суть логарифмического
дифференцирования.

1.6 Производные высших порядков

Производная
у’
= f
(х)
функции у
= f
(х)
есть также функция от х
и называется первой
производной,
или производной первого порядка.

Если
функция f
(х)
дифференцируема, то её производная
называется второй
производной,
или производной
второго порядка
и обозначается символами у,
f
(x)
или

.

Производная
от производной второго порядка, если
она существует, называется производной
третьего порядка
и обозначается у,
f
(x)
или

.

Вообще,
производной
n-го
порядка
функции f
(х)
называется первая производная от
производной (n-1)-го
порядка:

f
⁽ⁿ⁾
(x)
= [f
^(n-1)
(x)].

Пример
6.
Найти значение третьей производной
функции y
= е
^5x+3
в точке x
=
0.

Решение:
сначала найдём функцию y
= (f(x)
),
а затем вычислим её значение в точке x
=
0.

y
= (e^5x+3)
= 5e^5x+3,
y
= (e^5x+3)
= (5e^5x+3)
= 25e^5x+3,

y
= (25e^5x+3)
= 125e^5x+3,
y(0)
= 125e^50+3
= 125e³.

Пример
7. Найти
производную 13-го порядка функции y
= sin x.

Решение:
y
= (sin x)
= cos x
= sin(x+
),

y
= (cos x)
= —
sin x
= sin(x+


2),

y
= (sin x)
= —
cos x
= sin(x+


3),

y
^V
= (sin x)
= —
cos x
= sin(x+


4),

………………………………………..

y⁽¹³⁾
= sin(x+


13).

1.7 Механический смысл производной второго порядка

Пусть
материальная точка М
движется прямолинейно по закону S
= f (t).
Как уже известно, производная
S_t
равна
скорости точки в данный момент времени:
S_t
=
v.

Покажем,
что вторая производная от пути по
времени есть величина ускорения
прямолинейного движения точки, т.е.
S_t
=
а.

Пусть
в момент времени t
скорость
точки равна v,
а в момент t
+ t
– скорость
равна v
+
v,
т.е. за промежуток времени t
скорость
изменилась на величину v.

Отношение

выражает среднее ускорение движения
точки за время t.
Предел этого отношения при t

0 называется ускорением
точки М в
данный момент t
и обозначается
буквой а:

.
То есть v
= а. Но v
= S_t.
Поэтому а
= (S_t),
т.е. а
= S_t.

1.8 Производные высших порядков неявно заданной функции

Пусть
функция у
= f (х)
задана
неявно в виде уравнения F
(х;
у)
= 0.

Продифференцировав
это уравнение по х
и разрешив полученное уравнение
относительно у’,
найдём производную первого порядка.
Продифференцировав по х
первую
производную, получим вторую производную
от неявной функции. В неё войдут х,
у
и у’.
Подставляя уже найденное значение у’
в
выражение второй производной, выразим
у»
через
х
и
у.

Аналогично
поступаем для нахождения производной
третьего (и дальше) порядка.

Пример
8. Найти
у,
если
х
²
+
у
²
= 1.

Решение:
дифференцируем уравнение х
²
+
у
²
–
1 по х:
2
х
+ 2
уу’
= 0.

Отсюда

.
Далее имеем:

,
т.е.

(так как х²
+
у²
= 1), следовательно,

.

1.9 Производные высших порядков от функций, заданных параметрически

Пусть
функция у
= f (х)
задана
параметрическими уравнениями

Как
известно, первая производная у’_х
находится
по формуле
. (1.6)

Найдём вторую производную от функции
заданной параметрически. Из определения
второй производной и равенства (1.6)
следует, что

. (1.7)

Аналогично
получаем

,
y
^V
=

,
…

Пример
9. Найти
вторую производную функции

Решение:
по формуле (1.6)

ctg
t.

Тогда
по формуле (1.7)

.

1.10 Понятие дифференциала функции

Дифференциалом
функции
у
= f (х)
в
точке х
называется главная часть её приращения,
равная произведению производной функции
на приращение аргумента, и обозначается
dy
(или df
(x)): dy
= f 
(x)x.
(1.8)

Дифференциал
dy
называют
также дифференциалом
первого порядка.
Найдём
дифференциал независимой переменной
х,
т.е. дифференциал функции у
= х.

Так
как у’
=
х’
= 1,
то, согласно формуле (1.8), имеем dy
= dx = x,
т.е. дифференциал независимой переменной
равен приращению этой переменной: dx
= x.

Поэтому формулу
(1.8) можно записать так:

dy
= f 
(x)
dx, (1.9)

иными словами,
дифференциал функции равен произведению
производной этой функции на дифференциал
независимой переменной.

Из
формулы (1.9) следует равенство

.
Теперь обозначение производной

можно рассматривать как отношение
дифференциалов dy
и
dx.

Пример
10. Найти
дифференциал функции

.
Вычислить dy
при
х
=
0,
dx = 0,1.

Решение:
По формуле dy
= f 
(x)
dx
находим

.

Подставив
х
=
0 и
dx = 0,1,
получим

.

1.11 Геометрический смысл дифференциала функции

Выясним геометрический
смысл дифференциала.

Для
этого проведём к графику функции у
= f (х)
в
точке М
(х;
у)
касательную
МТ
и
рассмотрим ординату этой касательной
для точки х
+ х
(рис. 2).На рисунке АМ
=
х,
АМ₁
= у.
Из прямоугольного треугольника МАВ
имеем:

tg

=
,
т.е. АВ=
tg 
х.

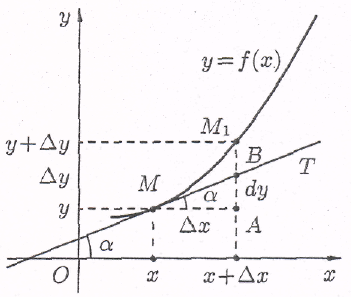
Рис. 2.

Но,
согласно геометрическому смыслу
производной, tg 
= f 
(х).
Поэтому
АВ
=
f 
(х)х.

Сравнивая полученный
результат с формулой (1.9), получаем
dy = АВ, т.е. дифференциал функции у
= f (х) в точке х равен приращению
ординаты касательной к графику функции
в этой точке, когда х получит
приращение х.

1.12 Основные теоремы о дифференциалах

Теорема
1. Дифференциал
суммы, произведения и частного двух
дифференцируемых функций определяются
следующими формулами:

d(u
+ v)
= du
+ dv,

d(uv)
= v
du + u
dv,

(v

0).

Теорема
2. Дифференциал
сложной функции равен произведению
производной этой функции по промежуточному
аргументу на дифференциал этого
промежуточного аргумента.

dy
= y_u

du.

1.13 Таблица дифференциалов

1. d(и
   ±
   v)
   = dи
   ±
   dv;

2. d(и
   
   v)
   = vdи
   +
   udv,

d(cu)
= c
du;

1. 
   ,

;

1. dу
   = у_х
   dx,
   если
   у
   =
   f
   (x);

2. dу
   =
   у_и
   
   du,
   если
   у
   =
   f
   (и),
   и = (х);

1. dc
   = 0;

2. d
   (и
   ^
   )
   =
   
   u
   ^–1
   
   du;

3. d
   (а
   ^и
   )
   = a
   ^u 
   ln
   a
   
   du,

d
(e
^и )
= e
^u 
du;

1. 
   ,

;

1. d
   (sin
   u)
   =
   cos
   u
   du;

2. d
   (cos
   u)
   = —
   sin u
   du;

3. d
   (tg
   u)
   =
   
   ;

13.
d
(ctg
u)
=

;

14.
d
(arcsin
u)
=

;

1. d
   (arcos
   u)
   =
   
   ;

2. d
   (arctg
   u)
   =
   
   ;

3. d
   (arcctg
   u)
   =
   
   ;

4. d
   (sh
   u)
   = ch u
   du;

5. d
   (ch
   u)
   = sh u
   du;

6. d
   (th
   u)
   =
   
   ;

7. d
   (cth
   u)
   =
   
   .

1.14 Применение дифференциала к приближённым вычислениям

Приращение
у
функции
у
= f (х)
в
точке х
можно
представить в виде у
=
f 
(х)

х,
где 

0 при х

0, или у
=
dy
+ 

х.
Отбрасывая бесконечно малую 

х
более
высокого порядка, чем х,
получаем
приближённое равенство

y

dy, (1.10)

причём
это равенство тем точнее, чем меньше
х.

Это равенство
позволяет с большой точностью вычислить
приблизительно приращение любой
дифференцируемой функции.

Дифференциал
обычно находится значительно проще,
чем приращение функции, поэтому формула
(1.10) широко применяется в вычислительной
практике.

Подставляя
в равенство (1.10) значения y
и
dy,
получим

f
(x₀+x)

f
(x₀)
+ f

(x₀)x (1.11)

Пример
11. Вычислить
приближённо агсtg (1,05).

Решение:
рассмотрим функцию f
(х)
=
агсtg
х.
По формуле (1.11) имеем:

агсtg
(x₀+x)

агсtg (х₀)
+ (агсtg (х₀))

x,
т.е. агсtg
(x₀+x)


 агсtg
(х₀)
+

.

Так
как х
= x₀
+
x
= 1,05,
то при х₀
= 1 и x
= 0,05
получаем:

aгсtg
(1,05) 
агсtg 1 +

=

+ 0,025 
0,810.

1.15 Дифференциалы высших порядков

Пусть
у
= f (х)
дифференцируемая
функция, а её аргумент х
—
независимая переменная.
Тогда
её первый дифференциал dy
= f
(x)
dx
есть
также функция от х;
можно найти дифференциал этой функции.

Дифференциал
от дифференциала функции у
= f (х)
называется
её вторым
дифференциалом
(или
дифференциалом
второго порядка)
и обозначается d
²y
или d
² f
(x):

d
² y
= f

(x)
dx
² (1.12)

Здесь
dx
²
обозначает
(dx)².

Аналогично
определяется и находится дифференциал
третьего порядка:

d
³ y
=
d
(d
² y)
= d (f

(x)
dx
² )
=
f

(x)
dx
³.

Вообще,
дифференциал n-го
порядка есть дифференциал от дифференциала
(n-1)—го
порядка: d
ⁿ
y = d (d
^{n
— 1}y)
= f
⁽ⁿ⁾
(x)
(dx)
ⁿ.

Отсюда
находим, что

.
В частности, при n
= 1, 2, 3 соответственно получаем:

,

,

,
т.е. производную функции можно
рассматривать как отношение её
дифференциала соответствующего порядка
к соответствующей степени дифференциала
независимой переменной.

Отметим,
что все приведённые выше формулы
справедливы только, если х
– независимая переменная.

Пример
12. Найти d
² y,
если y = e
^3x
и х
– независимая переменная.

Решение:
так как y
= 3e
^3x,
y
= 9e
^3x,
то по формуле (1.12) имеем d
²y
= 9e
^3x
dx
².

1.16 Правила Лопиталя

Правила
Лопиталя применяются для раскрытия
неопределённостей вида

и

,
которые называются основными.

Теорема
3.
(Правило Лопиталя раскрытия
неопределённостей вида

).

Пусть
функции f
(x)
и g
(x)
непрерывны и дифференцируемы в
окрестности точки х₀
и обращаются в нуль в этой точке: f
(x₀)
= g
(x₀)
= 0. Пусть g
(x)

0 в окрестности точки x₀.
Если существует предел

,
то

.

Пример
13.
Найти

.

Решение:

.

Теорема
4.
(Правило Лопиталя раскрытия
неопределённостей вида

).

Пусть
функции f
(x)
и g
(x)
непрерывны и дифференцируемы в
окрестности точки х₀
(кроме, может быть, точки х₀),
в этой окрестности

,
g
(x)

0. Если существует предел

,
то

.

Пример
14.
Найти

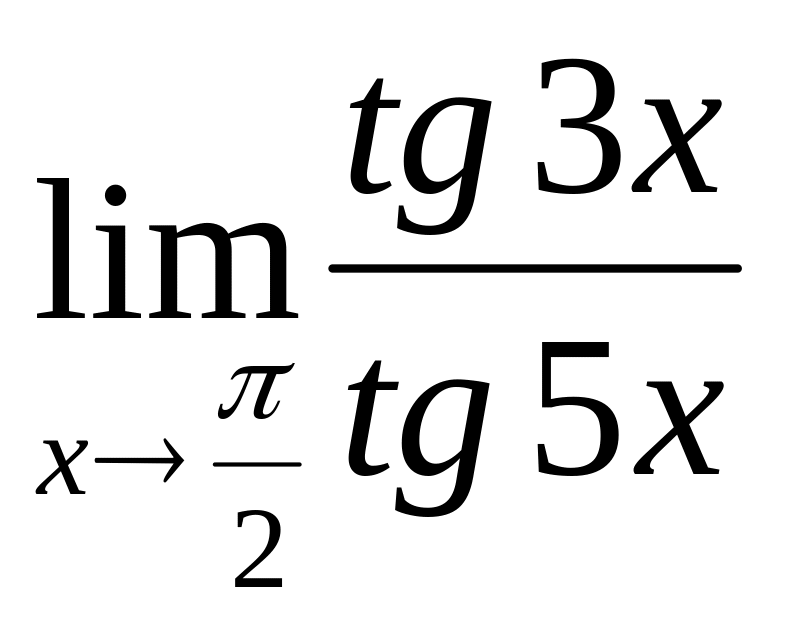
Решение:

.

Неопределённости
вида [0],
[

],
[1^],
[
⁰],
[0
⁰]
сводятся к двум основным путём
тождественных преобразований.

1. Пусть
   f
   (x)
   
   0, и g
   (x)
   
   0 при х
   
   х₀.
   Тогда очевидны следующие преобразования:

(или

).

Пример
15.
Найти

.

Решение:

.

1. Пусть
   f
   (x)
   
   ,
   и g
   (x)
   
   
   при х
   
   х₀.
   Тогда можно поступить так:

.

Пример
16.
Найти

.

Решение:

.

1. Пусть
   f
   (x)
   
   1, и g
   (x)
   
   ,
   или f
   (x)
   
   ,
   и g
   (x)
   
   0, или f
   (x)
   
   0, и g
   (x)
   
   0 при х
   
   х₀.
   Для нахождения предела вида
   

   вспомним свойство логарифма
   
   
   .

Пример
16.
Найти

.

Решение:

=




=

=

=

=

= [tg 2x

2x]
= =

=

.

Пример
17.
Найти

.

Решение:

= =

=

=

=
=
.

2. Исследование функций при помощи производных

2.1 Возрастание и убывание функций

Одним из приложений
производной является её применение к
исследованию функций и построению
графика функции.

Установим
необходимые и достаточные условия
возрастания и убывания функции.

Теорема
5 (необходимые
условия). Если дифференцируемая на
интервале (a;
b)
функция f
(x)
возрастает (убывает), то f

(x)

0 (f 
(x)

0) для любого х

(a;
b).

Теорема
6 (достаточные
условия). Если функция f
(x)
дифференцируема на интервале (a;
b)
и f 
(x)
> 0 (f 
(x)
< 0) для
любого х

(a;
b),
то эта функция возрастает (убывает) на
интервале (a;
b).

Посмотрим
на графики функций y
= f
(x),
y =
g (x)
и y
= 
(x),
изображённые на рис. 2 —
4.

Функции
f (x)
и g (x)
возрастают, но график, изображённый на
рис. 3, пологий на участке [а,
0], т.е. функция y
= f
(x)
меняется (растёт) медленно, график же
функции g
(x)
круто поднимается вверх на участке

,
т.е. g (x)
меняется (тоже растёт) быстро, с большей
скоростью. Проведём касательные к нашим
графикам в точке М₀.
Сравним углы ₁
и ₂,
которые образуют касательные к графикам
с положительным направлением оси Ох.
Так как углы ₁
и ₂
острые, то tg ₁
и tg ₂
положительны и по смыслу производной
это обозначает, что обе функции
возрастают в интервале от (a;
x₀).
Поскольку f
(x₀)

g
(x₀),
график второй функции “круче”, чем
график первой.

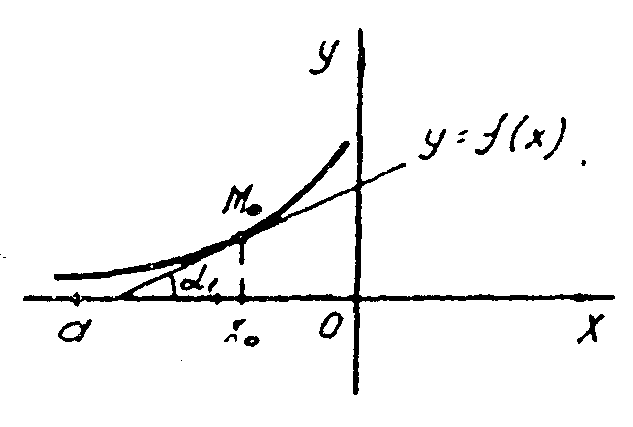
Рис. 3.

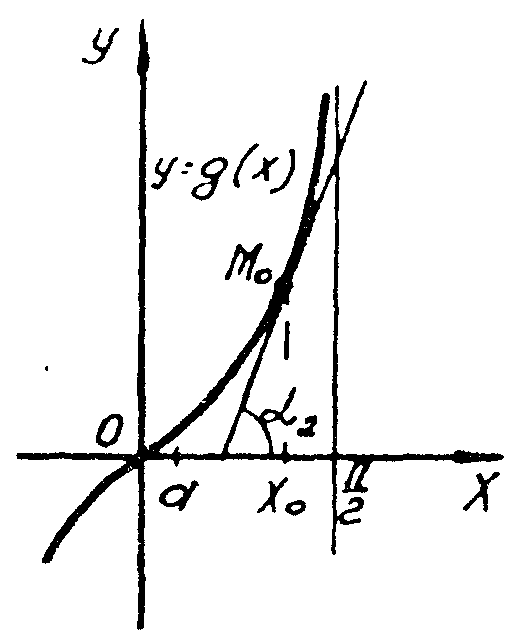
Рис. 4.

Эти
рисунки отражают общее явление: если
функция возрастает на интервале и имеет
производную в каждой точке этого
интервала, то производная неотрицательна;
если производная положительна во всех
точках интервала, то функция строго
возрастает на этом интервале.

Рис. 5.

Рассмотрим
теперь рис. 5. На нём изображён график
убывающей на [х₀,
а]
функции y =

(x).
Угол ₃
касательной с осью Ох
тупой и tg 
₃ = 

(x₀)

0.

Этот рисунок
отражает следующее общее явление: если
функция убывает на интервале, то во
всех точках этого интервала её производная
не положительна; если производная
отрицательна, то функция строго убывает.

В сформулированных
утверждениях следует строго различать
необходимые и достаточные условия.
Поясним это примерами.

Функция
у =
х
³ строго
возрастает на всей вещественной оси
(рис. 6). Для её производной имеем у
= 3х
². В
частности, у
= 0 при х
= 0. Это
означает, что положительность производной
является достаточным, но не является
необходимым условием (строгого)
возрастания. Кроме того, следует не
упускать из вида, что на участках
возрастания (убывания), строгого или
нет, могут встречаться точки, в которых
функция вообще не имеет производной.
Простейший пример даёт функция у
= 2х
+ х,
график которой имеет вид (рис. 7):

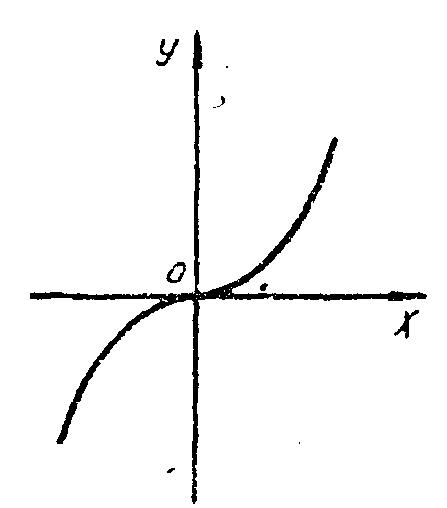
Рис. 6.

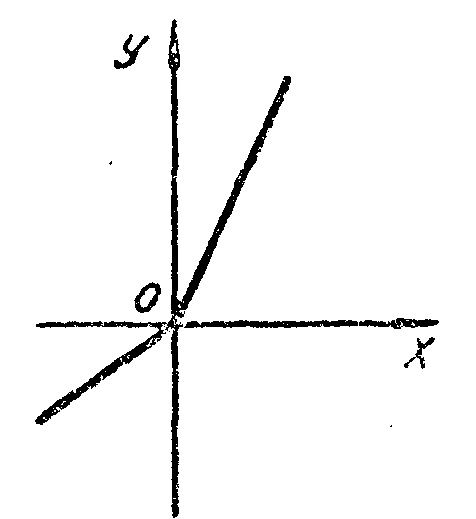
Рис. 7.

2.2 Экстремумы функций, наибольшее и наименьшее значения функции на отрезке

Если
есть функция у
= f (х),
которая имеет конечную производную в
каждой точке отрезка [а,
b]
(говорят, функция f
(х)
– дифференцируема на отрезке [а
,b]
), то её поведение можно исследовать с
помощью производной y
= f
(x).
Ранее мы отмечали, что интервалы
возрастания и убывания f
(x)
определяются знаком f

(x).

Как
видно из рис. 8, такими точками являются
точки х₁,
х₂,
х₃,
х₄.
Точка х₁,
например, обладает следующим свойством:
значение функции в точке х₁
больше значений функции во всех
«соседних» точках как слева, так и
справа от х₁.

Рис
8.

В
этом случае говорят, что функция имеет
в точке х₁
максимум. В точке х₃
функция тоже имеет максимум, а сами
точки х
= х₁
и х
= х₃
называют точками максимума.
И хотя значение функции в точке максимума
х₁
меньше, чем, например, в точке х₅,
важно отметить, что «по – соседству»
с х₁
имеем f
(x)
< f
(x₁).
Говорят, что функция у
=
f
(х)
имеет максимум (max) в точке х
= с,
если существует такая окрестность
точки х
= с,
что для всех точек х

с,
принадлежащих этой окрестности,
выполняется неравенство f
(x)
< f
(с).

Функция
у
=
f
(х)
имеет минимум (min) в точке х
= с,
если существует такая окрестность
точки х
= с,
что для всех точек х

с,
принадлежащих этой окрестности,
выполняется неравенство f
(x)
> f
(с).

Таким
свойством, очевидно, обладают точки х
= х₂
и х
= х₄,
эти точки называют точками минимума.
Точки максимума и минимума объединяют
под общим названием точки экстремума.

Точки
экстремума лежат внутри области
определения функции, их ещё называют
локальный
максимум
и локальный
минимум
(от латинского слова lokal – местный).
Точки же х
= b
и х
= х₂
на рис. 8 являются глобальным
максимумом
и глобальным
минимумом,
или, говорят, наибольшим и наименьшим
значением f
(x)
на замкнутом интервале [a,
b].
В нашем случае глобальный максимум
совпадает с концом интервала х
= b,
а глобальный минимум совпадает с
локальным в точке х
= х₂.
Функция, непрерывная на замкнутом
интервале, достигает своего наибольшего
и наименьшего значения.

Что
можно сказать о производной в точках
экстремума? (Мы рассматриваем случай,
когда производная существует во всех
точках [a,
b].)

Вспомним,
что производная f
(x₀)
связана с касательной, проведённой в
точке х₀.
В точках экстремума х₁,
х₂,
х₃,
х₄
(т.е. на «вершинах» и на «дне оврагов»)
касательные горизонтальны, т.е. f
(x₁)
= f
(x₂)
= f
(x₃)
= f
(x₄)
= 0.

Сформулируем
необходимый признак существования
экстремума.

Теорема
7
(необходимый признак существования
экстремума). Если f
(x)
имеет в точке х
= с
экстремум и дифференцируема в этой
точке, то f
(с)
= 0.

Не
следует думать, что верно и обратное
утверждение. Из того, что f

(с)
= 0 ещё не следует, что точка х
= с
является точкой минимума или максимума.

На
рис. 9 изображен график функции у
= х
³.
В точке х
=
0 касательная горизонтальна и производная

равна нулю, но в этой точке у функции
нет ни минимума, ни максимума. Из
сказанного следует, что обращение в
нуль производной в точке, еще не
достаточно, чтобы утверждать, что в
этой точке экстремум. Однако, искать
точки экстремума следует среди тех, в
которых производная равна нулю.

Такие
точки называют стационарными.

Чем
же отличается, например, точка х₃
на рис. 8 от точки х
=
0 на рис. 9?

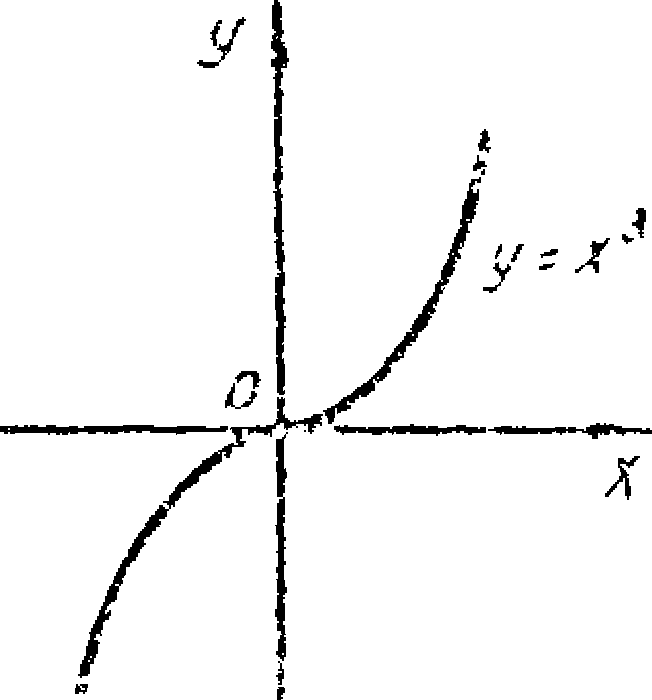
Рис.
9.

И
в той, и в другой точке касательные
параллельны оси Ох,
т.е. f
=
0, обе точки стационарные.

В
точке х
= х₃
(рис. функция f
(х)
меняет характер монотонности (с
возрастания на убывание), т.е. производная
слева от х₃
положительна, а справа – отрицательна.

В
точке х
=
0 (рис. 9) функция у
= х
³
характер монотонности не меняет, слева
и справа от стационарной точки функция
возрастает и её производная

= 3 х
²
сохраняет положительный знак.

Теорема
8
(достаточный признак существования
экстремума). Если непрерывная функция
у
=
f (х)
имеет производную f
(х)
во всех точках некоторого интервала,
содержащего стационарную точку х
= с,
и если производная f
(х)
при переходе аргумента слева направо
через стационарную точку х
= с
меняет знак с «плюса» на «минус», то
стационарная точка х
= с
есть точка максимума, а при перемене
знака с «минуса» на «плюс» – точка
минимума.

Пример
18.
Определить экстремум функции у
= х
³
– Зх
² +2
и найти её наименьшее и наибольшее
значение на отрезке [-0,5; 4].

Решение:
Областью существования функции является
вся числовая ось (;
).
Находим производную у
‘(х)
= З х
² —
6х.
Приравниваем производную нулю, находим
стационарные точки: 3 х
²
–
6 х
= 3 х
(х
—
2) = 0. Решаем это уравнение и получаем
х₁
= 0, х₂
= 2. Нанесём наши точки на числовую ось
и посмотрим как ведёт себя производная
у
‘ (х)
= 3х
(х
—
2) на отрезке [—0,5;
4].

Рассмотрим
интервалы (—0,5;
0), (0; 2), (2; 4).

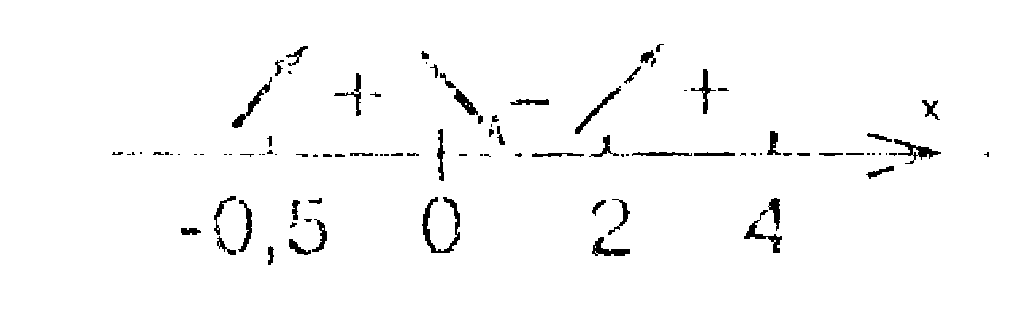
На
интервале (—0,5;
0) производная f

(х)
> 0, на интервале (0; 2) производная f

(х)
< 0. (Убедиться в этом можно, подставляя
в производную какую-нибудь точку из
рассматриваемых интервалов). Теперь
рассмотрим интервал (2; 4) и убедимся,
что f
(х)
> 0. Таким образом, переходя через точку
х
=
0, производная меняет знак с «плюса» на
«минус», т.е. стационарная точка х
=
0 является точкой максимума, а в точке
х
=
2 происходит смена знака производной
с «минуса» на «плюс» и х
=
2 – точка минимума. Значение функции в
точках х_min
и х_max
вычислим, подставив х
=
2 и х
=
0 в уравнение у
= х
³
– 3х
²
+ 2.

Получим,
х_max
= 0, у_max
= у(0) = 2; х_min
= 2, у_min
=
у(2)
= – 2.

Итак,
мы определили локальные экстремумы.

Чтобы
найти наибольшее и наименьшее значения
функции – глобальные
экстремумы
– применяется следующее правило:

1.
Находим все стационарные точки и точки,
в которых производная не существует,
вычисляем в них значения функции.

2.
Вычисляем значения функции на концах
отрезка, в точках х
= а,
х
= b.

3.
Сравнивая между собой вычисленные
значения функции, выбираем наибольшее
и наименьшее.

Так
как значения в стационарных точках
вычислены, подсчитаем значения функции
на концах отрезка [-0,5; 4], в точках х
= 0,5;
х
= 4.

у(0,5)
= ( 0,5)
³

3 (
0,5)²
+ 2 = +
;
у
(4 ) = 4 ³

34
²
+ 2 = 18

Сравниваем
значения функции у
(-0,5),
у
(0),
у
(2),
у
(4),
получаем, что наибольшее значение
достигается на правом конце у
(4)^:=18,
а наименьшее в точке локального минимума
у
(2)
= 2.

2.3 Выпуклость и вогнутость графика функции. Точки перегиба

Ещё
одной важной характеристикой функции
является характер её выпуклости.

График
дифференцируемой функции называется
вогнутым
в интервале (a,b),
если он расположен выше любой своей
касательной в этом интервале (рис. 10).

График
дифференцируемой функции называют
выпуклым
в интервале (a,
b),
если он расположен ниже любой своей
касательной в этом интервале (рис. 11).

Рис. 10.	Рис. 11

Так
парабола у
= х
²
– функция вогнута на всей числовой оси
(рис. 12), а полуокружность

(рис. 13) имеет выпуклый график на отрезке
[—1;
1].

Точка
М₀
(x₀,
f
(x₀)),
лежащая на графике и отделяющая выпуклую
часть графика от вогнутой, называется
точкой
перегиба
функции у
=
f
(x)
(рис. 14).

За
выпуклость (вогнутость) функции
«отвечает» вторая производная
функции у
=
f
(x).

Справедливо
следующее утверждение: если функция
у
=
f
(x)
имеет вторую производную f
(x)
во всех точках интервала (a,
b)
и если во всех точках этого интервала
f
(x)
< 0. то график функции в интервале (a,
b)
– выпуклый, если же f
(x)
> 0, то график функции вогнутый в этом
интервале.

Рис. 12	Рис. 13	Рис. 14

Точки
перегиба следует искать среди тех
точек, в которых вторая производная
у
= f
(x)
= 0.

Если
слева от такой точки и справа от нее f

(x)
имеет разные знаки, то найденная точка
будет точкой перегиба.

2.4 Асимптоты графика функции

Построение
графика функции значительно облегчается,
если знать его асимптоты.

Асимптотой
кривой называется прямая, расстояние
от которой до точки, лежащей на кривой,
стремится к нулю при неограниченном
удалении от начала координат этой точки
по кривой.

Асимптоты
могут быть вертикальными, наклонными
и горизонтальными.

Говорят,
что прямая является вертикальной
асимптотой
графика функции y
= f
(x),
если

,
или

,
или

.
То есть, для отыскания вертикальных
асимптот следует найти те значения х,
при которых функция обращается в
бесконечность (терпит бесконечный
разрыв).

Для
определения наклонной
асимптоты
y
= kx + b
числа k
(угловой коэффициент прямой) и b
находят из формул:

,

.

Но
если хотя бы один из этих пределов не
существует или равен бесконечности,
то кривая y
= f
(x)
наклонных асимптот не имеет.

Отметим,
что следует отдельно рассмотреть случаи
х
+ 
и х


.
Частным случаем наклонной асимптоты
при k
= 0 и

будет горизонтальная асимптота. Поэтому
y
= b
– уравнение горизонтальной
асимптоты.

Рассмотрим
график функции на рис. 15. Точки х
= х₂,
х
= х₄
– точки экстремумов функции, точка х
= х₁
– это точка перегиба. Точка х
= х₃
является особенной точкой для функции,
в ней f
(x)
терпит разрыв, а прямая х
= х₃
является вертикальной асимптотой
графика функции. Прямая y
= kx + b
тоже будет асимптотой графика, только
наклонной, прямая у
= 0 – горизонтальная асимптота графика.

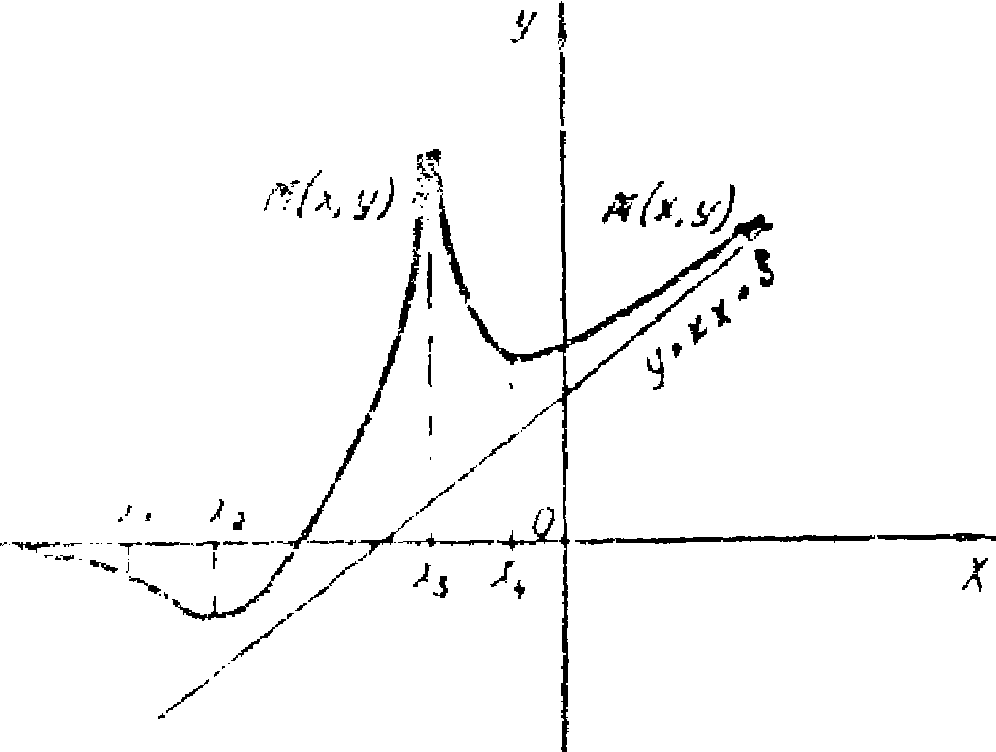
Рис.
15.

Если
точка М
(х,
у)
лежит на графике и неограниченно
удаляется от начала координат, то она
приближается к одной из этих прямых;
расстояние от точки М
(х,
у)
до асимптот стремится к нулю.

2.5 Общая схема исследования функции и построения графика

Для
общего исследования функции и построения
графика полезно придерживаться
следующего плана.

1. Найти
   область определения функции, точки
   разрыва функции и интервалы непрерывности

2. Найти
   (если это возможно) точки пересечения
   графика с осями координат.

3. Найти
   интервалы знакопостоянства функции
   (промежутки, на которых f
   (x)
   > 0 или f
   (x)
   < 0).

4. Решить
   вопрос о чётности, нечётности, симметрии,
   периодичности функции.

5. Если
   есть точки разрыва 2—го
   рода, найти вертикальные асимптоты.

6. Найти,
   если они есть, наклонные и горизонтальные
   асимптоты.

7. С
   помощью 1—ой
   производной найти точки экстремума и
   области возрастания и убывания данной
   функции. Найти экстремальные значения
   функции.

8. С
   помощью 2—ой
   производной найти точки перегиба,
   области выпуклости и вогнутости.

9. Построить
   график.

Пример
19.
Исследовать функцию

и построить её график.

Функция
определена на всей числовой оси за
исключением точки х
=
1, где знаменатель дроби обращается в
нуль. Так как область определения не
симметрична относительно начала
координат, то не имеет смысла говорить
о чётности (нечётности) функции.

Точка
х
=
1 является точкой разрыва функции.
Найдём пределы y
= f (x)
при х

1 (слева и справа) (рис. 16).

Рис.
16.

,

Если
функция в точке х
=
1 имеет бесконечный разрыв, то прямая
х
=
1 является для графика вертикальной
асимптотой.

Будем
искать наклонную асимптоту в виде y
= kx + b.

.

Теперь
найдём

.

;

.

Наклонная
асимптота графика y
= 5
—
x.

Найдём
первую производную у’
=

.

Найдём
сначала стационарные точки, т.е.
приравняем у’
= 0. Получим

,
х₁
=
3, х₂
=

1

Посмотрим,
меняет ли производная знак при переходе
через эти точки.

Результаты
схематически изображены на рис. 17.

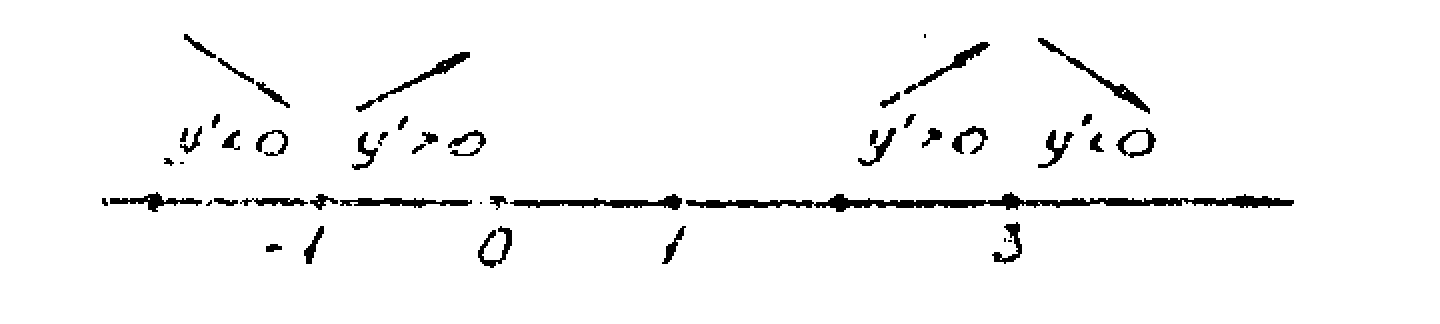
Рис.
17.

Вывод:
х
=

1 – точка минимума, у
(-1
) = 8; х
=
3 – точка максимума, у
(3)
= 0.

Исследование,
включающее вторую производную, проводить
не обязательно. Но мы всё же вычислим
у»

.

Вторая
производная в нуль не обращается, т.е.
точек перегиба график не имеет. На
интервале (,
1) вторая производная положительна и
график вогнутый, в интервале (1, +)
вторая производная меняет знак на
«минус», и график – выпуклый.

Здесь
легко найти точки, где функция пересекает
координатные оси: у
=
0 при х
= 3, а при х
=
0, у
= 9.

График
изображён на рис. 18.

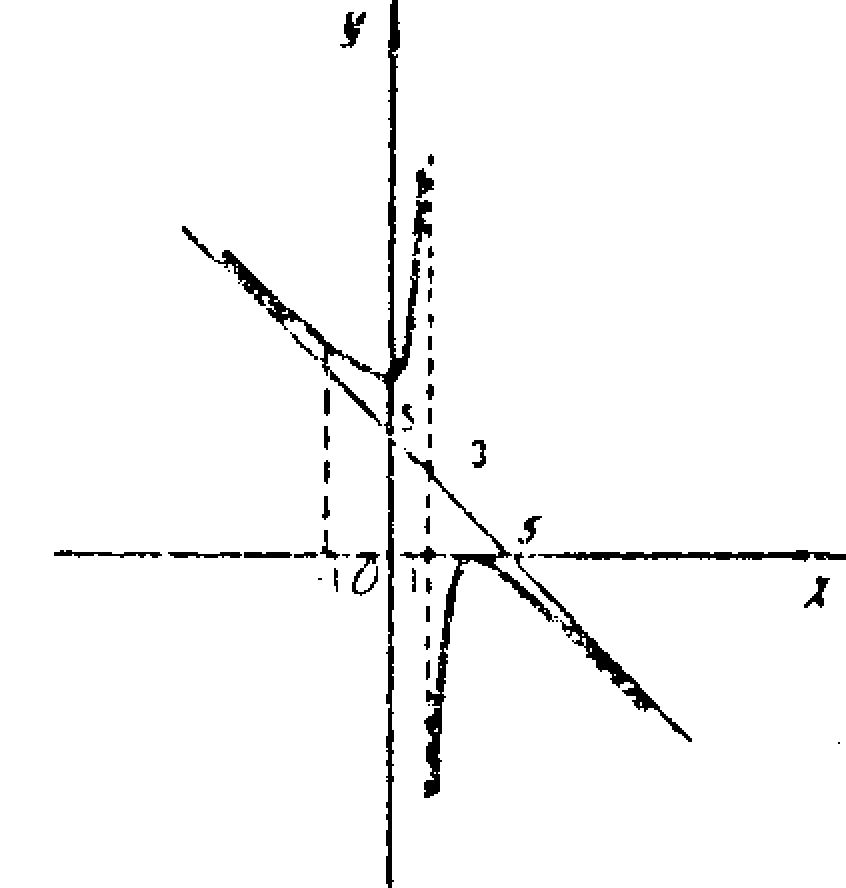
Рис.
18.

Пример
20.
Исследовать функцию y
= e

и построить её график.

Область
определения функции – вся числовая
ось (,
).
Функция всюду непрерывна, вертикальных
асимптот нет.

Найдём
наклонную асимптоту:

;

.

Асимптотой
является горизонтальная прямая у
=
0.

Найдём
экстремум функции и интервалы
монотонности.

;
у
= 0,
х
=
1.

Стационарная
точка х
=
1 будет точкой максимума функции, так
как при переходе через эту точку (слева
направо) производная меняет знак с
«плюса» на «минус».

y_max
=
y
(1)
= e
⁰ =
1.

Вычислим
у
и найдём точки перегиба:

.

Вторая
производная обращается в нуль при х
=
0 и при х
=
2. В обеих этих точках происходит смена
знака у»,
т.е. обе точки будут точками перегиба:

,

.

График
функции изображен на рис. 19.

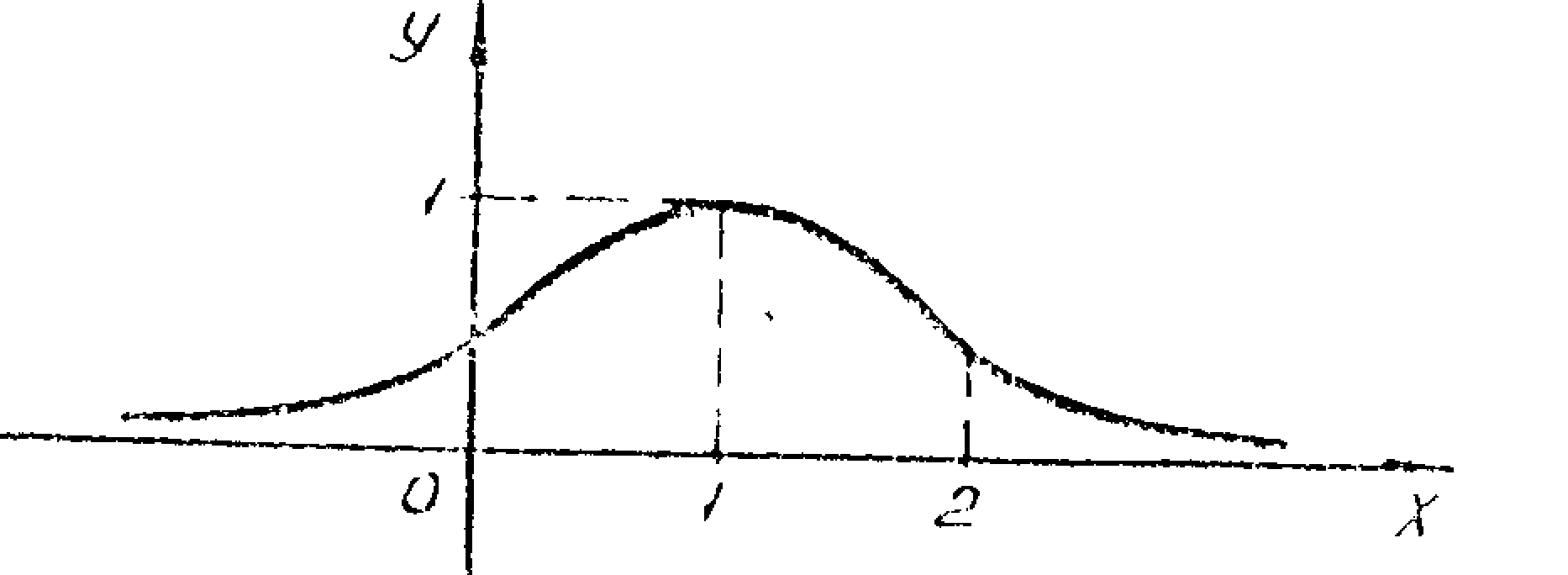
Рис. 19

3. Векторная функция скалярного аргумента

Простейшим
способом задания пространственной
кривой является задание её векторным
уравнением

,
где

– радиус—вектор
точки кривой, а t
– параметр, определяющий положение
точки на кривой. То есть при изменении
t
конец вектора

опишет в пространстве некоторую линию
(L)
(рис.20). Таким образом, переменный вектор

является функцией скалярного аргумента
t;
такие функции носят название векторных
функций скалярного аргумента.

Разлагая
вектор

по осям координат, можно уравнению
пространственной кривой

придать форму

,
где

,

,

– орты координатных осей, что даёт
возможность перейти от векторного
уравнения кривой к её параметрическим
уравнениям

x
= x (t),
y
= y (t),
z
= z (t).

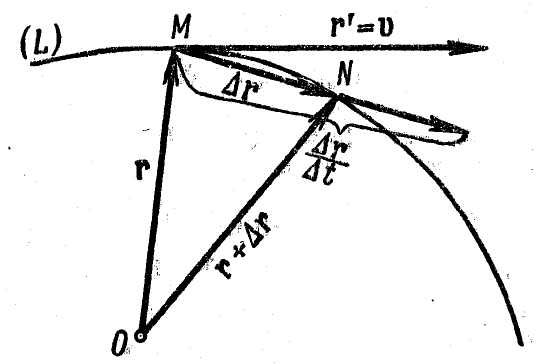
Рис. 20.

Переменную
t удобно
истолковывать как время. Тогда линия
(L)
будет представлять собой траекторию
движущейся точки. Эта линия называется
годографом
этой векторной функции (начало координат
называется полюсом
годографа).

Например,
уравнение

,
где

и

– постоянные векторы, определяет прямую
линию (рис. 21) и равномерное движение
по ней со скоростью

.
Проектируя это уравнение на оси
координат, получим параметрические
уравнения прямой линии:

х
= а_х
+ b_x
t,
y = a_y
+ b_y
t,
z = a_z
+ b_z
t.

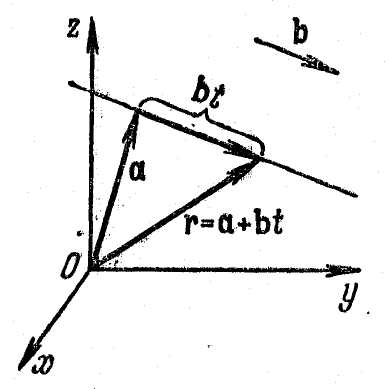
Рис. 21.

Рассмотрим
уравнения винтовой линии. Эта линия
получается в результате наложения
равномерного перемещения параллельно
некоторой оси и равномерного вращения
вокруг этой же оси (рис. 22). Приняв в
качестве этой оси ось z
и обозначив
поступательную скорость через v,
а вращательную через ,
получим x
= R
cos 
t; y
= R
sin 
t; z
= v t
или в векторном виде

.

Если
переменная t
получит приращение t,
то точка V
на линии (L)
перейдёт в положение N
(рис. 20); таким образом,

.
Отношение

(вектор
средней скорости),
поскольку t
– скаляр, также идёт по прямой MN.
Когда t
0,
то

(вектор
мгновенной скорости,
являющийся производной
от векторной функции

по аргументу
t );

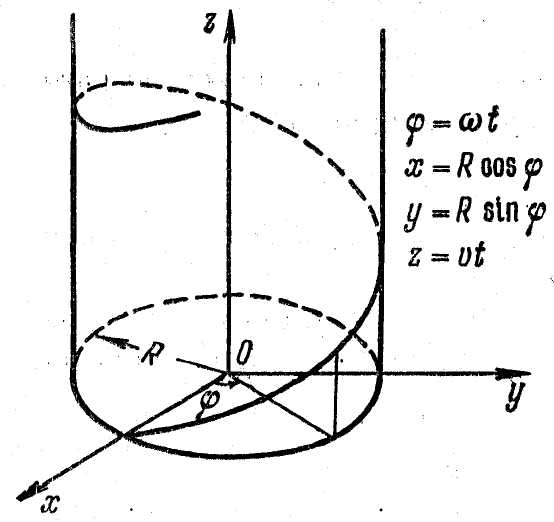
Рис. 22.

но
секущая MN,
будучи продолжена, поворачиваясь около
точки M,
стремится перейти в касательную к
траектории в точке М.
Таким образом, вектор мгновенной
скорости

направлен по касательной к траектории.
Векторно-параметрическое уравнение
касательной при некотором значнеии t
= t₀,
имеет вид (рис. 21)

,
где

,

.
Замена

на

означает переход от движения по линии
(L)
к равномерному движению по касательной
со скоростью, равной мгновенной скорости
в рассматриваемый момент, как будто на
движущуюся точку вдруг перестали
действовать все силы.

Если
воспользоваться разложением вектора

по ортам, то вектор

можно представить в виде

,
где

,

,

.
Отсюда, деля на t
и переходя к пределу при t
0,
найдём для производного вектора
следующее выражение

.

Исследуем
некоторые свойства производного вектора

.
Найдём его модуль:

.
Деля и умножая под знаком предела на
l
(где l
– длина дуги годографа, предполагаемого
спрямляемым) и учитывая, что при t0
также и l0,
находим

.
Но в силу предположения о спрямляемости
дуги годографа имеем

.
Поэтому

.
То есть модуль производного вектора
равен производной (по тому же аргументу)
от дуги годографа.

Если
через

обозначить единичный вектор, направленный
по касательной к годографу в сторону
возрастания параметра t,
то вектор

можно представить в виде

.

Если
за аргумент векторной функции принять
длину дуги годографа l,
отсчитываемую от некоторой выбранной
произвольно начальной точки годографа,
т.е. если положить

,
то из предыдущего равенства (так как

)
получим

.
То есть производная от векторной функции
по длине дуги годографа равна единичному
вектору касательной к годографу,
направленному в сторону возрастания
дуги.

Если
годограф векторной функции рассматривать
как траекторию движущейся точки, а
аргумент t
– как время движения, отсчитываемое
от некоторого начального момента, то
в этом случае производный вектор

по величине и по направлению совпадает
с вектором скорости движения

:

Итак,
производная

есть
вектор, направленный по касательной к
годографу вектора

в сторону возрастания параметра t.
Если t
есть время, то

– вектор скорости конца вектора

,
а

– вектор ускорения.

Координаты
вектора

суть направляющие косинусы касательной

,

,

.
Каноническое уравнение касательной
имеет вид:

.

Пример
21. Рассмотрим
винтовую линию x
= a
cos t;
y
= a
sin t;
z
= bt.
Вектор

есть направляющий вектор касательной.
Находим единичный вектор касательной

,
так что

,

,

.
Отсюда tg =
.

Уравнене
касательной имеет вид:

или

.

Плоскость
Р,
проходящая через точку М
линии (L),
называется нормальной
плоскостью
линии (L).
Направляющий вектор касательной

является нормальным
вектором
плоскости Р.
уравнение нормальной плоскости имеет
вид: (Х — х)
х
+ (Y
— y) y
+ (Z
— z) z
= 0.

Пример
22. Уравнение
нормальной плоскости к винтовой линии
x
= a
cos t;
y
= a
sin t;
z
= bt
имеет вид

(Х
— a
cos t)
(-a
sin t)
+ (Y
— a
sin t)
(a
cos t)
+ (Z
– b t)
b
= 0

или
–y
X + x Y + b Z – b z = 0.

Всякая
прямая, проходящая через точку М
пространственной линии (L)
и перпендикулярная к касательной МТ,
называется нормалью
линии (L)
в точке М.
Пространственная линия имеет бесчисленное
множество нормалей. Все они лежат в
нормальной плоскости. Если линия (L)
лежит в одной плоскости, из множества
нормалей выделяется одна (главная
нормаль),
лежащая в этой плоскости. У неплоской
линии тоже можно выделить главную
нормаль.

4. Комплексные числа

4.1 Понятие и представление комплексных чисел

Комплексным
числом
z
называется выражение вида z
= x + i y,
где х
и у
– действительные числа, а i
– мнимая
единица, i
²
= —
1.

Если
х
= 0, то число 0 + i
y = i y
называется чисто
мнимым;
если у
= 0, то число х
+ i0
отождествляется с действительным
числом.

Число
х
называется действительной
частью
комплексного числа z
и обозначается x
= Re z,
а у
– мнимой
частью
z,
y
= Im z.

Два
комплексных числа z₁
= x₁
+ iy₁
и z₂
= x₂
+ iy₂
называются равными
(z₁
= z₂)
тогда и только тогда, когда равны их
действительные части и равны их
мнимые части: х₁
= х₂,
у₁
= у₂.
Понятия «больше» и «меньше» для
комплексных чисел не вводятся.

Два
комплексных числа z
= x + iy
и z
=
x – iy,
отличающиеся лишь знаком мнимой части,
называются сопряжёнными.

Всякое
комплексное число z
= x + iy
можно изобразить точкой M
(x;
y)
плоскости Оху
такой, что x
= Re z,
y
= Im z.
И, наоборот, каждую точку M
(x;
y)
координатной плоскости можно рассматривать
как образ комплексного числа z
= x + iy.
Именно поэтому между двумя комплексными
числами z₁
= x₁
+ iy₁
и z₂
= x₂
+ iy₂
нельзя поставить знак « > » или « <
», но можно поставить знак « = », если
числа совпадают, т.е. если x₁
= x₂,
iy₁
= iy₂.

Плоскость,
на которой изображаются комплексные
числа, называется комплексной
плоскостью.
Ось абсцисс называется действительной
осью,
так как на ней лежат действительные
числа z
= x
+ 0i
= x.
Ось ординат называется мнимой
осью,
на ней лежат чисто мнимые комплексные
числа z
= 0 + iy.

Комплексное
число z
= x + iy
можно задавать с помощью радиус—вектора

.
Длина вектора

,
изображающего комплексное число
z,
называется модулем
этого числа и обозначается

или r.
Величина угла между положительным
направлением действительной оси и
вектором

,
изображающим комплексное число,
называется аргументом
этого комплексного числа и обозначается
arg z
или .

Запись
числа z
= x + iy
называют алгебраической
формой
комплексного числа.

Модуль
r
и аргумент 
комплексного числа можно рассматривать
как полярные координаты вектора

,
изображающего комплексное число z
= x + iy.
Тогда получаем x
= r
cos ,
y
= r
sin .
Следовательно, комплексное число
z
= x + iy
можно записать в виде z
= r
cos 
+
i r
sin 
или z
= r
(cos 
+
i
sin ).
Такая запись комплексного числа
называется тригонометрической
формой.

Модуль
r
=

однозначно определяется по формуле

.

Используя
формулу
Эйлера
e
^i
= cos

+ i sin
,
связывающую тригонометрические функции
с показательными, комплексное число z
= r
(cos 
+
i
sin )
можно записать в так называемой
показательной
(или экспоненциальной)
форме z
= r e
^{i },
где r
=

– модуль комплексного числа, а
угол 
=
arg z.

Пример
23. Записать
комплексные числа z₁
= —
1 + i

и z₂
= —
1 в тригонометрической и показательной
формах.

Решение:
для z
₁
имеем

,
arg z
= arctg

,
т.е.

.
Поэтому

.

Для
z
₂
имеем

,
arg z
= arg (- 1) = ,
т.е.

= .
Поэтому —
1
= cos 
+ i
sin 
= e
^{i }.

4.2 Действия над комплексными числами

Сложение
комплексных чисел

Суммой
двух комплексных чисел z₁
= x₁
+ iy₁
и z₂
= x₂
+ iy₂
называется комплексное число, определяемое
равенством

z₁
+ z₂
= (x₁
+ x₂)
+ i
(y₁
+ y₂). (3.1)

Сложение
комплексных чисел обладает переместительным,
(коммутативным) и сочетательным
(ассоциативным)
свойствами: z₁
+ z₂
=
z₂
+ z₁,

(z₁
+ z₂)
+ z₃
= z₁
+ (z₂
+ z₃).

Из определения
(3.1) следует, что геометрически комплексные
числа складываются как векторы (рис.
23).

Непосредственно
из рисунка видно, что
z₁
+ z₂z₁+z₂.
Это соотношение называется неравенством
треугольника.

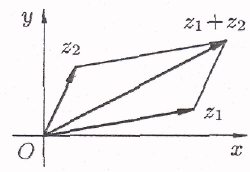
Рис.
23.

Вычитание
комплексных чисел

Вычитание
определяется как действие, обратное
сложению. Разностью
двух
комплексных чисел z₁
и z₂
называется
такое комплексное число z,
которое,
будучи сложенным с z₂,
дает число z₁,
т.е.
z
= z₁
—
z₂,
если z
+ z₂
= z₁.

Если
z₁
= x₁
+ iy₁
и z₂
= x₂
+ iy₂,
то
из этого определения легко получить
z:

z
= z₁
—
z₂
= (x₁
—
x₂)
+ i
(y₁
—
y₂). (3.2)

Из равенства (3.2) следует, что геометрически
комплексные числа вычитаются как
векторы (рис. 24).

Непосредственно
из рис.24 видно, что z₁
—
z₂z₁
—
z₂.
Отметим, что z₁
—
z₂
=

= d,
т.е. модуль разности двух комплексных
чисел равен расстоянию d
между точками, изображающими эти числа
на плоскости.

Поэтому, например, равенство z
— 2i = 1
определяет на комплексной плоскости
множество точек z, находящихся на
расстоянии 1 от точки z₀ = 2i,
т.е. окружность с центром в z₀
= 2i

и радиусом 1.

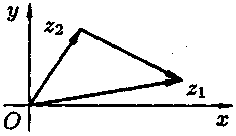
Рис. 24.

Умножение
комплексных чисел

Произведением
комплексных
чисел z₁
= x₁
+ iy₁
и z₂
= x₂
+ iy₂
называется комплексное число, определяемое
равенством z
= z₁
z₂
= (x₁
x₂
—
y₁
y₂)
+ i
(x₁
y₂
—
y₁
x₂).
(3.3)

Отсюда, в частности, следует важнейшее соотношение

i
²
= —
1 (3.4)

Умножение
комплексных чисел обладает переместительным,
сочетательным и распределительным
(дистрибутивным) свойствами:

z₁
z₂
= z₂
z₁,

(z₁
z₂)
z₃
= z₁
(z₂
z₃),

z₁
(z₂
+ z₃)
= z₁
z₂
+ z₁
z₃.

В этом легко
убедиться, используя определение (3.3).

Найдём
теперь произведение комплексных
чисел z₁
= r₁
(cos 
₁
+
i
sin 
₁)
и z₂
= r₂
(cos 
₂
+
i
sin 
₂),
заданных
в тригонометрической форме:

z₁
z₂
= r₁
(cos 
₁
+
i
sin 
₁)r₂
(cos 
₂
+
i
sin 
₂)
=

=
r₁
r₂
(cos

₁
cos 
₂
+ i
sin 
₁
cos 
₂
+
i
cos 
₁
sin 
₂
–
sin

₁


 sin

₂)
= r₁
r₂
((cos

₁
cos 
₂
—
sin 
₁
sin 
₂)
+ i
(sin 
₁
cos 
₂
+

+
cos 
₁
sin 
₂))
= r₁
r₂
(cos
(
₁
+ 
₂)
+ i
sin (
₁
+
₂)),

т.е.
z₁
z₂
= r₁
r₂
(cos
(
₁
+ 
₂)
+ i
sin (
₁
+
₂)).

Таким образом,
при умножении комплексных чисел их
модули перемножаются, а аргументы
складываются.

Это
правило распространяется на любое
конечное число множителей. В частности,
если есть п
множителей
и все они одинаковые, то

z
ⁿ
= (r
cos

+ i
sin )
ⁿ
= r
ⁿ
cos
n
₁
+ i
sin n). (3.5)

Формула
(3.5) называется формулой
Муавра.

Пример
24. Найти
(1 +


i)⁹.

Решение:
запишем сначала число z
= 1 +

i
в тригонометрической форме:

r
=


= 2;
arg z
= arctg


arg z
=

,

.

По формуле Муавра
имеем

z
⁹
= (1
+

i)
⁹
= 2⁹

=
2⁹(cos
3
+ i
sin
3)
= = 2⁹(—1)
= —512.

Деление комплексных
чисел

Деление
определяется как действие, обратное
умножению. Частным
двух комплексных чисел чисел z₁
и z₂

0 называется комплексное число z,
которое, будучи умноженным на z₂,
даёт число z₁,
т. е.

,
если z₂z
= z₁.

Если
положить z₁
= x₁
+ iy₁
и z₂
= x₂
+ iy₂

0,
z
= x
+ iy,
то из равенства (x₂
+ iy₂)
(x
+ iy)
= x₁
+ iy₁
следует

Решая
систему, найдём значения х
и у:

,

.

Таким
образом,



.

На практике частное
двух комплексных чисел находят путём
умножения числителя и знаменателя на
число, сопряжённое знаменателю
(«избавляются от мнимости в знаменателе»).

Пример
25. Выполнить
деление

.

Решение:

=

=

=

= 1+i.

Для тригонометрической
формы комплексного числа формула
деления имеет вид

=

.

То есть, при делении
комплексных чисел их модули, соответственно,
делятся, а аргументы, соответственно,
вычитаются.

Извлечение
корней из комплексных чисел

Извлечение
корня п-й
степени определяется как действие,
обратное возведению в натуральную
степень.

Корнем
п-й
степени
из комплексного числа z
называется комплексное число ,
удовлетворяющее равенству 
^п
= z,
т.е.

,
если 
^п
= z.

Если
положить z
= r
(cos 
+
i
sin ),
а 
= 
(cos 
+
i
sin ),
то, по определению корня и формуле
Муавра, получаем z
= 
^п
= 
^п
(cos п
+
i
sin п)
= r
(cos 
+
i
sin ).

Отсюда
имеем 
^п=
z,
п
=
+ 2
k,
k
= 0,
1,
2…
То есть

и

(арифметический корень).

Поэтому
равенство

принимает вид

,
k = 0,
1,…n-1.

Получим п различных значений корня.
При других значениях k, в силу
периодичности косинуса и синуса,
получатся значения корня, совпадающие
с уже найденными. Так, при k = n
имеем

 _п =

=

=

=

=  ₀

(k = 0).

Итак,
для любого z

0 корень п-й
степени из числа z
имеет
ровно п
различных
значений, которые изображаются на
комплексной плоскости в виде вершин
правильного п-угольника,
вписанного в окружность с центром в
начале координат.

Пример
26. Найти
значения

.

Решение:
запишем подкоренное выражение в
тригонометрической; форме:

=

=

.

Тогда,

=

=

=

=

=

.

При
k
= 0 имеем

=

=

,

при
k
= 1 имеем

=

=

=

=

,

при
k
= 2 имеем

=

=

=

,

при
k
= 3 имеем

=

=

=

.

Теоретический тест

1. Задачи, приводящие
   к понятию производной.

2. Определение
   производной, её механический и
   геометрический смысл.

3. Основные правила
   нахождения производных.

4. Таблица производных.

5. Производная
   сложной функции.

6. Дифференцирование
   функций, заданных неявно и параметрически.

7. Логарифмическое дифференцирование.

8. Производные высших порядков.

9. Понятие
   дифференциала.

10. Геометрический
    смысл дифференциала.

11. Дифференциал
    сложной функции.

12. Правила Лопиталя.

13. Необходимые и достаточные условия
    монотонности функций.

14. Необходимые и достаточные условия
    экстремума функций.

15. Нахождение
    наименьшего и наименьшего значений
    функции.

16. Нахождение
    интервалов выпуклости, вогнутости и
    точек перегиба.

17. Виды асимптот и
    их нахождение.

18. Производная
    векторной функции скалярного аргумента
    и её применение.

19. Алгебраическая,
    тригонометрическая и показательная
    формы комплексных чисел.

20. Действия над комплексными числами.

Практический тест

По теме «Производная»

Вариант 1

1. Найти
   

   от следующих функций:

а)

;
б)
y
= x²
sin x
+ 2x
cos²
x
– 2sin x;

в)
y
= sin 2xctg

—
cos²x;
г)

;
д)
y
= 3x²ln
x
– x³;

е)
y
= (x²
+ 2x
+ 2)³e
^–2
x;
ж)
y = (cos
x)^sin
x;
з)
y =

;

и)

;
к)
x
– y = arcsin
x
– arcsin
y;
л)
x⁴
+
y⁴
=
x²y²;

м)
log₂(x
+ y) = xy;
н)

;
о)

1. Найти
   

   от следующих функций:

а)

;
б)

3;
в) e^y+xy=e;
г)

1. Найти
   уравнение касательной к кривой у
   = 2 —
   4х
   – 3х²
   в точке с абсциссой х
   = —2.

2. По
   оси Ох
   движутся точки, имеющие законы движения
   

   и
   
   ,
   t
   > 0. С какой скоростью удаляются эти
   точки друг от друга в момент встречи?
   (х
   измеряется в сантиметрах, t
   – в секундах)

3. Найти дифференциал
   функции

,
x
> 0.

1. Вычислить
   приближённо: а)
   

   при х =
   0,1;

б)
tg 4530.

1. Найти пределы:

а)

; ж)

.

б)

;

в)

;

г)

;

д)

;

е)

;

Вариант 2

1. Найти

   от следующих функций:

а)

;
б)

;
в)

;

г)

;
д) y
= log
³₂ x
⁴; е)

;

ж)
y=(sin
x)^cos
x;
з)
y
=
(1 + x)
^{ln x}
; и)

;

к)
x²
– х y +
у²
= 1; л) у²
cos x
= a²
sin 3y;
м)

;

н)

;
о)

1. Найти

   от следующих функций:

а)

;
б) y =
(1 + x²)
arctgx;
в) x + y =
sin² y;
г)

1. В
   какой точке касательная к параболе у
   = х²
   + 4х
   параллельна оси Ох?
   Написать уравнения касательной и
   нормали в этой точке.

2. Тело,
   массой 3 кг
   движется прямолинейно по закону
   s = 1
   + t +
   t
   ² (s
   – в метрах, t
   – в секундах). Определить кинетическую
   энергию тела через 5 с
   после начала движения.

3. Найти
   дифференциал функции y
   = tg
   
   ,
   x
   > 0.

4. Вычислить
   приближённо:

а)

;
б) arctg 0.98.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 3

1. Найти

   от следующих функций:

а)

;
б)

;
в)

;

г)
y
= arctg
²
;
д)
y
= x(sin
ln x
– cos ln x);
е)
y
= 5
^{cos x}sin
x;

ж)
y = (х
² +
1)^sin
x;
з)
y =

;
и)


;
к)
tg y
= xy;
л)
arctg
;
м)
sin y
² =
x
² y;
н)

;

о)

1. Найти

   от следующих функций:

а)

;
б) y =
(arccos x)
²; в)

;
г)

1. Написать
   уравнения касательной и нормали к
   кривой
   

   в точке с координатами (2; 3).

2. Тело
   движется по прямой Ох
   по закону x(t)=t²—4t+1.
   Определить скорость и ускорение
   движения в произвольный момент времени.
   В какой момент времени тело меняет
   направление движения? (х
   измеряется в сантиметрах, t
   – в секундах)

3. Найти
   дифференциал функции
   
   .

4. Вычислить
   приближённо:

а)

при х=0,03;
б) sin 89.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 4

1. Найти

   от следующих функций:

а)

;
б)

;

в)
y
= sin(cos²(tg
x₃));

г)

;
д)

;
е)

;

ж)

;
з)
y=(ctg
x)^sin
x
; и)

;
к)
cos(xy)
=
ay;
л)
e^xsiny
– e^–ycos
x=0;
м)

;
н)

;
о)

1. Найти

   от следующих функций:

а)

;
б) y =
tg x;
в) xy
– y²
= a²;
г)

1. Написать
   уравнения касательной и нормали к
   линии
   

   в точке с абсциссой х
   = 2.

2. Точка
   движется прямолинейно по закону
   
   .
   Найти ускорение в конце 5-й с.
   (s
   измеряется в сантиметрах, t
   – в секундах)

3. Найти
   дифференциал функции
   
   .

4. Вычислить
   приближённо:

а)
arctg 0,97; б)

.
при х =
2,037.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 5

1. Найти

   от следующих функций:

а)

;
б) y
= (3 – 2sin x)⁴;
в)

;

г)

;
д)
y
= ln sin²(3
+ x);
е)
y
= 5^x
ln
5 –

;

ж)
y
=
(1 + x²)^arccos
x;
з)
y
=
(1 + x)
^x;
и)

;

к)
x²ln
(y²
+
1) = y;
л)
2y
= –1 + x²
y²;
м)

;

н)

;
о)

1. Найти

   от следующих функций:

а)
y =
x lnx
– x;
б) y =
arctg²
x;
в) x e ^y
= e ^2
y+1;
г)

1. Написать
   уравнения касательной и нормали к
   графику функции
   

   в точке его пересечения с осью Ох.
   Какой угол образует касательная с осью
   Ох?

2. В
   тонком неднородном стержне, имеющем
   длину 25 см,
   масса (в граммах) распределяется
   по закону g
   (l)
   = 4 l
   ² – 2
   l +
   5, где l
   – расстояние от начала стержня до
   любой его точки. Найти плотность стержня
   на расстоянии 4 см
   от начала стержня и среднюю плотность
   стержня.

3. Найти
   дифференциал функции
   
   ,
   х>0.

4. Вычислить
   приближённо: а)
   

   при х=2,02;

б) arcsin 0,09.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 6

1. Найти

   от следующих функций:

а)

;
б)
y
= sin(sin (sin x));
в)
y
= tg x
–

tg³
x
+

tg⁵
x;

г)
y
= arcsin(sin x
– cos x);
д)
y
= ln⁵
tg
;
е)

;

ж)
y =
(tg x)^ctg
x;
з) y =
(1+x²)
^1/x;
и)

;
к) xy – ln
y=1;
л)

;
м) xsin²y
+ y =
x²;
н)

;
о)

1. Найти

   от следующих функций:

а)
y=
x²
(2lnx
– 3); б) y=
;
в) sin(x+y)
= x+y;
г)

1. Найти
   угловые коэффициенты касательных,
   проведённых к параболе у
   = х ²
   в точках её пересечения с прямой у
   = 3х
   — 2. Написать
   уравнения касательных и нормалей в
   этих точках.

2. Тело
   движется прямолинейно
   по закону s
   (t)
   = 0,5t
   ⁴ — 5t
   ³ + 12t
   ² — 1.
   В какие моменты времени ускорение
   движения тела равно нулю? (s
   измеряется в метрах, t
   – в секундах)

3. Найти
   дифференциал функции
   
   .

4. Вычислить
   приближённо:

а)

;
б) arcsin 0,08.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 7

1. Найти

   от следующих функций:

а)

;
б)
y
= (2 – x²)
²cos
x
+ 2x
sin²
x;

в)

;
г)
y
= arcsin

;
д)

;
е)

;
ж)
y
=
(ctg 3 x
)
;
з)
y
=
x^sin
x;

и)

;
к)
y³
– e ^y
ln
x
=
x;
л)
arctg y
= x + y;

м)
x²
sin y
– cos y =
0; н)

;
о)

1. Найти

   от следующих функций:

а)
y
=
(2x

+
3)
;
б)
y
=
sin (ln x)
+ cos (ln x);

в)
x
²+y
² – x
y = 0; г)

1. Написать
   уравнения касательной и нормали к
   кривой
   

   в точке с абсциссой х
   = 0.

2. Тело
   движется по прямой Ох
   по закону х
   (t)
   =
   

   — 2
   t
   ² + 3 t.
   Определить скорость и ускорение
   движения в произвольный момент времени.
   В какие моменты тело меняет направление
   движения? (х
   измеряется в метрах, t
   – в секундах)

3. Найти
   дифференциал функции y
   = arctg (sh x)
   + sh xln
   ch x.

4. Вычислить
   приближённо:

а)

при х
=26,46; б) arctg 1,02.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 8

1. Найти

   от следующих функций:

а)

;
б)

;
в)

;

г)
y
= arcsin
;
д)

;

е)

;
ж)

;
з) y =
(ctg x)
^{ln x};

и)

;
к) ysin
x + xcos
y =
x;
л) x
² – 3 y
²+2tg
y = 0;
м)

;
н)

;
о)

1. Найти

   от следующих функций:

а)
y =
(2x +
5) ln ² x;
б)

;
в) 2y ln
y
= x;
г)

1. Какой
   угол образует с осью абсцисс касательная
   к кривой
   
   ,
   проведённая в точке с абсциссой х
   = 1? Написать
   уравнения касательной и нормали в этой
   в точке.

2. Угол
   (в радианах), на который повернётся
   колесо через t
   с 
   (t)
   = 3t
   ² – 12
   t +
   36. Найти угловую скорость 
   в момент
   t = 4c
   и определить, в какой момент времени
   колесо остановится.

3. Найти
   дифференциал функции y
   =
   
   .

4. Вычислить
   приближённо:

а)

при х
=1,97; б) arcctg 1,01.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 9

1. Найти

   от следующих функций:

а)

;
б) y
= sin³
x
;
в) y
= (tg

—
ctg
)²;

г)
y
= arctg
;
д)
y
= ln tg
;

е)

;
ж)

;
з)
y
=
(cos x)
^{tg x};

и)

;
к) y
= 1+ x e ^y;
л)

;

м)
2 y ln
y
= x
³; н)

;
о)

1. Найти

   от следующих функций:

а)

;
б) y =
arcsin ²
x;
в) tg y
= x+y;
г)

1. Написать
   уравнения касательных и нормалей
   к кривой у
   ³ = х
   ⁴ в точках
   с абсциссами х₁
   = 0, х₂
   = 1.

2. Тело
   движется по прямой
   по закону s
   (t)
   = 8 – 2 t +
   24 t
   ² – 0,3 t
   ⁵. Найти
   скорость движения тела в момент времени,
   когда ускорение равно нулю. (s
   измеряется в метрах, t
   – в секундах).

3. Найти
   дифференциал функции y
   =

   
   .

4. Вычислить
   приближённо:

а)

;
б) e
^0,05.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 10

1. Найти

   от следующих функций:

а)

;
б)

;

в)

;
г)

;

д)

;
е)

;
ж)
y
=
(sin x)^arcsin
x;

з)
y =
x
^х;
и)

;
к)

;
л) y sin
(x y)
= x
²; м) x³
+y³
— 3xy
= 0; н)

;
о)

1. Найти

   от следующих функций:

а)

;
б) y =
xcos
x²;
в)

;
г)

1. В
   какой точке касательная к параболе у
   = х
   ² + 7 х
   — 3 параллельна
   прямой 5 х
   + у – 3 = 0 ?
   Написать уравнения касательной и
   нормали в этой точке.

2. Закон
   движения точки по оси Ох
   есть х
   = 3 t — t
   ³. Найти
   перемещение точки за время, предшествующее
   изменению направления её движения.

3. Найти
   дифференциал функции y=
   .

4. Вычислить
   приближённо:

а)
х
³ + 4 х
² + 5 х
+ 3 при х
= 1,03; б) ln (x
² — 3)
при х =
1,9.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 11

1. Найти

   от следующих функций:

а)

;
б)

;

в)

;
г) y
= arctg
;

д)

;
е)

;
ж)

;

з)
y =
(sin x)
^{ln x};
и)

;
к) x
⁴ + y
⁴ = tg
² y;

л)
y
²
cos
x
=
a
² tg
2 y;
м)

;
н)

;

о)

1. Найти

   от следующих функций:

а)

;
б) y =
2 ^х+
2 ^{– x} ;
в) ln (x + y)
= y;
г)

1. В
   каких точках касательная к параболе
   у =
   х³
   образует с осью Ох
   угол в 45?
   Написать уравнения касательной и
   нормали в этой точке.

2. Законы
   движения двух тел вдоль одной прямой
   задаются уравнениями s₁
   (t)
   = 4 t
   ² + 2, s₂
   (t)
   = 3 t
   ² + 4 t
   — 1. Найти
   скорости движения тел в те моменты,
   когда тела «сходятся» в одной точке.

3. Найти
   дифференциал функции y
   =
   
   .

4. Вычислить
   приближённо:

а)
х
²¹ при х
= 0,998; б) arctg
(3 x — 2)
при х =
1,03.

1. Найти пределы:

а)

; ж)

.

б)

;

в)

;

г)

;

д)

;

е)

;

Вариант 12

1. Найти

   от следующих функций:

а)

;
б)

;

в)

;
г)

;
д)

;
е) y
= ln(e^—
x + xe
^{– x}); ж)
y = x^ln
x;

з)
y =
(arcsin x)
^x;
и)

;
к) ln x³
— e
^{x y} =
y +
1;

л)

;
м)

;
н)

;
о)

1. Найти

   от следующих функций:

а)
y = x +
sin 2 x;
б) y =
x
ln x;
в) arctg y
= x + y;
г)

1. В
   какой точке касательная к параболе у
   = х²
   перпендикулярна к прямой 2 х
   – 6 у
   + 5 = 0 ?
   Написать уравнения касательной и
   нормали в этой точке.

2. Закон
   прямолинейного движения материальной
   точки
   
   .
   Найти скорость в момент времени t
   = 9 c.
   (s
   измеряется в сантиметрах, t
   – в секундах).

3. Найти
   дифференциал функции y=
   .

4. Вычислить
   приближённо: а)
   

   при х =
   0,98;

б) arccos 0,08.

1. Найти пределы:

а)

; ж)

.

б)

;

в)

;

г)

;

д)

;

е)

;

Вариант 13

1. Найти

   от следующих функций:

а)

;
б)

;
в) y
= ctg (x
sin x);

г)
y
= arctg x
+

arctg
x³;
д)

;

е)
y
= (e
^{a x}
– e
^{– a x})²;
ж)
y
= (cos
x)
^{ctg x};
з)
y
=
(x
³ +
4)
^{tg x};

и)

;
к) x
² = y + arctg
y;
л) x
³ + 3 x
² y
+ y
³ = 9 x;

м)
sin² e
^x—cos²
e ^y=y;
н)

при t >
0; о)

1. Найти

   от следующих функций:

а)
y
= e
^{1 —
2
x}
sin
(2 + 3 x);
б)
y
=
x
(sin ln x
+ cos ln x);

в)
ln (x + e
^y ) = y;
г)

1. На
   кривой у =
   х²
   (х — 2)²
   найти точки, в которых касательные
   параллельны оси Ох.
   Написать уравнения касательной и
   нормали, проведённых в точке с абсциссой
   х =
   2.

2. Закон
   изменения количества электричества
   в проводнике в момент времени t
   даётся
   формулой Q
   (t) = 3 t
   ² + 5 t
   — 1. Найти
   силу тока в момент времени t
   = 5 c.
   (Q
   измеряется в кулонах, t
   – в секундах).

3. Найти
   дифференциал функции y
   =
   
   .

4. Вычислить
   приближённо:

а)
(1,98)⁶;
б) arcsin (1 – e
^x)
при х =
0,05.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 14

1. Найти

   от следующих функций:

а)

;
б)
y
= cos²
x
+ ln tg
;
в)
y
= tg(cos²
3x);

г)

;
д)

;

е)

;
ж)
y
= (1
+ е
^x)
^{ln x};
з)
y
=
(lg x)
^{sin x};

и)

;
к) x y = e
^x+y; л)

;

м)
y
² ln y
= x
²; н)

;
о)

1. Найти

   от следующих функций:

а)
y = e
^x +
2 e
^{2 x};
б) y =
5 – cos²
x;
в) y
² x =
ln y;
г)

1. В
   каких точках касательные к кривой у
   = х
   ³ + х
   — 2 параллельны
   прямой y=4x—1.
   Написать уравнения касательной и
   нормали к кривой в точке с абсциссой
   х=1.

2. Тело
   массой m_c
   движется
   прямолинейно по закону s
   (t)
   = 
   t ²+
   
   t + 
   (,
   ,
   
   – величины постоянные). Доказать, что
   сила, действующая на тело, постоянная.

3. Найти
   дифференциал функции
   y
   =

   
   .

4. Вычислить
   приближённо:

а)

;
б) sin (х
² + 3 х)
при х =
1.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 15

1. Найти

   от следующих функций:

а)

;
б) y
= (1 – cos 2x)

;

в)

;
г) y
= x (arcsin
x)
² – 2 x;

д)
y
=

(ln
³ x
+ 3 ln
² x
+ 6 ln x
+ 6); е)

;

ж)
; y = (1
– х
²)
^{ctg x}
з) y
= (arccos
x)

;
и)

;

к)
x
y = arctg

;
л)
y
– sin
y
= x;
м)

;

н)

;
о)

1. Найти

   от следующих функций:

а)
y
=
e
^–x +
cos x;
б) y
=
x
+
ln
² x;
в) y
=
x
+
arcsin y;
г)

1. В
   каких точках угловой коэффициент
   касательных к графику функции у
   = 2 х
   ³ – 2
   х
   ² + х — 1
   равен 3 ? Написать уравнения касательной
   и нормали к данной кривой в точке с
   абсциссой х
   = 1.

2. Угол,
   на который повернётся колесо
   за время t,
   
   (t)
   = 100 + 3 t — 0,01
   t
   ³. Найти
   ускорение в тот момент времени, когда
   колесо остановится.( 
   измеряется
   в радианах, t
   – в секундах).

3. Найти
   дифференциал функции y
   = 2 х
   + lnsin
   x + 2cos
   x.

4. Вычислить
   приближённо:

а)
cos 89;
б)

при х=1,012.

1. Найти пределы:

а)

; ж)

.

б)

;

в)

;

г)

;

д)

;

е)

;

Вариант 16

1. Найти

   от следующих функций:

а)

;
б)

;
в) y
= tg(3x
+ 1)³;

г)

;
д)

;

е)
y
= 5

cos
x;
ж)
y
= (sin
х)
^x;
з)
y
=
(x
⁵ +
5)
^{ctg x};

и)

;
к) x
⁴ – x y + y
⁴ = 1;
л) (х +
y)²
+ (2х
+у)³=1;
м) cos (x + y
² ) = y;
н)

;
о)

1. Найти

   от следующих функций:

а)
y = sin
xln
x;
б)

;
в)

;
г)

1. В
   каких точках касательная к графику
   функции
   

   образует с осью Оx
   угол 45?
   Написать уравнения касательной и
   нормали к данной кривой в точке с
   абсциссой х
   = 2.

2. Закон
   движения материальной точки по оси Оx
   x (t)
   = 7 t — t
   ³. Найти
   ускорение точки в момент времени, когда
   скорость движения равна (—5).(
   х
   измеряется в метрах, t
   – в секундах).

3. Найти
   дифференциал функции
   
   .

4. Вычислить
   приближённо:

а)

при х =
2,9; б) sh 1,05.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 17

1. Найти

   от следующих функций:

а)

;
б)

;
в)

;

г)

;
д)

;
е)

;

ж)

;
з) y
= (sin x)
;
и)

;

к)
arctg (x
+ y)
= x
y;
л)
y
² sin
x
=
х
² sin
y;
м)

;

н)

;
о)

1. Найти

   от следующих функций:

а)

;
б)

;
в) 2 x y +
y
³ = 1;

г)

1. Написать
   уравнения касательной и нормали к
   кривой
   

   в точке с абсциссой х
   = 2.

2. Зависимость
   между количеством вещества, получаемого
   в некоторой химической реакции, и
   временем t
   выражается формулой x
   (t)
   = А (1
   — е^{–k
   t} ).
   Определить скорость и ускорение
   реакции.

3. Найти
   дифференциал функции
   
   .

4. Вычислить
   приближённо: а)
   

   при х =
   2,56; б) сh 0,2.

5. Найти пределы:

а)

; ж)

.

б)

;

в)

;

г)

;

д)

;

е)

;

Вариант 18

1. Найти

   от следующих функций:

а)

;
б)

;

в)

;
г)

;

д)
y
= ln tg

—
cos xln
tg x;
е)

;

ж)
y
= (arcsin
х)
^{tg x};
з)
y
=
(1 + log₄
x)
^x;
и)

;

к)
y
² sin
x
+ y
³ cos
x
= 0;
л)

;
м)
x²
+
y²
=
arctg
² y;

н)

;
о)

1. Найти

   от следующих функций:

а)

;
б)

;
в) e
^x+y=x-y;
г)

1. Написать
   уравнения касательной и нормали к
   кривой
   

   в точке с абсциссой х
   = 2.

2. Колебательное
   движение материальной точки совершается
   по закону x
   (t)
   = a cos
   
   t. Определить
   скорость и ускорение движения при х
   = 
   а
   и х =
   0.

3. Найти
   дифференциал функции
   
   .

4. Вычислить
   приближённо:

а)

при х =
0,984; б) arccos (1 —
x) при х
= 1,08.

1. Найти пределы:

а)

(a
> 0);

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 19

1. Найти

   от следующих функций:

а)

;
б)

;
в) y
= tg³x
– 3tg x
+ 3x;

г)

;
д)

;
е)

;

ж)

;
з)

;
и)

;

к)
х
² y = ln
y;
л) (x — 2)
² + (y
— 1)
² = 2 y
³; м)

;

н)

;
о)

1. Найти

   от следующих функций:

а)
y = cos
(ln x);
б)

;
в) x
² + y
² = 2 a
y ³;
г)

1. Под
   каким углом к оси Оx
   наклонена касательная, проведённая к
   кривой у =
   2 х
   ³ – х +
   1 в точке её пересечения с осью Оy?
   Написать уравнения касательной и
   нормали этой в точке.

2. Тело
   массой 4 кг
   движется прямолинейно по закону
   
   .
   Определить кинетическую энергию этого
   тела в момент времени t
   = 3 с.
   (х
   измеряется в метрах)

3. Найти
   дифференциал функции
   
   .

4. Вычислить
   приближённо:

а)
sin (x
⁴ – 3
x
² + 2) при х
= 1,02; б)

при х =
6,64.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 20

1. Найти

   от следующих функций:

а)

;
б)

;
в) y =
ctg
³
;

г)

;
д) y
= ln (ln ² (ln
³ x));

е)

;
ж)

;

з)
y =
(ctg 
x) ^{sin
( x –
1)};
и)

;
к)

;

л)
x
arcsin y
= y
arcsin x;
м)

;
н)

;
о)

при t
> 0.

1. Найти

   от следующих функций:

а)
y
=
arctg x
²;
б)

;
в)
a
^x
y =
(xy)
^a;
г)

1. Определить
   под каким углом синусоида
   

   пересекает ось абсцисс в начале
   координат. Написать уравнения касательной
   и нормали к графику функции в этой
   точке.

2. Материальная
   точка движется по прямой по закону
   
   .
   В какие моменты времени её ускорение
   равно нулю? (s
   измеряется в метрах, t
   – в секундах)

3. Найти
   дифференциал функции
   
   .

4. Вычислить
   приближённо: а)
   

   при х =
   4,16;

б)
е

при х =
0,86.

1. Найти пределы:

а)

; д)

;

б)

; е)

;

в)

; ж)

.

г)

;

Вариант 21

1. Найти

   от следующих функций:

а)

;
б)

;
в)

;

г)
y
= arctg
;
д)

;
е) y
= arctg ²
e
^{2 x};
ж)

;
з)

;

и)

;
к) x
⁵ + x
y + y
⁵ = 6; л) e
^{x y} — x
² + y
³ = 0; м) arctg
ytg
x = y
²; н)

;
о)

1. Найти

   от следующих функций:

а)
y =
sin ²
x;
б)

;
в) y
² ln y
– x ln x
= 1; г)

1. Написать
   уравнения касательной и нормали к
   графику функции у
   = х ² е^{–
   х} в
   точке с абсциссой х
   = 1.

2. Закон
   изменения количества электричества
   в проводнике в момент времени t
   даётся формулой Q
   (t)
   = 2 t
   ² + 3 t
   + 1. Найти
   силу тока в момент времени t
   = 6. (Q
   измеряется в кулонах, t
   – в секундах)

3. Найти
   дифференциал функции
   
   .

4. Вычислить
   приближённо:

а)

при х =
0,8; б)

при х =
4,25.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 22

1. Найти

   от следующих функций:

а)

;
б)

;

в)

;
г)
y
= sin xarctg
(sin x);

д)

;
е)

;

ж)
y =
(tg x)^sin
x;
з)

;
и)

;

к)
x
² + y
² = tg y;
л)

;
м)

;
н)

;
о)

1. Найти

   от следующих функций:

а)
y =
ln ln x;
б)

;
в) y
² = x
— cos y;
г)

1. Написать
   уравнения касательной и нормали к
   графику функции у
   ² = – х y
   – 2 x
   ² = 0
   в точке с абсциссой х
   = 2.

2. Колесо
   вращается так, что угол поворота
   пропорционален квадрату времени.
   Первый оборот был сделан колесом за 8
   с.
   Определить угловую скорость колеса
   через 48 с
   после начала вращения.

3. Найти
   дифференциал функции
   
   .

4. Вычислить
   приближённо:

а)

при х =
0,16; б)

при х =
0,84.

1. Найти пределы:

а)

; ж)

.

б)

;

в)

;

г)

;

д)

;

е)

;

Вариант 23

1. Найти

   от следующих функций:

а)

;
б)

;
в)

;

г)
y =
x
arcsin
;
д)

;

е)
y
= 3
ln
cos x;
ж)
y
= x
;
з)
y
=
(1 —
x)
^{ln x};

и)

;
к)

;
л) arctg x +
arctg y = x y;
м)

;
н)

;
о)

1. Найти

   от следующих функций:

а)
y =
cos²
x²;
б)

;
в) 2 ^y
= x + y;
г)

1. Написать
   уравнения касательной и нормали к
   графику функции
   

   в точке с абсциссой х
   = 0.

2. Тело,
   выпущенное вертикально вверх, движется
   по закону h
   (t)
   = 4 + 8 t
   – 5 t
   ². Через
   сколько секунд тело достигнет наивысшей
   точки и на каком расстоянии от земли?

3. Найти
   дифференциал функции
   
   .

4. Вычислить
   приближённо:

а)

при х =
0,96; б)

при х =
92.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)

;

ж)

.

Вариант 24

1. Найти

   от следующих функций:

а)

;
б)

;
в) y
= tg (1+ tg (1+ tg x));

г)
y
= arccos³
;
д)

;

е)
y
= e

;
ж) y =
(1+ sin x)
^x; з) y
= (ln x)
^{lg x};

и)

;
к)

;
л) ln (x +
y)
= x – y;

м)
(x + y)
²x
= y ²;
н)

;
о)

1. Найти

   от следующих функций:

а)

;
б) y
=
x
sin
² 2
x;
в)

;

г)

1. Под
   каким углом к оси Оx
   наклонена касательная, проведённая к
   кривой у =
   х ³ —
   х ² –
   7 х
   + 6 в точке
   с координатами (2; —
   4)? Написать
   уравнения касательной и нормали к
   кривой функции в этой точке.

2. Две
   точки движутся по оси Оx
   по законам х₁
   =
   t ²
   + 6 t +
   8,
   
   .
   Найти скорости движения точек в момент
   времени, когда их координаты х₁
   и х₂
   равны (х₁
   и х₂
   измеряются в метрах, t
   – в секундах).

3. Найти
   дифференциал функции y
   = e ^x
   (cos 2 x
   + 2 sin 2 x).

4. Вычислить
   приближённо:

а)

при х =
1,87; б)

при х =
1,16.

1. Найти пределы:

а)

; ж)

.

б)

;

в)

;

г)

;

д)

;

е)

;

Вариант 25

1. Найти

   от следующих функций:

а)

;
б)

;

в)
y
= ln tg

+ cos x
+

cos
3x;
г)

;

д)

ctg²
x
+ ln sin x;
е) y
= 2

;
ж)

;
з)

;
и)

;
к)

;

л)
x
y
² =
y ³
–
sin
x;
м)
arctg y
² +
lny=
;
н)

;

о)

1. Найти

   от следующих функций:

а)
y
= e
;
б)

;
в)

;
г)

1. На
   графике функции у
   = х (х
   – 4)
   ² найти
   точки, в которых касательные параллельны
   оси Оx.
   Написать уравнения касательной и
   нормали в точке с абсциссой х
   = 4.

2. Прямолинейные
   движения двух материальных точек
   заданы уравнениями s₁
   = 2 t
   ³ – 5
   t
   ² – 3
   t,
   s₂
   = 2 t
   ³ – 3
   t
   ² – 11
   t +
   7. Найти ускорения движущихся материальных
   точек в момент времени, когда их скорости
   равны (s₁
   и s₂
   измеряются в метрах, t
   – в секундах).

3. Найти
   дифференциал функции y
   = x (sin ln x
   – cos ln x).

4. Вычислить
   приближённо:

а)

при х =
2,68; б)

при х =
1,16.

1. Найти пределы:

а)

; е)

;

б)

; ж)

.

в)

;

г)

;

д)

;

Вариант 26

1. Найти

   от следующих функций:

а)

;
б)

;

в)
y
=

tg
² sin
x
+ ln cos sin x;
г)
y
= arccos³
;

д)
y
= lg
³
x
²
+ ln tg
;
е)
y
= 10
;
ж)
y
= (ln
sh x)
^x;

з)

;
и)

;
к) x
² + x
⁴ y
⁵ + 5 y
³ = 0;

л)

;
м) ln ln y
= – y
² x;
н)

;
о)

1. Найти

   от следующих функций:

а)

;
б)

;
в) e
^{x y}
=
y;
г)

1. Под
   каким углом пересекается с прямой Оy
   кривая
   
   ?
   Написать уравнения касательной и
   нормали к кривой в этой точке пересечения.

2. Тело
   массой 4 кг
   движется прямолинейно по закону
   
   .
   Найти силу, действующую на тело, в
   момент времени t=1
   (s
   измеряется в метрах, t
   – в секундах).

3. Найти
   дифференциал функции
   
   
   .

4. Вычислить
   приближённо:

а)

при х =
0,02; б)

при х =
0,96.

1. Найти пределы:

а)

; д)

;

б)

; е)

;

в)

; ж)

.

г)

;

Вариант 27

1. Найти
   

   от следующих функций:

а)

;
б)
y
=

sin
² x
+

cos²
x
–

cos
2x;

в)
y
= tg
³ tg
x
+ 3 tg tg x;
г)
y
= arcsin (sin x
² )
+ arccos (cos x
² );

д)
y
= ln sin
²
x
– ln cos
²
x;
е)
у
= 7

;
ж)
y
= (cos
x)
^{lg x};

з)
у
= (х
² + 3)
;
и)

;
к) x
² = y
³x
+ sin y;

л)
x
³ +
3 x
y =
9 arctg x;
м)
sin
e
^x +
cos
e
^y
=
x
²y
²;

н)

при t >
0; о)

1. Найти

   от следующих функций:

а)
y
= e
^{1 –
2
x}
sin
² (1
–
2
x);
б)
y
=
x
(sin e
^x
+ cos e
^x);

в)
cos (x + e
^y) = y
+ e ^x;
г)

1. На
   кривой у =
   х
   ⁴ – 4
   х
   ³ + 6
   x
   ² найти
   точки, в которых касательные параллельны
   оси Ох.
   Написать уравнения касательной и
   нормали, проведённых в точке с
   абсциссой х
   = 1.

2. Закон
   изменения количества электричества
   в проводнике в момент времени t
   даётся
   формулой Q
   (t) = 8 t
   ³ + 3 t
   ² + t
   — 1. Найти
   силу тока в момент времени t
   = 4 c.
   (Q
   измеряется в кулонах, t
   – в секундах).

3. Найти
   дифференциал функции y
   =arctg
   .

4. Вычислить
   приближённо:

а)

;
б) arctg (1,05).

1. Найти пределы:

а)

; ж)

.

б)

;

в)

;

г)

;

д)

;

е)

;

Вариант 28

1. Найти

   от следующих функций:

а)

;
б)

;

в)
y
= (x
tg x
+ ln cos x)³;
г)

;

д)

;
е)

;
ж) y
= (x +
1)^{arcsin x}
; з) y = х

;
и) y
=

;
к) e
^x+y = xy;
л) arctg

= y +2;
м) x
² + y
² ln x
– 4 = 0; н)

;
о)

1. Найти

   от следующих функций: а) y
   = x²
   е
   ;

2. б)
   y
   =
   
   ;
   в) x
   ² + x
   y + y
   ² = 6; г)
   

3. Написать
   уравнения касательных к
   окружности х
   ² + у
   ² + 4 х
   – 4 у
   + 3 = 0 в точках
   пересечения её с осью Ох.

4. Зависимость
   пути от времени задана
   уравнением s
   = t ln (t
   + 1) (s
   измеряется в метрах, t
   – в секундах). Найти скорость движения
   в конце второй секунды.

5. Найти
   дифференциал функции у
   =
   
   
   .

6. Вычислить
   приближённо:

а)
arcsin 0,51; б)

.

1. Найти пределы:

а)

;

б)

;

в)

;

г)

;

д)

;

е)


;

ж)

.

Вариант 29

1. Найти

   от следующих функций:

а)

;
б)

;
в)

;

г)
y
= arctg
;
д)

;

е)
у = 6


;
ж) y
=

;
з) y
= (log₂x)
^{ch x};
и) y
=

;
к) e
^x + x y =
e ^y;
л) x
² sin y
+ y
² cos x
= 0; м) y
=

;
н)

;
о)

1. Найти

   от следующих функций: а) y
   = x
   ² sin
   
   ;

2. б)
   y
   = arcsin x
   ³; в) x
   ² + y
   ² – x
   y = 0; г)
   

3. Написать
   уравнения касательной и нормали к
   гиперболе
   
   ,
   проведённой в точке М
   (—
   9; —
   8).

4. Зависимость
   пути от времени при прямолинейном
   движении точки задана уравнением
   

   (s
   измеряется в метрах, t
   – в секундах). Определить скорость
   движения в конце второй секунды.

5. Найти
   дифференциал функции
   

6. Вычислить
   приближённо:

а)
arctg 0,95; б)

при х
= 1,02.

1. Найти пределы:

а)

; е)

;

б)

; ж)

.

в)

(n>0);

г)

;

д)

;

Вариант 30

1. Найти

   от следующих функций:

а)

;
б)

;
в)

;

г)

;
д)

;

е)

;
ж)
y
= (
sh x)
^ln
x;
з)
y
= (ctg

)
^{cos x};

и)

;
к) x
² + x
⁴ y
⁵ + 5 y
³ = 0;

л)

;
м) log ₂
sin y
= 2 y
³x;

н)

;
о)

1. Найти

   от следующих функций:

а)

;
б)

;
в) ln e
^{x y} = y
²; г)

1. Под
   каким углом пересекается с прямой Оу
   кривая
   
   ?
   Написать уравнения касательной и
   нормали к кривой в этой точке пересечения.

2. Тело
   массой 3 кг
   движется
   прямолинейно по закону s
   (t)
   = t
   – t
   ³. Найти
   силу, действующую на тело, в момент
   времени t =
   4 (s
   измеряется в метрах, t
   – в секундах).

3. Найти дифференциал
   функции

y
= arccos
+ln
.

1. Вычислить
   приближённо:

а)

при х =
0,03; б)

при х =
0,9.

1. Найти пределы:

а)

; е)

;

б)

; ж)

.

в)

;

г)

;

д)

;

Практический тест По теме «Приложения производной. Комплексные числа» Вариант 1

1. Провести полное
   исследование и построить графики
   функций:

а)
у =
2 х
³ + 3 х
² — 1;
б)

;
в)

.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [0; 3].

2. Из
   всех прямоугольников, вписанных в круг
   радиуса R
   найти тот, который имеет наибольшую
   площадь.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение движения
в момент времени t₀
= 
;

в)
составить уравнение касательной и
нормальной плоскости к годографу в
точке t₀
= .

1. Даны
   два комплексных числа z₁
   = 5
   + 3 i, z₂
   = 2
   + 4 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б)
изобразить их на комплексной плоскости
;

в) выполнить
следующие действия:

z₁
+ z₂;
z₁
— z₂;
z₁z₂;

;
(1 + i )⁵;

;

г)
найти х
и у
из уравнения 2 z₁
x +
3 z₂
y =
4.

Вариант 2

1. Провести полное
   исследование и построить графики
   функций:

а)
у =
х
⁴ – 10
х
² + 9; б)

;
в) y =
sin x +
cos x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [1; 4].

2. В
   полукруг радиуса R
   вписать прямоугольник наибольшей
   площади.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение движения
в момент времени t₀
=

;

в)
составить уравнение касательной и
нормальной плоскости к годографу в
точке t₀
=

.

1. Даны
   два комплексных числа z₁
   = 2
   + 4 i, z₂
   = 2
   + 8 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б)
изобразить их на комплексной плоскости
;

в) выполнить
следующие действия:

z₁
+ z₂;
z₁
— z₂;
z₁z₂;

;
(— 1
+ i )⁵;

;

г)
найти х
и у
из уравнения 2 z₁
x +
z₂
y =
2.

Вариант 3

1. Провести полное
   исследование и построить графики
   функций:

а)
у =
0,5 х
⁴ – 4
х
²; б)

;
в) y =
x – ln
(1 + x).

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [0; 6].

2. Сопротивление
   балки на сжатие пропорционально площади
   сечения. Из круглого бревна радиуса R
   вырубить балку наибольшего прямоугольного
   сечения.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение движения
в момент времени t₀
=

;

в)
составить уравнение касательной и
нормальной плоскости к годографу в
точке t₀
=

.

1. Даны
   два комплексных числа z₁
   = 5
   + 3 i, z₂
   = 2
   – 4
   i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б)
изобразить их на комплексной плоскости
;

в) выполнить
следующие действия:

z₁
+ z₂;
z₁
– z₂;
z₁z₂;

;
(1 – i )⁵;

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
3.

Вариант 4

1. Провести полное
   исследование и построить графики
   функций:

а)
у =
х
³ – 3
х
² + 2; б)

;
в) y =
x + ln
(1 + x
² ).

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [0; 4].

2. Сечение
   желоба имеет форму равнобедренной
   трапеции, основание и боковые стороны
   её равны а.
   Каков угол наклона стенки желоба к его
   высоте при наибольшей пропускной
   способности желоба?

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение движения в
момент времени t₀=
;

в)
составить уравнение касательной и
нормальной плоскости к годографу в
точке t₀=
.

1. Даны
   два комплексных числа z₁
   = 2
   + 3 i, z₂
   = 3
   – 2
   i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б)
изобразить их на комплексной плоскости
;

в) выполнить
следующие действия:

z₁
+ z₂;
z₁
— z₂;
z₁z₂;

;
(—1
– i )⁵;

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
3.

Вариант 5

1. Провести полное
   исследование и построить графики
   функций:

а)
у =
— х
⁴ + 2 х
² + 8; б)

;
в)


.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [0; 4].

2. Сумма
   двух положительных чисел равна а.
   Найти эти числа при наименьшем значении
   их произведения.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение движения
в момент времени t₀
=

;

в)
составить уравнение касательной и
нормальной плоскости к годографу в
точке t₀
=

.

1. Даны
   два комплексных числа z₁
   = 4
   + 2 i, z₂
   = 2
   + 4 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б)
изобразить их на комплексной плоскости
;

в) выполнить
следующие действия:

z₁
+ z₂;
z₁
— z₂;
z₁z₂;

;
(1 +

i)⁵;

;

г)
найти х
и у
из уравнения 2 z₁
x +
3 z₂
y =
4.

Вариант 6

1. Провести полное
   исследование и построить графики
   функций:

а)
у =
х
⁴ + 2 х
² + 8; б)

;
в)

.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—1;
   5].

2. В
   круг радиуса R
   вписан равнобедренный треугольник.
   При каком соотношении сторон треугольник
   будет иметь наибольшую площадь?

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение движения
в момент времени t₀
=

;

в)
составить уравнение касательной и
нормальной плоскости к годографу в
точке t₀
=

.

1. Даны
   два комплексных числа z₁
   = 7
   + 8 i, z₂
   = 8
   – 7
   i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б)
изобразить их на комплексной плоскости
;

в) выполнить
следующие действия:

z₁
+ z₂;
z₁
— z₂;
z₁z₂;

;
(—1
+

i)⁵;

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
4.

Вариант 7

1. Провести полное
   исследование и построить графики
   функций:

а)
у =
2 х
³ – 15
х
² + 36; б)

;
в)

.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [1; 9].

2. Найти
   радиус основания и высоту цилиндра,
   если его полная поверхность S
   наименьшая, а объём постоянен и равен
   V.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение движения
в момент времени t₀
=

;

в)
составить уравнение касательной и
нормальной плоскости к годографу в
точке t₀
=

.

1. Даны
   два комплексных числа z₁
   = 2
   + 6 i, z₂
   = 6
   – 2
   i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б)
изобразить их на комплексной плоскости
;

в) выполнить
следующие действия:

z₁
+ z₂;
z₁
— z₂;
z₁z₂;

;
(—1
—

i)⁵;

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
8.

Вариант 8

1. Провести полное
   исследование и построить графики
   функций:

а)
у =

х
⁵ – 4
х
²; б)

;
в) y = x
sin x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [0; 3].

2. Сумма
   двух положительных чисел равна а.
   Каковы эти числа, если сумма их кубов
   будет наименьшей?

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение движения
в момент времени t₀
=

;

в)
составить уравнение касательной и
нормальной плоскости к годографу в
точке t₀
=

.

1. Даны
   два комплексных числа z₁
   = 5
   + 4 i, z₂
   = 6
   – 2
   i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б)
изобразить их на комплексной плоскости
;

в) выполнить
следующие действия:

z₁
+ z₂;
z₁
— z₂;
z₁z₂;

;
(2 — 2
i)⁵;

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
7.

Вариант 9

1. Провести полное
   исследование и построить графики
   функций:

а)


;
б)

;
в) y = x + sin
x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—3,
   3].

2. Закон
   движения тела, брошенного вертикально
   вверх, задан уравнением
   
   .
   Найти наибольшую высоту подъёма тела.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 2 + 7 i,
   z₂
   = 3 –
   6 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁ 
z₂,

,

,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
8.

Вариант 10

1. Провести полное
   исследование и построить графики
   функций:

а)

;
б)

;
в) y =
ln cos x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [2, 4].

2. Произведение
   двух положительных чисел равно а.
   Найти эти числа при наименьшем значении
   их суммы.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 2 + 5 i,
   z₂
   = 5 –
   2 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(—2
– 2
i)⁵,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
6.

Вариант 11

1. Провести полное
   исследование и построить графики
   функций:

а)

;
б)

;
в) y = cos
x
– ln cos x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—1,
   2].

2. В
   треугольник, основание которого а,
   высота h,
   вписан прямоугольник наибольшей
   площади (основание прямоугольника
   лежит на основании треугольника). Найти
   стороны этого прямоугольника.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 3 + 4 i,
   z₂
   = 5 –
   6 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(—2
+ 2 i)⁵,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
5.

Вариант 12

1. Провести полное
   исследование и построить графики
   функций:

а)
у = х
⁷ + 7 х
+ 1; б)

;
в) y =
x
– 2 arctg x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—1,
   6].

2. Закон
   прямолинейного движения тела задан
   уравнением S
   = — t
   ³ + 9 t
   ² – 24
   t — 8.
   Найти наибольшую скорость движения
   тела (S
   – в метрах, t
   – в секундах).

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 9 + 5 i,
   z₂
   = 5 –
   9 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(3 – 3
i)⁵,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
10.

Вариант 13

1. Провести полное
   исследование и построить графики
   функций:

а)
у = х
⁴ + 6 х
²; б)

;
в) y =
xarctg
x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [1, 4].

2. Сопротивление
   балки на изгиб пропорционально
   произведению ширины х
   сечения на квадрат высоты h
   (т.е. Q
   = kxh²,
   где k
   – коэффициент пропорциональности).
   Из круглого бревна диаметром d
   вырезать прямоугольную балку с
   наибольшим сопротивлением на изгиб.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 1 + 4 i,
   z₂
   = 4 —
   i. Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁ 
z₂,

,
(—3
– 3
i)⁵,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
7.

Вариант 14

1. Провести полное
   исследование и построить графики
   функций:

а)

;
б)

;
в) y =
х
+ cos x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке

   ,
   [2, 4].

2. Найти
   основание и высоту треугольника,
   площадь которого наибольшая, если
   сумма основания и высоты равна а.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = —
   1 + 7 i,
   z₂
   = 7 + i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(—3
+ 3 i)⁵,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
16.

Вариант 15

1. Провести полное
   исследование и построить графики
   функций:

а)
у = х
³ – 3
х
² + 2; б)

;
в)

.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [1, 5].

2. На
   какой высоте h
   надо подвесить фонарь над центром
   круглой площадки радиуса R,
   чтобы площадка была максимально осещена
   у её границы? (Яркость освещения
   выражается формулой
   
   ,
   где 
   – угол наклона лучей, r
   – расстояние источника света от
   освещаемой площадки, k
   – сила источника света.)

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 1 + 5 i,
   z₂
   = 5 —
   i. Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(— 4
+ 4 i)⁵,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
8.

Вариант 16

1. Провести полное
   исследование и построить графики
   функций:

а)

;
б)

;
в)

arctg x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—1,
   1].

2. Из всех
   прямоугольников данного периметра
   найти тот, у которого площадь наибольшая.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁=—4+2i,
   z₂=2+4i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(— 4
– 4
i)⁵,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
18.

Вариант 17

1. Провести полное
   исследование и построить графики
   функций:

а)
у = (х
+ 14)
³; б)

;
в) y = (x
– 2) ln x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—4,
   —1].

2. Из
   всех конусов, вписанных в шар радиуса
   R
   найти тот, у которого объём наибольший.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = —
   4 —
   i, z₂
   = 4 —
   i. Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(4 – 4
i)⁵,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
4.

Вариант 18

1. Провести полное
   исследование и построить графики
   функций:

а)
у = (х
+ 4)
³; б)

;
в)

.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—2,
   4].

2. Из всех
   прямоугольников данного периметра
   найти тот, у которого диагональ
   наименьшая.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = —
   2 + 4i,
   z₂
   = 2 + 4i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,


,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
6.

Вариант 19

1. Провести полное
   исследование и построить графики
   функций:

а)
у = х
² (х
— 8); б)

;
в) y =
x+ arctg
x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—2,
   1].

2. Из
   всех круговых секторов, имеющих данный
   периметр Р
   найти сектор с наибольшей площадью.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 1 —
   2i,
   z₂
   = 1 + 2i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,

,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
7.

Вариант 20

1. Провести полное
   исследование и построить графики
   функций:

а)
у = х
² (х
— 3); б)

;
в) y =
sin x+

sin
2 x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—5,
   1].

2. Из
   всех прямых параллелепипедов с данной
   полной поверхностью S,
   в основании которых лежит квадрат,
   найти тот, объём которого наименьший.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = —
   5 + i,
   z₂
   = 6 + 2i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,

,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
5.

Вариант 21

1. Провести полное
   исследование и построить графики
   функций:

а)
у = х
³ — 3
х
²; б)

;
в) y=
cos x – cos²
x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [0, 4].

2. Боковые
   стороны и меньшее основание трапеции
   равны по 10 см.
   Определить её большее так, чтобы площадь
   трапеции была наибольшей.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 2 + 7i,
   z₂
   = 2 —
   i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,

,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
4.

Вариант 22

1. Провести полное
   исследование и построить графики
   функций:

а)
у = 6
х
² — х
⁴; б)

;
в) y=
sin x 
sin 2x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [1, 5].

2. Для
   ограждения клумбы, имеющей форму
   кругового сектора, выдано 20 м
   проволоки. Какой следует взять радиус
   круга, чтобы площадь была наибольшей?

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 5 + 6i,
   z₂
   = 4 —
   3i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,

,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
8.

Вариант 23

1. Провести полное
   исследование и построить графики
   функций:

а)
у = (х
– 1)²
(х
+ 2); б)

;
в) y =
ln sin x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [2, 5].

2. Из
   материала толщиной d
   изготовлен цилиндрический резервуар
   вместимостью V₀.
   При каких значениях радиуса основания
   и высоты цилиндра будет наименьший
   расход материала?

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 2 + 5i,
   z₂
   = 5 —
   2i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,

,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
5.

Вариант 24

1. Провести полное
   исследование и построить графики
   функций:

а)

;
б)

;
в) y =
cos xcos
2x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—2,
   2].

2. Из
   круга радиуса R
   вырезан сектор, из оставшейся части
   склеен конус. Какой угол должен иметь
   вырезанный сектор, чтобы объём конуса
   был наибольшим? Найти радиус основания
   и высоту конуса.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 4 + 5 i,
   z₂
   = 6 + 15 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
–
z₂,
z₁

z₂,

,

,

;

г)
найти х
и у
из уравнения 2 z₁
x +
3 z₂
y =
4.

Вариант 25

1. Провести полное
   исследование и построить графики
   функций:

а)
у = (х
² – 1)
³; б)

;
в)

+arctg
x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке

   ,
   [—2,
   2].

2. С
   начальной скоростью v₀
   под углом 
   к горизонту выпущено ядро. При каком
   угле 
   дальность полёта R
   будет наибольшей (
   ,
   0 < 
   < 2)?

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 2 + i,
   z₂
   = 1 —
   3i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,

,

;

г)
найти х
и у
из уравнения 2 z₁
x +
3 z₂
y =
3.

Вариант 26

1. Провести полное
   исследование и построить графики
   функций:

а)
y = x
⁴ – x
– 1; б)

;
в) y =
sin x
+ cos ²
x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [0, 4].

2. Проволока
   длиной l
   согнута в прямоугольник. Каковы размеры
   этого прямоугольника, если его площадь
   наибольшая?

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 1 + 2 i,
   z₂
   = 6 + 5 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(— 2
– 2
i )
⁵,

;

г)
найти х
и у
из уравнения 2 z₁
x +
4 z₂
y =
5.

Вариант 27

1. Провести полное
   исследование и построить графики
   функций:

а)
y = (x
+ 2) ² (x
+ 3)
²; б)

;
в) y=
cos x

.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—1,
   1].

2. Найти
   наибольший объём конуса, образующая
   которого равна l.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 4 + 3 i,
   z₂
   = 5 + 6 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(6 + 6
i)
⁵,

;

г)
найти х
и у
из уравнения z₁
x +
2 z₂
y =
12.

Вариант 28

1. Провести полное
   исследование и построить графики
   функций:

а)

;
б)

;
в) y =
x
+ arctg x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [1, 3].

2. Найти
   наибольший объём цилиндра, у которого
   полная поверхность равна S.

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 4 + 3 i,
   z₂
   = 5 –
   2 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(— 3
+ 3 i)
³,

;

г)
найти х
и у
из уравнения 3 z₁
x +
z₂
y =
7.

Вариант 29

1. Провести полное
   исследование и построить графики
   функций:

а)

;
б)

;
в) y =
х
ln x.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [—2,
   1].

2. Найти
   стороны прямоугольника наибольшей
   площади, который можно вписать в эллипс
   
   .

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 2 + 3 i,
   z₂
   = 5 –
   4 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(5 – 5
i)
⁵,

;

г)
найти х
и у
из уравнения 2 z₁
x +
3 z₂
y =
6.

Вариант 30

1. Провести полное
   исследование и построить графики
   функций:

а)
y
= 3 x
⁴ – 4 x
³ – 6 x
² + 12 x
– 20; б)

;

в)
y=

.

1. Найти
   наибольшее и наименьшее значения
   функции на заданном отрезке
   
   ,
   [1, 4].

2. Канал,
   ширина которого 27м,
   под прямым углом впадает в другой канал
   шириною 64м.
   Какова наибольшая длина брёвен, которые
   можно сплавлять по этой системе каналов?

3. Уравнение
   движения имеет вид
   
   ,
   где t
   – время. Требуется:

а) построить
годограф движения;

б)
найти скорость и ускорение в момент
времени

;

в)
составить уравнение касательной и
нормальной плоскостей к годографу в
точке

.

1. Даны
   два комплексных числа z₁
   = 3 + 5 i,
   z₂
   = 2 –
   3 i.
   Требуется:

а) записать эти
числа в тригонометрической и показательной
формах;

б) изобразить их
на комплексной плоскости;

в)
выполнить следующие действия:
z₁ +
z₂,
z₁
—
z₂,
z₁

z₂,

,
(— 5
– 5
i)⁶,

;

г)
найти х
и у
из уравнения z₁
x +
z₂
y =
7.

Литература

1. Бермант А.Ф.,
   Араманович И.Г. Краткий курс математического
   анализа для втузов: Учебное посо­бие
   для втузов: — М.: Наука, Главная редакция
   физико-математической литературы,
   1971 г.,736с.

2. Данко П.Е., попов
   А.Г., Кожевникова Т.Я. Высшая математика
   в упражнениях и задачах: Учеб. пособие
   для студентов втузов. Ч 1. М.: Высш. шк..,
   1986. – 304 с.

3. Минорский В.П.
   Сборник задач по высшей математике.
   М.: Наука, Главная редакция
   физико-математической литературы,
   1987. – 352 с.

4. Мышкис А.Д. Лекции
   по высшей математике. – М.: Наука, 1973.
   640 с.

5. Мышкис А.Д.
   Математика для вузов. Специальные
   курсы. – М.: Наука, 1971. – 632 с.

6. Пискунов Н.С.
   Дифференциальное и интегральное
   исчисления для втузов, Том 2: Учебное
   пособие для втузов.-13-е изд. -М. :Наука,
   Главная редак­ция физико-математической
   литературы, 1985.-560с.

7. Сборник задач
   по математике для вузов / Под ред. А.В.
   Ефимова, Б.П. Демидовича. Ч.1. – М.: Наука,
   1986. – 464 с.

8. Фролов С.В., Шостак
   Р. Я. Курс высшей математики. Т. 2. Учеб.
   пособие для втузов. М. :«Высшая школа»,
   1973. – 400 с.

9. В.С. Шипачёв Высшая
   математика: Учебное пособие для втузов:
   – М: Наука, Главная редакция
   физико-математической литературы,
   2002. – 471 с.

ПРИЛОЖЕНИЕ 1

Производная

Производная
– это

Правила
дифференцирования

Таблица производных

Производная
сложной
функции

.

Производная
функции,
заданной неявно

.
Дифференцируется левая часть как
сложная функция, и полученное уравнение
разрешается относительно

.

Производная
функции,
заданной параметрически

:

,

,

.

Геометрический
смысл производной

– тангенс угла наклона касательной.

– угол
между двумя кривыми в точке

.

Уравнение
касательной K

.

Уравнение
нормали N

.

Механический
смысл производной . Если

– закон движения точки, то

– скорость,

– ускорение.

Дифференциал
– главная часть приращения функции.

,

,

Приближённые
формулы

,

,

.

Правила
Лопиталя
раскрытия неопределённостей.

,

,

.

Если

,
то по формуле f(x)
= e
^{ln f(x)}
записываем

,
или функция

предварительно логарифмируется

,
затем находится предел

.

Если

,
то

.

ПРИЛОЖЕНИЕ
2

Комплексные числа и функции

z
= x + iy –
алгебраическая форма комплексного
числа,

где

,
x
– действительная часть (x
= Re z),

y
– мнимая часть (y
= Im z)
комплексного числа z.

 =
arctg

– аргумент (Arg z),

– модуль

.

z
= r(cos
+ i
sin)
– тригонометрическая форма числа z.

z
= r e ^{i }
– показательная форма числа z.

Формулы
Эйлера:
e
^{i }
= cos

+ isin
,
e
^{— i }
= cos

—
isin
,

,

.

Формула
Муавра:
если
z
= r e
^{i }
, то
z
ⁿ
= r
ⁿe
^in.

Комплексная
функция
z
= z(t)
= x(t)
+ i
y(t),

график
z(t)
есть линия

производная
z
(t)
= x
(t)
+ i y
(t).

ПРИЛОЖЕНИЕ 3

Приложения производной

Возрастание,
убывание и экстремумы функции y
= f(x)
определяются с помощью y.

>0,
f(x)
возрастает

f(x)
= <0,
f(x)
убывает

=0,
х
– критическая точка или f(x)
не существует.

Наибольшее
M
и наименьшее m
значения функции на отрезке [a;
b]
достигаются в точках экстремума или
на границах отрезка.

Направление
выпуклости и точки перегиба
функции y
= f(x)
определяются с помощью y.

>0,
f(x)
вогнута,

f(x)
= <0,
f(x)
выпукла,

=0,
х
– критическая точка или f(x)
не существует.

Асимптота
функции y
= f(x)
есть прямая.

Вертикальная
асимптота x
= a

.

Горизонтальная
асимптота y
= b

.

Наклонная
асимптота y
= k x +b

,

.

Вектор-функция

.

Годографом

называется линия, описываемая концом
вектора

.

– скорость,
направленная по касательной к годографу.

– ускорение.

Кривизна y
= f(x) в точке M₀

а) y = f(x)
б)

в) r = r()
г) F(x; y) = 0

Радиус кривизны
y = f(x) в точке M₀

.

Дифференциальные
характеристики пространственной
кривой

.

– направляющий вектор касательной, – направляющий вектор бинормали, – направляющий вектор главной нормали.

– основные единичные векторы кривой .

Производные.

Приложения
производных.

Комплексные числа

Учебно-методическое
пособие

Юлия Константиновна
Чернова,

Светлана
Александровна Крылова

Редактор

Компьютерная
вёрстка Крылов В.Г.

Подписано в
печать Формат 6086/16.

Печать оперативная.
Усл.п.л. Уч.-изд. л.

Тираж 500 экз.
Заказ №

Тольяттинский
государственный университет.

Тольятти,
Белорусская,14.

3

170

4

169

5

168

6

167

7

166

8

165

9

164

10

163

11

162

12

161

13

160

14

159

15

158

16

157

17

156

18

155

19

154

20

153

21

152

22

151

23

150

24

149

25

148

26

147

27

146

28

145

29

144

30

143

31

142

32

141

33

140

34

139

35

138

36

137

37

136

38

135

39

134

40

133

41

132

42

131

43

130

44

129

45

128

46

127

47

126

48

125

49

124

50

123

51

122

52

121

53

120

54

119

55

118

56

117

57

116

58

115

59

114

60

113

61

112

62

111

63

110

64

109

65

108

66

107

67

106

68

105

69

104

70

103

71

102

72

101

73

100

74

99

75

98

76

97

77

96

78

95

79

94

80

93

81

92

82

91

83

90

84

89

85

88

86

87