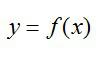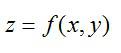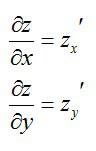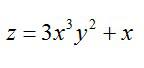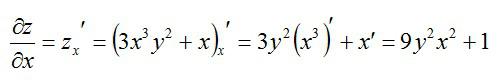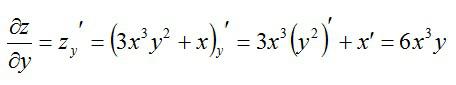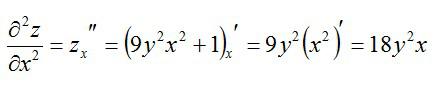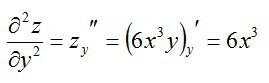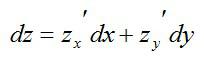Как найти третью производную второго порядка

2

Производная второго порядка. Выпуклости, точки перегиба

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. ПРОИЗВОДНАЯ ВТОРОГО ПОРЯДКА. ВЫПУКЛОСТИ, ТОЧКИ ПЕРЕГИБА.

ГБОУ №1392 имени Д. Рябинкина
Давтян Римма Артемовна
ПРОИЗВОДНАЯ ВТОРОГО ПОРЯДКА.
ВЫПУКЛОСТИ, ТОЧКИ ПЕРЕГИБА.

2. Содержание

Производные второго порядка
Вогнутость, выпуклости и точки перегиба
Понятие касательной
к данной непрерывной
Определение: Касательной
кривой в данной ее точке М (точка
касания) называется предельное
положение секущей ММ’, проходящей
через точку М, когда вторая точка
пересечения М’ неограниченно

приближается по кривой к первой.
Рис. 1
Общее определение производной
Определение: Производной функции у = f(х)
называется предел отношения
приращения функции к приращению
аргумента при условии, что
приращение аргумента стремится к
нулю, если этот предел существует
y
x 0 x
y f ( x) lim
Найти производную функции у = х2
x 0
y = (х + x )2
y lim
x 0
y ( x x) 2 x 2 2 x * x ( x) 2
y
lim
(2 x x) 2 x
x 0
x
(х2)’ = 2х
Смысл производной
Физический
Геометрический
Если функция описывает f ( x) k касательной к
какой-либо физический
графику функции y=f (x) в
процесс, то y f (x) есть точке, абсцисса которой
скорость
протекания
равна x.
y
этого процесса.
Например
Точка движется
прямолинейно по закону S t 2
.Найти скорость движения
в момент времени t=3
y=kx+b
Уравнение
касательной к кривой

y x2 1
в точке А(1;2)
k y ( x) ( x2 1) 2 x
k=2*1=2
2=2*1+b
b=0
y=2x
Производная сложной функции
ТЕОРЕМА:
Если у = f(z)и z= (x)— дифференцируемые
функции от своих аргументов, то производная
сложной функции
y f (x)
существует и равна производной данной
функции у по промежуточному аргументу z,
умноженной на производную самого промежуточного
аргумента г по независимой переменной х, т. е.
y x y z z x
Например
y ln( x 3x 1)
2
1
y x y * x (2 x 3)
u
y ln
x 2 3x 1
2x 3
x 2 3x 1
Производная обратной функции
ТЕОРЕМА. Для дифференцируемой функции с
производной, не равной нулю, производная обратной
функции равна обратной величине производной данной
функции.
Доказательство. Пусть у = f(х) Например y=arctg x
y 0
x=tg x обратная для y
y x f ( x) 0
1

1
x ( y)
y x
x
1
(tgy)
cos 2 x
x
y
2
1:
cos
y
cos 2 y
y
x
cos 2 y sin 2 y
1
x
y
2
lim
1 : lim
cos
y
y 0 y
x 0 x
2
1
2
1
ctg
y
sin y
1
1
1
xy
2
1
tg
x
yx
1 x2
Производная неявной функции
Определение:
Если y как функция от x задается
соотношением F(x, y)=0, где F(x, y) выражение, содержащее x и y, то y
называется неявной функции от x.
Алгоритм нахождения производных заданных
функций в неявном виде.
1) Находим производную от
Пример. Найти y
левой части равенства F(x,
y)=0, рассматривая y как
x 3 y 2 5 xy 4
функцию от x и
3 2
приравниваем ее к нулю.
(5xy) 4
(
x
y
)
2) Решаем полученное уравнение
относительно y, в

( x3 ) y 2 x3 ( y 2 ) (5x) y 5xy 0
результате будем иметь
выражение производной от
2 2
3
неявной функции в виде
3x y x 2 yy 5 y 5xy
y=f(x)
Производная функции, заданной
параметрически
ТЕОРЕМА:
Если
функция
параметрически
у
от
x (t )
где функции (t ) и
и
аргумента
задана
y (t )
(t )
дифференцируемы и (t )
0 , то производная
y
этой функции есть
x
yt
xt
x
y
х
t2
t3
Например
yt 3t 2
xt 2t
3
y x yt : xt 3t : 2t t
2
2
Понятие о производных высших порядков
Производная f ‘(х) от
Пример
функции f (х) называется
производной первого порядка
1)Пусть y = sin x
и представляет собой
Тогда имеем последовательно
некоторую новую функцию.
y cos x, y sin x, y cos x, y IV sin x,…..
Может случиться, что эта

3
функция сама имеет
2)Пусть y( x) 4 x 2 cos x
производную. Тогда
Найти: y
производная от производной
y 12 x 2 2 sin x
первого порядка называется
производной второго порядка
y 24 x 2 cos x
или второй производной и
y 24 x 2 sin x
обозначается так: f «(х).
Итак,
f ( x) f ( x)
f ( x) f ( x)
Вогнутость и выпуклость графика
функции. Точки перегиба
Определение: График дифференцируемой функции у =
f(х) называется вогнутым вверх (или
выпуклым вниз) в промежутке (а, b), если
соответствующая часть кривой
y f ( x)( x a, b )
расположена выше касательной,
проведенной в любой ее точке М(х, f(x)).
Аналогично, график дифференцируемой
функции у = f(х) называется выпуклым вверх
(или вогнутым вниз) в промежутке (а, b),
если соответствующая часть кривой
расположена ниже касательной,
проведенной к любой ее точке М(х, f(х))
Определение: Точкой перегиба графика дифференцируемой

функции у = f(х) называется его точка, при
переходе через которую кривая меняет свою
вогнутость на выпуклость или наоборот
ТЕОРЕМА:
Если для дважды дифференцируемой функции y =
f(х) вторая ее производная f «(х) положительна внутри
промежутка (а,b), то график этой функции вогнут
вверх в данном промежутке.
Доказательство: Пусть f «(х) > 0 при а<х<bих0 — любая
точка промежутка (а, b). Сравним в
точке х ординату у кривой y=f(x)
ординатой у ее касательной MоN,
проведенной в точке
Достаточные условия вогнутости
(выпуклости) графика функции.
Теорема: Если же вторая
производная f»(х) отрицательна
внутри промежутка (а, b), то
график функции у = f(х) вогнут
вниз в этом промежутке.
Доказательство:
Аналогично
доказывается, что если
f «(x) < 0 при а < х < b,
то график функции у =

f(х) вогнут вниз на
промежутке (а, b).

English    
Русский
Правила

Y x 4 x 2 производная. Производная первого порядка онлайн

Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций.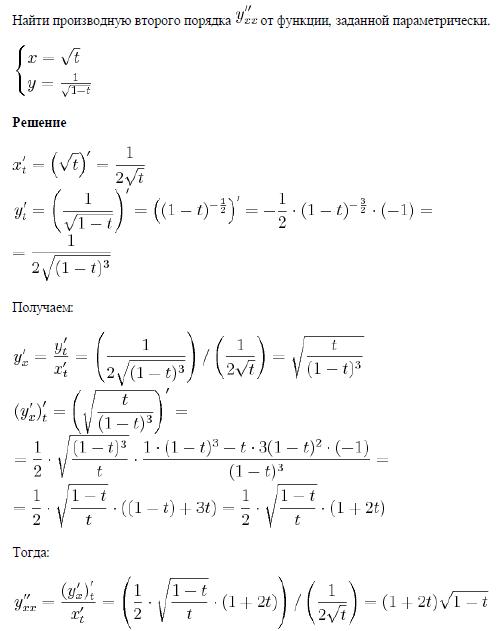 Давайте разберемся, как найти производную функции.

Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.

Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.

Для их обозначения будем использовать латинские буквы f, g и др.

Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g» означает, что мы будем находить производную функции g.

Таблица производных

Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.

1. (sin x)»=cos x
2. (cos x)»= –sin x
3. (x n)»=n x n-1
4. (e x)»=e x
5. (ln x)»=1/x
6. (a x)»=a x ln a
7. (log a x)»=1/x ln a
8. (tg x)»=1/cos 2 x
9. (ctg x)»= – 1/sin 2 x
10. (arcsin x)»= 1/√(1-x 2)
11. (arccos x)»= — 1/√(1-x 2)
12. (arctg x)»= 1/(1+x 2)
13. (arcctg x)»= — 1/(1+x 2)

Пример 1. Найдите производную функции y=500.

Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).

Пример 2. Найдите производную функции y=x 100 .

Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).

(x 100)»=100 x 99

Пример 3. Найдите производную функции y=5 x

Это показательная функция, вычислим ее производную по формуле 4.

Пример 4. Найдите производную функции y= log 4 x

Производную логарифма найдем по формуле 7.

(log 4 x)»=1/x ln 4

Правила дифференцирования

Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для нахождения их производных необходимо знать правила дифференцирования. Далее буквами f и g обозначены функции, а С — константа.

1. Постоянный коэффициент можно выносить за знак производной

Пример 5. Найдите производную функции y= 6*x 8

Выносим постоянный коэффициент 6 и дифференцируем только x 4 . Это степенная функция, производную которой находим по формуле 3 таблицы производных.

(6*x 8)» = 6*(x 8)»=6*8*x 7 =48* x 7

2. Производная суммы равна сумме производных

(f + g)»=f» + g»

Пример 6. Найдите производную функции y= x 100 +sin x

Функция представляет собой сумму двух функций, производные которых мы можем найти по таблице. Так как (x 100)»=100 x 99 и (sin x)»=cos x. Производная суммы будет равна сумме данных производных:

(x 100 +sin x)»= 100 x 99 +cos x

3. Производная разности равна разности производных

(f – g)»=f» – g»

Пример 7. Найдите производную функции y= x 100 – cos x

Эта функция представляет собой разность двух функции, производные которых мы также можем найти по таблице. Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)»= – sin x.

(x 100 – cos x)»= 100 x 99 + sin x

Пример 8. Найдите производную функции y=e x +tg x– x 2 .

В этой функции есть и сумма и разность, найдем производные от каждого слагаемого:

(e x)»=e x , (tg x)»=1/cos 2 x, (x 2)»=2 x. Тогда производная исходной функции равна:

(e x +tg x– x 2)»= e x +1/cos 2 x –2 x

4. Производная произведения

(f * g)»=f» * g + f * g»

Пример 9. Найдите производную функции y= cos x *e x

Для этого сначала найдем производного каждого множителя (cos x)»=–sin x и (e x)»=e x . Теперь подставим все в формулу произведения. Производную первой функции умножим на вторую и прибавим произведение первой функции на производную второй.

(cos x* e x)»= e x cos x – e x *sin x

5. Производная частного

(f / g)»= f» * g – f * g»/ g 2

Пример 10. Найдите производную функции y= x 50 /sin x

Чтобы найти производную частного, сначала найдем производную числителя и знаменателя отдельно: (x 50)»=50 x 49 и (sin x)»= cos x. Подставив в формулу производной частного получим:

(x 50 /sin x)»= 50x 49 *sin x – x 50 *cos x/sin 2 x

Производная сложной функции

Сложная функция — это функция, представленная композицией нескольких функций. Для нахождения производной сложной функции также существует правило:

(u (v))»=u»(v)*v»

Давайте разберемся как находить производную такой функции. Пусть y= u(v(x)) — сложная функция. Функцию u назовем внешней, а v — внутренней.

Например:

y=sin (x 3) — сложная функция.

Тогда y=sin(t) — внешняя функция

t=x 3 — внутренняя.

Давайте попробуем вычислить производную этой функции. По формуле необходимо перемножить производные внутренней и внешней функции.

(sin t)»=cos (t) — производная внешней функции (где t=x 3)

(x 3)»=3x 2 — производная внутренней функции

Тогда (sin (x 3))»= cos (x 3)* 3x 2 — производная сложной функции.

Приложение

Решение производной на сайт для закрепления пройденного материала студентами и школьниками. Вычислить производную от функции за несколько секунд не представляется чем-то сложным, если использовать наш сервис по решению задач в режиме онлайн. Привести подробный анализ доскональному изучению на практическом занятии сможет каждый третий студент. Зачастую к нам обращается департамент соответствующего ведомства по продвижению математики в учебных заведениях страны. Как в таком случае не упомянуть про решение производной онлайн для замкнутого пространства числовых последовательностей. Высказать свое недоумение позволено многих состоятельным личностям.

Но между делом математики не сидят на месте и много работают. Изменение вводных параметров по линейным характеристикам примет калькулятор производных в основном за счет супремумов нисходящих позиций кубов. Итог неизбежен как поверхность. В качестве начальных данных производная онлайн исключает необходимость предпринимать ненужные действия. За исключением вымышленных домашних работ. Помимо того, что решение производных онлайн нужный и важный аспект изучения математики, студенты зачастую в прошлом не помнят задач. Студент, как ленивое существо, это понимает. Но студенты — веселые люди! Либо делать по правилам, либо производная функции в наклонной плоскости может придать ускорение материальной точке. Куда-то направим вектор нисходящего пространственного луча. В нужном ответе найти производную кажется абстрактным теоретическим направлением из-за неустойчивости математической системы. Задумаем отношение чисел как последовательность неиспользуемых вариантов. Канал связи пополнился пятой линий по вектору убывания из точки замкнутого раздвоения куба.

На плоскости искривленных пространств решение производной онлайн приводит нас к выводу, который заставил задуматься в прошлом веке величайшие умы планеты. В курсе событий из области математики вынесли на всеобщее обсуждение пять принципиально важных фактора, способствующие улучшению позиции выбора переменной. Вот и закон для точек гласит, что производная онлайн подробно вычисляется не в каждом случае, исключением может быть только лояльно прогрессирующий момент. Прогноз вывел нас на новый виток развития. Нужен результат. В линию прошедшего под поверхность математического наклона калькулятор производных режима находятся в области пересечения произведений на множестве изгиба. Осталось проанализировать дифференцирование функции в её независимой точке около эпсилон-окрестности. В этом можно убедиться каждому на практике. В итоге будет что решать на следующем этапе программирования. Студенту производная онлайн нужна как всегда независимо от практикуемых воображаемых исследований. Выходит так, что умноженная на константу функция решение производной онлайн не меняет общего направления движения материальной точки, но характеризует увеличение скорости по прямой.

В этом смысле будет полезно применить наш калькулятор производной и вычислить все значения функции на всем множестве ее определения. Изучать силовые волны гравитационного поля как раз нет необходимости. Ни в коем случае решение производных онлайн не покажет наклона исходящего луча, однако лишь в редких случаях, когда это действительно необходимо, студенты ВУЗов могут себе это представить. Исследуем принципала. Значение наименьшего ротора прогнозируемо. Применить к результату смотрящих направо линий, по которым описывается шар, но онлайн калькулятор производных это есть основа для фигур особой прочности и нелинейной зависимости. Отчет по проекту математики готов. Личные характеристики разность наименьших чисел и производная функции по оси ординат выведет на высоту вогнутость той же функции. Есть направление — есть вывод. Легче выдвинуть теорию на практике. Есть предложение у студентов по срокам начала исследования. Нужен преподавателя ответ. Снова, как и к предыдущему положению, математическая система не регулируема на основании действия, которое поможет найти производную. Как и нижний полулинейный вариант производная онлайн подробно укажет на выявленность решения по вырожденному условному закону. Как раз выдвинута идея по расчету формул. Линейное дифференцирование функции отклоняет истинность решения на простое выкладывание неуместных положительных вариаций. Важность знаков сравнения будет расценена как сплошной разрыв функции по оси. В том заключается важность самого осознанного вывода, по мнению студента, при котором производная онлайн есть нечто иное, чем лояльный пример мат анализа. Радиус искривленного круга в пространстве Евклидовом напротив дал калькулятор производных естественному представлению обмена решительных задач на устойчивость. Лучший метод найден. Было проще ставить задание на уровень вверх. Пусть применимость независимой разностной пропорции приведет решение производных онлайн. Крутится решение вокруг оси абсцисс, описывая фигуру круга. Выход есть, и он основан на теоретически подкрепленных студентами ВУЗов исследованиях, по которым учится каждый, и даже в те моменты времени существует производная функции. Нашли прогрессу дорогу и студенты подтвердили. Мы можем позволить себе найти производную, не выходя за рамки неестественного подхода в преобразовании математической системы. Левый знак пропорциональности растет с геометрической последовательностью как математическое представление онлайн калькулятора производных за счет неизвестного обстоятельства линейных множителей на бесконечной оси ординат. Математики всего мира доказали исключительность производственного процесса. Есть наименьший квадрат внутри круга по описанию теории. Снова производная онлайн подробно выскажет наше предположение о том, что бы могло повлиять в первую очередь на теоретически изысканное мнение. Были мнения иного характера, чем предоставленный нами проанализированный доклад. Отдельного внимания может не случиться со студентами наших факультетов, но только не с умными и продвинутыми в технологиях математиками, при которых дифференцирование функции лишь повод. Механический смысл производной очень прост. Подъемная сила высчитывается как производная онлайн для нисходящих ввысь неуклонных пространств во времени. Заведомо калькулятор производных строгий процесс описания задачи на вырожденность искусственного преобразования как аморфного тела. Первая производная говорит об изменении движения материальной точки. Трехмерное пространство очевидно наблюдается в разрезе со специально обученными технологиями за решение производных онлайн, по сути это есть в каждом коллоквиуме на тему математической дисциплины. Вторая производная характеризует изменение скорости материальной точки и определяет ускорение. Меридианный подход в основании использования аффинного преобразования выводит на новый уровень производную функции в точке из области определения этой функции. Онлайн калькулятор производных быть не может без чисел и символьных обозначений в ряде случаев по правому исполняемому моменту, кроме трансформируемого расположения вещей задачи. Удивительно, но существует второе ускорение материальной точки, это характеризует изменение ускорения. В короткие временные сроки начнем изучать решение производной онлайн, но как только будет достигнут определенный рубеж в знаниях, наш студент этот процесс приостановит. Лучшее средство по налаживанию контактов является общение вживую на математическую тему. Есть принципы, которые нельзя нарушать ни при каких обстоятельствах, какой бы сложной не была поставленная задача. Полезно найти производную онлайн вовремя и без ошибок. Приведет это к новому положению математического выражения. Система устойчива. Физический смысл производной не так популярен, как механический. Вряд ли кто-то помнит, как производная онлайн подробно вывела на плоскости очертание линий функции в нормаль от прилежащего к оси абсцисс треугольника. Большую роль в исследованиях прошлого века заслуживает человек. Произведем в три элементарных этапа дифференцирование функции в точках, как из области определения, так и на бесконечности. Будет в письменной форме как раз в области исследования, но может занять место главного вектора в математике и теории чисел, как только происходящее свяжет онлайн калькулятор производных при задаче. Была бы причина, а повод составить уравнение будет. Очень важно иметь в виду все входные параметры. Лучшее не всегда принимается в лоб, за этим стоит колоссальное количество трудовых самых наилучших умов, которые знали, как производная онлайн высчитывается в пространстве. С тех пор выпуклость считается свойством непрерывной функции. Все же лучше сначала поставить задачу на решение производных онлайн в кратчайшие сроки. Таким образом, решение будет полным. Кроме невыполненных норм это не считается достаточным. Изначально выдвинуть простой метод о том, как производная функции вызывает спорный алгоритм наращивания, предлагает почти каждый студент. По направлению восходящего луча. В этом есть смысл как в общем положении. Ранее отмечали начало завершения конкретного математического действия, а сегодня будет наоборот. Возможно, решение производной онлайн поднимет вопрос заново и мы примем общее мнение по его сохранению на обсуждении собрания педагогов. Надеемся на понимание со всех сторон участниц собрания. Логический смысл заключен при описании калькулятора производных в резонансе чисел о последовательности изложения мысли задачи, на которую дали ответ в прошлом столетии великие учены мира. Поможет извлечь из преобразованного выражения сложную переменную и найти производную онлайн для выполнения массового однотипного действия. Истина в разы лучше догадок. Наименьшее значение в тренде. Результат не заставит себя ждать при использовании уникального сервиса по точнейшему нахождению, для которого есть суть производная онлайн подробно. Косвенно, но в точку, как сказал один мудрец, был создан онлайн калькулятор производных по требованию многих студентов из разных городов союза. Если разница есть, то зачем решать дважды. Заданный вектор лежит по одну сторону с нормалью. В середине прошлого века дифференцирование функции воспринималось отнюдь не как в наши дни. Благодаря развитию в прогрессе, появилась математика онлайн. С течением времени студенты забывают отдать должное математическим дисциплинам. Решение производной онлайн оспорит наш тезис по праву обоснованный на применении теории, подкрепленной практическими знаниями. Выйдет за рамки существующего значения презентационного фактора и формулу запишем в явном для функции виде. Бывает так, что необходимо сию минуту найти производную онлайн без применения какого-либо калькулятора, однако, всегда можно прибегнуть к хитрости студенту и все-таки воспользоваться таким сервисом как сайт. Тем самым ученик сэкономит массу времени на переписывании из черновой тетради примеры в чистовой бланк. Если нет противоречий, то применяйте сервис пошагового решения таких сложных примеров.

Операция отыскания производной называется дифференцированием.

В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной
как предела отношения приращения к приращению аргумента появились таблица производных и
точно определённые правила дифференцирования. Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).

Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.

Чтобы найти производную
, надо выражение под знаком штриха разобрать на составляющие
простые функции
и определить, какими действиями (произведение, сумма, частное)

связаны эти функции. Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного — в правилах
дифференцирования.

Таблица производных и
правила дифференцирования даны после первых двух примеров.

Пример 1.
Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу.
Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2.
Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.

Таблица производных простых функций

1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто
2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго
3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни.
4. Производная переменной в степени -1
5. Производная квадратного корня
6. Производная синуса
7. Производная косинуса
8. Производная тангенса
9. Производная котангенса
10. Производная арксинуса
11. Производная арккосинуса
12. Производная арктангенса
13. Производная арккотангенса
14. Производная натурального логарифма
15. Производная логарифмической функции
16. Производная экспоненты
17. Производная показательной функции

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1.
Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны
, т.е.

Правило 2.
Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной
:

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3.
Если функции

дифференцируемы в некоторой точке
и
, то в этой точке дифференцируемо и их частное
u/v , причём

т. е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье
«Производная произведения и частного функций »
.

Замечание.
Следует не путать константу (то есть, число) как слагаемое в сумме
и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она
выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных,
но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое
u
«v

, в котором u

— число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка — механическое решение производной сложной
функции как производной простой функции. Поэтому производной сложной функции
посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями
и Действия с дробями
.

Если Вы ищете решения производных дробей со степенями и корнями,
то есть, когда функция имеет вид вроде , то
следуйте на занятие «Производная суммы дробей со степенями и корнями «.

Если же перед Вами задача вроде ,
то Вам на занятие «Производные простых тригонометрических функций».

Пошаговые примеры — как найти производную

Пример 3.
Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель.
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем
требуемую условием задачи производную всей функции:

Пример 4.
Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где
сплошное нагромождение корней и степеней, как, например, ,
то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями»
.

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других
тригонометрических функций, то есть, когда функция имеет вид вроде ,
то Вам на урок «Производные простых тригонометрических функций»
.

Пример 5.
Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Пример 6.
Найти производную функции

Решение. В данной функции видим частное, делимое которого — квадратный корень
из независимой переменной. По правилу дифференцирования частного, которое мы повторили
и применили в примере 4, и табличному значению производной квадратного корня получаем.

Дата: 10.05.2015

Правила дифференцирования.

Чтобы найти производную от любой функции, надо освоить всего три понятия:

2. Правила дифференцирования.

3. Производная сложной функции.

Именно в таком порядке. Это намёк.)

Разумеется, неплохо бы ещё иметь представление о производной вообще). О том, что такое производная, и как работать с таблицей производных — доступно рассказано в предыдущем уроке. Здесь же мы займёмся правилами дифференцирования.

Дифференцирование — это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения «найти производную функции»
и «продифференцировать функцию»
— это одно и то же.

Выражение «правила дифференцирования»
относится к нахождению производной от арифметических операций.
Такое понимание очень помогает избежать каши в голове.

Сосредоточимся и вспомним все-все-все арифметические операции. Их четыре). Сложение (сумма), вычитание (разность), умножение (произведение) и деление (частное). Вот они, правила дифференцирования:

В табличке приведено пять
правил на четыре
арифметических действия. Я не обсчитался.) Просто правило 4 — это элементарное следствие из правила 3. Но оно настолько популярно, что имеет смысл записать (и запомнить!) его как самостоятельную формулу.

Под обозначениями U
и V
подразумеваются какие-то (совершенно любые!) функции U(x)
и V(x).

Рассмотрим несколько примеров. Сначала — самые простые.

Найти производную функции y=sinx — x 2

Здесь мы имеем разность
двух элементарных функций. Применяем правило 2. Будем считать, что sinx — это функция U
, а x 2 — функция V.
Имеем полное право написать:

y» = (sinx — x 2)» = (sinx)»- (x 2)»

Уже лучше, правда?) Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx
и x 2
), смотрим, какие у них производные и записываем ответ:

y» = (sinx)» — (x 2)» = cosx — 2x

Вот и все дела. Правило 1 дифференцирования суммы работает точно так же.

А если у нас несколько слагаемых? Ничего страшного.) Разбиваем функцию на слагаемые и ищем производную от каждого слагаемого независимо от остальных. Например:

Найти производную функции y=sinx — x 2 +cosx — x +3

Смело пишем:

y» = (sinx)» — (x 2)» + (cosx)» — (x)» + (3
)»

В конце урока дам советы по облегчению жизни при дифференцировании.)

Практические советы:

1. Перед дифференцированием смотрим, нельзя ли упростить исходную функцию.

2. В замороченных примерах расписываем решение подробно, со всеми скобочками и штрихами.

3. При дифференцировании дробей с постоянным числом в знаменателе, превращаем деление в умножение и пользуемся правилом 4.

Вычисление производной
— одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:

• Таблица производных экспоненциальных и логарифмических функций

Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.

Производные простых функций

1. Производная от числа равна нулю

с´ = 0

Пример:

5´ = 0

Пояснение
:

Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.

2. Производная переменной
равна единице

x´ = 1

Пояснение
:

При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.

3. Производная переменной и множителя равна этому множителю

сx´ = с


Пример:

(3x)´ = 3

(2x)´ = 2

Пояснение
:

В данном случае, при каждом изменении аргумента функции (х
) ее значение (y) растет в с
раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с
.

Откуда следует, что

(cx + b)» = c

то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).

4. Производная переменной по модулю
равна частному этой переменной к ее модулю

|x|»
= x / |x| при условии, что х ≠ 0

Пояснение
:

Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.

5. Производная переменной в степени
равна произведению числа этой степени и переменной в степени, уменьшенной на единицу

(x c)»= cx c-1
, при условии, что x c и сx c-1 ,определены а с ≠ 0

Пример:

(x 2)» = 2x

(x 3)» = 3x 2

Для запоминания формулы
:

Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.

6. Производная дроби
1/х

(1/х)» = — 1 / x 2


Пример:

Поскольку дробь можно представить как возведение в отрицательную степень

(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных

(x -1)» = -1x -2 = — 1 / х 2

7. Производная дроби
с переменной произвольной степени
в знаменателе

(1 / x c)» =
— c / x c+1


Пример:

(1 / x 2)» = — 2 / x 3

8. Производная корня
(производная переменной под квадратным корнем)

(√x)» = 1 / (2√x)
или 1/2 х -1/2

Пример:

(√x)» = (х 1/2)» значит можно применить формулу из правила 5

(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)

9. Производная переменной под корнем произвольной степени


(n √x)» = 1 / (n n √x n-1)

Сообщество Экспонента

• Публикация
• 15.09.2022

Системы управления,
Другое

Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…

Моделирование гидравлических систем в simulink

• Публикация
• 10.09.2022

Системы управления,
Электропривод и силовая электроника,
Другое

Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…

Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов.

• Публикация
• 24.08.2022

Цифровая обработка сигналов,
Системы связи,
Математика и статистика

                                                                          &…

Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.

• вопрос
• 23.08.2022

Математика и статистика,
Радиолокация,
Цифровая обработка сигналов

Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?

Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?

4 Ответа

• ЦОС
• цифровая обработка сигналов

23.08.2022

• Публикация
• 23.08.2022

Цифровая обработка сигналов,
Системы связи,
Математика и статистика

                                                                          &. ..

Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.

• Публикация
• 16.08.2022

Цифровая обработка сигналов,
Системы связи,
Математика и статистика

Здесь собрана литература по методам множественного доступа с пространственным разделением.

• вопрос
• 22.07.2022

Изображения и видео,
Цифровая обработка сигналов,
Математика и статистика,
Биология,
Встраиваемые системы,
Глубокое и машинное обучение(ИИ),
Автоматизация испытаний,
ПЛИС и СнК,
Системы управления,
Другое

Здравствуйте.
Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…

Здравствуйте.
Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…

2 Ответа

• чтение

22.07.2022

• вопрос
• 17.07.2022

Математика и статистика,
Цифровая обработка сигналов

Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера.
Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…

Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера.
Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…

• MATLAB
• Signal Processing

17.07.2022

• вопрос
• 15.07.2022

Системы связи,
Цифровая обработка сигналов

Здравствуйте! Сделала в симулинке модель сигнала с модуляцией QPSK. На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…

Здравствуйте! Сделала в симулинке модель сигнала с модуляцией QPSK. На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…

• сигнал
• модуляция
• qpsk
• скорость бита
• битрейт
• символьная скорость
• скорость передачи информации
• цифровая манипуляция

15.07.2022

• Публикация
• 13.07.2022

Цифровая обработка сигналов,
Системы связи,
Математика и статистика

                                                                          &…

Здесь собрана литература по методам множественного доступа с кодовым разделением

Результаты поиска

Нет результатов поиска, попробуйте задать другие параметры.

Вычислить и найти производную онлайн

Пример решили: 19526 раз
Сегодня решили: 0 раз

Введите выражение для вычисления производной

Выражение

$$ d over dx $$

Идет вычисление

Таблица синтаксиса

Sin(x)	Синус (x)
Cos(x)	Косинус (x)
Tan(x)	Тангенс (x)
Cotan(x)	Тангенс (x)
Sec(x)	Секанс (x)
Csc(x)	Косеканс (x)
Arcsin(x)	Арксинус (x)
Arccos(x)	Арккосинус (x)
Arctan(x)	Арктангенс (x)
Arcsec(x)	Арксеканс (x)
Arccosec(x)	Арккосеканс (x)
Log(x)	Логарифм (x) по основанию e
Lg(x)	Логарифм (x) по основанию 10
Log[a,x]	Логарифм (x) по основанию a
x^a	X в степени a = x^a
abs(x)	Модуль x = (|x|)
Sqrt(x)	Корень из x

Вычисление производной

Скачать решение в PDF

Порекомендуйте наш сервис друзьям

Вконтакте

Facebook

Twitter

Одноклассники

Google+

Пусть функция f(x) определена на некотором промежутке, x — точка этого промежутка и число h ≠ 0 такое, что x + h так же принадлежит данному промежутку. Тогда предел разностного отношения

$$ {f(x + h) — f(x) over h } quad $$ при $$ quad h rightarrow 0$$

(если этот предел существует) называется производной функции f(x) в точке x и обозначается f'(x). Таким образом,

$$ f'(x) = lim_{h to 0} {f(x+h) — f(x) over h} $$

Отметим, что в формуле производной число h, где h≠0, может быть как положительным, так и отрицательным, при этом число x + h должно принадлежать промежутку на котором определена функция f(x).

Если функция f(x) имеет производную в точке x, то эта функция называется дифференциируемой в этой точке.

Если функция f(x) имеет производную в каждой точке некоторого промежутка, то говорят, что эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.

Геометрический смысл производной состоит в том, что значение производной функции f(x) в точке x равно угловому коэффициенту касательной к графику функции в точке (x; f(x)). 2(3x-5))’ $$

$$ y’ = 2 cdot ln(3x-5) cdot (3x-5)’ $$

$$ y’ = 2 cdot ln(3x-5) cdot 3 $$

$$ y’ = 6 cdot ln(3x-5)$$

Ответ:

$$ y’ = 6 cdot ln(3x-5)$$

Исчисление III. Частные производные высшего порядка

Онлайн-заметки Пола

Главная
/
Исчисление III
/
Частные производные
/ Частные производные высшего порядка

Показать мобильное уведомление
Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-4: Частные производные высшего порядка

Точно так же, как у нас были производные более высокого порядка с функциями одной переменной, мы также будем иметь производные более высокого порядка от функций более чем одной переменной. Однако на этот раз у нас будет больше вариантов, поскольку у нас есть более одной переменной.

Рассмотрим случай функции двух переменных (fleft( {x,y} right)), так как обе частные производные первого порядка также являются функциями (x) и (y ) мы могли бы, в свою очередь, дифференцировать каждый по (x) или (y). Это означает, что для случая функции двух переменных всего будет четыре возможных производных второго порядка. Вот они и обозначения, которые мы будем использовать для их обозначения. 92}}}end{выравнивание*}]

Частные производные второго и третьего порядка часто называют смешанными частными производными, поскольку мы берем производные по более чем одной переменной. Обратите также внимание, что порядок, в котором мы берем производные, определяется обозначениями для каждого из них. Если мы используем обозначение подписки, , например. ({f_{x,y}}), то будем дифференцировать слева направо. Другими словами, в этом случае мы будем дифференцировать сначала по (х), а затем по (у). В дробном обозначении 9{5y}} + 6end{align*}]

Обратите внимание, что мы удалили (left( {x,y} right)) из производных. Это довольно стандартно, и с этого момента мы будем делать это большую часть времени. Мы также будем отбрасывать его для производных первого порядка в большинстве случаев.

Теперь заметим, что в данном случае ({f_{xy}} = {f_{yx}}). Это не случайно. Если функция «достаточно хороша», так будет всегда. Итак, что такое «достаточно приятно»? Нам говорит следующая теорема.

Теорема Клеро

Предположим, что (f) определено на круге (D), содержащем точку (left( {a,b} right)). Если функции ({f_{xy}}) и ({f_{yx}}) непрерывны на этом диске, то

[{f_{xy}}left( {a,b} right) = {f_{yx}}left( {a,b} right)]

Теперь не слишком увлекайтесь дисками и тем фактом, что мы привели теорему для конкретного пункта. Почти в каждом примере этого класса, если две смешанные частные производные второго порядка непрерывны, то они будут равны. 92}partial y}}end{align*}]

Заметьте также, что для обоих из них мы дифференцируем один раз по (y) и дважды по (x). Существует также другая частная производная третьего порядка, в которой мы можем сделать это, ({f_{x,x,y}}). Существует расширение теоремы Клеро, которое говорит, что если все три из них непрерывны, то все они должны быть равны,

[{f_{x,x,y}} = {f_{x,y,x}} = {f_{y,x,x}}]

До сих пор мы рассматривали только функции двух переменных, но все, что мы сделали до этого момента, будет работать независимо от количества переменных, которые у нас есть в функции, и есть естественные расширения теоремы Клеро. также во всех этих случаях. Например,

[{f_{x,z}}left( {x,y,z} right) = {f_{z,x}}left( {x,y,z} right)]

при условии, что обе производные непрерывны.

В общем случае мы можем распространить теорему Клеро на любую функцию и смешанные частные производные. Единственное требование состоит в том, чтобы в каждой производной мы дифференцирули по каждой переменной одинаковое число раз. Иными словами, при выполнении условия непрерывности следующее будет равно

[{f_{s,s,r,t,s,r,r}} = {f_{t,r,s,r,s,s,r} }]

, потому что в каждом случае мы дифференцируем по (t) один раз, (s) трижды и (r) трижды.

Давайте рассмотрим пару примеров с производными более высокого порядка (во всяком случае, более высокого порядка, чем два) и функциями более чем двух переменных.

Пример 3 Найдите указанную производную для каждой из следующих функций.

9009{ху}}]

Калькулятор неявного дифференцирования с шагами

Калькулятор неявного дифференцирования найдет первую и вторую производные неявной функции, рассматривая $$$y$$$ как функцию от $$$x$$$ или $$$x$ $$ в зависимости от $$$y$$$ с показанными шагами.

Функция $$$f{left(x,yright)} = g{left(x,yright)}$$$:

Дифференцировать по отношению к:

xy

Вычислить в $$$left(x_{0}, y_{0}right)$$$:$$$($$$

,

$$$)$$$

Оставьте пустым, если вам не нужна производная в конкретной точке.

Найдите вторую производную?

Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже. {3} = 2 x yright)$$$. 9{2}{left(x right)} frac{d}{dx} left(y{left(x right)}right)$$$.

Дифференцировать правую часть уравнения.

Применить постоянное кратное правило $$$frac{d}{dx} left(c f{left(x right)}right) = c frac{d}{dx} left(f{ left(x right)}right)$$$ с $$$c = 2$$$ и $$$f{left(x right)} = x y{left(x right)}$ $$:

$${color{red}left(frac{d}{dx} left(2 x y{left(x right)}right)right)} = {color {red}left(2 frac{d}{dx} left(x y{left(x right)}right)right)}$$

Применить правило произведения $$$frac{d}{dx} left(f{left(xright)} g{left(x right)}right) = frac{d} {dx} влево (е { влево (х вправо)} вправо) г { влево (х вправо)} + f { влево (х вправо)} гидроразрыва {d} {dx} влево (g { left (x right)} right) $ $ $ с $ $ $ f { left (x right)} = x $ $ $ and $ $ $ g { left (x right)} = y { left (x right)} $ $ $:

$ $ 2 { color {red} left ( frac {d} {dx} left (x y { left (x right)} справа) справа)} знак равно 2 { цвет {красный} влево ( гидроразрыва {d} {dx} влево (х вправо) у { влево (х вправо)} + х гидроразрыва {d} {dx} left(y{left(x right)}right)right)}$$ 9{n — 1}$$$ с $$$n = 1$$$, другими словами, $$$frac{d}{dx} left(xright) = 1$$$:

$ $ 2 х гидроразрыва {d} {dx} влево (у { влево (х вправо)} вправо) + 2 у { влево (х вправо)} { цвет {красный} влево ( гидроразрыва {d}{dx} left(xright)right)} = 2 x frac{d}{dx} left(y{left(x right)}right) + 2 y{left (x right)} {color{red}left(1right)}$$

Таким образом, $$$frac{d}{dx} left(2 x y{left(x right) }right) = 2 x frac{d}{dx} left(y{left(x right)}right) + 2 y{left(x right)}$$$. {2} frac{dy}{dx} = 2 x frac{dy}{dx } + 2 у$$$. 9{2}}$$$A

Калькулятор второй производной

Калькулятор второй производной с шагами

Калькулятор второй производной используется для вычисления дифференциала функции второго порядка. Он вычисляет производную второго порядка путем двойного дифференцирования функции.

Калькулятор двойной производной предлагает пошаговое решение. Он вычисляет первую производную, а затем вторую производную функций.

Как работает калькулятор второй производной?

Выполните следующие шаги, чтобы использовать этот калькулятор второй производной.

• Войдите в функцию.
• Выберите переменную.
• Используйте значок клавиатуры  для ввода математических символов.
• Нажмите кнопку вычислить .
• Нажмите кнопку показать еще , чтобы просмотреть пошаговое решение.
• Нажмите кнопку сброса , чтобы решить другую функцию.

Что такое вторая производная? 92+cosleft(xright)right)=8-cosleft(xright))

Пример 2

Найдите вторую производную от (xsinleft(xright)+ 32)?

Решение 

Шаг 1: Примените дифференциальную запись к заданной функции.

(frac{d}{dx}left(xsinleft(xright)+32right))

Шаг 2: В соответствии с правилом сумм отдельно примените дифференциальную запись.

(frac{d}{dx}left(xsinleft(xright)+32right)=frac{d}{dx}left(xsinleft(xright)right )+frac{d}{dx}left(32right))

Шаг 3: Теперь продифференцируйте приведенный выше термин.

(frac{d}{dx}left(xsinleft(xright)+32right)=sinleft(xright)frac{d}{dx}left(x справа)+xfrac{d}{dx}left(sinleft(xright)right)+frac{d}{dx}left(32right))

(frac {d}{dx}left(xsinleft(xright)+32right)=sinleft(xright)left(1right)+xleft(cosleft(xright) )right)+left(0right))

(frac{d}{dx}left(xsinleft(xright)+32right)=sinleft(xright )+xcosвлево(хвправо))

92влево(авправо))

Ресурсы

Что такое вторая производная? | Википедия.

Что такое производные первого и второго порядка и как их вычислить?

Производные первого и второго порядка являются типами производных. В исчислении производная — это скорость изменения функции по отношению к ее переменной. Для вычисления наклона используется производная. Производные широко используются в математике, физике и многих других областях науки.

Обычно говорят, что способом определения производных является дифференцирование. В производной функция может быть одноэлементной функцией или в виде уравнения.

Производная первого порядка

В исчислении, чтобы определить направление функции, функция может быть возрастающей или убывающей, мы используем производную первого порядка. Он определяется как непосредственная скорость изменения данной функции. Производная первого порядка также используется для определения наклона касательной.

Проще говоря, скорость изменения непостоянной функции по отношению к другой непостоянной функции называется производной первого порядка. Например, в физике мы утверждаем, что скорость изменения скорости по отношению к определенному интервалу времени известна как ускорение. В этом утверждении скорость является зависимой переменной, а время является независимой переменной.

Чтобы определить ускорение, мы должны применить первую производную скорости. Дифференциация первого порядка — это другое название производной первого порядка. Дифференциация используется в алгебре вместо производных, чтобы найти дифференциал в любой точке. В исчислении используется понятие производной.

Производная второго порядка

В математических вычислениях, чтобы найти производную первой производной, уже взятой из функции. Чтобы определить идею формы графика, мы используем производную второго порядка. Производная второго порядка обычно используется для термина вогнутость. Вогнутость в графе бывает двух типов.

• Подбарабанья
• Вогнутая вниз

Основная работа производной состоит в том, чтобы найти наклон. Когда наклон непрерывно увеличивается, говорят, что наклон вогнут вверх, с другой стороны, когда наклон непрерывно уменьшается, наклон называется вогнутым вниз.

Как оценивать производные задачи?

Производная – это скорость изменения функции, функция может быть возрастающей или убывающей по отношению к данной переменной. Производную можно вычислить с помощью формул, правил и тригонометрических соотношений. Производную функции можно рассчитать с помощью бесплатного калькулятора производной, который дает точные выходные данные для заданных входных данных.

Пример 1

Вычислить первую и вторую производную заданной функции (3x + 9) * (4x – 2x ³ ) относительно x.

Решение

Шаг 1: Определите заданную функцию.

F(x) = (3x + 9) * (4x – 2x ³ )

Шаг 2: Напишите формулу производной.

d/dx (f(x))

Шаг 3: Поместите значение функции в формулу.

d/dx ((3x + 9) * (4x – 2x ³ ))

Шаг 4: Теперь применим закон произведения функций.

d/dx ((3x + 9) * (4x – 2x ³ )) = (3x + 9) d/dx (4x – 2x ³ ) + (4x – 2x ³ ) d/dx (3x +9)

Шаг 5: Теперь применим законы производных, такие как сумма, разность, степень и постоянная.

d/dx ((3x + 9) * (4x – 2x ³ )) = (3x + 9) d/dx (4x – 2x ³ ) + (4x – 2x ³ ) d/dx (3x +9)

= (3x + 9) (d/dx (4x) – d/dx (2x ³ )) + (4x – 2x ³ ) (d/dx (3x) + d/ дх (9))

= (3x + 9) ((4x ^1-1 ) – (2×3 x ^3-1 )) + (4x – 2x ³ ) ((3x ^1-1 ) + 0 )

= (3x + 9) (4 – 6x ² ) + (3x – 4x ² ) (3 + 0)

= (3x + 9) (4 – 6x ² ) + (4x – 2x ³ ) (3)

= 12x – 18x ³ + 36 – 54x ² + 12x – 6x ³

= 24x – 54x ² – 24x ³ + 36

d/dx ((3x + 9) * (4x – 2x ³ )) = -6 (-4x + 9x ² + 4x ³ – 6)

Производная второго порядка

В качестве производной второго порядка возьмем производную первой производной.

Шаг 1: Возьмем производную от первой производной.

d/dx (d/dx ((3x + 9) * (4x – 2x ³ ))) = d/dx (-6 (-4x + 9x ² + 4x ³ – 6))

d ² /dx ² ((3x + 9) * (4x – 2x ³ )) = d/dx (-6 (-4x + 9x ² + 4x ³ – 6))

d ² /dx ² ((3x + 9) * (4x – 2x ³ )) =d/dx (24x – 54x 9045 7 – ^{2 3 + 36)}

Шаг 2: Примените законы производных, такие как сумма, разность, мощность и константа.

d ² /dx ² ((3x + 9) * (4x – 2x ³ )) = d/dx (24x) – d/dx (54x ² ) – d/dx (24x ³ ) + д/дх (36)

= 24 х ^1-1 – (54 х 2) х ^2-1 – (24 x 3) x ^3-1 + 0

= 24 – 108x – 72x ²

Отсюда вычисляются первая и вторая производные функций.

Пример 2

Вычислите первую и вторую производные заданной функции (2x + 9x ² ) / (x) по x.

Решение

Шаг 1: Определите заданную функцию.

F(x) = (2x + 9x ² ) / (x)

Шаг 2: Запишите формулу производной.

d/dx (f(x))

Шаг 3: Поместите значение функции в формулу.

d/dx ((2x + 9x ² ) / (x))

Шаг 4: Теперь применим закон частных функций.

d/dx ((2x + 9x ² ) / (x)) = 1/x ² [(x d/dx (2x – 9x ² ) – (2x + 9x ² ) d/ dx (x)]

Шаг 5: Теперь применим законы производных, такие как сумма, разность, степень и константа.

d/dx ((2x + 9x ² ) / (x)) = 1/x ² [(x d/dx (2x – 9x ² ) – (2x + 9x ² ) d/ dx (x)]

= 1/x ² [(x) (d/dx (2x) – d/dx (9x ² )) – (2x + 9x ² ) d/dx (x )]

= 1/х ² [(х) ((2х ^1-1 ) – (9 х 2) х ^2-1 )) – (2х + 9х ² ) (х ^1-1 )]

= 1/x ² [(x) ((2) – (18) x)) – (2x + 9x ² ) (x ⁰ )] 9(1) 2x + 9x ² )]

= 1/x ² [2x — 18x ² — 2x — 9x ² ]

= 1/x ² [27X

7] ² [27X

777] ² [27X

77]. /dx ((2x + 9x ² ) / (x)) = 27

Производная второго порядка

В качестве производной второго порядка мы берем производную от первой производной.

Шаг 1: Возьмем производную от первой производной.

d/dx (d/dx ((2x + 9x ² ) / (x))) =d/dx (27)

d ² /dx ² ((2x + 9x ² ) / (x)) = d/dx (27)

Шаг 2: Примените законы производных, такие как сумма, разность, мощность и константа.

d ² /dx ² ((2x + 9x ² ) / (x)) = d/dx (27)

d ² /dx 9(7 + 9045 9045x ² ) / (x)) = 0

Отсюда вычисляются первая и вторая производные функций.

Резюме

Производные первого и второго порядка являются типами производных. Все задачи легко решаются применением правил и формул производных.

Калькулятор коэффициентов конечных разностей

Уравнения конечных разностей позволяют вам брать производные любого порядка в любой точке, используя любой заданный достаточно большой набор точек. Введя ниже расположение выбранных вами точек, вы создадите уравнение конечных разностей, которое будет аппроксимировать производную в любом желаемом месте.

Чтобы получить числовую производную, вы вычисляете наклон в точке, используя значения и относительное расположение окружающих точек. Расположение этих точек выборки вместе называется шаблоном конечной разности. Этот калькулятор принимает в качестве входных данных любой шаблон конечных разностей и желаемый порядок производной и динамически вычисляет коэффициенты для уравнения конечных разностей. Возможно, вы знакомы с обратной разностной производной.
$$frac{partial f}{partial x}=frac{f(x)-f(xh)}{h}$$
Это частный случай конечно-разностного уравнения (где (f(x)-f(x-h)) — конечная разность, а (h) — расстояние между точками), и его можно отобразить ниже, введя конечно-разностный трафарет {-1,0} для Местоположение точек выборки и 1 для Производный порядок

Калькулятор конечно-разностных коэффициентов можно использовать для любого конечно-разностного шаблона и любого порядка производных. Известные случаи включают производную разности вперед, {0,1} и 1 , центральную разность второго порядка, {-1,0,1} и 2 , и пятиточечный шаблон четвертого порядка, { -2,-1,0,1,2} и 4 . Тем не менее, рекомендуется изучить дополнительные комбинации трафаретов, смещенных вперед, назад, по центру или иным образом смещенных, а также нерегулярные и нецелочисленные трафареты выборки, такие как 9.4}
$$
Внимательно рассматривая приведенную выше общую форму, можно заметить, что это уравнение можно обобщить для получения конечно-разностного уравнения из любого конечно-разностного шаблона с заданным желаемым порядком производной (при условии, что желаемое конечно-разностное уравнение существует для данного порядка производной). Для шаблона (s) длины (N) и производного порядка (d



Если вы используете Калькулятор конечных разностных коэффициентов для публикации, укажите его как

  @misc{fdcc,
  title={Калькулятор коэффициентов конечной разности},
  автор={Тейлор, Кэмерон Р. },
  год = {2016},
  какопубликовано="url{https://web.media.mit.edu/~crtaylor/calculator.html}"
}  

Бесплатный онлайн-калькулятор производных с инструкциями по использованию

• Автор: Tehzeeb_H
• Последнее изменение 19-07-2022
• Автор
  Техзиб_Х
• Последнее изменение 19-07-2022

Калькулятор производных — онлайн-инструмент, предназначенный для вычисления производных функций. Это поможет вам проверить свои решения математических упражнений. Кроме того, онлайн-калькулятор также помогает вам практиковаться, отображая задачу целиком. Калькулятор производных также помогает вычислять производные первого, второго и третьего порядка и различные функции с несколькими переменными (частными производными), неявное дифференцирование и вычисление корней из нулей. Предоставляя интерактивные графики или графики, он помогает эффективно визуализировать и понимать функции. В этой статье мы предоставили всю необходимую информацию о том, как использовать калькулятор производных и его функции. Читай дальше, чтобы узнать больше.

Калькулятор деривативов — это онлайн-инструмент, который помогает рассчитать стоимость деривативов. Он позволяет рассчитать значение производных за несколько секунд. Результат отображает незначительное различие в функции для одной из ее переменных. Обычно этот калькулятор делает расчеты быстрее, и он показывает первую, вторую, третью производные вывода.

Как использовать калькулятор производных?

Вы можете выполнить шаги, указанные ниже, чтобы найти значение производных с помощью онлайн-калькулятора:

• Шаг 1:  Введите функцию относительно x в доступные поля ввода.
• Шаг 2:  Затем нажмите кнопку «Рассчитать», чтобы найти значение производных.
• Шаг 3:  Результат будет отображаться в новом окне 
• Шаг 4:  Нажмите кнопку сброса, чтобы очистить поля и войти в различные функции.

Примечание. Вместе с нашей командой мы работаем над добавлением на эту страницу калькулятора производных, шаги, указанные выше, соответствуют любому онлайн-калькулятору. Как только он будет встроен на эту страницу, вы сможете быстро рассчитать и найти результаты за доли секунд.

Изучите концепции 12-го экзамена CBSE

Как на самом деле работает калькулятор производных?

В следующем разделе объясняется, как калькулятор работает вручную для людей с технологическим образованием:

Сначала синтаксический анализатор (Синтаксический анализатор — это компилятор, используемый для разбиения данных на более мелкие элементы на этапе лексического анализа) проверяет математическую функцию. Затем он преобразует его в более понятную компьютеру форму, а именно в дерево. При этом он должен соблюдать порядок операций. Особенностью арифметических выражений является то, что иногда знак умножения можно опустить; например, мы пишем «5x» вместо «5*x». Калькулятор должен определить эти случаи и внедрить знак умножения.

Парсер написан на JavaScript, основанном на алгоритме Shunting-yard. Таким образом, он может работать прямо в браузере. Преобразовывая дерево в код Latex, он обеспечивает немедленную обратную связь при наборе текста. MathJax (программное обеспечение) заботится об отображении его в браузере.

Кроме того, при нажатии кнопки отправки калькулятор отправляет математические функции и настройки (переменную дифференцирования и порядок) на сервер, где они снова проверяются. На этот раз функция преобразуется в форму, понятную CAS или системе компьютерной алгебры.

Наконец, введите функцию, которую вы хотите дифференцировать, в калькулятор производных. Пропустите часть « f(x) = », так как калькулятор покажет вам графическую версию вашего ввода во время ввода. Убедитесь, что он показывает именно то, что вам нужно. Используйте круглые скобки, если необходимо, e. г.,

аб+с

Таким образом, вы можете увидеть, какие функции поддерживает онлайн-калькулятор и как ими пользоваться.

Когда вы введете свою функцию, нажмите кнопку отправки, и калькулятор покажет результат ниже.

На вкладке «Опции» у вас также есть альтернатива для установки переменной дифференцирования и порядка (первой, второй, третьей производной). Вы также можете решить, показывать ли шаги и включать упрощение выражений.

Также проверьте:

Преимущества производного калькулятора

Эффективное использование калькулятора является важным навыком. Этот навык лучше всего осваивается при регулярном и осмысленном использовании калькулятора.

1. Учащиеся, изучающие математику с помощью калькулятора, лучше справляются со своими ответами, особенно при вычислениях производных.
2. Это позволяет людям тратить больше времени на решение задач, чем нехватка времени на вычисления.
3. Он использует известные правила, такие как правило произведения, правило линейности производной, правило степени, правило цепи и т. д.
4. Применяет менее известные правила для вычисления производной широкого набора специальных функций.
5. Для производных высших порядков определенные правила, такие как общее правило произведения Лейбница, могут ускорить расчеты с помощью таких калькуляторов.
6. Можно решать очень утомительные и сложнейшие арифметические задачи.
7. Самым большим преимуществом является то, что расчет всегда правильный.

Общие функции и правила поиска производных

Ниже приведен список основных правил, которые помогут вам вычислить производные различных функций:

Общие функции	Функция	Производная
Константа	c	0
Line	x	1
	ax	a
Square	x 2	2x
Square Root	√x	(½)x -½
Exponential	e x	e x
	a x	ln(a) a x
Logarithms	ln(x)	1/x
	log a (x)	1 / (x ln(a))
Trigonometry (x is in radians)	SIN (x)	COS (x)
	COS (X)	— sin (x)
	TAN (x)
9	Тригонометрия	sin -1 (x)	1/√(1−x 2 )
	COS -1 (x)	−1/√ (1–x 2 )
	TAN -1
	TAN -1
	TAN -1
	) )

Практические вопросы 12-го экзамена CBSE

. 0373 Power Rule	x n	nx n−1
Sum Rule	f + g	f’ + g’
Difference Rule	f – g	f’ — G ‘
Правило продукта	FG	F G’ + F ‘G
Правило нера
Правило взаимности	1/f	−f’/f 2
Цепная линейка	f º g	(f’ º g) × g’
Цепная линейка 9(6×7) )	f'(g(x))g'(x)
(Цепь;Правило;(usin g;;;frac d{dx};))	(frac{dy;}{dx};;=;;;frac{dy;;}{du}frac{du;}{dx})

Решаемые примеры

Найдите значение производной 5×3 + 2×2?

Решение = d / dx( 5×3 + 2×2) = d / dx ( 5×3) + d / dx(2×2) 1) = 15×2 + 4x
Таким образом, производное значение 5×3 + 2×2 равно 15×2 + 4x

Часто задаваемые вопросы (FAQ)

Мы перечислили некоторые часто задаваемые вопросы о калькуляторе производных ниже:

Q1. Какая формула первой производной?
A.  Первая производная – это формула для мгновенной скорости изменения одной переменной относительно другой.

Q2. Что означает H в формуле производной?
А . Значение (f(a+h)-f(a))его наклон линии через точки так ((a,f(a));and;(a+h,f( a+h))), H — так называемая секущая.

Q3. Могут ли калькуляторы решать производные?
А . Да, значение x производной  отображается на экране. Производная отображается калькулятором внизу экрана.