Как найти тригонометрическую формулу комплексного числа

Тригонометрическая форма комплексных чисел

29 ноября 2021

Второй урок по комплексным числам. Если вы только начинаете изучать эту тему (что такое комплексная единица, модуль, сопряжённые), см. первый урок: «Что такое комплексное число».

Сегодня мы узнаем:

  1. Что такое тригонометрическая форма
  2. Умножение и деление комплексных чисел в тригонометрической форме
  3. Формула Муавра (возведение в степень)
  4. Дополнение 1. Геометрический подход, чтобы не путать, где синус, а где косинус
  5. Дополнение 2. Как быстро и надёжно искать аргумент комплексного числа?

Начнём с ключевого определения.

1. Тригонометрическая форма

Определение. Тригонометрическая форма комплексного числа — это выражение вида

[z=left| z right|cdot left( cos text{ }!!varphi!!text{ }+isin text{ }!!varphi!!text{ } right)]

где $left| z right|$ — модуль комплексного числа, $text{ }!!varphi!!text{ }$ — некоторый угол, который называется аргумент комплексного числа (пишут $text{ }!!varphi!!text{ }=arg left( z right)$).

Любое число $z=a+bi$, отличное от нуля, можно записать с тригонометрической форме. Для этого нужно вычислить модуль и аргумент. Например:

Записать в тригонометрической форме число $z=sqrt{3}+i$.

Переписываем исходное число в виде $z=sqrt{3}+1cdot i$ и считаем модуль:

[left| z right|=sqrt{{{left( sqrt{3} right)}^{2}}+{{1}^{2}}}=2]

Выносим модуль за скобки:

[z=sqrt{3}+1cdot i=2cdot left( frac{sqrt{3}}{2}+frac{1}{2}cdot i right)]

Вспоминаем тригонометрию, 10-й класс:

[frac{sqrt{3}}{2}=cos frac{text{ }!!pi!!text{ }}{6};quad frac{1}{2}=sin frac{text{ }!!pi!!text{ }}{6}]

Окончательный ответ:

[z=2cdot left( cos frac{text{ }!!pi!!text{ }}{6}+icdot sin frac{text{ }!!pi!!text{ }}{6} right)]

Понятно, что вместо $frac{text{ }!!pi!!text{ }}{6}$ с тем же успехом можно взять аргумент $frac{13text{ }!!pi!!text{ }}{6}$. Синус и косинус не поменяется. Главное — выбрать такой аргумент, чтобы в тригонометрической форме не осталось никаких минусов. Все минусы должны уйти внутрь синуса и косинуса. Сравните:

Записать в тригонометрической форме число $z=-1-i$.

Правильно:

[z=sqrt{2}cdot left( cos frac{5text{ }!!pi!!text{ }}{4}+isin frac{5text{ }!!pi!!text{ }}{4} right)]

Неправильно:

[begin{align} & z=-sqrt{2}cdot left( cos frac{text{ }!!pi!!text{ }}{4}+isin frac{text{ }!!pi!!text{ }}{4} right) \ & z=sqrt{2}cdot left( -cos frac{text{ }!!pi!!text{ }}{4}-isin frac{text{ }!!pi!!text{ }}{4} right) \ & z=sqrt{2}cdot left( cos frac{3text{ }!!pi!!text{ }}{4}-isin frac{3text{ }!!pi!!text{ }}{4} right) \ end{align}]

2. Умножение и деление комплексных чисел

Комплексные числа, записанные в тригонометрической форме, очень удобно умножать и делить.

Теорема. Пусть даны два комплексных числа:

[begin{align} & {{z}_{1}}=left| {{z}_{1}} right|cdot left( cos alpha +isin alpha right) \ & {{z}_{2}}=left| {{z}_{2}} right|cdot left( cos beta +isin beta right) \ end{align}]

Тогда их произведение равно

[{{z}_{1}}cdot {{z}_{2}}=left| {{z}_{1}} right|cdot left| {{z}_{2}} right|cdot left( cos left( alpha +beta right)+isin left( alpha +beta right) right)]

А если ещё и $left| {{z}_{2}} right|ne 0$, то их частное равно

[frac{{{z}_{1}}}{{{z}_{2}}}=frac{left| {{z}_{1}} right|}{left| {{z}_{2}} right|}cdot left( cos left( alpha -beta right)+isin left( alpha -beta right) right)]

Получается, что при умножении комплексных чисел мы просто умножаем их модули, а аргументы складываем. При делении — делим модули и вычитаем аргументы. И всё!

Найти произведение и частное двух комплексных чисел:

[begin{align} & {{z}_{1}}=2cdot left( cos frac{pi }{3}+isin frac{pi }{3} right) \ & {{z}_{2}}=5cdot left( cos frac{pi }{6}+isin frac{pi }{6} right) \ end{align}]

Считаем произведение:

[begin{align} {{z}_{1}}cdot {{z}_{2}} & =2cdot 5cdot left( cos left( frac{pi }{3}+frac{pi }{6} right)+isin left( frac{pi }{3}+frac{pi }{6} right) right)= \ & =10cdot left( cos frac{pi }{2}+isin frac{pi }{2} right) \ end{align}]

Считаем частное:

[begin{align} frac{{{z}_{1}}}{{{z}_{2}}} & =frac{2}{5}cdot left( cos left( frac{pi }{3}-frac{pi }{6} right)+isin left( frac{pi }{3}-frac{pi }{6} right) right)= \ & =0,4cdot left( cos frac{pi }{6}+isin frac{pi }{6} right) \ end{align}]

По сравнению со стандартной (алгебраической) формой записи комплексных чисел экономия сил и времени налицо.:)

3. Формула Муавра

Пусть дано комплексное число в тригонометрической форме:

[z=left| z right|cdot left( cos text{ }!!varphi!!text{ }+isin text{ }!!varphi!!text{ } right)]

Возведём его в квадрат, умножив на само себя:

[begin{align} {{z}^{2}} & =zcdot z = \ & =left| z right|left| z right|cdot left( cos left( text{ }!!varphi!!text{ + }!!varphi!!text{ } right)+isin left( text{ }!!varphi!!text{ + }!!varphi!!text{ } right) right)= \ & ={{left| z right|}^{2}}cdot left( cos 2text{ }!!varphi!!text{ }+isin 2text{ }!!varphi!!text{ } right) \ end{align}]

Затем возведём в куб, умножив на себя ещё раз:

[{{z}^{3}}={{left| z right|}^{3}}cdot left( cos 3varphi +isin 3varphi right)]

Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.

Формула Муавра. При возведении всякого комплексного числа

[z=left| z right|cdot left( cos varphi +isin varphi right)]

в степень $nin mathbb{N}$ получим

[{{z}^{n}}={{left| z right|}^{n}}cdot left( cos left( nvarphi right)+isin left( nvarphi right) right)]

Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $nin mathbb{R}$, а не только натуральном. Но об этом позже. Сейчас примеры:

Вычислить:

[{{left( sqrt{3}-i right)}^{16}}]

Представим первое число в тригонометрической форме:

[begin{align} sqrt{3}-i & = 2cdot left( frac{sqrt{3}}{2}+icdot left( -frac{1}{2} right) right)= \ & =2cdot left( cos left( -frac{pi }{6} right)+isin left( -frac{pi }{6} right) right) \ end{align}]

По формуле Муавра:

[begin{align} & {{left( 2cdot left( cos frac{11pi }{6}+isin frac{11pi }{6} right) right)}^{16}}= \ & ={{2}^{16}}cdot left( cos frac{88pi }{3}+isin frac{88pi }{3} right)= \ & ={{2}^{16}}cdot left( cos frac{4pi }{3}+isin frac{4pi }{3} right) \ end{align}]

Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.

Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:

Вычислить:

[{{left( left( -frac{sqrt{2}}{2} right)+left( -frac{sqrt{2}}{2} right)i right)}^{2022}}]

Теперь второе число запишем в комплексной форме:

[begin{align} & left( -frac{sqrt{2}}{2} right)+left( -frac{sqrt{2}}{2} right)i= \ & =1cdot left( cos frac{5pi }{4}+isin frac{5pi }{4} right) \ end{align}]

По формуле Муавра:

[begin{align} & {{left( 1cdot left( cos frac{5pi }{4}+isin frac{5pi }{4} right) right)}^{2022}}= \ & ={{1}^{2022}}cdot left( cos frac{5055pi }{2}+isin frac{5055pi }{2} right)= \ & =1cdot left( cos frac{3pi }{2}+isin frac{3pi }{2} right)=-i \ end{align}]

Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.

4. Дополнение 1. Геометрический подход

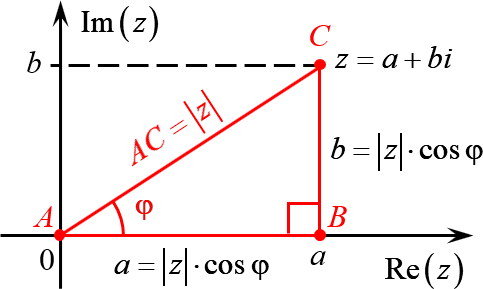
Многие путают местами косинус и синус. Почему комплексная единица стоит именно у синуса? Вспомним, что есть декартова система координат, где точки задаются отступами по осям $x$ и $y$:

А есть полярная система координат, где точки задаются поворотом на угол $varphi $ и расстоянием до центра $r$:

А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:

Комплексное число $z=a+bi$ задаёт на плоскости точку $C$, удалённую от начала координат на расстояние

[AC=sqrt{{{a}^{2}}+{{b}^{2}}}=left| z right|]

Треугольник $ABC$ — прямоугольный. Пусть $angle BAC=varphi $. Тогда:

[begin{align} & AB=ACcdot cos varphi =left| z right|cdot cos varphi \ & BC=ACcdot sin varphi =left| z right|cdot sin varphi \ end{align}]

С другой стороны, длины катетов $AB$ и $BC$ — это те самые отступы $a$ и $b$, с помощью которых мы задаём комплексное число. Поэтому:

[begin{align} a+bi & =left| z right|cos varphi +icdot left| z right|sin varphi = \ & =left| z right|left( cos varphi +isin varphi right) \ end{align}]

Итак, мы перешли от пары $left( a;b right)$ к паре $left( left| z right|;varphi right)$, где $left| z right|$ — модуль комплексного числа, $varphi $ — его аргумент (проще говоря, угол поворота).

Важное замечание. А кто сказал, что такой угол $varphi $ существует? Возьмём число $z=a+bi$ и вынесем модуль за скобку:

[begin{align} z & =a+bi= \ & =sqrt{{{a}^{2}}+{{b}^{2}}}cdot left( frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}}+icdot frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}} right)= \ & =left| z right|cdot left( cos text{ }!!varphi!!text{ }+isin text{ }!!varphi!!text{ } right) \ end{align}]

Осталось подобрать такой угол $varphi $, чтобы выполнялось два равенства:

[begin{align} & frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}}=cos text{ }!!varphi!!text{ } \ & frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}}=sin text{ }!!varphi!!text{ } \ end{align}]

Такой угол обязательно найдётся, поскольку выполняется основное тригонометрическое тождество:

[begin{align} {{sin }^{2}}text{ }!!varphi!!text{ } & +{{cos }^{2}}text{ }!!varphi!!text{ }= \ & ={{left( frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}} right)}^{2}}+{{left( frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}} right)}^{2}}= \ & =frac{{{a}^{2}}}{{{a}^{2}}+{{b}^{2}}}+frac{{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}=frac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}=1 \ end{align}]

На практике основная трудность заключается именно в поиске подходящего аргумента.

5. Дополнение 2. Как найти аргумент?

В учебниках пишут много разной дичи, типа вот этой:

Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.

5.1. Точки на координатных осях

Для начала рассмотрим точки, лежащие осях координат.

Тут всё очевидно:

  • На положительной полуоси абсцисс $varphi =0$ (фиолетовая точка $A$).
  • На отрицательной — $varphi =pi $ (синяя точка $B$).
  • На положительной полуоси ординат $varphi =frac{pi }{2}$ (зелёная точка $B$).
  • На отрицательной — $varphi =frac{3pi }{2}$ (красная точка $C$). Однако ничто не мешает рассмотреть $varphi =-frac{pi }{2}$ — результат будет тем же самым.:)

5.2. Точки с арктангенсом

А если точки не лежат на осях, то в записи комплексного числа $a+bi$ числа $ane 0$ и $bne 0$. Рассмотрим вспомогательный угол

[{{varphi }_{1}}=operatorname{arctg}left| frac{b}{a} right|]

Очевидно, это острый угол:

[0 lt operatorname{arctg}left| frac{a}{b} right| lt frac{pi }{2}]

Зная знаки чисел $a$ и $b$, мы немедленно определим координатную четверть, в которой располагается искомая точка. И нам останется лишь отложить вспомогательный угол ${{varphi }_{1}}$ от горизонтальной оси в эту четверть.

В правой полуплоскости мы откладываем от «нулевого» луча:

Точка $Aleft( 3;4 right)$ удалена от начала координат на расстояние 5:

[begin{align} 3+4i & =5cdot left( cos varphi +isin varphi right) \ varphi & =operatorname{arctg}frac{4}{3} end{align}]

Для точки $Bleft( 6;-6 right)$ арктангенс оказался табличным:

[6-6i=6sqrt{2}cdot left( cos left( -frac{pi }{4} right)+isin left( -frac{pi }{4} right) right)]

В левой полуплоскости откладываем от луча, соответствующего углу $pi $:

Итого для точки $Cleft( -2;5 right)$ имеем:

[begin{align} -2+5i & =sqrt{29}cdot left( cos varphi +isin varphi right) \ varphi & =pi -operatorname{arctg}frac{5}{2} end{align}]

И, наконец, для точки $Dleft( -5;-3 right)$:

[begin{align} -5-3i & =sqrt{34}cdot left( cos varphi +isin varphi right) \ varphi & =pi +operatorname{arctg}frac{3}{5} end{align}]

Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.

А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)

Смотрите также:

  1. Как извлекать корни из комплексных чисел
  2. Комплексные числа — первый и самый важный уок
  3. Тест к параграфу «Что такое логарифм» (легкий)
  4. Тест к уроку «Площади многоугольников без координатной сетки» (средний)
  5. Четырехугольная пирамида: как найти координаты вершин
  6. Задача C1: тригонометрические уравнения и формула двойного угла
Источник

Комплексные числа в тригонометрической
и показательной формах

Тригонометрическая форма комплексного числа

Каждому комплексному числу z=x+iy геометрически соответствует точка M(x,y) на плоскости Oxy. Но положение точки на плоскости, кроме декартовых координат (x,y), можно зафиксировать другой парой — ее полярных координат (r,varphi) в полярной системе (рис. 1.3,a).

Величина r является неотрицательной и для данной точки определяется единственным образом, а угол varphi может принимать бесчисленное множество значений (при этом zne0): если точке соответствует некоторое значение varphi_0, то ей также соответствуют значения varphi=varphi_0+2kpi,~ k=0,pm1,pm2,ldots. Например, если для точки z=-1-i (см. рис. 1.1) выбрать varphi_0=frac{5pi}{4}, то ей соответствует любое varphi=frac{5pi}{4}+2kpi,~ k=0,pm1,ldots, в частности varphi=-frac{3pi}{4} при k=-1. Если же выбрать varphi_0=-frac{3pi}{4}, то varphi=-frac{3pi}{4}+2kpi,~ k=0,pm1,ldots, а при k=1 получаем varphi=frac{5pi}{4}.

Положение точки на плоскости в полярных координатах

Используя связь декартовых и полярных координат точки Mcolon begin{cases} x=rcosvarphi,\ y=rsinvarphiend{cases} (рис. 1.3,б), из алгебраической формы записи комплексного числа z=x+iy получаем тригонометрическую форму:

z=r bigl(cosvarphi+isinvarphibigr).

(1.3)

Показательная форма комплексного числа

Если обозначить комплексное число z, у которого operatorname{Re}z= cosvarphi, а operatorname{Im}z=sinvarphi, через e^{i,varphi}, то есть cosvarphi+isinvarphi=e^{i,varphi}, то из (1.3) получим показательную форму записи комплексного числа:

z=r,e^{i,varphi}.

(1.4)

Равенство e^{i,varphi}= cosvarphi+isinvarphi называется формулой Эйлера.

Заметим, что геометрически задание комплексного числа z=(r,varphi) равносильно заданию вектора overrightarrow{OM}, длина которого равна r, то есть bigl|overrightarrow{OM}bigr|=r, а направление — под углом varphi к оси Ox (рис. 1.3,б).

Модуль комплексного числа

Число r — длина радиуса-вектора точки M(x,y) называется модулем комплексного числа z=x+iy. Обозначение: |z|=r.

Из рис. 1.3,б получаем формулу для нахождения модуля числа, заданного и алгебраической форме z=x+iycolon

|z|=sqrt{x^2+y^2},.

(1.5)

Геометрический смысл модуля комплексного числа

Очевидно, что |z|geqslant0 и |z|=0 только для числа z=0~(x=0,,y=0).

С помощью правила вычитания запишем модуль числа z=z_1-z_2, где z_1=x_1+iy_1 и z_2=x_2+iy_2,colon

bigl|z_1-z_2bigr|= sqrt{(x_1-x_2)^2+(y_1-y_2)^2},.

А это, как известно, есть формула для расстояния между точками M_1(x_1,y_1) и M_2(x_2,y_2).

Таким образом, число |z_1-z_2| есть расстояние между точками z_1 и z_2 на комплексной плоскости.

Пример 1.13. Найти модули комплексных чисел:

bold{1)}~z_1=2,~z_2=-2+sqrt{3},;qquad bold{2)}~z_3=-2i,~ z_4=(2-sqrt{3})i,;qquad bold{3)}~ z_5=-1+2i,.

Решение

Аргумент комплексного числа

Полярный угол varphi точки M(x,y) называется аргументом комплексного числа z=x+iy. Обозначение: varphi=arg z.

В дальнейшем, если нет специальных оговорок, под arg z будем понимать значение varphi, удовлетворяющее условию -pi<varphileqslantpi. Так, для точки z=-1-i (см. рис. 1.1) arg z=-frac{3pi}{4}.

Формулу для нахождения аргумента комплексного числа z=x+iy, заданного в алгебраической форме, получаем, используя связь декартовых и полярных координат точки M(x,y) (см. рис. 1.3,б). Для точек, не лежащих на мнимой оси, т.е. для z, у которых xne0, получаем operatorname{tg}varphi= frac{y}{x}; для точек мнимой положительной полуоси, т.е. для z, у которых x=0,~ y>0, имеем varphi=frac{pi}{2}; для точек мнимой отрицательной полуоси, т.е. для z, у которых x=0,~ y<0, соответственно varphi=-frac{pi}{2}.

Аргумент числа z=0 — величина неопределенная.

Нахождение аргумента при xne0 сводится к решению тригонометрического уравнения operatorname{tg}varphi= frac{y}{x}. При y=0, т.е. когда z=x — число действительное, имеем varphi=0 при x>0 и varphi=pi при x<0. При yne0 решение уравнения зависит от четверти плоскости Oxy. Четверть, в которое расположена точка z, определяется по знакам operatorname{Re}z и operatorname{Im}z. В результате получаем:

Аргумент комплексного числа

arg z= begin{cases}operatorname{arctg}dfrac{y}{x},& x>0;\ pi+operatorname{arctg}dfrac{y}{x},& x<0,ygeqslant0;\ -pi+operatorname{arctg}dfrac{y}{x},& x<0,y<0;\ dfrac{pi}{2},& x=0,~y>0;\ -dfrac{pi}{2},& x=0,~y<0.end{cases}

(1.6)

При решении примеров удобно пользоваться схемой, которая изображена на рис. 1.5.

Пример 1.14. Найти аргументы чисел из примера 1.13.

Решение

Пример 1.15. Найти модуль и аргумент числа z=2-i.

Решение. Находим |z|=sqrt{2^2+(-1)^2}= sqrt{5}. Так как operatorname{Re}z=2>0,~ operatorname{Im}z=-1<0, т.е. точка расположена в четвертой четверти, то из равенства operatorname{tg}varphi=-frac{1}{2} получаем varphi= operatorname{arctg}!left(-frac{1}{2}right) (рис. 1.5).

Главное значение аргумента комплексного числа

Аргумент комплексного числа определяется неоднозначно. Это следует из неоднозначности задания величины угла varphi для данной точки, а также из тригонометрической формы записи комплексного числа и свойства периодичности функций sinvarphi и cosvarphi.

Всякий угол, отличающийся от arg z на слагаемое, кратное 2pi, обозначается operatorname{Arg}z и записывается равенством:

operatorname{Arg}z=arg z+2kpi,quad k=0,pm1,pm2,ldots,

(1.7)

где arg z — главное значение аргумента, -pi<arg zleqslantpi.

Комплексные числа с нулевыми вещественными и мнимыми частями

Пример 1.16. Записать arg z и operatorname{Arg}z для чисел z_1=1,~ z_2=-1,~ z_3=i,~ z_4=-i.

Решение. Числа z_1 и z_2 — действительные, расположены на действительной оси (рис. 1.6), поэтому

arg z_1=0,~~ operatorname{Arg}z_1=2kpi;qquad arg z_2=pi,~~ operatorname{Arg}z_2= pi+2kpi,quad k=0,pm1,pm2,ldots;

числа z_3 и z_4 — чисто мнимые, расположены на мнимой оси (рис. 1.6), поэтому

arg z_3=frac{pi}{2},~~ operatorname{Arg}z_3=frac{pi}{2}+2kpi;qquad arg z_4=-frac{pi}{2},~~ operatorname{Arg}z_4= -frac{pi}{2}+2kpi,quad k=0,pm1, pm2,ldots

Пример 1.17. Записать комплексные числа из примера 1.16:

а) в тригонометрической форме;

б) в показательной форме.

Решение

Модули всех чисел, очевидно, равны 1. Поэтому, используя решение предыдущего примера и формулы (1.3) и (1.4), получаем:

а) 1=cos2kpi+ isin2kpi;~~ -1=cos(pi+2kpi)+ isin(pi+2kpi);~~ k=0,pm1,pm2,ldots

i=cos!left(frac{pi}{2}+2kpiright)+ isin!left(frac{pi}{2}+2kpiright);quad -i=cos!left(-frac{pi}{2}+2kpiright)+ isin!left(-frac{pi}{2}+2kpiright);

б) 1=e^{2kpi i};~~ -1=e^{(pi+2kpi)i};~~ i=e^{left(frac{pi}{2}+2kpiright)i};~~ -i=e^{left(-frac{pi}{2}+2kpiright)i},~~ k=0,pm1,pm2,ldots.

Пример 1.18. Записать в тригонометрической форме числа z_1=-1-i,~ z_2=cosfrac{pi}{5}-isinfrac{pi}{5},~ z_3= ileft(cosfrac{pi}{5}-isinfrac{pi}{5}right).

Решение

Числа z_1 и z_2 записаны в алгебраической форме (заметим, что заданная запись числа z_2 не является тригонометрической формой записи (сравните с (1.3)). Находим модули чисел по формуле (1.5):

|z_1|= sqrt{(-1)^2+(-1)^2}= sqrt{2},,qquad |z_2|=sqrt{cos^2 frac{pi}{5}+ left(-sin frac{pi}{5}right)^2}=1.

Далее находим аргументы. Для числа z_1 имеем operatorname{tg}varphi=1 и, так как operatorname{Re}z_1<0,~ operatorname{Im}z_1<0 (точка расположена в третьей четверти), получаем arg z_1=-pi+frac{pi}{4}=-frac{3pi}{4} (см. рис. 1.5). Для числа z_2 имеем operatorname{tg}varphi=-operatorname{tg}frac{pi}{5}, или operatorname{tg}varphi= operatorname{tg}left(-frac{pi}{5}right), и, так как operatorname{Re}z_2>0,~ operatorname{Im}z_2<0 (точка расположена в четвертой четверти (см. рис. 1.5)), получаем arg z_2=-frac{pi}{5}.

Записываем числа z_1 и z_2 в тригонометрической форме

begin{gathered}z_1= sqrt{2} left[cosleft(-frac{3pi}{4}+2kpiright)+ isinleft(-frac{3pi}{4}+2kpiright)right];\[5pt] z_2= cosleft(-frac{pi}{5}+2kpiright)+ isinleft(-frac{pi}{5}+ 2kpiright)!,quad k=0,pm1,pm2,ldots end{gathered}

Заметим, что для числа z_2 решение можно найти иначе, а именно используя свойства тригонометрических функций: cosalpha=cos(-alpha),~ -sinalpha=sin(-alpha).

Число z_3 является произведением двух чисел. Выполнив умножение, получим алгебраическую форму записи (найдем operatorname{Re}z_3 и operatorname{Im}z_3): z_3=sin frac{pi}{5}+ icos frac{pi}{5}. Здесь, как и для числа z_2, при решении удобно использовать преобразования тригонометрических выражений, а именно sinfrac{pi}{5}= cos!left(frac{pi}{2}-frac{pi}{5}right)!,~ cosfrac{pi}{5}= sin!left(frac{pi}{2}-frac{pi}{5}right).

Рассуждая, как выше, найдем |z_3|=1,~ arg z_3=frac{pi}{2}-frac{pi}{5}= frac{3pi}{10}. Для числа z_3=sin frac{pi}{5}+ icos frac{pi}{5}, записанного в алгебраической форме, получаем тригонометрическую форму:

z_3= cos!left(frac{3pi}{10}+2kpiright)+ isin!left(frac{3pi}{10}+2kpiright)!,quad k=0,pm1,pm2,ldots

Равенство комплексных чисел в тригонометрической форме

Условия равенства комплексных чисел получаем, используя геометрический смысл модуля и аргумента комплексного числа, заданного в тригонометрической форме. Так, для чисел z_1=r_1(cosvarphi_1+ isinvarphi_1), z_2=r_2(cosvarphi_2+ isinvarphi_2), из условия z_1=z_2. очевидно, следует:

r_1=r_2;qquad varphi_1-varphi_2=2kpi,quad k=0,pm1,pm2,ldots

или

|z_1|=|z_2|,quad operatorname{Arg}z_1-operatorname{Arg}z_2= 2kpi,quad k=0,pm1,pm2,ldots

(1.8)

Аргументы равных комплексных чисел либо равны (в частности равны главные значения), либо отличаются на слагаемое, кратное 2pi.

Для пары сопряженных комплексных чисел z и overline{z} справедливы следующие равенства:

|overline{z}|= |z|,qquad argoverline{z}=-arg z,.

(1.9)

Умножение комплексных чисел в тригонометрической форме

Зададим два комплексных числа в тригонометрической форме z_1=r_1(cosvarphi_1+ isinvarphi_1) и z_2=r_2(cosvarphi_2+isinvarphi_2) и перемножим их по правилу умножения двучленов:

begin{aligned}z_1cdot z_2&= r_1cdot r_2cdot (cosvarphi_1+ isinvarphi_1)cdot (cosvarphi_2+isinvarphi_2)=\ &= r_1cdot r_2 bigl(cosvarphi_1cosvarphi_2- sinvarphi_1 sinvarphi_2+ i(cosvarphi_1 sinvarphi_2+ sinvarphi_1 cosvarphi_2)bigr) end{aligned}

или

z_1cdot z_2= r_1cdot r_2cdot bigl(cos(varphi_1+varphi_2)+ isin(varphi_1+ varphi_2)bigr).

Получили новое число z, записанное в тригонометрической форме: z=r(cosvarphi+ isinvarphi), для которого r=r_1cdot r_2,~ varphi= varphi_1+ varphi_2.

Правило умножения. При умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:

|z_1cdot z_2|= |z_1|cdot |z_2|,qquad operatorname{Arg}(z_1cdot z_2)= arg z_1+arg z_2.

(1.10)

В результате умножения чисел может получиться аргумент произведения, не являющийся главным значением.

Пример 1.19. Найти модули и аргументы чисел:

bold{1)}~ z=-2i left(cosfrac{4pi}{7}- isinfrac{4pi}{7}right)!;qquad bold{2)}~ z=(1+i)(sqrt{3}-i).

Решение

Каждое из заданных чисел записано в виде произведения. Найдем модули и аргументы сомножителей и воспользуемся правилом (1.10) умножения чисел, заданных в тригонометрической форме:

bold{1)}quad z=z_1cdot z_2,quad z_1=-2i,quad z_2= cosfrac{4pi}{7}- isinfrac{4pi}{7}= cos!left(-frac{4pi}{7}right)+ isin!left(-frac{4pi}{7}right),.

Для чисел z_1 и z_2 находим модули и аргументы: |z_1|=2,~ arg z_1=-frac{pi}{2};~ |z_2|=1,~ arg z_2=-frac{4pi}{7}. Используя формулы (1.10), получаем

|z|=|z_1|cdot|z_2|=2,quad operatorname{Arg}z= arg z_1+arg z_2= -frac{pi}{2}-frac{4pi}{7};quad arg z= 2pi- frac{15pi}{14}= frac{13pi}{14}

б) z=z_1cdot z_2,~ z_1=1+i,~ z_2=sqrt{3}-i. Для числа z_1 имеем: |z_1|=sqrt{2},~ arg z_1=frac{pi}{4}; для числа z_2colon, |z_2|=2,~ operatorname{tg}varphi_2=-frac{1}{sqrt{3}}, и так как operatorname{Re}z_2>0,~ operatorname{Im}z_2<0 (точка расположена в четвертой четверти), то arg z_2=-frac{pi}{6}. Используя формулы (1.10), получаем |z|=2sqrt{2},~ arg z=frac{pi}{4}-frac{pi}{6}=frac{pi}{12}.

Заметим, что для решения этой задачи можно раскрыть скобки, записать каждое число в алгебраической форме, а затем найти |z| и arg z, используя формулы (1.5), (1.6).

Деление комплексных чисел в тригонометрической форме

Рассмотрим частное комплексных чисел frac{z_1}{z_2}, заданных в тригонометрической форме. Из определения частного z=frac{z_1}{z_2} имеем z_1=zcdot z_2 и, применяя к произведению правило умножения (формулы (1.10)), получаем r=frac{r_1}{r_2},~ varphi=varphi_1-varphi_2.

Правило деления. Модуль частного, полученного в результате деления чисел, заданных в тригонометрической форме, равен частному от деления модуля числителя на модуль знаменателя, а аргумент частного равен разности аргументов делимого и делителя:

left|frac{z_1}{z_2}right|= frac{|z_1|}{|z_2|},qquad operatorname{Arg}frac{z_1}{z_2}= arg z_1-arg z_2.

(1.11)

В результате деления чисел по формуле (1.11) может получиться аргумент честного, не являющийся главным значением.

Пример 1.20. Записать в тригонометрической форме комплексное число frac{1+i}{sqrt{3}-i}.

Решение. Обозначим z=frac{z_1}{z_2},~ z_1=1+i,~ z_2=sqrt{3}-i. Для чисел z_1 и z_2 находим модули и аргументы: |z_1|=sqrt{2},~ arg z_1=frac{pi}{4}; |z_2|=2,~ arg z_2=-frac{pi}{6} (см. пример 1.19). По формуле (1.11) получаем |z|=frac{|z_1|}{|z_2|}=frac{sqrt{2}}{2},~ arg z=arg z_1-arg z_2=frac{pi}{4}-left(-frac{pi}{6}right)= frac{5pi}{12} и

frac{1+i}{sqrt{3}-i}= frac{sqrt{2}}{2}left(cosleft(frac{5pi}{12}+2kpiright)+ isinleft(frac{5pi}{12}+2kpiright)right)!,~ k=0,pm1,pm2,ldots

Возведение в степень комплексного числа в тригонометрической форме

Из определения степени z^n и правила умножения чисел, записанных в тригонометрической форме (формула (1.10)), получаем

|z^n|=r^n,quad operatorname{Arg}z^n=nvarphi, где z=r(cosvarphi+ isinvarphi).

Правило возведения в степень. При возведении в степень комплексного числа в эту степень возводится модуль числа, а аргумент умножается на показатель степени:

|z^n|= |z|^n,qquad operatorname{Arg}z^n= narg z,.

(1.12)

Записывая число z^n в тригонометрической форме z^n= r^n(cos nvarphi+ isin nvarphi), получаем формулу возведения в степень:

bigl[r(cosvarphi+ isinvarphi)bigr]^n= r^n(cos nvarphi+ isin nvarphi).

(1.13)

При r=1 это равенство принимает вид и называется формула Муавра

(cosvarphi+ isinvarphi)^n= cos nvarphi+ isin nvarphi,.

(1.14)

Пример 1.21. Найти модуль и аргумент комплексного числа (1+i)^5.

Решение. Обозначим z=z_1^5,~ z_1=1+i. Находим модуль и аргумент числа z_1colon, |z_1|=sqrt{2},~ arg z_1=frac{pi}{4}. Поэтому |z|= (sqrt{2})^5 и operatorname{Arg}z=5arg z_1=frac{5pi}{4}. Так как по определению для главного значения аргумента выполняется условие -pi<arg zleqslantpi, то arg z= frac{5pi}{4}-2pi=-frac{3pi}{4}.

Пример 1.22. Записать в тригонометрической форме число (1+i)^5(sqrt{3}-i)^7.

Решение

Пример 1.23. Используя формулу Муавра, найти выражения для cos3varphi и sin3varphi через тригонометрические функции угла varphi.

Решение

Из формулы (1.14) при n=3 имеем (cosvarphi+ isinvarphi)^3= cos3varphi+isin3varphi. Возведем левую часть в степень, учитывая, что i^3=-i (см. пример 1.8):

begin{aligned}cos^3varphi+ i3cos^2varphisinvarphi- 3cosvarphi sin^2varphi+ i^3sin^3varphi&= cos3varphi+ isin3varphi,\ (cos^3varphi-3cosvarphisin^2varphi)+ i(3cos^2varphisinvarphi-sin^3varphi)&= cos3varphi+ isin3varphi.end{aligned}

Используя условие равенства комплексных чисел, получаем:

cos3varphi= cos^3varphi- 3cosvarphisin^2varphi,qquad sin3varphi= 3cos^2varphi sinvarphi- sin^3varphi.

Извлечение корня из комплексного числа в тригонометрической форме

Рассмотрим задачу извлечения корня из комплексного числа, заданного в показательной или тригонометрической форме z=r,e^{ivarphi}, или z=r(cosvarphi+ isinvarphi). Искомое число w=sqrt[LARGE{n}]{z} также запишем в показательной форме: w=rho,e^{ivarphi},~ rho=|w|,~ theta=arg w. Используя определение операции извлечения корня z=w^n и условия (1.8), получаем соотношения

rho^n=r,qquad ncdottheta= varphi+2kpi,quad k=0,pm1,pm2,ldots

или

rho= sqrt[LARGE{n}]{r},quad theta= frac{varphi+2kpi}{n},quad k=0,pm1,pm2,ldots

(1.15)

Правило извлечения корня. Чтобы извлечь корень из комплексного числа, нужно извлечь корень (арифметический) той же степени из модуля данного числа, а аргумент (operatorname{Arg}z) разделить на показатель корня:

bigl|sqrt[LARGE{n}]{z}bigr|= sqrt[LARGE{n}]{|z|},qquad operatorname{Arg}sqrt[LARGE{n}]{z}= frac{operatorname{Arg}z}{n},.

(1.16)

Теперь можно записать число w=sqrt[LARGE{n}]{z} в показательной форме:

sqrt[LARGE{n}]{z}= sqrt[LARGE{n}]{|z|}cdot exp frac{i operatorname{Arg}z}{n},.

Если записать это соотношение в тригонометрической форме, то, учитывая периодичность тригонометрических функций, нетрудно убедиться, что выражение sqrt[LARGE{n}]{z} принимает только n различных значений. Для их записи достаточно в формуле (1.15) взять n последовательных значений k, например k=0,1,2,ldots,n-1. В результате получаем формулу извлечения корня из комплексного числа в тригонометрической форме, где r=|z|,~ varphi=arg z:

sqrt[LARGE{n}]{z}= sqrt[LARGE{n}]{r} left(cos frac{varphi+2kpi}{n}+ isin frac{varphi+2kpi}{n}right)!,quad 0,1,2,ldots,n-1.

(1.17)

Значения корня комплексного числа

Замечания 1.1

1. Рассмотренная задача извлечения корня степени n из комплексного числа равносильна решению уравнения вида z^n-a=0, где, очевидно, z=sqrt[LARGE{n}]{a}.

Для решения уравнения нужно найти n значений sqrt[LARGE{n}]{a}, а для этого необходимо найти r=|a|,~ varphi=arg a и использовать формулу извлечения корня.

2. Исследование формулы (1.17) показывает, что все комплексные числа w_k,~ k=1,2,ldots,n (значения sqrt[LARGE{n}]{z}) имеют равные модули, т.е. геометрически расположены на окружности радиуса R=sqrt[LARGE{n}]{r},~ r=|z|. Аргументы двух последовательных чисел отличаются на frac{2pi}{n}, так как arg w_{k+1}-arg w_k= frac{2pi}{n}, т.е. каждое последующее значение w_{k+1} может быть получено из предыдущего w_k поворотом радиуса-вектора точки w_k на frac{2pi}{n}.В этом заключается геометрический смысл формулы (1.17), что можно сформулировать следующим образом.

Точки, соответствующие значениям sqrt[LARGE{n}]{z}, расположены в вершинах правильного n-угольника, вписанного в окружность с центром в начале координат, радиус которой R= sqrt[LARGE{n}]{|z|}, причем аргумент одного из значений w_k равен frac{arg z}{n}= frac{varphi}{n} (рис. 1.7).

Алгоритм решения комплексных уравнений вида z^n-a=0

1. Найти модуль и аргумент числа acolon, r=|a|,~ varphi=arg a.
2. Записать формулу (1.17) при заданном значении ncolon, sqrt[LARGE{n}]{a}= sqrt[LARGE{n}]{r} left(cos frac{varphi+2kpi}{n}+ isin frac{varphi+2kpi}{n}right).
3. Выписать значения корней уравнения z_k, придавая значения k=0,1,2,ldots,n-1.

Пример 1.24. Решить уравнения: a) z^6-1=0; б) z^3-i=0.

Решение

Задача равносильна задаче нахождения всех значений корня из комплексного числа. Решаем в каждом случае по алгоритму.

а) Найдем z=sqrt[LARGE{6}]{1}.
1. Определим модуль и аргумент числа 1colon, r=1,~ varphi=0.
2. При полученных значениях r и varphi записываем формулу (1.17):

z= sqrt[LARGE{6}]{1}= sqrt[LARGE{6}]{1} left(cosfrac{2kpi}{6}+ isinfrac{2kpi}{6}right)!,qquad k=0,1,2,3,4,5.

Заметим, что справа стоит sqrt[LARGE{6}]{1} — арифметический корень, его единственное значение равно 1.

3. Придавая k последовательно значения от 0 до 5, выписываем решения уравнения:

begin{array}{ll}z_1= cos0+isin0=1,&qquad z_2=cos dfrac{pi}{3}+isindfrac{pi}{3}= dfrac{1}{2}+ i,dfrac{sqrt{3}}{2},\[7pt] z_3= cosdfrac{2pi}{3}+ isindfrac{2pi}{3}= -dfrac{1}{2}+ i,dfrac{sqrt{3}}{2},&qquad z_4=cospi+isinpi=-1,\[10pt] z_5= cosdfrac{4pi}{3}+ isindfrac{4pi}{3}= -dfrac{1}{2}-i,dfrac{sqrt{3}}{2},&qquad z_6= cosdfrac{5pi}{3}+ isindfrac{5pi}{3}= dfrac{1}{2}-i,dfrac{sqrt{3}}{2}.end{array}

Геометрически соответствующие точки расположены в вершинах правильного шестиугольника, вписанного в окружность радиуса R=1, одна из точек (соответствует k=0) z_1=1. Строим шестиугольник (рис. 1.8,в). Отметим свойства корней этого уравнения с действительными коэффициентами — его комплексные корни являются попарно сопряженными: z_6= overline{z}_2,~ z_5= overline{z}_3,~ z_1 и z_4 — действительные числа.

б) Найдем z=sqrt[LARGE{3}]{i}.
1. Определим модуль и аргумент числа rcolon, r=|i|=1,~ varphi=arg i=frac{pi}{2}.
2. По формуле (1.17) имеем

sqrt[LARGE{3}]{i}= 1cdot left(cosfrac{frac{pi}{2}+2kpi}{3}+ isin frac{frac{pi}{2}+2kpi}{3}right)= cos!left(frac{pi}{6}+ frac{2}{3}kpiright)+ isin!left(frac{pi}{6}+ frac{2}{3}kpiright)!,quad k=0,1,2.

3. Выписываем корни z_1,,z_2,,z_3colon, z_1= frac{sqrt{3}}{2}+i frac{1}{2},~ z_2= -frac{sqrt{3}}{2}+i frac{1}{2},~ z_3=-i.

Геометрический смысл комплексных корней

Для геометрического представления решения уравнения достаточно изобразить одно значение, например z_1=cosfrac{pi}{6}+ isinfrac{pi}{6} (при k=0) — это точка окружности |z|=1, лежащая на луче varphi=frac{pi}{6}. После этого строим правильный треугольник, вписанный в окружность |z|=1 (рис. 1.8,б).

Пример 1.25. Найти корень уравнения z^4-1+i=0, для которого operatorname{Re}z<0,~ operatorname{Im}z>0.

Решение

Геометрическая интерпретация корней комплексного уравнения

Задача равносильна задаче нахождения z=sqrt[LARGE{4}]{1-i} при условие operatorname{Re}z<0,~ operatorname{Im}z>0.

1. Находим модуль и аргумент числа 1-icolon, r=|1-i|=sqrt{2},~ varphi=arg(1-i)=-frac{pi}{4}.

2. По формуле (1.17) имеем: z_{k+1}= sqrt[LARGE{4}]{1-i}= sqrt[LARGE{8}]{2}e^{left(-frac{pi}{16}+frac{2kpi}{4}right) i},~ k=0,1,2,3.

3. Для нахождения искомого решения нет необходимости выписывать все значения корня. Нужно выбрать значение k~(k=0,1,2,3), при котором выполняется условие frac{pi}{2}< arg zleqslantpi (соответствующая точка — точка второй четверти). Удобно при этом использовать чертеж (рис. 1.9).

Условию поставленной задачи удовлетворяет корень z_3 (при k=2): z_3= sqrt[LARGE{8}]{2}e^{left(pi-frac{pi}{16}right)i}= sqrt[LARGE{8}]{2}e^{frac{15pi}{16},i}.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Алгебра и начала математического анализа, 11 класс

Урок №40. Тригонометрическая форма комплексного числа.

Перечень вопросов, рассматриваемых в теме

1) понятие модуля комплексного числа;

2) понятие тригонометрической формы комплексного числа;

3) перевод комплексного числа в тригонометрическую форму.

Глоссарий по теме

Модулем комплексного числа z называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.

Аргументом комплексного числа z называется угол φ между положительной полуосью действительной оси Re z и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: z=0.

Для этого рассмотрим формулы для нахождения в зависимости от а и b.

1.

2.

3.

4.

5.

6.

7.

8.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., Учебник комплект под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е.Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2017. 

Теоретический материал для самостоятельного изучения

Комплексные числа имеют три формы, две из них мы уже изучили — алгебраическую и геометрическую.

Но в электротехнике, электрооборудовании, электронике, автоматике и других дисциплинах комплексное число записывается в тригонометрической форме.

Например: при работе трансформатора идет нагрев обмоток — активное сопротивление R, катушка выделяет электромагнитные волны — реактивное сопротивление. Сняли замеры трансформатора

2 + 7 i ,

где 2 Ом — активное сопротивление,

7 Ом — реактивное сопротивление

Тригонометрическая форма комплексного числа r(cos φ+sin φ).

На любом трансформаторе стоит маркировка cos φ=. Это энергетический показатель ГОС стандартов. Он показывает эффективность работы, КПД, cos φ- активный показатель мощности, тока, напряжения. sin φ- реактивный показатель.

Любое комплексное число (кроме нуля) z=a+bi  можно записать в тригонометрической форме: z=|z|∙(cosφ+isinφ), где |z| – это модуль комплексного числа, а φ – аргумент комплексного числа.

Изобразим на комплексной плоскости число z=a+bi  . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что a>0, b>0 :

Модулем комплексного числа z называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.

Модуль комплексного числа z стандартно обозначают: |z| или r.

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедлива для любых значений a и b.

Аргументом комплексного числа z называется угол φ между положительной полуосью действительной оси Re z и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: z=0.

Аргумент комплексного числа z стандартно обозначают: φ или arg z.

Из геометрических соображений получается следующая формула для нахождения аргумента:

Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой.

Для этого рассмотрим формулы для нахождения в зависимости от а и b.

1.

2.

3.

4.

5.

6.

7.

8.

Пример Представим в тригонометрической форме число z= -2+4i. Найдем его модуль и аргумент.

Поскольку a<0, b>0, то   – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение arctg 2, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:

— число z в тригонометрической форме.

Разбор решения заданий тренировочного модуля

№1. Тип задания: единичный выбор

Представить в тригонометрической форме число z= -1+2i.

Найдем его модуль и аргумент.

Поскольку a<0, b>0, то – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение arctg 2, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:

— число z в тригонометрической форме.

Значит, верный ответ 1

№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Найдите куб суммы z= (3+4i)3=_____________

Решение:

Возведем данное выражение в третью степень

Упрощаем полученное выражение, учитывая, что i2=-1

Ответ:

Источник

Тригонометрическая и показательная форма комплексного числа

Тригонометрической формой комплексного числа $z = x+iy$ называется выражение вида $$z = |z|(cos varphi + isin varphi),$$где $|z|$ — модуль и $varphi$ — аргумент комплексного числа.

Показательной формой комплексного числа $z = x+iy$ называется выражение вида $$z = |z|e^{varphi i},$$ где $|z|$ — модуль и $varphi$ — аргумент.

Пример 1
Записать в тригонометрической и показательной форме комплексное число $z = 2-i$.
Решение

В условии задачи дано комплексное число в алгебраической форме. Чтобы его перевести в тригонометрическую форму нужно найти модуль и аргумент. 

Вычисляем модуль по формуле корень квадратный из суммы квадратов действительной и мнимой части комплексного числа $$|z| = sqrt{x^2 + y^2} = sqrt{2^2 + (-1)^2} = sqrt{5}.$$

Для нахождения аргумента нужно учитывать, что в данном комплексном числе $x = 2 > 0$, поэтому формула $varphi = arctg frac{y}{x}$. Более подробнее о формуле можно прочитать в статье аргумент комплексного числа. $$varphi = arctg frac{y}{x} = arctg frac{-1}{2} = -frac{pi}{6}$$

Теперь можно записать тригонометрическую форму $$z = sqrt{5}(cos (-frac{pi}{6})+isin(-frac{pi}{6})),$$и показательную $$z = sqrt{5}e^{frac{pi}{6}i}.$$
Ответ
$$z = sqrt{5}(cos (-frac{pi}{6})+isin(-frac{pi}{6}))$$ $$z = sqrt{5}e^{frac{pi}{6}i}$$
Пример 2
Перевести комплексное число в тригонометрическую и показательную форму $z = -2 + sqrt{3}i$.
Решение

Находим модуль $$|z| = sqrt{(-2)^2 + (sqrt{3})^2} = sqrt{4 + 3} = sqrt{7}.$$

Вычисляем аргумент по формуле $varphi = pi + arctgfrac{y}{x}$, так как $x<0$ и $y>0$ $$varphi = pi + arctg frac{sqrt{3}}{-2} = pi — frac{pi}{4} = frac{3pi}{4}$$

И наконец, записываем тригонометрическую форму на основании полученных значений $$z = sqrt{7} (cos frac{3pi}{4} + isin frac{3pi}{4}),$$и теперь показательную форму $$z = sqrt{7}e^{ frac{3pi}{4}i}.$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$z = sqrt{7} (cos frac{3pi}{4} + isin frac{3pi}{4})$$ $$z = sqrt{7}e^{ frac{3pi}{4}i}$$
Источник

Содержание:

  • Алгебраическая форма комплексного числа
  • Тригонометрическая форма комплексного числа
  • Показательная форма комплексного числа

Алгебраическая форма комплексного числа

Запись комплексного числа $z$ в виде
$z=a+b i$, где
$a$ и
$b$ — действительные числа, называется
алгебраической формой комплексного числа.

Например. $z=1-i$

Подробнее о данной форме записи комплексных чисел по ссылке →

Тригонометрическая форма комплексного числа

Если $|z|=sqrt{a^{2}+b^{2}}$ —
модуль комплексного числа
$z=a+b i$, а
$phi$ — его аргумент, то тригонометрической формой
комплексного числа $z$ называется выражение

$z=|z|(cos phi+i sin phi)$

Пример

Задание. Записать число $z=1-i$ в тригонометрической форме.

Решение. Для получения тригонометрической формы заданного комплексного числа найдем вначале его модуль и аргумент.
Так как $a=operatorname{Re} z=1$,
$b=operatorname{Im} z=-1$, то

$|z|=sqrt{a^{2}+b^{2}}=sqrt{1^{2}+(-1)^{2}}=sqrt{2}$

$arg z=operatorname{arctg} frac{b}{a}=operatorname{arctg} frac{1}{-1}=operatorname{arctg}(-1)=-operatorname{arctg} 1=-frac{pi}{4}$

Тогда тригонометрическая форма заданного числа $z=1-i$
имеет вид:

$z=1-i=sqrt{2}left(cos left(-frac{pi}{4}right)+i sin left(-frac{pi}{4}right)right)=sqrt{2}left(cos frac{pi}{4}-i sin frac{pi}{4}right)$

Ответ. $z=sqrt{2}left(cos frac{pi}{4}-i sin frac{pi}{4}right)$

Подробнее о данной форме записи комплексных чисел по ссылке →

Показательная форма комплексного числа

Показательной формой комплексного числа $z=a+b i$
называется выражение

$z=|z| e^{i phi}$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Комплексное число $z=2 i$ записать в показательной форме.

Решение. Найдем модуль и аргумент заданного комплексного числа:

$|z|=sqrt{a^{2}+b^{2}}=sqrt{0^{2}+2^{2}}=sqrt{4}=2$

$arg z=operatorname{arctg} frac{b}{a}=operatorname{arctg} frac{2}{0}=operatorname{arctg} infty=frac{pi}{2}$

А тогда имеем, что

$z=2 e^{i frac{pi}{2}}$

Ответ. $z=2 e^{i frac{pi}{2}}$

Заметим, что показательную и тригонометрическую формы комплексного числа связывает
формула Эйлера:

$e^{i phi}=cos phi+i sin phi$

Читать дальше: алгебраическая форма записи комплексного числа.

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти угловую скорость по графику
  • Как можно найти работу в омске
  • Как найти мою избирательную комиссию
  • Как найти значение выражения с корнями примеры
  • Как правильно составить конспект занятия в подготовительной группе