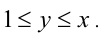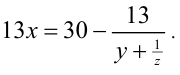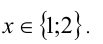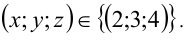Как найти тройку чисел удовлетворяющих условию - Исправление недочетов и поиск решений вместе с Examum.ru

Метод оценок

При решении задач в целых числах иногда используется подход, основанный на построении и применении различного рода оценок выражений, входящих в условия задач. Рассмотрим примеры.

Пример №55.

Доказать, что уравнение

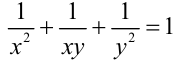
не имеет целых положительных решений.

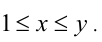
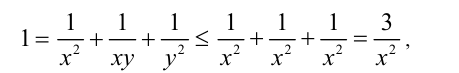
Доказательство. Пусть, ради определённости, Тогда

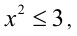
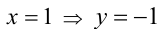
откуда находим оценку т.е. — не удовлетворяет условию задачи. Аналогично рассматривается случай

Пример №56.

Сумма обратных величин трёх натуральных чисел равна 1. Найти эти числа (наборы, а не упорядоченные тройки).

Решение:

Пусть x,y,z — искомые натуральные числа. Условия задачи приводят к уравнению

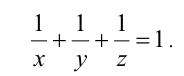
Очевидно, что для того чтобы это равенство выполнялось, необходимо, чтобы хотя бы одно из чисел не превосходило 3. Без ограничения общности будем считать, что 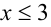. Тогда X = 2 или X = 3 .

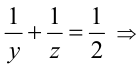
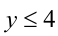
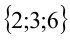
1) Пусть X = 2 , тогдахотя бы одно из чисел у или z не превосходит 4. Ради определённости, пусть это . Тогда у = 3 или у = 4 . В первом случае z = 6 , и имеем три числа . Во втором случае Z = 4 , и находим ещё одну тройку {2;4;4}.

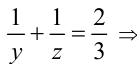
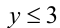
2) Пусть теперь X = 3, тогдахотя бы одно из чисел у или z не превосходит 3. Ради определённости, пусть это . Тогда у = 2 или у = 3. В первом случае z = 6 , и имеем числа {3;2;6} — уже было. Во втором случае z = 3 , и получаем набор { 3;3;3} .

Ответ: это наборы чисел {2;3;6}, {2;4;4}, {3;3;3}.

Пример №57.

Найти все упорядоченные тройки (x,y,z) натуральных чисел, удовлетворяющих равенству

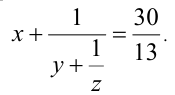
Решение:

Приведём уравнение к виду

Так как 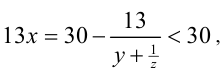, то получаем:

1) Если x = 1, то, подставляя в уравнение, находим 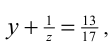, что невозможно, так левая часть в этом равенстве больше 1, а правая — меньше 1.

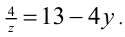
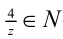
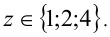
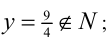
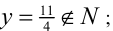
2) Если x = 2 , то получаем Справа стоит целое число, следовательно, , откуда При z = 1 имеем при z = 2 имеем при z = 4 находим у = 3 . Ответ:

Пример №58.

Непустое множество X состоит из конечного числа N натуральных чисел. Чётных чисел в X меньше двух третей от N , а нечётных не больше 36% от N . Какое минимальное значение может принимать число N ?

Решение:

Пусть n — число нечётных чисел в X . По условию,

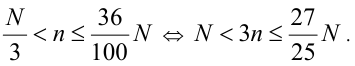
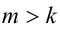
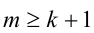
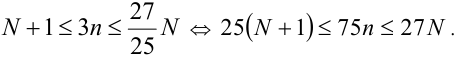
Воспользуемся тем свойством, что для целых чисел m,k строгое неравенство равносильно нестрогому . Поэтому

По свойству транзитивности из последнего неравенства получаем, как следствие, оценку

Далее действуем перебором (с проверкой).

Если N = 13 , то, подставив в неравенство (1), получим: 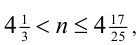что невозможно при целых n .

Если N = 14, то, подставив в неравенство (1), получим: 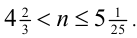Этому условию удовлетворяет n= 5 (т.е. нашлось n). Ответ:

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Предмет математика

Эти страницы возможно вам будут полезны:

Источник

Попробую изложить логику вычислений (она может быть не идеальной).
1) Произведение и сумма чисел в условии должна равняться n, то есть x, y, z однозначно меньше числа n.
2) Мне надо перебрать все возможные значения этих чисел x, y, z. Для этого я запускаю три цикла подбора-перебора этих чисел. Поэтому он их не с потолка берет, а подбирает в этих циклах

Pascal

1
2
3

 for x:=1 to n do
  for y:=1 to n do
   for z:=1 to n do

3)После того, как некие значения x, y, z (а точнее, любые значения x, y, z) выбраны, необходимо проверить, подходят ли они по условию. Поэтому

Pascal

1	if (xy+5z)=n then

4) Если они по условию подходят, мне необходимо вывести их на экран

Pascal

1	writeln (x, ' ', y, ' ', z);

5) Кроме вывода на экран подходящих значений x, y, z мне надо учесть вариант, когда решений нет. Именно для этого я использую k. k — это счетчик возможных решений.Изначально я считаю,что решений у данной задачи нет, поэтому k=0. Как только программа находит хоть одно решение, к принимает ненулевое значение и, собственно говоря, необходимость в нем отпадает…

Источник

Необходимо написать программу, которая определяет количество троек натуральных чисел (x,y,z), таких что:

0 < x < y < z < N,

Где N — натуральное число, 0 < N < 1000

Понимаю, что задача состоит в правильном использовании комбинаторных формул. Однако идей нет. Вариант в лоб (через 3 цикла и перебор не подходит для меня). Нет идей. Не нужно ничего писать, если можно подтолкните к правильному решению.

задан 22 янв 2018 в 10:37

Как уже написали в комментариях, посчитать число троек (x, y, z) натуральных чисел, таких что

0 < x < y < z < N

можно так:

Сначала уберём условие упорядоченности, то есть посчитаем число троек (x, y, z), таких что каждое из трёх чисел больше нуля и меньше N

Получится N - 1 * N - 2 * N - 3 троек (первое число можно выбрать N - 1 способами, второе N - 2 способами, …)
Теперь рассмотрим три различных числа, например {1, 2, 3}. Всего троек, составленных из этих чисел будет 6 = 3 * 2 * 1 штук (следствие предыдущего пункта для N равного 3+1). Нам подходит ровно одна из этих шести троек — когда числа стоят по возрастанию

Таким образом, ответ равен (N - 1) * (N - 2) * (N - 3) / 6

Источник

1/а + 1/х + 1/у = 1 (чтобы не переключать раскладку).

Пусть а — число, меньше которого нет среди а, х. у.

а равно 2 или 3, так как 1/4 + 1/4 + 1/4 < 1.

Пусть а = 2. Тогда х = 2 + 4/(у — 2)

4/(у — 2) — целое, если в знаменателе -4, -2, -1, 1, 2 или 4.

Первые 3 отпадают; 2 тройки: 2; 4; 4 и 2, 3, 6.

Пусть а = 3. Тогда 2х = 3 + 9/(2у — 3) (целое).

Отсюда тройка: 3; 3; 3.

Источник

Var A:array[1..100] of real;
    i,n:byte;
Begin
    write('Введите n: ');readln(n);
    For i:=1 to n do
    Begin
      write('A[',i,'] = ');
      readln(A[i]);
    End;
    For i:=2 to n-1 do
     if A[i]<=((A[i+1]+A[i-1])/2) then writeln(A[i]:6:2,A[i-1]:6:2,A[i+1]:6:2);
    readln;
End.

Источник