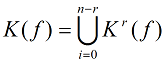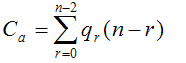Как найти тупиковую днф карты карно - Исправление недочетов и поиск решений вместе с Examum.ru

5.3.1. Алгоритм Квайна

Алгоритм
Квайна строит сокращенную ДНФ по СДНФ.
На первом этапе к СДНФ применяется
операция неполного склеивания:
.
После того, как операция применена к
каждой паре конъюнкций из СДНФ, к которой
она применима, с помощью операции
поглощения

удаляются те конъюнкции ранга n,
которые можно удалить таким образом. В
результате получается некоторая ДНФ
.
Если проведено

этапов, то на
-м
этапе операции неполного склеивания и
поглощения применяются к конъюнкциям
ранга

для
ДНФ
.
В результате получится ДНФ
.
Алгоритм Квайна заканчивает работу,
если
.

Пример 6

Применим алгоритм
Квайна к СДНФ функции из примера 1.

5.3.2. Карта Карно

Этот
метод применим для функций, зависящих
от небольшого числа (не более 4) переменных.
Функция задается прямоугольной таблицей,
в которой наборы значений переменных
расположены в таком порядке, чтобы при
переходе к следующему столбцу или строке
изменялась бы только одна компонента
решения. Нахождение простых импликант
сводится к выделению максимальных по
включению прямоугольников, состоящих
из единиц. Считается, что каждая клетка,
примыкающая к одной из сторон, является
соседней к клетке, примыкающей к
противоположной стороне и расположенной
в той же строке (или в том же столбце).
соседних
клеток, содержащих единицы и расположенных
по вертикали или горизонтали в виде
прямоугольника или квадрата, соответствуют
одной элементарной конъюнкции, ранг
которой меньше n
на k
единиц.

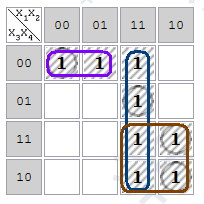
Пример 7

Рассмотрим
карту Карно для функции

со значениями (1110 0101 0100 1101)

Рис.
2.2. Пример
построения карты Карно

Максимальными
являются интервалы:

,
,
,
,
.

Сокращенная ДНФ
имеет вид

5.3.3. Таблица Квайна для построения тупиковых днф

Строки этой таблицы
соответствуют простым импликантам
функции
,
а столбцы 
наборам из множества
.
На пересечении строки, соответствующей
импликанте

и столбца, соответствующего набору
,
стоит 1, если

и 0, если
.
Минимальное покрытие столбцов таблицы
строками так, чтобы в него попали все
единицы, соответствует тупиковой ДНФ.
Минимальной ДНФ соответствует покрытие,
обладающее минимальной суммой рангов
конъюнкций, соответствующих строкам,
вошедшим в покрытие. Для построения
всех тупиковых ДНФ функции

составим КНФ

по следующему правилу: поставим в
соответствие столбцу

элементарную дизъюнкцию
,
где


все такие простые импликанты
,
что
.
Положим
.
Раскрывая скобки с помощью закона
дистрибутивности и применяя эквивалентности

и
,
получим из КНФ

ДНФ
,
слагаемые которой соответствуют
тупиковым ДНФ функции
.

Пример 8

Рассмотрим
.
Сокращенная ДНФ функции
:
.
Составим таблицу Квайна.

Простые импликанты	Единичный набор
(001)	(010)	(100)	(011)	(101)	(110)
	0	0	1	0	1	0
	0	0	1	0	0	1
	0	1	0	1	0	0
	0	1	0	0	0	1
	1	0	0	1	0	0
	1	0	0	0	1	0

Тогда

и

Функция

имеет пять тупиковых ДНФ. Из них две ДНФ

и
,
соответствующие слагаемым

и
,
являются минимальными.

Соседние файлы в папке 120_Гусев(уч.пос)

Источник

Построение минимальных ДНФ

СДНФ, которая строится по таблице булевой функции, зачастую оказывается весьма сложной, т.е. она содержит достаточно много элементарных конъюнкций и литералов. Необходимо уметь находить в определенном смысле минимальную ДНФ, представляющую исходную функцию. Уточним задачу.

Определение 6.5. Булеву функцию называют импликантой булевой функции , если для любых наборов значений переменных из g=1 следует f=1 .

Замечание 6.7. Напомним, что функции и можно рассматривать как функции от одного и того же числа переменных. Обозначая это число через , можно так уточнить понятие импликанты: функция $gin mathcal{P}_{2,n}$ есть импликанта функции $gin mathcal{P}_{2,n}$ если для каждого набора a $widetilde{alpha}inmathbb{B}^n$ из g(widetilde{alpha})=1 следует f(widetilde{alpha})=1 . Термин «импликанта» естественным образом ассоциируется и с логической связкой, называемой импликацией, и с одноименной булевой функцией. Действительно, если д импликанта , то из (gto f)=1 и g=1 следует, что f=1 , т.е. истинно высказывание

$(forallwidetilde{alpha}inmathbb{B}^n)bigl((g(widetilde{alpha})=1)Rightarrow (f(widetilde{alpha})=1)bigr).$

Если функция представлена СДНФ, то любая ее элементарная конъюнкция (констпигпуентпа единицы функции ) будет ее импликантой. Полезно заметить также, что если g_1 и g_2 — импликанты , то дизъюнкция g_1lor g_2 также является импликантой . Действительно, если g_1lor g_2=1 , то g_1=1 или g_2=1 . Но тогда, поскольку каждая из этих функций есть импликанта , и есть импликанта .

Из определения 6.5 и понятия равных булевых функций (см. определение 6.2) следует, что булевы функции и равны, если и только если каждая из них служит импликантой другой: f=1Leftrightarrow g=1 .

Определение 6.6. ДНФ называют минимальной, если она содержит наименьшее число литералов среди всех ДНФ, эквивалентных ей.

Обратим внимание на то, что под числом литералов в ДНФ понимают число всех подформул этой ДНФ, которые являются литералами. Так, СДНФ (6.9) содержит 12 литералов (по три литерала в каждой из четырех элементарных конъюнкции).

Пример 6.10. ДНФ $x_1x_2lor overline{x}_1x_2$ не является минимальной, так как ее можно преобразовать к эквивалентной ДНФ, не содержащей ни одного из литералов $widetilde{x}_1:$

$x_1x_2lor overline{x}_1x_2=(x_1lorwidetilde{x}_1)x_2=x_2,.$

Вместо четырех литералов в исходной ДНФ получаем ДНФ, состоящую из одного литерала.
Определение 6.7. Длиной ДНФ называют число входящих в нее элементарных конъюнкций.
ДНФ называют кратчайшей, если она имеет наименьшую длину среди всех эквивалентных ей ДНФ.

Заметим, что кратчайшая ДНФ не обязана быть в то же время минимальной среди всех ДНФ, эквивалентных исходной функции. Но поиск минимальных ДНФ, как мы сейчас увидим, проводится среди кратчайших ДНФ.

Наша задача состоит в том, чтобы описать метод построения минимальной ДНФ, эквивалентной заданной булевой функции. Мы рассмотрим простейший метод такого рода, основанные на алгоритме Квайна — Мак-Клоски. Этот алгоритм исходит обязательно из СДНФ, которая строится по таблице функции так, как это было описано ранее.

Алгоритм Квайна–Мак-Клоски

Опишем последовательно этапы, составляющие алгоритм Квайна–Мак-Клоски.

1. Склейка. Пусть K_1 и K_2 — две элементарные конъюнкции, входящие в исходную СДНФ Ф, которая представляет функцию , причем для некоторого переменного и некоторой элементарной конъюнкции выполняются равенства K_1=xK и $K_2=overline{x}K$ . Тогда имеем, согласно тождествам булевой алгебры,

$K_1lor K_2=xKlor overline{x}=(xlor overline{x})K=K,.$

Мы получаем элементарную конъюнкцию , которая содержит на один литерал меньше, чем K_1 и K_2 , и является, как и обе конъюнкции K_1 и K_2 , импликантой . Образно говоря, мы «склеили» две импликанты в одну, в которой число литералов на единицу меньше.

Операцию получения по K_1 и K_2 , описанную выше, можно провести и для любых двух элементарных конъюнкций подобного вида, составляющих любую ДНФ, эквивалентную исходной функции. Такую операцию называют простой склейкой импликант K_1 и K_2 по переменному .

Установим геометрический смысл простой склейки* (с точки зрения структуры, или «геометрии», булева куба).

Из доказательства теоремы о представлении булевой функции в виде ДНФ (см. теорему 6.2) мы знаем, что существует взаимно однозначное соответствие между множеством элементарных конъюнкций СДНФ, представляющей функцию , и множеством C_f^1 ее конституент единицы. Это соответствие, напомним, таково, что каждому набору $widetilde{alpha}=(alpha_1,ldots,alpha)in C_f^1$ отвечает элементарная конъюнкция $K_{widetilde{alpha}}=x_{1}^{alpha_1}cdotldots x_{n}^{alpha_n}$ , принимающая значение 1 только на наборе . Тогда простая склейка может быть применена только к таким двум элементарным конъюнкциям $K_{widetilde{alpha}}$ и $K_{widetilde{beta}}$ , соответствующим наборам $widetilde{alpha}, widetilde{beta}in C_f^1$ , что для некоторого i~(1leqslant ileqslant n)

$begin{aligned}widetilde{alpha}&= (alpha_1,ldots, alpha_{i-1},alpha_{i}, alpha_{i+1}, ldots, alpha_{n}),\[2pt] widetilde{beta}&= (alpha_1,ldots, alpha_{i-1}, overline{alpha}_{i}, alpha_{i+1}, ldots, alpha_{n}).end{aligned}$

Это значит, что наборы widetilde{alpha}, widetilde{beta} таковы, что один из них доминирует над другим (они различаются значением только одной компоненты), т.е. они образуют ребро булева куба $mathbb{B}^n$ .

Следовательно, простой склейке, применяемой к элементарным конъюнкциям исходной СДНФ, представляющей функцию , подлежат те и только те элементарные конъюнкции, которые соответствуют элементам какого-либо ребра булева куба, на котором функция принимает единичное значение. Образно говоря, две соседние вершины куба, на которых функция равна 1, псклеиваются» в ребро, их «соединяющее».

С алгебраической же точки зрения мы из двух элементарных конъюнкций $K_{widetilde{alpha}}$ и $K_{widetilde{beta}}$ получаем новую элементарную конъюнкцию $x_{1}^{alpha_1}ldots x_{i-1}^{alpha_{i-1}} x_{i+1}^{alpha_{i+1}}ldots x_{n}^{alpha_n}$ , лишенную литерала $x_{i}^{alpha_i}$ .

Итак, применяя простую склейку к исходной СДНФ Phi , получаем новую ДНФ Phi_1 ; к ней также применяем простую склейку — получаем ДНФ Phi_2 ; продолжаем выполнять эту операцию до тех пор, пока не окажется, что для некоторого в ДНФ Phi_k уже нельзя склеить никакие две элементарные конъюнкции. Такое всегда найдется, так как СДНФ Phi состоит из конечного числа элементарных конъюнкций, а они, в свою очередь, состоят из конечного числа литералов. Полученную в результате ДНФ Phi_k называют сокращенной ДНФ функции , а ее элементарные конъюнкции — простыми импликантами булевой функции .

Замечание 6.8. Понятие простой импликанты определено через процедуру многократного повторения простой склейки. Иногда простую импликанту булевой функции определяют независимо от понятия о склейке как такую элементарную конъюнкцию в составе некоторой ДНФ, представляющей функцию , что удаление из нее любого литерала лишает ее свойства «быть импликантой». Например, конъюнкция $x_1x_2 overline{x}_3$ не является простой импликантой мажоритарной функции, так как из ее СДНФ (6.9) можно удалить литерал $overline{x}_3$ и получить конъюнкцию x_1x_2 , которая будет снова импликантой функции, но уже, как будет показано далее, простой.

Можно доказать, что эти два определения простой импликанты равносильны.

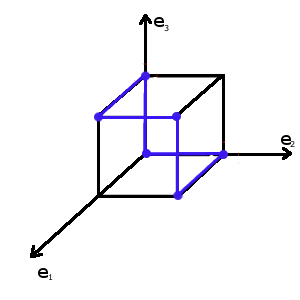
Геометрия описанного выше многократного повторения простой склейки, как можно показать, состоит в дальнейшем «склеивании» каждой пары соседних ребер {граней размерности 1), на которых значение функции равно 1, в грани размерности 2, соседних граней размерности 2 в грани размерности 3 и т.д. Разбираемый ниже пример поясняет эту идею.

Пример 6.11. Зададим функцию от трех переменных следующей СДНФ:

$f=overline{x}_1overline{x}_2overline{x}_3lor overline{x}_1overline{x}_2 x_3lor x_1overline{x}_2overline{x}_3lor x_1overline{x}_2x_3,.$

(6.11)

Подвергнем простой склейке первую и третью, а также вторую и четвертую элементарные конъюнкции в (6.11):

$f=overline{x}_2overline{x}_3loroverline{x}_2x_3,.$

(6.12)

Склейка первой и третьей конъюнкций в формуле

С геометрической точки зрения склейка первой и третьей конъюнкций в формуле (6.11) означает, что функция принимает единичное значение на ребре [000,100] (рис. 6.6), а склейка второй и четвертой конъюнкций точно так же определяет ребро [001,101], Эти ребра являются соседними, и, кроме того, оказывается, что функция / принимает единичное значение и на другой паре соседних ребер: [000, 001] и [100,101]. Здесь сказывается существенное отличие «геометрии» булева куба от классической: в булевом кубе ребро — это пара вершин, между которыми нет никаких «точек». Тогда любая пара соседних ребер образует грань размерности 2, любая пара соседних граней размерности 2 образует грань размерности 3 и т.д. Таким образом, если функция принимает единичное значение на двух соседних ребрах булева куба, то она равна 1 в любой точке образуемой ими грани размерности 2, если она равна 1 на двух параллельных соседних гранях размерности 2, то она равна 1 на соответствующей грани размерности 3 и т.д.

Применяя простую склейку к (6.12) (по переменному x_3 ), получаем $f(x_1,x_2,x_3)=overline{x}_2$ . Побочным результатом склейки явилось и удаление фиктивных переменных функции x_1 и x_3 .

Пример 6.12. Рассмотрим СДНФ мажоритарной функции (6.9).
Имеем следующие склейки:

$overline{x}_1x_2x_3lor x_1x_2x_3=x_2x_3,qquad x_1overline{x}_2x_3lor x_1x_2x_3=x_1x_3,qquad x_1x_2overline{x}_3lor x_1x_2x_3=x_1x_2.$

В данном случае сразу получаем сокращенную ДНФ: Phi_1=x_1x_2lor x_1x_3lor x_2x_3 .

Карты Карно

Для булевых функций от трех и четырех переменных процедура склейки наглядно и просто выполняется на так называемых картах Карио. Форма карт Карно, представляющих собой прямоугольные таблицы, для функции от трех переменных показана на рис. 6.7, а для функции от четырех переменных — на рис. 6.8. На рис. 6.7 строки отмечены наборами значений переменного x_1 , а столбцы — x_2,x_3 , а на рис. 6.8 строки — наборами значений переменных x_1,x_2 , а столбцы — x_3,x_4 .

Форма карт Карно для функций от трех и четырёх переменных

Карта Карно есть не что иное, как форма таблицы для определения булевой функции. Каждая клетка карты задается своим набором значений переменных, причем в клетках, соответствующих конституентам единицы данной функции, ставится единица, тогда как остальные клетки остаются пустыми. Карта Карно устроена так, что наборы, определяющие любые две соседние клетки, различаются в точности в одной позиции (т.е. различаются значениями ровно одной компоненты), причем клетки (одной и той же строки или одного и того же столбца), примыкающие к противоположным сторонам прямоугольника, также являются соседними в только что определенном смысле. Это можно представить себе так, что карта закручивается» в цилиндр» по обоим направлениям, т.е. в «тор».

С геометрической точки зрения карта Карно есть способ изображения булева куба (размерностей 3 и 4). Любая пара соседних клеток (с учетом «закрученности» карты) определяет некоторое ребро булева куба, а любой прямоугольник, состоящий из 2^k клеток (или, как говорят, прямоугольник с площадью 2^k ) для некоторого , определяет грань размерности .

Можно построить карты Карно и для размерностей 5 и 6, но они используются весьма редко. Может быть построена и простейшая карта Карно для функции от двух переменных, но для таких функций не возникает нетривиальных задач построения минимальной ДНФ.

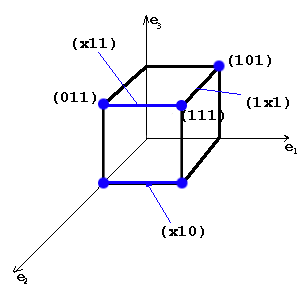
Пусть булева функция задана таблицей, представленной в форме карты Карно. Описанный выше итерационный процесс склейки, в результате которого получается сокращенная ДНФ, представляющая функцию , проводится на карте Карно так: любые две соседние клетки, содержащие единицы, обводятся, и «поглотивший» их прямоугольник (он и есть обозначение результата склейки на карте) представляется словом, содержащим «0», «1» и «×» («крестик»), причем «крестик» занимает позицию того переменного, по которому произведена склейка (рис. 6.9).

Булева функция, заданая таблицей, представленной в форме карты Карно

С геометрической точки зрения такой прямоугольник площади 2 соответствует ребру булева куба, в каждой вершине которого функция принимает значение 1. Запись прямоугольника в виде слова можно понимать как обозначение соответствующего ребра. Так, на карте, показанной на рис. 6.9, прямоугольник 11× обозначает ребро [110,111], прямоугольники же 1×1 и ×11 — ребра [101,111] и [011,111] соответственно.

По таким обозначениям легко получить и ту импликанту, которая является результатом простой склейки: для этого достаточно записать литерал x_i (соответственно $overline{x}_i$ ), если в i-й позиции стоит 1 (соответственно 0), и пропустить литерал ж», если в i-й позиции стоит «крестик». Так, по слову 1×0 получим импликанту $x_1overline{x}_3$ .

Наличие на карте Карно двух прямоугольников площади 2, находящихся в соседних столбцах или строках, показывает, что функция принимает значение 1 на некоторой паре соседних ребер, т.е. на некоторой грани размерности 2. Тогда они могут быть объединены в один большой прямоугольник площади 4 (рис. 6.10).

Наличие на карте Карно двух прямоугольников площади и их объединение

Этот прямоугольник можно записать в виде слова хОх, показывая тем самым, что соответствующая грань (размерности 2) образована любой из двух пар соседних ребер: (×00, ×01) (два вертикальных прямоугольника площади 2) или (00×, 10×) (два горизонтальных прямоугольника площади 2).

Точно так же можно объединять в один прямоугольник площади 8 два соседних прямоугольника площади 4 (рис. 6.11).

Карты Карно

Если такие большие прямоугольники находить сразу, то «поглощаемые» ими меньшие прямоугольники уже не рассматриваются. Тем самым, находя на карте Карно прямоугольники максимальной площади и не содержащиеся друг в друге, мы находим грани максимальных размерностей и максимальные по включению, такие, на которых заданная функция принимает единичное значение. Поскольку грань размерности имеет 2^k вершин, то выделяемые описанным способом прямоугольники могут состоять только из 2^k клеток (для некоторого , не превышающего числа переменных). Так, на карте, приведенной на рис. 6.12, получим два прямоугольника площади 4: ×0×0 и 0×0×, соответствующие граням размерности 2, и один прямоугольник 01×1, отвечающий ребру, которое не содержится ни в одной из указанных выше граней. Подчеркнем еще раз, что соседство клеток, прямоугольников и само выделение прямоугольников на карте Карно производится с учетом ее «закрученности». В этой связи интересен » прямоугольник» на карте, приведенной на рис. 6.12, обозначенный ×0×0. Он образован двумя парами противоположных угловых клеток.

Таким образом, если на карте Карно сразу выделять все максимальные (в указанном выше смысле) прямоугольники площади 2^k (для некоторого kgeqslant0 и не превышающего числа переменных), то тем самым мы «геометрически» реализуем описанный ранее алгебраический итерационный процесс склейки и в результате получаем все простые импликанты исходной функции (составляющие сокращенную ДНФ). Эти импликанты восстанавливаются по записям прямоугольников точно так же, как описано выше для простой склейки. Так, для карты, приведенной на рис. 6.12, получим сокращенную ДНФ в виде

$overline{x}_2 overline{x}_4lor overline{x}_1 overline{x}_3lor overline{x}_1x_2x_4,.$

2. Определение ядра. Говорят, что элементарная конъюнкция покрывает элементарную конъюнкцию (и пишут Ksucc L ), если любой литерал, входящий в , входит в . Так,

$x_1x_2succ x_1x_2x_3,qquad x_1x_3succ x_1 overline{x}_2x_3$ , но $x_1x_3nsucc x_1x_2overline{x}_3$ .

Поскольку вторая конъюнкция содержит литерал $overline{x}_3$ , отсутствующий в первой конъюнкции. Легко понять, что если Ksucc L , то Klor L=K (согласно тождествам поглощения).

Каждая входящая в сокращенную ДНФ простая импликанта покрывает некоторую элементарную конъюнкцию исходной С ДНФ. На карте Карно этому отвечает прямоугольник, п закрывающий» соответствующую единицу.

Простую импликанту называют ядровой, если она покрывает некоторую элементарную конъюнкцию исходной СДНФ, не покрываемую никакой другой простой импликантой. На карте Карно прямоугольник, соответствующий ядровой импли-канте, отыскивается очень просто: это такой прямоугольник, удалив который получим единицу, не закрытую никаким другим прямоугольником. Тогда ни одна ядровая импликанта не может быть удалена из искомой минимальной ДНФ исходной функции, т.е. все ядровые импликанты обязательно войдут в минимальную ДНФ.

Множество всех ядровых импликант (склеек) сокращенной ДНФ называют ядром.

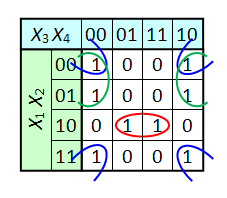
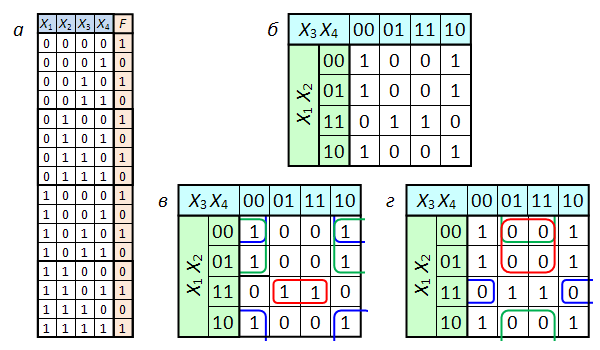
Пример 6.13. а. У мажоритарной функции все импликанты являются ядровыми. Напротив, у функции, изображенной на карте Карно на рис. 6.13, ядро пусто, т.е. ядровых импликант нет вовсе.

Две карты Карно

б. На карте Карно на рис. 6.14 в ядро попадают склейки 0times,times1,~ 0times1times,~ 1times00 .

Если все простые импликанты оказались в ядре, то сокращенная ДНФ и есть единственная минимальная и кратчайшая ДНФ для данной функции. Именно так обстоит дело с мажоритарной функцией (см. пример 6.12). В противном случае смотрят, не эквивалентна ли ДНФ, построенная как дизъюнкция всех ядровых импликант, исходной СДНФ. Это будет иметь место тогда и только тогда, когда ядровые импликанты покрывают в совокупности все элементарные конъюнкции исходной СДНФ. На карте Карно тогда каждая клетка, содержащая единицу, должна быть закрыта прямоугольником, отвечающим некоторой ядровой импликанте. Если это так, то ДНФ, построенная по ядру, как описано выше, есть минимальная и кратчайшая (склейки ядра закрыли все единицы карты Карно). При этом импликанты, не попавшие в ядро, все оказываются «избыточными», т.е. их удаление из сокращенной ДНФ не приводит к нарушению эквивалентности этой последней с исходной СДНФ.

В остальных случаях переходят к отысканию так называемых тупиковых ДНФ.

3. Перечисление тупиковых ДНФ. Простую импликанту называют избыточной (относительно некоторой ДНФ, содержащей только простые импликанты и эквивалентной исходной СДНФ), если ее можно удалить из этой ДНФ без потери эквивалентности ее исходной СДНФ. Так, сокращенная ДНФ (см. рис. 6.14) содержит избыточные импликанты: импликанта, соответствующая прямоугольнику 10times0 , или импликанта, соответствующая прямоугольнику times010 , может быть удалена (но не обе сразу!). Это значит, что каждая из этих импликант является избыточной относительно сокращенной ДНФ, но удаление одной из них приводит к новой ДНФ, относительно которой вторая из упомянутых импликант уже не будет избыточной. В том случае, когда каждую элементарную конъюнкцию исходной СДНФ покрывает некоторая ядровая импликанта, импликанты, не вошедшие в ядро, можно удалить одновременно.

Тогда можно представить процесс пошагового удаления избыточных импликант, начиная с сокращенной ДНФ, в результате которого получится некоторая ДНФ, уже не содержащая ни одной избыточной склейки.

Любую ДНФ, эквивалентную исходной СДНФ, содержащую все ядровые импликанты и не содержащую ни одной избыточной импликанты, называют тупиковой.

Заметим, что в силу конечности множества всех импликант тупиковая ДНФ обязательно существует, т.е. в упомянутом выше процессе мы рано или поздно доберемся до такого момента, когда удаление хотя бы одной склейки приведет к тому, что «откроется» какая-то единичная клетка на карте Карно и тем самым будет потеряна эквивалентность полученной таким образом ДНФ исходной СДНФ.

Для СДНФ, карта Карно которой приведена на рис. 6.14, имеются две тупиковые ДНФ (первые три конъюнкции соответствуют ядру):

$begin{gathered}overline{x}_1x_4lor overline{x}_1x_3lor x_1overline{x}_3cdot overline{x}_4lor overline{x}_2 x_3 overline{x}_4,\[2pt] overline{x}_1x_4lor overline{x}_1x_3lor x_1overline{x}_3cdot overline{x}_4lor x_1overline{x}_2cdot overline{x}_4. end{gathered}$

В общем случае для перечисления всех тупиковых ДНФ может быть использован следующий алгоритм. Мы изложим его в терминах карт Карно и, допуская вольность речи, будем отождествлять максимальные прямоугольники на карте Карно с соответствующими простыми импликантами.

Присвоим каждой простой импликанте сокращенной ДНФ некоторое имя: т.е. обозначим их, например, как K_1,K_2,ldots,K_m . Для любой единицы карты Карно, не покрываемой ядром, перечислим все простые импликанты, которые ее покрывают, записав их в виде элементарной дизъюнкции, в которой переменными считаются введенные выше имена простых импликант. Переменное, именующее данную простую импликанту, принимает, по определению, значение 1, если данная простая импликанта выбирается для покрытия рассматриваемой единицы
карты Карно.

Записав все элементарные дизъюнкции, составим из них КНФ. Рассмотрим карту Карно на рис. 6.13. Обозначив

$begin{array}{lll}K_1=x_1overline{x}_2(10times),&qquad K_2= overline{x}_2 x_3(times01), &qquad K_3= overline{x}_1x_3(0times1),\[2pt] K_4= overline{x}_1 x_2(01times), &qquad K_5=x_2overline{x}_3(times10),&qquad K_6= x_1overline{x}_3(1times0), end{array}$

получим

(K_1lor K_6)land (K_1lor K_2)land (K_2lor K_3)land (K_3lor K_4)land (K_4lor K_5)land (K_5lor K_6).

(6.13)

Тем самым мы образуем вспомогательную функцию (представленную КНФ вида (6.13)), называемую функцией Патрика. Раскрывая скобки в КНФ (6.13) и используя тождества булевой алгебры (в частности, тождество поглощения), получим ДНФ, в которой каждая элементарная конъюнкция соответствует некоторой тупиковой ДНФ и, наоборот, каждой тупиковой ДНФ может быть сопоставлена одна из этих конъюнкций.

Для нашего примера поступим так: вычислим конъюнкцию первой и второй скобки в выражении (6.13), а также третьей и четвертой, пятой и шестой скобок, после чего получим

$begin{aligned}(K_1lor K_1 K_2lor K_6 K_1lor K_6 K_2) &land (K_2 K_3lor K_2 K_4lor K_3lor K_3 K_4)land\[2pt] &land (K_4 K_5lor K_4 K_6lor K_5lor K_5 K_6). end{aligned}$

(6.14)

Используя тождества поглощения, в первой скобке в формуле (6.14) мы можем удалить все члены, содержащие K_1 , во второй скобке — все члены, содержащие K_3 , в третьей скобке — все члены, содержащие K_5 . Проделав это, раскрыв все три скобки и применив еще раз поглощение, окончательно получим

K_1 K_3 K_5lor K_1 K_3 K_4 K_6lor K_1 K_2 K_4 K_5lor K_2 K_3 K_5 K_6lor K_2 K_4 K_6.

(6.15)

Элементарные конъюнкции в (6.15) определяют тупиковые ДНФ. Более того, так как в данном случае отсутствуют ядровые импликанты, найденные конъюнкции исчерпывают тупиковые ДНФ. Первая тупиковая ДНФ состоит из конъюнкций K_1,,K_3 и K_5 , т.е. имеет вид $x_1 overline{x}_2lor overline{x}_1x_3lor x_2 overline{x}_3$ . Точно так же определяются остальные тупиковые ДНФ.

Обоснование описанного выше алгоритма может быть получено из следующих соображений. Функция Патрика, представленная КНФ, принимает значение 1 тогда и только тогда, когда каждая элементарная дизъюнкция принимает значение 1. А элементарная дизъюнкция принимает значение 1 в том и только в том случае, когда хотя бы одно ее переменное принимает значение 1. Согласно определению функции Патрика, это значит, что хотя бы одна простая импликанта выбрана для покрытия соответствующей единицы на карте Карно. Поскольку таким образом перебираются все не покрываемые ядром единицы карты Карно, то гарантируется эквивалентность искомой ДНФ исходной СДНФ. Однако, когда функция Патрика представлена ДНФ и мы выбираем в точности одну из ее элементарных конъюнкций, полагая, что все входящие в нее переменные равны 1, мы тем самым из всех возможных вариантов покрытия каждой единицы на карте Карно выбираем в точности один вариант. Значит, полученная в результате такого выбора ДНФ для исходной (минимизируемой) СДНФ действительно будет тупиковой.

Но нужно заметить, что перечисление тупиковых ДНФ является самым неприятным и трудоемким этапом всего алгоритма минимизации. Если число единичных клеток карты Карно, не покрываемых ядром, достаточно велико, то функция Патрика будет весьма сложной и ее упрощение сопоставимо по трудоемкости со всем процессом минимизации.

4. Отыскание среди тупиковых ДНФ кратчайших и минимальных. Среди найденных тупиковых ДНФ находят кратчайшие и минимальные. Можно легко показать, что минимальная ДНФ всегда является кратчайшей, но обратное неверно. Так, $x_1x_2loroverline{x}_2=x_1lor overline{x}_2$ и первая ДНФ кратчайшая, но не минимальная. Действительно, легко сообразить, что вторая из записанных ДНФ минимальна. Следовательно, представляемую ею функцию нельзя представить ДНФ, содержащей менее двух элементарных конъюнкций. Но в первой ДНФ три литерала, а во второй — два. Из пяти тупиковых ДНФ, соответствующих функции Патрика (6.15), кратчайшими являются две. Каждая из них минимальна, так как обе они имеют одинаковое число литералов.

Карта Карно

Пример 6.14. Рассмотрим карту Карно на рис. 6.15. В результате проведения склейки получим следующую сокращенную ДНФ*:

$overline{x}_1overline{x}_3lor overline{x}_1overline{x}_2lor overline{x}_2 overline{x}_4lor overline{x}_2overline{x}_3lor overline{x}_3x_4lor x_1x_2x_4lor x_1x_2x_3lor x_1x_3overline{x}_4,.$

Ядро составляют склейки (простые импликанты) $overline{x}_1overline{x}_3$ и $overline{x}_1overline{x}_3$ .

Шесть клеток, содержащих единицу, на карте Карно остаются непокрытыми ядровыми склейками. Для неядровых склеек (обозначенных K_1,ldots,K_6 ) составляем функцию Патрика в виде

(K_3lor K_4) (K_4lor K_5) (K_5lor K_6) (K_1lor K_2) (K_2lor K_3) (K_1lor K_6).

Преобразуя ее аналогично функции (6.13), получаем

K_1K_3K_5lor K_2K_4K_6lor K_2K_3K_5K_6lor K_1K_2K_4K_5lor K_1K_3K_4K_6,.

Имеем, следовательно, пять тупиковых ДНФ. Запишем их, для наглядности, так:

$underbrace{overline{x}_1overline{x}_3lor overline{x}_1 overline{x}_2}_{text{yadro}}lor begin{cases}overline{x}_2overline{x}_4lor overline{x}_3x_4lor x_1x_2x_3,\ overline{x}_2overline{x}_3lor x_1x_2x_4lor x_1x_3overline{x}_4,\ overline{x}_2 overline{x}_3lor overline{x}_3x_4lor x_1x_2x_3lor x_1x_3overline{x}_4,\ overline{x}_2 overline{x}_4lor overline{x}_2overline{x}_3lor x_1x_2x_4lor x_1x_2x_3,\ overline{x}_2 overline{x}_4lor overline{x}_3x_4lor x_1x_2x_4lor x_1x_3overline{x}_4. end{cases}$

Из этих пяти тупиковых ДНФ кратчайшими являются первая и вторая. Из них, в свою очередь, минимальной является первая, так как она содержит на один литерал меньше. В итоге получаем минимальную ДНФ в виде

$overline{x}_1overline{x}_3lor overline{x}_1overline{x}_2lor overline{x}_2 overline{x}_4lor overline{x}_3x_4lor x_1x_2x_3,.$

«Обратим еще раз внимание на то, что каждый выделяемый прямоугольник на карте Карно имеет площадь, равную некоторой степени двойки. Поэтому, например, три соседние единичные клетки не могут быть объединены в один прямоугольник, а их «накроют» два прямоугольника площадью 2, пересекающиеся по одной клетке.

В данном случае минимальная ДНФ оказалась единственной, хотя, как это мы видели в ранее разобранных примерах, в общем случае могут существовать несколько минимальных ДНФ.

Метод Блейка

Техника карт Карно является удобным и наглядным (при определенных ограничениях на число переменных минимизируемой функции) способом реализации алгоритма Квайна–Мак-Клоски. Но существуют и другие способы проведения склейки, т.е. получения сокращенной ДНФ для исходной функции. Одним из таких способов является чисто алгебраический метод Блейка, состоящий в том, что к любой ДНФ, представляющей функцию, применяются следующие тождества:

$begin{cases}xK_1lor overline{x}K_2= xK_1lor overline{x}K_2lor K_1K_2,\ K_1lor K_1K_2=K_1.end{cases}$

Первое из тождеств (6.16) называют тождеством (или правилом) обобщенного склеивания, второе — тождеством (или правилом) поглощения.

«Технология» использования метода Блейка такова: применяют тождество обобщенного склеивания до тех пор, пока не перестанут появляться новые элементарные конъюнкции (вида К1К2). После этого применяют тождество поглощения.

Таблицы Квайна

Как только сокращенная ДНФ тем или иным способом найдена, приступают к нахождению ядра. Ядро можно определить (без использования карты Карно) с помощью так называемой таблицы Квайна. Столбцы этой таблицы соответствуют элементарным конъюнкциям исходной СДНФ, а строки — простым импликантам сокращенной ДНФ. На пересечении строки и столбца проставляется знак «+» (плюс), если простая импликанта данной строки покрывает элементарную конъюнкцию данного столбца. Ядро вычисляется так: отмечаем столбцы с единственным знаком «+», тогда простые импликанты тех и только тех строк, в которые попал этот знак, образуют ядро. Для примера 6.13.6 (см. рис. 6.14) получим таблицу Квайна, изображенную на рис. 6.16. (В целях экономии места элементарные конъюнкции в таблице заменены цифровыми обозначениями соответствующих вершин и граней булева куба — точно так же как при обозначении прямоугольников на картах Карно. Ядровые импликанты выделены жирным шрифтом.)

Таблица Квайна

По таблице Квайна можно составить и функцию Патрика для перечисления тупиковых ДНФ. Для этого нужно отметить все столбцы таблицы, в которых на пересечении со строками, соответствующими ядровым импликантам, не стоит знак «+». Для разбираемого примера таковым является только последний столбец. Чтобы покрыть соответствующую элементарную конъюнкцию СДНФ, можно выбрать одну из двух простых импликант: $x_1 overline{x}_2 overline{x}_4$ или $overline{x}_2x_3overline{x}_4$ .

Построение минимальных ДНФ частичных булевых функций

В заключение рассмотрим очень кратко применение карт Карно к построению минимальных ДНФ частичных булевых функций, т.е. частичных отображений из множества ${0;1}^n$ в множество {0;1} .

Частичная булева функция может быть задана посредством карты Карно, в которой кроме клеток с единицами и пустых клеток будут клетки, заполненные прочерками (–). Такой прочерк означает, что на соответствующем наборе функция не определена.

Склейка для частичной функции (заданной картой Карно) проводится таким образом, что выделяются прямоугольники максимальной площади (содержащие 2^k клеток, для некоторого ), каждая клетка которых содержит либо единицу, либо прочерк, причем существует по крайней мере одна единичная клетка.

Пример 6.15. Пусть частичная функция f(x_1,x_2,x_3) задана картой Карно, приведенной на рис. 6.17. Прямоугольник максимальной площади (равной 4), состоящий из единицы и прочерков, записывается как 0times,times . Следовательно, минимальная ДНФ для заданной функции будет $overline{x}_1$ .

Частичная булевая функция, заданная картой Карно

По поводу рассмотренного примера возникает такой вопрос: почему не принят во внимание другой прямоугольник (площади 2), содержащий клетку с единицей и клетку с прочерком: times00 ? Связано это вот с чем. Перед тем как выделять упомянутые выше прямоугольники, мы на самом деле доопределяем исходную частичную функцию (получая обычную булеву функцию) так, чтобы в максимальном числе клеток, в которых стоят прочерки (но не нули!), появились единицы. Точнее говоря, среди прямоугольников (с прочерками), содержащих данную единицу, выбирают для замены прочерков единицами такой, который имеет максимальную площадь. Прочерки же в остальных прямоугольниках заменяют нулями.

В примере 6.15 мы доопределяем исходную функцию так, что получается функция f_1 , задаваемая картой Карно, приведенной на рис. 6.18. Эта функция имеет минимальную ДНФ $overline{x}_1$ . Следовательно, и частичная исходная функция может быть представлена такой ДНФ, поскольку на всех наборах, на которых она определена, она принимает такое же значение, как и функция f_1 .

Карты Карно 2

Конечно, мы могли бы доопределить функцию по-другому, так, чтобы получилась функция f_2 , заданная картой Карно, приведенной на рис. 6.19. Ясно, что $f_2= overline{x}_2overline{x}_3$ поэтому и частичная функция может быть определена такой ДНФ. Но эта ДНФ не минимальна для данной частичной (именно частичной!) функции, поскольку первый способ доопределения дал ДНФ, содержащую лишь один литерал.

Таким образом, в отличие от минимизации булевых функций при минимизации частичных булевых функций не следует выделять все максимальные прямоугольники с прочерками, содержащие данную единичную клетку карты Карно, достаточно выбрать произвольно любой из таких прямоугольников. Но, конечно, не нужно забывать о том, что каждая единица на карте должна быть покрыта некоторой склейкой.

Пример 6.16. Для карты на рис. 6.20 следует взять обе склейки на четыре позиции: 00times,times и times,times00 , получив для заданной этой картой частичной функции минимальную ДНФ в виде $overline{x}_1 overline{x}_2lor overline{x}_3 overline{x}_4$ .

Карта Карно булевой функции четырех переменных

Заметим, что без использования склеек с прочерками мы вообще не могли бы минимизировать данную функцию. Нужно также отметить, что не всегда использование «частичности» функции позволяет получить минимальную ДНФ для нее. Так, на представленной на рис. 6.20 карте в случае, если мы переместим нижнюю единицу на строку выше, обычная склейка на две позиции дает лучший результат: $overline{x}_1overline{x}_3overline{x}_4$ , а записанная выше ДНФ уже не будет минимальной (и даже кратчайшей).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Калькулятор

Метод Квайна

В основе две операции:

где под p понимается некоторая элементарная конъюнкция.

Теорема.
Если в СДНФ какой-либо переключательной функции выполнить все возможные операции неполного попарного склеивания и элементарного поглощения, то в результате получится СкДНФ(сокращенная дизъюнктивная нормальная форма), эквивалентная исходной функции.

Итерационый алгоритм. Задача в нахождении по полной системе импликант (конституэнт единицы) полной системы простых импликант.

Алгоритм:

Исходным является множество конституэнт единицы функции — импликанты нулевого ранга.
Выполняются все возможные операции неполного попарного склеивания для элементарных конъюнкций длины n. (где n-кол-во аргументов).
Согласно соотношениям «a.» и «b.» результат — дополнительная импликанта p.
Выполняются все возможные операции элементарного поглощения для элементарных конъюнкций длины n-1. (общая часть «p» имеет длину n-1)
В результате получилось множество элементарных конъюнкций, разделяемых на два подмножества(по длине):
- подмножество элементарных конъюнкций длины n (оставшиеся)
- подмножество элементарных конъюнкций длины n-1
Элементарные конъюнкции длины n не участвовали в склеивания, а, следовательно, и в поглощении (т.к. поглощаются собственной частью те, которые участвовали в склеивании).
Следовательно, подмножество элементарных конъюнкций длины n входит в множество простых импликант (импликант нулевого ранга).
Если множество элементарных конъюнкций длины n-1 не пусто, то выполняются шаги со второго для конъюнкций длины n-1 и т.д.

Алгоритм завершается, когда подмножество является пустым, либо нельзя выполнить ни одной операции неполного попарного склеивания.

Таким образом, получаем систему простых импликант функции.

Нахождение тупиковых ДНФ

Стратегическая задача нахождения приведенной системы простых импликант заключается в нахождении наилучших покрытий единиц функции простыми импликантами.

Для системы простых импликант для заданной функции может быть получено несколько приведенных систем. Следует считать, что среди них есть такая, которая дает тупиковую нормальную форму минимальной длины.

Алгоритм нахождения приведенных систем простых импликант также является переборным. Задача в том, чтобы обеспечить направленный перебор. Для этого алгоритм строится в виде итерационной процедуры, которая содержит следующие шаги:

Находятся такие единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант (для каждой единицы считаем сколько ее покрывает импликант и отмечаем их).
Этим импликанты образуют, так называемое, ядро функции. Такие импликанты будут входить в приведенную систему простых импликант. Следовательно, конъюнкции будут входить во все ТДНФ( в том числе минимальные).
Исключаются из рассмотрения все единицы функции, покрываемые ядром.
Осталось множество непокрытых ядром единицы функции и множество простых импликант, которые не вошли в ядро.
Повторяем шаг 1 и шаг 2 для оставшихся множеств (находится псевдоядро). Но перед повторением должен быть дополнительный шаг, который уменьшает перебор. (выкидываем из тех, которые покрывают одни и те же единицы(из оставшихся) ту импликанту, которая имеет наибольшую длину)

И так далее до тех пор, пока не будут покрыты все единицы функции.

Велика вероятность, что на каком-то шаге не найдется ни одной единицы функции, которая покрывается одной импликантой. В этом случае ищется наилучшее (наименьшей длины) покрытие оставшихся единиц функции методом перебора:

Если единица функции покрывается импликантами A,B,C,…
- Пусть A входит в ТДНФ, а B,C,… нет.
- Пусть В входит в ТДНФ, а A,C,… нет.
- Пусть C входит в ТДНФ, а A,B,… нет.
- …
Таким образом, получаем множество ТДНФ. Затем выбираем из них ДНФ наименьшей длины — получаем {МДНФ}.

Пример минимизации переключательной функции методом Квайна

Функция задана вектором: 883F. Запишем 16-ричное число 883F в двоичной виде в столбец значений функции таблицы истинности.

Таблица истинности исходной функции

Набор>	Значение исходной функции	Набор>	Значение исходной функции

0000	1	1000	0
0001	0	1001	0
0010	0	1010	1
0011	0	1011	1
0100	1	1100	1
0101	0	1101	1
0110	0	1110	1
0111	0	1111	1

Цена ДНФ является суммой длин всех входящих в нее конъюнкций.

Минимизация функции методом Квайна.

На данном шаге все импликанты участвовали в операциях попарного неполного склеивания и были поглощены своими собственными частями. Поэтому простые импликанты на этом шаге не получены.

В результате на данном шаге получаем простые импликанты:
,

СкДНФ:
v v v

Нахождение тупиковых форм.

Обозначения:

Единицы ДНФ, покрываемые импликантами СкДНФ, обозначаются «+».Импликанты, попадающие в ядро помечаются «*».
Единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант, помечаются “>”.
Единицы функции, покрываемые ядром, но не покрываемые только какой-то одной импликантой из системы простых импликант, помечаются “>>”.

	>	>>	>	>	>>	>	>>	>>
^*	+	+
		+			+
^*			+	+			+	+
^*					+	+	+	+

Ядро: v v

МДНФ: v v , цена=7

Графический метод минимизации — Карты Карно

Карты Карно — это графическое представление операций попарного неполного склеивания и элементарного поглощения.

Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции.

Карты Карно — определенная плоская развертка n-мерного булева куба.

Строится таблица истинности функции определенным образом. Каждая клетка таблицы соответствует вполне определенной вершине булева куба. Нулевые значения не записываются.

Карта Карно для функции 4-х переменных:

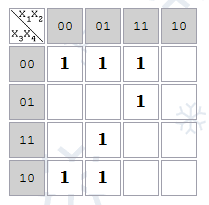
Карта Карно рассматривается как поверхность фигуры под названием тор («бублик»).

p-клетки — клетки карты Карно, соответствующие единичному значению функции.

Соседние наборы — наборы, которые различаются только одним аргументом (одной орбитой).

Любой паре соседних наборов в Карте Карно соответствуют соседние клетки.

Две соседние p-клетки на карте Карно дают импликанту первого ранга. Например, клетки 1100 и 1101 отличаются только значением переменной x₃, следовательно, они дают импликанту 124.

Две соседние импликанты первого ранга образуют импликанту второго ранга.

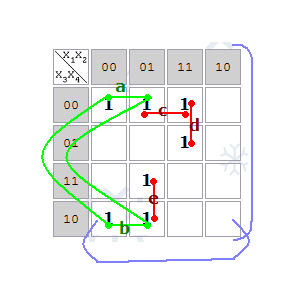
На этой карте соседние клетки образуют импликанты a,b,c,d,e. При этом импликанты a и b являются соседними, поэтому они образуют импликанту второго ранга.

Если функция имеет 5 переменных, то рисуются 2 Карты Карно: для x₅=0 и для x₅=1. Если 6 переменных — 4 Карты, так чтобы в соседних картах соседние клетки имели одинаковые координаты:

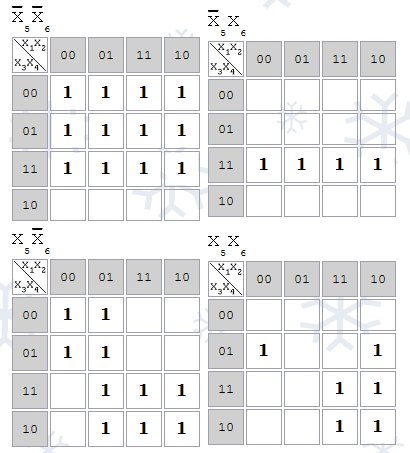
Соседние p-клетки, соответствующие импликанте образуют компактную группу.

Количество p-клеток в компактной группе является степенью двойки.

Задача минимизации переключательной функции с помощью карт Карно заключается в нахождении импликант высшего ранга (соответствующих компактным группам наибольшей размерности), покрывающих p-клетки функции наилучшим образом.

Если на картах Карно выделить все компактные группы наибольшей размерности, то дизъюнкция соответствующих конъюнкций даст СкДНФ.

Пример минимизации функции 4-х переменных методом Карт Карно

Компактных групп размера 4 — 2
Компактных групп размера 2 — 2

Нахождение тупиковых форм.

Обозначения:

Цветом выделены компактные группы наибольшей размерности, вошедшие в ядро.

Ядро: v v
МДНФ: v v , цена=7

Машинно-ориентированные методы минимизации переключательных функций.

Основаны на применении соответствующих алгебр(или соответствующих алгебраический преобразований).

Вопрос 1. Интервальная форма задания функции. Постановка задачи минимизации.

Геометрический представление: (отображение функции на n-мерный булев куб)
Любому набору значений аргументов соответствует элементарная конъюнкция, содержащая все эти переменные — конституента единицы.

Те вершины n-мерного булева куба, в которых функция принимает единичное значение называются 0-кубами.

Два 0-куба образуют 1-куб, если соответствующие булевы вектора(их координаты) отличаются между собой значением только одной координаты(или одной компоненты). Эти координаты носят название свободной координаты. Обозначение x, остальные координаты 0-куба называются связанными и имеют либо 1, либо 0 значение. 0-кубы, образующие 1-куб называются его гранями. Два 1-куба образуют 2-куб, если свободная координата у них одинакова и они различаются значением только одной связанной компоненты.( 1-кубы — грани соответствующего 2-куба).

…

И так далее до n-куба( в случае тавтологии).

В общем случае, r-куб-это такой куб в булевом пространстве, у которого r свободных компонент и n-r связанных компонент.

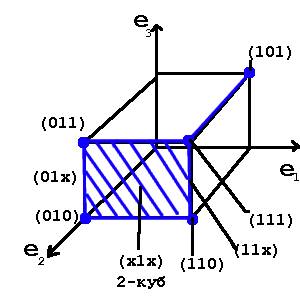
Пример:
(1x1xx1) — 3-куб
(1x1x01),(1x1x11)- два 2-куба. Они являются гранями этого 3-куба(образуют его).

Если для какой-то функции взять все возможные кубы одинаковой размерности, то получаем множество кубов(или комплекс кубов).
K^r(f) — комплекс r-кубов функции f/

Для некоторой функции всегда есть комплекс

(Если Kⁿ(f) содержит куб, то f — константа 1

оператор граней:

C^r=(a₁a₂…a_n-1a_n)-куб,

где a∈{0,1,x}, тогда для этого куба можно вычислить грани этого куба. Грани куба:

∂_i^p(a₁a₂…a_n-1a_n)=		a₁a₂…a_i-1 p a_i+1…a_n-1a_n, a_i=x, p∈{0;1}
∅, a_i ≠ x

где C-получаемый куб.

При a_i=x есть две грани (вместо i-ой либо 0, либо 1).

Оператор сограней

позволяет вычислить куб большей размерности, гранью которого может быть этот куб.

δ_i(a₁a₂…a_n-1a_n)=		a₁a₂…a_i-1 x a_i+1…a_n-1a_n, a_i≠x, C^r+1⊆K(f)
∅, a_i=x, C^r+1⊄K(f)

Подмножество вершин булева куба, соответствующие кубу размерности r называется интервалом булева пространства ранга r. (интервал 1 ранга — 1×1, интервал 2 ранга — x1x)

Для нашего примера:
K⁰(f)={101,110,111,010,011}
K¹(f)={01x,11x,1×1,x11,x10}
K²(f)={x1x}

В общем случае комплекс кубов определенного ранга не является покрытием исходной функции(за исключением K⁰).

В нашем примере K² не является покрытием, хотя K¹ — покрытие.
K(f)=K⁰∪K¹∪K² — для нашей функции

Куб большей размерности покрывает кубы меньшей размерности, если они могут быть получены из него последовательным применением оператора граней.

(x1x) имеет грани (01x) и (11x), которые имеют грани : (010),(011) и (110),(111)

Если взять интервал булева пространства, то аналитически его можно описать в виде соответствующих элементарных конъюнкций.

Некоторый комплекс кубов — L, таких, что каждая вершина из комплекса K⁰(f) включена по крайней мер в один из кубов комплекса L, называется покрытием комплекса K функции f.

Каждое покрытие комплекса K(f) определяет некоторую ДНФ переключательной функции.

Покрытие можно рассматривать (с точки зрения реализации), как двухуровневую схему.

Уровни схемы:

Аргументы (0-ой уровень)

конъюнктивные члены(элементарные конъюнкции) (1-ый уровень)

дизъюнкция (2-ой уровень)

Не учитывается инверсия аргументов на нулевом уровне.

Минимизация
Цена r-куба: c=n-r — число связанных переменных, количество символов в элементарной конъюнкции(совпадает с ценой в смысле Квайне)

—цена покрытия, где q_r-количество кубов размерности r в покрытии L.

-вторая функция цены покрытия(учитывает число кубов)

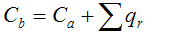
Задача минимизации: Найти такое покрытие L комплекса K(f), цена которого будет минимальна — минимизация в смысле Квайне.

Задача решается алгебраически, вводится свой математический аппарат. Это аппарат исчисления кубических комплексов (задает операции над кубами).

Каждая операция проходит в два этапа:

I Этап. Предварительное вычисление путем покоординатной обработки кубов по правилам, задаваемым с помощью таблиц покоординатной обработки.

II Этап. Окончательный.

Зададим операции над кубами:
a = (a₁ a₂ … a_n)

b = (b₁ b₂ … b_n)

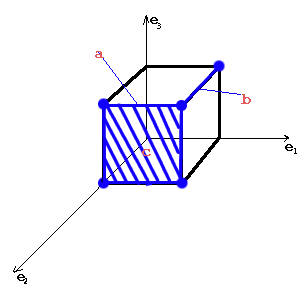
Операция *: c=a*b

По содержанию * — это нахождение куба некоторой размерности r, грани которого содержаться в кубах a и b.

c_i=a_i*b_i
	0	1	x
0	0	y	0
1	y	1	1
x	0	1	x

a*b =		∅, если ∑α_i^c_i>1
c, если ∑α_i^c_i≤1

где α_i^c_i =		0, c_i≠y
1, c_i=y

c = ([a₁*b₁] … [a_n*b_n]).

При чем, если результат операции — y, то y заменяется на x.

(101)*(111)
после предварительной обработки:
=(1y1)
Окончательный вариант:
=(1×1)

(x11)*(101)=(1×1)

(x10)
(101)
(1yy)
∅	— нет общих граней

Операция пересечения кубов.

c = a ∩ b

покоординатно!

c_i=a_i∩b_i
	0	1	x
0	0	∅	0
1	∅	1	1
x	0	1	x

a ∩ b =		∅, если ∃i (a_i∩b_i = ∅
c в противном случае

Пересечение — нахождение общей части булева пространства, покрываемой этими кубами (т.е. куба или грани какого-то уровня)

(1×1)∩(x1x)=(111)

Операция вычитания кубов (#).

c_i=a_i#b_i
	0	1	x
0	z	y	z
1	y	z	z
x	1	0	z

* и ∪ обладают свойством коммутативности, но a#b ≠ b#a !

Операция вычитания кубов удаляет из куба a общую часть кубов уменьшаемого и вычитаемого (т.е. пересечение кубов a и b).

В результате вычитания можем иметь несколько кубов.

Если куб a входит в куб b, то результат — ∅

Пример:

a#b = (1×1)#(x11) = (z0z) = (101)

c#b = (1xx)#(x11) = (z00) = {(10x),(1×0)}

Нахождение множества простых импликант

K(f)=K⁰∪K¹∪…∪Kⁱ∪…∪K^n-1 — комплекс K функции f

z⊆K является простой импликантой этого комплекса, если δ_i(z)=∅ (δ_i — оператор сограней), то есть не существует какого-либо другого куба, который бы включал в себя исходный куб z.

Z(f)={z} — множество импликант для функции f

Необходимо получить весь комплекс K функции f, используя операторы граней и сограней.

Берем куб z из K и проверяем, есть ли какой-то куб, гранью которого является рассматриваемый.

Операция *(«звездочка») позволяет получить множество Z — кубов, соответствующих простым импликантам функции.

Алгоритм (*) — нахождение множества кубов, соответствующих простым импликантам функции.

Предположим есть некоторый комплекс Ĉ₀, являющийся покрытием комплекса K(f), т.е.

Ĉ₀(f) — неупорядоченное покрытие

причем одна и та же единица функции может покрываться несколькими кубами
C₀ = Ĉ₀ — {c₁ | c₁ ∈ Ĉ₀ ∧ c₂ ∈ Ĉ₀ ∧ c₁ ⊆ c₂}

(тоже, что и поглощение в методе Квайне)
C₀*C₀ попарно
в результате 3) находится множество 0-кубов:
Z₀ = { c⁰ | c⁰ * C₀ не содержит никаких 1-кубов }

— это такие кубы, которые в результате операции * не дают никаких 1-кубов
вычисляется Ĉ₁:

Ĉ₁ = C₀ ∪ (C₀*C₀)
C₁ = Ĉ₁ — { c | c ⊆ d, c,d∈Ĉ₁ } — {0-кубы, получившиеся в результате операции *, и Z₀}

( (1×1)*(x11)= (111) )
C₁ * C₁
Z₁
Ĉ₂
C₂ (удаляем 0-кубы и 1-кубы)

и так далее (итерационный процесс)

Ĉ₀(f) — исходное покрытие K(f)

C₁(f) и т.д. в общем случае покрытием функции не являются

C₁(f) ∪ Z₀ ⊆ K — является покрытием K(f)

Алгоритм заканчивается, когда на каком-то шаге получаем множество C, содержащее один куб.

Результат — множество Z — множество простых импликант.

Z = ∪Z_i

Алгоритм извлечения

ИЗ множества простых импликант извлечь те (выбрать такое подмножество кубов) простые импликанты, которые:

Является покрытием исходного множества кубов функции;
С минимальной ценой покрытия, если покрытий несколько.

Для решения этой задачи исходные данные фактически — исходный комплекс функции, то есть некоторый исходный комплекс K⁰(f) и Z(f).

Определение: возьмем некоторую вершину d∈K₀. Говорят, что эта вершина является обособленной вершиной комплекса на множестве простых импликант Z, если существует такой куб z∈Z, что вершина d накрывается только этой импликантой z.

Такая импликанта будет простая. Вершина d называется различающей. А импликанта получила название экстремаль.

Любое минимальное покрытие содержит экстремали нулевого ранга.

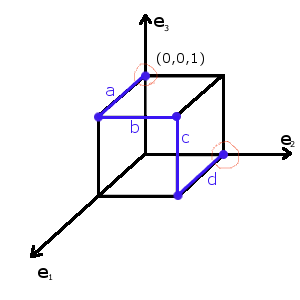
Пример:

Различающие вершины: (0;0;1) и (0;1;0)

E₀={ a, d}, осталось покрыть одну вершину — (1;1;1)

Задача минимизации: необходимо найти все обособленные вершины и выделить импликанты, накрывающие эти обособленные вершины.

Такие импликанты образуют множество экстремалей.

Задача решается, если известно K⁰(f), то есть все вершины.

В общем случае задачи минимизации функция задана некоторым комплексом K(f), который состоит не только из 0-кубов. Тогда можно найти все 0-кубы и решить задачу, а можно и не находить.

Некоторая простая импликанта e∈Z является экстремалью, если e∩K ≠ e∩U'(e,Z)∩K, а e∩K ≠ ∅,

U'(e,Z) = U(e,Z) — e,

U(e,Z) = { z | z∈Z, Z∩e ≠ ∅}.

Z — множество простых импликант,

U(e,Z) — окрестность куба e, т.е. все простые импликанты из Z, которые имеют общие части с импликантой e.

U'(e,Z) — окрестность без самой импликанты.

Функция может быть не полностью определена:

L — комплекс, где функция определена и равна 1,

D — комплекс, где значение функции не определено,

тогда K=L∪D.

но чаще экстремали вычисляют по одному соотношению:
[e#(Z-e)]∩K≠∅

e#(Z-e) — те вершины булева куба, которые накрываются только e и не накрываются всех оставшейся частью Z.

+ эти вершины присутствуют в комплексе K (или L для неполностью определенной функции)

Если из простой импликанты e удалить все подкубы (Z-e), и остается, по крайней мере, одна вершина булева куба, которая содержится в исходном комплексе функции, то оставшиеся вершины является выделенными, или отмеченными.

Алгоритм нахождения экстремалей также итерационный.

Нахождение множества экстремалей

Каждая простая импликанта проверяется на наличие в ней выделенной вершины, т.е. вычисляется e#(Z-e), если результат вычитания кубов не пустой, то такая импликанта может быть экстремалью.
Как правило, вычитание e#(Z-e) сводится в таблицу.
Каждый кандидат на экстремаль проверяется на пересечение с комплексом единичных значений функции.
Если результат пересечения не пустой, значит в L (комплексе единичных значений) имеются обособленные вершины, а e является экстремалью.

Получаем множество экстремалей нулевого ранга — E₀ = {e}. В смысле Квайна оно соответствует ядру функции.
Находим ₁ = Z₀ — E₀

Т.е. из множества простых импликант удаляем множество экстремалей нулевого ранга.

Находим L₁ = L₀ # E₀, т.е. находятся все вершины, не покрытые экстремалями.

₁ — оставшаяся часть множества простых импликант, неупорядоченное множество простых импликант.

Операция, которая позволяет сократить в последующем перебор и исключить из _i не максимальные кубы — упорядочивание.

Пусть u∈₁, v∈₁. Говорят, что u1 удовлетворяет условию u∩L₁ ⊆ v∩L₁.

( вершины из L₁, покрываемые u, покрываются и кубов v )

В этом случае из кубов u,v выбираем при упорядочивание куб v.

Если кубы разной размерности, а вершины покрывают одинаковые — то оставляем куб большей размерности ( цена = n — r ).

Таким образом, ₁ => Z₁ (находится Z₁ — упорядоченной множество оставшихся простых импликант), применением процедуры упорядочивания.
Остались Z₁ и L₁
(Z₁,L₁) => E₁ по тому же алгоритму.

Затем ₂ => Z₂; L₂ = L₁#E₁; (Z₂,L₂) => E₂ и т.д.

Два варианта окончания алгоритма:

L = ∅ => покрытие единственное

E = ∪E_i
L ≠ ∅ Если проверка на экстремальность не дает результата, т.е. ни одна простая импликанта не содержит квазеопорных вершин, а операция упорядочивания не дает результата.

Пример:

В этом случае не остается никакого другого варианта решения, кроме волюнтаристского.

Берется любая простая импликанта, для которой выдвигается две гипотезы (Алгоритм ветвления):
1. простая импликанта входит в минимальное покрытие
  e∈E
  
  находим L_i+1=L_i#{e}, упорядочиваем Z и вновь применяем алгоритм извлечения (возможно еще ветвление).
2. простая импликанта не входит в минимальное покрытие
  e∉E
  
  удаляем e из Z_i (находим _i+1), упорядочиваем _i+1 => Z_i+1
  
  L_i+1 = L_i
  
  И применяем алгоритм извлечения.
Таким образом, при ветвление получаем множество покрытий, сравниваем по цене и выбираем наименьшей.

Все вычисления в ручном варианте сводятся к вычислениям над таблицами.

Минимизация функции методом кубических покрытий.

Рассмотрим комплекс кубов К(f) = L D, где L – множество единичных наборов, D – множество наборов, на которых ДНФ не определена.

Будем выполнять операцию «*» для получения множества простых импликант.

Таблица операции C₀*C₀

	0000	0010	0100	0110	1010	1100	1101	1110
0000	—	00×0	0x00	Ø	Ø	Ø	Ø	Ø
0010	00×0	—	Ø	0x10	x010	Ø	Ø	Ø
0100	0x00	Ø	—	01×0	Ø	x100	Ø	Ø
0110	Ø	0x10	01×0	—	Ø	Ø	Ø	x110
1010	Ø	x010	Ø	Ø	—	Ø	Ø	1×10
1100	Ø	Ø	x100	Ø	Ø	—	110x	11×0
1101	Ø	Ø	Ø	Ø	Ø	110x	—	Ø
1110	Ø	Ø	Ø	x110	1×10	11×0	Ø	—

Z₀=Ø
Ĉ₁=C₀∪(C₀*C₀)
C₁=>

Таблица операции C₁*C₁

	00×0	0x00	0x10	x010	01×0	x100	x110	1×10	110x	11×0
00×0	—	0000	0010	0010	0xx0	0x00	0x10	x010	Ø	Ø
0x00	0000	—	0xx0	00×0	0100	0100	01×0	Ø	x100	x100
0x10	0010	0xx0	—	0010	0110	01×0	0110	xx10	Ø	x110
x010	0010	00×0	0010	—	0x10	Ø	xx10	1010	Ø	1×10
01×0	0xx0	0100	0110	0x10	—	0100	0110	x110	x100	x1x0
x100	0x00	0100	01×0	Ø	0100	—	x1x0	11×0	1100	1100
x110	0x10	01×0	0110	xx10	0110	x1x0	—	1110	11×0	1110
1×10	x010	Ø	xx10	1010	x110	11×0	1110	—	11×0	1110
110x	Ø	x100	Ø	Ø	x100	1100	11×0	11×0	—	1100
11×0	Ø	x100	x110	1×10	x1x0	1100	1110	1110	1100	—

Z₁=
Ĉ₂=C₁∪(C₁*C₁)
C₂=>

Таблица операции C₂*C₂

	0xx0	xx10	x1x0
0xx0	—	0x10	01×0
xx10	0x10	—	x110
x1x0	01×0	x110	—

Z₂=
Ĉ₃=C₂∪(C₂*C₂)
C₃=>Ø
Z = Z₀∪Z₁∪Z₂
Z=>

Нахождение тупиковых форм.

Таблица операции вычитания

	110x	0xx0	xx10	x1x0
110x	—	110x	110x	1101	v
0xx0	0xx0	—	0x00	0000	v
xx10	xx10	1×10	—	1010	v
x1x0	x110 01×0	1110	Ø	—

E₀:
L₁=L₀#E₀

Получение L₁:

	110x	0xx0	xx10
0000 0010 0100 0110 1010 1100 1101 1110	0000 0010 0100 0110 1010 1110	1010 1110	Ø

L₁:Ø
₁=Z₀-E₀

₁ => Z₁
Z₁:

МДНФ: v v , цена=7

Содержание

Постановка задачи
Решение задачи
1. Анализ переключательной функции
2. Метод Квайна
3. Карты Карно
4. Кубические покрытия
Анализ полученных результатов
Список литературы

1. Постановка задачи

Минимизировать переключательную функцию шести аргументов. Функция задана в виде наборов, на которых значения функции равны единице либо не определены. Наборы задаются в шестнадцатеричной системе счисления. В скобках заданы наборы, на которых значение функции не определено:

y => (2) v (3B) v (20) v (21) v (1D) v (6) v (1B) v (D) v (24) v (2C) v (23) v (B) v 36 v 1C v 3A v 7 v A v 8 v 10 v 38 v 12 v 15 v 5 v 1F v 3F v 1A v 17 v 3E v 3D v 39 v 9 v 37 v 19 v 2A v 11 v 18 v 4 v 3C v 2E v 29 v 0 v 2D v 28 v 25 v 14 v 1E

Необходимо выполнить следующие задачи:

Доопределить функцию нулями, минимизировать полученную функцию методом Квайна;
Доопределить функцию единицами и произвести минимизацию, используя карты Карно;
Минимизировать исходную функцию методом кубических покрытий;
Проанализировать полученные результаты;

2. Решение задачи

2.1 Анализ переключательной функции

Представим исходную последовательность в виде таблицы истинности.

Исходная последовательность:

(2) v (3B) v (20) v (21) v (1D) v (6) v (1B) v (D) v (24) v (2C) v (23) v (B) v 36 v 1C v 3A v 7 v A v 8 v 10 v 38 v 12 v 15 v 5 v 1F v 3F v 1A v 17 v 3E v 3D v 39 v 9 v 37 v 19 v 2A v 11 v 18 v 4 v 3C v 2E v 29 v 0 v 2D v 28 v 25 v 14 v 1E

Таблица истинности исходной функции

Набор	Значение исходной функции	Набор	Значение исходной функции
`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆
000000	1	100000	?
000001	0	100001	?
000010	?	100010	0
000011	0	100011	?
000100	1	100100	?
000101	1	100101	1
000110	?	100110	0
000111	1	100111	0
001000	1	101000	1
001001	1	101001	1
001010	1	101010	1
001011	?	101011	0
001100	0	101100	?
001101	?	101101	1
001110	0	101110	1
001111	0	101111	0
010000	1	110000	0
010001	1	110001	0
010010	1	110010	0
010011	0	110011	0
010100	1	110100	0
010101	1	110101	0
010110	0	110110	1
010111	1	110111	1
011000	1	111000	1
011001	1	111001	1
011010	1	111010	1
011011	?	111011	?
011100	1	111100	1
011101	?	111101	1
011110	1	111110	1
011111	1	111111	1

‘?’ обозначено значение наборов, на которых функция не определена.

Цена ДНФ является суммой длин всех входящих в нее конъюнкций.

2.2 Минимизация функции методом Квайна.

Доопределим функцию нулями, получим конституэнты единицы, затем выполним операции попарного неполного склеивания и элементарного поглощения.

No	Эл. Конъюнкция	Поглощение
1	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
2	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
3	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
4	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
5	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
6	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
7	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
8	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
9	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
10	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
11	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
12	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
13	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
14	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
15	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
16	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
17	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
18	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
19	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
20	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
21	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
22	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
23	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
24	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
25	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
26	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
27	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
28	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
29	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
30	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
31	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
32	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
33	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+
34	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	+

Номера скл.	Результат склеивания
1 — 2	`x`₁`x`₂`x`₃`x`₅`x`₆
1 — 5	`x`₁`x`₂`x`₄`x`₅`x`₆
1 — 8	`x`₁`x`₃`x`₄`x`₅`x`₆
2 — 3	`x`₁`x`₂`x`₃`x`₄`x`₅
2 — 11	`x`₁`x`₃`x`₄`x`₅`x`₆
3 — 4	`x`₁`x`₂`x`₃`x`₄`x`₆
3 — 12	`x`₁`x`₃`x`₄`x`₅`x`₆
3 — 20	`x`₂`x`₃`x`₄`x`₅`x`₆
4 — 13	`x`₁`x`₃`x`₄`x`₅`x`₆
5 — 6	`x`₁`x`₂`x`₃`x`₄`x`₅
5 — 7	`x`₁`x`₂`x`₃`x`₄`x`₆
5 — 14	`x`₁`x`₃`x`₄`x`₅`x`₆
5 — 21	`x`₂`x`₃`x`₄`x`₅`x`₆
6 — 15	`x`₁`x`₃`x`₄`x`₅`x`₆
6 — 22	`x`₂`x`₃`x`₄`x`₅`x`₆
7 — 16	`x`₁`x`₃`x`₄`x`₅`x`₆
7 — 23	`x`₂`x`₃`x`₄`x`₅`x`₆
8 — 9	`x`₁`x`₂`x`₃`x`₄`x`₅
8 — 10	`x`₁`x`₂`x`₃`x`₄`x`₆
8 — 11	`x`₁`x`₂`x`₃`x`₅`x`₆
8 — 14	`x`₁`x`₂`x`₄`x`₅`x`₆
9 — 12	`x`₁`x`₂`x`₃`x`₅`x`₆
9 — 15	`x`₁`x`₂`x`₄`x`₅`x`₆
10 — 16	`x`₁`x`₂`x`₄`x`₅`x`₆
11 — 12	`x`₁`x`₂`x`₃`x`₄`x`₅
11 — 17	`x`₁`x`₂`x`₄`x`₅`x`₆
12 — 13	`x`₁`x`₂`x`₃`x`₄`x`₆
13 — 19	`x`₁`x`₂`x`₄`x`₅`x`₆
13 — 27	`x`₂`x`₃`x`₄`x`₅`x`₆
14 — 15	`x`₁`x`₂`x`₃`x`₄`x`₅
14 — 16	`x`₁`x`₂`x`₃`x`₄`x`₆
14 — 17	`x`₁`x`₂`x`₃`x`₅`x`₆
14 — 28	`x`₂`x`₃`x`₄`x`₅`x`₆
15 — 29	`x`₂`x`₃`x`₄`x`₅`x`₆
16 — 18	`x`₁`x`₂`x`₃`x`₅`x`₆
16 — 30	`x`₂`x`₃`x`₄`x`₅`x`₆
17 — 18	`x`₁`x`₂`x`₃`x`₄`x`₆
17 — 31	`x`₂`x`₃`x`₄`x`₅`x`₆
18 — 19	`x`₁`x`₂`x`₃`x`₄`x`₅
18 — 33	`x`₂`x`₃`x`₄`x`₅`x`₆
19 — 34	`x`₂`x`₃`x`₄`x`₅`x`₆
20 — 24	`x`₁`x`₂`x`₄`x`₅`x`₆
21 — 22	`x`₁`x`₂`x`₃`x`₄`x`₅
21 — 23	`x`₁`x`₂`x`₃`x`₄`x`₆
21 — 28	`x`₁`x`₃`x`₄`x`₅`x`₆
22 — 24	`x`₁`x`₂`x`₃`x`₅`x`₆
22 — 29	`x`₁`x`₃`x`₄`x`₅`x`₆
23 — 25	`x`₁`x`₂`x`₃`x`₅`x`₆
23 — 30	`x`₁`x`₃`x`₄`x`₅`x`₆
24 — 32	`x`₁`x`₃`x`₄`x`₅`x`₆
25 — 33	`x`₁`x`₃`x`₄`x`₅`x`₆
26 — 27	`x`₁`x`₂`x`₃`x`₄`x`₅
26 — 33	`x`₁`x`₂`x`₄`x`₅`x`₆
27 — 34	`x`₁`x`₂`x`₄`x`₅`x`₆
28 — 29	`x`₁`x`₂`x`₃`x`₄`x`₅
28 — 30	`x`₁`x`₂`x`₃`x`₄`x`₆
28 — 31	`x`₁`x`₂`x`₃`x`₅`x`₆
29 — 32	`x`₁`x`₂`x`₃`x`₅`x`₆
30 — 33	`x`₁`x`₂`x`₃`x`₅`x`₆
31 — 32	`x`₁`x`₂`x`₃`x`₄`x`₅
31 — 33	`x`₁`x`₂`x`₃`x`₄`x`₆
32 — 34	`x`₁`x`₂`x`₃`x`₄`x`₆
33 — 34	`x`₁`x`₂`x`₃`x`₄`x`₅

No	Эл. Конъюнкция	Поглощение
1	`x`₁`x`₂`x`₃`x`₅`x`₆	+
2	`x`₁`x`₂`x`₄`x`₅`x`₆	+
3	`x`₁`x`₃`x`₄`x`₅`x`₆	+
4	`x`₁`x`₂`x`₃`x`₄`x`₅	+
5	`x`₁`x`₃`x`₄`x`₅`x`₆	+
6	`x`₁`x`₂`x`₃`x`₄`x`₆	+
7	`x`₁`x`₃`x`₄`x`₅`x`₆	+
8	`x`₂`x`₃`x`₄`x`₅`x`₆	—
9	`x`₁`x`₃`x`₄`x`₅`x`₆	+
10	`x`₁`x`₂`x`₃`x`₄`x`₅	+
11	`x`₁`x`₂`x`₃`x`₄`x`₆	+
12	`x`₁`x`₃`x`₄`x`₅`x`₆	+
13	`x`₂`x`₃`x`₄`x`₅`x`₆	+
14	`x`₁`x`₃`x`₄`x`₅`x`₆	+
15	`x`₂`x`₃`x`₄`x`₅`x`₆	+
16	`x`₁`x`₃`x`₄`x`₅`x`₆	+
17	`x`₂`x`₃`x`₄`x`₅`x`₆	+
18	`x`₁`x`₂`x`₃`x`₄`x`₅	+
19	`x`₁`x`₂`x`₃`x`₄`x`₆	+
20	`x`₁`x`₂`x`₃`x`₅`x`₆	+
21	`x`₁`x`₂`x`₄`x`₅`x`₆	+
22	`x`₁`x`₂`x`₃`x`₅`x`₆	+
23	`x`₁`x`₂`x`₄`x`₅`x`₆	+
24	`x`₁`x`₂`x`₄`x`₅`x`₆	+
25	`x`₁`x`₂`x`₃`x`₄`x`₅	+
26	`x`₁`x`₂`x`₄`x`₅`x`₆	+
27	`x`₁`x`₂`x`₃`x`₄`x`₆	+
28	`x`₁`x`₂`x`₄`x`₅`x`₆	+
29	`x`₂`x`₃`x`₄`x`₅`x`₆	+
30	`x`₁`x`₂`x`₃`x`₄`x`₅	+
31	`x`₁`x`₂`x`₃`x`₄`x`₆	+
32	`x`₁`x`₂`x`₃`x`₅`x`₆	+
33	`x`₂`x`₃`x`₄`x`₅`x`₆	+
34	`x`₂`x`₃`x`₄`x`₅`x`₆	+
35	`x`₁`x`₂`x`₃`x`₅`x`₆	+
36	`x`₂`x`₃`x`₄`x`₅`x`₆	+
37	`x`₁`x`₂`x`₃`x`₄`x`₆	+
38	`x`₂`x`₃`x`₄`x`₅`x`₆	+
39	`x`₁`x`₂`x`₃`x`₄`x`₅	+
40	`x`₂`x`₃`x`₄`x`₅`x`₆	+
41	`x`₂`x`₃`x`₄`x`₅`x`₆	+
42	`x`₁`x`₂`x`₄`x`₅`x`₆	—
43	`x`₁`x`₂`x`₃`x`₄`x`₅	+
44	`x`₁`x`₂`x`₃`x`₄`x`₆	+
45	`x`₁`x`₃`x`₄`x`₅`x`₆	+
46	`x`₁`x`₂`x`₃`x`₅`x`₆	+
47	`x`₁`x`₃`x`₄`x`₅`x`₆	+
48	`x`₁`x`₂`x`₃`x`₅`x`₆	+
49	`x`₁`x`₃`x`₄`x`₅`x`₆	+
50	`x`₁`x`₃`x`₄`x`₅`x`₆	+
51	`x`₁`x`₃`x`₄`x`₅`x`₆	+
52	`x`₁`x`₂`x`₃`x`₄`x`₅	+
53	`x`₁`x`₂`x`₄`x`₅`x`₆	+
54	`x`₁`x`₂`x`₄`x`₅`x`₆	+
55	`x`₁`x`₂`x`₃`x`₄`x`₅	+
56	`x`₁`x`₂`x`₃`x`₄`x`₆	+
57	`x`₁`x`₂`x`₃`x`₅`x`₆	+
58	`x`₁`x`₂`x`₃`x`₅`x`₆	+
59	`x`₁`x`₂`x`₃`x`₅`x`₆	+
60	`x`₁`x`₂`x`₃`x`₄`x`₅	+
61	`x`₁`x`₂`x`₃`x`₄`x`₆	+
62	`x`₁`x`₂`x`₃`x`₄`x`₆	+
63	`x`₁`x`₂`x`₃`x`₄`x`₅	+

Номера скл.	Результат склеивания
1 — 20	`x`₁`x`₃`x`₅`x`₆
2 — 21	`x`₁`x`₄`x`₅`x`₆
3 — 5	`x`₁`x`₃`x`₅`x`₆
3 — 12	`x`₁`x`₄`x`₅`x`₆
4 — 25	`x`₁`x`₃`x`₄`x`₅
5 — 7	`x`₁`x`₃`x`₄`x`₅
6 — 27	`x`₁`x`₃`x`₄`x`₆
7 — 9	`x`₁`x`₃`x`₄`x`₆
10 — 30	`x`₁`x`₃`x`₄`x`₅
10 — 43	`x`₂`x`₃`x`₄`x`₅
11 — 31	`x`₁`x`₃`x`₄`x`₆
11 — 44	`x`₂`x`₃`x`₄`x`₆
12 — 14	`x`₁`x`₃`x`₄`x`₅
12 — 16	`x`₁`x`₃`x`₄`x`₆
12 — 45	`x`₃`x`₄`x`₅`x`₆
13 — 15	`x`₂`x`₃`x`₄`x`₅
13 — 17	`x`₂`x`₃`x`₄`x`₆
13 — 33	`x`₃`x`₄`x`₅`x`₆
14 — 47	`x`₃`x`₄`x`₅`x`₆
15 — 34	`x`₃`x`₄`x`₅`x`₆
16 — 49	`x`₃`x`₄`x`₅`x`₆
17 — 36	`x`₃`x`₄`x`₅`x`₆
18 — 25	`x`₁`x`₂`x`₃`x`₅
18 — 30	`x`₁`x`₂`x`₄`x`₅
19 — 31	`x`₁`x`₂`x`₄`x`₆
20 — 22	`x`₁`x`₂`x`₃`x`₅
20 — 32	`x`₁`x`₂`x`₅`x`₆
21 — 23	`x`₁`x`₂`x`₄`x`₅
21 — 24	`x`₁`x`₂`x`₄`x`₆
21 — 26	`x`₁`x`₂`x`₅`x`₆
28 — 54	`x`₂`x`₄`x`₅`x`₆
29 — 41	`x`₂`x`₄`x`₅`x`₆
30 — 55	`x`₂`x`₃`x`₄`x`₅
31 — 37	`x`₁`x`₂`x`₃`x`₆
31 — 56	`x`₂`x`₃`x`₄`x`₆
32 — 35	`x`₁`x`₂`x`₃`x`₆
32 — 57	`x`₂`x`₃`x`₅`x`₆
33 — 34	`x`₂`x`₃`x`₄`x`₅
33 — 36	`x`₂`x`₃`x`₄`x`₆
33 — 38	`x`₂`x`₃`x`₅`x`₆
35 — 59	`x`₂`x`₃`x`₅`x`₆
36 — 40	`x`₂`x`₃`x`₅`x`₆
37 — 61	`x`₂`x`₃`x`₄`x`₆
38 — 40	`x`₂`x`₃`x`₄`x`₆
39 — 63	`x`₂`x`₃`x`₄`x`₅
40 — 41	`x`₂`x`₃`x`₄`x`₅
43 — 55	`x`₁`x`₃`x`₄`x`₅
44 — 56	`x`₁`x`₃`x`₄`x`₆
45 — 47	`x`₁`x`₃`x`₄`x`₅
45 — 49	`x`₁`x`₃`x`₄`x`₆
46 — 58	`x`₁`x`₃`x`₅`x`₆
47 — 50	`x`₁`x`₃`x`₅`x`₆
48 — 59	`x`₁`x`₃`x`₅`x`₆
49 — 51	`x`₁`x`₃`x`₅`x`₆
52 — 63	`x`₁`x`₂`x`₄`x`₅
53 — 54	`x`₁`x`₂`x`₄`x`₅
55 — 60	`x`₁`x`₂`x`₃`x`₅
56 — 61	`x`₁`x`₂`x`₃`x`₆
57 — 58	`x`₁`x`₂`x`₃`x`₅
57 — 59	`x`₁`x`₂`x`₃`x`₆
60 — 63	`x`₁`x`₂`x`₃`x`₄
61 — 62	`x`₁`x`₂`x`₃`x`₄

В результате на данном шаге получаем простые импликанты:
x₂x₃x₄x₅x₆ , x₁x₂x₄x₅x₆

No	Эл. Конъюнкция	Поглощение
1	`x`₁`x`₃`x`₅`x`₆	—
2	`x`₁`x`₄`x`₅`x`₆	—
3	`x`₁`x`₃`x`₄`x`₅	—
4	`x`₁`x`₃`x`₄`x`₆	—
5	`x`₁`x`₃`x`₄`x`₅	+
6	`x`₂`x`₃`x`₄`x`₅	+
7	`x`₁`x`₃`x`₄`x`₆	+
8	`x`₂`x`₃`x`₄`x`₆	+
9	`x`₃`x`₄`x`₅`x`₆	+
10	`x`₃`x`₄`x`₅`x`₆	+
11	`x`₃`x`₄`x`₅`x`₆	+
12	`x`₁`x`₂`x`₃`x`₅	—
13	`x`₁`x`₂`x`₄`x`₅	—
14	`x`₁`x`₂`x`₄`x`₆	—
15	`x`₁`x`₂`x`₅`x`₆	—
16	`x`₂`x`₄`x`₅`x`₆	—
17	`x`₂`x`₃`x`₄`x`₅	+
18	`x`₁`x`₂`x`₃`x`₆	+
19	`x`₂`x`₃`x`₄`x`₆	+
20	`x`₂`x`₃`x`₅`x`₆	+
21	`x`₂`x`₃`x`₅`x`₆	+
22	`x`₂`x`₃`x`₄`x`₆	+
23	`x`₂`x`₃`x`₄`x`₅	—
24	`x`₁`x`₃`x`₄`x`₅	+
25	`x`₁`x`₃`x`₄`x`₆	+
26	`x`₁`x`₃`x`₅`x`₆	—
27	`x`₁`x`₃`x`₅`x`₆	—
28	`x`₁`x`₂`x`₄`x`₅	—
29	`x`₁`x`₂`x`₃`x`₅	—
30	`x`₁`x`₂`x`₃`x`₆	+
31	`x`₁`x`₂`x`₃`x`₄	—

Номера скл.	Результат склеивания
5 — 24	`x`₃`x`₄`x`₅
6 — 17	`x`₃`x`₄`x`₅
7 — 25	`x`₃`x`₄`x`₆
8 — 19	`x`₃`x`₄`x`₆
9 — 10	`x`₃`x`₄`x`₅
9 — 11	`x`₃`x`₄`x`₆
18 — 30	`x`₂`x`₃`x`₆
19 — 22	`x`₂`x`₃`x`₆
20 — 21	`x`₂`x`₃`x`₆

В результате на данном шаге получаем простые импликанты:
x₁x₃x₅x₆ , x₁x₄x₅x₆ , x₁x₃x₄x₅ , x₁x₃x₄x₆ , x₁x₂x₃x₅ , x₁x₂x₄x₅ , x₁x₂x₄x₆ , x₁x₂x₅x₆ , x₂x₄x₅x₆ , x₂x₃x₄x₅ , x₁x₃x₅x₆ , x₁x₃x₅x₆ , x₁x₂x₄x₅ , x₁x₂x₃x₅ , x₁x₂x₃x₄

No	Эл. Конъюнкция	Поглощение
1	`x`₃`x`₄`x`₅	—
2	`x`₃`x`₄`x`₆	—
3	`x`₂`x`₃`x`₆	—

В результате на данном шаге получаем простые импликанты:
x₃x₄x₅ , x₃x₄x₆ , x₂x₃x₆

СкДНФ:
x₂x₃x₄x₅x₆ v x₁x₂x₄x₅x₆ v x₁x₃x₅x₆ v x₁x₄x₅x₆ v x₁x₃x₄x₅ v x₁x₃x₄x₆ v x₁x₂x₃x₅ v x₁x₂x₄x₅ v x₁x₂x₄x₆ v x₁x₂x₅x₆ v x₂x₄x₅x₆ v x₂x₃x₄x₅ v x₁x₃x₅x₆ v x₁x₃x₅x₆ v x₁x₂x₄x₅ v x₁x₂x₃x₅ v x₁x₂x₃x₄ v x₃x₄x₅ v x₃x₄x₆ v x₂x₃x₆

Нахождение тупиковых форм.

Обозначения:

Единицы ДНФ, покрываемые импликантами СкДНФ, обозначаются «+».Импликанты, попадающие в ядро помечаются «*».
Единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант, помечаются “>”.
Единицы функции, покрываемые ядром, но не покрываемые только какой-то одной импликантой из системы простых импликант, помечаются “>>”.

x₁x₂x₃x₄x₅x₆

x₁x₂x₃x₄x₅x₆^>>

x₁x₂x₃x₄x₅x₆^>

x₁x₂x₃x₄x₅x₆^>>

x₁x₂x₃x₄x₅x₆^>

x₁x₂x₃x₄x₅x₆^>>

x₁x₂x₃x₄x₅x₆

x₁x₂x₃x₄x₅x₆^>

x₁x₂x₃x₄x₅x₆

x₁x₂x₃x₄x₅x₆^>>

x₁x₂x₃x₄x₅x₆

x₁x₂x₃x₄x₅x₆^>>

x₁x₂x₃x₄x₅x₆

x₁x₂x₃x₄x₅x₆^>

x₁x₂x₃x₄x₅x₆^>>

x₁x₂x₃x₄x₅x₆

x₁x₂x₃x₄x₅x₆^>>

x₂x₃x₄x₅x₆

x₁x₂x₄x₅x₆

x₁x₃x₅x₆

x₁x₄x₅x₆

x₁x₃x₄x₅

x₁x₃x₄x₆^*

x₁x₂x₃x₅

x₁x₂x₄x₅

x₁x₂x₄x₆^*

x₁x₂x₅x₆

x₂x₄x₅x₆

x₂x₃x₄x₅

x₁x₃x₅x₆

x₁x₃x₅x₆^*

x₁x₂x₄x₅^*

x₁x₂x₃x₅

x₁x₂x₃x₄

x₃x₄x₅^*

x₃x₄x₆^*

x₂x₃x₆

Ядро: x₁x₃x₄x₆ v x₁x₂x₄x₆ v x₁x₃x₅x₆ v x₁x₂x₄x₅ v x₃x₄x₅ v x₃x₄x₆
До упорядочивания:

	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆
`x`₂`x`₃`x`₄`x`₅`x`₆								+
`x`₁`x`₂`x`₄`x`₅`x`₆								+	+
`x`₁`x`₃`x`₅`x`₆	+	+		+
`x`₁`x`₄`x`₅`x`₆	+
`x`₁`x`₃`x`₄`x`₅		+		+
`x`₁`x`₂`x`₃`x`₅			+	+
`x`₁`x`₂`x`₄`x`₅			+
`x`₁`x`₂`x`₅`x`₆				+	+
`x`₂`x`₄`x`₅`x`₆							+
`x`₂`x`₃`x`₄`x`₅						+	+
`x`₁`x`₃`x`₅`x`₆									+		+
`x`₁`x`₂`x`₃`x`₅										+	+
`x`₁`x`₂`x`₃`x`₄										+	+
`x`₂`x`₃`x`₆					+	+				+

После упорядочивания:

	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆^>	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆^>	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆^>	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆^>>	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆^>>	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆^>	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆^>	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆^>>	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆
`x`₁`x`₂`x`₄`x`₅`x`₆^*								+	+
`x`₁`x`₃`x`₅`x`₆^*	+	+		+
`x`₁`x`₂`x`₃`x`₅^*			+	+
`x`₁`x`₂`x`₅`x`₆				+	+
`x`₂`x`₃`x`₄`x`₅^*						+	+
`x`₁`x`₃`x`₅`x`₆									+		+
`x`₁`x`₂`x`₃`x`₅										+	+
`x`₂`x`₃`x`₆					+	+				+

Псевдоядро: x₁x₂x₄x₅x₆ v x₁x₃x₅x₆ v x₁x₂x₃x₅ v x₂x₃x₄x₅
До упорядочивания:

	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆
`x`₁`x`₂`x`₅`x`₆	+
`x`₁`x`₃`x`₅`x`₆			+
`x`₁`x`₂`x`₃`x`₅		+	+
`x`₂`x`₃`x`₆	+	+

После упорядочивания:

	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆^>	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆^>>	`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆^>
`x`₁`x`₂`x`₃`x`₅^*		+	+
`x`₂`x`₃`x`₆^*	+	+

Псевдоядро: x₁x₂x₃x₅ v x₂x₃x₆

МДНФ: x₁x₃x₄x₆ v x₁x₂x₄x₆ v x₁x₃x₅x₆ v x₁x₂x₄x₅ v x₃x₄x₅ v x₃x₄x₆ v x₁x₂x₄x₅x₆ v x₁x₃x₅x₆ v x₁x₂x₃x₅ v x₂x₃x₄x₅ v x₁x₂x₃x₅ v x₂x₃x₆, цена=46

2.3 Минимизация функции методом Карт Карно.

Дополним функцию единицами и построим Карты Карно.

Компактных групп размера 16 — 1
Компактных групп размера 8 — 9
Компактных групп размера 4 — 13
Компактных групп размера 2 — 1

Нахождение тупиковых форм.

Обозначения:

Ядро: x₁x₂x₃x₄x₆ v x₁x₂x₄x₅ v x₁x₄x₆ v x₁x₃x₄ v x₁x₂x₅ v x₁x₃x₆ v x₂x₃
Псевдоядро: x₁x₂x₃x₄ v x₁x₃x₄x₆
Псевдоядро: x₁x₂x₅
Псевдоядро: x₃x₅x₆
МДНФ: x₁x₂x₃x₄x₆ v x₁x₂x₄x₅ v x₁x₄x₆ v x₁x₃x₄ v x₁x₂x₅ v x₁x₃x₆ v x₂x₃ v x₁x₂x₃x₄ v x₁x₃x₄x₆ v x₁x₂x₅ v x₃x₅x₆, цена=37

2.4 Минимизация функции методом кубических покрытий.

Будем выполнять операцию «*» для получения множества простых импликант.

K(f) =

000000, 000010, 000100
000101, 000110, 000111
001000, 001001, 001010
001011, 001101, 010000
010001, 010010, 010100
010101, 010111, 011000
011001, 011010, 011011
011100, 011101, 011110
011111, 100000, 100001
100011, 100100, 100101
101000, 101001, 101010
101100, 101101, 101110
110110, 110111, 111000
111001, 111010, 111011
111100, 111101, 111110
111111

=> C₀ =>

Таблица операции C₀*C₀

000000

000010

000100

000101

000110

000111

001000

001001

001010

001011

001101

010000

010001

010010

010100

010101

010111

011000

011001

011010

011011

011100

011101

011110

011111

100000

100001

100011

100100

100101

101000

101001

101010

101100

101101

101110

110110

110111

111000

111001

111010

111011

111100

111101

111110

111111

000000

—

0000×0

000×00

00×000

0x0000

x00000

000010

0000×0

—

000×10

00×010

0x0010

000100

000×00

—

00010x

0001×0

0x0100

x00100

000101

00010x

—

0001×1

00×101

0x0101

x00101

000110

000×10

0001×0

—

00011x

000111

0001×1

00011x

—

0x0111

001000

00×000

—

00100x

0010×0

0x1000

x01000

001001

00100x

—

0010×1

001×01

0x1001

x01001

001010

00×010

0010×0

—

00101x

0x1010

x01010

001011

0010×1

00101x

—

0x1011

001101

00×101

001×01

—

0x1101

x01101

010000

0x0000

—

01000x

0100×0

010×00

01×000

010001

01000x

—

010×01

01×001

010010

0x0010

0100×0

—

01×010

010100

0x0100

010×00

—

01010x

01×100

010101

0x0101

010×01

01010x

—

0101×1

01×101

010111

0x0111

0101×1

—

01×111

x10111

011000

0x1000

01×000

—

01100x

0110×0

011×00

x11000

011001

0x1001

01×001

01100x

—

0110×1

011×01

x11001

011010

0x1010

01×010

0110×0

—

01101x

011×10

x11010

011011

0x1011

0110×1

01101x

—

011×11

x11011

011100

01×100

011×00

—

01110x

0111×0

x11100

011101

0x1101

01×101

011×01

01110x

—

0111×1

x11101

011110

011×10

0111×0

—

01111x

x11110

011111

01×111

011×11

0111×1

01111x

—

x11111

100000

x00000

—

10000x

100×00

10×000

100001

10000x

—

1000×1

100×01

10×001

100011

1000×1

—

100100

x00100

100×00

—

10010x

10×100

100101

x00101

100×01

10010x

—

10×101

101000

x01000

10×000

—

10100x

1010×0

101×00

1×1000

101001

x01001

10×001

10100x

—

101×01

1×1001

101010

x01010

1010×0

—

101×10

1×1010

101100

10×100

101×00

—

10110x

1011×0

1×1100

101101

x01101

10×101

101×01

10110x

—

1×1101

101110

101×10

1011×0

—

1×1110

110110

—

11011x

11×110

110111

x10111

11011x

—

11×111

111000

x11000

1×1000

—

11100x

1110×0

111×00

111001

x11001

1×1001

11100x

—

1110×1

111×01

111010

x11010

1×1010

1110×0

—

11101x

111×10

111011

x11011

1110×1

11101x

—

111×11

111100

x11100

1×1100

111×00

—

11110x

1111×0

111101

x11101

1×1101

111×01

11110x

—

1111×1

111110

x11110

1×1110

11×110

111×10

1111×0

—

11111x

111111

x11111

11×111

111×11

1111×1

11111x

—

Z₀=Ø
Ĉ₁=C₀∪(C₀*C₀)
C₁=>

0000×0, 000×00, 00×000
0x0000, x00000, 000×10
00×010, 0x0010, 00010x
0001×0, 0x0100, x00100
0001×1, 00×101, 0x0101
x00101, 00011x, 0x0111
00100x, 0010×0, 0x1000
x01000, 0010×1, 001×01
0x1001, x01001, 00101x
0x1010, x01010, 0x1011
0x1101, x01101, 01000x
0100×0, 010×00, 01×000
010×01, 01×001, 01×010
01010x, 01×100, 0101×1
01×101, 01×111, x10111
01100x, 0110×0, 011×00
x11000, 0110×1, 011×01
x11001, 01101x, 011×10
x11010, 011×11, x11011
01110x, 0111×0, x11100
0111×1, x11101, 01111x
x11110, x11111, 10000x
100×00, 10×000, 1000×1
100×01, 10×001, 10010x
10×100, 10×101, 10100x
1010×0, 101×00, 1×1000
101×01, 1×1001, 101×10
1×1010, 10110x, 1011×0
1×1100, 1×1101, 1×1110
11011x, 11×110, 11×111
11100x, 1110×0, 111×00
1110×1, 111×01, 11101x
111×10, 111×11, 11110x
1111×0, 1111×1, 11111x

Таблица операции C₁*C₁

0000×0

000×00

00×000

0x0000

x00000

000×10

00×010

0x0010

00010x

0001×0

0x0100

x00100

0001×1

00×101

0x0101

x00101

00011x

0x0111

00100x

0010×0

0x1000

x01000

0010×1

001×01

0x1001

x01001

00101x

0x1010

x01010

0x1011

0x1101

x01101

01000x

0100×0

010×00

01×000

010×01

01×001

01×010

01010x

01×100

0101×1

01×101

01×111

x10111

01100x

0110×0

011×00

x11000

0110×1

011×01

x11001

01101x

011×10

x11010

011×11

x11011

01110x

0111×0

x11100

0111×1

x11101

01111x

x11110

x11111

10000x

100×00

10×000

1000×1

100×01

10×001

10010x

10×100

10×101

10100x

1010×0

101×00

1×1000

101×01

1×1001

101×10

1×1010

10110x

1011×0

1×1100

1×1101

1×1110

11011x

11×110

11×111

11100x

1110×0

111×00

1110×1

111×01

11101x

111×10

111×11

11110x

1111×0

1111×1

11111x

0000×0

—

000000

000010

000×00

000xx0

000×00

000×10

00×000

00x0x0

00×000

00×010

0x0000

0x00x0

0x0000

0x0010

x00000

000×00

000000

—

000000

000xx0

0000×0

000100

00010x

0001×0

00×000

0x0000

0x0x00

0x0000

0x0100

x00000

x00x00

x00000

x00100

00×000

000000

—

000000

0000×0

00x0x0

0000×0

000×00

001000

00100x

0010×0

0x0000

0xx000

0x1000

x00000

x0x000

x01000

0x0000

000000

—

000000

0000×0

0x00x0

000×00

0x0x00

000×00

00×000

0xx000

00×000

010000

01000x

0100×0

010×00

01×000

x00000

000000

—

0000×0

000×00

x00x00

00×000

x0x000

0x0000

100000

10000x

100×00

10×000

000×10

000010

000xx0

0000×0

—

000010

0001×0

000110

0001×0

00011x

000110

00011x

00×010

0x0010

00×010

000010

0000×0

00x0x0

0000×0

000010

—

000010

000×10

0010×0

001010

0010×0

00101x

001010

00101x

0x0010

0xx010

0x1010

x01010

0x0010

000010

0000×0

0x00x0

0000×0

000010

—

000×10

00×010

0xx010

00×010

0100×0

010010

0100×0

010010

01×010

00010x

000×00

000100

000×00

0001×0

—

000100

000101

0001xx

0001×1

00×101

0x0100

0x0101

0x010x

0x0100

0x0101

x00100

x00101

x0010x

x00100

x00101

0001×0

000xx0

000100

000×00

000110

000×10

000100

—

000100

0001xx

00010x

000110

00011x

0x0100

x00100

0x0100

000×00

000100

000×00

0x0x00

000×00

0001×0

000100

—

000100

00010x

0x010x

00010x

0001×0

010×00

010100

010×00

01010x

010100

01010x

01×100

x00100

000×00

000100

000×00

x00x00

0001×0

000100

—

00010x

x0010x

0001×0

0x0100

100×00

100100

100×00

10010x

100100

10010x

10×100

0001×1

00010x

00011x

000101

0001xx

00010x

—

000101

000111

00×101

0x0101

0x01x1

0x0101

0x0111

x00101

00×101

00010x

000101

00010x

000101

—

000101

0001×1

001×01

001101

001×01

001101

0x0101

0xx101

0x1101

x00101

x0x101

x01101

0x0101

00010x

000101

00010x

0x010x

00010x

000101

—

000101

0001×1

0x01x1

00×101

0xx101

00×101

010×01

01010x

010101

010×01

010101

01010x

010101

0101×1

01×101

x00101

00010x

000101

00010x

x0010x

000101

—

0001×1

00×101

x0x101

0x0101

100×01

10010x

100×01

100101

100×01

100101

10010x

100101

10×101

00011x

000×10

0001×0

000110

000×10

0001xx

000110

0001×0

000111

0001×1

—

000111

0x0111

00011x

0001×1

00011x

000111

0001×1

0x01x1

0001×1

000111

—

0101×1

010111

0101×1

010111

01×111

x10111

00100x

00×000

001000

00×000

0010×0

001×01

—

001000

001001

0010xx

0010×0

0010×1

001×01

0x1000

0x1001

0x100x

0x1000

0x1001

x01000

x01001

x0100x

x01000

x01001

0010×0

00x0x0

00×000

001000

00×000

00×010

001010

00×010

001000

—

001000

0010xx

00100x

001010

00101x

0x1000

0x1010

0x1000

0x10x0

0x1000

0x1010

x01000

x010x0

x01000

x01010

0x1000

00×000

001000

0xx000

00×000

0010×0

001000

—

001000

00100x

0x100x

00100x

0010×0

0x10x0

0010×0

01×000

011000

01100x

0110×0

011×00

011000

01100x

0110×0

011×00

x01000

xx1000

x11000

x01000

00×000

001000

00×000

x0x000

0010×0

001000

—

00100x

x0100x

0010×0

x010x0

0x1000

xx1000

10×000

101000

10100x

101×00

101000

10100x

1010×0

101×00

1×1000

0010×1

00100x

00101x

001×01

001001

0010xx

00100x

—

001001

001011

00101x

001011

001×01

0x1001

0x10x1

0x1001

0x1011

x01001

001×01

00100x

00×101

001101

00×101

001001

00100x

001001

—

001001

0010×1

001101

0x1001

0x1101

0x1001

0x1x01

0x1001

0x1101

x01001

x01101

x01001

x01x01

x01001

x01101

0x1001

00100x

001×01

001001

00100x

0x100x

00100x

001001

—

001001

0010×1

0x10x1

0x1x01

001×01

01×001

01100x

01×001

011001

011×01

011001

01100x

011001

0110×1

011×01

x01001

xx1001

x11001

x01001

00100x

001×01

001001

00100x

x0100x

001001

—

0010×1

001×01

x01x01

0x1001

xx1001

10×001

10100x

10×001

101001

101×01

101001

10100x

101001

101×01

1×1001

00101x

00×010

0010×0

00×010

001010

00×010

0010xx

001010

0010×0

001011

0010×1

—

001010

001011

0x1010

0x1011

0x101x

0x1010

0x1011

x01010

0x1010

00×010

0010×0

00×010

001010

0xx010

0010×0

001010

0x10x0

0010×0

00101x

001010

—

001010

0x101x

01×010

0110×0

011010

0110×0

011010

0110×0

01101x

011010

01101x

011×10

x01010

xx1010

x11010

x01010

00×010

0010×0

00×010

001010

00×010

0010×0

001010

0010×0

x010x0

00101x

001010

—

00101x

0x1010

xx1010

1010×0

101010

1010×0

101010

101×10

1×1010

0x1011

00101x

0010×1

00101x

001011

0010×1

0x10x1

0010×1

001011

0x101x

00101x

—

0110×1

01101x

011×11

0110×1

01101x

011011

0110×1

011011

01101x

011011

011×11

x11011

0x1101

00×101

001101

0xx101

00×101

001×01

001101

0x1x01

001×01

—

001101

01×101

011×01

01×101

01110x

01×101

011101

0111×1

011×01

01110x

011×01

011101

011×01

0111×1

011101

01110x

011101

0111×1

x01101

xx1101

x11101

x01101

00×101

001101

00×101

x0x101

001×01

001101

001×01

x01x01

001101

—

0x1101

xx1101

10×101

101×01

10×101

10110x

101101

101×01

10110x

101101

101×01

101101

10110x

101101

1×1101

01000x

0x0000

010000

0x0000

0100×0

010×00

010×01

01×000

01×001

—

010000

010001

0100×0

010x0x

010×00

010×01

01x00x

01×000

01×001

0100×0

0x00x0

0x0000

010000

0x0000

0x0010

010010

010×00

01×000

01×010

010000

—

010000

01000x

010010

010×00

01×000

01x0x0

01×000

01×010

010×00

0x0000

0x0x00

0x0000

010000

0x0000

0100×0

0x0100

010100

0x0100

01010x

01×000

010000

—

010000

010x0x

01000x

0100×0

010100

01010x

01×000

01xx00

01×000

01×100

01×000

0x0000

0xx000

010000

0x0000

0100×0

010×00

0x1000

011000

0x1000

01100x

0110×0

010000

—

01000x

01x00x

01x0x0

010×00

01xx00

011000

01100x

0110×0

011×00

x11000

010×01

01000x

0x0101

01010x

0x0101

010101

0x0101

0101×1

01×001

01×101

010001

01000x

010x0x

01000x

—

010001

010101

01010x

010101

0101×1

01×001

01xx01

01×001

01×101

01×001

01000x

010×01

0x1001

01100x

0x1001

011001

0x1001

0110×1

011×01

010001

01000x

01x00x

010001

—

010×01

01xx01

011001

01100x

011001

0110×1

011×01

x11001

01×010

0x0010

0100×0

0x0010

0xx010

010010

0x1010

0110×0

0x1010

011010

0x1010

01101x

0100×0

010010

0100×0

01x0x0

—

0110×0

011010

0110×0

01101x

011010

01101x

011×10

x11010

01010x

0x0100

010×00

0x010x

0x0100

010100

0x0100

0x0101

010101

0x0101

0101×1

01×101

010x0x

010×00

010100

010×00

010101

010×01

—

010100

010101

0101×1

01×100

01×101

01x10x

01×100

01×101

01×100

0x0100

010×00

0x0100

010100

0x0100

01010x

011×00

01110x

010×00

010100

01xx00

01010x

010100

—

01010x

01x10x

011×00

011100

011×00

01110x

0111×0

011100

01110x

0111×0

x11100

0101×1

0x0101

01010x

0x01x1

0x0101

010101

0x0101

0x0111

010111

01×101

010×01

01010x

010101

010×01

010101

01010x

—

010101

010111

01×101

01×111

01×101

01x1x1

01×101

01×111

x10111

01×101

0x0101

01010x

0x0101

0xx101

010101

0x0101

0101×1

0x1101

011×01

011101

0x1101

010×01

01010x

010101

01xx01

010101

01x10x

010101

—

01x1x1

0101×1

011×01

01110x

011×01

011101

011×01

0111×1

011101

01110x

011101

0111×1

x11101

01×111

0x0111

0101×1

0x0111

010111

011×11

0111×1

0101×1

010111

01x1x1

—

010111

011×11

0111×1

011×11

01111x

011111

011×11

0111×1

01111x

011111

0111×1

011111

01111x

011111

x10111

x1x111

x11111

x10111

0x0111

0101×1

0x0111

010111

0101×1

010111

0101×1

010111

—

01×111

x1x111

110111

11011x

110111

11×111

01100x

0x1000

01×000

0x100x

0x1000

011000

0x1000

0x1001

011001

0x1001

0110×0

0110×1

011×01

01x00x

01×000

011000

01×001

011001

0110×0

011×00

011×01

—

011000

011001

0110xx

0110×0

0110×1

011x0x

011×00

011×01

x11000

x11001

x1100x

x11000

x11001

0110×0

0x1000

01×000

0x1010

01×010

0x1000

0x10x0

011000

0x1000

01100x

0x1010

011010

0x1010

01101x

01×000

01x0x0

01×000

011000

01100x

011010

011×00

011000

—

011000

0110xx

01100x

011010

01101x

011×00

011xx0

011×00

011×10

x11000

x11010

x11000

x110x0

x11000

x11010

011×00

0x1000

01×000

01×100

0x1000

011000

0x1000

01100x

0110×0

01110x

01×000

01xx00

011000

01100x

0110×0

01×100

011100

01110x

011000

—

011000

01100x

011x0x

01100x

0110×0

011xx0

0110×0

011100

01110x

0111×0

x11000

x11100

x11000

x11x00

x11100

x11000

0x1000

01×000

0x1000

011000

xx1000

01100x

0110×0

01×000

011000

01100x

0110×0

011×00

011000

—

01100x

x1100x

0110×0

x110x0

011×00

x11x00

1×1000

111000

11100x

1110×0

111×00

111000

11100x

1110×0

111×00

0110×1

0x1001

01100x

0x10x1

0x1001

011001

0x1001

0x1011

01101x

011011

011×01

01×001

01100x

01×001

011001

01101x

011×01

011×11

011001

0110xx

01100x

—

011001

011011

01101x

011011

011×01

011xx1

011×01

011×11

x11001

x110x1

x11001

x11011

011×01

0x1101

01×101

0x1001

01100x

0x1001

0x1x01

011001

0x1001

0110×1

011101

0x1101

01×001

01100x

01xx01

011001

01×101

01110x

01×101

011101

0111×1

011001

01100x

011x0x

01100x

011001

—

011001

0110×1

011xx1

0110×1

011101

01110x

011101

0111×1

x11001

x11101

x11001

x11x01

x11101

x11001

0x1001

01100x

0x1001

011001

xx1001

0110×1

011×01

01×001

01100x

01×001

011001

011×01

011001

01100x

x1100x

011001

—

0110×1

x110x1

011×01

x11x01

1×1001

11100x

1×1001

111001

111×01

111001

11100x

111001

1110×1

111×01

01101x

0x1010

01×010

0x1010

0110×0

0x1011

0110×1

0x101x

011010

0x1010

011011

01×010

0110×0

0110×1

011010

011×11

0110xx

011010

0110×0

011011

0110×1

—

011010

011011

011×10

011×11

011x1x

011×10

011×11

x11010

x11011

x1101x

x11010

x11011

011×10

0x1010

01×010

0x1010

0110×0

0x1010

011010

0x1010

01101x

01×010

0110×0

011010

0111×0

01111x

0110×0

011010

011xx0

0110×0

01101x

011010

—

011010

011x1x

01101x

0111×0

011110

0111×0

01111x

011110

01111x

x11010

x11110

x11010

x11x10

x11110

x11010

0x1010

01×010

0x1010

0110×0

0x1010

011010

xx1010

01101x

01×010

0110×0

011010

0110×0

011010

0110×0

x110x0

01101x

011010

—

01101x

x1101x

011×10

x11x10

1×1010

1110×0

1×1010

111010

111×10

1110×0

111010

1110×0

11101x

111010

11101x

111×10

011×11

01×111

0x1011

0110×1

0x1011

01101x

011011

0111×1

0110×1

01101x

01×111

0111×1

011111

01×111

0110×1

01101x

011011

011xx1

0110×1

011011

011x1x

01101x

—

011011

0111×1

01111x

011111

0111×1

011111

01111x

011111

x11111

x11011

x11x11

x11111

x11011

0x1011

0110×1

0x1011

01101x

011011

0110×1

01101x

011×11

0110×1

01101x

011011

0110×1

x110x1

011011

01101x

x1101x

011011

—

011×11

x11x11

1110×1

11101x

111×11

1110×1

11101x

111011

1110×1

111011

11101x

111011

111×11

01110x

01×100

0x1101

01×101

011×00

0x1101

011×01

011101

0x1101

01×100

011×00

01×101

011×01

01x10x

011100

01×101

011101

0111×1

011x0x

011×00

011100

011×00

011×01

011101

011×01

0111×0

0111×1

—

011100

011101

0111xx

0111×0

0111×1

x11100

x11101

x11100

x11101

x1110x

x11100

x11101

0111×0

01×100

011×00

011×10

01110x

01×100

011×00

011×10

01×100

011100

01110x

01111x

011×00

011xx0

011100

011×00

01110x

011×10

011110

011×10

01111x

011100

—

011100

0111xx

01110x

011110

01111x

x11100

x11110

x11100

x11110

x11100

x111x0

x11110

x11100

01×100

011×00

01110x

01×100

011×00

01×100

011100

01110x

011×00

011100

x11x00

01110x

0111×0

011100

—

01110x

x1110x

0111×0

x111x0

1×1100

111×00

1×1100

111100

11110x

1111×0

111×00

111100

11110x

1111×0

111100

11110x

1111×0

0111×1

0x1101

01×101

01×111

0x1101

011×01

011×11

011101

0x1101

01×101

011×01

01×101

01110x

01x1x1

011101

011111

01×111

011×01

01110x

011xx1

011101

011×01

011×11

01111x

011111

011×11

011101

0111xx

01110x

—

011101

011111

01111x

011111

x11101

x11111

x11101

x11111

x11101

x111x1

x11111

x11101

0x1101

01×101

0x1101

011×01

011101

xx1101

01×101

011×01

01×101

01110x

01×101

011101

0111×1

011×01

01110x

011×01

011101

x11x01

0111×1

011101

01110x

x1110x

011101

—

0111×1

x111x1

1×1101

111×01

1×1101

11110x

111101

1111×1

111×01

11110x

111×01

111101

1111×1

111101

11110x

111101

1111×1

01111x

01×111

011×10

011×11

0111×1

011×10

0111×0

01×111

0111×1

011111

01×111

011×10

0111×0

011×11

0111×1

011x1x

011110

011×10

011111

011×11

0111xx

011110

0111×0

011111

0111×1

—

011110

011111

x11110

x11111

x11110

x11111

x11110

x11111

x1111x

x11110

011×10

0111×0

01111x

011×10

0111×0

011×10

011110

x11x10

01111x

0111×0

011110

x111x0

01111x

011110

—

x1111x

1×1110

111×10

1×1110

1111×0

111110

11×110

111110

11111x

111×10

1111×0

111×10

111110

11111x

1111×0

111110

11111x

111110

x11111

01×111

011×11

0111×1

01×111

0111×1

011111

x1x111

011×11

0111×1

011×11

01111x

011111

x11x11

0111×1

01111x

011111

x111x1

011111

x1111x

—

1111×1

11111x

11×111

11111x

111111

111×11

1111×1

111×11

11111x

111111

1111×1

11111x

111111

10000x

x00000

100000

100×00

100×01

10×000

10×001

—

100000

100001

100x0x

100×00

100×01

10x00x

10×000

10×001

100×00

x00000

x00x00

x00000

100000

x00100

100100

10010x

10×000

100000

—

100000

10000x

100x0x

10000x

100100

10010x

10×000

10xx00

10×000

10×100

10×000

x00000

x0x000

x00000

100000

100×00

x01000

101000

10100x

1010×0

1×1000

100000

—

10000x

10x00x

100×00

10xx00

101000

10100x

1010×0

101×00

1×1000

1000×1

10000x

100×01

10×001

100001

10000x

—

100001

100×01

10×001

100×01

10000x

x00101

10010x

x00101

100101

10×001

10×101

100001

100x0x

10000x

100001

—

100001

100101

10010x

100101

10×001

10xx01

10×001

10×101

10×001

10000x

100×01

x01001

10100x

x01001

101001

101×01

1×1001

100001

10000x

10x00x

100001

—

100×01

10xx01

101001

10100x

101001

101×01

1×1001

10010x

x00100

100×00

x0010x

x00100

100100

x00101

100101

10×101

100x0x

100100

100×00

100×01

100101

100×01

—

100100

100101

10×100

10×101

10x10x

10×100

10×101

10×100

x00100

100×00

x00100

100100

10010x

101×00

10110x

1×1100

100×00

100100

10xx00

10010x

100100

—

10x10x

101×00

101100

101×00

10110x

1011×0

101100

10110x

1011×0

1×1100

10×101

x00101

10010x

x00101

x0x101

x00101

100101

x01101

101×01

x01101

101101

1×1101

100×01

10010x

100×01

100101

10xx01

100101

10x10x

—

101×01

10110x

101101

101×01

101101

10110x

101101

1×1101

10100x

x01000

10×000

x0100x

x01000

101000

x01001

101001

1010×0

101×01

1×1000

1×1001

10x00x

10×000

101000

10×001

101001

101×00

101×01

—

101000

101001

1010×0

101x0x

101×00

101×01

1x100x

1×1000

1×1001

1010×0

x01000

10×000

x01010

x01000

x010x0

x01000

101000

10100x

x01010

101010

1×1000

1×1010

10×000

101000

10100x

101×00

101000

—

101000

10100x

101010

101×00

101xx0

101×00

101×10

1×1000

1x10x0

1×1000

1×1010

101×00

x01000

10×000

10×100

x01000

101000

10100x

1010×0

10110x

1×1000

1×1100

10×000

10xx00

101000

10100x

10×100

101100

10110x

101000

—

101000

101x0x

10100x

101xx0

1010×0

101100

10110x

1011×0

1×1000

1x1x00

1×1100

1×1000

x01000

10×000

x01000

xx1000

101000

10100x

1010×0

x11000

111000

11100x

1110×0

111×00

10×000

101000

10100x

101×00

101000

—

10100x

1x100x

1010×0

1x10x0

101×00

1x1x00

111000

11100x

1110×0

111×00

101×01

x01101

10×101

x01001

10100x

x01001

x01x01

x01001

101001

x01101

101101

1×1001

1×1101

10×001

10100x

10×001

10xx01

101001

10×101

10110x

101101

101001

10100x

101x0x

10100x

—

101001

101101

10110x

101101

1×1001

1x1x01

1×1101

1×1001

x01001

10100x

x01001

xx1001

101001

101×01

x11001

11100x

x11001

111001

1110×1

111×01

10×001

10100x

10×001

101001

101×01

101001

10100x

1x100x

101001

—

101×01

1x1x01

111001

11100x

111001

1110×1

111×01

101×10

x01010

1010×0

x01010

101010

1×1010

1×1110

1010×0

1011×0

1010×0

101010

101xx0

1010×0

—

101010

1011×0

101110

1011×0

101110

1×1110

1×1010

1x1x10

1×1110

1×1010

x01010

1010×0

x01010

xx1010

101010

x11010

1110×0

x11010

111010

11101x

111×10

1010×0

101010

1010×0

1x10x0

101010

—

101×10

1x1x10

111×10

1110×0

111010

1110×0

11101x

111010

11101x

111×10

10110x

10×100

x01101

10×101

101×00

x01101

101×01

x01101

101101

1×1100

1×1101

10×100

101×00

10×101

101×01

10x10x

101100

101101

101x0x

101×00

101100

101×00

101101

101×01

1011×0

—

101100

101101

1011×0

1×1100

1×1101

1x110x

1×1100

1×1101

1011×0

10×100

101×00

101×10

10110x

1×1100

1×1110

10×100

101×00

10×100

101100

10110x

101×00

101xx0

101100

101×00

10110x

101110

101×10

101100

—

101100

10110x

101110

1×1110

1×1100

1×1110

1×1100

1x11x0

1×1110

1×1100

10×100

101×00

10110x

x11100

111×00

x11100

111100

11110x

1111×0

10×100

101×00

10×100

101100

10110x

101×00

101100

1x1x00

10110x

1011×0

101100

—

1x110x

1x11x0

1111×0

111×00

111100

11110x

1111×0

111100

11110x

1111×0

1×1101

x01101

10×101

x01101

101×01

xx1101

101101

x11101

111×01

x11101

11110x

x11101

111101

1111×1

10×101

101×01

10×101

10110x

101101

101×01

10110x

101101

1x1x01

101101

10110x

1x110x

—

1111×1

111×01

11110x

111×01

111101

1111×1

111101

11110x

111101

1111×1

1×1110

101×10

x11110

111×10

x11110

1111×0

x11110

111110

11111x

1011×0

101×10

1011×0

101110

1x1x10

1011×0

101110

1x11x0

—

11×110

111110

11111x

111×10

1111×0

111×10

111110

11111x

1111×0

111110

11111x

111110

11011x

x10111

110111

11×110

11×111

11×110

—

110110

110111

11×110

11×111

11×110

11×111

11x11x

11×110

11011x

x11110

111×10

x11110

1111×0

x11110

111110

11111x

1×1110

111×10

1×1110

1111×0

111110

110110

—

11x11x

111×10

1111×0

111×10

111110

11111x

1111×0

111110

11111x

111110

11×111

x10111

x1x111

110111

x11111

111×11

x11111

1111×1

x11111

11111x

111111

1111×1

11111x

110111

11x11x

—

111×11

1111×1

111×11

11111x

111111

1111×1

11111x

111111

11100x

x11000

1×1000

x11001

1×1001

x11000

x11001

x1100x

x11000

111000

x11001

111001

1110×0

1110×1

111×00

111×01

1×1000

1×1001

1x100x

1×1000

111000

1×1001

111001

1110×0

111×00

111×01

—

111000

111001

1110xx

1110×0

1110×1

111x0x

111×00

111×01

1110×0

x11000

1×1000

x11010

1×1010

x11000

x11010

x11000

x110x0

x11000

111000

11100x

x11010

111010

11101x

111×00

111×10

1×1000

1x10x0

1×1000

111000

11100x

1×1010

111010

111×00

111×10

111000

—

111000

1110xx

11100x

111010

11101x

111×00

111xx0

111×10

111×00

x11000

1×1000

x11000

x11100

x11000

x11x00

111000

11100x

1110×0

x11100

111100

11110x

1111×0

1×1000

1×1100

1×1000

1x1x00

111000

11100x

1110×0

1×1100

111100

11110x

1111×0

111000

—

11100x

111x0x

1110×0

111xx0

111100

11110x

1111×0

1110×1

x11001

1×1001

x11011

x11001

11100x

x110x1

x11001

111001

x11011

11101x

x11011

111011

111×01

111×11

1×1001

11100x

1×1001

111001

11101x

111×01

111×11

111001

1110xx

11100x

—

111001

111011

11101x

111011

111×01

111xx1

111×11

111×01

x11001

1×1001

x11101

1×1101

x11001

x11101

x11001

11100x

x11001

x11x01

111001

1110×1

x11101

11110x

x11101

111101

1111×1

1×1001

1×1101

1×1001

11100x

1x1x01

111001

1×1101

11110x

111101

1111×1

111001

11100x

111x0x

111001

—

1110×1

111xx1

111101

11110x

111101

1111×1

11101x

x11010

1×1010

x11011

x11010

1110×0

x11011

1110×1

x1101x

x11010

111010

x11011

111011

111×10

111×11

1×1010

1110×0

1110×1

1×1010

111010

111×10

111×11

1110xx

111010

1110×0

111011

1110×1

—

111010

111011

111×10

111×11

111x1x

111×10

x11010

1×1010

x11010

1110×0

x11010

x11x10

111010

11101x

x11110

1111×0

x11110

111110

11111x

1×1010

1110×0

1x1x10

111010

1×1110

1111×0

111110

11×110

111110

11111x

1110×0

111010

111xx0

11101x

111010

—

111x1x

1111×0

111110

11111x

111110

111×11

x11011

x11111

11×111

x11011

1110×1

x11011

11101x

x11x11

111011

x11111

1111×1

x11111

11111x

111111

1110×1

11101x

1111×1

11111x

11×111

11111x

111111

1110×1

11101x

111011

111xx1

111011

111x1x

—

1111×1

11111x

111111

11110x

x11101

1×1101

x11100

x11101

x11100

111×00

x11101

111×01

x1110x

x11100

111100

x11101

111101

1111×0

1111×1

1×1100

1×1101

1×1100

111×00

1×1101

111×01

1x110x

1×1100

111100

111101

1111×0

1111×1

111x0x

111×00

111100

111×01

111101

1111×0

1111×1

—

111100

111101

1111xx

1111×0

x11100

111×00

x11110

111×10

x11100

x111x0

111100

11110x

x11110

111110

11111x

1×1100

111×00

1×1110

111×10

1×1100

1x11x0

111100

11110x

111110

11×110

111110

11111x

111×00

111xx0

111100

11110x

111×10

111110

11111x

111100

—

1111xx

111110

1111×1

x11101

1×1101

x11101

x11111

11×111

x11101

111×01

x11111

111×11

x11101

11110x

x111x1

111101

x11111

11111x

111111

1×1101

111×01

1×1101

11110x

111101

11111x

11×111

11111x

111111

111×01

11110x

111xx1

111101

111×11

11111x

111111

111101

1111xx

—

111111

11111x

x11111

11×111

x11110

111×10

x11111

111×11

x11110

1111×0

x11111

1111×1

x1111x

111110

111111

1×1110

111×10

1×1110

1111×0

1111×1

111110

11x11x

111110

111111

111×10

1111×0

111×11

1111×1

111x1x

111110

111111

1111xx

111110

111111

—

Z₁=
Ĉ₂=C₁∪(C₁*C₁)
C₂=>

000xx0, 00x0x0, 0x00x0
0x0x00, x00x00, 0xx000
x0x000, 0xx010, 0001xx
0x010x, x0010x, 0x01x1
0xx101, x0x101, 0010xx
0x100x, x0100x, 0x10x0
x010x0, xx1000, 0x10x1
0x1x01, x01x01, xx1001
0x101x, xx1010, xx1101
010x0x, 01x00x, 01x0x0
01xx00, 01xx01, 01x10x
01x1x1, x1x111, 0110xx
011x0x, x1100x, 011xx0
x110x0, x11x00, 011xx1
x110x1, x11x01, 011x1x
x1101x, x11x10, x11x11
0111xx, x1110x, x111x0
x111x1, x1111x, 100x0x
10x00x, 10xx00, 10xx01
10x10x, 101x0x, 1x100x
101xx0, 1x10x0, 1x1x00
1x1x01, 1x1x10, 1x110x
1x11x0, 11x11x, 1110xx
111x0x, 111xx0, 111xx1
111x1x, 1111xx

Таблица операции C₂*C₂

000xx0

00x0x0

0x00x0

0x0x00

x00x00

0xx000

x0x000

0xx010

0001xx

0x010x

x0010x

0x01x1

0xx101

x0x101

0010xx

0x100x

x0100x

0x10x0

x010x0

xx1000

0x10x1

0x1x01

x01x01

xx1001

0x101x

xx1010

xx1101

010x0x

01x00x

01x0x0

01xx00

01xx01

01x10x

01x1x1

x1x111

0110xx

011x0x

x1100x

011xx0

x110x0

x11x00

011xx1

x110x1

x11x01

011x1x

x1101x

x11x10

x11x11

0111xx

x1110x

x111x0

x111x1

x1111x

100x0x

10x00x

10xx00

10xx01

10x10x

101x0x

1x100x

101xx0

1x10x0

1x1x00

1x1x01

1x1x10

1x110x

1x11x0

11x11x

1110xx

111x0x

111xx0

111xx1

111x1x

1111xx

000xx0

—

0000×0

000×00

000000

000010

0001×0

000100

0001xx

00010x

00x0x0

00×000

00x0x0

00×000

00×010

0x0x00

0x0000

0x00x0

0x0x00

0x0100

x00x00

x00000

x00x00

x00100

00x0x0

0000×0

—

0000×0

000000

00×000

00×010

000xx0

000×00

0010×0

001000

0010×0

001000

0010xx

00100x

001010

0x0000

0xx000

0xx0x0

0xx000

0x10x0

0x1000

0x10x0

0x1000

0x1010

x00000

x0x000

x01000

x010x0

x01000

x01010

0x00x0

0000×0

—

0x0000

000000

0x0000

000000

0x0010

000xx0

0x0x00

000×00

00x0x0

0xx000

00×000

0xx0x0

00x0x0

0xx000

0xx010

010000

0100×0

010000

01000x

010×00

01x0x0

01×000

01x0x0

01×000

01×010

x00000

0x0x00

000×00

000000

0x0000

—

000×00

0x0000

000000

0x00x0

000100

0x0100

000100

0x010x

00010x

00×000

0xx000

00×000

0xx000

00×000

0xx000

010×00

010000

010×00

010x0x

010100

01010x

01×000

01xx00

01×000

01xx00

01×000

01xx00

01×100

x00x00

x00000

x00x00

x00100

x00x00

000×00

000000

000×00

—

000000

x00000

0000×0

000100

x00100

00010x

x0010x

00×000

x0x000

00×000

x0x000

0x0x00

0x0000

0x0x00

0x0100

100×00

100000

100×00

100x0x

100100

10xx00

10×000

10xx00

10×000

10xx00

10×100

0xx000

000000

00×000

0x0000

000000

—

00×000

0xx0x0

000×00

0x0x00

000×00

001000

0x1000

001000

0x1000

001000

0x1000

0x100x

00100x

0x100x

0x10x0

010000

01×000

01x00x

01xx00

011000

01100x

0110×0

011×00

x00000

x0x000

x01000

xx1000

x01000

xx1000

x11000

x0x000

000000

00×000

000000

x00000

00×000

—

00x0x0

000×00

x00x00

001000

x01000

001000

x01000

00100x

x0100x

0010×0

x010x0

0x0000

0xx000

0x1000

xx1000

0x1000

xx1000

100000

10×000

10x00x

10xx00

101000

10100x

1010×0

101×00

1×1000

0xx010

000010

00×010

0x0010

0x00x0

0000×0

0xx0x0

00x0x0

—

000×10

001010

0x10x0

0010×0

0x1010

001010

0x10x0

0x101x

0x1010

0100×0

01x0x0

01×010

01x0x0

011010

0110×0

011010

0110×0

01101x

011010

01101x

011×10

x01010

xx1010

x11010

0001xx

0001×0

000xx0

000100

000×00

000×10

—

00010x

0001×1

000101

00×101

0x010x

0x0100

0x0101

0x010x

0x01x1

0x0111

x0010x

x00100

x00101

x0010x

0x010x

000100

000×00

0x0x00

0x0100

000100

0x0x00

000×00

00010x

—

00010x

0x0101

000101

0xx101

00×101

0xx101

01010x

010x0x

010×00

010100

010101

01010x

010101

0101×1

01x10x

01×100

01×101

01x10x

01×100

01×101

x0010x

x00100

x00101

x0010x

000100

000×00

000100

x00100

000×00

x00x00

00010x

—

000101

x00101

00×101

x0x101

0x010x

0x0100

0x0101

0x010x

0x0101

10010x

100x0x

100100

100101

10010x

10x10x

10×100

10×101

10x10x

10×100

0x01x1

0001xx

0x010x

00010x

0001×1

0x0101

000101

—

0x0101

000101

0xx101

00×101

0xx101

010101

010×01

01010x

010101

0101×1

010111

01×101

01x1x1

01×101

01×111

01x1x1

01×101

01x1x1

01×111

x00101

x10111

0xx101

00010x

0x010x

00010x

000101

0x0101

000101

0x0101

—

00×101

001×01

0x1x01

001×01

0x1x01

0x1101

001101

0x1x01

0x1101

010101

01xx01

01x10x

01×101

01x1x1

011×01

011101

011×01

01110x

011101

011×01

011101

0111×1

011101

01110x

011101

0111×1

x00101

x0x101

x01101

xx1101

x11101

x0x101

00010x

x0010x

000101

x00101

000101

00×101

—

001×01

x01x01

001×01

001101

x01101

x01x01

x01101

0x0101

0xx101

0x1101

xx1101

0x1101

xx1101

100101

10xx01

10x10x

10×101

101101

101×01

10110x

101101

10110x

1×1101

0010xx

00x0x0

0010×0

00x0x0

00×000

001000

001010

001×01

—

00100x

0010×0

001000

0010×1

001001

00101x

001010

001×01

0x100x

0x10x0

0x1000

0x1001

0x10xx

0x100x

0x10x0

0x1000

0x10x1

0x1001

0x101x

0x1010

0x1011

x0100x

x01000

x01001

x0100x

x010x0

x01000

x01001

x01010

0x100x

00×000

001000

0xx000

00×000

0x1000

001000

0x10x0

0x1x01

001×01

00100x

—

00100x

0x1000

001000

0x1000

0x1001

001001

0x1001

0x10xx

0x10x0

0x1x01

01x00x

01100x

011000

011001

011x0x

011×01

01100x

011000

011001

0110xx

0110×0

0110×1

011x0x

011×00

011×01

x0100x

x01000

x01001

x0100x

xx100x

x01000

xx1000

xx1001

x1100x

x11000

x11001

x0100x

00×000

001000

00×000

x0x000

001000

x01000

0010×0

001×01

x01x01

00100x

—

001000

x01000

001001

x01001

0010xx

x010x0

x01x01

0x100x

0x1000

0x1001

0x100x

xx100x

0x1000

xx1000

0x1001

xx1001

10x00x

10100x

101000

101001

101x0x

10100x

101000

101001

1010×0

101x0x

101×00

1x100x

1×1000

1×1001

0x10x0

00x0x0

0010×0

0xx0x0

0xx000

00×000

0x1000

001000

0x1010

0010×0

0x1000

001000

—

0010×0

0x1000

0x10xx

0x100x

00100x

0x100x

0x1010

01×000

011000

0110×0

011000

01100x

011×00

0110×0

011000

0110×0

011000

0110xx

01100x

011010

01101x

011xx0

011×00

011xx0

011×10

x01000

xx1000

x010x0

xx10x0

xx1000

xx1010

x110x0

x11000

x110x0

x11010

x010x0

00x0x0

0010×0

00x0x0

00×000

x0x000

001000

x01000

001010

0010×0

001000

x01000

0010×0

—

x01000

0010xx

00100x

x0100x

001010

x01010

0x1000

0x10x0

0x1000

0x10x0

0x1000

xx1000

0x10x0

xx10x0

xx1000

0x1010

xx1010

10×000

101000

10100x

101×00

101000

1010×0

101000

10100x

101010

101×00

101xx0

1x10x0

1×1000

1x10x0

1×1010

xx1000

00×000

001000

0xx000

x0x000

0x1000

x01000

0x10x0

001000

0x1000

x01000

0x1000

x01000

—

0x100x

x0100x

xx100x

0x10x0

xx10x0

01×000

011000

01100x

011×00

011000

x11000

011000

x11000

01100x

x1100x

0110×0

x110x0

011×00

x11x00

10×000

101000

10100x

101×00

101000

1×1000

101000

1×1000

1x100x

1x10x0

1x1x00

111000

11100x

1110×0

111×00

0x10x1

0010xx

0x100x

00100x

0x101x

0x1x01

001×01

0010×1

0x1001

001001

0x10xx

0010xx

0x100x

—

0x1001

001001

0x1001

0x1011

0x101x

0x1x01

01×001

011001

0110xx

01100x

011001

011×01

011xx1

011×11

0110×1

011001

0110xx

01100x

0110×1

011001

011011

01101x

011011

011xx1

011×01

011xx1

011×11

x01001

xx1001

x110x1

x11001

x110x1

x11011

0x1x01

00100x

0x100x

00100x

00×101

0xx101

00×101

0xx101

0x1101

001101

001001

0x1001

001001

0x100x

00100x

0x100x

0x1001

—

001×01

0x1001

0x10x1

0x1101

01xx01

011001

01100x

011x0x

011×01

011101

0111×1

011001

011×01

011001

011x0x

01100x

011x0x

011×01

011001

011×01

011xx1

0110×1

011xx1

011101

01110x

011101

0111×1

x01001

x01x01

x01101

x01x01

xx1001

xx1x01

xx1101

x11001

x11x01

x11101

x01x01

00100x

x0100x

00×101

x0x101

00×101

001101

x01101

001001

x01001

00100x

x0100x

001001

001×01

—

x01001

0010×1

x01101

0x1001

0x1x01

0x1101

0x1001

0x1x01

xx1001

0x1x01

xx1001

xx1x01

0x1101

xx1101

10xx01

101001

101x0x

101×01

101101

101×01

101001

101x0x

10100x

101x0x

101×01

101101

10110x

1×1001

1x1x01

1×1101

xx1001

00100x

0x100x

x0100x

0x1x01

x01x01

001001

0x1001

x01001

0x100x

x0100x

xx100x

0x1001

x01001

—

0x10x1

xx1x01

01×001

011001

01100x

011001

011×01

011001

x11001

01100x

x1100x

011001

x11001

0110×1

x110x1

011×01

x11x01

10×001

101001

10100x

101001

101×01

101001

1×1001

10100x

1x100x

1×1001

1x1x01

111001

11100x

111001

1110×1

111×01

0x101x

00×010

001010

0xx010

0x10x0

0010×0

0x1010

00101x

0x10xx

0010xx

0x1010

001010

0x10x0

0x1011

0x10x1

0010×1

0x10x1

—

0x1010

0110xx

011010

0110×0

0110×1

011×11

01101x

0110xx

011010

0110×0

011011

0110×1

01101x

011010

011011

011x1x

011×10

011×11

011x1x

x01010

xx1010

x1101x

x11010

x11011

x1101x

xx1010

00×010

001010

0xx010

0x10x0

x010x0

0x1010

001010

0x10x0

x010x0

0x1010

x01010

xx10x0

0x101x

0x1010

—

0110×0

011010

0110×0

011010

0110×0

x110x0

011010

x11010

x110x0

01101x

x1101x

011010

x11010

x1101x

011×10

x11x10

1010×0

1x10x0

101010

1×1010

1x10x0

1×1010

1x1x10

111×10

111010

1110×0

111010

11101x

111010

111×10

xx1101

00×101

0xx101

x0x101

0xx101

0x1101

x01101

001×01

0x1x01

x01x01

0x1x01

0x1101

x01101

xx1x01

—

01×101

011×01

01110x

011101

x111x1

011×01

011101

x11x01

01110x

x1110x

011101

x11x01

x11101

0111×1

x111x1

011101

x11101

x1110x

x11101

x111x1

10×101

101×01

10110x

101101

1x1x01

10110x

1x110x

1×1101

1x110x

1111×1

111×01

111101

11110x

111101

1111×1

111101

010x0x

0x0x00

0x0000

010000

010×00

0x0x00

010000

0x0000

0100×0

0x010x

01010x

0x010x

010101

0x0101

01x00x

01×000

01×001

01xx01

01×001

01×101

—

01000x

010000

010×00

010×01

01010x

010101

0101×1

01x00x

01xx0x

01x00x

01xx00

01×000

01xx00

01xx01

01×001

01xx01

01x10x

01×100

01×101

01x00x

0x0000

0xx000

010000

0x0000

01×000

0xx000

01x0x0

010x0x

010×01

01xx01

0x100x

01100x

0x100x

011000

0x1000

011000

011001

0x1001

011001

0110xx

0110×0

011×01

01000x

—

01×000

01×001

01xx0x

01xx01

01100x

011000

011001

0110xx

0110×0

0110×1

011x0x

011×00

011×01

x1100x

x11000

x11001

x1100x

x11000

x11001

01x0x0

0x00x0

0xx0x0

0100×0

010000

0x0000

01×000

0xx000

01×010

010×00

0x10x0

011000

0x1000

0110×0

0x10x0

011000

0110xx

01100x

011010

010000

01×000

—

01×000

01x00x

01xx00

0110×0

011000

0110×0

011000

0110xx

01100x

011010

01101x

011xx0

011×00

011xx0

011×10

x11000

x110x0

x11000

x11010

x110x0

x11000

x110x0

x11010

01xx00

0x0x00

0xx000

010000

010×00

0x0x00

01×000

0xx000

01x0x0

0x0100

010100

0x0100

01010x

01x10x

0x1000

011000

0x1000

011000

0x1000

011000

01100x

011x0x

01100x

0110×0

01110x

010×00

01×000

—

01xx0x

01×100

01x10x

011000

011×00

011000

011×00

011000

011×00

011x0x

01100x

011x0x

011xx0

0110×0

011xx0

011100

01110x

0111×0

x11000

x11x00

x11100

x11000

x11x00

x11100

01xx01

01000x

010x0x

01x00x

0x0101

010101

0x0101

010101

01×101

0xx101

0x1001

011001

0x1001

01100x

011001

011×01

0x1x01

011001

0110×1

011101

010×01

01×001

01x00x

01xx0x

—

01×101

01x1x1

011001

011×01

011001

011x0x

01100x

011x0x

011×01

011001

011×01

011xx1

0110×1

011xx1

011101

01110x

011101

0111×1

x11001

x11x01

x11101

x11001

x11x01

x11101

01x10x

0x0100

010×00

010100

0x0100

01xx00

0x010x

01010x

0x010x

010101

01×101

0xx101

011x0x

011×00

011×01

011101

0x1101

011×01

011101

01010x

01xx0x

01xx00

01×100

01×101

—

01×101

01x1x1

011x0x

01110x

011x0x

011100

011×00

011100

011101

011×01

011101

0111xx

0111×0

0111×1

01110x

011100

011101

0111xx

x11100

x11101

x1110x

x11100

x1110x

x11100

x11101

x1110x

01x1x1

01010x

0x01x1

010101

0x0101

0101×1

01×101

0xx101

011×01

011xx1

011101

0x1101

011×01

011×11

011101

010101

01xx01

01x10x

01×101

—

01×111

011xx1

011101

011×01

0111xx

01110x

0111×1

011xx1

011101

011111

011×11

01111x

011111

0111×1

011101

0111xx

0111×1

011111

x11101

x1x111

x11101

x111x1

x11111

x111x1

x1x111

0x0111

0101×1

010111

01x1x1

011×11

0111×1

011×11

x111x1

0101×1

01x1x1

01×111

—

011×11

0111×1

01111x

011111

x11x11

x111x1

011111

x11x11

x1111x

x11111

011111

x111x1

x1111x

x11111

1111×1

11111x

1111×1

11111x

11×111

111×11

1111×1

11111x

111111

0110xx

0x10x0

01x0x0

01×000

011000

0x1000

011010

011×01

0x10xx

01100x

0x100x

0110×0

0x10x0

011000

0110×1

011001

0x1001

011001

01101x

011010

011×01

01x00x

01100x

0110×0

011000

011001

011x0x

011xx1

011×11

—

01100x

0110×0

011000

0110×1

011001

01101x

011010

011011

011xxx

011x0x

011xx0

011xx1

011x1x

x1100x

x110x0

x11000

x11001

x11010

x110xx

x1100x

x110x0

x110x1

x1101x

011x0x

0x1000

01×000

01xx00

011000

0x1000

0110×0

01x10x

01×101

011101

0x1101

0x100x

01100x

0x100x

011000

0x1000

011000

011001

011×01

0x1x01

011001

0110xx

0110×0

011101

01xx0x

01100x

011000

011×00

011×01

01110x

011101

0111×1

01100x

—

01100x

011×00

011000

011×00

011×01

011001

011×01

011xxx

0110xx

011xx0

011xx1

01110x

011100

011101

0111xx

x1100x

x11000

x11x00

x11x01

x1110x

x11100

x1100x

x11x0x

x11x00

x11x01

x1110x

x1100x

0x1000

01×000

011000

xx1000

0110×0

011×01

0x100x

01100x

xx100x

011000

xx1000

x11000

011001

xx1001

x11001

0110xx

x110x0

x11x01

01x00x

01100x

011000

011001

011x0x

011×01

01100x

—

011000

x11000

011001

x11001

0110xx

x110xx

x110x0

x110x1

011x0x

x11x0x

x11x00

x11x01

1x100x

1×1000

1×1001

1x100x

11100x

1×1000

111000

111001

1110×0

111x0x

111×00

11100x

111000

111001

1110xx

111x0x

011xx0

0x10x0

01x0x0

01xx00

011000

0x1000

011010

01×100

01110x

0x10x0

011000

0x1000

0110×0

0x10x0

011000

0110xx

011x0x

01100x

011010

01110x

01xx00

011000

0110×0

011×00

011x0x

011100

0111xx

01111x

0110×0

011×00

011000

—

0110×0

011×00

011xxx

0110xx

011x0x

011×10

011010

011×10

011x1x

0111×0

011100

0111×0

0111xx

011110

x11000

x110x0

x11x00

x11x10

x11100

x111x0

x11110

x110x0

x11x00

x11xx0

x11x10

x111x0

x110x0

0x10x0

01x0x0

01×000

011000

xx1000

011010

0x10x0

011000

xx1000

0110×0

xx10x0

x11000

0110xx

01100x

x1100x

011010

x11010

01×000

011000

0110×0

011000

01100x

011×00

0110×0

011000

x11000

0110×0

—

x11000

0110xx

x110xx

x1100x

011010

x11010

x1101x

011xx0

x11x00

x11xx0

x11x10

1×1000

111000

1x10x0

1110×0

111000

11100x

111010

111×00

111xx0

111×10

1110×0

111000

1110×0

1110xx

111010

111xx0

x11x00

0x1000

01×000

01xx00

011000

xx1000

0110×0

01×100

01110x

0x1000

011000

xx1000

011000

xx1000

x11000

01100x

011x0x

x1100x

0110×0

x110x0

x1110x

01xx00

011000

011×00

011x0x

011100

01110x

011000

011×00

x11000

011×00

x11000

—

011x0x

x1100x

x11x0x

011xx0

x110x0

x11xx0

011100

x11100

x1110x

x111x0

1×1000

1x1x00

1×1100

1x1x00

111000

1x1x00

111000

111×00

111x0x

111xx0

111100

1111×0

111000

111×00

111x0x

111xx0

111100

011xx1

01100x

01101x

01×101

01x1x1

011101

0x1101

0x10x1

011001

0x1001

0110xx

01100x

0110×1

011×01

0x1x01

011001

011011

01101x

011101

01xx01

011001

0110xx

011x0x

011×01

011101

0111×1

011111

0110×1

011×01

011001

011xxx

0110xx

011x0x

—

0110×1

011×01

011×11

011011

011x1x

011×11

0111×1

011101

0111xx

0111×1

011111

x11001

x11x01

x11101

x11111

x110x1

x11x01

x11xx1

x11x11

x111x1

x110x1

01100x

01101x

011×01

0x10x1

011001

xx1001

0110xx

x1100x

0110×1

011001

xx1001

x11001

011011

x1101x

x11x01

01×001

011001

0110xx

01100x

011001

011×01

011xx1

x11x11

0110×1

011001

x11001

0110xx

x110xx

x1100x

0110×1

—

x11001

011011

x11011

x1101x

x11011

011xx1

x11x01

x11xx1

x11x11

1×1001

111001

1110xx

11100x

111001

11101x

111×01

111×11

1110×1

111001

1110xx

1110×1

111011

111xx1

x11x01

01100x

01×101

011101

xx1101

0x1001

011001

xx1001

01100x

x1100x

011001

011×01

xx1x01

x11001

0110×1

x11101

01xx01

011001

01100x

011x0x

011×01

011101

x111x1

011001

011×01

x11001

011x0x

x1100x

x11x0x

011×01

x11001

—

011xx1

x110x1

x11xx1

011101

x11101

x1110x

x11101

x111x1

1×1001

1x1x01

1×1101

1x1x01

111001

11100x

111x0x

111×01

111101

11110x

1111×1

111001

111×01

111x0x

111×01

111xx1

111101

011x1x

0x1010

01×010

0110×0

011010

01×111

0111×1

0x101x

0110xx

011010

0x1010

0110×0

011011

011xx1

0110×1

01101x

011010

0111×1

0110xx

011010

011xx0

011xx1

0111xx

011111

01101x

011xxx

0110xx

011×10

011010

011xx0

011×11

011011

011xx1

—

01101x

011×10

011×11

01111x

0111xx

011110

011111

01111x

x11010

x11x10

x11110

x1111x

x1101x

x11x10

x11x11

x11x1x

x1111x

x1101x

0x1010

01×010

0110×0

011010

0x101x

0110xx

011010

xx1010

x110x0

011011

0110×1

x110x1

01101x

x11010

0110xx

011010

0110×0

0110×1

011×11

x11x11

01101x

0110xx

x110xx

011010

x11010

x110x0

011011

x11011

x110x1

01101x

—

x11010

x11011

011x1x

x11x10

x11x11

x11x1x

1110xx

1×1010

111010

1110×0

1110×1

111010

111×10

111x1x

11101x

1110xx

111010

111011

11101x

111x1x

x11x10

0x1010

01×010

0110×0

011010

0x1010

0110×0

011010

xx1010

x110x0

01101x

011010

x11010

0110×0

011010

011xx0

0111×0

01111x

x1111x

011010

011xx0

x110x0

011×10

x11010

x11xx0

011x1x

x1101x

011×10

x11010

—

x11x1x

011110

x111x0

x11110

x1111x

x11110

1110×0

1x1x10

111010

111xx0

111×10

1111×0

111110

111010

111xx0

111×10

111x1x

111×10

111110

x11x11

01101x

01×111

0111×1

0x1011

0110×1

01101x

011011

011xx1

x110x1

011011

x1101x

x111x1

0110×1

01101x

011xx1

0111×1

011111

x11111

011011

011xx1

x110x1

011x1x

x1101x

011×11

x11011

x11xx1

011×11

x11011

x11x1x

—

011111

x111x1

x1111x

x11111

1110×1

11101x

111xx1

111x1x

1111×1

11111x

111111

111011

111xx1

111x1x

111×11

111111

0111xx

01×100

011×00

011×10

01x10x

01x1x1

011101

0x1101

011x0x

011xx0

011×00

011xx1

011101

0x1101

011×01

011x1x

011×10

011101

01x10x

011x0x

011xx0

011100

011101

01110x

0111×1

011111

011xxx

01110x

011x0x

0111×0

011xx0

011100

0111×1

011xx1

011101

01111x

011x1x

011110

011111

—

01110x

0111×0

0111×1

01111x

x11100

x11101

x11110

x1110x

x111x0

x1111x

x1110x

x111x0

x111x1

x1111x

x111xx

x1110x

01×100

011×00

01x10x

01×101

011101

xx1101

011x0x

011×00

x11x00

011×01

011101

xx1101

x11x01

x11101

01x10x

011x0x

011×00

011100

011101

01110x

011101

x111x1

011x0x

01110x

x11x0x

011100

x11x00

x11100

011101

x11x01

x11101

0111xx

x111x0

x111x1

01110x

—

x11100

x11101

x111xx

1×1100

1×1101

1x110x

111x0x

1×1100

111×00

111100

111101

1111×0

11110x

111100

1111xx

111x0x

11110x

111100

111101

1111xx

11110x

x111x0

01×100

011×00

011×10

01×100

01110x

011×00

011xx0

x11x00

01110x

011×10

x11x10

x1110x

01×100

011×00

011xx0

011100

01110x

011100

0111xx

x1111x

011xx0

011100

x11x00

0111×0

x11xx0

x11100

0111xx

x1110x

011110

x11x10

x11110

x1111x

0111×0

x11100

—

x111xx

x11110

1×1100

111×00

1x11x0

111xx0

111100

11110x

111110

111100

1111×0

111110

111xx0

111100

1111×0

1111xx

111110

1111×0

x111x1

01×101

01x1x1

011101

xx1101

011×01

011xx1

011101

xx1101

x11x01

011×11

x11101

01×101

011×01

01110x

011101

0111×1

x11111

011xx1

011101

x11x01

0111xx

x1110x

0111×1

x11xx1

x11101

011111

x11x11

x1111x

x11111

0111×1

x11101

x111xx

—

x11111

1×1101

111×01

11110x

111101

11111x

111101

1111xx

111111

111xx1

111101

1111xx

1111×1

111111

1111×1

x1111x

011×10

01×111

0111×1

011×10

011×11

0111×1

011x1x

x11x10

x111x1

011×10

0111×0

0111×1

0111xx

011111

x11111

011x1x

0111xx

011110

x11x10

x111x0

011111

x11x11

x111x1

01111x

x11x1x

x11110

x11111

01111x

x111xx

x11110

x11111

—

1×1110

111×10

1111×0

1111×1

111110

1111xx

111110

11111x

111x1x

1111xx

111110

111111

11111x

100x0x

x00x00

x00000

x00x00

100×00

x00000

100000

x0010x

10010x

x00101

100101

10x00x

10×000

10xx01

10×001

10×101

—

10000x

100×00

100×01

10010x

10xx0x

10x00x

10xx00

10×000

10xx00

10xx01

10x10x

10×100

10x00x

x00000

x0x000

x00000

100000

x0x000

10×000

100x0x

10xx01

x0100x

10100x

x01000

101000

x01001

101001

1010×0

101×01

1x100x

1×1000

1×1001

10000x

—

10×000

10×001

10xx0x

10100x

101000

101001

1010×0

101x0x

101×00

1x100x

1×1000

1×1001

10xx00

x00x00

x0x000

x00000

x00x00

100×00

x0x000

10×000

x00100

100100

10x10x

x01000

101000

x01000

101000

101x0x

10100x

1010×0

10110x

1×1000

1x1x00

1×1100

100×00

10×000

—

10xx0x

10×100

101×00

101000

101×00

101000

101×00

101x0x

101xx0

101100

1×1000

1x1x00

1×1100

10xx01

100x0x

10x00x

x00101

100101

x00101

x0x101

10×101

x01001

101001

10100x

x01001

x01x01

101×01

101001

101101

1×1001

1x1x01

1×1101

100×01

10×001

10xx0x

—

10×101

101×01

101001

101x0x

10100x

101x0x

101×01

101101

10110x

1×1001

1x1x01

1×1101

10x10x

x00100

100100

10xx00

x0010x

10010x

x00101

x0x101

10×101

101x0x

101×00

x01101

101101

101×01

101101

1×1100

1×1101

1x110x

1×1100

1×1101

10010x

10xx0x

10×100

10×101

—

10110x

101x0x

101100

101×00

101100

101101

1011×0

10110x

101100

1x110x

1×1100

1×1101

1x110x

101x0x

x01000

10xx00

x01000

101000

10x10x

x01101

101101

x0100x

10100x

x01000

101000

x01001

x01x01

101×01

101001

1010×0

101101

1x100x

1×1000

1x1x00

1×1001

1x1x01

1x110x

1×1100

1×1101

10xx0x

10100x

101×00

101×01

10110x

—

10100x

101×00

101000

101×00

101×01

101xx0

10110x

101100

1x100x

1x1x0x

1x1x00

1x1x01

1x110x

1x100x

x01000

10×000

xx1000

101000

101×01

x0100x

xx100x

10100x

xx1000

101000

1×1000

xx1001

101001

1×1001

1x10x0

1x1x01

x1100x

x11000

x11001

x1100x

11100x

x11000

111000

x11001

111001

1110xx

1110×0

1110×1

111x0x

111×00

111×01

10x00x

10100x

101000

101001

101x0x

10100x

—

101000

1×1000

1×1001

1x10x0

1x1x0x

1x1x00

11100x

111000

111001

1110xx

111x0x

101xx0

x010x0

10xx00

x01000

101000

x01010

10×100

10110x

x010x0

x01000

101000

x010x0

1010×0

101000

101x0x

10100x

x01010

101010

10110x

1×1000

1x10x0

1x1x00

1×1010

1x1x10

1×1100

1x11x0

1×1110

10xx00

101000

101×00

101x0x

101100

101×00

101000

—

1010×0

101×00

101x0x

101×10

101100

1011×0

1×1110

1x10x0

1x1x00

1x1xx0

1x1x10

1x11x0

1x10x0

x010x0

10×000

xx1000

101000

xx1010

x010x0

xx1000

101000

xx10x0

1010×0

1×1000

10100x

1x100x

xx1010

1×1010

x11000

x110x0

x11000

x110x0

x11000

111000

x110x0

1110×0

111000

1110xx

11100x

x11010

111010

11101x

111×00

111xx0

111×10

10×000

101000

10100x

101×00

101000

1×1000

1010×0

—

1×1000

1x100x

1×1010

1x1x00

1x1xx0

111×10

1110×0

111000

1110×0

1110xx

111010

111xx0

1x1x00

x01000

10xx00

xx1000

101000

10×100

10110x

x01000

xx1000

101000

xx1000

101000

1×1000

101x0x

1x100x

1x10x0

1x110x

x11000

x11x00

x11100

x11000

x11x00

111000

x11x00

111000

111×00

11100x

111x0x

1110×0

111xx0

x11100

111100

11110x

1111×0

10xx00

101000

101×00

101x0x

101100

101×00

1×1000

101×00

1×1000

—

1x1x0x

1x1xx0

1×1100

1111×0

111000

111×00

111x0x

111xx0

111100

1x1x01

10100x

10×101

xx1101

101101

x01001

xx1001

101001

10100x

1x100x

xx1001

xx1x01

101×01

1×1001

1×1101

x11001

x11x01

x11101

1111×1

x11001

x11x01

111001

11100x

111x0x

x11x01

111001

111×01

1110×1

111xx1

x11101

111101

11110x

111101

1111×1

10xx01

101001

101x0x

101×01

101101

101×01

1×1001

101x0x

1x100x

1x1x0x

—

1×1101

1x110x

1111×1

111001

111×01

111x0x

111×01

111xx1

111101

1x1x10

x01010

1010×0

xx1010

x01010

1010×0

xx1010

101010

1x10x0

xx1010

1×1010

x11010

11111x

x11010

1110×0

x11x10

111010

111xx0

11101x

x11x10

111010

111×10

111x1x

x11110

1111×0

111110

11111x

111110

1010×0

101xx0

1011×0

101xx0

1x10x0

101×10

1×1010

1x1xx0

—

1x11x0

1×1110

111110

111010

111xx0

111×10

111x1x

111×10

111110

1x110x

10×100

101×00

10x10x

xx1101

101101

101x0x

101×00

1x1x00

xx1101

101101

1x1x01

1×1101

x11100

x11101

x1110x

x11101

1111×1

x1110x

111x0x

x11100

111×00

111100

x11101

111×01

111101

1111×0

1111×1

x1110x

11110x

111100

111101

1111xx

10x10x

101x0x

101100

101101

10110x

1x1x0x

101100

1x1x00

1×1100

1×1101

1x11x0

—

1×1100

1111xx

111x0x

11110x

111100

111101

1111xx

11110x

1x11x0

10×100

101×00

10×100

10110x

101×00

101xx0

1x1x00

10110x

1x1x10

1x110x

x11100

11111x

x11100

111×00

x111x0

111xx0

111100

11110x

x11110

111×10

111110

11111x

x111x0

111100

1111×0

1111xx

111110

10×100

101×00

101100

10110x

101100

1x1x00

1011×0

1x1xx0

1×1100

1x110x

1×1110

1×1100

—

111110

111xx0

111100

1111×0

1111xx

111110

1111×0

11x11x

x10111

111×10

1111×1

x1x111

11×111

x11110

111×10

1111×0

x11111

111×11

1111×1

x1111x

111x1x

111110

111111

x1111x

1111xx

111110

111111

11111x

1×1110

111×10

1111×0

1111×1

111110

1111xx

111110

—

111x1x

1111xx

111110

111111

11111x

1110xx

x11000

1×1000

x11010

x1100x

1x100x

x110x0

1x10x0

111000

x110x1

x11001

1×1001

111001

x1101x

111010

111×01

x1100x

x110x0

x11000

x11001

111×11

x110xx

x1100x

11100x

x110x0

1110×0

111000

x110x1

1110×1

111001

x1101x

11101x

111010

111011

111x0x

111xx0

111xx1

111x1x

1x100x

1×1000

1×1001

1x100x

11100x

1x10x0

1110×0

111000

111001

111010

111x0x

111xx0

111x1x

—

11100x

1110×0

1110×1

11101x

111xxx

111x0x

x11000

1×1000

x11101

1×1101

x1100x

1x100x

x11000

1×1000

111000

x11001

x11x01

1x1x01

111001

1110×0

111101

x1100x

x11000

x11x00

x11x01

x1110x

x11101

1111×1

x1100x

x11x0x

11100x

x11x00

111000

111×00

x11x01

111001

111×01

1110xx

111xx0

111xx1

x1110x

11110x

111100

111101

1111xx

1x100x

1x1x00

1x1x01

1x110x

1x1x0x

11100x

1x1x00

111000

111×00

111×01

111xx0

11110x

111100

1111xx

11100x

—

111×00

111×01

111xxx

11110x

111xx0

x11000

1×1000

x11010

x11000

1×1000

x110x0

1x10x0

111000

11100x

x11010

111010

11110x

x11000

x110x0

x11x00

x11100

11111x

x110x0

x11x00

111000

x11xx0

1110×0

111×00

1110xx

111x0x

x11x10

111010

111×10

111x1x

x111x0

111100

1111×0

1111xx

111110

1×1000

1x1x00

1×1100

1x1x00

111000

1x1xx0

1110×0

111×00

111x0x

111×10

111100

1111×0

111110

1110×0

111×00

—

111xxx

111×10

1111×0

111xx1

x11101

1×1101

x11001

1×1001

11100x

x110x1

x11x01

1x1x01

111001

x11011

11101x

111101

x11001

x11x01

x11101

x111x1

111111

x110x1

x11x01

111001

1110xx

111x0x

x11xx1

1110×1

111×01

x11x11

111011

111x1x

111×11

x111x1

111101

1111xx

1111×1

111111

1×1001

1x1x01

1×1101

1x1x01

111001

1110xx

111x0x

111×01

111x1x

111101

1111xx

111111

1110×1

111×01

111xxx

—

111×11

1111×1

111x1x

x11010

1×1010

1110×0

x11011

1110×1

x1101x

111010

1111×1

x11010

x11111

111111

x1101x

1110xx

x11x10

111010

111xx0

x11x11

111011

111xx1

x11x1x

11101x

111×10

111×11

x1111x

1111xx

111110

111111

11111x

1110xx

1x1x10

111010

111xx0

111xx1

111×10

1111xx

111110

11111x

11101x

111xxx

111×10

111×11

—

11111x

1111xx

x11101

1×1101

111×00

x11101

1×1101

111×01

111×10

111101

x11100

x11101

x1110x

x111x1

111111

x1110x

111x0x

x111x0

111xx0

111100

x111x1

111xx1

111101

x1111x

111x1x

111110

111111

x111xx

11110x

1111×0

1111×1

11111x

1×1100

1×1101

1x110x

111x0x

1x11x0

111xx0

111100

111101

111110

11110x

1111×0

11111x

111xxx

11110x

1111×0

1111×1

11111x

—

Z₂=
Ĉ₃=C₂∪(C₂*C₂)
C₃=>

0xx0x0, 0x10xx, xx100x
xx10x0, xx1x01, 01xx0x
011xxx, x110xx, x11x0x
x11xx0, x11xx1, x11x1x
x111xx, 10xx0x, 1x1x0x
1x1xx0, 111xxx

Таблица операции C₃*C₃

0xx0x0

0x10xx

xx100x

xx10x0

xx1x01

01xx0x

011xxx

x110xx

x11x0x

x11xx0

x11xx1

x11x1x

x111xx

10xx0x

1x1x0x

1x1xx0

111xxx

0xx0x0

—

0x10x0

0x1000

0x10x0

0x100x

01×000

0110×0

011000

0110×0

0110xx

011010

011xx0

x0x000

xx1000

xx10x0

x110x0

0x10xx

0x10x0

—

0x100x

0x10x0

0x1001

01100x

0110xx

01100x

0110×0

0110×1

01101x

011xxx

x0100x

xx100x

xx10x0

x110xx

xx100x

0x1000

0x100x

—

xx1000

xx1001

01100x

x1100x

x11000

x11001

x110xx

x11x0x

10100x

1x100x

1×1000

11100x

xx10x0

0x10x0

xx1000

—

xx100x

011000

0110×0

x110x0

x11000

x110x0

x110xx

x11010

x11xx0

101000

1×1000

1x10x0

1110×0

xx1x01

0x100x

0x1001

xx1001

xx100x

—

011×01

x11001

x11x01

x11x0x

x11x01

x11xx1

x11101

101×01

1x1x01

1x1x0x

111×01

01xx0x

01×000

01100x

011000

011×01

—

011x0x

01100x

011x0x

011×00

011×01

011xxx

01110x

x11x0x

x11x00

x11x0x

011xxx

0110×0

0110xx

01100x

0110×0

011×01

011x0x

—

0110xx

011x0x

011xx0

011xx1

011x1x

0111xx

x11x0x

x11xx0

x11xxx

x110xx

0110×0

0110xx

x1100x

x110x0

x11001

01100x

0110xx

—

x1100x

x110x0

x110x1

x1101x

x11xxx

1x100x

11100x

1110×0

1110xx

x11x0x

011000

01100x

x1100x

x11000

x11x01

011x0x

x1100x

—

x11x00

x11x01

x11xxx

x1110x

1x1x0x

111x0x

111×00

111x0x

x11xx0

0110×0

x11000

x110x0

x11x0x

011×00

011xx0

x110x0

x11x00

—

x11xxx

x11x10

x111x0

1x1x00

111×00

111xx0

x11xx1

0110xx

0110×1

x11001

x110xx

x11x01

011×01

011xx1

x110x1

x11x01

x11xxx

—

x11x11

x111x1

1x1x01

111×01

111xxx

111xx1

x11x1x

011010

01101x

x110xx

x11010

x11xx1

011xxx

011x1x

x1101x

x11xxx

x11x10

x11x11

—

x1111x

111xxx

111×10

111x1x

x111xx

011xx0

011xxx

x11x0x

x11xx0

x11101

01110x

0111xx

x11xxx

x1110x

x111x0

x111x1

x1111x

—

1x110x

11110x

1111×0

1111xx

10xx0x

x0x000

x0100x

10100x

101000

101×01

1x100x

1x1x0x

1x1x00

1x1x01

1x110x

—

101x0x

101×00

1x1x0x

xx1000

xx100x

1x100x

1×1000

1x1x01

x11x0x

11100x

111x0x

111×00

111×01

111xxx

11110x

101x0x

—

1x1x00

111x0x

1x1xx0

xx10x0

1×1000

1x10x0

1x1x0x

x11x00

x11xx0

1110×0

111×00

111xx0

111xxx

111×10

1111×0

101×00

1x1x00

—

111xx0

111xxx

x110x0

x110xx

11100x

1110×0

111×01

x11x0x

x11xxx

1110xx

111x0x

111xx0

111xx1

111x1x

1111xx

1x1x0x

111x0x

111xx0

—

Z₃=
Ĉ₄=C₃∪(C₃*C₃)
C₄=>

Таблица операции C₄*C₄

	x11xxx
x11xxx	—

Z₄=
Ĉ₅=C₄∪(C₄*C₄)
C₅=>Ø
Z = Z₀∪Z₁∪Z₂∪Z₃∪Z₄
Z=>

1000×1, 000xx0, 0x0x00
x00x00, x0x000, 0001xx
0x010x, x0010x, 0x01x1
0xx101, x0x101, 01x1x1
x1x111, 11x11x, 0xx0x0
0x10xx, xx100x, xx10x0
xx1x01, 01xx0x, 10xx0x
1x1x0x, 1x1xx0, x11xxx

Нахождение тупиковых форм.

Таблица операции вычитания

1000×1

000xx0

0x0x00

x00x00

x0x000

0001xx

0x010x

x0010x

0x01x1

0xx101

x0x101

01x1x1

x1x111

11x11x

0xx0x0

0x10xx

xx100x

xx10x0

xx1x01

01xx0x

10xx0x

1x1x0x

1x1xx0

x11xxx

1000×1

—

1000×1

100011

000xx0

—

000×10

000010

0x0x00

010×00

—

010×00

010000

x00x00

100×00

—

100100

x0x000

x01000
10×000

x01000
101000

—

x01000
101000

101000

0001xx

0001×1

—

000111

0x010x

0x0101
01010x

0x0101
010101

010101

—

010101

x0010x

x00101
10010x

x00101
100101

100101

—

100101

0x01x1

0101×1

010111

—

010111

0xx101

0x1101
01×101

0x1101
011101

—

011101

x0x101

x01101
10×101

x01101
101101

101101

—

101101

01x1x1

01×111
0111×1

011111
0111×1

011111

—

x1x111

x11111
11×111

111111
11×111

—

11x11x

11×110

—

11×110

110110

0xx0x0

0x10x0
01x0x0

0x10x0
01×010
0110×0

0x1010
0110×0
01×010

—

010010

0x10xx

0x10x1
0x101x
0110xx

0x10x1
0x1011
0110×1

—

0x1011
011011

001011

xx100x

xx1001
x1100x

xx1001
x11001
11100x

1×1001
111001
11100x

—

1×1001
111001

xx10x0

xx1010
x110x0

1×1010
1110×0

1×1010
111010

—

1×1010
111010

xx1x01

xx1001
1x1x01

xx1001
1×1001
111×01

1×1001
111×01

111101

—

111101

01xx0x

01xx01
011x0x

01×001
011×01
011x0x

01×001
011001
011×00
01100x

01×001
011001
011100

010001
011100

—

010001
011100

010001

10xx0x

10xx00
10x10x
101x0x

101×00
10×101
10110x
101x0x

101100
10×101
10110x
101×01

101100
101101
10110x
101×01

101100
101001

101100

—

1x1x0x

1x1x01
1x110x
111x0x

1×1001
111×01
1×1100
11110x
111x0x

111101
1×1100
11110x

1×1100
111100

111100

—

1x1xx0

1x1x10
1x11x0
111xx0

1×1010
101×10
1×1100
1011×0
111×00
1110×0

1×1010
101×10
1×1100
1011×0
111100
111010

101110
1×1100
1011×0
111100

101110
111100

101110

—

101110

x11xxx

x11xx0
x11x1x
x110xx
111xxx

x11xx0
x11x10
x1101x
111x1x
x110xx
111xxx

x11xx0, x11x10, x1101x
111×10, 11101x, x110xx
111xx0, 111x0x, 1110xx

x11x00, x110x0, 011xx0
x11010, 011×10, x1101x
111010, 11101x, x110xx
111×00, 1110×0, 111x0x
1110xx

x11100, 111×00, 1110×0
0111×0, 111010, 011110
x11011, 11101x, x110x1
1110xx, 111x0x

x11100, 111×00, 1110×0
0111×0, 111010, 011110
111011, 11101x, 1110×1
1110xx, 111x0x

x11100
111100
111010
0111×0
011110
111011
11101x
11110x

x11100
111100
0111×0
011110
111011
11110x

x11100
111100
0111×0
011110
111011

111100
011110
111011

011110
111011

—

E₀:
L₁=L₀#E₀

Получение L₁:

	11x11x	0xx0x0	01xx0x	1x1xx0	x11xxx
000000, 000100, 000101 000111, 001000, 001001 001010, 010000, 010001 010010, 010100, 010101 010111, 011000, 011001 011010, 011100, 011110 011111, 100101, 101000 101001, 101010, 101101 101110, 110110, 110111 111000, 111001, 111010 111100, 111101, 111110 111111	000000, 000100, 000101 000111, 001000, 001001 001010, 010000, 010001 010010, 010100, 010101 010111, 011000, 011001 011010, 011100, 011110 011111, 100101, 101000 101001, 101010, 101101 101110, 111000, 111001 111010, 111100, 111101	000100, 000101, 000111 001001, 010001, 010100 010101, 010111, 011001 011100, 011110, 011111 100101, 101000, 101001 101010, 101101, 101110 111000, 111001, 111010 111100, 111101	000100, 000101, 000111 001001, 010111, 011110 011111, 100101, 101000 101001, 101010, 101101 101110, 111000, 111001 111010, 111100, 111101	000100, 000101, 000111 001001, 010111, 011110 011111, 100101, 101001 101101, 111001, 111101	000100 000101 000111 001001 010111 100101 101001 101101

L₁:
₁=Z₀-E₀
До упорядочивания:

	000100	000101	000111	001001	010111	100101	101001	101101
1000×1
000xx0	+
0x0x00	+
x00x00	+
x0x000
0001xx	+	+	+
0x010x	+	+
x0010x	+	+				+
0x01x1		+	+		+
0xx101		+
x0x101		+				+		+
01x1x1					+
x1x111					+
0x10xx				+
xx100x				+			+
xx10x0
xx1x01				+			+	+
10xx0x						+	+	+
1x1x0x							+	+

После упорядочивания:

	000100	000101	000111	001001	010111	100101	101001	101101
0001xx	+	+	+
x0010x	+	+				+
0x01x1		+	+		+
x0x101		+				+		+
xx1x01				+			+	+
10xx0x						+	+	+

₁ => Z₁
Z₁:

Таблица операции вычитания

	0001xx	x0010x	0x01x1	x0x101	xx1x01	10xx0x
0001xx	—	00011x	000110	000110	000110	000110	v
x0010x	10010x	—	10010x	100100	100100	Ø
0x01x1	0101×1	0101×1	—	0101×1	0101×1	0101×1	v
x0x101	x01101 10×101	x01101 101101	x01101 101101	—	Ø	Ø
xx1x01	xx1x01	xx1x01	xx1x01	xx1001 x11x01	—	x11001 0x1001 x11x01	v
10xx0x	10xx0x	10x00x 101x0x	10x00x 101x0x	10x00x 101×00 10100x	10×000 10000x 101×00 101000	—	v

E₁:
L₂=L₁#E₁

Получение L₂:

	0x01x1	xx1x01
000100 000101 000111 001001 010111 100101 101001 101101	000100 001001 100101 101001 101101	000100 100101

L₂:
₂=Z₁-E₁
До упорядочивания:

	000100	100101
0001xx	+
x0010x	+	+
x0x101		+
10xx0x		+

После упорядочивания:

	000100	100101
x0010x	+	+
10xx0x		+

₂ => Z₂
Z₂:

Таблица операции вычитания

	x0010x	10xx0x
x0010x	—	00010x	v
10xx0x	10x00x 101x0x	—	v

E₂:
L₃=L₂#E₂

Получение L₃:

	x0010x
000100 100101	Ø

L₃:Ø
₃=Z₂-E₂

₃ => Z₃
Z₃:

МДНФ:x₁x₂x₄x₅ v x₁x₄x₆ v x₁x₂x₅ v x₁x₃x₆ v x₂x₃ v x₁x₃x₄x₆ v x₃x₅x₆ v x₂x₃x₄x₅, цена=26

3. Анализ полученных результатов

Все результаты:

Результат метода Квайна
f₁ = x₁x₃x₄x₆ v x₁x₂x₄x₆ v x₁x₃x₅x₆ v x₁x₂x₄x₅ v x₃x₄x₅ v x₃x₄x₆ v x₁x₂x₄x₅x₆ v x₁x₃x₅x₆ v x₁x₂x₃x₅ v x₂x₃x₄x₅ v x₁x₂x₃x₅ v x₂x₃x₆, цена=46

Результат метода Карно
f₂ = x₁x₂x₃x₄x₆ v x₁x₂x₄x₅ v x₁x₄x₆ v x₁x₃x₄ v x₁x₂x₅ v x₁x₃x₆ v x₂x₃ v x₁x₂x₃x₄ v x₁x₃x₄x₆ v x₁x₂x₅ v x₃x₅x₆, цена=37

Результат метода Кубических покрытий
f₃ = x₁x₂x₄x₅ v x₁x₄x₆ v x₁x₂x₅ v x₁x₃x₆ v x₂x₃ v x₁x₃x₄x₆ v x₃x₅x₆ v x₂x₃x₄x₅, цена=26

Общая таблица истинности

Набор	Исходная	После Квайна	После Карно	После Кубических покрытий
`x`₁`x`₂`x`₃`x`₄`x`₅`x`₆	f₀	f₁	f₂	f₃
000000	1	1	1	1
000001	0	0	0	0
000010	?	0	1	1
000011	0	0	0	0
000100	1	1	1	1
000101	1	1	1	1
000110	?	0	1	0
000111	1	1	1	1
001000	1	1	1	1
001001	1	1	1	1
001010	1	1	1	1
001011	?	0	1	0
001100	0	0	0	0
001101	?	0	1	1
001110	0	0	0	0
001111	0	0	0	0
010000	1	1	1	1
010001	1	1	1	1
010010	1	1	1	1
010011	0	0	0	0
010100	1	1	1	1
010101	1	1	1	1
010110	0	0	0	0
010111	1	1	1	1
011000	1	1	1	1
011001	1	1	1	1
011010	1	1	1	1
011011	?	0	1	1
011100	1	1	1	1
011101	?	0	1	1
011110	1	1	1	1
011111	1	1	1	1
100000	?	0	1	0
100001	?	0	1	0
100010	0	0	0	0
100011	?	0	1	0
100100	?	0	1	1
100101	1	1	1	1
100110	0	0	0	0
100111	0	0	0	0
101000	1	1	1	1
101001	1	1	1	1
101010	1	1	1	1
101011	0	0	0	0
101100	?	0	1	1
101101	1	1	1	1
101110	1	1	1	1
101111	0	0	0	0
110000	0	0	0	0
110001	0	0	0	0
110010	0	0	0	0
110011	0	0	0	0
110100	0	0	0	0
110101	0	0	0	0
110110	1	1	1	1
110111	1	1	1	1
111000	1	1	1	1
111001	1	1	1	1
111010	1	1	1	1
111011	?	0	1	1
111100	1	1	1	1
111101	1	1	1	1
111110	1	1	1	1
111111	1	1	1	1

АНАЛИЗ

По таблице истинности видно, что минимизация функции проведена верно.

В результате минимизации получили минимальные дизъюнктивные нормальные формы:

Доопределив функцию нулями, методом Квайна получили МДНФ цены 46
Доопределив функцию единицами, методом карт Карно получили МДНФ цены 37
Доопределяя функцию по ходу выполнения алгоритма, методом кубических покрытий получили МДНФ цены 26

Метод кубических покрытий приводит к наименьшей МДНФ. Это связано с тем, что минимизируется не полностью определенная функция. В результате минимальная форма принимает на наборах, на которых исходная функция не определена, такие значения, которые соответствуют наиболее оптимальному покрытию. Из всех методов наиболее трудоемким оказывается также метод кубических покрытий, но он удобен для программной реализации минимизации. Наименее трудоемким оказался метод Квайне.

4 Список литературы

http://www.google.com/search?q=минимизация+переключательных+функций
file:///C:/Users/Viktor/Desktop/tmp2/minsf/index.html#24

Источник

Носитель элементарной конъюнкции ранга R будем называть интервалом ранга R.

Интервал ранга R содержит 2N-R векторов.

N – количество рассматриваемых векторов.

Интервал – носитель элементарной конъюнкции.

Теорема

Носитель дизъюнкции двух функций равен объединению носителей этих функций.

Доказательство.

» a Î Nf V g Þ f(a) V g(a) = 1 Þ f(a) = 1 ИЛИ g(a) = 1 Þ a Î Nf ИЛИ a Î N g

Ч. т.д.

Носитель ДНФ является объединением интервалов.

Допустимым интервалом для данной функции называется интервал, который целиком содержится в носителе этой функции.

Nf = I1 V I2 V … V Ik

Интервал для данной функции является максимальным, если он не содержится целиком ни в каком другом допустимом интервале.

Элементарная конъюнкция, носителем которой является допустимый интервал, называется импликантой.

ЭК, N – максимальный интервал – простая импликанта.

Представление носителя в виде объединения максимальных интервалов будем называть Покрытием носителя максимальными интервалами.

Дизъюнкция всех возможных простых импликант называется Сокращенной ДНФ функции.

Покрытие носителя интервалами будем называть Неприводимым, если ни один нельзя отбросить из правой части равенства, не нарушив это равенство.

ДНФ, которая соответствует неприводимому покрытию, называется Тупиковой ДНФ.

Утверждение.

Минимальная ДНФ Содержится среди тупиковых ДНФ.

Определение

Максимальный интервал называется ядровым, если он содержит хотя бы одну вершину из носителя функции, которая не принадлежит больше никакому другому максимальному интервалу.

Элементарная конъюнкция, соответствующая ядровому интервалу – ядровая импликанта.

Объединение всех ядровых интервалов – ядро функции.

Дизъюнкция всех ядровых импликант — ядровая ДНФ.

Ядро функции обязательно входит в любое неприводимое покрытие.

Алгоритм получения минимальной ДНФ.

1. Выделяем носитель функции.

2. Выделяем все возможные интервалы.

3. Выписываем все простые импликанты.

4. Выделяем ядровый интервал.

5. Используя ядро функции и комбинацию неядровых интервалов, получаем все неприводимые покрытия, для каждого из которых выписываем тупиковую ДНФ.

6. Среди тупиковых ДНФ выбираем минимальную.

X1	X2	X3	F
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	1

Выделение всех возможных интервалов.

1. Для булева куба размерности 3 интервалом ранга 1 могут быть 4 вершины, лежащие в одной грани.

2. Ранга 2 – любые 2 вершины, соединенные ребром.

3. Ранга 3 – любая отдельная вершина.

1. Нет _

2. I1 = { 001 011} <-> П1 = x1x3 — ядровый

I2 = { 011 111} <-> П2 = x2x3

Если координата вектора меняет значения, то переменная не входит

I3 = { 111 110} <-> П3 = x1x2

I4 = { 110 100} <-> П4 = x1x3

Dсокр. = П1 V П2 V П3 V П4

Nf = I1 U I4 U I2 (U – объединение)

Получили неприводимое покрытие, добавив к ядру недостающие интервалы так, чтобы все единичные вершины были задействованы.

D1= П1 V П4 V П2

Nf = I1 U I4 U I3

D2= П1 V П4 V П3

Сосчитаем ранги тупиковых ДНФ

R1 = 6

R2 = 6

Dmin = D1 = D2

Метод карт Карно для нахождения минимальной ДНФ

N = 4

Карта Карно – плоскостная интерпретация 4-мерного булева куба.

Считаем, что левый край склеен с правым, а верхний – с нижним.

Если таблицу Карно свернуть таким образом, то получится тор (torus — геометрическая фигура, напоминающая бублик).

Правила поиска интервалов.

1. Интервалом ранга 1 могут быть 2 соседних строки (2 соседних столбца)

2. Интервалом ранга 2 может быть вся строка, весь столбец или квадрат 2х2.

3. Интервалом ранга 3 – любые 2 соседние по горизонтали и вертикали клетки.

4. Одна отдельно взятая вершина будет интервалом ранга 4.

Алгоритм – тот же самый.

< Предыдущая		Следующая >

Источник

Схемотехника. Минимизация логических функций

Зачем это нужно?

Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок.

К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки.

В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.

Минимизация логических функций при помощи карт Карно

Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.

Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.

В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

Возможность поглощения следует из очевидных равенств

Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.

Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.

На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:

В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.

Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

В общем случае можно сказать, что 2K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.

Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.

Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):

Объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2 n (n целое число = 0…) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
Не смежные области расположенные симметрично оси(ей) могут объединяться в одну;
Область должна быть как можно больше, а кол-во областей как можно меньше;
Области могут пересекаться;
Возможно несколько вариантов накрытия.

Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):

Порядок работы с картой Карно

Лекция №11

Упрощение логических выражений методом карт Карно

2. Принцип минимизации.

3. Порядок работы с картой Карно.

Куб Карно

Куб Карно́ — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.

Принцип минимизации

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

Аналогично для КНФ:

Возможность поглощения следует из очевидных равенств

Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе 2 N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.

Таблица не верна. Верной будет: 1 1 0 0 1 1 0 0. Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

В общем случае можно сказать, что 2 K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.

Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом, появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

Аналогичным образом можно работать с функциями пяти, семи (обязательно простое число) и т.д., используя не визуализируемые многомерные булевы кубы.

Порядок работы с картой Карно

Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, задавая её значения на всех возможных 2 N наборах входных переменных X₁ . X_N. Карта Карно также содержит 2 N клеток, каждая из которых ассоциируется с уникальным набором входных переменных X₁ . X_N. Таким образом, между таблицей истинности и картой Карно имеется взаимно однозначное соответствие, и карту Карно можно считать соответствующим образом отформатированной таблицей истинности.

В данном разделе в качестве примера используется функция четырёх переменных, заданная таблицей истинности, изображённой на рис. 2а. Карта Карно для той же функции изображена на рис. 2б.

Рис. 2. Пример работы с картой Карно

Принципы склейки

· Склейку клеток карты Карно можно осуществлять по единицам (если необходимо получить ДНФ) или по нулям (если требуется КНФ).

· Склеивать можно только прямоугольные области с числом единиц (нулей) 2 n , где n — целое число. Для карт Карно с числом переменных более четырёх могут получаться более сложные области, о чём будет сказано в следующих разделах.

· Область, которая подвергается склейке должна содержать только единицы (нули).

· Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой (топологически карта Карно для четырёх переменных представляет собой тор) и могут объединяться в прямоугольники. Следствием этого правила является смежность всех четырёх угловых ячеек карты Карно для N=4. Если во всех четырёх угловых ячейках стоят единицы (нули) они могут быть объединены в квадрат, как показано на рис. 2в.

· Все единицы (нули) должны попасть в какую-либо область.

· С точки зрения минимальности ДНФ (КНФ) число областей должно быть как можно меньше (каждая область представляет собой терм), а число клеток в области должно быть как можно больше (чем больше клеток в области, тем меньше переменных содержит терм. Терм размером 2 n ячеек содержит N–n переменных).

· Одна ячейка карты Карно может входить сразу в несколько областей. Это следует из очевидного свойства булевых функций: повторение уже существующего слагаемого (сомножителя) не влияет на функцию:

· В отличие от СДНФ (СКНФ), ДНФ (КНФ) не единственны. Возможно несколько эквивалентных друг другу ДНФ (КНФ), которые соответствуют разным способам покрытия карты Карно прямоугольными областями.

Описание

Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути, Карта Карно — это таблица истинности, составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.е. вся Карта Карно сворачивается в фигуру тор (бублик) (рис.4.1).

Рис. 4.1. Метод скручивания карты Карно

На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки, которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):

1. Объединяем смежные клетки, содержащие единицы, в область так, чтобы одна область содержала ( целое число = 0… ) клеток (помним про то, что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток, содержащих нули;

2. Область должна располагаться симметрично оси (ей) (оси располагаются через каждые четыре клетки);

3. Несмежные области, расположенные симметрично оси(ей), могут объединяться в одну;

4. Область должна быть как можно больше, а количество областей как можно меньше;

5. Области могут пересекаться;

6. Возможно несколько вариантов покрытия.

Далее берём первую область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например (для Карт на 2 переменные):

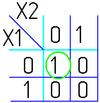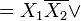Для КНФ всё то же самое, только рассматриваем клетки с нулями, неменяющиеся переменные в пределах одной области объединяем в дизъюнкции (инверсии проставляем над единичными переменными), а дизъюнкции областей объединяем в конъюнкцию. На этом минимизация считается законченной. Так для Карты Карно на рис.1 выражение в формате ДНФ будет иметь вид:

Так же из ДНФ в КНФ и обратно можно перейти использовав Законы де Моргана.

Пример 1.

Упростить полученную СДНФ, используя склеивание, а так же применить карту Карно для получения ДНФ.

, применено свойство и склеивание по «z» и по «y».

Дизъюнкции в скобках получены по парам наборов переменных (0,0,0), (0,0,1) и (0,0,0), (0,1,0). Наборы в каждой паре отличаются только в одной позиции и называются соседними. После упрощения остаются совпадающие в паре переменные. Карты Карно представляют собой таблицу истинности, в которой соседние наборы переменных расположены рядом (метод скользящей единицы при этом нарушается).

Для нашей функции имеем

Карты Карно позволяют получить ДНФ минимальную по числу переменных или их отрицаний. Для этого необходимо заключить в круги рядом стоящие значения функции равные 1, причём

1) Каждый руг может содержать только 2 K (к = 0, 1, 2,…) единиц, например16, 8, 4, 2, 1.

2) Круги должны быть наибольшего размера.

3) Число кругов наименьшее, покрывающее все единицы.

4) Так как наборы (0,0) и (1,0) соседние. То края карты соединяются друг с другом.

5) По каждому из кругов составляется простая конъюнкция, входящая в ДНФ. При этом оставляются только те переменные, которые сохраняют свое значение во всем круге и как обычно, если х_i = 1, то пишем х_i , если х_i = 0, то .

Построим круги для нашего примера.

yz x
1 1	1 2

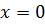
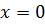
Имеем две конъюнкции. Для первого круга и сохраняют свое значение, получаем . Во втором круге не меняется и , получаем . Окончательно .

Пример 2

У мальчика Коли есть мама, папа, дедушка и бабушка. Коля пойдёт гулять на улицу, если ему разрешат хотя бы двое родственников.
Для краткости обозначим родственников Коли через буквы:
мама — х1
папа — х2
дедушка — х3
бабушка — х4
Условимся обозначать согласие родственников единицей, несогласие — нулём. Возможность пойти погулять обозначим буквой f, Коля идёт гулять — f = 1, Коля гулять не идёт — f = 0.
Составим таблицу истинности:

Перерисуем таблицу истинности в 2-х мерный вид:

Переставим в ней строки и столбцы в соответствии с кодом Грея. Получили Карту Карно:

Заполним её значениями из таблицы истинности:

Минимизируем в соответствии с правилами:

1. 1. Все области содержат 2^n клеток;

2. 2. Так как Карта Карно на четыре переменные, оси располагаются на границах Карты и их не видно (подробнее смотри пример Карты на 5 переменных);

3. 3. Так как Карта Карно на четыре переменные, все области симметрично осей — смежные между собой (подробнее смотри пример Карты на 5 переменных);

4. 4. Области S3, S4, S5, S6 максимально большие;

5. 5. Все области пересекаются (необязательное условие);

6. 6. В данном случае рациональный вариант только один.

Теперь по полученной минимальной ДНФ можно построить логическую схему:

Из-за отсутствия в наличии шести — входового элемента ИЛИ, реализующего функцию дизъюнкции, пришлось каскадировать пяти- и двух-входовые элементы (D7, D8).

Составим мин. КНФ:

Для минимизации логических функций возможно использовать разные методы:

карта Карно (Вейча)
Квайна
Квайна- Мак-Класки
Петрика

Отличие метода карт Карно от карт Вейча заключается в способе обозначения строк и столбцов карт. У карт Карно строки и столбцы обозначаются с помощью кода Грея. Однако, принципиальной разницы между ними нет.

Метод минимизационных карт Карно (или карт Вейча) хорошо работает при числе аргументов 3,4 и даже 5 и обеспечивает простоту получения результата. Этот метод основан на зрительном анализе таблиц (карт) и не может быть применен для обработки вычислительной техникой.

1. Минимизировать нижеприведённые функции, представленные картами Карно.

Не заполненные клетки соответствуют нулю. Переменные, обозначенные буквами, соответствуют прямому значению, а не обозначенные — инверсному.

1. Определение куба Карно.

2. Кем и в каком году были изобретены карты Карно?

3. Основной метод минимизации логических функций?

4. Принципы склейки карты Карно.

5. В какую фигуру сворачивается карта Карно?

Минимальная ДНФ булевой функции

На этой странице вы найдете готовые примеры по булевой алгебре , связанные с минимизацией нормальных формул булевой функции (обычно это задания вроде «найти минимальную ДНФ. «). Помимо минимальной ДНФ, в процессе решения могут быть найдены тупиковые и сокращенные ДНФ, ядерные импликанты (и ядро функции), функция Патрика и т.п.

Основные методы получения минимальной ДНФ функции это: равносильные преобразования, метод карт Карно, метод Квайна (или Квайна-МакКласки), преобразования по булевому кубу. Все они разобраны ниже. В некоторых задачах также построены релейно-контактные или функциональные схемы.

Типовые задачи снабжены подробным решением, формулами, пояснениями. Используйте их, чтобы научиться решать подобные задачи или закажите решение своей работы нам.

Другие примеры решений о булевых функциях:

Задачи и решения о минимизации ДНФ булевых функций

Задача 1. Применяя равносильные преобразования привести булеву функцию $f=(bar x to bar y)to (yz to bar xz)$ к минимальной ДНФ.

Задача 2. Для заданной логической функции: $$F= overline <(bar A vee Bcdot bar C)>cdot overline<( overline <(B downarrow C)>cdot D> $$ — найти дизъюнктивную нормальную форму;
— составить таблицу истинности и построить диаграмму Карно;
— получить минимальную дизъюнктивную нормальную форму;
— от минимальной дизъюнктивной нормальной формы перейти к конъюнктивной нормальной форме.

Задача 3. Для функции $f(x_1,x_2,x_3,x_4)$, заданной списком номеров наборов из $Nf$ методом Квайна найти сокращенную и минимальные ДНФ.
Список номеров: 0,1,2,3,6,7,8,9,11,15.

Задача 4. С помощью карт Карно найдите сокращенную, все тупиковые и минимальные ДНФ или КНФ булевой функции f(x1,x2,x3,x4), заданной вектором своих значений.
(1100 0101 0011 0011)

Задача 5. Найти минимальные КНФ булевых функций, зависящих от аргументов $A, B, C, D$. В квадратных скобках указаны неопределенные состояния

$$f = ( 1, 2, 5, 6, 14), [4, 9, 11, 12, 15].$$

Задача 6. Найти минимальные ДНФ и КНФ булевых функций, зависящих от аргументов $A, B, C, D$

$$f = (1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14, 15).$$

Задача 7. Для булевой функции $f(x, y, z)$ найти методом преобразования минимальную ДНФ. По таблице истинности построить СКНФ. По минимальной ДНФ построить релейно-контактную схему.

$$f(x,y,z)=(bar x vee bar y)wedge (bar y vee bar z) to (bar x vee bar z)$$

Задача 8. Переключательная функция от трех аргументов задана номером в десятичной системе счисления. Получить номер ПФ в двоичном, восьмеричном и шестнадцатеричном кодах, таблицу истинности, определить СДНФ, СКНФ, символическую форму функции с восьмеричной нумерацией наборов. Минимизировать функцию по кубу соседних чисел и карте Карно. Определить свойства функции. Реализовать функцию переключательной схемой на функциональных элементах в базисах а) И, ИЛИ, НЕ, б) И-НЕ, в) ИЛИ-НЕ.

Задача 9. Для булевой функции f, заданной в таблице 1:
а) найти сокращённую ДНФ;
б) найти ядро функции;
в) получить все тупиковые ДНФ и указать, какие из них являются минимальными;
г) на картах Карно указать ядро и покрытия, соответствующие минимальным ДНФ.

Задача 10. Двумя способами: с помощью карты Карно и методом Квайна найти сокращенную, ядровую и все минимальные дизъюнктивные нормальные формы булевой функции $f$, заданной вектором значений 0101101001001110. Построить минимальную функциональную (над системой $<vee, wedge, neg>$ ) и минимальную контактную схемы для функции $f$.

Решение задач о минимальной ДНФ на заказ

Выполняем для студентов очников и заочников решение заданий, контрольных и практических работ о минимизации булевых функций. Также оказываем помощь в сдаче тестов. Подробное оформление, таблицы, графики, пояснение, использование специальных программ при необходимости. Стоимость примера от 150 рублей , оформление производится в Word, срок от 2 дней.

Сокращенная и минимальная ДНФ

Сокращенная ДНФ — форма записи булевой функции, для которой 1) любые два слагаемых различаются как минимум в двух позициях, 2) ни один из конъюнктов не содержится в другом. Для булевой функции может существовать несколько сокращенных ДНФ

Минимальная ДНФ — такая сокращенная ДНФ, в которой содержится минимальное количество вхождений переменных.

источники:

http://lektsii.org/16-81366.html

http://www.matburo.ru/ex_dm.php?p1=bfmin

Источник