В данной публикации мы рассмотрим, что такое тупой угол, а также разберем примеры задач, в которых он участвует.
- Определение тупого угла
- Примеры задач
Определение тупого угла
Угол является тупым, если его градусная мера находится между 90 и 180 градусами.
∠α – тупой, если 90° < α < 180°.
То есть тупой угол больше прямого (90°), но меньше развернутого (180°).
Примеры задач
Задание 1
Дан треугольник, у которого известны два угла – 34° и 27°. Найдем третий и определим, является ли он тупым.
Решение:
Примем неизвестную величину за “α“. Как мы знаем, сумма углов треугольника равняется 180 градусам, значит:
α = 180° – 34° – 27° = 119°.
Следовательно, угол α – тупой.
Задание 2
Дан ромб, площадь (S) которого составляет 12,5 см2, а длина (a) стороны – 5 см. Найдем его углы и определим, являются ли они тупыми.
Решение:
Синус угла ромба (α) можно найти следующим образом (выведено из формулы расчета площади фигуры):
Следовательно, α = 30° (arcsin 0,5), является острым.
Как мы знаем, сумма соседних углов ромба составляет 180 градусов, значит второй угол β равен 150° (180° – 30°), и он является тупым.
Угол, который полностью помещается внутри прямого угла, называется острым.
— острый угол.
Угол, внутри которого полностью помещается прямой угол, называется тупым углом.
— тупой угол.
Обрати внимание!
В ромбе, если он не является квадратом, два угла острых и два угла тупых.
Углы (ABC) и (ADC) — острые.
Углы (BAD) и (BCD) — тупые.
Источники:
Рис. 1. Углы, угольник, ромб. © ЯКласс
Определение
Тупой угол — это угол, больший прямого, но меньший развёрнутого.
Градусная мера тупого угла — от 90º до 180º.
Например,
∠ABC, ∠DEF, ∠PTK — тупые углы.
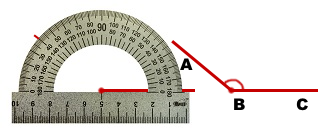
Построить тупой угол заданной градусной меры можно с помощью транспортира.
Пример.
Построить с помощью транспортира угол 140º.
1) Отмечаем точку — вершину угла.
2) От точки проводим луч — сторону угла.
3) Отметку в центре транспортира (у разных моделей отметка может располагаться в разных местах) совмещаем с вершиной угла таким образом, чтобы отметка 0º находилась на стороне угла.
4) Находим 140º на той шкале, где находится 0º, и ставим точку.
5) От вершины угла к отмеченной точке проводим луч — вторую сторону угла.
На рисунках показано построение угла 140º с началом отсчёта по разным шкалам — по нижней и по верхней.
∠ABC=140º
∠MNK=140º
Чтобы найти тупой угол на рисунке при помощи угольника, нужно приложить вершину угольника к вершине угла так, чтобы сторона угольника проходила вдоль одной из сторон угла. Если угол тупой, то его другая сторона выйдет за вторую сторону угольника.
Содержание:
- Определение тупого угла
- Примеры решения задач с тупыми углами
Определение тупого угла
Определение
Угол называется тупым, если его
градусная мера лежит в пределах от
$90^{circ}$ до
$180^{circ}$ (рис. 1).
$angle alpha$ — тупой, если
$90^{circ} lt angle alpha < 180^{circ}$.
То есть тупой угол больше
прямого и меньше, чем
развернутый.
Примеры решения задач с тупыми углами
Пример
Задание. Найти тупой угол параллелограмма
$ABCD$, если известно, что его
острый угол равен
$30^{circ}$.
Решение. Известно, что сумма углов параллелограмма, прилежащих к одной стороне, равна
$180^{circ}$. Тогда искомый тупой угол равен
$$angle alpha=180^{circ}-30^{circ}=150^{circ}$$
Ответ. $angle alpha=150^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два угла треугольника равны
$30^{circ}$ и
$40^{circ}$. Найти третий угол треугольника, определить
тупым или острым он является.
Решение. Пусть $alpha$ — искомый угол.
Согласно теореме про сумму углов треугольника имеем, что
$$angle alpha+30^{circ}+40^{circ}=180^{circ}$$
Отсюда получаем
$$angle alpha=110^{circ}$$
Так как $90^{circ} < angle alpha=110^{circ} < 180^{circ}$, то он является тупым.
Ответ. $angle alpha=110^{circ}$
Читать дальше: что такое плоский угол.
- Учебники
- 2 класс
- Математика 👍
- Моро
- №5
авторы: Моро, Бантова, Бельтюкова, Волкова, Степанова.
издательство: «Просвещение» 2014
Раздел:
- Часть 2
- ЧИСЛА ОТ 1 ДО 100
- Умножение и деление
- Деление
- страница 76
1) Вычисли периметр каждого многоугольника.
2) Выпиши номера тупых углов многоугольника.
reshalka.com
ГДЗ учебник по математике 2 класс Моро. Часть 2. Страница 76. Номер №5
Решение 1
1) 4 * 3 = 12 (см) − периметр синего многоугольника;
2) 2 * 3 + 2 = 6 + 2 = 8 (см) − периметр красного многоугольника;
3) 6 * 2 = 12 (см) − периметр зеленого многоугольника.
Ответ: 12 см; 8 см; 12 см.
Решение 2
Номера тупых углов многоугольников:
синий: 1; 3.
красный: нет тупых углов.
зеленый: 8; 9; 10; 11; 12; 13.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом