Как найти у равнобедреной трапеции в которую - Исправление недочетов и поиск решений вместе с Examum.ru

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

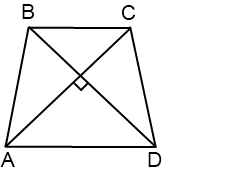
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

Признаки равнобедренной трапеции

∠ABC = ∠BCD и ∠BAD = ∠ADC

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

Основные свойства равнобедренной трапеции

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD

9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

a = b + 2 h ctg α = b + 2 c cos α

b = a — 2 h ctg α = a — 2 c cos α

c =	h	=	a — b
sin α	2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d ₁ 2 — c 2	b =	d ₁ 2 — c 2	c = √ d ₁ 2 — ab
b	a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	— b b =	2S	— a
h	h

4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

m = a — h ctg α = b + h ctg α = a — √ c 2 — h 2 = b + √ c 2 — h 2

2. Формула средней линии трапеции через площадь и сторону:

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

1. Формула высоты через стороны:

h =	1	√ 4 c 2 — ( a — b ) 2
2

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a — b	tg β	= c sin β
2

Диагонали равнобедренной трапеции

Формулы длины диагоналей равнобедренной трапеции:

d ₁ = √ a 2 + c 2 — 2 ac cos α

d ₁ = √ b 2 + c 2 — 2 bc cos β

4. Формула длины диагонали через высоту и основания:

d ₁ =	1	√ 4 h 2 + ( a + b ) 2
2

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

1. Формула площади через стороны:

S =	a + b	√ 4 c 2 — ( a — b ) 2
4

2. Формула площади через стороны и угол:

S = ( b + c cos α ) c sin α = ( a — c cos α ) c sin α

3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:

S =	4 r 2	=	4 r 2
sin α	sin β

4. Формула площади через основания и угол между основой и боковой стороной:

5. Формула площади ранобедренной трапеции в которую можно вписать окружность:

S = ( a + b ) · r = √ ab ·c = √ ab ·m

6. Формула площади через диагонали и угол между ними:

S =	d ₁ 2	· sin γ	=	d ₁ 2	· sin δ
2	2

7. Формула площади через среднюю линию, боковую сторону и угол при основании:

S = mc sin α = mc sin β

8. Формула площади через основания и высоту:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d ₁
4√ p ( p — a )( p — c )( p — d ₁)

где

a — большее основание

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Вписанная в равнобедренную трапецию окружность

Какими свойствами обладает вписанная в равнобедренную трапецию окружность?

1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.

То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.

Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:

2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.

Если MN —

3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.

По свойству равнобедренной трапеции,

Из прямоугольного треугольника ABF по теореме Пифагора

4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство

5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.

Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,

источники:

http://ru.onlinemschool.com/math/formula/trapezium_isosceles/

Вписанная в равнобедренную трапецию окружность

Источник

Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.

1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.

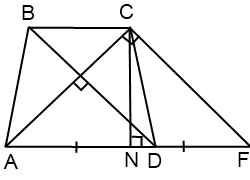
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.

Четырехугольник BCFD — параллелограмм ( BC∥DF как основания трапеции, BD∥CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.

Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то

$[CN = frac{1}{2}AF = frac{{AD + BC}}{2},]$

что в общем виде можно записать как

$[h = frac{{a + b}}{2},]$

где h — высота трапеции, a и b — ее основания.

2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.

Так как средняя линия трапеции m равна полусумме оснований, то

3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).

Так как площадь трапеции находится по формуле

$[S = frac{{a + b}}{2} cdot h]$

а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:

$[h = frac{{a + b}}{2} = m,]$

то

$[S = {h^2}]$

$[S = {(frac{{a + b}}{2})^2}]$

$[S = {m^2}.]$

4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.

Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле

$[S = frac{1}{2}{d_1}{d_2}sin varphi ]$

sin 90º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна

$[S = frac{1}{2}{d^2}.]$

откуда

$[frac{1}{2}{d^2} = {(frac{{a + b}}{2})^2} = {h^2} = {m^2},]$

$[{d^2} = frac{{{{(a + b)}^2}}}{2}.]$

Источник

Углы равнобедренной трапеции. Здравствуйте! В этой статье речь пойдёт о решении задач с трапецией. Данная группа заданий входит в состав экзамена, задачки простые. Будем вычислять углы трапеции, основания и высоты. Решение ряда задач сводится к решению прямоугольного треугольника, как говориться: куда мы без теоремы Пифагора, синуса и косинуса?

Работать будем с равнобедренной трапецией. У неё равны боковые стороны и углы при основаниях. О трапеции есть статья на блоге, посмотрите.

Отметим небольшой и важный нюанс, который в процессе решения самих заданий подробно расписывать не будем. Посмотрите, если у нас дано два основания, то большее основание высотами, опущенными к нему, разбивается на три отрезка – один равен меньшему основанию (это противолежащие стороны прямоугольника), два других равны друг другу (это катеты равных прямоугольных треугольников):

Простой пример: дано два основания равнобедренной трапеции 25 и 65. Большее основание разбивается на отрезки следующим образом:

*И ещё! В задачах не введены буквенные обозначения. Это сделано умышленно, чтобы не перегружать решение алгебраическими изысками. Согласен, что это математически неграмотно, но цель донести суть. А обозначения вершин и прочих элементов вы всегда можете сделать сами и записать математически корректное решение.

Рассмотрим задачи:

zadacha

27439. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.

Для того чтобы найти угол необходимо построить высоты. На эскизе обозначим данные в условии величины. Нижнее основание равно 65, высотами оно разбивается на отрезки 7, 51 и 7:

В прямоугольном треугольнике нам известна гипотенуза и катет, можем найти второй катет (высоту трапеции) и далее уже вычислить синус угла.

По теореме Пифагора указанный катет равен:

Таким образом:

Ответ: 0,96

zadacha

27440. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.

Построим высоты и отметим данные в условии величины, нижнее основание разбивается на отрезки 15, 43 и 15:

Ответ: 21

zadacha

27441. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (2√10)/7. Найдите меньшее основание.

Построим высоты. Для того чтобы найти меньшее основание нам необходимо найти чему равен отрезок являющийся катетом в прямоугольном треугольнике (обозначен синим):

Можем вычислить высоту трапеции, а затем найти катет:

По теореме Пифагора вычисляем катет:

Таким образом, меньшее основание равно:

Ответ: 22

zadacha

27442. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.

Построим высоты и отметим данные в условии величины. Нижнее основание разбивается на отрезки:

1010

Что делать? Выражаем тангенс известного нам угла при основании в прямоугольном треугольнике:

Ответ: 10

zadacha

27443. Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8. Найдите большее основание.

Строим высоты и вычисляем чему равен катет:

Таким образом большее основание будет равно:

Ответ: 71

zadacha

27444. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.

Строим высоты и отмечаем известные величины на эскизе. Нижнее основание разбивается на отрезки 35, 17, 35:

По определению тангенса:

Ответ: 0,4

zadacha

77152. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.

Построим эскиз, построим высоты и отметим известные величины, большее основание разбивается на отрезки 3, 6 и 3:

Выразим гипотенузу обозначенную как х через косинус:

Из основного тригонометрического тождества найдём cosα

Таким образом:

Ответ: 5

zadacha

27818. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50⁰? Ответ дайте в градусах.

Из курса геометрии нам известно, что если имеем две параллельные прямые и секущую, что сумма внутренних односторонних углов равна 180⁰_. В нашем случае это

C условии сказано, что разность противолежащих углов равна 50⁰, то есть

Так как у равнобедренной трапеции углы при основании равны, то есть угол А равен углу В, то можем записать

Имеем два уравнения с двумя неизвестными, можем решить систему:

*Конечно, эту задачу можно было легко решить просто перебирая пары углов )

zadacha

27833. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 60⁰. Найдите меньшее основание.

Построим высоты DE и CF:

Меньшее основание равно отрезку EF, так как DC и EF это противолежащие стороны прямоугольника. Отрезок EF мы можем найти если вычислим АЕ. Выразим этот катет прямоугольного треугольника ADE через функцию косинуса:

Так как AE=FB=5, то EF=25–5–5=15. Следовательно и DC=15.

Ответ: 15

zadacha

27837. Основания равнобедренной трапеции равны 15 и 9, один из углов равен 45⁰. Найдите высоту трапеции.

Из точек D и C опустим две высоты:

Как уже сказано выше они разбивают большее основание на три отрезка: один равен меньшему основанию, два других равны друг другу.

В данном случае они равны 3, 9 и 3 (в сумме 15). Кроме того, отметим что высотами отсекаются прямоугольные треугольники, причём они являются равнобедренными, так как углы при основании равны по 45⁰. Отсюда следует, что высота трапеции будет равна 3.

Ответ: 3

На этом всё! Успеха вам!

С уважением, Александр.

P.S: Расскажите о сайте в социальных сетях!

Источник

Трапеция — геометрическая фигура представляет собой выпуклый четырехугольник с параллельными
противоположными сторонами. Они называются основаниями. Две другие стороны — боковые.
Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон
образует у основания угол в 90 градусов-прямоугольной.

Прямая линия, проведенная от одного основания
к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.
Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции
они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.

Угол трапеции при основании через высоту и прилегающую
боковую сторону
Угол трапеции через нижнее основание, боковую сторону и
диагональ
Угол равнобедренной трапеции через нижнее основание,
среднию линию и боковую сторону
Угол равнобедренной трапеции через среднию линию, верхнее
основание и боковую сторону
Острый угол при нижнем основании прямоугольной трапеции
через высоту и два основания
Острый угол при нижнем основании прямоугольной трапеции
через два основания и боковую сторону

Угол трапеции при основании через высоту и прилегающую боковую сторону

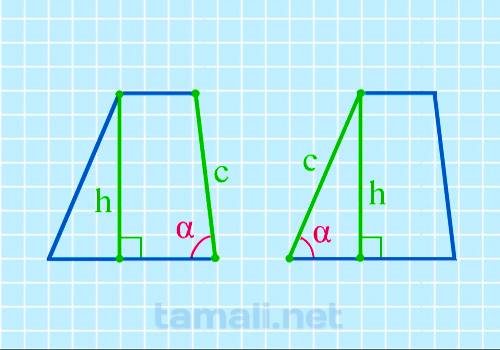
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с
помощью формулы

sin α = h/с

где: h — высота трапеции, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна
9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α =
55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует
величине 55 градусов.

Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции

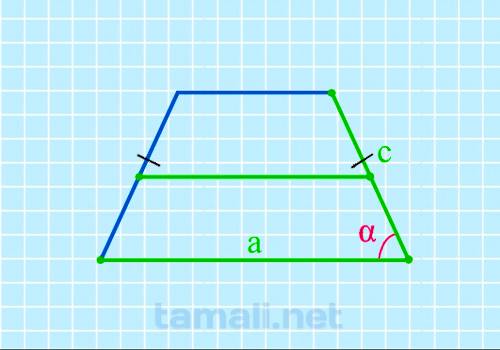
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по
формуле:

cos α = (2a-2m) / 2c

где а — нижнее основание, m — средняя линия, с — боковая сторона.

Цифр после
запятой:

Результат в:

Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8
см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65
градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α =
65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее
особенность.

Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали

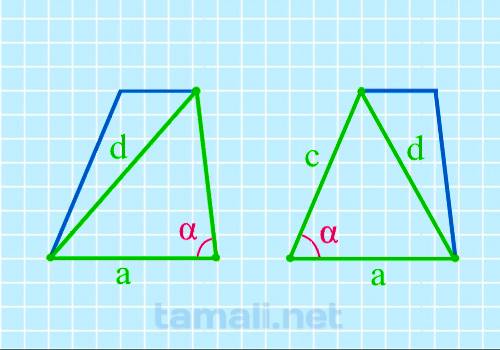
Если известны эти величины, воспользуемся формулой:

cos α= (a²+c²-d²) / 2ac

где а-нижнее основание, d-диагональ, с-боковая сторона.

Цифр после
запятой:

Результат в:

Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см,
боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по
таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534,
отсюда α = 85º.

Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции

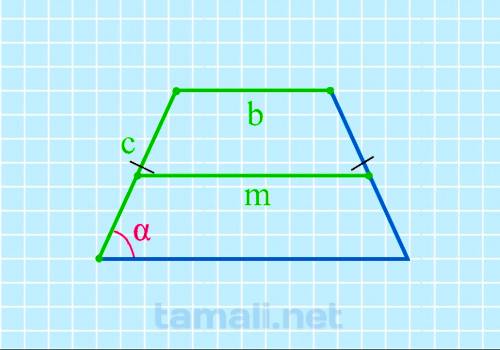
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону
выполняется по предложенной формуле:

cos α = (2m-2b) / 2c

где m — средняя линия, b — верхнее основание, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции
верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5.
Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5,
отсюда α = 60º

Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции

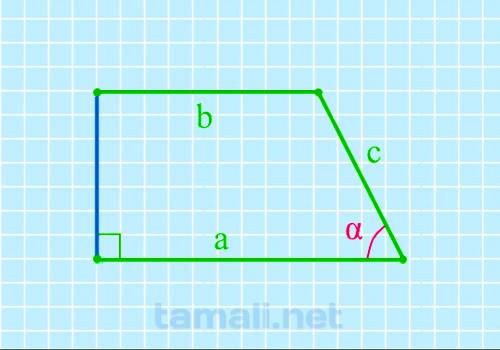
Находится по формуле

cos α = (a — b) / c

где a,b — основания, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный
пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой
стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833.
Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º

Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции

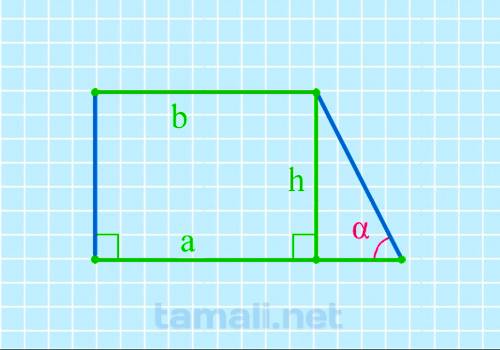
При известных указанных величинах воспользуемся следующей формулой:

tg(α) = h / (a-b)

где h — высота, a,b — верхнее и нижнее основания.

Цифр после
запятой:

Результат в:

Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15.
По таблице функций показатель соответствует 86 градусам.

Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла,
общая сумма которых составляет 360 градусов.

Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми
одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие —
острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением
высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению
высоты к боковой стороне.

Источник

Это свойство равнобедренной трапеции удобно доказать в общем виде в начале изучения темы, чтобы в дальнейшем использовать его при решении задач.

Утверждение.

Высота равнобедренной трапеции, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.

AD=a,