Интервалы возрастания и убывания функции
С помощью данного сервиса можно найти интервалы возрастания и убывания функции в онлайн режиме с оформлением решения в Word.
- Решение онлайн
- Видеоинструкция
Исследование функции с помощью производной
Определение: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)>f(x).
Определение: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)<f(x).
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная f′(x) обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции y=f(x) с помощью первой производной
- Найти производную функции f′(x).
- Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
- Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
- Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
- Вычислить значения функции в точках минимума и максимума.
С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
Пример №1: Найти промежутки монотонности и экстремумы функции: f(x)=x3–3x2.
Решение: Найдем первую производную функции f′(x)=3x2–6x.
Найдем критические точки по первой производной, решив уравнение 3x2–6x=0; 3x(x-2)=0 ;x = 0, x = 2
Исследуем поведение первой производной в критических точках и на промежутках между ними.
| x | (-∞, 0) | 0 | (0, 2) | 2 | (2, +∞) |
| f′(x) | + | 0 | — | 0 | + |
| f(x) | возрастает | max | убывает | min | возрастает |
f(0) = 03 – 3*02 = 0
f(2) = 23 – 3*22 = -4
Ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2);
точка минимума функции (2;-4); точка максимума функции (0;0).
Правило нахождения экстремумов функции y=f(x) с помощью второй производной
- Найти производную f′(x).
- Найти стационарные точки данной функции, т.е. точки, в которых f′(x)=0.
- Найти вторую производную f″(x).
- Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
- Вычислить значения функции в точках экстремума.
Отсюда следует, что дважды дифференцируемая функция f(x) выпукла на отрезке [a, b], если вторая производная f»(x) ≥ 0 при всех х [a, b].
Все вычисления можно проделать в онлайн режиме.
Пример №2. Исследовать на экстремум с помощью второй производной функцию: f(x) = x2 – 2x — 3.
Решение: Находим производную: f′(x) = 2x — 2.
Решая уравнение f′(x) = 0, получим стационарную точку х=1. Найдем теперь вторую производную: f″(x) = 2.
Так как вторая производная в стационарной точке положительна, f″(1) = 2 > 0, то при x = 1 функция имеет минимум: fmin = f(1) = -4.
Ответ: Точка минимума имеет координаты (1; -4).
1.Если производная функции y
= f(x)
положительна (отрицательна) во всех
точках промежутка, то функцияy
= f(x)
монотонно возрастает (убывает)на этом промежутке.
2.Точкаx0называется точкоймаксимума (минимума)
функцииy = f(x),
если существует интервал, содержащий
точкуx0, такой,
что для всехxиз этого
интервала имеет место неравенствоf(x0)≥ f(x),(f(x0)≤ f(x)).
Точки максимума и точки минимума
называются точкамиэкстремума.
3. Необходимое условие экстремума:
в точке экстремума функции ее производная
либо равна нулю(f
′(x)=0), либо
не существует.
4.Первое достаточное условие
экстремума: если в точке x0функцияy = f(x)
непрерывна, а производная f
′(x)при
переходе через точкуx0меняет знак, то точкаx0– точка экстремума: максимума, если
знак меняется с «+» на «-», и минимума,
если с «–» на «+».
Если при переходе через точку x0производная не меняет знак, то в точкеx0экстремума нет.
5.Второе достаточное условие
экстремума: если в точкеx0
,
а
,
тоx0является точкой
максимума функции. Если
,
а
,
тоx0является точкой
минимума функции.
6.Схема исследования функции
на экстремум:
1) найти производную
;
2) найти критические точки функции, в
которых производная равна нулю или не
существует;
3) исследовать знак производной слева
и справа от каждой критической точки и
сделать вывод о наличии экстремумов
функции;
4) найти экстремальные значения функции.
При исследовании функции на экстремум
с помощью 2-го достаточного условия п.
1), 2), 4) сохраняются, а в п. 3) необходимо
найти вторую производную
и определить ее знак в каждой критической
точке.
7.Чтобы найтинаибольшее и наименьшее
значение(глобальный максимум и
минимум) функции
на отрезке [a,b]
следует выбрать наибольшее (наименьшее)
из значений функции в критических
точках, находящихся в интервале (a,b)
и на концах отрезка (в точкахaиb).
8.Если дифференцируемая на интервале
(a,b) функция
имеетединственнуюточку экстремума,
то в этой точке достигается наибольшее
или наименьшее значение (глобальный
максимум или минимум) функции на интервале
(a,b).
8.35. Найти интервалы монотонности
и экстремумы функции
.
Решение. В соответствии со схемой
исследования (п. 6) найдем
.Очевидно, производная существует при
всех значенияхx. Приравниваяy′ к нулю, получаем
уравнение
откуда
и
— критические точки. Знаки производной
имеют вид (рис. 8.1):
Рис. 8.1
На интервалах
и
производная
и функция возрастает, на интервале
и функция убывает;
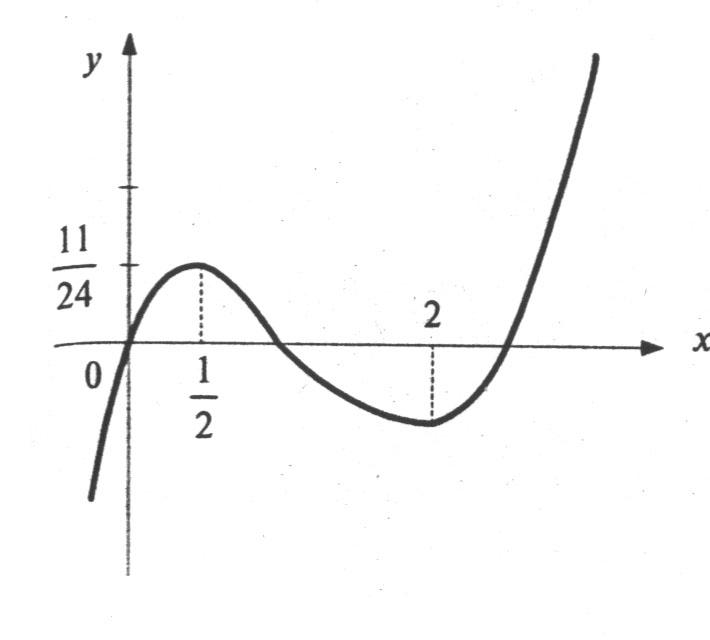
Рис. 8.2
— точка максимума и
— точка минимума и
,
так как при переходе через эти точки
производная меняет свой знак соответственно
с «+» на «-» и с «-» на «+».
Замечание.Установить
существование экстремума в критических
точках
и
,
в которых
можно было и с помощью второй производной
(см.
п. 5). Так как
,
а
,
то
— точка максимума, а
— точка минимума.
График данной функции схематично показан
на рисунке 8.2.
8.36. Найти экстремумы и интервалы
монотонности функции
.
Решение.
.
Производная существует во всех точках,
в которых существует и сама функция,
т.е. при x> 0. Точки, в
которых производная обращается в нуль,
задаются равенствамиlnx=0,lnx-1
= 0, откудаx1 =1,x2
= е – критические точки. Знаки
производной указаны на рис. 8.3.
Рис.8.3
Таким образом, функция монотонно
возрастает на промежутках (0;1) и (е;+
)
и монотонно убывает на промежутке (1;е).
Точкаx= 1 – точка максимума
и
,
точка х = е – точка минимума и
.
8.37. Найти экстремумы и интервалы
монотонности функции
Решение.
.
Производная не существует приcosx=1 т.е. при
и равна нулю при
.
Знак производной совпадает со знакомsin(x); таким
образом у’ >0 при
иy'<0 при
.
Это, соответственно, интервалы возрастания
и убывания функции.
— точки максимума
,
— точки минимума
.
8.38. Найти наибольшее значение
(глобальный максимум) функции
на интервале (10;18).
Решение. Найдем
.
На интервале (10;18) имеется всего одна
критическая точкаx= 6.
Производная при переходе через эту
точку меняет знак с «+» на «-», т.е.x= 6 – точка максимума. Следовательно,
функция достигает наибольшего значения
приx= 16, т.е.
.
(Заметим, что наименьшего значения
(глобального минимума) данной функции
на указанном интервале не существует.)
8.40. Забором длиной 24 метра требуется
огородить с трех сторон прямоугольный
палисадник наибольшей площади. Найти
размеры палисадника.
Решение.Пусть длины сторон палисадникаx,y. Тогда
2x+y= 24, т.е.y= 24-2x.
Площадь палисадникаS=xy=x(24-2x)
= 24x-2x2,
где 0<x<12 (ибо 24-2x>0).
Таким образом, задача свелась к отысканию
значенияx, при которомS(x) принимает
наибольшее значение на интервале (0;12).
НайдемS'(x)
= 24-4x= 0 приx= 6. Легко видеть, чтоx= 6
– единственная точка экстремума –
максимума функцииS(x).
Это означает, что на интервале (0;12)S(x)
принимает наибольшее значение приx= 6, т.е. искомые размеры палисадника 6 м
и 24- 2 — 6 = 12 м.
Найти интервалы
монотонности и экстремумы функции:
8.41.
.8.42.
.8.43.
.
8.44.
.8.45.
8.46.
.
8.47.
.8.48.
.8.49.
.
8.50.
.8.51.
.8.52.
.
8.53.
.8.54.
.8.55.
.
8.56.
.8.57.
.8.58.
.
8.59.
.8.60.
.
Найти наибольшее
и наименьшее значение (глобальный
максимум и минимум) функции
на отрезке [a,b]:
8.61.
8.62.
8.63.
8.64.
8.65.
8.66.
8.67.
8.68.
Найти наибольшее
или наименьшее значение (глобальный
максимум или минимум) функции
на интервале(a,b):
8.69.
8.70.
8.71.
8.72.
8.73.
8.74.
8.75. Рассматриваются всевозможные
прямоугольные параллелепипеды, основания
которых являются квадратами, а каждая
из боковых сторон имеет периметр, равный
6 см. найти среди них параллелепипед с
наибольшим объемом и найти этот объем.
8.76. Определить размеры открытого
бассейна с квадратным дном, при которых
на облицовку стен и дна пойдет наименьшее
количество материала. Объем бассейнаVфиксирован.
8.77. Требуется огородить два участка:
один в форме правильного треугольника,
другой в форме полукруга. Длина изгороди
фиксирована и равна Р. Определить размеры
участков (сторону треугольника и радиус
полукруга) так, чтобы сумма площадей
этих участков была бы наименьшей.
8.78. В треугольнике с основаниемaи высотойh вписан
прямоугольник, основание которого лежит
на основании треугольника, а две вершины
— на боковых сторонах. Найти наибольшую
площадь вписанного прямоугольника.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Алгебра и начала математического анализа, 11 класс
Урок №15. Возрастание и убывание функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение промежутков монотонности функции,
2) Определение алгоритма нахождения промежутков возрастания и убывания функции,
3) Решение задачи на нахождения промежутков возрастания и убывания функции
Глоссарий по теме
Алгоритм нахождения промежутков возрастания и убывания функции y = f(x)
- Найти D(f)
- Найти f‘(x).
- Определить, при каких значениях хf‘(x) ≥ 0 (на этих промежутках функция возрастает); при каких значениях х f‘(x) ≤ 0 (на этих промежутках функция убывает))
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
1. Функция y = f(x), определенная на промежутке Х, называется возрастающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) <f(x2)
2. Функция y = f(x), определенная на промежутке Х, называется убывающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) >f(x2)
Теоремы
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≥ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) возрастает на промежутке Х.
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≤ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) убывает на промежутке Х.
Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежутки монотонности функции
у = -3х3 + 4х2 + х – 10.
Решение
1.Найдем область определения функции.
D(y) = 
2.Найдем производную функции.
y’ = (x – 1)(-9x – 1)
3.Определим, на каких промежутках производная положительна (на этих промежутках функция возрастает), на каких – отрицательна (на этих промежутках функция убывает).
Применим для этого метод интервалов. Для определения знака на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Так как на интервале 
производная функции отрицательна, то на этом интервале функция убывает.
Так как на интервале 
производная функции положительна, то на этом интервале функция возрастает.
Так как на интервале 
производная функции отрицательна, то на этом интервале функция убывает.
Так как в точках 
функция непрерывна, то эти точки входят в промежутки возрастания и убывания данной функции.
Следовательно, функция возрастает на 
; функция убывает на 
и на 
.
Ответ: Функция возрастает на 
Функция убывает на 
и на 
.
№2. Определите промежутки монотонности функции
у = х5–5х4 +5х3 – 4.
Решение:
y‘ =
- Функция возрастает на
; функция убывает на .
; функция убывает на 
.Ответ: Функция возрастает на 
;
функция убывает на 
.
Тема курса Применение
производной при исследовании и построении графиков функций
Тема
урока №22. Возрастание и убывание функций.
Экстремум функций
Возрастание и убывание функции.
Экстремум функций
Возрастание и убывание функции.
Приведем
формулировки теорем, используемых при исследовании функций.
Достаточное условие строгого
возрастания (убывания) функции.
Если () в интервале , то строго
возрастает (убывает) в этом интервале.
Промежутки, в которых функция возрастает (убывает),
называются промежутками монотонности функции. Чтобы найти промежутки
монотонности функции необходимо:
1. найти область определения функции;
2. найти производную функции;
3. приравнять производную к нулю и определить ее корни
(стационарные точки), а также найти точки, в которых производная не
существует, а функция определена;
4. определить знак производной в каждом из
промежутков, на которые разбивается полученными точками область определения
функции.
Экстремумы функций.
Внутренняя точка интервала называется
точкой максимума (минимума) функции , если существует такое ,
что для всех из интервала , содержащегося внутри интервала , выполняется
неравенство (). Точки максимума и минимума называют точками экстремума
(локального экстремума) функции. Точки, в которых производная обращается в
ноль, называют стационарными точками.
Необходимое условие экстремума
функции
Если функция дифференцируема в
точке и достигает в этой точке 
максимума (минимума), то .
Точками экстремума могут быть
только те точки, в которых производная равна нулю, либо не существует. Точки, в
которых производная равна нулю или не существует, называют точками,
подозрительными на экстремум, или 
критическими точками.
Достаточные условия экстремума
функции
Если при переходе через точку ,
подозрительную на экстремум, производная меняет знак, то точка является точкой
экстремума. При этом если в некоторой окрестности точки для и для , то является
точкой максимума. Если же в этой окрестности для и для , то – точка
минимума.
Другим достаточным признаком существования экстремума в
стационарной точке является условие (тогда это точка максимума) и (тогда это
точка минимума). При этом считается, что имеет непрерывную вторую производную
в некоторой окрестности точки .
Примеры. Исследовать функции на минимум и максимум.
. Область определения
функции D(y)=R.
. Область определенияНайдем производную заданной функции 
Определим критические точки 
. Производная не существует при х2=
0. Следовательно, критические точки: 0 и 2/5. Нанесем их на числовую ось и
определим знак производной на каждом из полученных промежутков.
Критическая точка функции x =3. Точка x= –1
не входит в область определения функции.
Преподаватель: Г.Б.Слямова