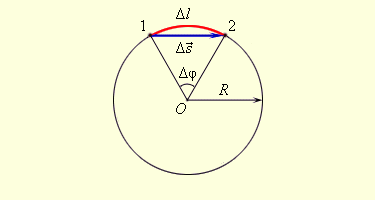
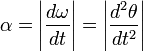Угловое перемещение (угол поворота) — это угол, на который переместился радиус-вектор при перемещении тела из точки 1 в точку 2.
Δφ=φ-φ0
Угловое Δφ перемещения при движении тела по окружности.
Единица измерения угла поворота — 1 радиан [1 рад]. Радиан — это угол, опирающийся на дугу окружности, равную ее радиусу.
Длина дуги связана с углом поворота соотношением Δl = RΔφ.
Считая, что в начальный момент времени φ0=0, угловое перемещение (угол поворота) часто обозначают φ.
Зная угловую скорость и время, за которое был совершен поворот, можно определить угол поворота:
φ=ωt
Обозначения:
Δφ, φ— угловое перемещение (угол поворота)
Δl — длина дуги
R — радиус окружности
ω — угловая скорость
t — время, за которое был совершен поворот
We’ll look at how a body moves in a circular direction in this section. The rotational motion is shown in this diagram. These motions have a displacement that is not the same as a linear motion’s displacement. Because the displacement in such motion takes the form of an angle, it’s called angular displacement. The angular displacement formula will be discussed in this topic with examples. Now let’s get started!
What is Angular Displacement?
The angle sketched out by the radius vector at the center of the circular route at a certain time is defined as the angular displacement of the object moving around a circular path in that time.
A vector quantity is an Angular Displacement. It has both magnitude and direction. It is depicted as a circular arrow pointing in either a clockwise or anti-clockwise direction from the starting point to the ending point.
Unit of Angular Displacement: Radian or Degrees is the unit of Angular Displacement. 2π radians equal 360 degrees. The SI unit for displacement is the meter. Because Angular Displacement is concerned with curvilinear motion, the SI unit for it is Degrees or Radian.
Angular Displacement Formula
The following formula can be used to calculate a point’s angular displacement:
Angular Displacement = θf – θi
where, θ = s/r
Here, r is the radius of curvature of the specified path, s is the distance travelled by the object on the circular path, and is the angular displacement of the object through which the movement happened.
We can use the following formula if we know the object’s acceleration (α), starting angular velocity (ω), and the time (t) at which the displacement is to be determined.
θ = ωt + 1/2(αt2)
Derivation of Angular Displacement
Consider an item ‘A’ moving in a straight line with an initial velocity of ‘u’ and an acceleration of ‘a’. Let us state that the object’s ultimate velocity is ‘v’ and its total displacement is ‘s’ after time t.
We all know that acceleration is the rate at which velocity changes. Therefore,
a = dv/dt
∴dv = a × dt
On both sides, integrating
∫uv dv = a ∫0t dt
∴ v – u = at
Also,
a = dv/dt
∴ a = (dv/dx) × (dx/dt)
we have, v = dx/dt
∴ a = (dv/dx)v
∴ v dv = a dx
On both sides, integrating
∴ ∫uv v dv = ∫0s a dx
∴ v2 – u2 = 2as ⇢(Equation 1)
we have, v – u =at
∴ u = v – at
put value of u in equation 1,
v2 – (v – at)2 = 2as
∴ 2vat – a2t2 = 2as
Divide both sides by 2a,
∴ s = vt – 1/2(at2)
we use the value of v instead of u, we get
∴ s = ut + 1/2(at2)
Sample Questions
Question 1: Minakshi travels around a 12-m-diameter circular track. What is her angular displacement if she runs around the entire track for 70 m?
Answer:
Given : s = 70 m, d = 12 m = r = 6 m
Find : θ
Solution :
We have,
θ = s/r
∴ θ = 70/6
∴ θ = 11.66 radians
Question 2: Dhanraj purchased a pizza with a radius of 0.3 meters. A fly lands on the pizza and wanders 60 centimetres around the edge. Calculate the fly’s angular displacement.
Answer:
Given : r = 0.3 m, s = 60 cm = 0.06 m
Find : θ
Solution :
We have,
θ = s/r
∴ θ = 0.06/0.3
∴ θ = 0.2 radians
Question 3: In a certain case Angular displacement is 0.267 radians and the radius is 6 m. Find the distance travelled by the object on the circular path.
Answer:
Given : θ = 0.267 radians, r = 6 m
Find : s
Solution :
We have,
θ = s/r
∴ s = θ × r
∴ s = 0.267 × 6
∴ s = 1.602 m
Question 4: In a certain case Angular displacement is 34.2 radians and the distance travelled by the object on the circular path is 23 m. Find the radius of curvature of the specified path.
Answer:
Given : θ = 34.2 radians, s = 23 m
Find : r
Solution :
We have,
θ = s/r
∴ r = s/θ
∴ r = 23/34.2
∴ r = 0.67 m
Question 5: What is the definition of Angular Displacement as a Vector?
Answer:
There is no such thing as an angular displacement vector.
A vector is a quantity that has both direction and magnitude and satisfies the rules of vector algebra. Although angular displacement appears to be a quantity that can only be expressed in one direction, you can specify directions to establish conventions like the right-hand rule of thumb. The term “magnitude” refers to the quantity of spin. However, it does not follow all of the principles of vector algebra, particularly the commutative law: u + v = v + u for the vector and u and v. Choose a 3D object, such as a cell phone, with the screen facing you upright. Rotate it clockwise so that the screen is still horizontal but faces you (landscape adjustment). Rotate the screen once more so that it faces the ceiling. Due to the sum of two angular displacements, this occurs. The ultimate orientation will be different if the rotation order is changed. Angular displacement in a different order will provide various outcomes that violate commutability.
Question 6: What Are Some Angular Displacement Examples?
Answer:
Example of angular displacement: If a dancer dances around a pole in a full rotation, their angular rotation will be 360 degree. The displacement will be 1800 if the rotation is half. This will be a vector quantity, which implies that it will have both a magnitude and a direction. A 360-degree displacement done clockwise versus anticlockwise, for example, is extremely different.
Last Updated :
10 Feb, 2022
Like Article
Save Article
-
Угловое перемещение, угловая скорость, угловое ускорение, их связь
с
линейными величинами.
Угловое
перемещение —
векторная величина, характеризующая
изменение угловой координаты в процессе
её движения.
Углова́я
ско́рость
— векторная физическая величина,
характеризующая скорость вращения
тела. Вектор угловой скорости по величине
равен углу поворота тела в единицу
времени:
,
а
направлен по оси вращения согласно
правилу буравчика, то есть, в ту сторону,
в которую ввинчивался бы буравчик с
правой резьбой, если бы вращался в ту
же сторону.
Единица
измерения угловой скорости, принятая
в системах СИ и СГС) — радианы в секунду.
(Примечание: радиан, как и любые единицы
измерения угла, — физически безразмерен,
поэтому физическая размерность угловой
скорости — просто [1/секунда]). В технике
также используются обороты в секунду,
намного реже — градусы в секунду, грады
в секунду. Пожалуй, чаще всего в технике
используют обороты в минуту — это идёт
с тех времён, когда частоту вращения
тихоходных паровых машин определяли,
просто «вручную» подсчитывая число
оборотов за единицу времени.
Вектор
(мгновенной) скорости любой точки
(абсолютно) твердого тела, вращающегося
с угловой скоростью
определяется формулой:
где
— радиус-вектор к данной точке из начала
координат, расположенного на оси вращения
тела, а квадратными скобками обозначено
векторное произведение. Линейную
скорость (совпадающую с модулем вектора
скорости) точки на определенном расстоянии
(радиусе) r от оси вращения можно считать
так: v = rω. Если вместо радианов применять
другие единицы углов, то в двух последних
формулах появится множитель, не равный
единице.
В
случае плоского вращения, то есть когда
все векторы скоростей точек тела лежат
(всегда) в одной плоскости («плоскости
вращения»), угловая скорость тела всегда
перпендикулярна этой плоскости, и по
сути — если плоскость вращения заведомо
известна — может быть заменена скаляром
— проекцией на ось, ортогональную
плоскости вращения. В этом случае
кинематика вращения сильно упрощается,
однако в общем случае угловая скорость
может менять со временем направление
в трехмерном пространстве, и такая
упрощенная картина не работает.
Производная
угловой скорости по времени есть угловое
ускорение.
Движение
с постоянным вектором угловой скорости
называется равномерным вращательным
движением (в этом случае угловое ускорение
равно нулю).
Угловая
скорость (рассматриваемая как свободный
вектор) одинакова во всех инерциальных
системах отсчета, однако в разных
инерциальных системах отсчета может
различаться ось или центр вращения
одного и того же конкретного тела в один
и тот же момент времени (то есть будет
различной «точка приложения» угловой
скорости).
В
случае движения одной единственной
точки в трехмерном пространстве можно
написать выражение для угловой скорости
этой точки относительно выбранного
начала координат:
,
где
— радиус-вектор точки (из начала
координат),
— скорость этой точки.
—
векторное произведение,
— скалярное произведение векторов.
Однако эта формула не определяет угловую
скорость однозначно (в случае единственной
точки можно подобрать и другие векторы
,
подходящие по определению, по другому
— произвольно — выбрав направление
оси вращения), а для общего случая (когда
тело включает более одной материальной
точки) — эта формула не верна для угловой
скорости всего тела (так как дает разные
для каждой точки, а при вращении абсолютно
твёрдого тела по определению угловая
скорость его вращения — единственный
вектор). При всём при этом, в двумерном
случае (случае плоского вращения) эта
формула вполне достаточна, однозначна
и корректна, так как в этом частном
случае направление оси вращения заведомо
однозначно определено.
В
случае равномерного вращательного
движения (то есть движения с постоянным
вектором угловой скорости) декартовы
координаты точек вращающегося так тела
совершают гармонические колебания с
угловой (циклической) частотой, равной
модулю вектора угловой скорости.
При
измерении угловой скорости в оборотах
в секунду (об/с), модуль угловой скорости
равномерного вращательного движения
совпадает с частотой вращения f, измеренной
в герцах (Гц)
(то
есть в таких единицах
).
В
случае использования обычной физической
единицы угловой скорости — радианов в
секунду
—
модуль угловой скорости связан с частотой
вращения так:
Наконец,
при использовании градусов в секунду
связь с частотой вращения будет:
Углово́е
ускоре́ние
— псевдовекторная физическая величина,
характеризующая быстроту изменения
угловой скорости твёрдого тела.
При
вращении тела вокруг неподвижной оси,
угловое ускорение по модулю равно:
Вектор
углового ускорения α направлен вдоль
оси вращения (в сторону
при ускоренном вращении и противоположно
— при замедленном).
При
вращении вокруг неподвижной точки
вектор углового ускорения определяется
как первая производная от вектора
угловой скорости ω по времени, то есть
,
и
направлен по касательной к годографу
вектора
в соответствующей его точке.
Существует
связь между тангенциальным и угловым
ускорениями:
где
R — радиус кривизны траектории точки в
данный момент времени. Итак, угловое
ускорении равно второй производной от
угла поворота по времени или первой
производной от угловой скорости по
времени. Угловое ускорение измеряется
в рад/сек2 .
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вращательное движение (Движение тела по окружности)
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
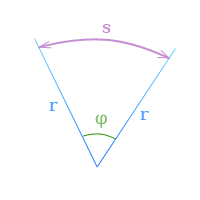
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
[
φ = frac{s}{r}
]
Соотношение между единицами угла
[ frac{φ_{рад}}{φ_{°}} = frac{π}{180°} ]
|
$ 1 enspace рад = 57.3° $ |
$ 1° = 17.45 enspace мрад $ |
$ 1´ = 291 enspace мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
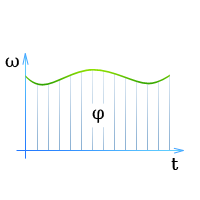
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t).
Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
[ [n] = [f] = frac{Обороты}{Секунда} = frac{(об)}{с} = frac{1}{c} = Герц ]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
[
T = frac{1}{f} = frac{1}{n}
]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
[
φ = 2 π N
]
Угловая скорость
Из формулы для одного оборота следует:
[
ω = 2 π f = frac{2π}{T}
]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Вращательное движение (движение тела по окружности) |
стр. 422 |
|---|