Как найти угловое смещение

Вращение твердого тела P вокруг фиксированной оси O.

Угловое смещение тела — это угол в радианах (градусов, оборотов ), через который точка вращается вокруг центра или линия была повернута в определенном смысле относительно указанной оси . Когда тело вращается вокруг своей оси, движение нельзя просто анализировать как частицу, поскольку при круговом движении оно претерпевает изменяющуюся скорость и ускорение в любой момент времени (t). Когда речь идет о вращении тела, становится проще считать само тело твердым. Тело обычно считается твердым, когда расстояние между всеми частицами остается постоянным на протяжении всего движения тела, например, части его массы не разлетаются. В реальном смысле все может быть деформируемым, однако это воздействие минимально и незначительно. Таким образом, вращение твердого тела над фиксированной осью называется вращательным движением.

Содержание

• 1 Пример
• 2 Измерения
• 3 Трехмерные
  • 3.1 Матричные обозначения
• 4 Матрицы бесконечно малых вращений
  • 4.1 Генераторы вращений
  • 4.2 Связь с алгебрами Ли
  • 4.3 Экспоненциальное отображение
• 5 См. Также
• 6 Ссылки

Пример

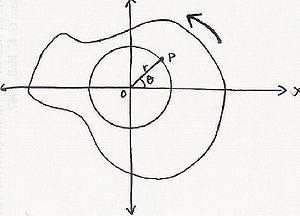
В примере, показанном на справа (или выше в некоторых мобильных версиях) частица или тело P находится на фиксированном расстоянии r от начала координат O, вращаясь против часовой стрелки. Затем становится важным представить положение частицы P в терминах ее полярных координат (r, θ). В этом конкретном примере значение θ изменяется, а значение радиуса остается прежним. (В прямоугольных координатах (x, y) и x, и y меняются со временем). Когда частица движется по окружности, она проходит длину дуги s, которая становится связанной с угловым положением через соотношение: —

s = r θ { displaystyle s = r theta , }

Измерения

Угловое смещение может быть измерено в радианах или градусах. Использование радианов обеспечивает очень простую связь между расстоянием, пройденным по окружности, и расстоянием r от центра.

θ = sr { displaystyle theta = { frac {s} {r}}}

Например, если тело вращается на 360 ° по окружности радиуса r, угловое смещение определяется расстоянием прошел по окружности, равной 2πr, деленной на радиус: θ = 2 π rr { displaystyle theta = { frac {2 pi r} {r}}}что легко упрощается до: θ = 2 π { displaystyle theta = 2 pi}. Следовательно, 1 оборот равен 2 π { displaystyle 2 pi}радиан.

Когда частица перемещается из точки P в точку Q за δ t { displaystyle delta t}, как на иллюстрации слева, радиус круг проходит через изменение угла Δ θ = θ 2 — θ 1 { displaystyle Delta theta = theta _ {2} — theta _ {1}}, что равно угловому смещение.

Три измерения

Рисунок 1 : теорема Эйлера о вращении. Большой круг при вращении превращается в другой большой круг, всегда оставляя диаметр сферы в исходном положении. Рисунок 2 : Вращение, представленное осью Эйлера и углом.

В трех измерениях, угловой смещение — это сущность с направлением и величиной. Направление определяет ось вращения, которая всегда существует в силу теоремы вращения Эйлера ; величина определяет вращение в радианах вокруг этой оси (используя правило правой руки для определения направления). Этот объект называется ось-угол.

. Несмотря на направление и величину, угловое смещение не является вектором , потому что оно не подчиняется закону коммутативности для сложения. Тем не менее, имея дело с бесконечно малыми вращениями, бесконечно малые величины второго порядка можно отбросить, и в этом случае появляется коммутативность.

Существует несколько способов описания углового смещения, таких как матрицы вращения или углы Эйлера. См. Диаграммы на SO (3) для других.

Матричная запись

Учитывая, что любой кадр в пространстве может быть описан матрицей вращения, смещение между ними также может быть описано матрицей вращения. Поскольку A 0 { displaystyle A_ {0}}и A f { displaystyle A_ {f}}две матрицы, матрица углового смещения между ними может можно получить как Δ A = A f. A 0–1 { displaystyle Delta A = A_ {f}.A_ {0} ^ {- 1}}. Когда это произведение выполняется с очень небольшой разницей между обоими кадрами, мы получим матрицу, близкую к единице.

В пределе у нас будет бесконечно малая матрица вращения.

Матрицы бесконечно малого вращения

Бесконечно малое угловое смещение — это матрица бесконечно малого вращения :

• Поскольку любая матрица вращения имеет единственное действительное собственное значение, равное +1, это собственное значение показывает ось вращения.
• Его модуль может быть выведен из значения бесконечно малого вращения.
• Форма матрицы следующая:

A = (1 — d ϕ z (t) d ϕ y (t) d ϕ z (t) 1 — d ϕ x (t) — d ϕ y (t) d ϕ x (t) 1) { displaystyle A = { begin {pmatrix} 1 -d phi _ {z} (t) d phi _ {y} (t) \ d phi _ {z} (t) 1 -d phi _ {x} (t) \ — d phi _ {y} (t) d phi _ {x} (t) 1 \ end {pmatrix}}}

Здесь мы можем ввести тензор бесконечно малых угловых смещений или генератор вращения связан:

d Φ (t) = (0 — d ϕ z (t) d ϕ y (t) d ϕ z (t) 0 — d ϕ x (t) — d ϕ y (T) d ϕ Икс (T) 0) { Displaystyle d Phi (t) = { begin {pmatrix} 0 -d phi _ {z} (t) d phi _ {y} (t) d phi _ {z} (t) 0 -d phi _ {x} (t) \ — d phi _ {y} (t) d phi _ {x} (t) 0 \ end {pmatrix}}}

Такой что соответствующая матрица вращения имеет вид A = I + d Φ (t) { displaystyle A = I + d Phi (t)}. Если его разделить на время, получится вектор угловой скорости.

Генераторы вращений

Предположим, мы задаем ось вращения единичным вектором [x, y, z], и предположим, что у нас бесконечно малый поворот угла Δθ об этом векторе. Расширяя матрицу вращения как бесконечное сложение и используя подход первого порядка, матрица вращения ΔR представлена ​​как:

Δ R = [1 0 0 0 1 0 0 0 1] + [0 z — y — z 0 ху — х 0] Δ θ = I + A Δ θ. { displaystyle Delta R = { begin {bmatrix} 1 0 0 \ 0 1 0 \ 0 0 1 end {bmatrix}} + { begin {bmatrix} 0 z -y \ — z 0 x \ y -x 0 end {bmatrix} } , Delta theta = mathbf {I} + mathbf {A} , Delta theta.}

Конечный поворот на угол θ вокруг этой оси можно рассматривать как последовательность небольших вращений вокруг та же ось. Аппроксимируя Δθ как θ / N, где N — большое число, поворот θ вокруг оси можно представить как:

R = (1 + A θ N) N ≈ e A θ. { Displaystyle R = left ( mathbf {1} + { frac { mathbf {A} theta} {N}} right) ^ {N} приблизительно e ^ { mathbf {A} theta}.}

Можно видеть, что теорема Эйлера по существу утверждает, что все повороты могут быть представлены в этой форме. Произведение A θ { displaystyle mathbf {A} theta}является «генератором» конкретного поворота, будучи вектором (x, y, z), связанным с матрицей A. Это показывает, что матрица вращения и формат оси угол связаны экспоненциальной функцией.

Можно вывести простое выражение для генератора G. Начнем с произвольной плоскости, определяемой парой перпендикулярных единичных векторов a и b. В этой плоскости можно выбрать произвольный вектор x с перпендикуляром y. Затем вычисляется y в терминах x, и подстановка в выражение для вращения в плоскости дает матрицу вращения R, которая включает генератор G = ba — ab.

x = a cos ⁡ (α) + b sin ⁡ (α) y = — a sin ⁡ (α) + b cos ⁡ (α) cos ⁡ (α) = a T x sin ⁡ (α) = b T xy = — ab T x + ba T x = (ba T — ab T) xx ′ = x cos ⁡ (β) + y sin ⁡ (β) = [I cos ⁡ (β) + (ba T — ab T)) sin ⁡ (β)] x R = I cos ⁡ (β) + (ba T — ab T) sin ⁡ (β) = I cos ⁡ (β) + G sin ⁡ (β) G = ba T — ab T { Displaystyle { begin {выровнен} х = а соз влево ( альфа вправо) + б грех влево ( альфа вправо) \ у = — а грех влево ( альфа вправо) + b cos left ( alpha right) \ cos left ( alpha right) = a ^ {T} x \ sin left ( alpha right) = b ^ {T } x \ y = — ab ^ {T} x + ba ^ {T} x = left (ba ^ {T} -ab ^ {T} right) x \\ x ‘= x cos left ( beta right) + y sin left ( beta right) \ = left [I cos left ( beta right) + left (ba ^ {T} -ab ^ {T} right) sin left ( beta right) right] x \\ R = I cos left ( beta right) + left (ba ^ {T} -ab ^ { T} right) sin left ( beta right) \ = I cos left ( beta right) + G sin left ( beta right) \\ G = ba ^ {T} -ab ^ {T} \ end {align}}}

Чтобы включить векторы вне плоскости во вращение необходимо изменить приведенное выше выражение для R, включив два оператора проекции , которые разделяют пространство. Эту модифицированную матрицу вращения можно переписать как экспоненциальную функцию.

P ab = — G 2 R = I — P ab + [I cos ⁡ (β) + G sin ⁡ (β)] P ab = e G β { displaystyle { begin {align} P_ {ab} = — G ^ {2} \ R = I-P_ {ab} + left [I cos left ( beta right) + G sin left ( beta right) right] P_ {ab} = e ^ {G beta} \ конец {выровнено}}}

С помощью этих генераторов анализ часто бывает проще, чем с полным матрица вращения. Анализ в терминах генераторов известен как алгебра Ли группы вращений.

Связь с алгебрами Ли

Матрицы в алгебре Ли сами по себе не являются вращениями; кососимметричные матрицы — это производные, пропорциональные разности поворотов. Фактическое «дифференциальное вращение» или матрица бесконечно малого вращения имеет вид

I + A d θ, { displaystyle I + A , d theta ~,}

где dθ исчезающе мала и A ∈ so (n), например, с A = L x,

d L x = [1 0 0 0 1 — d θ 0 d θ 1]. { displaystyle dL_ {x} = left [{ begin {smallmatrix} 1 0 0 \ 0 1 -d theta \ 0 d theta 1 end {smallmatrix}} right].}

Правила вычисления следующие обычно, за исключением того, что бесконечно малые второго порядка обычно отбрасываются. С этими правилами эти матрицы не удовлетворяют всем тем же свойствам, что и обычные матрицы конечного вращения при обычном рассмотрении бесконечно малых. Оказывается, порядок, в котором применяются бесконечно малые вращения, не имеет значения. Чтобы увидеть этот пример, обратитесь к бесконечно малым вращениям SO (3).

Экспоненциальное отображение

Соединение алгебры Ли с группой Ли — это экспоненциальное отображение, которое определяется с использованием стандартная матричная экспоненциальная серия для e Для любой кососимметричной матрицы A, exp (A) всегда является матрицей вращения.

Важным практическим примером является 3 × 3 случай. В группе вращений SO (3) показано, что можно идентифицировать каждый A ∈, поэтому (3) с вектором Эйлера ω = θ u, где u = (x, y, z) — вектор единичной величины.

По свойствам идентификации su (2) ≅ ℝ, u находится в нулевом пространстве A. Таким образом, u является остается инвариантным по exp (A) и, следовательно, является осью вращения.

Использование формулы вращения Родригеса в матричной форме с θ = ⁄ 2 + ⁄ 2 вместе со стандартным double формулы углов получаем,

exp ⁡ (A) = exp ⁡ (θ (u ⋅ L)) = exp ⁡ ([0 — z θ y θ z θ 0 — x θ — y θ x θ 0 ]) Знак равно I + 2 соз ⁡ θ 2 грех ⁡ θ 2 u ⋅ L + 2 грех 2 ⁡ θ 2 (и ⋅ L) 2, { displaystyle { begin {align} exp (A) {} = exp ( theta ({ boldsymbol {u cdot L}})) = exp left ( left [{ begin {smallmatrix}} 0 -z theta y theta \ z theta 0 -x theta \ — y theta x theta 0 end {smallmatrix}} right] right) = { boldsymbol {I}} + 2 cos { frac { theta} {2}} sin { frac { theta} {2}} ~ { boldsymbol {u cdot L}} + 2 sin ^ {2} { frac { theta} {2}} ~ ({ boldsymbol {u cdot L}}) ^ {2}, end {align}}}

где c = cos ⁄ 2, s = sin ⁄ 2.

Это матрица для поворота вокруг оси u на угол θ в полуугловой форме. Для получения полной информации см. экспоненциальная карта SO (3).

Обратите внимание, что для бесконечно малых углов члены второго порядка могут быть проигнорированы и остаются exp (A) = I + A

См. Также

Ссылки

1. ^Kleppner, Daniel; Коленков, Роберт (1973). Введение в механику. Макгроу-Хилл. стр. 288 –89.
2. ^в евклидовом пространстве
3. ^(Goldstein, Poole Safko 2002, §4.8) harv error: no target: CITEREFGoldsteinPooleSafko2002 (help )
4. ^(Wedderburn 1934, §8.02) ошибка harv: нет цели: CITEREFWedderburn1934 (help )

From Wikipedia, the free encyclopedia

Angular displacement of a body is the angle (in radians, degrees or turns) through which a point revolves around a centre or a specified axis in a specified sense. When a body rotates about its axis, the motion cannot simply be analyzed as a particle, as in circular motion it undergoes a changing velocity and acceleration at any time (t). When dealing with the rotation of a body, it becomes simpler to consider the body itself rigid. A body is generally considered rigid when the separations between all the particles remains constant throughout the body’s motion, so for example parts of its mass are not flying off. In a realistic sense, all things can be deformable, however this impact is minimal and negligible. Thus the rotation of a rigid body over a fixed axis is referred to as rotational motion.

Example[edit]

In the example illustrated to the right (or above in some mobile versions), a particle or body P is at a fixed distance r from the origin, O, rotating counterclockwise. It becomes important to then represent the position of particle P in terms of its polar coordinates (r, θ). In this particular example, the value of θ is changing, while the value of the radius remains the same. (In rectangular coordinates (x, y) both x and y vary with time). As the particle moves along the circle, it travels an arc length s, which becomes related to the angular position through the relationship:

Measurements[edit]

Angular displacement may be measured in radians or degrees. Using radians provides a very simple relationship between distance traveled around the circle and the distance r from the centre.

For example, if a body rotates 360° around a circle of radius r, the angular displacement is given by the distance traveled around the circumference — which is 2πr — divided by the radius: which easily simplifies to: . Therefore, 1 revolution is radians.

When a particle travels from point P to point Q over , as it does in the illustration to the left, the radius of the circle goes through a change in angle which equals the angular displacement.

Three dimensions[edit]

In three dimensions, angular displacement is an entity with a direction and a magnitude. The direction specifies the axis of rotation, which always exists by virtue of the Euler’s rotation theorem; the magnitude specifies the rotation in radians about that axis (using the right-hand rule to determine direction). This entity is called an axis-angle.

Despite having direction and magnitude, angular displacement is not a vector because it does not obey the commutative law for addition.^[1] Nevertheless, when dealing with infinitesimal rotations, second order infinitesimals can be discarded and in this case commutativity appears.

Several ways to describe angular displacement exist, like rotation matrices or Euler angles. See charts on SO(3) for others.

Given that any frame in the space can be described by a rotation matrix, the displacement among them can also be described by a rotation matrix. Being and two matrices, the angular displacement matrix between them can be obtained as . When this product is performed having a very small difference between both frames we will obtain a matrix close to the identity.

In the limit, we will have an infinitesimal rotation matrix.

Infinitesimal rotation matrices[edit]

See also[edit]

• Angular distance
• Angular position
• Angular velocity
• Infinitesimal rotation
• Linear elasticity
• Second moment of area

Notes[edit]

References[edit]

Sources[edit]

• Goldstein, Herbert; Poole, Charles P.; Safko, John L. (2002), Classical Mechanics (third ed.), Addison Wesley, ISBN 978-0-201-65702-9
• Wedderburn, Joseph H. M. (1934), Lectures on Matrices, AMS, ISBN 978-0-8218-3204-2

• Формулы
• упражнения
• Первое упражнение
• Второе упражнение
• Третье упражнение
• Ссылки

Вращение

Пусть нам дана плоскость, а на ней — прямая, а на прямой — точка $O$. Отбросим ту часть прямой, которая расположена по какую-либо одну сторону от этой точки. Оставшаяся часть называется лучом с началом в точке $O$. Если нам к тому же дано, что луч проходит через точку $A$, то он обозначается как «луч $OA$» или, более кратко, $[OA)$.

Представим себе, что луч $OA$ вращается вокруг своего начала, точки $O$, наподобие стрелки часов, оставаясь всё время в заданной плоскости. Вращение — это особый тип движения, при котором смещение определяется не расстоянием, а углом. Такое угловое смещение естественнее всего измерять числом оборотов. Например, минутная стрелка часов делает за сутки $24$ оборота. Впрочем, правильнее было бы сказать не «$24$ оборота», а «$-24$ оборота», потому что в математике за положительное принято направление вращения против часовой стрелки.

Нельзя не заметить, что, сделав $-24$ оборота, стелка оказывается в точности в том же самом положении, в котором она находилась в самом начале. Спрашивается: можно ли на этом основании утверждать, что

$-24$ оборота = $0$ оборотов?

Ответ зависит от того, какие задачи перед нами стоят. Если мы решаем задачу на движение и нас интересует, например, скорость вращения стрелки, то в этом случае ставить здесь знак равенства, конечно, неправильно. Но если мы рассматриваем только неподвижные картинки и история вопроса никакой роли не играет, тогда почему бы и нет? Впрочем, обычно так уж явно не пишут:

$0$ оборотов ${= 1}$ оборот ${= -1}$ оборот ${= 2}$ оборота ${=-2}$ оборота ${=~…}$

или

$^1!/!_4$ оборота ${= -^3!/!_4}$ оборота ${= 1^1!/!_4}$ оборота ${=-1^3!/!_4}$ оборота ${=~…}$,

но это как бы подразумевается. Обычно стараются как можно меньше иметь дело с подобными «чудны́ми» равенствами, и поэтому угловое смещение задают таким образом, чтобы его величина $alpha$ находилась в следующих пределах:

$-^1!/!_2$ оборота $< alpha leqslant~^1!/!_2$ оборота.

Однако совсем уж избежать «чудны́х» равенств нам не удастся, как это ясно видно, например, из следующего примера на сложение:

$-^1!/!_2$ оборотa ${+~^1!/!_4}$ оборота ${=~^3!/!_4}$ оборота ${= -^1!/!_4}$ оборота.

Угол

Пусть даны два луча $OA$ и $OB$ с общим началом в точке $O$. Такая геометрическая конструкция называется углом (в самом первоначальном смысле этого слова). Для нее применяется обозначение ${angle AOB}$. Лучи $OA$ и $OB$ называются сторонами угла, а точка $O$ — его вершиной.

Ясно, что одну сторону угла можно перевести в другую посредством вращения вокруг вершины. Поэтому мы можем говорить об угловом расстоянии между сторонами. Оно равно угловому смещению, необходимому для перевода одной стороны в другую, взятому по абсолютной величине. (При этом не важно, переводим ли мы луч $OA$ в луч $OB$ или, наоборот, луч $OB$ в луч $OA$, поскольку в обоих случаях абсолютная величина углового смещения одинакова). Вместо слов «угловое расстояние» говорят также «величина угла» или, для краткости, просто «угол». Для обозначения величин углов используют, как правило, строчные греческие буквы: $alpha$, $beta$, $gamma$ и т.д. Углы, отличающиеся на целое число оборотов, фактически совпадают. Обычно величину угла $alpha$ выбирают так, чтобы она не превосходила пол-оборота:

$0$ оборотов ${leqslant alpha leqslant~^1!/!_2}$ оборота,

но это ограничение не является строго обязательным.

Помимо оборотов, в качестве единицы измерения углов часто используется градус, обозначаемый значком «$^circ$»:

$1$ оборот = $360^circ$,

$1^circ =~^1!/!_{360}$ оборота.

Угол в пол-оборота ($180^circ$) называется развернутым.

Угол величиной четверть оборота ($90^circ$) называется прямым.

Углы меньше прямого называются острыми.

Углы больше прямого, но меньше развернутого называются тупыми.

В школе на уроках математики углы измеряются с помощью транспортира, который обеспечивает точность около одного градуса. Таким образом, все возможные результаты измерений представлены в следующем конечном ряду:

$0^circ!, 1^circ!, 2^circ!, …, 180^circ$.

В нашем воображении, однако, мы всегда можем представить себе углы, которые выражаются произвольными действительными числами.

Пересечение прямых

При пересечении двух прямых образуется четыре угла, как показано на рисунке:

В этой конструкции два соседних угла, у которых одна сторона общая, называются смежными. Их сумма, очевидно, равна пол-оборота ($180^circ$). Так, в обозначениях, указанных на рисунке:

$,alpha,$$:+:$$,beta,$$:= 180^circ$,

$,beta,$$:+:$$,gamma,$$:= 180^circ$,

$,gamma,$$:+:$$,delta,$$:= 180^circ$,

$,delta,$$:+:$$,alpha,$$:= 180^circ$.

Два противоположных угла, не имеющих общих сторон, называются вертикальными. Вертикальные углы равны по величине между собой, потому что они переходят друг в друга при вращении на пол-оборота вокруг точки пересечения прямых:

$,alpha,$$:=:$$,gamma,$

$,beta,$$:=:$$,delta,$

Хотя определение угла было дано для лучей, очень часто приходится слышать такое выражение, как «угол между прямыми». В качестве углового расстояния между двумя прямыми можно с одинаковым успехом взять любой из четырех углов $alpha$, $beta$, $gamma$ и $delta$, образующихся при их пересечении. Знание одного из них позволяет моментально вычислить все остальные. Фактически, выбор приходится делать только между двумя смежными углами $alpha$ и $beta$, поскольку ${gamma = alpha}$ и $delta = beta$. Обычно выбирают тот из них, который меньше, но это необязательно.

Отметим, что если хотя бы один из четырех углов является прямым, то это означает, что и все остальные углы тоже прямые:

$alpha = beta = gamma = delta =~^1!/!_2$ оборота $= 90^circ$.

Прямые, пересекающиеся под углом $90^circ$, называются перпендикулярными.

Замечание. К сожалению, в геометрии прилагательное «прямой» употребляется в двух совершенно разных, не связанных друг с другом смыслах. Прямыми могут быть углы и прямыми могут быть линии. Будем внимательны, чтобы не запутаться.

Конспект

1. Луч ($[OA)$) с началом в точке $O$: «половинка прямой», то есть усеченная прямая $(OA)$, в которой сохранена только точка $O$ и точки, расположенные от $O$ с той же стороны, что и точка $A$.

2. Вращение луча [OA) вокруг своего начала $O$ характеризуется угловым смещением, которое измеряется в оборотах. Направление вращения против часовой стрелки принято за положительное. Угловые смещения, отличающиеся на целое число оборотов, фактически совпадают.

3. Угол (${angle AOB}$): два луча [OA) и [OB) с общим началом O. Лучи [OA) и [OB) называются сторонами угла.

4. Величина угла (или же угловое расстояние между сторонами): угловое смещение, необходимое для перевода одной стороны в другую, взятое по абсолютной величине. Вместо слов «величина угла» или «угловое расстояние» часто говорят просто «угол». Величина угла определена неоднозначно (так как добавление целого числа оборотов фактически ничего не меняет), но обычно ее выбирают так, чтобы она не превосходила пол-оборота.

5. Градус ($^circ$): еще одна единица измерения углов, равная $^1!/!_{360}$ оборота.

6. Развернутый угол ${=~^1!/!_2}$ оборота ${= 180^circ}$.

Прямой угол ${=~^1!/!_4}$ оборота ${= 90^circ}$.

$0 <$ острый угол $<$ прямой угол.

Прямой угол < тупой угол < развернутый угол.

7. При пересечении двух прямых образуется четыре угла с общей вершиной. Соседние углы, у которых одна сторона общая, называются смежными. Их сумма равна ${180^circ}$. Противоположные углы, не имеющие общих сторон, называются вертикальными. Противоположные углы равны между собой.

8. Угол между двумя прямыми: величина любого из четырех углов (обычно наименьшего), образующихся при пересечении этих прямых. Если один из углов прямой, то и все остальные тоже прямые. Прямые, пересекающиеся под прямым углом, называются перпендикулярными.