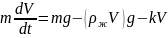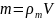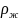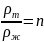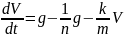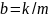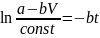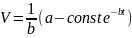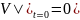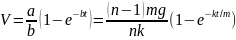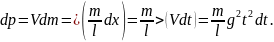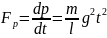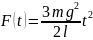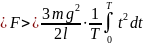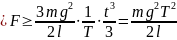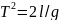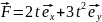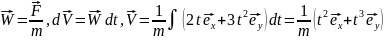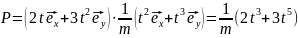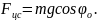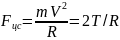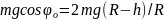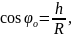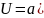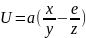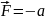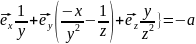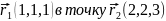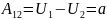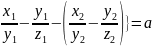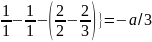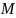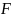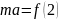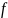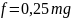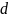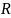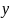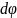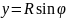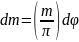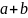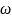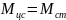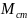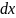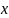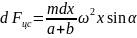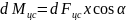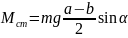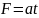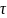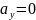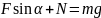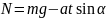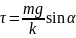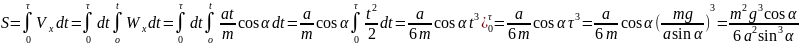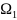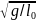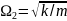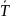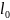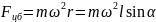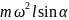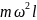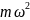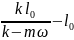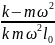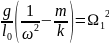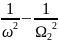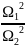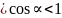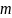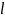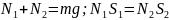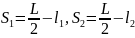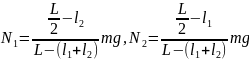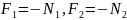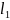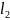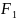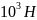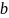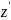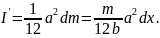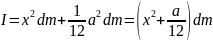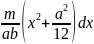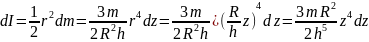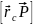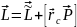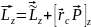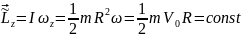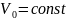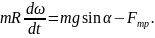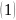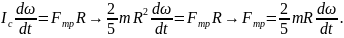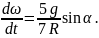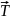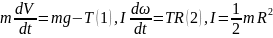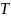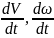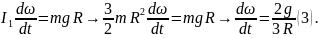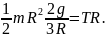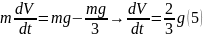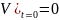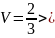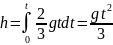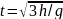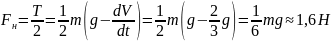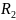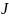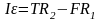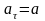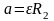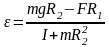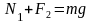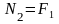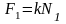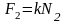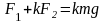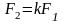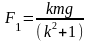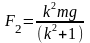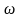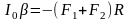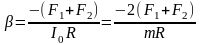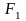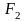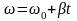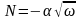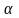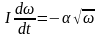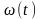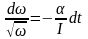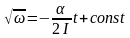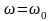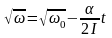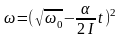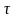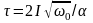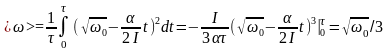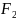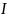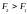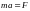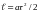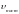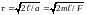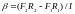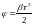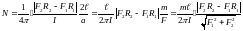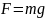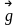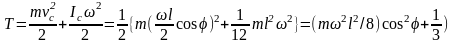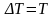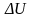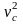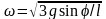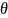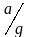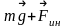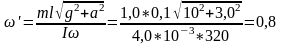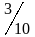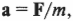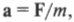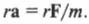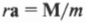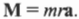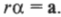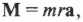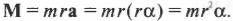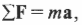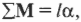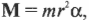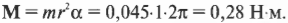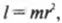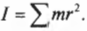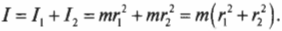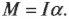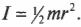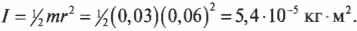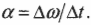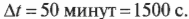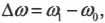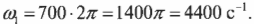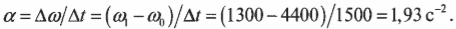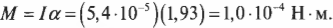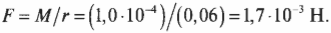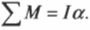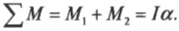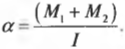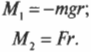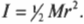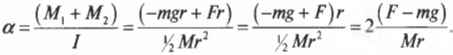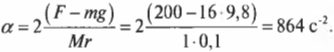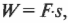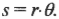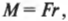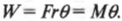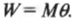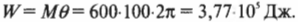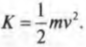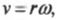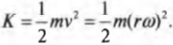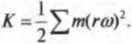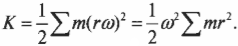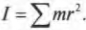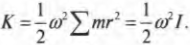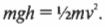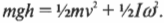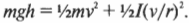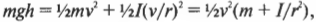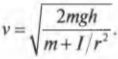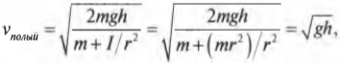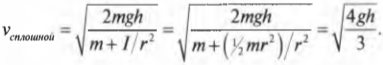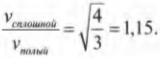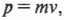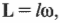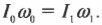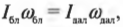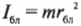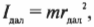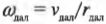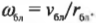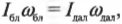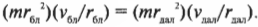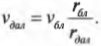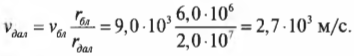Как найти угловое ускорение блока с грузом

Спрятать решение

Источник: Са­вчен­ко О. Я. За­да­чи по фи­зи­ке, М.: «Наука», 1988 (2.7.9*)

Главная
→ Форумы » Физика » Решение задач по физике » Вращательное движение твердого тела

Вращательное движение твердого тела

Автор

Сообщение

Crash

#10761
2012-05-07 11:00 GMT

Пользователи

7 сообщений

Репутация 0 [-][+]

Определить угловое ускорение блока радиусом R с моментом инерции J, через который перекинута нить с грузами массой m1 и m2. Трением пренебречь

Личное сообщение

iskander

#10799
2012-05-10 14:29 GMT

Администраторы

3361 сообщений
http://alexandr4784.narod.ru/

Откуда: Псков
Кто: книгоиздательство

Репутация 179 [-][+]

Пусть груз 1 движется вниз, ось ОХ направлена вниз, тогда:

(m_1g-T_1=m_1a)

(m_2g-T_2=-m_2a)

(Jvarepsilon=RT_1-RT_2=R(T_1-T_2))

(a=varepsilon{R})

Думаю, этого достаточно.

Личное сообщение

2.1.
Шарик массы m
помещен в высокий сосуд с некоторой
жидкостью и отпущен без толчка. Плотность
жидкости в n
раз меньше плотности шарика. При движении
шарика возникает сила сопротивления
среды, пропорциональная скорости
движения: F
= — kV.

а)
Описать качественно характер движения
шарика.

б)
Найти зависимость скорости шарика V
от времени t.

Решение.
На
падающий в жидкости шарик действует
три силы — тяжести, Архимеда и
сопротивления. Уравнение движения
шарика имеет вид

(1), где

— масса шарика, V
— его объем;

и

— плотности тела и жидкости. Равенство
(1) поделим на m
и учтем, что

.
При этом уравнение (1) получит вид

,
или

,

.
Отсюда путем интегрирования получим:

=>
.
Из начального условия

следует, что const
= a
и затем

.

2.2.
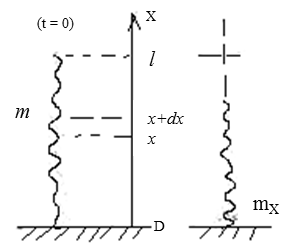
Тонкая стальная цепочка с очень мелким
звеньями висит вертикально, касаясь
нижним концом стола. Масса цепочки m,
длина L.
В момент t
= 0 цепочку отпускают. Считая цепочку
однородной по длине, найти:

а)
мгновенное значение силы F(t),
с которой цепочка действует на стол;

б)
среднее значение <F>
этой силы за время падения.

Р
ешение.
Предварительно
отметим: при растяжении цепочки между
ее звеньями возникают упругие силы; при
падении в поле тяжести звенья не
взаимодействуют, каждое звено падает
с ускорение

независимо друг от друга. Согласно
условиям, сила действия цепочки на стол
в начале падения равна нулю, в конце
падения эта сила получает максимальное
значение 3mg.
Обратимся к рисунку и сделаем следующие
вычисления. Элементы цепочки, падая с
высоты х, независимо от других элементов
приобретают скорость V
= gt
и соответствующий импульс

При падении элемент цепочки действует
на поверхность стола силой

.
Помимо этой силы на поверхность стола
действует сила тяжести упавшей части
цепочки к моменту времени t,
равная

Суммарная сила

Итак,

.
Средняя сила

,
где T
— время падения цепочки. Таким образом,

.
Поскольку

,
то <F>
= mg.

2.3.
Тело массы m
начинает двигаться под действием силы

.
Найти мощность P(t),
развиваемую силой в момент времени t.

Решение.
Мощность
P
силы

вычислим по формуле P
=

,
где

— скорость поступательного движения
тела. В рассматриваемом случае

.
Отсюда ускорение и скорость тела:

.
Начальные условия: при t
= 0 величины F,

и

равны нулю. Мощность силы

.

2.4.
Небольшое тело начинает скользить без
трения с вершины сферы радиуса R
вниз. На какой высоте h
над центром сферы тело отделится от
поверхности сферы и полетит свободно?

Р
ешение.
На
рисунке изображены сила тяжести тела

и сила нормальной реакции

.
Трения скольжения нет. Центростремительная
сила, действующая на тело, равна

.
При отрыве тела от поверхности сферы N
= 0 и

Как известно,

,
где Т — кинетическая энергия. На основании
закона сохранения механической энергии
тела в потенциальном поле сил тяжести
Т = mg(R
— h).
Таким образом получаем соотношение

(*). Если учесть, что

то из (*) найдем: h
= 2(R
— h)
=>h
= (2/3)R.

2.5.
Потенциальная
энергия частицы имеет вид:
),
где

— константа. Найти:

а)
силу F, действующую на частицу,

б)
работу А, совершаемую над частицей
силами поля при переходе частицы из
точки (1, 1, 1) в точку (2, 2, 3)

Решение.
Имеется связь между силой и потенциальной
энергией частицы в силовом поле, а именно

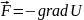
В
декартовых координатах

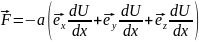
В
рассматриваемом случае
.

Поэтому

{
{

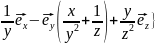
Работа,
совершаемая силами поля при перемещении
частицы из точки

,
равна

{
{
.

2.6.
На
столе лежит доска массы

= 1 кг, а на доске – груз массы m = 2 кг.
Какую силу

нужно приложить к доске, чтобы доска
выскользнула из-под груза? Коэффициент
трения между грузом и доской 1
= 0,25 , а между доской и столом 2
= 0,5.

Р
ешение.
Механическая
система с указанием действующих на нее
сил показана на рисунке. Уравнение
движения доски:

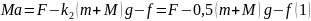
И
уравнение движения груза:

,где

—
сила трения между грузом и доской,

– ускорение.

Максимальное
значение

;
следовательно, максимальное ускорение
груза 0,25
,
и максимальная сила

,
при которой еще будет происходить
движение груза и доски как целого, должна
сообщать доске и грузу ускорение

.
А для этого, согласно уравнению (1), сила

должна быть равна

Для
m=2кг,

=1кг
сила

=22,5H.

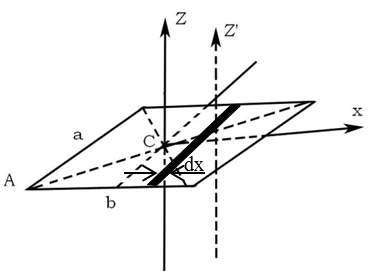
2.7.
Определить
расстояние

центра масс полуокружности радиуса

от стягивающего её диаметра.

Решение.
Ясно,
что центр масс данного полукольца
находится на оси

(см.рис.).
Ордината выделенного углом

элемента полукольца равна

,
масса этого элемента

.
Ордината центра масс полукольца равна

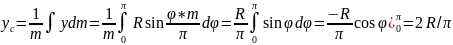
Итак,
координаты центра масс:

2
.8.
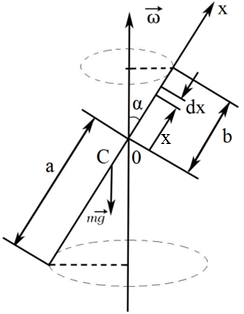
Тонкий
стержень длиной

шарнирно
закреплен в точке, отстоящей на расстояние
«b»
от одного из его концов, и вращается с
угловой скоростью

вокруг вертикальной оси, описывая
круговой конус (см. рис.). Определить
угол отклонения стержня от вертикали.

Решение.
В
системе координат, вращающейся вокруг
вертикальной оси с угловой скоростью

,
условие равновесия стержня можно
записать в виде

,
где

– момент центробежной силы и

– момент силы тяжести относительно
точки закрепления стержня (шарнира О).
Центробежная сила инерции, действующая
на элемент стержня

,
находящийся на расстоянии

от точки закрепления, будет равна
,
а
соответствующий момент этой силы можно
записать в виде
.

При
этом полный момент центробежной силы
инерции равен

Приравнивая
эту величину моменту силы тяжести

,
получим:

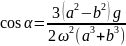
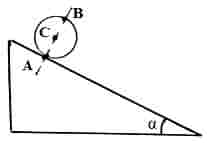
2.9.
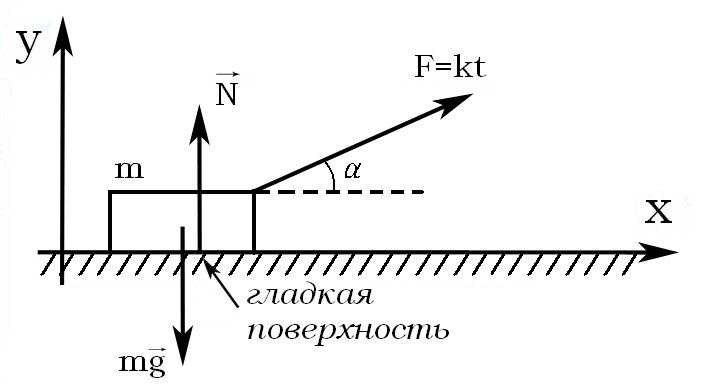
На
небольшое тело массы m, лежащее на гладкой
горизонтальной плоскости, в момент

= 0 начала действовать сила, зависящая
от времени по закону

,
где

— постоянная. Направление этой силы все
время составляет угол α с горизонтом.
Найти:

а)
скорость тела в момент отрыва от
плоскости;

б)
путь, пройденный телом к этому моменту.

Р
ешение.

До
некоторого момента времени

тело движется горизонтально с ускорением

,
при этом

и

,
т.е.

.
В момент отрыва

и

.

а)
Скорость тела в момент времени

равна

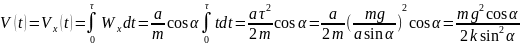
б)
Путь за время

равен

.

2
.10.
Шарик
массы m подвешен на идеальной пружине
жесткости k
и начальной длины l
над центром платформы центробежной
машины. Затем шарик начинает вращаться
вместе с машиной с угловой скоростью
ω. Какой угол α образует при этом пружина
с вертикалью?

Решение.
Данную
механическую систему ещё до вращения
можно рассматривать как колебательную
с двумя степенями свободы, характеризующуюся
двумя частотами

=

и

.
Вопросы колебательных движений данной
системы не так просты и мы их опустим.
Будем считать, что в начальный момент
времени система находилась в покое,
колебания не совершались. Далее будем
приводить систему во вращательное
движение до заданной угловой скорости

очень медленно, полагая, что колебания
в системе не возникнут.

Для
получения ответа на поставленный вопрос
перейдем во вращающуюся систему
координат, приложив к шарику еще
дополнительную центробежную силу
инерции. В этой системе координат в
принятых условиях шарик будет находиться
в состоянии покоя (равновесия).

Пусть

– упругая сила натяжения пружины. По
величине она равна T=k(l-
),
где l
– длина пружины в состоянии растяжения,

– её длина в недеформированном состоянии.
Центробежная сила

,
где r
= lsinα.
В состоянии равновесия имеем соотношения:
T
sinα
=

→
T =

;Tcosα
= mg.

Итак,
имеется три уравнения: T=k(l-
),
T
=

,
Tcosα
= mg.
Отсюда находим cos
α: k(l-
)
=

→ l
= k
/(k-
);T=k(
)
=

;
cosα
= mg/T
= mg*

=

(
)
=

(
-1).Здесь
0
,
т.е.

.Отсюда

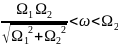
2
.11.
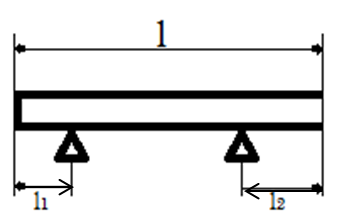
Балка
массы

=300
кг и длины

=8,00
м лежит на двух опорах (рис.) Расстояния
от концов балки до опор:
₁=2,00
м,
₂=1,00
м. Найти силы

₁
и
₂,
с которыми балка давит на опоры.

Решение.
Балка при действии на нее сил тяжести
и нормальных реакций со стороны опор
находится в равновесии (покое).

В
этом состоянии результирующая сила и
результирующий момент сил относительно
любой точки (например, центра масс) равны
нулю. Поэтому можно написать:

,
где

– плечи действия сил

.
Из системы этих уравнений находим:

.

При
этом силы давления на опоры равны:
.
Для m=300кг,
l=8м,

=2м,

=1м:
|
|=1,76*
|
=1,18*
.

2.12.
Найти
момент инерции однородной прямоугольной
пластинки массы

,
длины

и ширины

относительно перпендикулярной к ней
оси, проходящей через: а) центр
пластинки, б) одну из вершин пластинки.

Р
ешение.
Выделим
полоску шириной

параллельно, например, стороне «
»
прямоугольника; масса этой полоски

=

.
Момент инерции этого элемента пластинки
относительно оси

:
d

По теореме Штейнера момент инерции того
же элемента относительно оси

:
d

=

.
Момент инерции пластинки в целом
относительно оси

:

=

.

Момент
инерции относительно оси, проходящей
через вершину пластинки и перпендикулярную
ей, равен:I=

.

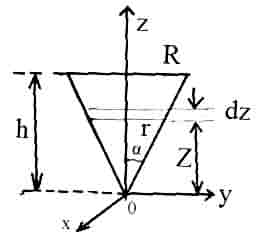
2.13.
Прямой
круглый однородный конус имеет массуm
и радиус основания R. Найти момент инерции
I
конуса относительно его оси.

Решение.
Объем
конуса разбиваем на тонкие круглые
диски, перпендикулярные оси симметрии

.
Радиус элементарного диска
,

е
го
масса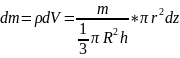

Момент
инерции:
.Момент
инерции конуса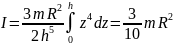

2
.14.
Однородный
цилиндр массы m и радиуса r катится без
скольжения по горизонтальной плоскости.
Центр цилиндра движется со скоростью

(см.рис.).
Найти модуль момента импульса цилиндра
относительно точек 1, 2 и 3, которые лежат
в перпендикулярной к цилиндру плоскости,
проходящей через его центр.

Решение.
Момент импульса тела относительно
произвольно заданной неподвижной точки
( например, 1, 2 или 3) определяется суммой
собственного момента импульса

и момента импульса

,
обусловленного поступательным движением
тела как целого, т.е.

.
В проекциях на ось z,
которую проведем перпендикулярно
плоскости рисунка и от нас, это равенство
представим в виде

.

В
рассматриваемом случае

при

.
Моменты импульса катящегося цилиндра
относительно точек 1, 2, 3 соответственно
равны:

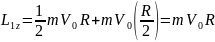
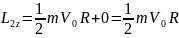
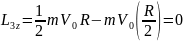
2.15.
Однородный
шарик помещен на плоскость, образующую
угол α=30,0° с горизонтом.

1.
При каких значениях коэффициента трения

шарик будет скатываться с плоскости
без скольжения?

2.
Полагая

=0,100,
а) определить характер движения шарика,
б) найти значения скоростей точек A,
В и С шарика спустя

=1,00
с после начала движения.

Р
ешение.
Напишем уравнения поступательного
движения шарика вдоль наклонной плоскости
и вращательного движения вокруг оси

,
полагая, что скольжения нет:

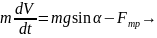
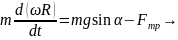
Уравнения
(1) и (2) совместно дают:

Подставляя
(3) в (1), получим

(4).

Скольжение
отсутствует, если

.
Максимальная сила трения

.
Итак, имеем:

При

шарик
будет скользить по наклонной плоскости,
вращаясь одновременно.

2.16.
Однородный
сплошной цилиндр массы

=1,00
кг висит в горизонтальном положении на
двух намотанных на него невесомых нитях
(рис.). Цилиндр отпускают без толчка.

а)
За сколько времени

цилиндр опустится на расстояние

=50,0
см?

б
)
Какое натяжение

испытывает при опускании цилиндра
каждая из нитей?

Решение.
На рисунке вектор

определяет силу натяжения обеих нитей.
В данной системе цилиндр совершает
поступательное движение вертикально
вниз и вращательное движение вокруг
оси

.
Соответствующие уравнения имеют вид:

.

В
уравнениях (1) и (2) содержится 3 неизвестных
величины: сила

и ускорения

.
Поэтому напишем уравнение вращательного
движения тела относительно оси А:

Подставляем (3) в (2):

Отсюда
находим

(4). Из (1) и (4) получаем ускорение опускания
цилиндра:

.
Из (5) с учетом начального условия

следует:

.
При этом за время t
цилиндр опустится навысоту

.
Отсюда

.
Для h=0,5м
t=0,4с.
На основании (1) и (5) находим силу натяжения
одной нити:

.

2.17.
На
ступенчатый блок (см.рис)
намотаны
в противоположных направлениях две
нити. На конец одной нити действуют
постоянной силой

,
а к концу другой нити прикреплен груз
массы m. Известны радиусы ступенчатого
блока
,
,
момент инерции блока относительно оси
вращения

.
Трения нет. Найти угловое ускорение
блока.

Р
ешение.
Обозначим
силу натяжения правого участка нити
через Т и напишем уравнение движения
тел данной системы:

1)
для груза mMa=mg-T
(1),

2)
для блока

(2).

Здесь

– угловое ускорение блока, которое
связано с тангенциальным ускорением

соотношением

(3).
Исключая из системы равенств (1) и (2)
величину Т с учетом соотношения (3),
получим:

.

2.18.
Однородный цилиндр радиуса

раскрутили вокруг его оси до угловой
скорости

 и
поместили затем в угол (см.рис). Коэффициент
трения между стенками угла и цилиндром
равен

.
Сколько времени цилиндр будет вращаться
в этом положении?

Решение.Действующие
на данное тело силы показаны на рисунке.
Поскольку данное тело не совершает
поступательного движения, то

,

.
Если учесть, что силы трения

,

,
то из предыдущих соотношений следует:

,

.
Отсюда получаем:
,

.

Т
еперь
нам необходимо найти угловую скорость

замедленного вращения цилиндра. Из
динамического уравнения

угловое ускорение

.
Подставляя выражения для
и

,
получим

.
Угловая скорость в произвольный момент
времени

.
В момент остановки

.
Следовательно, время вращения цилиндра
до остановки будет равно

.

2.19.
Маховик с начальной угловой скоростью

начинает
тормозиться силами, момент которых
относительно его оси пропорционален
квадратному корню из его угловой
скорости. Найти среднюю угловую скорость
маховика за все время торможения.

Решение.
Согласно
условию момент тормозящих сил, действующих
на раскрученный маховик,

,
где

>0
– некоторая постоянная,

— модуль мгновенной угловой скорости
вращения. Из уравнения

вращательного движения маховика
относительно неподвижной оси легко
установить зависимость

:
,
.
Для t
= 0

,
следовательно,

и

,
т. е.

.
Длительность

вращения маховика найдём из условия

:

.
При этом средняя скорость вращения
маховика равна

.

2.20.
Двухступенчатый
блок радиусов

и

положили
на гладкую горизонтальную поверхность.
На ступени блока плотно намотаны нити,
к концам которых приложили постоянные,
взаимно перпендикулярные силы

и

(рис., вид сверху). Сколько оборотов
совершит блок за время, в течение которого
его ось С переместится на расстояние

?
Масса данного блока

,
его момент инерции относительно оси С
равен

.

Решение.
Результирующее
движение ступенчатого блока рассматриваем
как наложение поступательного движения
и его вращения вокруг собственной оси
С. Уравнения этих движений имеют вид,
полагая, что

:

,
где

.
Время перемещения блока на расстояние

найдем из соотношения

,
F=const,

=const,начальные

и

равны нулю:

.
Угловое ускорение

.
Угловой путь блока за время

равен

,
а совершенное число оборотов

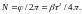
Подставляя
сюда выражения для

и

,
получим:

.

2.21.
Сплошному
однородному цилиндру массы

и радиуса

сообщили вращение вокруг его оси с
угловой скоростью

,
затем его положили боковой поверхностью
на горизонтальную плоскость и предоставили
самому себе. Коэффициент трения равен

.
Найти: а) время, в течение которого
движение цилиндра будет происходить
со скольжением; б) полную работу силы
трения скольжения.

Р
ешение.
На
первой стадии угловая скорость вращения
цилиндра ω>v/R,
где
v—
скорость
качения. Под действием тормозящего
момента сил трения через некоторый
промежуток времени τ угловая скоростьω(τ)
= v(τ)/R.
(1)

Отсюда
видно, что для определения времени τ
необходимо предварительно установить
зависимости ω(t)
и
v(t)
на
стадии скольжения цилиндра. Из уравнений
поступательного и вращательного движений
цилиндра та=F_тр
= kmgи

mR²
β= —RF_mp=-kmgRнаходим
ускоренияа=kgи
β=-2kg/R.
‘Гак
как а
и
β
константы, то v=at=kgt(v₀=0)

и
ω=ω₀+βt=ω₀
—
2kgt/R.
Удовлетворяя
условию (1), получим τ=ω₀R/3kg.
При
этом ω(τ)=ω₀/3.

Работа
сил трения скольжения равна прирщению
кинети­ческой энергии данного тела:

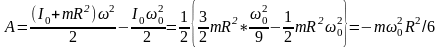
2.22.
На
гладкой горизонтальной поверхности
лежит однородный стержень массы

и длины

.
На один из его концов начали действовать
постоянной, направленной все время
вертикально вверх силой

.
Найти угловую скорость стержня в
зависимости от угла

его поворота.

Решение.
В
отношении положительной к стержню силы

=-m
необходимо
принять одно из дополнительных условий:
вектор силы может перемещаться в
горизонтальном направлении, оставаясь
параллельным самому себе или точка
приложения этого вектора остается на
одной и той же вертикали. Рассмотрим
сначала первый вариант.

1. В

   этом случае центр масс стержня под
   действием приложенной силы получает
   только вертикальное перемещение (см.
   рисунок). Пусть в процессе движения
   угол поворота стержня равен φ.
   При
   этом значении угла поворота центр масс
   стержня поднимется на высоту h_c=(l/2)sinφ,
   aero
   скорость будет равна v_c=dh_c/
   dt=(ωl/2)cosφ,
   где
   ω — угловая скорость поворота стержня
   в рассматриваемый момент времени. К
   этому моменту стержень приобретает
   кинетическую энергию

При
этом, совершенная силой

=-m
работа,
равна А=Flsinφ=mglsinφ.
Эта
работа пойдет на приращение кинетической
энергии

и
потенциальной энергии стержня

=mgh_c=(mgl/2)sinφ.
Итак,
имеем равенство
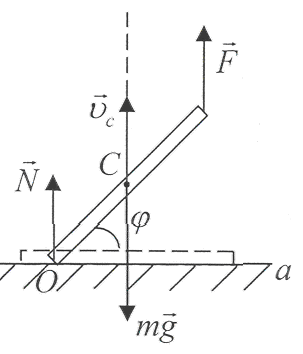
mglsinφ=(mω²l²/8)(cos²φ+1/3)+(mgl/2)sinφ.
Отсюда
следует, что gsinφ(ω²/4)(cos²φ+1/3)
и φ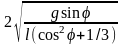

2)
Теперь рассмотрим случай, когда центр
масс стержня одновременно перемещается
вверх и в сторону вертикали, вдоль
которой действует приложенная сила

.

Обращаясь
к рисунку, запишем координаты центра
масс стержня:
Х_с=(l—lcosφ)+(l/2)cosφ=(l/2)(2-cosφ),y_t=(l/2)sinφ.
(1)

Д
ифференцируя
равенства (1) по времени, получим компоненты
и модуль скорости центра масс стержня:
v_сх=(ωl.2)sinφ,
v_су=(ωl/2)cosφ,
v_c=
ωl/2.

Кинетическая
энергия стержня для φповорота
равна Т=т
/2+I_cω²/2=тω²l²/6.
Из энергетического соотношения
А=Flsinφ=Т+mglsinφ/2
найдем угловую скорость стержня

.

2.23.
Волчок
массы

= 0,50 кг, ось которого наклонена под углом

= 30° к вертикали, прецессирует под
действием силы тяжести. Момент инерции
волчка относительно его оси симметрии

= 2,0 г*м²,
угловая скорость вращения вокруг этой
оси

= 350 1/с, расстояние от точки опоры до
центра масс волчка

= 10 см. Найти: а) угловую скорость прецессии
волчка; б) модуль и направление
горизонтальной составляющей силы
реакции, действующей на волчок в точке
опоры.

Р
ешение.
Угловая
скорость прецессии волчка вокруг
вертикальной оси. проходящей через
неподвижную точку О(см. рис.), равна

,
где l=ОС,
точка С — центр масс волчка. Во вращающейся
системе координат с угловой скоростью
ωгоризонтальная составляющая силы
реакции в точке О равна центробежной
силе инерции, обусловленной прецессионным
вращением волчка, т.е. R=тω’2lsinθ.
При
числовых значениях данных величин
ω’=0,7
,
R=10
мН.

2.24.
Волчок,
масса которого

= 1,0 кг и момент инерции относительно
собственной оси

= 4,0г*м²,
вращается с

= 320 рад/с. Его точка опоры находится на
подставке, которую перемещают в
горизонтальном направлении с ускорением

= 3,0 м/с².
Расстояние между точкой опоры и центром
масс волчка

= 10 см. Найти модуль и направление вектора

‘
— угловой скорости прецессии волчка.

Р
ешение.
Относительно
ускоряющейся платформы создается
однородное результирующее поле сил
тяжести и инерции, которому можно
сопоставить ускорение, модуль которого
равен

.
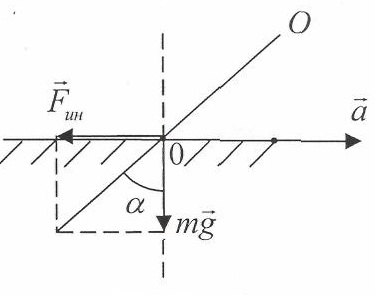
Ускорение

образует с земной вертикалью угол
а=arctg
(см.
рисунок). Ось 00, проходящая через
неподвижную точку О гироскопа и
параллельная вектору

,
будет являться ось прецессии. При этом
угловая скорость прецессии гироскопа
будет равна

1/c;

Угол,
образуемый вектором

с вертикалью, равен a=arctg
=arctg
=17°.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

= 120 см = 1,2 м.

m = 8 кг.

m1 = 500 г = 0,5 кг.

m2 = 1,3 кг.

g = 9,8 м/с^2.

ε — ?

Угловое ускорение ε определяется формулой: ε = M / I, где M — момент силы, который действует на блок, I — момент инерции блока.

Блок будем считать диском, поэтому момент инерции диска I определяется формулой: I = m * R^2/2, где m — масса диска, R — радиус диска.

R = D / 2.

R = 1,2 м / 2 = 0,6 м.

M = M2 — M1, где M1 — момент силы первого груза, M2 — момент силы второго груза.

M1 = m1 * g * R, M2 = m2 * g * R.

M = m2 * g * R — m1 * g * R = (m2 — m1) * g * R.

ε = 2 * (m2 — m1) * g * R / m * R^2 = 2 * (m2 — m1) * g / m * R.

ε = (1,3 кг — 0,5 кг) * 9,8 м/с^2 / 8 кг * 0,6 м = 1,63 рад / с^2.

Ответ: угловое ускорение блока ε = 1,63 рад / с^2.

В этой главе…

• Переходим от динамики поступательного движения к динамике вращательного движения
• Вычисляем момент инерции
• Определяем работу вращательного движения
• Находим связь между работой и изменением кинетической энергии
• Изучаем закон сохранения момента импульса

Эта глава посвящена динамике вращательного движения, т.е. описанию сил и их влияния на характер вращательного движения. Здесь рассматриваются основные законы динамики вращательного движения по аналогии с законами динамики поступательного движения. Например, описывается аналог второго закона Ньютона (см. главу 5), представлено новое понятие “момент инерции”, исследуется связь между работой и кинетической энергией и т.п.

Применяем второй закон Ньютона для вращательного движения

Согласно второму закону Ньютона (см. главу 5), ускорение объекта под действием силы пропорционально величине силы и обратно пропорционально массе объекта:

где ​( mathbf{a} )​ — это вектор ускорения, ( mathbf{F} ) — вектор силы, а ​( m )​ — масса объекта. Подробнее о векторах рассказывается в главе 4. Соблюдается ли этот закон для вращательного движения?

В главе 10 мы уже познакомились характеристиками вращательного движения, которые являются эквивалентами (аналогами) некоторых характеристик поступательного движения. А как будет выглядеть аналог у второго закона Ньютона? Похоже, что во вращательном движении роль ускорения ( mathbf{a} ) играет угловое ускорение ( alpha ), а роль силы ( mathbf{F} ) — момент силы ( mathbf{M} )? Не вдаваясь в подробности, скажем лишь, что это действительно так. А что же с массой? Оказывается, что для этого используется новое понятие — момент инерции ​( l )​. Известно, что второй закон Ньютона для вращательного движения принимает следующий вид:

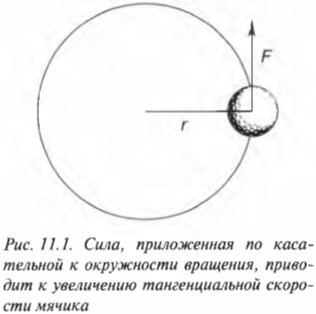
Рассмотрим простой пример. Пусть привязанный нитью мячик для игры в гольф вращается по окружности, как показано на рис. 11.1. Допустим, что к мячику приложена направленная по касательной к окружности тангенциальная сила, которая приводит к увеличению тангенциальной скорости мячика. (Обратите внимание, что речь идет не о нормальной силе, направленной вдоль радиуса окружности вращения. Более подробно нормальная и тангенциальная скорости, а также нормальное и тангенциальное ускорения рассматриваются в главе 10.)

Поскольку:

то, умножая обе части этой формулы на радиус окружности ​( r )​, получим:

Поскольку ​( rmathbf{F}=mathbf{M} )​ то

или

Таким образом, частично совершен переход от второго закона Ньютона для поступательного движения к его аналогу для вращательного движения. (Следует отметить, что это выражение справедливо для материальной точки, т.е. объекта, размерами которого можно пренебречь по сравнению с величиной радиуса окружности ​( r )​. Для протяженного объекта следует использовать другие формулы, которые описываются далее в этой главе. — Примеч. ред.)

Преобразуем тангенциальное ускорение в угловое

Чтобы полностью перейти от описания поступательного движения к описанию вращательного движения, необходимо использовать связь между угловым ускорением ​( alpha )​ и тангенциальным ускорением ​( mathbf{a} )​. Как нам уже известно из главы 10, они связаны следующим соотношением:

Подставляя это выражение в приведенную выше формулу

получим:

Итак, мы получили связь момента силы, действующей на материальную точку, и ее углового ускорения. Коэффициент пропорциональности между ними, ​( l=mr^2 )​, называется моментом инерции материальной точки. Таким образом, мы получили эквивалент второго закона Ньютона для вращательного движения, где роль силы играет момент силы, роль ускорения — угловое ускорение, а роль массы — момент инерции.

Пример: вычисляем момент силы для обеспечения углового ускорения

Если на объект действует несколько сил, то второй закон Ньютона имеет следующий вид:

где ​( mathbf{sum!F} )​ обозначает векторную сумму всех сил, действующих на объект.

Аналогично, если на объект действует несколько моментов сил, то второй закон Ньютона имеет вид:

где ( mathbf{sum! M} ) обозначает векторную сумму всех моментов сил, действующих на объект. Аналог массы, т.е. момент инерции, измеряется в кг·м².

Помните, что аналогом второго закона Ньютона при описании вращательного движения является формула ​( mathbf{sum! M}=lalpha )​, т.е. угловое ускорение прямо пропорционально сумме всех моментов сил, действующих на вращающийся точечный объект, и обратно пропорционально моменту инерции.

Пусть мячик из предыдущего примера (см. рис. 11.1) имеет массу 45 г, а длина нити равна 1 м. Какой момент сил необходимо приложить, чтобы обеспечить угловое ускорение — ​( 2pi с^{-2} )​? Подставляя значения в уже известную нам формулу

получим:

Как видите, для решения этой задачи достаточно было поступить, как при определении силы, необходимой для обеспечения ускорения поступательного движения (где нужно было бы умножить массу на ускорение), т.е. умножить угловое ускорение на момент инерции.

Вычисляем момент инерции протяженного объекта

Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения ​( r )​. В таком случае момент инерции имеет знакомый вид:

где ( r ) — это расстояние, на котором сосредоточена вся масса мячика ( m ).

Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине. Вообще говоря, для определения момента инерции протяженного объекта нужно просуммировать моменты инерции всех материальных точек объекта:

Например, момент инерции ​( l )​ системы из двух “точечных” мячиков для игры в гольф с одинаковой массой ​( m )​ на расстояниях ​( r_1 )​ и ​( r_2 )​ равен сумме их отдельных моментов инерции ​( l_1=mr_1^2 )​ и ( l_2=mr_2^2 ):

А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.

Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.

Пример: замедление вращения компакт-диска

Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:

Момент инерции диска с радиусом ​( r )​, вращающегося относительно своего центра в плоскости диска, выражается формулой:

Подставляя значения, получим:

Теперь нужно определить угловое ускорение, которое определяется следующей формулой:

Изменение угловой скорости ​( Deltaomega )​ произошло за промежуток времени:

В данном примере изменение угловой скорости:

где ​( omega_1 )​ — конечная, а ( omega_0 ) — начальная угловая скорость компакт-диска.

Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит ​( 2pi )​ радиан:

Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит ( 2pi ) радиан:

Подставляя значения в формулу углового ускорения, получим:

Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:

Итак, средний момент равен 10^-4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:

Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.

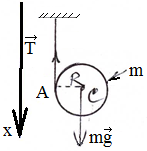
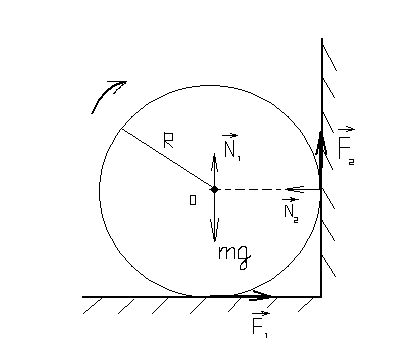
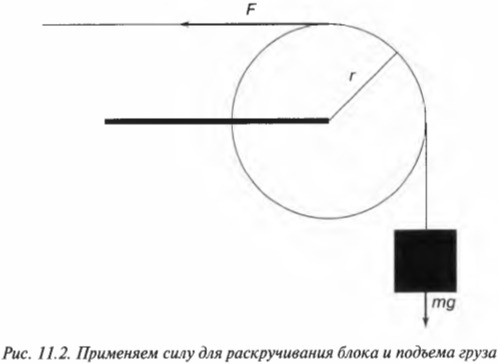
Еще один пример: поднимаем груз

Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис. 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.

В данном примере нужно вычислить сумму всех моментов сил ​( mathbf{sum! M} )​, которые действуют на веревку:

В данном примере на веревку действует два момента сил: один ​( M_1 )​ со стороны груза весом ​( mg )​, а другой ( M_2 ) — со стороны горизонтальной силы ​( F )​:

Отсюда получаем формулу для углового ускорения:

Эти моменты ​( M_1 )​ и ( M_2 ) имеют одинаковое плечо, равное радиусу блока ​( r )​, поэтому:

Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:

Подставляя выражения для ​( l )​, ​( M_1 )​ и ​( M_2 )​ в формулу для углового ускорения, получим:

Подставляя значения, получим:

 

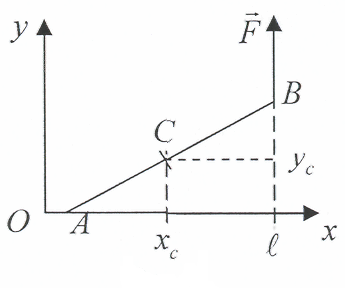
Вычисляем энергию и работу при вращательном движении

При изучении поступательного движения в главе 8 мы познакомились с понятием работа. Она равна произведению силы на перемещение под действием этой силы. Можно ли выразить работу при вращательном движении на основе его характеристик? Конечно можно, и для этого потребуется преобразовать силу в момент силы, а перемещение — в угол. В этом разделе демонстрируется такое преобразование, а также связь работы с изменением энергии.

Работа при вращательном движении

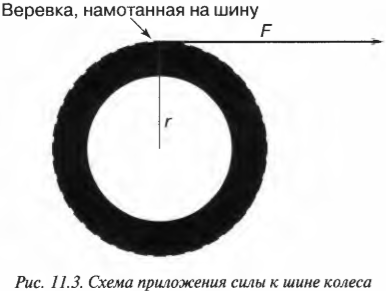
Допустим, что инженеру в области автомобилестроения необходимо рассчитать параметры революционно новой шины колеса. Для начала он решил оценить работу, которую необходимо выполнить для ускоренного раскручивания этой шины. Как связать работу при поступательном движении и работу при вращательном движении? Инженер предложил простую, как все гениальное, идею: “связать” шину веревкой. Точнее говоря, он предложил намотать веревку на шину, потянуть за веревку с помощью внешней силы и раскрутить шину. Так, приравнивая работу внешней силы при поступательном движении веревки и работу ускорения вращательного движения шины, можно, образно говоря, “связать” их веревкой.

Пусть шина имеет радиус ​( r )​ и для ее вращения используется сила ​( F )​, как показано на рис. 11.3.

Чему равна работа этой силы? Применим знакомую нам формулу:

где ​( s )​ — это перемещение веревки под действием этой силы. В данном примере перемещение ​( s )​ равно произведению радиуса ​( r )​ на угол поворота шины ​( theta )​:

Подставляя это выражение в формулу работы, получим:

Поскольку момент ​( M )​, создаваемой этой силой, равен:

то получаем для работы:

Таким образом, работа при вращательном движении равна произведению момента силы и угла поворота. Она измеряется в тех же единицах, что и работа при поступательном движении, т.е. в джоулях.

Учтите, что для описания вращательного движения в этих формулах работы угол нужно указывать в радианах.

Вот еще один пример. Пусть пропеллер самолета совершает 100 поворотов с постоянным моментом силы 600 Н·м. Какую работу выполняет двигатель самолета? Для ответа на этот вопрос начнем с уже известной нам формулы:

Полный оборот соответствует повороту на угол ​( 2pi )​. Подставляя значения в формулу, получим:

Что происходит с выполненной таким образом работой? Она преобразуется в кинетическую энергию вращательного движения.

Изучаем кинетическую энергию вращательного движения

Из главы 8 нам уже известно, что объект массы ​( m )​, движущийся поступательно со скоростью ​( v )​, обладает кинетической энергией:

А как получить формулу кинетической энергии для вращающегося объекта? Нужно применить данную формулу для всех его частичек.

При описании вращательного движения аналогом массы является момент инерции, а аналогом скорости — угловая скорость.

Как известно (см. главу 10), тангенциальная скорость ​( v )​ и угловая скорость ​( omega )​ связаны соотношением:

где ​( r )​ — это радиус окружности вращения.

Подставляя это соотношение в предыдущую формулу, получим:

Однако эта формула справедлива только для бесконечно малой материальной точки. Чтобы определить кинетическую энергию протяженного объекта, нужно просуммировать кинетические энергии всех его мельчайших материальных точек, т.е. вычислить сумму:

Как можно было бы упростить эту формулу? Предположим, что все составляющие частички протяженного объекта вращаются с одинаковой угловой скоростью. Тогда угловую скорость можно вынести за знак суммирования и получим:

Здесь начинается самое интересное. Ранее в этой главе уже приводилась формула момента инерции:

Теперь совсем нетрудно сделать подстановку в предыдущей формуле кинетической энергии:

Итак, кинетическая энергия вращательного движения вычисляется аналогично кинетической энергии поступательного движения, если вместо массы использовать момент инерции, а вместо тангенциальной скорости — угловую скорость. Примеры кинетической энергии вращательного движения окружают повсюду. Спутник на космической орбите и бочка пива, которую скатывают по наклонной плоскости, обладают определенной кинетической энергией вращательного движения. Особенности вращательного движения бочки пива более подробно описываются в следующем разделе.

Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости

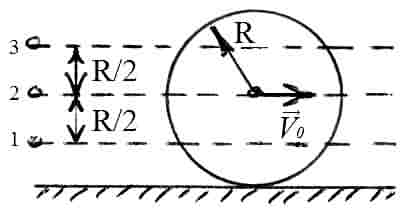
Итак, нам уже известно, что объекты могут двигаться поступательно и вращательно, причем двигаться так, что без знания строгих законов физики порой трудно понять их поведение. Да ну? Действительно, если бочка скользит вниз по наклонной плоскости, то ее потенциальная энергия превращается в кинетическую энергию поступательного движения (см. главу 8). А если бочка скатывается вниз по наклонной плоскости, то ее потенциальная энергия превращается не только в кинетическую энергию поступательного движения, но и в кинетическую энергию вращательного движения.

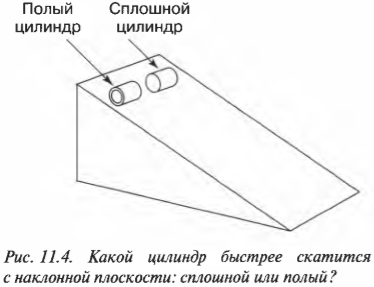
На рис. 11.4 показан случай, когда с наклонной плоскости высотой ​( h )​ скатываются сплошной и полый цилиндры с одинаковой массой ​( m )​. Какой цилиндр достигнет нижнего конца наклонной плоскости?

Иначе говоря: какой цилиндр будет обладать большей скоростью в конце наклонной плоскости? Поскольку действующие на цилиндры силы постоянны, то постоянны и их ускорения, а значит, большая скорость в конце пути означает меньшее время его прохождения. В случае только поступательного движения цилиндра и при отсутствии трения уменьшение потенциальной энергии ​( mgh )​ преобразуется в увеличение кинетической энергии только поступательного движения ​( {}^1!/!_2mv^2 )​, т.е.:

Однако в данном примере эта формула не годится, потому что цилиндры скатываются без проскальзывания. Это значит, что часть уменьшения потенциальной энергии будет преобразовываться в увеличение кинетической энергии поступательного движения ( {}^1!/!_2mv^2 ), а часть — в кинетическую энергию вращательного движения ( {}^1!/!_2Iomega ^2 ). Тогда предыдущее равенство принимает следующий вид:

Сделаем подстановку ​( omega=v/r )​ и получим:

Путем несложных алгебраических преобразований получим:

откуда легко получить выражение для скорости цилиндра:

Для обоих цилиндров все параметры одинаковы, кроме момента инерции ​( I )​. Как это повлияет на скорость цилиндров? Согласно данным из табл. 11.1, полый цилиндр имеет момент инерции ​( mr^2 )​, а сплошной — ​( {}^1!/!_2mr^2 )​.

Итак, для полого цилиндра получим:

а для сплошного цилиндра:

А их отношение равно:

Как видите, скорость сплошного цилиндра в 1,15 раза больше скорости полого цилиндра, а значит, сплошной цилиндр быстрее достигнет конца наклонной плоскости.

Как на пальцах объяснить полученный результат? Все очень просто. В полом цилиндре вся масса сосредоточена на расстоянии радиуса цилиндра, а в сплошном цилиндре значительная часть масса распределена ближе радиуса. Это значит, что при одинаковой угловой скорости в полом цилиндре больше материала будет обладать большей тангенциальной скоростью, а для этого потребуется потратить больше энергии.

Не можем остановиться: момент импульса

Допустим, нам нужно остановить космический корабль с массой 40 т, который находится на околоземной орбите. Для этого потребуется затратить немалые усилия. Почему? Все дело во вращательном импульсе космического корабля.

В главе 9 подробно описывается понятие импульс материальной точки, который выражается следующей формулой:

где ​( m )​ — это масса, a ​( v )​ — скорость материальной точки.

По аналогии, при описании вращательного движения физики используют понятие вращательный импульс (который в русскоязычной научной литературе чаще называют моментом импульса материальной точки. — Примеч. ред.):

где ​( l )​ — это момент инерции, а ​( omega )​ — угловая скорость материальной точки.

Следует помнить, что момент импульса (или вращательный импульс) является вектором, направление которого совпадает с направлением вектора угловой скорости.

Момент импульса в системе СИ измеряется в кг·м²·с^-1 (более подробно системы единиц измерения описываются в главе 2). Одним из наиболее важных свойств момента импульса является закон сохранения момента импульса.

Сохраняем момент импульса

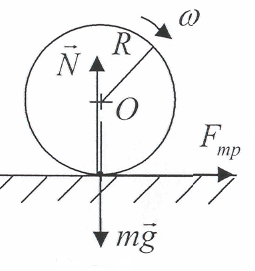
Закон сохранения момента импульса гласит: момент импульса сохраняется, если равна нулю сумма всех моментов внешних сил. Этот закон проявляется во многих обыденных ситуациях. Например часто приходится видеть, как мастера фигурного катания на льду вращаются с широко разведенными в стороны руками, а затем резко приближают их к своему телу и сильно ускоряют свое вращение. Дело в том, что таким образом они уменьшают свой момент инерции и, согласно закону сохранения момента импульса, увеличивают свою угловую скорость. Зная начальную угловую скорость вращения фигуриста ​( omega_0 )​ и его моменты инерции в позе с разведенными руками ​( I_0 )​ и в позе с сомкнутыми руками ​( I_1 )​, легко найти конечную угловую скорость ​( omega_1 )​ по формуле:

Однако этот закон удобно использовать не только в таких простых ситуациях. Возвращаясь к примеру с космическим кораблем на околоземной орбите, следует отметить, что его орбита далеко не всегда является строго круглой. Чаще всего орбиты спутников Земли и других планет имеют эллиптическую форму. Поэтому без закона сохранения момента импульса было бы гораздо сложнее определять параметры их орбитального движения.

Пример закона сохранения момента импульса: вычисляем скорость спутника

Предположим, что космический корабль вращается на эллиптической орбите вокруг Плутона. Причем в самой близкой к Плутону точке орбиты спутник находится на расстоянии 6·10⁶ м от центра Плутона и имеет скорость 9·10³ м/с. Вопрос: какой будет скорость спутника в самой далекой точке эллиптической орбиты на расстоянии 2·10⁷ м от центра Плутона?

Для ответа на этот вопрос нужно воспользоваться законом сохранения момента импульса, поскольку на спутник не действуют никакие внешние моменты сил (сила гравитационного притяжения направлена параллельно радиусу и не создает момента). Однако закон сохранения момента импульса нужно преобразовать так, чтобы вместо угловых скоростей в его формулировке фигурировали тангенциальные скорости.

Итак, рассмотрим формулу закона сохранения момента импульса:

где ​( I_{бл} )​ — это момент инерции спутника в самой близкой точке, ( I_{дал} ) — это момент инерции спутника в самой далекой точке, ( omega_{бл} ) — угловая скорость спутника в самой близкой точке, а ( omega_{дал} ) — угловая скорость спутника в самой далекой точке.

Предположим, что размеры спутника гораздо меньше расстояния до центра Плутона и спутник можно считать материальной точкой. Тогда его моменты инерции равны:

и

где ​( r_{бл} )​ — это расстояние от спутника до центра Плутона в самой близкой точке эллиптической орбиты, а ( r_{дал} ) — это расстояние от спутника до центра Плутона в самой далекой точке эллиптической орбиты.

Кроме того:

и

Подставляя все перечисленные соотношения в формулу закона сохранения момента импульса

получим:

Отсюда путем несложных алгебраических преобразований, получим:

Подставляя значения, получим:

Итак, в ближайшей к Плутону точке орбиты спутник будет иметь скорость 9000 м/с, а в самой дальней — 2700 м/с. Этот результат мы легко получили только благодаря знанию закона сохранения момента импульса.