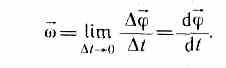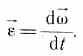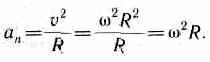Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:
Приняв вектор k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.
Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
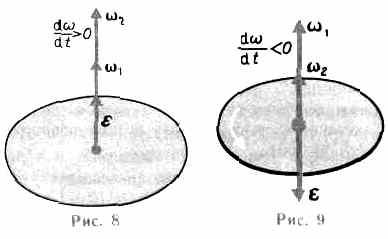
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.
Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Угловое ускорение – что это?
Угловое ускорение (varepsilon) – физическая величина, характеризующая изменение угловой скорости при движении тела.
Единица измерения: (lbrackvarepsilonrbrack=frac1{с^2}) или (с^{-2})
Угловая скорость
Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Угловая скорость (omega) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.
При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).
Вектор угловой скорости направлен вдоль оси вращения.
Основные формулы для вычисления угловой скорости
Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):
- (omega=frac nt), где (n) – количество оборотов за единицу времени (t).
- (omega=fracvarphi t), где (varphi) – угол поворота, (t) – время, за которое он совершен.
- (omega=frac{2pi}T), где (Т) – период обращения (время, за которое тело/точка совершает один оборот).
- (omega=2pinu), где (nu) – числом оборотов в единицу времени.
Единица измерения угловой скорости в СИ: (lbrackomegarbrack=frac{рад}с)
Связь между угловой скоростью и нормальным (центростремительным) ускорением
Центростремительное (нормальное) ускорение (a_n) – это составляющая полного ускорения, которая характеризует изменение направления вектора скорости при криволинейном движении. Другим компонентом полного ускорения является тангенциальное ускорение, оно характеризует изменение величины скорости.
Центростремительное ускорение определяется по формуле:
(a_n=frac{V^2}R),
где (V) – скорость движения, (R) – радиус окружности.
Единица измерения в СИ: (lbrack a_nrbrack=frac м{с^2})
Итак, формула связывающая эти две величины:
(a_n=omega^2R)
Основные формулы для расчета углового ускорения
Значение углового ускорения в определенный момент времени вычисляется как первая производная от угловой скорости или вторая производная от угла поворота по времени.
(varepsilon=lim_{triangle trightarrow0}frac{triangleomega}{triangle t}=frac{domega}{dt}=frac{d^2varphi}{dt}=overset.omega=overset{..}varphi)
Угловое ускорение маховика
(varepsilon=fracomega t=frac{2pi n}t), где (n) – количество оборотов за единицу времени (t).
Среднее угловое ускорение
Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.
(leftlanglevarepsilonrightrangle=frac{triangleomega}{triangle t})
Тангенциальное ускорение
Тангенциальным (касательным) ускорением (a_tau) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.
(a_tau=varepsilon r), где (varepsilon) – угловое ускорение, (r) – радиус кривизны траектории в заданной точке.
Мгновенное угловое ускорение
Мгновенное угловое ускорение (alpha) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.
(alpha=tg(varepsilon)=frac{;domega}{dt}=frac{d^2phi}{dt^2})
Download Article
Different ways to calculate rotation speed
Download Article
Most people have a general understanding of the idea of velocity and acceleration. Velocity is the measure of how fast an object is moving, and acceleration is the measure of how quickly the object’s velocity is changing (i.e., speeding up or slowing down). When the object is moving in a circle, such as a spinning tire or a rotating CD, velocity and acceleration are generally measured by the angle of rotation. They are then called angular velocity and angular acceleration. If you know the object’s velocity over some period of time, you can calculate its average angular acceleration. Alternatively, you may have a function to calculate the object’s position. With this information, you can calculate its angular acceleration at any chosen instant.
-
1
Determine the function for angular position. In some cases, you may be provided with a function or formula that predicts or assigns the position of an object with respect to time. In other cases, you may derive the function from repeated experiments or observations. For this article, we assume that the function has been provided or previously calculated.[1]
-
2
Find the function for angular velocity. Velocity is the measure of how fast an object changes its position. In layman’s terms, we think of this as its speed. In mathematical terms, the change of position over time can be found by finding the derivative of the position function. The symbol for angular velocity is
. Angular velocity is generally measured in units of radians divided by time (radians per minute, radians per second, etc.).[2]
Advertisement
-
3
Find the function for angular acceleration. Acceleration is the measure of how fast an object’s velocity is changing over time. You can mathematically calculate the angular acceleration by finding the derivative of the function for angular velocity. Angular acceleration is generally symbolized with
, the Greek letter alpha. Angular acceleration is reported in units of velocity per time, or generally radians divided by time squared (radians per second squared, radians per minute squared, etc.).[3]
-
4
Apply the data to find instantaneous acceleration. Once you have derived the function for instantaneous acceleration as the derivative of velocity, which in turn is the derivative of position, you are ready to calculate the instantaneous angular acceleration of the object at any chosen time.[4]
Advertisement
-
1
-
2
Measure final angular velocity. The second piece of information that you need is the angular velocity of the spinning or rotating object at the end of the time period that you want to measure. This is to be called the “final” velocity.[6]
- A compact disc plays in the machine by rotating at an angular velocity of 160 radians per second.
- The roller coaster, after applying its brakes to the spinning wheels, ultimately reaches an angular velocity of zero when it stops. This will be its final angular velocity.
-
3
Measure the elapsed time. To calculate the average angular velocity of the spinning or rotating object, you need to know the amount of time that passes during your observation. This can be found by direct observation and measurement, or the information can be provided for a given problem.[7]
- The owner’s manual for the CD player provides the information that the CD reaches its playing speed in 4.0 seconds.
- From observations of roller coasters being tested, it has been found that they can come to a complete stop within 2.2 seconds from when the brakes are initially applied.
-
4
Calculate the average angular acceleration. If you know the initial angular velocity, the final angular velocity, and the elapsed time, fill that data into the equation and find the average angular acceleration.[8]
- For the example of the CD player, the calculation is as follows:
- For the roller coaster example, the calculation looks like this:
- Note that acceleration is always going to be in units of some distance measurement “per” time squared. With angular acceleration, the distance is generally measured in radians, although you could convert that to number of rotations if you wish.
Advertisement
-
1
Understand the concept of angular motion. When people think of the speed of an object, they often consider linear motion — that is, objects traveling mostly in a straight line. This would include a car, a plane, a ball that is thrown or any number of other objects. However, angular motion describes objects that spin or rotate. Think of the earth spinning on its axis. The position or speed of the earth can be measured with angular quantities. A spinning compact disc (or record player, if you’re old enough), electrons on their axes, or the wheels of a car on the axle are other examples of rotating objects that can be measured through angular motion.[9]
-
2
Visualize angular position. When you measure the position of a moving vehicle, for example, you can measure the distance traveled in a straight line from the starting point. With a rotating object, the measurement is generally done in terms of the angle around a circle. By convention, the starting or “zero” point is generally a horizontal radius from the center to the right side of the circle. The distance traveled is measured by the size of the angle
, measured from that horizontal radius.[10]
- The angle that is being measured is commonly represented by
, the Greek letter theta.
- Positive motion is measured in a counterclockwise direction. Negative motion is measured in a clockwise direction.
- The angle that is being measured is commonly represented by
-
3
Measure angular motion in radians. Linear travel is generally measured in some unit of distance, such as miles, meters, inches or some other unit of length. Rotational or angular motion is generally measured in units called radian. A radian is a fraction of the circle. For standard reference, mathematicians use the “unit circle,” which has a standard radius of 1 unit.[11]
- One full rotation around the unit circle is said to measure 2π radians. Therefore, a half circle is π radians, and a quarter circle is π/2 radians.
- Sometimes it is useful to convert from radians to degrees. If you recall that a full circle is 360 degrees, you can find the conversion as follows:
- Thus, one radian is about equal to 57.3 degrees.
-
4
Understand the concept of angular acceleration. Angular acceleration is the measurement of how fast or slow a rotating object is changing its velocity. In other words, is the spinning speeding up or slowing down? If you know the angular velocity at a starting time and then at a later ending time, you can calculate the average angular acceleration over that time interval. If you know the function for the object’s position, you can use calculus to derive the instantaneous angular acceleration at any chosen time.[12]
- People often use the word “acceleration” to mean speeding up, and “deceleration” to mean slowing down. In mathematical and physical terms, however, only the word “acceleration” is used. If the object is speeding up, the acceleration is positive. If it is slowing down, the acceleration is negative.
Advertisement
Add New Question
-
Question
What are the formulas to find the initial acceleration of an object?
Initial acceleration generally has to be given as a condition of the problem or the experiment.
-
Question
What is the direction of radial and tangential acceleration and how do they affect each other?
Angular (or radial) measurements are generally counterclockwise. Tangential acceleration means the straight line direction of the tangent at some measured point along the circle. The tangent is a line that is perpendicular to the radius at that point.
-
Question
How can you find angular acceleration in revolutions per second squared?
This article shows how to find acceleration in radians per second squared. To convert the number of radians to the number of revolutions, recall that 1 full circle (or 1 revolution) is equal to 2pi radians. This is roughly equivalent to 6.28 radians per revolution. If you know the acceleration in radians per second squared, divide that answer by 6.28 to get revolutions per second squared.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Remember to express final results with the proper units. Angular position is usually expressed in radians. Angular velocity is expressed in radians per time. Angular acceleration is expressed in units of radians per time squared.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate instantaneous angular acceleration, start by determining the function for angular position, or the position of the object with respect to time. Next, find the angular velocity, which is the measure of how fast the object changes its position. Then, find the derivative of the function for angular velocity in order to determine the function for angular acceleration. Finally, plug in the data to find the instantaneous acceleration of the object at any chosen time. To learn more, including how to calculate average angular acceleration, read on.
Did this summary help you?
Thanks to all authors for creating a page that has been read 91,183 times.
Did this article help you?
Угловое ускорение объекта обусловлено вращательным движением объекта вокруг своей оси из точки центра тяжести, а крутящий момент отвечает за вращательное движение объекта.
Поскольку сила приложена к телу по касательной, эквивалентная сила действует на точку, расположенную напротив нее, и действует в противоположном направлении, что стремится вращать ее с угловым ускорением, и, следовательно, крутящий момент и угловое ускорение входят в картину в картине. случае вращающегося тела.
Связь между крутящим моментом и угловым ускорением
Чистый крутящий момент, действующий на объект, прямо пропорционален угловому ускорению объекта и обратно пропорционален инерции вращения вокруг его оси вращения.
Скорость, приобретаемая объектом, зависит от крутящего момента, приложенного к телу, и угловое ускорение — это изменение угловой скорости со временем вращения объекта вокруг оси.
Формула крутящего момента и углового ускорения
We знать, что крутящий момент является произведением силы, приложенной к объекту, и того, насколько далеко он смещен от приложенной силы.
τ = сила * перемещение
И F=ма
Рассмотрим круглый диск радиуса ‘r’, и к диску приложена сила F, чтобы вращать его вокруг оси, создающей крутящий момент τ, движущийся с угловым ускорением α.
θ является угловое смещение диска при приложении крутящего момента, ω — угловая скорость а — ускорение диска.
Пусть смещение равно ‘r’ от оси вращения, тогда получим
т = ма*р
Если объект вращается с угловой скоростью ω, то угловая скорость связана с угловым ускорением как α=ω/t а ускорение объекта связано с угловым ускорением как
а=ра
Используя это в приведенном выше уравнении, мы имеем
т = г-н2
Термин г-н2 есть не что иное, как момент инерции объекта, распространенный во всех измерениях объекта. Следовательно,
а=Iα
Это уравнение, обозначающее связь между крутящим моментом и угловым ускорением объекта.
График крутящего момента и углового ускорения
Ссылаясь на уравнение, дающее связь крутящего момента и углового ускорения объекта, которое мы нашли выше, мы можем построить график крутящего момента и углового ускорения.
Предположим, что момент инерции равен I=0.67 кг·м.2, затем
Если α=10, то
τ=Iα
=0.67*10=6.7 Нм
Если α=20, то
τ= 0.67* 20=13.4 Нм
Если α =30, то
τ= 0.67* 30=20.1 Нм
Следовательно, мы получаем график зависимости крутящего момента от углового ускорения в секунду, как показано ниже:
Наклон графика зависимости крутящего момента от углового ускорения, очевидно, даст нам момент инерции тела, и видно, что угловое ускорение линейно возрастает с увеличением крутящего момента.
Следовательно, если мы узнали крутящий момент, придаваемый объекту, и угловое ускорение, которое приобретает объект, то можем узнать момент инерции объекта, построив график зависимости крутящего момента от углового ускорения.
Крутящий момент и направление углового ускорения
Если мы внимательно посмотрим на приведенную ниже диаграмму, мы сможем понять, что сила приложена к объекту с касательной к нему и соответствующий ей объект начинает вращаться с угловым ускорением, перпендикулярным приложенной к объекту силе.
Крутящий момент, создаваемый на оси вращения, показан на диаграмме, которая перпендикулярна силе, а также угловому ускорению объекта.
То же самое мы можем изобразить на трех осях, как показано ниже:
На этой диаграмме мы ясно видим, что сила, угловое ускорение и крутящий момент лежат перпендикулярно друг другу.
Если сила приложена к оси x, то направление углового ускорения объекта будет перпендикулярно силе в направлении y, а соответствующий крутящий момент будет приложен по азимутальной оси, которая перпендикулярна оси z к обеим сторонам. .
Эту же мысль можно запомнить, используя правило большого пальца правой руки.
Если вы держите правую руку, как показано на рисунке выше, большой палец обозначает направление крутящего момента, действующего на объект, изогнутые пальцы представляют направление углового ускорения объекта, а сила, перпендикулярная обоим, обозначается ладонь вашей руки.
Как найти крутящий момент с угловым ускорением?
Угловое ускорение объекта является результатом действия крутящего момента на его тело.
Крутящий момент легко найти, зная угловое ускорение объекта и момент инерции по формуле τ=Iα, где τ — крутящий момент, действующий на тело, I — момент инерции, а альфа — угловое ускорение объекта.
Момент инерции представляет собой произведение суммы всех масс частицы, составляющей объект, на квадрат расстояния от точки углового ускорения края объекта до оси вращения и является тенденцией объект для снижения углового ускорения.
Если твердый диск массой 1 кг и радиусом 12 см вращается с угловым ускорением 2π рад/с2 тогда какой крутящий момент приложен к диску?
Данный: м =1кг
г = 12 см = 0.12 м
а =2π рад/с2
Момент инерции диска равен
Теперь мы можем рассчитать крутящий момент, действующий на диск, как
Следовательно, крутящий момент, приложенный к объекту, составляет 0.045 Нм.
Как найти угловое ускорение по крутящему моменту?
Как только к телу будет приложен крутящий момент, оно начнет вращаться с некоторым угловым ускорением, зависящим от момента инерции тела.
Угловое ускорение можно рассчитать исходя из величины крутящего момента, приложенного к объекту, по формуле α= τ/I . Приложенный крутящий момент создаст угловое ускорение, в то время как момент инерции тела попытается одновременно противодействовать этому угловому ускорению.
Каково угловое ускорение шара для боулинга массой 800 г и радиусом 12 см, если крутящий момент 3.5 раз 10-4 Nm применяется к мячу?
Данный: т=3.5 *10-4 Nm
г = 12 см = 0.12 м
м = 800 г = 0.8 кг
Теперь давайте сначала рассчитаем момент инерции шара для боулинга. Так как шар для боулинга имеет сферическую форму
Следовательно, угловое ускорение шара для боулинга равно
Угловое ускорение шара для боулинга равно 0.076 м/с.2.
Возникает ли угловое ускорение за счет крутящего момента?
Угловое ускорение является результатом вращательного движения объекта, которое достигается за счет приложения к телу крутящего момента.
Крутящий момент создается приложением силы, перпендикулярной оси вращения тела, и тело начинает вращаться вокруг своей оси вращения, образуя угол 90 градусов к направлению приложенного крутящего момента.
Крутящий момент и угловое ускорение маховика
Маховик — это механизм, используемый для хранения энергии внутри него и вырабатывающий большое количество электроэнергии, когда ему придается крутящий момент для ускорения.
Рассмотрим маховик, вращающийся по часовой стрелке, когда на него действует сила F, как показано на рисунке ниже. Радиус маховика равен «r», а его ось вращения расположена в центре.
Крутящий момент, действующий на маховик, равен
τ=сила*смещение
Сила тяжести, действующая на маховик, равна F=mg, а радиальное смещение маховика происходит по его радиусу ‘r’.
Отсюда получаем выражение для крутящего момента в виде
τ=мгр
Так как маховик поднят на высоту h, потери потенциальной энергии в машине равны mgh.
Кинетическая энергия вращающегося маховика, вращающегося с угловой скоростью ω, равна
КЭ =1/2Iω2
Где I — момент инерции, а ω — угловая скорость объекта.
Угловое ускорение объекта представляет собой изменение угловой скорости во времени и определяется выражением
α=dω/dt
Крутящий момент на маховике равен
τ=Iα
Замена на альфа
τ =Idω/dt
Это уравнение не зависит от углового ускорения.
We знать, что крутящий момент прямо пропорционально угловому ускорению по уравнению
τ=Iα
Следовательно, угловое ускорение есть отношение крутящего момента к моменту инерции объекта.
α =τ/I
Итак, мы нашли уравнение крутящего момента для маховика, давайте подставим его сюда в это уравнение, чтобы найти угловое ускорение.
α =мгр/I
Умножая r в числителе и знаменателе, получаем
α = г-н2г/л
Так как я=мистер2 используя это в уравнении выше
α =Ig/Ir
α=г/р
Компания угловое ускорение обратно пропорционально к радиусу объекта; это означает, что если диаметр объекта больше, угловое ускорение объекта будет меньше.
Крутящий момент и угловое ускорение для твердого тела
Твердое тело — это твердый объект, который не деформируется ни в какой последовательности, а масса непрерывно распределяется в твердом теле.
Момент инерции твердого тела постоянен и прямо пропорционален угловому моменту вращающегося тела. Он задается соотношением как
I=L/ω
Следовательно, крутящий момент на твердом теле равен
А крутящий момент связан с моментом инерции уравнением
Подставляя сюда уравнение момента импульса в это уравнение, получаем
ω есть не что иное, как угловая скорость и равна угловому ускорению во времени.
Отсюда получаем, что крутящий момент, действующий на твердое тело, также равен моменту количества движения тела в единицу времени.
Следовательно, теперь мы можем найти угловое ускорение объекта как
По этой формуле можно найти угловое ускорение твердого тела.
Каковы угловое ускорение и крутящий момент на цилиндрическом стержне твердой массы?
Рассмотрим цилиндрический стержень длиной «L», вращаемый по часовой стрелке, тогда крутящий момент, действующий на цилиндрический стержень массы м
Сила гравитации равна F=mg, а r составляет половину длины стержня, расстояние от оси вращения до точки, в которой действует сила.
Поскольку угол, образуемый вращающейся осью с угловым ускорением объекта, составляет 90 градусов,
Sin900=1
Крутящий момент к угловому ускорению стержня равен
Теперь приравнивая оба уравнения,
Следовательно, мы получили угловое ускорение жесткого цилиндрического стержня.
Часто задаваемые вопросы
Каковы крутящий момент и угловое ускорение, если ребенок массой 21 кг сидит на карусели массой 60 кг радиусом 1.2 м и для ее вращения приложена сила 230 Н?
Данный: Вес ребенка m=21кг
Вес карусели М=60кг.
Радиус карусели r=1.2м.
F = 230 Н
Момент инерции карусели равен
Момент инерции ребенка, сидящего на карусели, равен
Следовательно, полный момент инерции равен
Крутящий момент, действующий на карусель, равен
Отсюда угловое ускорение карусели от крутящего момента 276 Нм равно
Угловое ускорение карусели равно 4.76 м / с2.
Каковы угловое ускорение и крутящий момент потолочного вентилятора массой 5.4 кг, имеющего 3 лопасти длиной 1 м и центральный диск радиусом 12 см? Масса каждой лопасти составляет 800 граммов, а центр тяжести весит 3 кг.
Данный: Масса лопастей m=800г=0.8кг.
Масса диска М =3кг
Длина 3-х лопастей L = 1м
Радиус диска r = 12 см = 0.12 м
Общая масса вентилятора 5.4 кг.
Крутящий момент лопастей вентилятора
Момент инерции лопасти
Следовательно, момент инерции 3-х лопастей равен
Момент инерции диска равен
Следовательно, полный момент инерции равен
Следовательно, теперь мы можем вычислить угловое ускорение вентилятора
Компания угловое ускорение потолочный вентилятор 64.33 рад/с2.
Рассмотрим
твердое тело, которое вращается
вокруг неподвижной оси. Тогда отдельные
точки этого тела будут описывать
окружности разных радиусов, центры
которых лежат на оси вращения. Пусть
некоторая точка движется по окружности
радиуса R
(рис.6).
Ее положение через промежуток времени
t
зададим
углом .
Элементарные (бесконечно малые) углы
поворота рассматривают как векторы.
Модуль вектора d
равен
углу поворота, а его направление совпадает
с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения
точки по окружности, т. е. подчиняется
правилу
правого, винта (рис.6).
Векторы, направления которых связываются
с направлением вращения, называются
псевдовекторами
или
аксиальными
векторами. Эти
векторы не имеют определенных точек
приложения: они могут откладываться
из любой точки оси вращения.
Угловой
скоростью называется
векторная величина, равная первой
производной угла поворота тела по
времени:
Вектор
«в направлен вдоль оси вращения по
правилу правого винта, т. е. так же, как
и вектор d
(рис. 7). Размерность угловой скорости
dim=T-1,
a .
ее единица — радиан в секунду (рад/с).
Линейная скорость
точки (см. рис. 6)
В векторном виде
формулу для линейной скорости можно
написать как векторное произведение:
При
этом модуль векторного произведения,
по определению, равен
,
а
направление совпадает с
направлением
поступательного движения правого винта
при его вращении от
к R.
Если
=const,
то
вращение равномерное и его можно
характеризовать периодом
вращения Т
—
временем, за которое точка совершает
один полный оборот, т. е. поворачивается
на угол 2.
Так как промежутку времени t=T
соответствует =2,
то =
2/Т,
откуда
Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называется частотой
вращения:
Угловым
ускорением называется
векторная величина, равная первой
производной угловой скорости по
времени:
При вращении тела
вокруг неподвижной оси вектор углового
ускорения направлен вдоль оси вращения
в сторону вектора элементарного
приращения угловой скорости. При
ускоренном движении вектор
13
сонаправлен
вектору
(рис.8),
при замедленном.— противонаправлен
ему (рис. 9).
Тангенциальная
составляющая ускорения
Нормальная
составляющая ускорения
Таким
образом, связь между линейными (длина
пути s,
пройденного
точкой по дуге окружности радиуса R,
линейная
скорость v,
тангенциальное
ускорение а,
нормальное ускорение аn)
и угловыми величинами (угол поворота
,
угловая скорость (о, угловое ускорение
)
выражается следующими формулами:
В
случае равнопеременного движения точки
по окружности (=const)
где
0
— начальная угловая скорость.
Контрольные
вопросы
• Что
называется материальной точкой? Почему
в механике вводят такую модель?
• Что
такое система отсчета?
• Что
такое вектор перемещения? Всегда ли
модуль вектора перемещения равен отрезку
пути,
пройденному точкой?
• Какое
движение называется поступательным?
вращательным?
• Дать
определения векторов средней скорости
и среднего ускорения, мгновенной
скорости
и мгновенного
ускорения. Каковы их направления?
• Что
характеризует тангенциальная
составляющая ускорения? нормальная
составляющая
ускорения? Каковы
их модули?
• Возможны
ли движения, при которых отсутствует
нормальное ускорение? тангенциальное
ускорение? Приведите
примеры.
• Что
называется угловой скоростью? угловым
ускорением? Как определяются их
направления?
• Какова
связь между линейными и угловыми
величинами?
Задачи
1.1.
Зависимость
пройденного телом пути от времени
задается уравнением s
= A+Вt+Сt2+Dt3
(С
= 0,1 м/с2,
D
= 0,03 м/с3).
Определить: 1) через какое время после
начала движения ускорение а тела будет
равно 2 м/с2;
2) среднее ускорение <а>
тела за этот промежуток времени. [ 1) 10
с; 2) 1,1 м/с2]
1.2.
Пренебрегая сопротивлением воздуха,
определить угол, под которым тело брошено
к горизонту, если максимальная высота
подъема тела равна 1/4 дальности его
полета. [45°]
1.3.
Колесо
радиуса R
=
0,1 м вращается так, что зависимость
угловой скорости от времени задается
уравнением
= 2At+5Вt4
(A=2
рад/с2
и B=1
рад/с5).
Определить полное ускорение точек обода
колеса через t=1
с после начала вращения и число оборотов,
сделанных колесом за это время. [а =
8,5 м/с2;
N
= 0,48]
14
1.4.
Нормальное ускорение точки, движущейся
по окружности радиуса r=4
м,
задается уравнением аn=А+-Bt+Ct2
(A=1
м/с2,
В=6
м/с3,
С=3
м/с4).
Определить: 1) тангенциальное ускорение
точки; 2) путь, пройденный точкой за время
t1=5
с после начала движения; 3) полное
ускорение для момента времени t2=1
с. [ 1) 6 м/с2;
2) 85 м; 3) 6,32 м/с2]
1.5.
Частота
вращения колеса при равнозамедленном
движении за t=1
мин
уменьшилась от 300 до 180 мин-1.
Определить: 1) угловое ускорение колеса;
2) число полных оборотов, сделанных
колесом за это время. [1)
0,21 рад/с2;
2) 360]
1.6.
Диск
радиусом R=10
см вращается вокруг неподвижной оси
так, что зависимость угла поворота
радиуса диска от времени задается
уравнением =A+Bt+Ct2+Dt3
(B
= l рад/с,
С=1
рад/с2,
D=l
рад/с3).
Определить для точек на ободе колеса к
концу второй секунды после начала
движения: 1) тангенциальное ускорение
а;
2) нормальное ускорение аn;
3) полное ускорение а. [ 1) 0,14 м/с2;
2) 28,9 м/с2;
3) 28,9 м/с2]
Соседние файлы в папке Трофимова
- #
- #
- #
- #
- #
- #