Как найти угловое ускорение шкива

Принцип возможных
перемещений дает общий метод решения
задач статики. Принцип Даламбера
использует методы статики для решения
задач динамики. Применяя два эти принципа
одновременно, можно получить общий
метод решения задач динамики.

При движении
механической системы с идеальными
связями сумма элементарных работ
заданных сил и сил инерции на любом
возможном перемещении системы равна
нулю
(18.1) или.
(18.2)

Рисунок 60

При наличии сил
трения их нужно причислить к задаваемым
силам. С помощью общего уравнения
динамики можно определять силы по
заданному движению (прямая задача
динамики) или определять движение по
заданным силам (обратная задача динамики).
Для решения задач с помощью общего
уравнения динамики необходимо:

1. показать на схеме
   активные силы и реакции неидеальных
   связей (например, силы трения);

2. добавить к активным
   силам силы инерции;

3. дать возможное
   перемещение точкам системы, выражая
   перемещение всех точек через возможное
   перемещение одной из точек системы;

4. составить общее
   уравнение динамики, вычисляя сумму
   элементарных работ всех активных сил
   и сил инерции на возможном перемещении
   точки их приложения;

5. решить полученное
   уравнение в соответствии с условием
   задачи

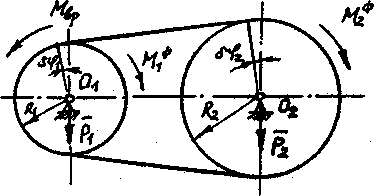
ПРИМЕР 26.

К шкиву 1 ременной
передачи (рис. 61) приложен вращающий
момент М_вр=3Нм.
Массы шкивов равномерно распределены
по их ободам и соответственно равны
m₁=1кг
и m₂=2кг.
Радиус шкива 1 R₁=0,1м.
Пренебрегая трением, определить угловое
ускорение шкива 1.

Рисунок 61

РЕШЕНИЕ.

1. Массы шкивов
равномерно распределены по их ободам
и пропорциональны размерам:

;(1)

,

где
—
плотность материала шкивов. Используя
выражение (1), можно определить размер
второго шкива

;

м.

2. Силы инерции
точек шкивов приводятся к моментам сил
инерции, которые соответственно равны
;
(2)

.
(3)

Угловые ускорения
колес обратно пропорциональны их
радиусам, т.е.

или
.
Тогда.
(4)

3. Запишем общее
уравнение динамики
.
(5) Дадим системе возможное
перемещение: шкив 1 повернется на угол,
шкив 2—на угол.
Вычислим работу активных сил и сил
инерции на возможном перемещении системы.
(6) Выразим возможное
перемещениешкива 2 через:.
Тогда, с учетом (2) и (4), получим:.
(7) Так как,
приравниваем нулю выражение,
из которого находим угловое ускорение
шкива 1:с^-2.

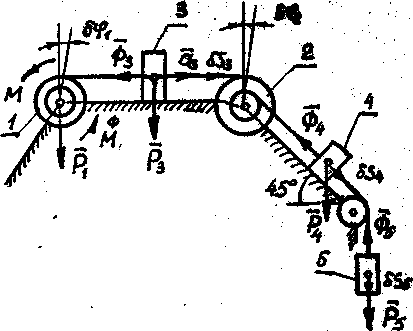
ПРИМЕР 27.

Механическая
система состоит из однородных ступенчатых
шкивов 1 и 2, обмотанных нитями, грузов
3, 4 и 5, прикрепленных к этим нитям, и
невесомого блока 2. Система движется в
вертикальной плоскости под действием
сил тяжести и пары сил с моментом М=12Нм.,
приложенных к шкиву 1. Радиусы ступеней
шкива равны: R₁=0,2м,
r₁=0,1м,
а шкива 2—R₂=0,3м
и r₂=0,15м;радиус
инерции шкива 1 относительно оси вращения
=0,1м
(рис. 62). Пренебрегая трением, определить
ускорение груза 3, если Р₁=30Н,
Р₃=40Н,
Р₄=20Н,
Р₅=10Н.

РЕШЕНИЕ.

1. Рассмотрим
движение механической системы, состоящей
из тел 1, 2, 3, 4, 5, соединенных нитями.
Система имеет одну степень свободы.
Связи, наложенные на тела системы,
относятся к идеальным. Для определения
ускорения груза 3 применим общее уравнение
динамики:

Рисунок 62

,

(1) где
—
сумма элементарных работ активных сил;

—
сумма элементарных работ сил инерции.

2. Покажем активные
силы:
,,,и пару сил с моментом М. Зададим направление
ускорения груза 3 и покажем силы инерции,,и момент сил инерции:;

;

;

(2)

.

3. Дадим системе
возможное перемещение и составим
уравнение (1).
.
Выразим все перемещения через:;

;

;
(3)

.
С учетом выражений
(2) и (3) уравнение (1) примет вид:
(4) или.
(5)

Выразим
,,через искомое ускорение груза:

;

;.
(6) Так как,
с учетом (6) приравниваем нулю выражение
(5):.
Откуда определим ускорениегруза 3:.

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
   
2. если задан угол поворота φ за единицу времени:
   
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
   

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

Содержание:

1. Поступательное и вращательное движение твердого тела
2. Порядок решения задач на вращательное движение твердого тела
3. Примеры решения задач
4. Задания темы К2
5. Пример решения задания темы К2
6. Поступательное движение твердого тела
7. Вращательное движение твердого тела
8. Равномерное и равнопеременное вращательное движение тела
9. Скорость и ускорение точек вращающегося тела
10. Примеры решения задач

Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе. Одинаковыми остаются при поступательном движении перемещение, траектория, путь, скорость, ускорение. 3. Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой перпендикулярной плоскостям этих окружностей.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Поступательное и вращательное движение твердого тела

Краткие сведения по теории:

Поступательным называется такое движение твердого тела по траектории произвольной формы, при котором любая прямая, проведенная в этом теле, при
перемещении вместе с телом остается параллельной самой себе.

Главное свойство поступательного движения тела определяется теоремой, согласно которой при поступательном движении тела все его точки движутся по одинаковым (при
наложении совпадают) траекториям и имеют в каждый момент времени одинаковые векторы скоростей и одинаковые векторы ускорений:

Таким образом, поступательное движение твердого тела полностью определяется движением любой его точки, движение которой было рассмотрено в теме К1.
 

Вращательным называется такое движение твердого тела, при котором все его точки, что принадлежат определенной неизменно связанной с телом прямой,
которую называют осью вращения, остаются неподвижными, а траекториями остальных точек тела будут концентрические круги в плоскостях, перпендикулярные оси вращения, и с центрами, которые лежат на этой оси.

Положение тела при его вращении вокруг оси относительно исходного положения в любой момент времени определяется углом поворота тела. Таким образом,
кинематическим уравнением вращательного движения тела является
зависимость от времени его угла повороту 

Единицей угла поворота тела в системе СИ является радиан:

Кинематическими характеристиками вращательного движения твердого тела являются  его угловая скорость  и угловое ускорение 
 

Угловая скорость  характеризует изменение угла поворота тела за единицу времени и в настоящее момент времени равен первой производной от угла поворота по времени:

Единицей угловой скорости в системе СИ является радиан разделен на секунду: 

Знак угловой скорости  определяет направление вращения тела. Если то с положительного направления оси вращения движение тела будет видно против хода часовой стрелки, а если  то — наоборот.

В технике угол поворота пропорционален количеству оборотов  что сделало тело за некоторый промежуток времени. В этом случае угол поворота тела  в радианах можно найти по зависимости:

Угловую скорость вращения тела часто задают числом оборотов за одну минуту 

Угловую скорость в этом случае определяют по формуле:

где n — подставляют в об/мин.

Угловое ускорение  характеризует изменение угловой скорости тела со временем и в данный момент времени,  численно равно первой производной от угловой скорости или второй производный от угла поворота по времени:

Единицей углового ускорения в системе СИ является радиан разделен на секунду в квадрате:

Знак углового ускорения   зависит от характера вращения тела. Если вращение тела ускоренное, то знаки  и  совпадают, а если вращение замедленное, то знаки  и разные.

В случае равномерного вращательного движения тела его угловая скорость будет устойчивой  а угловое ускорение равно нулю 

Угол поворота тела в этом случае вычисляется по формуле :

где  начальный угол поворота тела при t= 0.

В случае равномерно переменного вращательного движения тела его угловое ускорение будет постоянным 

Угловая скорость и угол поворота тела в этом случая вычисляются по формулам:

где  соответственно угол поворота тела и угловая
скорость в момент времени t=0.

Линейной или круговой скоростью любой точки М  тела, вращающегося  есть произведение  угловой скорости тела на расстояние ОМ от оси вращения до
этой точки (радиус круга, по которому движется точка):

Направленная линейная скорость (рис. К2.1) по касательной к окружности (перпендикулярно  к радиусу), что пишет точка тела, которое вращается, в сторону движения тела (в сторону угловой скорости).
 

Полное ускорение произвольной точки М тела, что вращается, и которая не лежит на оси
вращения, можно разложить на две составляющие по осям природной системы координат  и n:

тангенциальное (или касательное) ускорение, которое направлено по касательной к траектории точки тела (перпендикулярно к  радиусу) в сторону углового ускорения  и определяется по формуле:

и нормальное (или центростремительное) ускорение, которое направлено вдоль радиуса к оси вращения тела и определяется по формуле:

Полное ускорение точки соответственно равно:

Порядок решения задач на вращательное движение твердого тела

При решении задач на вращение твердого тела вокруг неподвижной оси рекомендуется соблюдать такую последовательность:

1. Выбрать систему координат таким образом, чтобы одна из осей (как правило ось z) совпадала с осью вращения.

2. Составить уравнение вращательного движения твердого тела (зависимость угла поворота  от времени t).

3. Дифференцируя по времени зависимость для угла поворота, определить величину угловой скорости 

4. Определить вторую производную от угла поворота по времени, найти величину углового ускорения 

5. Воспользовавшись угловой скоростью определить линейную скорость нужной точки тела и ее нормальное ускорение 
6. Воспользовавшись угловым ускорением  определить касательное ускорение  нужной точки тела.
7. Найти величину и направление полного ускорения этой точки.

Примеры решения задач

Задача 1

Вал начинает вращаться с постоянным ускорением с состояния покоя. За первые 5 секунд вал делает N = 12,5 оборота.

Определить угловую скорость вала в конце промежутка времени, которое рассматривается.
 

Решение. При равноускоренном вращении тела угловая скорость   меняется по закону:

Поскольку по условию задачи  то 

Таким образом, для определения угловой скорости вала надо найти его угловое ускорение 

Угол поворота тела при равноускоренном вращении определяется по формуле:

Поскольку  и  то

Угол поворота вала за число оборотов N равняется:

Тогда:

Подставив выражение для  в формулу для  

С учетом числовых данных:

Ответ:  

Задача 2

Шкив ременной передачи начинает вращаться из состояния спокойствия с устойчивым угловым ускорением и через 10 минут от начала движения имеет угловую скорость, которая соответствует 120 об/мин.

Определить число оборотов N, которые сделал шкив  за 10 минут.
 

Решение. Число оборотов N можно определить, если известен угол  на который вернулся шкив за 10 минут.
Поскольку то 
Угол поворота тела при равноускоренном вращении равен:

Поскольку  и  то

Таким образом:

Для определения углового ускорения  воспользуемся формулой для угловой скорости при равноускоренном вращении тела:

Поскольку то 
С другой стороны, из-за числа оборотов в минуту

Тогда:

Если подставить  в формулу для N, получим:

При n =120 об/мин и t=600 с, найдем:

Ответ: N = 600 об.

Задача 3

Колесо радиусом R = 0, 2 м начинает вращаться с состояния покоя с постоянным ускорением. Через t = 10 c от  начала движения точка, лежащая на ободе колеса, имеет линейную скорость V = 10 м/с.
 

Определить скорость, нормальное и касательное ускорение точек обода колеса в момент времени  от начала движения.
 

Решение. Для определения   и  воспользуемся зависимостями вращательного движения:

Таким образом, для определения  и  надо найти угловую скорость и угловое ускорение колеса в момент времени  

Определим угловую скорость в момент времени 

Поскольку при  скорость точки обода колеса то:

При равноускоренном вращении тела  угловая скорость меняется по закону:

Поскольку  то 
В момент времени   угловая скорость тела соответственно будет равняться:

Тогда:

На рис. 1 показаны направления определенных векторов.

Поскольку  и  направление  и  совпадают. Нормальное ускорение
 направлено в центр вращения шкива.
 

Ответ: 

Задача 4

Вращательное движение вала радиусом  вызывается грузом P, подвешенным к нитке, которая намотана на вал (рис.1). Груз Р движется вертикально по закону где  расстояние от тела до точки совпадения нити с поверхности вала в метрах, t — время в секундах.
 

Определить угловую скорость  и угловое ускорение  вала и полное ускорение  точки на поверхности вала в произвольный момент времени t.
 

Решение. Величина скорости точки M обода вала равняется скорости нити,
что сматывается с поверхности вала при опускании груза P, а также скорости груза Р. Скорость же груза P определим путем дифференцирования его закона движения:

Касательное ускорение  точки M равняется ускорению груза P, поскольку с этим ускорением сбегает нить с поверхности вала:

По известным линейной скоростью и касательным ускорением точки M поверхности вала можно определить угловую скорость  и угловое ускорение  вала:

Тогда, нормальное ускорение точки M будет равняться:

Для полного ускорения расположенной на M точки поверхности вала, получим:

Ответ: 

 

Задача 5

Передача состоит из трех шкивов: 1, 2 и 3 (рис. 1). Передача вращательного движения от первого шкива на второй происходит за счет сил трения в точке A соприкосновения
шкивов. Причем, вращение происходит без проскальзывания одного шкива относительно второго. Второй и третий шкив жестко насажены на один вал (ось вала ).
Угол поворота первого шкива меняется по закону:

 

Определить угловые скорости и угловые ускорения шкивов передачи и скорости и ускорения точек касания шкивов в момент времени если радиусы
шкивов: 

Решение. Определим угловую скорость и угловое ускорение шкива 1:

В момент времени 

Знак минус при значении  указывает на то, что направление угловой скорости в момент времени  в противоположную сторону от положительного
направления отсчета угла  Поскольку знаки  и  разные, то угловое
ускорение направлено в противоположную сторону от угловой скорости.

На рис. 1 положительное направление отсчета угла  выбрано против хода часовой стрелки. Тогда направление  будет за ходом часовой стрелки, а  против хода часовой стрелки. По модулю же  и соответственно равны:

Скорость и ускорение точки А соприкосновения первого шкива определим по формулам:

Скорость направленная (рис. 1) перпендикулярно к радиусу 
по направлению угловой скорости  Касательное ускорение  направленное тоже
перпендикулярно  к  но по направлению  Нормальное ускорение направлено вдоль радиуса  к центру вращения 

Поскольку шкивы 1 и 2 вращаются без проскальзывания в точке соприкосновения, то скорость и касательное ускорение точки А второго шкива будут равняться скорости и касательному ускорению точки А первого шкива, то есть:

Тогда:

Вычислим нормальное ускорение точки А второго шкива:

Направленное нормальное ускорение точки А второго шкива вдоль радиуса 
в центр вращения 

Направление угловой скорости второго шкива определяется направлением скорости точки А, то есть будет против хода часовой стрелки. Направление же углового ускорения определяется направлением касательного ускорения, то есть будет по ходу часовой стрелки.

Полные ускорения точек соприкосновения шкивов:

Поскольку шкивы 2 и 3 жестко насажены на один вал, то их угловые скорости и угловые ускорения будут одинаковыми, то есть:

 

Ответ: 

 

Задания темы К2

Механизм (рыс.К2.2), состоит из зубчатой рейки 1, которая в зацеплении со ступенчатым колесом 3, или груза 1, который прикреплен к нитке, которая намотана на колесо 2. Колеса 2 и 3 связаны между собой либо ременной передачей, либо находятся в зацеплении. Радиусы ступенчатых колес соответственно равны: для колеса 2 — меньше колесо больше колесо  для колеса 3 — меньше колесо больше колесо  Если колеса 3 и 2 одноступенчатые, то их радиусы равны  и  кроме схемы 0, для которой  На ободе одного из колес показана точка М.

В таблице К3 задан закон движения или одного из колес 2 или 3, или груза 1. Закон движения колес задается в виде или угла поворота: или изменения угловой скорости: Закон движения груза задается в виде или перемещения  или изменения скорости 

За положительное направление для отсчета  и  для которых закон движения задан, принять движение против хода часовой стрелки, а для  скорости груза и рельсы
1 — движение вниз. (В законах движения: в метрах;  в метрах в секунду, в радианах; t — в секундах.)
 

Определить в момент времени  величины, что указаны в соответствующей графе таблицы К3.

Схема механизма выбирается из рис. К2.2 по первой цифре шифра, а номер условия из таблицы К3 по второй.

Замечания. Эта задача на исследование простых видов движения твердого тела: поступательного и вращательного. При решении задачи необходимо иметь в виду, что в случае зубчатого зацепления двух колес точки зацепления каждого из колес имеют одинаковые скорости и одинаковые тангенциальные ускорения. В случае же ременной передачи скорости всех точек ремня и точек   колес за величиной одинаковые (принимается, что ремень не скользит по колесу).

Пример решения задания темы К2

Рейка 1 (рис. К2.3) движется в вертикальных направляющих по закону 
Колесо 3 радиуса  находится в зацеплении с одной стороны с рейкой 1, а со второй — с малым колесом радиуса  который сблокирован с шкивом 2 радиуса  На шкив
намотана нерастяжимая нить с грузом 4 на конце.

Дано: 

Определить: 

1. По известному закону движения рельсы 1 определим скорость точки С1, которая ей принадлежит:

В момент времени 

2. Поскольку рейка 1 и колесо 3 находятся в зацеплении, то  и, учитывая то, что  линейная скорость точки на ободе колеса, что вращается  3 получим:

Откуда:

Поскольку колеса 2 и 3 тоже находятся в зацеплении в точке К то  С другой стороны:

или, с учетом выражения для  получим:

Из этого уравнения с учетом значения для  найдем 

Подставив время в выражения для и   получим:

4. Определим ускорение точки С1 рельсы:

5. Ускорение точки С1 рельса равно касательному ускорению точки С3 на ободе колеса 3 (поскольку они находятся в зацеплении), то есть:

Поскольку   найдем угловое ускорение  колеса 3:

Аналогично определяем угловое ускорение  колеса 2, исходя из того, что то есть:

В момент времени   получим:

6. Определим нормальное и касательное ускорение точки М, лежащей на внешнем ободе колеса 2 (при 

Для полного ускорения точки М в момент времени  получим:

7. Учитывая то, что  находим ускорение груза 4:

Векторы ускорения точек и направления угловых ускорений показаны на рис. К2.5.

Ответ:  

Поступательное движение твердого тела

Поступательным называется такое движение твердого тела, при котором любая прямая, неизменно связанная с телом, все время остается параллельной своему изначальному положению.

Для твердого тела (рис.2.1) прямая , соединяющая две произвольные его точки, во время поступательного движения не изменяется ни по длине, ни по направлению. Это значит, что при поступательном движении точки и тела имеют одинаковые траектории (при наложении совпадают) и в каждый момент времени одинаковыми будут их скорости и ускорения, то есть:

Таким образом, поступательное движение твердого тела полностью определяется движением любой точки этого тела, то есть задача определения кинематических характеристик поступательного движения твердого тела сводится к задаче кинематики точки.

Вращательное движение твердого тела

Вращательным движением называется такое движение твердого тела, при котором любые две точки тела остаются неподвижными.

Если закрепить две точки тела и (рис.2.2), то будут неподвижными все точки прямой , которая называется осью вращение.

Траекториями всех остальных точек тела , например , будут окружности с центрами на оси вращения.

Проведем через ось вращения (рис.2.3) две плоскости: одну неподвижную — , а вторую плоскость , жестко свяжем с телом, которое вращается. Двугранный угол между этими двумя плоскостями однозначно определяет положение вращающегося тела.

Для определения знака угла на оси вращения выбирают положительное направление (на рис.2.3 – вверх). Угол считается положительным, если с положительного направления оси вращения угол относительно неподвижной плоскости отложен против хода часовой стрелки и отрицательный, если по ходу.

Когда тело вращается, угол непрерывно изменяется с временами. Таким образом, для полной характеристики вращательного движения надо задать уравнение вида:

Уравнение (2.1) называется уравнением вращательного движения тела.

Изменение угла поворота тела с течением времени характеризует угловая скорость .

Мгновенная угловая скорость является первой производной от угла поворота по времени:

Единицей измерения угловой скорости является радиан разделен на секунду и обозначается как , или , или .

Направлена угловая скорость в сторону мгновенного вращения тела и , если совпадает с направлением отсчета угла , и , если противоположна направлению отсчета .

В технике угол поворота пропорционален количеству оборотов , что сделало тело за некоторый промежуток времени. В этом случае угол поворота тела в радианах можно найти по зависимости:

Угловую скорость вращения тела часто задают числом оборотов за одну минуту (об/мин).

Угловую скорость в этом случае определяют по формуле:

где  — подставляют в об/мин.

Изменение угловой скорости с течением времени характеризует угловое ускорение .

Мгновенное угловое ускорение определяется как первая производная от угловой скорости по времени, или вторая производная от угла поворота тела:

Единицей измерения углового ускорения является радиан, разделен на секунду в квадрате, и обозначается , или , или .

Направлено угловое ускорение по направлению угловой скорости, если знаки и совпадают, и против направления угловой скорости, если знаки и различны.

Равномерное и равнопеременное вращательное движение тела

В случае равномерного вращательного движения тела его угловая скорость будет постоянной , а угловое ускорение равно нулю

Угол поворота тела в этом случае вычисляется по формуле:

где — начальный угол поворота тела при .

В случае равномерно переменного вращательного движения тела его угловое ускорение будет постоянным

Угловая скорость и угол поворота тела в этом случае вычисляются по формулам:

где  — соответственно угол поворота тела и угловая скорость в момент времени .

Скорость и ускорение точек вращающегося тела

Если для вращающегося тела известны угловая скорость и угловое ускорение , то можно найти скорость и ускорение любой его точки.

Скорость точки вращающегося тела равна произведению угловой скорости тела на расстояние от точки к оси вращения:

Вектор скорости точки направлен под прямым углом к радиусу вращения (рис.2.4) в сторону вращения тела (в сторону угловой скорости ).

Поскольку точка вращающегося тела движется по криволинейной траектории (окружности с радиусом кривизны ), то ускорение точки можно разложить на две составляющие: тангенциальную (касательную) и нормальную (центростремительную) (рис.2.4).

Подставив в формулы для  и (1.14) выражение для (2.9) получим:

Нормальное ускорение направлено от точки вдоль радиуса к центру вращения. Касательное ускорение направлено перпендикулярно радиусу в сторону углового ускорения .

Полное же ускорение точки соответственно равно:

Примеры решения задач

Задача №1

Вал начинает вращаться с постоянным ускорением из состояния покоя. За первые 5 секунд вал делает 12,5 оборота.

Определить угловую скорость вала в конце промежутка времени, что рассматривается.

Решение. При равноускоренном вращении тела угловая скорость изменяется по закону: 

Поскольку по условию задачи , то 

Таким образом, для определения угловой скорости вала надо найти его угловое ускорение .

Угол поворота тела при равноускоренном вращении определяется по формуле:

Поскольку  и , то

Угол поворота вала за число оборотов равен:

Тогда: 

Подставив выражение для в формулу для получим:

С учетом числовых данных:

Ответ: 

Задача № 2

Шкив ременной передачи начинает вращаться из состояния покоя с постоянным угловым ускорением и через 10 минут от начала движения имеет угловую скорость, которая соответствует 120 об/мин.

Определить число оборотов , которые сделал шкив за 10 минут.

Решение. Число оборотов можно определить, если известен угол , на который вернулся шкив за 10 минут.

Поскольку , то 

Угол поворота тела при равноускоренном вращении равен:

Поскольку и , то 

Таким образом:

Для определения углового ускорения  воспользуемся формуле для угловой скорости при равноускоренном вращении тела:

Поскольку , то 

С другой стороны, через число оборотов в минуту

Тогда:

Если подставить в формулу для , получим:

При об/мин и , найдем:

Ответ: 

Задача №3

Колесо радиусом начинает вращаться из состояния покоя с постоянным ускорением. Через от начала движения точка, лежащая на ободе колеса, имеет линейную скорость

Определить скорость, нормальное и касательное ускорение точек обода колеса в момент времени от начала движения.

Решение. Для определения и воспользуемся зависимостями вращательного движения:

Таким образом, для определения и надо найти угловую скорость и угловое ускорение колеса в момент времени .

Определим угловую скорость в момент часа . Поскольку при скорость точки обода колеса , то:

При равноускоренном вращении тела угловая скорость изменяется по закону:

Поскольку , то

В момент времени угловая скорость тела соответственно будет равна:

Тогда:

На рис. 2.5. показаны направления определенных векторов.

Поскольку и , то направления и совпадают. Нормальное же ускорение направлено в центр вращения шкива.

Ответ:  

Задача№4

Вращательное движение вала радиусом вызывается грузом , что подвешен к нити, которая намотана на вал (рис.2.6). Груз движется вертикально по закону , где — расстояние от тела к точке совпадения нити с поверхности вала в метрах, — время в секундах. 

Определить угловую скорость и угловое ускорение вала и полное ускорение точки на поверхности вала в произвольный момент времени .

Решение. Величина скорости точки обода вала равна скорости нити, сматываемой с поверхности вала при опускании груза , а также скорости груза . Скорость же груза определим путем дифференцирования его закона движения:

Касательное ускорение точки равна ускорению груза , поскольку с этим ускорением совпадает нить с поверхности вала:

По известным линейной скорости и касательному ускорению точки поверхности вала можно определить угловую скорость и угловое ускорение вала :

Тогда, нормальное ускорение точки будет равно:

Для полного ускорения точки , лежащей на поверхности вала, получим:

Ответ: 

Задача №5

Передача состоит из трех шкивов: 1, 2 и 3 (рис.2.7). Передача вращательного движения от первого шкива на второй происходит за счет сил трения в точке прикосновения шкивов. Причем, вращение происходит без проскальзывания одного шкива относительно второго. Второй и третий шкив жестко насажены на один вал (ось вала ). Угол поворота первого шкива меняется по закону: 

Определить угловые скорости и угловые ускорения шкивов передачи и скорости и ускорения точек касания шкивов в момент времени , если радиусы шкивов:

Решение. Определим угловую скорость и угловое ускорение шкива 1:

В момент времени :

Знак минус при значении указывает на то, что направление угловой скорости в момент времени в противоположную сторону от положительного направления отсчета угла . Поскольку знаки и разные, то угловое ускорение направлено в противоположную сторону от угловой скорости.

На рис 2.7 положительное направление отсчета угла выбрано против хода часовой стрелки. Тогда направление будет по ходу часовой стрелки, а против хода часовой стрелки. По модулю же и соответственно равны:

Скорость и ускорение точки прикосновения первого шкива определим по формулам:

Скорость направлена (рис 3.7) перпендикулярно радиусу по направлению угловой скорости . Касательное ускорение направлено тоже перпендикулярно , только по направлению . Нормальное ускорение направлено вдоль радиуса  к центру вращения .

Поскольку шкивы 1 и 2 вращаются без проскальзывания в точке касания, то скорость и касательное ускорение точки второго шкива будут равняться скорости и касательному ускорению точки первого шкива, то есть:

Тогда: 

Вычислим нормальное ускорение точки второго шкива:

Направлено нормальное ускорение точки второго шкива вдоль радиуса к центру  вращения .

Направление угловой скорости второго шкива определяется направлением скорости точки , то есть будет против хода часовой стрелки. Направление же углового ускорения определяется направлением касательного ускорения, то есть будет по ходу часовой стрелки.

Полные ускорения точек соприкосновения шкивов:

Поскольку шкивы 2 и 3 жестко насажены на один вал, то их угловые скорости и угловые ускорения будут одинаковыми, то есть:

Ответ:  

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Произвольная пространственная система сил
12. Плоская система сходящихся сил
13. Пространственная система сходящихся сил
14. Равновесие тела под действием пространственной системы сил
15. Естественный способ задания движения точки
16. Центр параллельных сил
17. Параллельные силы
18. Система произвольно расположенных сил
19. Сосредоточенные силы и распределенные нагрузки
20. Кинематика
21. Кинематика твердого тела
22. Движения твердого тела
23. Динамика материальной точки
24. Динамика механической системы
25. Динамика плоского движения твердого тела
26. Динамика относительного движения материальной точки
27. Динамика твердого тела
28. Кинематика простейших движений твердого тела
29. Общее уравнение динамики
30. Работа и мощность силы
31. Обратная задача динамики
32. Плоскопараллельное (плоское) движение твёрдого тела
33. Сферическое движение твёрдого тела
34. Движение свободного твердого тела
35. Сложное движение твердого тела
36. Сложное движение точки
37. Плоское движение тела
38. Статика твердого тела
39. Равновесие составной конструкции
40. Равновесие с учетом сил трения
41. Центр масс
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки