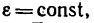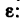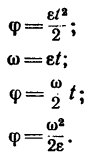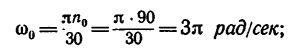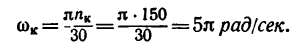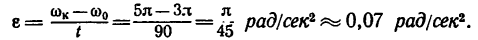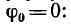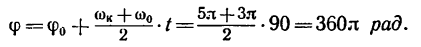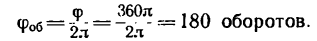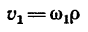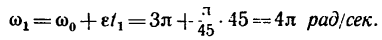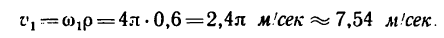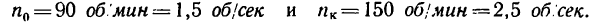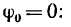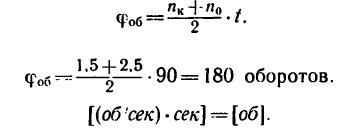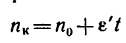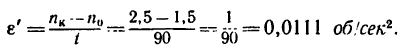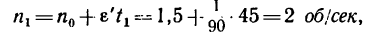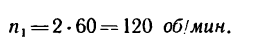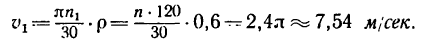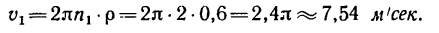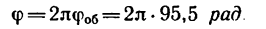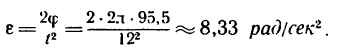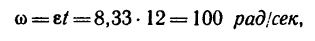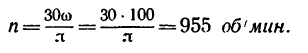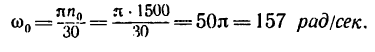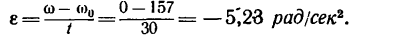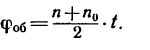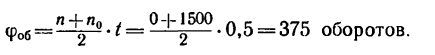Как найти угловое ускорение торможение

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

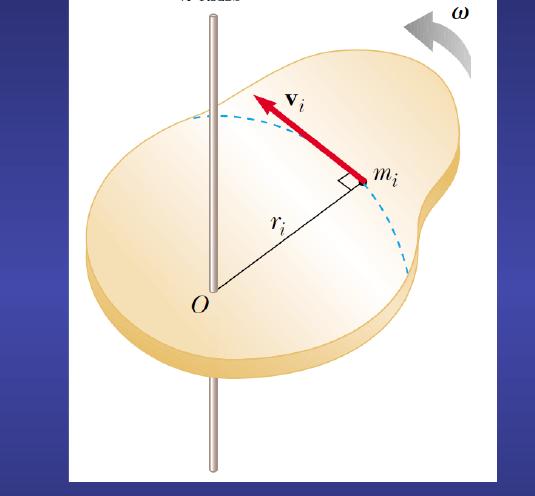
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

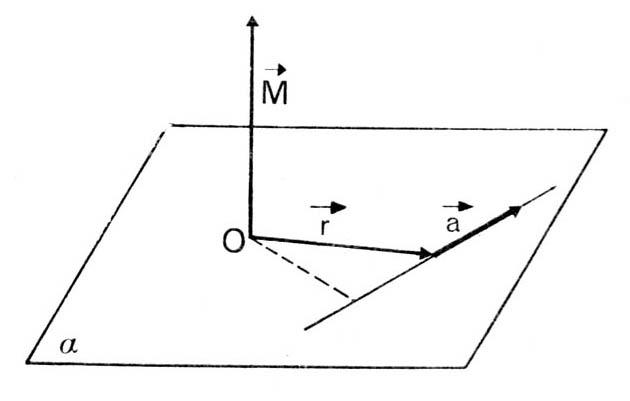
Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
   
2. если задан угол поворота φ за единицу времени:
   
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
   

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

Равнопеременное вращательное движение:

Вращательное движение с переменной угловой скоростью называется неравномерным. Если же угловое ускорение

и уравнение, выражающее угловую скорость тела в любой момент времени,

представляют совокупность основных формул вращательного равнопеременного движения тела.

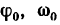
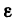
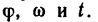
В эти формулы входят всего шесть величин: три постоянных для данной задачи и и три переменных Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.

Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.

Исключим из (1) и (2) угловое ускорение

Исключим из (1) и (2) время t:

В частном случае равноускоренного вращения, начавшегося из состояния покоя, 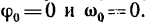Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:

Задача №1

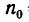
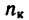
Маховик, вращающийся с угловой скоростью = 90 об/мин, с некоторого момента начинает вращаться равноускоренно и через 1,5 мин достигает угловой скорости = — 150 об/мин. Определить угловое ускорение маховика. Сколько всего оборотов делает маховик за 1,5 мин? Какую скорость имеют точки на цилиндрической поверхности маховика через 45 сек после начала равноускоренного движения, если диаметр маховика 1,2 м?

Решение 1. Все угловые величины выражаем в радианном измерении.

1.    Если 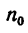=90 об/мин, то

если 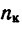=150 об/мин, то

2.    Из уравнения (2) находим угловое ускорение, учитывая, что изменение угловой скорости от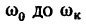 происходит за t=1,5 мин =  90 сек:

3.    Определяем из формулы (3) угол поворота тела за t = 1,5 мин = 90 сек, принимая

4.    Находим, какому числу оборотов соответствует этот угол поворота:

Следовательно, за время равноускоренного вращения маховик успеет совершить 180 оборотов.

5.    Прежде чем найти по формуле

скорость точек на ободе маховика в момент времени t=45 сек после начала равноускоренного вращения, необходимо найти угловую скорость маховика 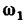в этот момент:

Зная, что 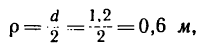получаем

Решение 2—угловые величины выражаются в оборотах, а время — в сек (t=1,5 мин — 90 сек).

1.    Выражаем данные угловые скорости в об/сек.

2.    Представим формулу (3) в ином виде, приняв
Тогда

3.    Обозначив 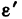—угловое ускорение, выраженное через обороты, формулу (2) можно представить в виде

и тогда

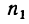
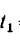
4.    Найдем — угловую скорость маховика через = 45 сек после начала равноускоренного вращения:

что соответствует

Теперь находим при этой угловой скорости маховика скорость точек на его ободе:

Если же 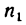выражено в об/сек, то

Задачу можно решить и не переводя заданное время из минут в секунды, т. е. решить при заданных числовых величинах

Этот вариант решения рекомендуем выполнить самостоятельно

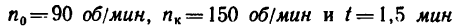
Задача №2

Вал, вращающийся равноускоренно из состояния покоя, в первые 12 сек совершает 95,5 оборота. С каким угловым ускорением вращается вал и какую угловую скорость он приобретает?

Решение.

1.    Угловое перемещение за время t=12 сек равноускоренного движения составляет

2.    Из формулы (5) находим угловое ускорение вала:

3.    К концу 12-й секунды вал приобретает угловую скорость [см. формулу (6)):

что соответствует

Задачу можно решить и в другой последовательности, а также выражая величины через обороты.

Задача №3

Колесо, вращающееся со скоростью 1500 об/мин, при торможении начинает вращаться равнозамедленно и через 30 сек останавливается. Определить угловое ускорение и число оборотов колеса с момента начала торможения до остановки.

Решение.

1.    Выразим начальную угловую скорость в рад/сек:

Найдем угловое ускорение из формулы (2):

2.    Представим формулу (3) в виде

Тогда число оборотов вала за t = 30 сек — 0,5 мин

Угловое ускорение – что это?

Угловое ускорение (varepsilon) – физическая величина, характеризующая изменение угловой скорости при движении тела.

Единица измерения: (lbrackvarepsilonrbrack=frac1{с^2}) или (с^{-2})

Угловая скорость

Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Угловая скорость (omega) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.

При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).

Вектор угловой скорости направлен вдоль оси вращения.

Основные формулы для вычисления угловой скорости

Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):

1. (omega=frac nt), где (n) – количество оборотов за единицу времени (t).
2. (omega=fracvarphi t), где (varphi) – угол поворота, (t) – время, за которое он совершен.
3. (omega=frac{2pi}T), где (Т) – период обращения (время, за которое тело/точка совершает один оборот).
4. (omega=2pinu), где (nu) – числом оборотов в единицу времени.

Единица измерения угловой скорости в СИ: (lbrackomegarbrack=frac{рад}с)

Связь между угловой скоростью и нормальным (центростремительным) ускорением

Центростремительное (нормальное) ускорение (a_n) – это составляющая полного ускорения, которая характеризует изменение направления вектора скорости при криволинейном движении. Другим компонентом полного ускорения является тангенциальное ускорение, оно характеризует изменение величины скорости.

Центростремительное ускорение определяется по формуле:

 (a_n=frac{V^2}R),

где (V) – скорость движения, (R) – радиус окружности.

Единица измерения в СИ: (lbrack a_nrbrack=frac м{с^2})

Итак, формула связывающая эти две величины:

(a_n=omega^2R)

Основные формулы для расчета углового ускорения

Угловое ускорение маховика

(varepsilon=fracomega t=frac{2pi n}t), где (n) – количество оборотов за единицу времени (t).

Среднее угловое ускорение

Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.

(leftlanglevarepsilonrightrangle=frac{triangleomega}{triangle t})

Тангенциальное ускорение

Тангенциальным (касательным) ускорением (a_tau) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.

(a_tau=varepsilon r), где (varepsilon) – угловое ускорение, (r) –  радиус кривизны траектории в заданной точке.

Мгновенное угловое ускорение

Мгновенное угловое ускорение (alpha) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.

(alpha=tg(varepsilon)=frac{;domega}{dt}=frac{d^2phi}{dt^2})

Вращение тел является одним из важных типов механического движения в технике и природе. В отличие от линейного перемещения, оно описывается собственным набором кинематических характеристик. Одной из них является угловое ускорение. Охарактеризуем эту величину в статье.

Движение вращения

Прежде чем говорить об угловом ускорении, опишем тип движения, к которому оно применяется. Речь идет о вращении, которое представляет собой перемещение тел по круговым траекториям. Чтобы вращение происходило, необходимо выполнение некоторых условий:

• наличие оси или точки вращения;
• наличие центростремительной силы, которая бы удерживала на круговой орбите тело.

Примерами этого типа движения являются различные аттракционы, например карусель. В технике вращение проявляет себя при движении колес и валов. В природе самым ярким примером этого типа движения является вращение планет вокруг собственной оси и вокруг Солнца. Роль центростремительной силы в названных примерах играют силы межатомного взаимодействия в твердых телах и гравитационное взаимодействие.

Кинематические характеристики вращения

К этим характеристикам относятся три величины: угловое ускорение, угловая скорость и угол поворота. Будем обозначать их греческими символами α, ω и θ соответственно.

Так как тело движется по окружности, то удобно рассчитывать угол θ, на который оно повернется за определенное время. Этот угол выражается в радианах (реже в градусах). Поскольку окружность имеет 2 × pi радиан, то можно записать равенство, связывающее θ с длиной дуги L поворота:

L = θ × r

Где r — радиус вращения. Эту формулу несложно получить, если вспомнить соответствующее выражение для длины окружности.

Угловая скорость ω, как и ее линейный аналог, описывает быстроту поворота вокруг оси, то есть она определяется согласно следующему выражению:

ω¯ = d θ / d t

Величина ω¯ является векторной. Направлена она вдоль оси вращения. Единицей ее измерения является радиан в секунду (рад/с).

Наконец, угловое ускорение — это физическая характеристика, которая определяет быстроту изменения величины ω¯, что математически записывается так:

α¯ = d ω¯/ d t

Вектор α¯ направлен в сторону изменения вектора скорости ω¯. Далее будет сказано, что угловое ускорение направлено в сторону вектора момента силы. Измеряют эту величину в радианах в квадратную секунду (рад/с²).

Момент силы и ускорение

Если вспомнить закон Ньютона, который связывает в единое равенство силу и линейное ускорение, то, перенеся этот закон на случай вращения, можно записать следующее выражение:

M¯ = I × α¯

Здесь M¯ — момент силы, представляющий собой произведение силы, которая стремится раскрутить систему, на рычаг — расстояние от точки приложения силы до оси. Величина I является аналогом массы тела и называется моментом инерции. Записанная формула называется уравнением моментов. Из него угловое ускорение можно вычислить так:

α¯ = M¯/ I

Поскольку I — это скаляр, то α¯ всегда направлено в сторону действующего момента силы M¯. Направление M¯ определяется по правилу правой руки или правилу буравчика. Вектора M¯ и α¯ перпендикулярны плоскости вращения. Чем больший момент инерции имеет тело, тем меньшее значение углового ускорения способен сообщить системе фиксированный момент M¯.

Кинематические уравнения

Чтобы понять, какую важную роль играет угловое ускорение для описания движения вращения, запишем формулы, связывающие изученные выше кинематические величины.

В случае равноускоренного вращения справедливы следующие математические соотношения:

ω = α × t;

θ = α × t² / 2

Первая формула показывает, что угловая скорость будет расти во времени по линейному закону. Второе выражение позволяет рассчитать угол, на который повернется тело за известное время t. Графиком функции θ(t) является парабола. В обоих случаях угловое ускорение — это постоянная величина.

Если воспользоваться приведенной в начале статьи формулой связи между L и θ, то можно получить выражение для α через линейное ускорение a:

α = a / r

Если α является постоянным, то при возрастании расстояния от оси вращения r будет пропорциональным образом увеличиваться линейное ускорение a. Именно поэтому для вращения пользуются угловыми характеристиками, в отличие от линейных, они не изменяются с увеличением или уменьшением r.

Пример задачи

Металлический вал, вращаясь с частотой 2 000 оборотов в секунду, начал замедлять свое движение и через 1 минуту полностью остановился. Необходимо рассчитать, с каким угловым ускорением происходил процесс торможения вала. Также следует вычислить количество оборотов, которые вал сделал до того, как остановиться.

Процесс замедления вращения описывается таким выражением:

ω = ω₀ — α × t

Начальная угловая скорость ω₀ определяется через частоту вращения f таким образом:

ω₀ = 2 × pi × f

Поскольку время торможения нам известно, тогда получаем значение ускорения α:

α = ω₀ / t = 2 × pi × f / t = 209,33 рад/с²

Это число следует взять со знаком минус, поскольку речь идет о торможении системы, а не об ее ускорении.

Для определения числа оборотов, которые вал сделает во время торможения, применим выражение:

θ = ω₀ × t — α × t² / 2 = 376 806 рад.

Полученное значение угла поворота θ в радианах просто переводится в число сделанных оборотов валом до его полной остановки с помощью простого деления на 2 × pi:

n = θ / (2 × pi) = 60 001 оборот.

Таким образом, мы получили все ответы на вопросы задачи: α = -209,33 рад/с², n = 60 001 оборот.