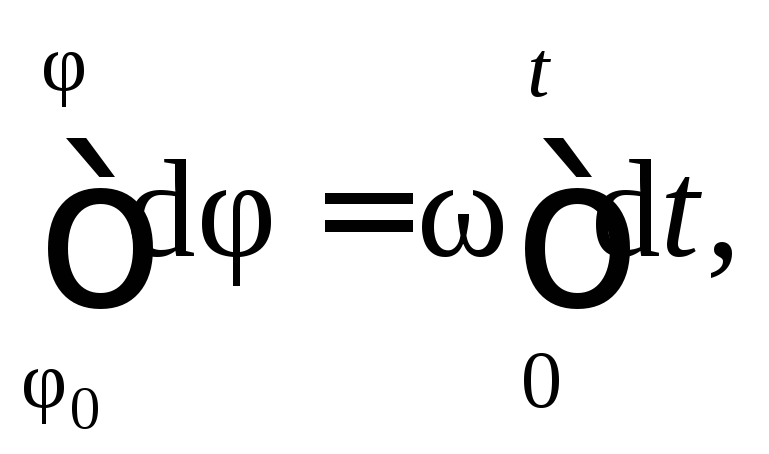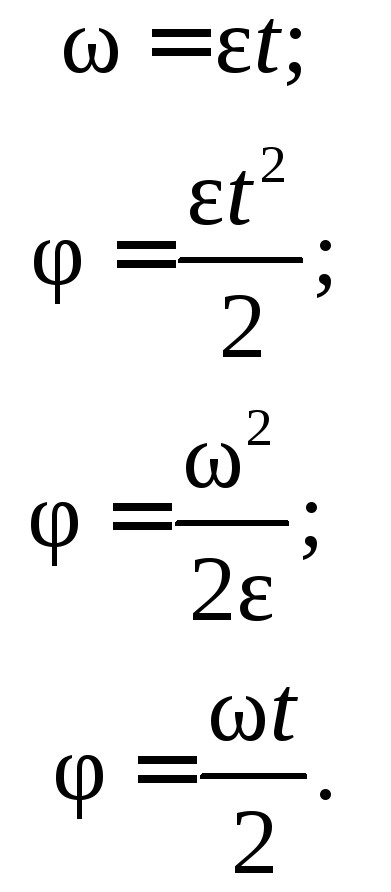Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:
Приняв вектор k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.
Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.
Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Download Article
Different ways to calculate rotation speed
Download Article
Most people have a general understanding of the idea of velocity and acceleration. Velocity is the measure of how fast an object is moving, and acceleration is the measure of how quickly the object’s velocity is changing (i.e., speeding up or slowing down). When the object is moving in a circle, such as a spinning tire or a rotating CD, velocity and acceleration are generally measured by the angle of rotation. They are then called angular velocity and angular acceleration. If you know the object’s velocity over some period of time, you can calculate its average angular acceleration. Alternatively, you may have a function to calculate the object’s position. With this information, you can calculate its angular acceleration at any chosen instant.
-
1
Determine the function for angular position. In some cases, you may be provided with a function or formula that predicts or assigns the position of an object with respect to time. In other cases, you may derive the function from repeated experiments or observations. For this article, we assume that the function has been provided or previously calculated.[1]
-
2
Find the function for angular velocity. Velocity is the measure of how fast an object changes its position. In layman’s terms, we think of this as its speed. In mathematical terms, the change of position over time can be found by finding the derivative of the position function. The symbol for angular velocity is
. Angular velocity is generally measured in units of radians divided by time (radians per minute, radians per second, etc.).[2]
Advertisement
-
3
Find the function for angular acceleration. Acceleration is the measure of how fast an object’s velocity is changing over time. You can mathematically calculate the angular acceleration by finding the derivative of the function for angular velocity. Angular acceleration is generally symbolized with
, the Greek letter alpha. Angular acceleration is reported in units of velocity per time, or generally radians divided by time squared (radians per second squared, radians per minute squared, etc.).[3]
-
4
Apply the data to find instantaneous acceleration. Once you have derived the function for instantaneous acceleration as the derivative of velocity, which in turn is the derivative of position, you are ready to calculate the instantaneous angular acceleration of the object at any chosen time.[4]
Advertisement
-
1
-
2
Measure final angular velocity. The second piece of information that you need is the angular velocity of the spinning or rotating object at the end of the time period that you want to measure. This is to be called the “final” velocity.[6]
- A compact disc plays in the machine by rotating at an angular velocity of 160 radians per second.
- The roller coaster, after applying its brakes to the spinning wheels, ultimately reaches an angular velocity of zero when it stops. This will be its final angular velocity.
-
3
Measure the elapsed time. To calculate the average angular velocity of the spinning or rotating object, you need to know the amount of time that passes during your observation. This can be found by direct observation and measurement, or the information can be provided for a given problem.[7]
- The owner’s manual for the CD player provides the information that the CD reaches its playing speed in 4.0 seconds.
- From observations of roller coasters being tested, it has been found that they can come to a complete stop within 2.2 seconds from when the brakes are initially applied.
-
4
Calculate the average angular acceleration. If you know the initial angular velocity, the final angular velocity, and the elapsed time, fill that data into the equation and find the average angular acceleration.[8]
- For the example of the CD player, the calculation is as follows:
- For the roller coaster example, the calculation looks like this:
- Note that acceleration is always going to be in units of some distance measurement “per” time squared. With angular acceleration, the distance is generally measured in radians, although you could convert that to number of rotations if you wish.
Advertisement
-
1
Understand the concept of angular motion. When people think of the speed of an object, they often consider linear motion — that is, objects traveling mostly in a straight line. This would include a car, a plane, a ball that is thrown or any number of other objects. However, angular motion describes objects that spin or rotate. Think of the earth spinning on its axis. The position or speed of the earth can be measured with angular quantities. A spinning compact disc (or record player, if you’re old enough), electrons on their axes, or the wheels of a car on the axle are other examples of rotating objects that can be measured through angular motion.[9]
-
2
Visualize angular position. When you measure the position of a moving vehicle, for example, you can measure the distance traveled in a straight line from the starting point. With a rotating object, the measurement is generally done in terms of the angle around a circle. By convention, the starting or “zero” point is generally a horizontal radius from the center to the right side of the circle. The distance traveled is measured by the size of the angle
, measured from that horizontal radius.[10]
- The angle that is being measured is commonly represented by
, the Greek letter theta.
- Positive motion is measured in a counterclockwise direction. Negative motion is measured in a clockwise direction.
- The angle that is being measured is commonly represented by
-
3
Measure angular motion in radians. Linear travel is generally measured in some unit of distance, such as miles, meters, inches or some other unit of length. Rotational or angular motion is generally measured in units called radian. A radian is a fraction of the circle. For standard reference, mathematicians use the “unit circle,” which has a standard radius of 1 unit.[11]
- One full rotation around the unit circle is said to measure 2π radians. Therefore, a half circle is π radians, and a quarter circle is π/2 radians.
- Sometimes it is useful to convert from radians to degrees. If you recall that a full circle is 360 degrees, you can find the conversion as follows:
- Thus, one radian is about equal to 57.3 degrees.
-
4
Understand the concept of angular acceleration. Angular acceleration is the measurement of how fast or slow a rotating object is changing its velocity. In other words, is the spinning speeding up or slowing down? If you know the angular velocity at a starting time and then at a later ending time, you can calculate the average angular acceleration over that time interval. If you know the function for the object’s position, you can use calculus to derive the instantaneous angular acceleration at any chosen time.[12]
- People often use the word “acceleration” to mean speeding up, and “deceleration” to mean slowing down. In mathematical and physical terms, however, only the word “acceleration” is used. If the object is speeding up, the acceleration is positive. If it is slowing down, the acceleration is negative.
Advertisement
Add New Question
-
Question
What are the formulas to find the initial acceleration of an object?
Initial acceleration generally has to be given as a condition of the problem or the experiment.
-
Question
What is the direction of radial and tangential acceleration and how do they affect each other?
Angular (or radial) measurements are generally counterclockwise. Tangential acceleration means the straight line direction of the tangent at some measured point along the circle. The tangent is a line that is perpendicular to the radius at that point.
-
Question
How can you find angular acceleration in revolutions per second squared?
This article shows how to find acceleration in radians per second squared. To convert the number of radians to the number of revolutions, recall that 1 full circle (or 1 revolution) is equal to 2pi radians. This is roughly equivalent to 6.28 radians per revolution. If you know the acceleration in radians per second squared, divide that answer by 6.28 to get revolutions per second squared.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Remember to express final results with the proper units. Angular position is usually expressed in radians. Angular velocity is expressed in radians per time. Angular acceleration is expressed in units of radians per time squared.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate instantaneous angular acceleration, start by determining the function for angular position, or the position of the object with respect to time. Next, find the angular velocity, which is the measure of how fast the object changes its position. Then, find the derivative of the function for angular velocity in order to determine the function for angular acceleration. Finally, plug in the data to find the instantaneous acceleration of the object at any chosen time. To learn more, including how to calculate average angular acceleration, read on.
Did this summary help you?
Thanks to all authors for creating a page that has been read 91,142 times.
Did this article help you?
Чивилёв В.И. Кинематика вращательного движения //Квант. — 1986. — № 11. — С. 17-18.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Содержание
- 1 Линейные и угловые величины
- 2 Связь линейных и угловых величин
- 3 Формулы кинематики для равноускоренного вращательного движения
Медленно проехав перекресток, троллейбус стал удаляться по улице, плавно увеличивая свою скорость…
Движение колеса троллейбуса — лишь один из многих примеров сложного механического движения в окружающем нас мире. Оказывается, любое сложное движение можно представить как сумму двух простых движений — поступательного и вращательного. Понимать это следует так: всегда можно подобрать такую поступательно движущуюся систему отсчета, относительно которой движение выглядит только как вращение вокруг некоторой неподвижной оси.
Какую же в нашем случае надо выбрать систему отсчета, чтобы в ней колесо троллейбуса совершало чистое вращение? Какими физическими величинами описывается это вращение, как эти величины связаны друг с другом и как зависят от времени? Такие вопросы могут возникнуть не только на пешеходном переходе, но и на уроке, экзамене, при решении конкретной задачи.
На первый вопрос ответить легко, догадавшись, что поступательно движущуюся систему отсчета можно связать с самим троллейбусом (его корпусом). Перед тем как ответить на остальные вопросы, заметим, что в нашем примере колесо вращается неравномерно — модуль скорости любой точки колеса меняется со временем.
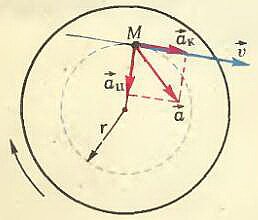
Рассмотрим некоторую точку М колеса, находящуюся на расстоянии r от оси вращения и имеющую в некоторый момент времени скорость (~vec upsilon) и ускорение (~vec a) (рис. 1). Из физических соображений разумно ускорение (~vec a) представить как сумму двух составляющих: одна из них (~vec a_c) направлена по радиусу к центру окружности — центростремительное ускорение, вторая (~vec a_k) направлена по касательной к окружности — касательное ускорение. Оба эти ускорения имеют определенный физический смысл — касательное ускорение характеризует быстроту изменения модуля скорости, а центростремительное характеризует быстроту изменения направления скорости. Можно показать, что модуль центростремительного ускорения (~a_c = frac{upsilon^2}{r}) («Физика 8», §16), а модуль касательного ускорения (~a_k = frac{Delta upsilon}{Delta t}), где Δυ — изменение модуля υ скорости точки за сколь угодно малое время Δt.
Рис. 1
Линейные и угловые величины
Как уже говорилось, нам надо ввести такие физические величины, которые характеризовали бы неравномерное вращение колеса (в системе отсчета, связанной с троллейбусом). Попробуем это сделать по аналогии с прямолинейным неравномерным движением.
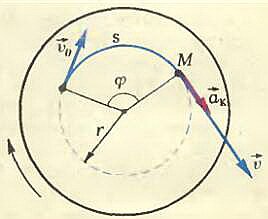
Проследим за точкой М колеса в течение малого промежутка времени Δt. За это время точка пройдет по дуге окружности путь s и будет иметь скорость υ и касательное ускорение ak (рис. 2). Три величины s, υ и ak, называемые линейными величинами, характеризуют движение точки М, но не могут служить для описания вращения всего колеса, так как в один и тот же момент времени другие точки, расположенные на других расстояниях от оси вращения, имеют другие линейные скорости, и касательные ускорения и пройденные ими пути тоже не одинаковы. Поэтому кроме линейных вводятся так называемые угловые величины, которые одинаковы для всех точек вращающегося колеса: угол поворота φ радиуса, соединяющего точку М с центром окружности, угловая скорость (~omega = frac{Delta varphi}{Delta t}) (Δφ — изменение угла поворота за время Δt) и угловое ускорение (~varepsilon = frac{Delta omega}{Delta t}) (Δω — изменение угловой скорости).
Рис. 2
Очевидно, что введенными здесь угловыми величинами можно описывать вращение не только троллейбусного колеса, но и любого другого тела. При этом с течением времени может изменяться не только угол поворота φ, но и угловая скорость ω и угловое ускорение ε. В частности, если угловое ускорение не зависит от времени, то угловая скорость изменяется равномерно и в таком случае говорят, что имеет место равноускоренное вращение. Когда же угловая скорость остается постоянной, то угловое ускорение оказывается равным нулю и говорят о равномерном вращении тела.
Связь линейных и угловых величин
Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.
При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь
(~s = r varphi) . (1)
За малое время Δt точка проходит расстояние (~Delta s = r varphi_2 — r varphi_1) , где φ2 и φ1 — углы поворота в конце и в начале интервала Δt. Разделив последнее равенство на Δt и учитывая, что (~frac{Delta s}{Delta t} = upsilon) и (~frac{varphi_2 — varphi_1}{Delta t} = frac{Delta varphi}{Delta t} = omega), получим
(~upsilon = r omega) . (2)
Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δt есть (~Delta upsilon = r omega_2 — r omega_1) , где ω2 и ω1 — угловые скорости в конце и в начале промежутка Δt. Разделим последнее равенство на Δt и учтем, что (~frac{Delta upsilon}{Delta t} = a_k) и (~frac{omega_2 — omega_1}{Delta t} = frac{Delta omega}{Delta t} = varepsilon), тогда касательное ускорение
(~a_k = r varepsilon) . (3)
Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.
Формулы кинематики для равноускоренного вращательного движения
Найдем зависимость угловой скорости ω и угла поворота φ колеса троллейбуса от времени t для случая вращения колеса с постоянным угловым ускорением ε.
Пусть начальная угловая скорость равна ω0. Тогда точка М, имея начальную скорость υ0 = rω0, будет двигаться с постоянным по модулю касательным ускорением ak = rε. По аналогии с прямолинейным равноускоренным движением для линейной скорости υ и пути s получим равенства
(~upsilon = upsilon_0 + a_k t) , (4)
(~s = upsilon_0 t + frac{a_k t^2}{2}) , (5)
из которых после исключения времени t следует полезное соотношение:
(~upsilon^2 — upsilon^2_0 = 2 a_k s) . (6)
Подставив в равенства (4)-(6) s = rφ, υ = rω, ak = rε, υ0 = rω0 и упростив, получим соотношения
(~begin{matrix} omega = omega_0 + varepsilon t \ varphi = omega_0 t + frac{varepsilon t^2}{2} \ omega^2 — omega^2_0 = 2 varepsilon varphi end{matrix}) .
Это и есть формулы кинематики для. вращательного движения любого тела (а не только колеса троллейбуса) с постоянным угловым ускорением.
Движение
твердого тела, при котором все его точки
перемещаются по окружности, центры
которой расположены на перпендикулярной
этим окружностям неподвижной прямой,
называется вращательным.
Неподвижная прямая, на которой лежат
центры круговых траекторий точек
тела, называется его осью
вращения.
Для образования оси вращения достаточно
закрепить какие-либо две точки тела. В
качестве примеров вращательного движения
тел можно привести движение дверей
или створок окон при их открывании или
закрывании.
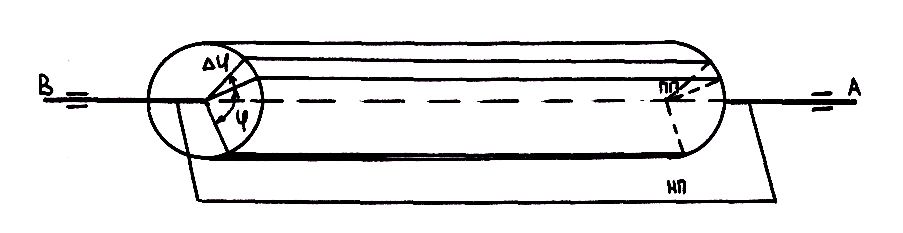
Представим
себе тело в виде цилиндра, ось AB
которого лежит в подшипниках (рис. 7.3).
Рис. 7.3. К
анализу вращательного движения твердого
тела
Движением одной
какой-либо точки однозначно определить
вращательное движение тела нельзя.
Для
установления закона вращательного
движения тела, по которому можно
определять его положение в данный
момент, проведем через ось вращения
тела связанную только с нею неподвижную
полуплоскость НП, а внутри тела отметим
подвижную полуплоскость, которая
вращается около оси вместе с телом,
теперь угол
φ,
образуемый в каждый данный момент
времени полуплоскостями НП и ПП, точно
определяет положение тела в пространстве
(см. рис. 7.3). Угол φ
называется углом
поворота
и выражается в радианах. Чтобы определять
положение тела в пространстве в любой
момент времени, необходимо знать
зависимость между углом поворота φ
и временем t,
т. е. знать закон вращательного движения
тела:
Быстрота
изменения угла поворота во времени
характеризуется величиной, которая
называется угловой
скоростью.
Представим,
что в некоторый момент времени t
положение
вращающегося тела определяется углом
поворота φ,
а в момент t
+ Δt –
углом поворота φ
+ Δ φ.
Следовательно, за время Δt
тело повернулось на угол Δ
φ,
и величина
называется
средней
угловой скоростью.
Единицей
угловой скорости является 1 рад/с.
Характеристикой быстроты изменения
угловой скорости служит угловое
ускорение,
обозначаемое
.
Среднее ускорение
;
.
Единица
углового ускорения 1 рад/с2.
Условимся
угол поворота, отсчитываемый против
хода часовой
стрелки,
считать положительным, а отсчитываемый
по ходу часовой стрелки – отрицательным.
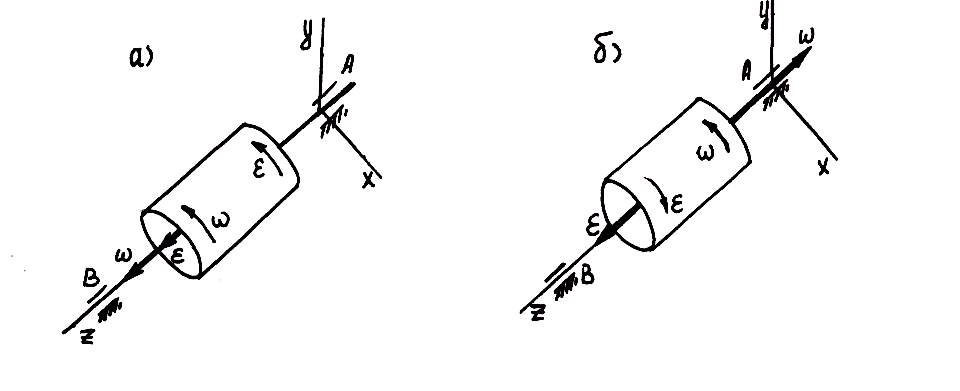
б
а
Рис. 7.4. К
определению вида вращательного движения
Векторы
и
– это скользящие векторы, которые
направлены по оси вращения, чтобы, глядя
из конца вектора
(или
),
видеть вращение, происходящее против
часовой стрелки.
Если
векторы
и
направлены в одну сторону (рис. 7.4,
а),
то вращательное движение тела ускоренное
– угловая скорость возрастает. Если
векторы
и
направлены в противоположные стороны,
то вращение тела замедленное
–
угловая скорость уменьшается (рис. 7.4,
б).
7.3. Частные случаи вращательного движения
1. Равномерное
вращательное движение.
Если угловое ускорение
и, следовательно, угловая скорость
,
(7.1)
то
вращательное движение называется
равномерным. Из выражения (7.1) после
разделения переменных получим
Если
при изменении времени от 0 до t
угол поворота изменялся от φ0
(начальный угол поворота) до φ,
то, интегрируя уравнение в этих пределах:
получаем уравнение
равномерного вращательного движения
,
которое в
окончательном виде записывается так:
.
Если
,
то
.
Таким
образом, при равномерном вращательном
движении угловая скорость
или при
.
2. Равнопеременное
вращательное движение.
Если угловое ускорение
(7.2)
то
вращательное движение называется
равнопеременным. Производя разделение
переменных в выражении (7.2):
и
приняв, что при изменении времени от 0
до t
угловая скорость изменилась от
(начальная угловая скорость) до
,
проинтегрируем уравнение в этих пределах:
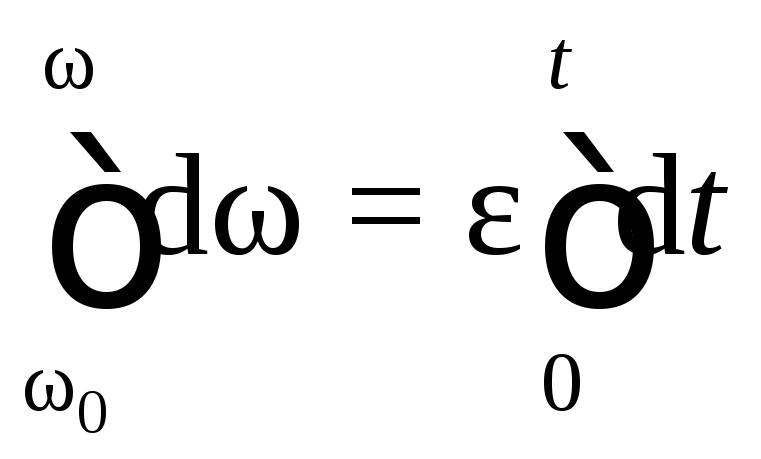
,
т. е.
получим уравнение
(7.3)
выражающее значение
угловой скорости в любой момент времени.
Закон
равнопеременного вращательного движения
или, с учетом уравнения (7.3):
Полагая,
что в течение времени от 0 до t
угол поворота изменялся от
до
,
проинтегрируем уравнение в этих пределах:
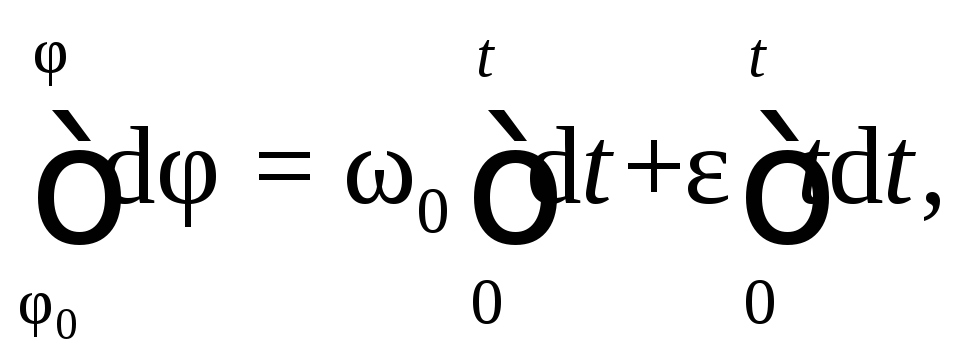
Уравнение
равнопеременного вращательного движения
в окончательном виде
(7.4)
Первую
вспомогательную формулу получим,
исключив из формул (7.3)
и
(7.4) время:
(7.5)
Исключив
из тех же формул угловое ускорение
,
получим вторую вспомогательную формулу:
(7.6)
где
–
средняя угловая скорость при
равнопеременном вращательном
движении.
Когда
и
,
формулы (7.3)–(7.6) приобретают более
простой вид:
В
процессе конструирования угловое
перемещение выражают не в радианах, а
просто в оборотах.
Угловая
скорость, выражаемая количеством
оборотов в минуту, называется частотой
вращения
и обозначается n.
Установим зависимость между
(с–1)
и n
(мин–1).
Так как
,
то при n
(мин–1)
за t
=
1 мин = 60 с угол поворота
.
Следовательно:
.
При
переходе от угловой скорости
(с–1)
к частоте вращения n
(мин–1)
имеем
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нам уже известно понятие ускорения тела. Так именуют величину, характеризующую изменение его скорости. Также нам известно понятие угловой скорости. Для характеристики этого изменения используют величину, называемую угловым ускорением. Рассмотрим его особенности и использование.
Определения углового ускорения тела. Среднее и мгновенное угловое ускорение
Определение 1
Угловым ускорением называется кинематическая величина, характеризующая изменение угловой скорости с течением времени. Обозначают его обычно греческой буквой ε.
Слово «кинематическая» означает, что движение рассматривается без учёта действия на тело сил, независимо от них. Обозначим промежуток времени как Δt. Изменение угловой скорости за этот промежуток обозначим как Δω. Отношение Δω/Δt называют средним угловым ускорением. Среднее угловое ускорение равно угловой скорости за определённый интервал времени. Однако, как она себя вела, например, в самом его начале, середине или конце ничего не скажешь.
Если мы будем выбранный нами интервал времени постоянно уменьшать, изменение скорости получится описывать всё более и более точно. В идеале, чтобы Δt вообще стремился к нулю:
ε = lim (Δt→0)(Δω/Δt) = dω/dt = d2φ /d2t
Так мы перешли ко второму определению углового ускорения, только оно уже не среднее, а, как говорят, мгновенное.
Определение 2
Угловое ускорение тела есть первая производная его угловой скорости по времени или вторая производная его углового перемещения. Ещё раз перепишем формулы, но уже в качестве официального определения.
Угловое ускорение тела равно:
ε = dω/dt = d2φ /d2t
Размерностью величины будет 1/T2 (1/время2). Измеряют его обычно в радианах на секунду в квадрате, рад/с2 или 1/с2 (с-2).
Обязательно следует отметить, что ε может рассматриваться, в качестве вектора, т. е. ему приписывается направление. Хотя в отличие от направления обычной скорости, воспринимается это несколько сложнее, ведь наглядность отсутствует.
Угловое ускорение через радиус выражается как a = ε*R, где a – ускорение, направленное по касательной траектории.
Определения
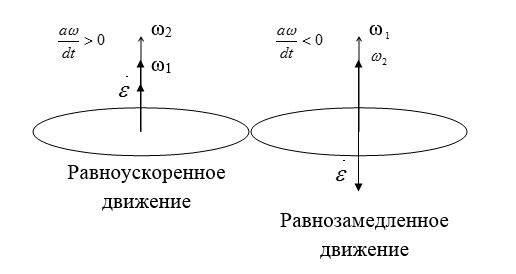
Если тело вращается всё быстрее и быстрее, то это значит, что модуль его угловой скорости с течением времени увеличивается. Такое вращение называют ускоренным. При нём вектора угловых скорости и ускорения имеют одно и то же направление.
Если тело вращается всё медленнее и медленнее, то это значит, что модуль его угловой скорости со временем уменьшается. Такое вращение называют замедленным. При нём вектора угловой скорости и углового ускорения направлены противоположно.
Угловое ускорение и формула закона движения при равнопеременном вращении
Определение 5
Равнопеременным вращением называют вращение, при котором угловое ускорение не меняется с течением времени, т. е. является константой [(ε=const)].
Выведем его закон. Пусть в начальный момент времени (t=0) равен φ0, а его начальная скорость ω0.
Из определений выше следует
ε = dω/dt следует, что dω = ε dt.
Чтобы найти угловую скорость нам нужно найти первообразную от этого выражения по времени. Получаем
ω = εt + С1.
С1 – некоторая постоянная. В нашем случае, по начальным условиям, она равна начальной угловой скорости тела, ω0.
Поэтому
ω = εt + ω0
Напомним, что мгновенная угловая скорость равна: ω = dφ /dt
Отсюда
dφ /dt = εt + ω0
φ = (εt + ω0)dt
Находим первообразную по времени
φ = εt2/2 + ω0t + С2
С2 – некоторая постоянная. Исходя из начальных условий она равна φ0. Приходим к выражению
φ = εt2/2 + ω0t + φ0
Это и есть закон равнопеременного вращательного движения.
Нет времени решать самому?
Наши эксперты помогут!
Примеры
Пример. 1
Колесо стало вращаться с постоянным угловым ускорением и, спустя 10 оборотов от начала вращения, получило скорость 20 рад/с. Чему равно угловое ускорение?
Решение:
Применим к вращению колеса формулу равнопеременного движения, исходя из того, что его начальная угловая скорость ω0 была равна нулю. Формулы, с которыми нам придётся иметь дело:
φ = εt2/2; ω = εt; φ = 2πN
Из первой формулы выражаем ε
ε = (φ/t2)
Из второй формулы выражаем время
t = ω/ε
Подставляем его в формулу выше.
ε = (2*φ)/(ω/ε)2 = ( 2* φ * ε2)/ω2
Проводим необходимые сокращения и приходим к формуле углового ускорения:
ε = ω2/2φ
Вместо угла φ подставляем в выражение третью формулу
ε = ω2/2*2πN = ω2/4πN
После подстановки численных значений получим ε = 3,2 рад/c2
Ответ: Угловое ускорение колеса равно 3,2 рад/c2.
Пример. 2
Тело вокруг собственной оси вращается по следующему закону:
φ = 10 + 20*t – 2*t2
Нужно найти угловое и полное ускорение точки, находящейся в 109 см. от оси вращения через 4 секунды после начала движения.
Решение:
Формулы, с которыми нам придётся иметь дело:
[a=sqrt{a_{n}^{2}+a_{T}^{2}}]
At = dv/dt = Rε
an = v2/R = ω2R
Если известен закон движения, то ω и ε не составляет труда выразить через производные. Сначала находим ω.
ω = d(10 + 20t – 2t2)/dt = 20 – 4t
Ускорение находим, дифференцируя последнее полученное выражение:
ε = d(20 — 4t)/dt = (- 4 )рад/с2
Смотрим на формулу нахождения полного a и выражение ε через радиус, после чего делаем соответствующие подстановки.
[a=sqrt{R^{2} varepsilon^{2}+omega^{4} R^{2}}]
После численных подстановок выясняем, что a точки равно 1,65 м/с2.
Ответ: Угловое ускорение точки равно (-4) рад/с2, а полное её ускорение – 1,65 м/с2.