Как найти угловой коэффициент касательной графику функции - Исправление недочетов и поиск решений вместе с Examum.ru

Касательная к графику функции f, дифференцируемой в точке x_о, — это прямая, проходящая через точку (x_о; f(x_о)) и имеющая угловой коэффициент f ′(x_о).

Угловой коэффициент имеет прямая вида y = kx + b. Коэффициент k и является угловым коэффициентом этой прямой.

Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс: k = tgα

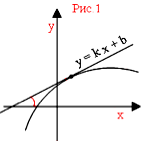
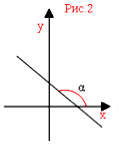
Здесь угол α – это угол между прямой y = kx + b и положительным (то есть против часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой (рис.1 и 2).

Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).

Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).

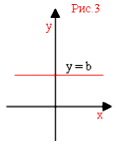
Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3).

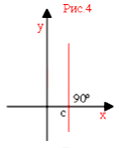
Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c, где c – некоторое действительное число (рис.4).

Уравнение касательной к графику функции y = f(x) в точке x_о:

y = f(x_о) + f ′(x_о) (x – x_о)

Алгоритм решения уравнения касательной к графику функции y = f(x):

Вычислить f ( x₀ )
Вычислить производные f ‘( x) и f ‘( x₀ )
Внести найденные числа x₀, f ( x₀ ) ,f ‘( x₀ ) в уравнение касательной и решить его

Пример: Найдем уравнение касательной к графику функции f(x) = x³ – 2x² + 1 в точке с абсциссой 2.

Решение.

Следуем алгоритму.

1) Точка касания x_оравна 2. Вычислим f(x_о):

f(x_о) = f(2) = 2³ – 2 ∙ 2² + 1 = 8 – 8 + 1 = 1

2) Находим f ′(x). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х² = 2х, а х³ = 3х². Значит:

f ′(x) = 3х² – 2 ∙ 2х = 3х² – 4х.

Теперь, используя полученное значение f ′(x), вычислим f ′(x_о):

f ′(x_о) = f ′(2) = 3 ∙ 2² – 4 ∙ 2 = 12 – 8 = 4.

3) Итак, у нас есть все необходимые данные: x_о = 2, f(x_о) = 1, f ′(x_о) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:

у = f(x_о) + f ′(x_о) (x – x_о) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.

Ответ: у = 4х – 7.

Найти угловой коэффициент касательной к графику функции в точке с абсциссой x₀ =

Найдите угловой коэффициент касательной к графику функции в точке с абсциссой x₀ = 2

Найдите тангенс угла наклона касательной, проведенной к графику функции в его точке с абсциссой (-1)

Дана функция f(x)=х2- 4x+1. Найдите координаты точки, в которой угловой коэффициент касательной к графику функции равен 2

Укажите абсциссу точки графика функции у = 12 -3х + х2 в которой угловой коэффициент касательной равен 2.

Источник

Задачи на нахождение производной касательной включены в ЕГЭ по математике и встречаются там ежегодно. При этом статистика последних лет показывает, что подобные задания вызывают у выпускников определенные затруднения. Поэтому, если учащийся рассчитывает получить достойные баллы по итогам прохождения ЕГЭ, то ему непременно стоит научиться справляться с задачами из раздела «Угловой коэффициент касательной как значение производной в точке касания», подготовленными специалистами образовательного портала «Школково». Разобравшись с алгоритмом их решения, ученик сможет успешно преодолеть аттестационное испытание.

Основные моменты

Приступая к решению задач ЕГЭ по данной теме, необходимо вспомнить основное определение: производная функции в точке равна угловому коэффициенту касательной к графику функции в этой точке. В этом и состоит геометрический смысл производной.

Необходимо освежить в памяти и другое важное определение. Оно звучит следующим образом: угловой коэффициент равняется тангенсу угла наклона касательной к оси абсцисс.

Какие еще важные моменты стоит отметить в этой теме? При решении задач на нахождение производной в ЕГЭ необходимо помнить, что угол, который образует касательная, может быть меньше, больше 90 градусов или равняться нулю.

Как подготовиться к экзамену?

Для того, чтобы задания в ЕГЭ на тему «Угловой коэффициент касательной как значение производной в точке касания» давались вам достаточно легко, воспользуйтесь при подготовке к выпускному испытанию информацией по этому разделу на образовательном портале «Школково». Здесь вы найдете необходимый теоретический материал, собранный и понятно изложенный нашими специалистами, а также сможете попрактиковаться в выполнении упражнений.

Для каждого задания, например, задач на тему «Угловой коэффициент касательной как тангенс угла наклона», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут выполнять упражнения различного уровня сложности в режиме онлайн. В случае необходимости задачу можно сохранить в разделе «Избранное», чтобы потом обсудить ее решение с преподавателем.

Источник

п.1. Уравнение касательной

Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin{gather*} (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end{gather*}

Уравнение касательной к кривой (y=f(x)) в точке (x_0) имеет вид: $$ y=f'(x_0)(x-x_0)+f(x_0) $$ при условии, что производная (f'(x_0)=aneinfty) — существует и конечна.

Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace{f'(x_0)}_{=k}x+underbrace{f(x_0)-f'(x_0)cdot x_0}_{=b} $$

Уравнение касательной с угловым коэффициентом: begin{gather*} y=kx+b\ k=f'(x_0), b=f(x_0)-f'(x_0)cdot x_0 end{gather*}

п.2. Алгоритм построения касательной

На входе: уравнение кривой (y=f(x)), абсцисса точки касания (x_0).
Шаг 1. Найти значение функции в точке касания (f(x_0))
Шаг 2. Найти общее уравнение производной (f’ (x))
Шаг 3. Найти значение производной в точке касания (f'(x_0 ))
Шаг 4. Записать уравнение касательной (y=f’ (x_0)(x-x_0)+f(x_0)), привести его к виду (y=kx+b)
На выходе: уравнение касательной в виде (y=kx+b)

Например:

Пусть (f(x)=x^2+3).
Найдем касательную к этой параболе в точке (x_0=1).

(f(x_0)=1^2+3=4 )
(f'(x)=2x )
(f'(x_0)=2cdot 1=2)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: (y=2x+2)

п.3. Вертикальная касательная

В случае, если производная (f'(x_0)=pminfty) — существует, но бесконечна, в точке (x_0) проходит вертикальная касательная (x=x_0).

Внимание!

Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода (x_0notin D), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку (x_0in D), входящую в область определения. График функции и касательная имеют одну общую точку ((x_0,y_0)).

Вертикальные касательные характерны для радикалов вида (y=sqrt[n]{x}).

Например:

Пусть (f(x)=sqrt[5]{x-1}+1).
Найдем касательную к этой кривой в точке (x_0=1).

(f(x_0)=sqrt[5]{1-1}+1=1)
(f'(x)=frac15(x-1)^{frac15-1}+0=frac15(x-1)^{-frac45}=frac{1}{5(x-1)^{frac45}} )
(f'(x_0)=frac{1}{5(1-1)^{frac45}}=frac10=+infty)
В точке (x_0) проходит вертикальная касательная.
Её уравнение: (x=1)
Ответ: (y=2x+2)

п.4. Примеры

Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0Rightarrow 2x(x+2)=0Rightarrow left[ begin{array}{l} x=0\ x=-2 end{array} right. $$ Две точки на оси: (0;0) и (-2;0).
Касательная в точке (x_0=0): begin{gather*} f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot 0+4=4\ y=4(x-0)+0=4x end{gather*} Касательная в точке (x_0=-2): begin{gather*} f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot (-2)+4=-4\ y=-4(x+2)+0=-4x-8 end{gather*}

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

Общее уравнение касательной: (f'(x)=4x+4)
По условию (f'(x_0)=tgalpha=tg45^circ=1)
Решаем уравнение: $$ 4x_0+4=1Rightarrow 4x_0=-3Rightarrow x_0=-frac34 $$ Точка касания (x_0=-frac34) begin{gather*} f(x_0)=2cdotleft(-frac34right)^2+4cdotleft(-frac34right)=frac98-3=-frac{15}{8} end{gather*} Уравнение касательной: begin{gather*} y=1cdotleft(x+frac34right)-frac{15}{8}=x-frac98 end{gather*}

в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: (y=-2x+6Rightarrow k=-2).
Касательная должна быть параллельной, значит, её угловой коэффициент тоже (k=-2). Получаем уравнение: begin{gather*} f'(x_0)=-2\ 4x_0+4=-2Rightarrow 4x_0=-6Rightarrow x_0=-frac32 end{gather*} Точка касания (x_0=-frac32) begin{gather*} f(x_0)=2cdotleft(-frac32right)^2+4cdotleft(-frac32right)=\ =frac92-6=-frac32 end{gather*} Уравнение касательной: begin{gather*} y=-2cdotleft(x+frac32right)-frac32=-2x-frac92 end{gather*} Или, в каноническом виде: begin{gather*} 2x+y+frac92=0 end{gather*}

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой (k=0).
Получаем уравнение: (f'(x_0)=0). begin{gather*} 4x_0+4=0Rightarrow 4x_0=-4Rightarrow x_0=-1 end{gather*} Точка касания (x_0=-1) begin{gather*} f(x_0)=2cdot(-1)^2+4cdot(-1)=-2 end{gather*} Уравнение касательной: begin{gather*} y=0cdot(x+1)-2=-2 end{gather*}

Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)

Пример 2. Напишите уравнение касательной к графику функции в заданной точке:
a) ( f(x)=frac5x+frac x5, x_0=4 ) begin{gather*} f(x_0)=frac54+frac45=frac{25+16}{20}=frac{41}{20}\ f'(x)=left(frac5xright)’+left(frac x5right)’=-frac{5}{x^2}+frac15=frac{-25+x^2}{5x^2}=frac{x^2-25}{5x^2}\ f'(x_0)=frac{4^2-25}{5cdot 4^2}=-frac{9}{80} end{gather*} Уравнение касательной: $$ y=-frac{9}{80}(x-4)+frac{41}{20}=-frac{9}{80}x+frac{9}{20}+frac{41}{20}=-frac{9}{80}x+2,5 $$
б) ( f(x)=frac{x^2+5}{3-x}, x_0=2 ) begin{gather*} f(x_0)=frac{2^2+5}{3-2}=frac91=9\ f'(x)=frac{(x^2+5)'(3-x)-(x^2+5)(3-x)’}{(3-x)^2}=frac{2x(3-x)+(x^2+5)}{(3-x)^2}=\ =frac{6x-2x^2+x^2+5}{(3-x)^2}=frac{-x^2+6x+5}{(3-x)^2}\ f'(x_0)=frac{-2^2+6cdot 2+5}{(3-2)^2}=13 end{gather*} Уравнение касательной: $$ y=13(x-2)+9=13x-26+9=13x-17 $$

Пример 3*. Найдите точку, в которой касательная к графику функции (f(x)=frac{x^2+2}{x+3}-x) перпендикулярна прямой (y=11x+3). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой (k_1=11).
Угловой коэффициент перпендикулярной прямой (k_2=-frac{1}{k_1}=-frac{1}{11}) begin{gather*} f'(x)=left(frac{x^2+2}{x+3}right)’-x’=frac{2x(x+3)-(x^2+2)cdot 1}{(x+3)^2}-1=frac{2x^2+6x-x^2-2-(x+3)^2}{(x+3)^2}=\ =frac{x^2+6x-2-x^2-6x-9}{(x+3)^2}=- frac{11}{(x+3)^2} end{gather*} В точке касания: begin{gather*} f'(x_0)=k_2Rightarrow=-frac{11}{(x+3)^2}=-frac{1}{11}Rightarrow (x+3)^2=121Rightarrow (x+3)^2-11^2=0Rightarrow\ Rightarrow (x+14)(x+8)=0Rightarrow left[ begin{array}{l} x=-14\ x=8 end{array} right. end{gather*}
Уравнение касательной при (x_0=-14) begin{gather*} f(x_0)=frac{(-14)^2+2}{-14+3}+14=frac{198}{-11}+14=-18+14=-4\ y=-frac{1}{11}(x+14)-4=-frac{x+58}{11} end{gather*} Уравнение касательной при (x_0=8) begin{gather*} f(x_0)=frac{8^2+2}{8+3}-8=frac{66}{11}-8=-2\ y=-frac{1}{11}(x-8)-2=-frac{x+14}{11} end{gather*}
Ответ: точка касания (-14;-4), уравнение (y=-frac{x+58}{11})
и точка касания (8;-2), уравнение (-frac{x+14}{11})

Пример 4*. Найдите уравнения общих касательных к параболам (y=x^2-5x+6) и (y=x^2+x+1). Укажите точки касания.

Найдем производные функций: begin{gather*} f_1′(x)=2x-5, f_2′(x)=2x+1 end{gather*} Пусть a – абсцисса точки касания для первой параболы, b — для второй.
Запишем уравнения касательных (g_1(x)) и (g_2(x)) через эти переменные. begin{gather*} g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\ \ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) end{gather*} Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: begin{gather*} begin{cases} 2a-5=2b+1\ 6-a^2=1-b^2 end{cases} Rightarrow begin{cases} 2(a-b)=6\ a^2-b^2=5 end{cases} Rightarrow begin{cases} a-b=3\ (a-b)(a+b)=5 end{cases} Rightarrow begin{cases} a-b=3\ a+b=frac53 end{cases} Rightarrow \ Rightarrow begin{cases} 2a=3+frac53\ 2b=frac53-3 end{cases} Rightarrow begin{cases} a=frac73\ b=-frac23 end{cases} end{gather*} Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2cdotfrac73-5=-frac13, b=6-a^2=6-frac{49}{9}=frac59 $$ Уравнение общей касательной: $$ y=-frac x3+frac59 $$
Точки касания: begin{gather*} a=frac73, f_1(a)=left(frac73right)^2-5cdotfrac73+6=frac{49}{9}-frac{35}{3}+6=frac{49-105+54}{9}=-frac29\ b=-frac23, f_2(b)=left(-frac23right)^2-frac23+1=frac49-frac23+1frac{4-6+9}{9}=frac79 end{gather*}
Ответ: касательная (y=-frac x3+frac59); точки касания (left(frac73;-frac29right)) и (left(-frac23;frac79right))

Пример 5*. Докажите, что кривая (y=x^4+3x^2+2x) не пересекается с прямой (y=2x-1), и найдите расстояние между их ближайшими точками.

Решим уравнение: (x^4+3x^2+2x=2x-1) begin{gather*} x^4+3x^2+1=0Rightarrow D=3^2-4=5Rightarrow x^2=frac{-3pmsqrt{5}}{2} end{gather*} Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, (xinvarnothing) — решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом (k=2), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой (y=2x-1).
Строим уравнение касательной. По условию: (f'(x)=4x^3+6x+2=2) begin{gather*} 4x^3+6x=0Rightarrow 2x(2x^2+3)=0Rightarrow left[ begin{array}{l} x=0\ 2x^2+3=0 end{array} right. Rightarrow left[ begin{array}{l} x=0\ x^2=-frac32 end{array} right. Rightarrow left[ begin{array}{l} x=0\ xinvarnothing end{array} right. Rightarrow x=0 end{gather*} Точка касания (x_0=0, y_0=0^4+3cdot 0^2+2cdot 0=0).
Уравнение касательной: (y=2(x-0)+0=2x)

Ищем расстояние между двумя параллельными прямыми:
(y=2x) и (y=2x-1).
Перпендикуляр из точки (0;0) на прямую (y=2x-1) имеет угловой коэффициент (k=-frac12), его уравнение: (y=-frac12 x+b). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и (b=0).

Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin{gather*} 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac{0,4}{2}=-0,2 end{gather*} Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt{0,4^2+(-0,2)^2}=0,2sqrt{2^2+1^2}=frac{sqrt{5}}{5})
Ответ: (frac{sqrt{5}}{5})

Источник

Цель:
Составить уравнение касательной к
графику функции в заданной точке.

Теоретический материал:

Углом наклона
прямой y
= kx+b называют
угол

,
отсчитываемый от положительного
направления оси абсцисс до прямой y
= kx+b в
положительном направлении (то есть,
против часовой стрелки). Угловым
коэффициентом прямой
y = kx+b
называют числовой коэффициент k.
Угловой коэффициент
прямой равен тангенсу угла наклона
прямой, то
есть,

.

Угол наклона прямой
равен нулю, когда прямая параллельна
оси абсцисс. В этом случае нулю равен и
угловой коэффициент, так как тангенс
нуля есть ноль. Следовательно, уравнение
прямой будет иметь вид y
= b.

Когда угол наклона
прямой y =
kx+b является
острым (

),
то угловой коэффициент k
является положительным числом (так как
тангенс острого угла

принимает
положительные значения

)
и указывает на возрастание графика
прямой.

В случае, когда
прямая располагается перпендикулярно
оси абсцисс (параллельно оси ординат)
и задается равенством x
= c, где c
— некоторое действительное число.

Когда угол наклона
прямой y =
kx+b является
тупым (

),
то угловой коэффициент k
является отрицательным числом и указывает
на убывание графика прямой.

Касательной к
графику функции y
= f(x) в
точке

называют
прямую, проходящую через точку

,
с отрезком которой практически сливается
график функции при значениях х
сколь угодно близких к

.
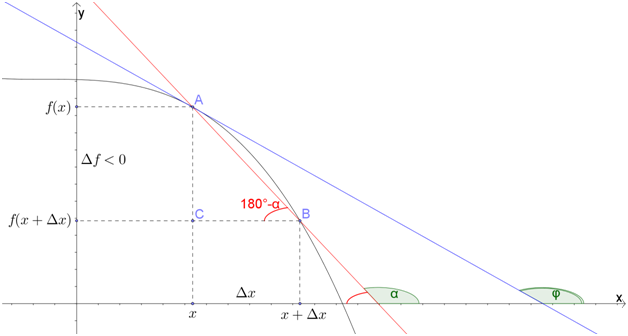
Для этого покажем, что будет происходить
с секущей АВ,
если точку В
бесконечно приближать к точке А.

Рисунок ниже
иллюстрирует этот процесс.

Секущая АВ
(показана синей пунктирной прямой) будет
стремиться занять положение касательной
прямой (показана синей сплошной линией),
угол наклона секущей

(показан
красной прерывистой дугой) будет
стремиться к углу наклона касательной

(изображен
красной сплошной дугой). Таким образом,
касательная
к графику функции y
= f(x) в точке
А
– это предельное положение секущей
AB
при

.

Геометрический смысл производной функции в точке.

Рассмотрим секущую
АВ
графика функции y
= f(x) такую,
что точки А
и В
имеют соответственно координаты

и

,
где

—
приращение аргумента. Обозначим через

приращение
функции. Отметим все на чертеже:

Из прямоугольного
треугольника АВС
имеем

.
Так как по определению касательная –
это предельное положение секущей, то

.
Вспомним определение
производной функции в точке:
производной функции y
= f(x) в точке

называется
предел отношения приращения функции к
приращению аргумента при

,
обозначается

.
Следовательно,

,
где

—
угловой коэффициент касательной. Таким
образом, существование производной
функции y =
f(x) в точке

эквивалентно
существованию касательной к графику
функции y =
f(x) в точке
касания

,
причем угловой
коэффициент касательной равен значению
производной в точке

,
то есть

Составление уравнения касательной прямой

Для записи уравнения
любой прямой на плоскости достаточно
знать ее угловой коэффициент и точку,
через которую она проходит. Уравнение
касательной к графику функции y
= f(x) в точке

имеет
вид:

Алгоритм
составления уравнения касательной к
графику функции y = f(x)

1. Обозначить
буквой a абсциссу точки касания.

2. Найти
f(a).

3. Найти f ‘(x) и f ‘(a).

4. Подставить
найденные числа a, f(a), f ‘(a) в общее
уравнение касательной y — f(a) = f ‘(a)(x
– a).

Примеры составления
уравнения касательной.

Пример 1. Составьте
уравнение касательной в точке M(3; – 2)
к графику функции

Решение. Точка
M(3; – 2) является точкой касания, так
как

1. a = 3 – абсцисса
точки касания.

2. f(3) = – 2.

3. f ‘(x)
= x²
– 4, f ‘(3) = 5.

y = – 2 + 5(x – 3), y = 5x –
17 – уравнение касательной.

Задание для
практической работы по теме «Нахождение
углового коэффициента касательной к
графику функции в указанной точке.
Составление уравнения касательной».
Составить уравнения касательных к
графикам функции в заданной точке с
абсциссой а=2:

Вариант 1	Вариант 2	Вариант 3	Вариант 4
Уровень А. Уровень А. Y=3x³-x Уровень B Уровень B	Уровень А. Уровень А. Y=-x³+x Уровень B Уровень B	Уровень А. Уровень А. Y=2x²-8x Уровень B Уровень B	Уровень А. Уровень А. Y=-3x²+12x Уровень B Уровень B
Вариант 5	Вариант 6	Вариант 7	Вариант 8
Уровень А. Уровень А. Y=x²+5x+4 Уровень B Уровень B	Уровень А. Уровень А. Y=-x²+2x+15 Уровень B Уровень B	Уровень А. Уровень А. Y=1/3x³-9 Уровень B Уровень B	Уровень А. Уровень А. Y=x³-3x Уровень B Уровень B

Практическое
Занятие №3

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или угловому коэффициенту этой касательной: (f'(x_0)=tgvarphi=k).

Это и есть геометрический смысл производной.

Касательная прямая – прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

Прямая, проходящая через точку касания перпендикулярно касательной, называется нормалью к кривой.

Уравнение касательной к графику функции (y = f(x)) в точке (x_0): (y — y_0 = f'(x_0)(x — x_0)), или (y = f'(x_0)(x — x_0) + f(x_0)).

Из геометрии известно, что произведение угловых коэффициентов перпендикулярных прямых равно −1. Поэтому, зная уравнение касательной, можно сразу записать уравнение нормали в виде: (y — {y_0} = — frac{1}{{f’left( {{x_0}} right)}}left( {x — {x_0}} right)).

Алгоритм решения уравнения касательной к графику функции (y = f(x)):

Вычислить (f(x_0)).
Вычислить производные (f ′(x) и f ′(x_0)).
Внести найденные числа (x_0, f(x_0), f ′(x_0) ) в уравнение касательной и решить его.

Пример. Найдите уравнение касательной к графику функции (f(x) = x^3 – 2x^2 + 1) в точке с абсциссой 2.

Решение:

1) Точка касания (x_0=2). Вычислим (f(x_0)): (f(x_0) = f(2) = 2^3 – 2 cdot 2^2 + 1 = 8 — 8 + 1 = 1).

2) Находим (f ′(x)). Для этого применяем формулы дифференцирования: (f ′(x) = 3x^2 – 2 cdot 2x = 3x^2 – 4x).

Теперь, используя полученное значение (f ′(x)), вычислим (f ′(x_0)): (f ′(x_0) = f ′(2) = 3 cdot2^2 – 4 cdot 2 = 12 – 8 = 4).

3) Итак, у нас есть все необходимые данные: (x_0 = 2, f(x_0) = 1, f ′(x_0) = 4). Подставляем эти числа в уравнение касательной и находим окончательное решение:

(y= f(x_0) + f ′(x_0) (x – x_0) = 1 + 4 cdot(x – 2) = 1 + 4x – 8 = –7 + 4x = 4x – 7).

Ответ: (y = 4x– 7).

Источник