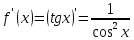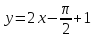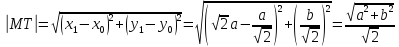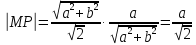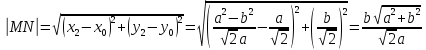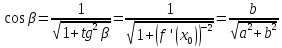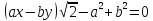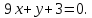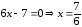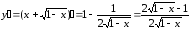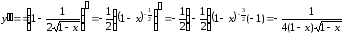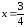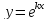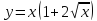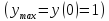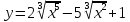Рассмотрим
кривую, уравнение которой имеет вид
Уравнение
касательной к данной кривой в точке
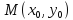

Нормалью
к кривой в данной точке называется
прямая, проходящая через данную точку,
перпендикулярную к касательной в этой
точке.
Уравнение
нормали к данной кривой в точке


Длина
отрезка касательной, заключенного между
точкой касания и осью абсцисс называется
длиной
касательной,
проекция этого отрезка на ось абсцисс
называется подкасательной.
Длина
отрезка нормали, заключенного между
точкой касания и осью абсцисс называется
длиной
нормали,проекция
этого отрезка на ось абсцисс называется
поднормалью.
Пример
17
Написать
уравнения касательной и нормали к кривой


Решение:
Найдем
значение функции в точке

Найдем
производную заданной функции в точке
Уравнение
касательной найдем по формуле (34):
Уравнение
нормали найдем по формуле (35):
Ответ:
Уравнение
касательной :
Уравнение
нормали :
Пример
18
Написать
уравнения касательной и нормали, длины
касательной и подкасательной, длины
нормали и поднормали для эллипса
в
точке

для которой
Решение:
Найдем

параметрически по формуле (10):
Найдем
координаты точки касания

и значение производной в точке касания

Уравнение
касательной найдем по формуле (34):
Найдем
координаты


касательной с осью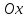
Длина
касательной равна длине отрезка

Согласно
определению, подкасательная

Где
угол
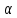
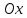

равный
Таким
образом, подкасательная

Уравнение
нормали найдем по формуле (35):
Найдем
координаты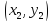

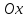
Длина
нормали равна длине отрезка

Согласно
определению, поднормаль
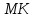
Где
угол

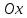

Поэтому,
поднормаль
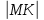
Ответ:
Уравнение
касательной :
Уравнение
нормали :
Длина
касательной

подкасательная
Длина
нормали

Задания
7. Написать
уравнения касательной и нормали:
1. К параболе в точке, абсцисса которой

2.
К окружности

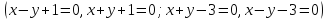
3.
К циклоиде


4.
В каких точках кривой

а)
оси Оx; б) прямой

10.
Промежутки монотонности функции.
Экстремумы функции.
Условие
монотонности функции:
Для
того, чтобы дифференцируемая на


чтобы во всех точках, принадлежащих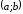

Для
того, чтобы дифференцируемая на

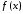
чтобы во всех точках, принадлежащих
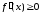
Промежутки,
на которых производная функции сохраняет
определенный знак, называются промежутками
монотонности
функции
Пример
19
Найти
промежутки монотонности функции

Решение:
Найдем
производную функции
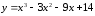
Найдем
промежутки знакопостоянства полученной
производной. Для этого
разложим полученный
квадратный трехчлен на множители:

Исследуем
знак полученного выражения, используя
метод интервалов.
Таким
образом, получаем согласно (36), (37),что
заданная функция возрастает на

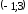
Ответ:
Заданная
функция

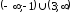

Определение
Функция


максимум (минимум),
если существует такая окрестность
точки

что для всех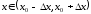
(
Локальный
минимум или максимум функции

экстремумом.
Необходимое
условие существования экстремума.
Пусть
функция
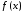
точки
Если функция
в точке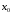
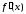

Точка

точкой
функции

если производная

Достаточные
условия наличия экстремума в критической
точке
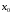
Пусть
точка

Первое
достаточное условие экстремума:
Пусть
функция




Точка

при переходе через
производная
функции меняет знак с плюса на минус.
Точка

переходе через
производная
функции меняет знак с минуса на плюс.
Пример
20
Найти
экстремумы функции

Решение:
Найдем
производную заданной функции
Приравнивая
в полученной производной к нулю числитель
и знаменатель, найдем критические точки:
Исследуем
знак производной, используя метод
интервалов.

Из
рисунка видно, что при переходе через
точку

минус. Следовательно, в точке
локальный максимум.
При
переходе через точку

плюс.
Следовательно,
в точке

локальный минимум.
При
переходе через точку

критическая точка
функции.
Ответ:

локальный максимум,
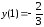
локальный минимум.
Второе
достаточное условие экстремума:
Если
первые
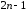

производная функции



причем,
если
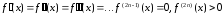
(38)
то
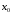
минимум
если

(39)
то
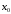
максимум.
Пример
21
Найти
экстремумы функции, пользуясь второй
производной

Решение:
ОДЗ:

Найдем
первую производную заданной функции
Найдем
критические точки функции:
Точку

определена только в левой окрестности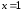
Найдем
вторую производную
Находим
Таким
образом, на основании (39) делаем вывод
о том, что при

Ответ:

локальный максимум.
Задания
8.
Исследовать
на возростание и убывание функции:
|
1. |
2. |
3. |
|
4. |
5. |
6. |
Исследовать
на экстремумы функции:
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вывод уравнения нормали к графику функции
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Замечание 1
Нормаль — это прямая, которая образует с касательной к графику функции угол в $90°$.
Рисунок 1. Нормальный перпендикуляр к графику касательной. Автор24 — интернет-биржа студенческих работ
В связи с тем, что нормаль перпендикулярна к касательной, её угловой коэффициент будет величиной, обратной к угловому коэффициенту касательной:
$k_{норм}=- frac{1}{k_{к}}= -1 frac{1}{f’(x_0)}$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пользуясь полученным выводом, запишем уравнение нормали к графику функции:
$y – y_0 = — frac{1}{f’(x_0)} cdot (x – x_0) left(1right) $, здесь $x_0$ и $y_0$ — координаты точки для которой строится искомая линия, при этом производная в этой точке $f’(x_0) ≠ 0$.
Порядок действий при поиске уравнения нормальной прямой если задана координата $x_0$:
- Вычисляется, чему равен нулевой игрек $y(x_0)$ для функции.
- Затем нужно определить производную.
- Нужно высчитать затем, чему равен $f’(x)$ в точке $x_0$, найденное значение — коэффициент касательной.
- Все найденные значения подставляются в формулу $(1)$.
Напомним также как выглядит само уравнение касательной:
$y – y_0 = f’(x_0) cdot (x – x_0)$.
Пример 1
Найдите уравнение нормали для функции $y=x^2$ в точке $x_0=2$.
Решение:
Производная данной функции составит $y’(x) = 2x$, затем найдём, чему равен наш подопытный кролик-функция в заданной точке $y_0= x^2 = 2^2 = 4$.
Теперь нужно высчитать производную функции в точке $x_0$: $y’(2) = 2 x = 2 cdot 2= 4$.
Все полученные значения расставляем по своим местам в формулу $(1)$:
$y-4=-frac{1}{4} cdot (x – 2)$
Уравнение нормали найдено.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 07.05.2023
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Касательная и нормаль к графику функции
Основные формулы
Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной
Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓
Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓
Определения
Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.
Определение касательной приводится здесь. Уравнение касательной:
.
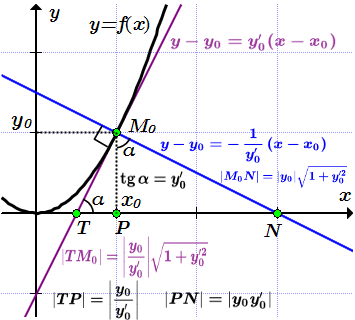
.
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .
Полезные формулы из аналитической геометрии
Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.
Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.
Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .
Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :
Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.
Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.
Уравнение прямой в отрезках, пересекающей оси координат в точках :
.
Примеры решения задач
Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓
Пример 1
Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.
Находим значение функции при :
.
Находим производную:
.
Находим производную в точке :
;
.
Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .
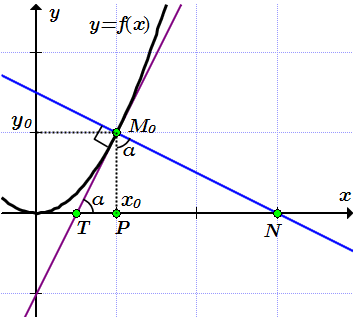
Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.
Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .
Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.
Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка поднормали . Из прямоугольника имеем:
.
Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.
Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .
Пример 2
Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .
Находим значения переменных при .
;
.
Обозначим эту точку как .
Находим производные переменных x и y по параметру t .
;
;
;
;
.
Подставляя , находим производную y по x в точке .
.
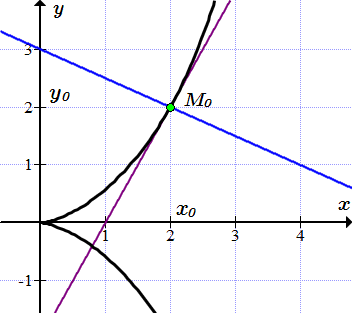
Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.
Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.
Уравнение касательной: .
Уравнение нормали: .
Пример 3
Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .
Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.
Находим производную в заданной точке, подставляя .
;
.
Находим уравнение касательной по формуле (2).
;
;
;
.
Находим уравнение нормали по формуле (3).
;
;
;
.
Касательная и нормаль к циссоиде изображены на рисунке ⇑.
Уравнение касательной: .
Уравнение нормали: .
Пример 4
Найти угол между кривыми и .
Найдем множество точек пересечения кривых, решая систему уравнений.
Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .
Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.
Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.
Вывод формулы для угла между кривыми
Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .
Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .
Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.
В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .
На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .
При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.
1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).
2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:
.
Этот случай изображен на рисунке ⇑.
3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).
Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.
Автор: Олег Одинцов . Опубликовано: 30-06-2021
Нормальный вектор прямой, координаты нормального вектора прямой
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
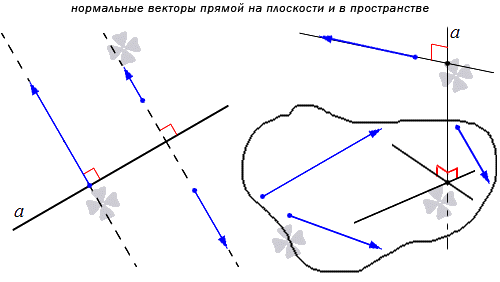
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .
Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Задана прямая вида 2 x + 7 y — 4 = 0 _, найти координаты нормального вектора.
По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Указать нормальный вектор для заданной прямой y — 3 = 0 .
По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y — 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .
Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.
Найти координаты нормального вектора, если дано уравнение прямой x 1 3 — y = 1 .
Для начала необходимо перейти от уравнения в отрезках x 1 3 — y = 1 к уравнению общего вида. Тогда получим, что x 1 3 — y = 1 ⇔ 3 · x — 1 · y — 1 = 0 .
Отсюда видно, что координаты нормального вектора имеют значение 3 , — 1 .
Ответ: 3 , — 1 .
Если прямая определена каноническим уравнением прямой на плоскости x — x 1 a x = y — y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0
Для решения можно выбирать любой удобный способ.
Найти нормальный вектор заданной прямой x — 2 7 = y + 3 — 2 .
Из прямой x — 2 7 = y + 3 — 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , — 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , — 2 ) .
Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , — 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x — 2 · n y = 0 .
Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 — 2 · n y = 0 ⇔ n y = 7 2 .
Значит, нормальный вектор имеет координаты 1 , 7 2 .
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
x — 2 7 = y + 3 — 2 ⇔ 7 · ( y + 3 ) = — 2 · ( x — 2 ) ⇔ 2 x + 7 y — 4 + 7 3 = 0
Полученный результат координат нормального вектора равен 2 , 7 .
Ответ: 2 , 7 или 1 , 7 2 .
Указать координаты нормального вектора прямой x = 1 y = 2 — 3 · λ .
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
x = 1 y = 2 — 3 · λ ⇔ x = 1 + 0 · λ y = 2 — 3 · λ ⇔ λ = x — 1 0 λ = y — 2 — 3 ⇔ x — 1 0 = y — 2 — 3 ⇔ ⇔ — 3 · ( x — 1 ) = 0 · ( y — 2 ) ⇔ — 3 · x + 0 · y + 3 = 0
Отсюда видно, что координаты нормального вектора равны — 3 , 0 .
Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .
Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .
Нормальный вектор прямой
Вы будете перенаправлены на Автор24
В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.
Нормаль – синоним для слова перпендикуляр.
Общее уравнение прямой на плоскости выглядит как $Ax + By + C = 0$. Подставляя в него различные значениях $A$, $B$ и $C$, в том числе нулевые, можно определить любые прямые.
Можно выразить уравнение прямой и другим способом:
Это уравнение прямой с угловым коэффициентом. В нем геометрический смысл коэффициента $k$ заключается в угле наклона прямой по отношению к оси абсцисс, а независимого члена $b$ — в расстоянии, на которое прямая отстоит от центра координатной плоскости, т.е. точки $O(0; 0)$.
Рисунок 1. Варианты расположения прямых на координатной плоскости. Автор24 — интернет-биржа студенческих работ
Нормальное уравнение прямой можно выразить и в тригонометрическом виде:
$x cdot cos <alpha>+ y cdot sin <alpha>- p = 0$
где $alpha$ — угол между прямой и осью абсцисс, а $p$ — расстояние от начала координат до рассматриваемой прямой.
Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:
- когда угловой коэффициент положителен, направляющий вектор прямой идёт снизу вверх;
- когда угловой коэффициент отрицателен, направляющий вектор прямой идёт сверху вниз;
- когда угловой коэффициент равен нулю, описываемая им прямая параллельна оси абсцисс;
- для прямых, параллельных оси ординат, углового коэффициента не существует, поскольку тангенс 90 градусов является неопределенной (бесконечной) величиной.
Готовые работы на аналогичную тему
Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.
Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:
$y — y_0 = k cdot (x — x_0)$
Таким образом, геометрически прямую на координатной всегда можно выразить с помощью угла и расстояния от начала координат. В этом и заключается смысл нормального вектора к прямой — самого компактного способа записи ее положения, если известны координаты хотя бы одной точки, принадлежащей этой прямой.
Вектором нормали к прямой, иначе говоря, нормальным вектором прямой, принято называть ненулевой вектор, перпендикулярный рассматриваемой прямой.
Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.
Обозначив нормальный вектор прямой как $vec(n_1; n_2)$, а координаты точки как $x_0$ и $y_0$, можно представить общее уравнение прямой на плоскости по точке и вектору нормали к прямой как
$n_1 cdot (x — x_n) + n_2 cdot (y — y_0) = 0$
Таким образом, координаты вектора нормали к прямой пропорциональны числам $A$ и $B$, присутствующим в общем уравнении прямой на плоскости. Следовательно, если известно общее уравнение прямой на плоскости, то можно легко вывести и вектор нормали к прямой. Если прямая, задана уравнением в прямоугольной системе координат
то нормальный вектор описывается формулой:
При этом говорят, что координаты нормального вектора «снимаются» с уравнения прямой.
Нормальный к прямой вектор и ее направляющий вектор всегда ортогональны по отношению друг к другу, т.е. их скалярные произведения равны нулю, в чем легко убедиться, вспомнив формулу направляющего вектора $bar
(-B; A)$, а также общее уравнение прямой по направляющему вектору $bar
(p_1; p_2)$ и точке $M_0(x_0; y_0)$:
В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:
$bar
cdot bar = -B cdot A + A cdot B = 0 implies bar
perp bar$
Всегда можно составить уравнение прямой, зная координаты принадлежащей ей точки и нормального вектора, поскольку направление прямой следует из его направления. Описав точку как $M(x_0; y_0)$, а вектор как $bar(A; B)$, можно выразить уравнение прямой в следующем виде:
$A(x — x_0) + B(y — y_0) = 0$
Составить уравнение прямой по точке $M(-1; -3)$ и нормальному вектору $bar(3; -1)$. Вывести уравнение направляющего вектора.
Для решения задействуем формулу $A cdot (x — x_0) + B cdot (y — y_0) = 0$
Подставив значения, получаем:
$3 cdot (x — (-1)) — (-1) cdot (y — (-3)) = 0$ $3 cdot (x + 1) — (y + 3) = 0$ $3x + 3 — y — 3 = 0$ $3x — y = 0$
Проверить правильность общего уравнения прямой можно «сняв» из него координаты для нормального вектора:
$3x — y = 0 implies A = 3; B = -1 implies bar(A; B) = bar(3; -1),$
Что соответствует числам исходных данных.
Подставив реальные значения, проверим, удовлетворяет ли точка $M(-1; -3)$ уравнению $3x — y = 0$:
Равенство верно. Осталось лишь найти формулу направляющего вектора:
$bar
(-B; A) implies bar
(1; 3)$
Ответ: $3x — y = 0; bar
(1; 3).$
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 03 2022
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnyj-vektor-prjamoj-koordinaty-normalnogo-vek/
http://spravochnick.ru/matematika/normalnyy_vektor_pryamoy/
Рассмотрим график функции в декартовой системе координат
(рис. 10.2). Возьмем на графике точку
и точку
. Проведем через эти точки прямую
. Эта прямая называется Секущей. Ее уравнением будет
, а угловой коэффициент этой прямой равен тангенсу угла наклона секущей:
Если то секущая MN поворачивается вокруг точки
и переходит в касательную с угловым коэффициентом
Если , то секущая MN поворачивается вокруг точки М и в пределе переходит в касательную с угловым коэффициентом

Угловой коэффициент касательной к графику функции в данной точке равен значению производной функции в этой
точке: .
Геометрический смысл производной состоит в том, что производная равна угловому коэффициенту касательной к графику функции в данной точке.
Значение производной в точке
равно тангенсу угла наклона касательной (рис. 10.3).
Нормаль – это прямая, перпендикулярная к касательной в точке касания (рис. 10.3).
Уравнение касательной к кривой в точке
запишем как уравнение прямой, которая проходит через заданную точку:
.
Уравнение нормали к кривой в точке
запишем так:

Пример 1. Напишите уравнение касательной к графику функции в точке с абсциссой
.
Решение. 1) Найдем значение функции, если :
.
2) Найдем первую производную функции: .
3) Найдем значение производной, если :
.
4) Запишем уравнение касательной, которая проходит через данную точку :
или
.
Ответ. Уравнение касательной: .
Пример 2. Напишите уравнение нормали к графику функции в точке с абсциссой
.
Решение. 1) Найдем значение функции, если :
.
2) Найдем первую производную функции: .
3) Найдем значение производной, если :
.
4) Запишем уравнение нормали, которая проходит через данную точку :

.
Ответ. Уравнение нормали: .
Рассмотрим задачу о свободном падении тела и найдем мгновенную скорость его движения.
Из физики мы знаем, что 
За время тело проходит расстояние

– расстояние

, откуда
.
Приращение функции будет равно:
Найдем предел отношения приращения функции к приращению ее аргумента T , если ΔT Стремится к нулю:

В левой части равенства мы получили значение производной функции , а в правой части значение мгновенной скорости тела в момент времени T0.
Физический смысл производной. Производная функции в точке
есть мгновенная скорость изменения функции в точке
, т. е. скорость протекания процесса, который описывается зависимостью
.
Например, если дана функция , то ее производная будет
, тогда значение производной в точке
будет
, а значение производной в точке
будет
. Это значит, что в точке
функция изменяется в 4 раза быстрее аргумента
, а в точке
изменяется в 6 раз быстрее (т. е. различная скорость изменения функции или протекания процесса). В этом и состоит физический смысл производной.
Операция нахождения (взятия) производной функции называется Дифференцированием функции.
Ответьте на вопросы
1. Что показывает угловой коэффициент K в уравнении прямой ?
2. Чему равен угловой коэффициент касательной к кривой в точке ?
3. Как найти угловой коэффициент нормали к кривой в точке ?
4. В чем состоит геометрический смысл производной?
5. В чем состоит физический смысл производной?
| < Предыдущая | Следующая > |
|---|