6.1 Цель работы
Исследование дисперсии стеклянной призмы и определение показателя преломления прозрачного вещества по углу наименьшего отклонения луча призмой.
6.2 Теоретическое введение
6.2.1 Прохождение света через границу раздела двух сред
При падении света на границу раздела двух сред световые волны частично отражаются, возвращаясь обратно в первую среду (отражение света), частично переходят во вторую среду, причем при наклонном падении изменяется направление распространения волн (преломление света на рисунке 6.1).
|
Падающий луч i i’ |
Отраженный луч |
|||||
|
Преломленный луч |
||||||
|
r |
||||||
Рисунок 6.1 − Отражение и преломление лучей на границе двух прозрачных сред
Отражение и преломление света происходит с соблюдением соответствующих закономерностей [1].
Закон отражения света. Отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной к границе раздела двух сред в точке падения; угол отражения i′равен углу падения i:
i′= i.
Закон преломления света. Преломленный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной к границе
55

раздела двух сред в точке падения; отношение синуса угла падения i к синусу угла преломления r есть величина постоянная для данных веществ:
|
sin i |
= n21 , |
(6.1) |
|
sin r |
где n21 − величина постоянная, не зависящая от угла падения и называемая показателем преломления второй среды, относительно первой. Численное значение n21 определяется свойствами обеих сред, через границу раздела которых проходит свет, а также зависит от длины волны света.
В случае преломления света, как и при отражении, имеет место принцип обратимости световых лучей. Согласно этому принципу луч, падающий на границу раздела из второй среды под углом r, переходит в первую среду, преломившись под углом i, то есть луч, идущий в обратном направлении, проходит тот же путь, что и прямой луч. Закон преломления для обратного луча будет иметь вид:
|
sin r = n |
, |
(6.2) |
|
sin i |
12 |
|
где n12 − показатель преломления первой среды относительно второй.
Из сравнения формул (6.1) и ( 6.2) следует, что величины n21 и n12 являются взаимообратными:
n21 = n1 .
12
Показатель преломления среды относительно вакуума называют
абсолютным показателем преломления этой среды. Абсолютный показатель преломления самого вакуума считают равным единице. Очень близок к единице абсолютный показатель преломления воздуха, поэтому значения показателей преломления веществ относительно воздуха близки к значениям абсолютных показателей преломления.
Согласно волновой теории между относительными показателями преломления n21 и n12 двух сред и скоростями света υ1 и υ2 в этих средах имеет место следующая зависимость:
|
n |
21 |
= |
υ1 |
(6.3) |
|||
|
υ |
|||||||
|
и |
2 |
||||||
|
υ2 |
|||||||
|
n |
= |
. |
(6.4) |
||||
|
12 |
υ |
||||||
|
1 |
56

Абсолютный показатель преломления среды определяется по формуле:
|
n = |
c |
, |
(6.5) |
|
υ |
где с − скорость света в вакууме, υ − скорость света в данной среде. Соотношения (6.3), (6.4) и ( 6.5) выражают физический смысл
показателей преломления. Исходя из них, можно найти связь между относительными n21 и n12 и абсолютными n1 и n2 показателями преломления двух сред. Учитывая, что n1=с/υ1 и n2=с/υ2, получаем:
|
n1 |
= |
υ2 |
. |
(6.6) |
|
|
n2 |
|||||
|
υ1 |
Из сравнения формул ( 6.3) и ( 6.4) с ( 6.6) следует, что
n21 = n2
n1
и
n12 = n1 ,
n2
то есть относительные показатели преломления двух сред равны отношению их абсолютных показателей преломления.
Известно, что световые волны распространяются в вакууме с
постоянной скоростью с = 3 108 м/с. При переходе из вакуума в какуюлибо среду скорость света изменяется. Это обусловлено взаимодействием световых электромагнитных волн с заряженными частицами (электронами и ионами) вещества. Совершая вынужденные колебания, эти частицы создают вторичную электромагнитную волну. При сложении первичной и вторичной волн образуется результирующая волна, скорость распространения которой зависит от соотношения частоты падающего света и частоты собственных колебаний частиц. При близких или совпадающих частотах скорость света в веществе значительно отличается от его скорости в вакууме.
Согласно электромагнитной теории скорость света в любой среде определяется ее диэлектрической ε и магнитной µ проницаемостями [1]:
|
υ = |
c |
. |
(6.7) |
|||||
|
ем |
||||||||
|
Из сравнения формул (6.5) и (6.7) следует, что |
||||||||
|
n = |
. |
(6.8) |
||||||
|
ем |
||||||||
|
Так как |
ε и |
µ |
зависят от частоты электромагнитных колебаний, то |
|||||
|
скорость |
света, |
а |
вместе с ней и |
показатель преломления |
среды, |
57
оказываются функциями этой частоты. Но поскольку λ0=с/ν, где λ0−длина волны в вакууме; ν −частота, то
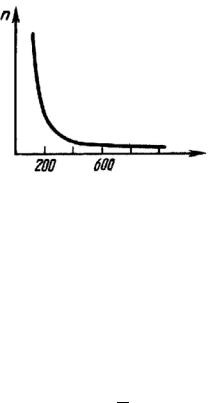
Дисперсией света называется зависимость показателя преломления n вещества от частоты ν (длины волны λ0) света или зависимость фазовой скорости υ световых волн от частоты ν. На рисунке 6.2 приведена зависимость (6.9) в видимой части спектра для всех прозрачных бесцветных веществ. С уменьшением длины волны показатель преломления увеличивается со все возрастающей скоростью dn/dλ0. Величина dn/dλ0 называется дисперсией вещества. Если модуль dn/dλ0
λo, нм
Рисунок 6.2 − Зависимость показателя преломления от длины волны
с уменьшением λ0 увеличивается, то дисперсия носит название нормальной. Рисунок 6.2 соответствует случаю нормальной дисперсии. Для большинства прозрачных сред магнитная проницаемость µ близка к единице. Чем больше частота колебаний, тем ближе µ к единице. Для световых частот формула (6.8) имеет вид:
n = 
где ε − значение диэлектрической проницаемости, найденное для электромагнитных колебаний световой частоты, то есть та часть общего его значения, которая обусловлена смещением зарядов в атомах и молекулах вещества под действием световых колебаний.
Диэлектрические и магнитные свойства, а вместе с ними и показатель преломления среды, зависят от различных других ее свойств, например, от плотности (газы), состава примесей (стекло), концентрации (прозрачные растворы), температуры и др. Изменение этих свойств среды приводит к изменению ее преломляющей способности. Иногда оказываются необходимыми материалы, показатель преломления которых зависит от тех или иных свойств, например, температуры и др. В других случаях
58
требуются материалы, не обладающие подобной зависимостью n от этих факторов. В то же время, зная преломляющие свойства среды, можно судить о других ее свойствах, например, концентрации раствора.
Значения показателей преломления для некоторых веществ относительно воздуха приведены в таблице 6.1 (данные относятся к желтому цвету).
Таблица 6.1 − Показатель преломления
|
Вещество |
Показатель преломления |
|
Вода (при 20 0С) |
1,33 |
|
Кедровое масло (при 20 0С) |
1,52 |
|
Сероуглерод (при 20 0С) |
1,63 |
|
Лед |
1,31 |
|
Каменная соль |
1,54 |
|
Кварц |
1,54 |
|
Рубин |
1,76 |
|
Алмаз |
2,42 |
|
Различные сорта стекла |
От 1,47 до 2,04 |
6.2.2 Преломление света в трехгранной призме
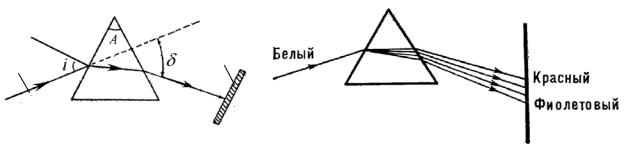
Рассмотрим ход монохроматического луча сквозь трехгранную призму, показанный на рисунке 6.3. Двухгранный угол, заключенный между двумя боковыми гранями призмы, на которых луч преломляется, называется преломляющим углом, а ребро этого угла − преломляющим ребром призмы. От положения призмы относительно направления падающего луча зависит, какой ее угол оказывается преломляющим. Так для луча на рисунке 6.3 преломляющим будет угол А.
Рисунок 6.3 − Преломление света в Рисунок 6.4 − Разложение белого света
призме с помощью призмы
59
В результате двух преломлений вышедший из призмы луч света отклоняется на угол δ по отношению к направлению падающего луча.
Угол отклонения δ зависит от угла падения i, преломляющего угла призмы А, а также от вещества призмы и длины волны света. Можно показать, что при симметричном прохождении света через призму угол отклонения имеет минимальное значение δmin. В этом случае показатель преломления n определяется формулой [2]:
|
sin |
A +δmin |
|||||
|
n( λ ) = |
. |
(6.10) |
||||
|
2 |
||||||
|
sin |
A |
|||||
|
2 |
||||||
Таким образом, если известен угол А, то определение показателя преломления призмы для каждой длины световой волны сводится к измерению соответствующего угла δmin.
Теперь рассмотрим особенности прохождения белого луча через призму, показанные на рисунке 6.4. Белый луч состоит из множества монохроматических лучей, каждому из которых соответствует определенная величина показателя преломления (см. рисунок 6.2, формула (6.10)). Вследствие этого при преломлении на поверхности призмы происходит разложение белого луча света на составляющие монохроматические лучи. Изображение светящейся щели принимает вид спектра. Больше других из видимых лучей преломляется фиолетовый, меньше − красный.
В данной работе выражение (6.10) представляет расчетную формулу для определения n(λ).
6.2.3 Угловая дисперсия призмы
Зависимость показателя преломления от длины волны света позволяет использовать трехгранную призму в качестве спектрального прибора, с помощью которого излучение исследуемого источника света разлагается в спектр по длинам волн. Одна из основных характеристик спектрального прибора − угловая дисперсия. Она характеризует способность прибора пространственно разделять пучки лучей различных длин волн. Мерой угловой дисперсии является отношение dδ / dλ, то есть
величина, равная производной угла отклонения по длине волны; dδ − угловое расстояние между двумя спектральными линиями, отличающи-
60
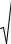
мися по длинам волн на dλ . Для трехгранной призмы угловая дисперсия вблизи угла наименьшего отклонения равна [2]:
|
dδmin |
dδmin |
dn |
2sin |
A |
dn |
|||||||||||
|
= |
= |
2 |
. |
(6.11) |
||||||||||||
|
dλ |
dn |
dλ |
dλ |
|||||||||||||
|
−n2sin2 |
A |
|||||||||||||||
|
1 |
||||||||||||||||
|
2 |
||||||||||||||||
Формула (6.11) показывает, что угловая дисперсия призмы с данным преломляющим углом А тем больше, чем больше показатель преломления n и чем больше дисперсия dn / dλ вещества призмы. Поэтому призмы спектрографов делают из стекол с возможно большим показателем преломления и возможно большей дисперсией (из так называемых тяжелых флинтов).
6.2.4 Фазовая и групповая скорости света
В диспергирующей среде, то есть среде, у которой показатель преломления зависит от длины волны n(λ), свет с различными длинами волн распространяется с различными скоростями. Действительно, согласно выражению (6.5), любая монохроматическая составляющая света распространяется со скоростью
|
υ = |
c |
. |
(6.12) |
|
n |
|||
|
А так как n=n(λ), то и υ=υ(λ). Скорость, определяемую |
соотношени- |
ем (6.12), называют фазовой; она характеризует скорость распространения определенной фазы монохроматической световой волны.
Любая реальная световая волна представляет собой суперпозицию монохроматических составляющих с длинами волн от λ − λ до λ + λ (ее называют поэтому группой волн). Чем менее монохроматичен свет, тем шире у него этот спектральный интервал, и наоборот. Так как в диспергирующей среде отдельные составляющие группы волн распространяются с различными скоростями, то форма светового импульса с течением времени будет изменяться. Максимум распределения энергии в световом импульсе совпадает с его «центром тяжести», где амплитуда результирующего колебания максимальна. Как показал Рэлей, скорость, с которой распространяется максимум амплитуды группы волн, определяются формулой [3]:
|
u =υ −λ |
dυ |
, |
(6.13) |
|
|
dλ |
||||
61
где все величины в правой части уравнения (фазовая скорость υ, длина
волны λ и dυ/dλ) относятся к середине спектрального интервала данной группы волн.
Эта скорость называется групповой; она характеризует скорость распространения энергии в реальной световой волне.
Имея в виду, что фазовая скорость υ=c/n, формулу (6.13) нетрудно преобразовать к другому виду:
|
λ |
dn |
|||
|
u =υ 1+ |
n |
. |
(6.14) |
|
|
dλ |
Следовательно, чем больше дисперсия вещества dn/dλ, тем больше групповая скорость отличается от фазовой. Так как практически все приемники света реагируют на усредненное значение квадрата напряженности электрического поля Е2 , то на опыте всегда измеряется групповая скорость u (метод Физо, Майкельсона и т.д.). Фазовую скорость нельзя измерить непосредственно. Эту величину определяют из соотношения n = c/υ, где n предварительно измеряется тем или иным способом.
Итак, зная зависимость n(λ), можно определить зависимость фазовой скорости от длины волны (то есть закон дисперсии света для данной среды) и групповую скорость света.
Измерение преломляющего угла А призмы и угла наименьшего отклонения δmin производится при помощи гониометра (от греч. Gōnia − угол и…метр).
6.3 Описание установки
Работа выполняется на гониометре − приборе, предназначенном для измерений углов. Прибор показан на рисунке 6.5. Он состоит из коллиматора К, зрительной трубы Т, столика С, на котором располагается изучаемый объект, лимба (круга с угловыми делениями), скрытого в корпусе, и отсчетного микроскопа М. Зрительная труба укреплена на подвижном кронштейне − алидаде А. Лимб, алидада и столик прибора могут вращаться вокруг вертикальной оси. Коллиматор представляет собой трубу, на одном конце которой имеется объектив О, на другом − узкая щель, и служит для создания параллельного пучка света. Для этого
62
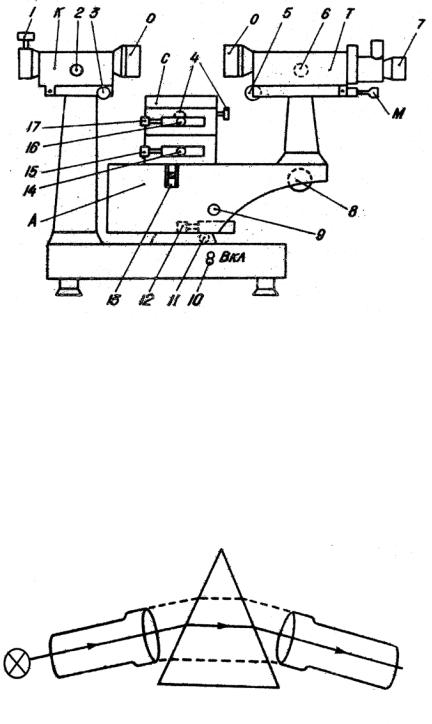
щель должна быть установлена в фокальной плоскости системы линз коллиматора.
1−микрометрический винт; 2,6 − фокусировочные винты; 3,5 − юстировочные винты;
|
4 |
− винты наклона |
столика; |
7 − окуляр; |
8 − маховичок отсчетного |
микрометра; |
|
9 |
− маховичок самостоятельного |
вращения |
лимба; 10 − общий выключатель; 11, |
||
|
14, 16 − стопорные |
винты; |
13 − |
механизм соединения лимба |
с алидадой; |
|
|
12, 15, 17 − микрометрические винты |
Рисунок 6.5 − Общий вид гониометра
Ход лучей в установке показан на рисунке 6.6. Из коллиматора К на
П
Рисунок 6.6 − Ход лучей в установке
грань призмы П направляют пучок лучей и в фокальной плоскости объектива зрительной трубы Т получают изображение щели в отраженном или преломленном (этот случай изображен на рисунке) свете. По шкале лимба отмечают положение зрительной трубы. Отсчет делений по лимбу производится с помощью отсчетного микроскопа. Поле зрения отсчетного микроскопа приведено на рисунке 6.7. Чтобы снять отсчет по лимбу,
63
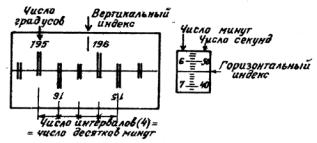
необходимо повернуть маховичок 8 (см. рисунок 6.5) оптического микрометра М настолько, чтобы верхние и нижние штрихи лимба в левом
Рисунок 6.7 − Поле зрения отсчетного микроскопа
окне точно совместились. Тогда число градусов будет равно ближайшей цифре, видимой слева от вертикального индекса верхней шкалы (195). Число десятков минут равно числу интервалов, заключенных между верхним штрихом, который соответствует отсчитанному числу градусов, и нижним оцифрованным штрихом (15), отличающимся от верхнего на 180 0. Число единиц минут отсчитывается по шкале микрометра в правом окне по левому ряду чисел (ближайшее число от горизонтального индекса сверху). Число десятков секунд − в том же окне по правому ряду чисел (по штриху, соответствующему отсчитанному числу единиц минут). Число единиц секунд равно числу делений между штрихом, соответствующим отсчету десятков секунд, и неподвижным горизонтальным индексом. Положение, показанное на рисунке 6.7, соответствует отсчету 195046′36′′.
В качестве источника света с линейчатым спектром используется ртутная лампа. Ее наиболее характерные спектральные линии указаны в таблице 6.4.
6.4 Указания по технике безопасности
Перед щелью коллиматора устанавливается ртутная лампа высокого давления, которая питается от универсального источника питания. Источник питания включается в сеть переменного тока 220 В. Лампа для защиты окружающих от осколков стекла при взрыве помещена в защитный кожух.
Перед началом работы необходимо надежно заземлить корпуса гониометра и источника питания ртутной лампы.
6.5 Задание 1. Определение преломляющего угла призмы
6.5.1 Измерение преломляющего угла призмы методом отражения
Пусть на призму перпендикулярно грани, лежащей против преломляющего угла А, падает пучок параллельных лучей как показано на рисунке 6.8). Луч 1-й (изображение щели) отражается от правой грани, луч 2-й −
64
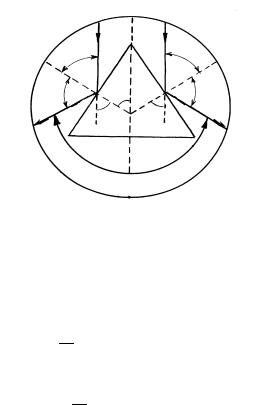
от левой (если смотреть со стороны падающего луча). Лимб на рисунке изображен в виде окружности. На поверхности лимба по часовой стрелке нанесена шкала с делениями от 00 до 3600.
|
1800 |
||||||
|
I |
A |
II |
γ |
|||
|
γ |
||||||
|
900 |
γ |
D |
γ |
γ |
γ |
2700 |
|
γ |
C |
|||||
|
α1 |
α2 |
|||||
|
00 |
||||||
|
3600 |
Рисунок 6.8 − К выводу соотношения (6.17)
Из ADC определим угол А:
A2 +γ + 900 =1800 ,
A2 = 900 −γ ,
A =1800 − 2γ ,
где γ − угол падения.
Обозначим через α1 и α2 отсчеты по лимбу. Тогда
α2 = α1 + 4γ.
Откуда
Подставляя выражение (6.16) в формулу (6.15), получим:
|
А = 1800 − |
α2 −α1 |
при α1 < α2 , |
(6.17) |
|||
|
2 |
||||||
|
А = 180 |
0 |
− |
3600 |
−(α1 −α2 ) |
при α1 > α2 . |
(6.18) |
|
2 |
||||||
65
Из выражений (6.17) и (6.18) следует, что для определения преломляющего угла А нужно снять отсчеты α1 и α2 по лимбу.
6.5.2 Порядок выполнения работы
6.5.2.1 Установить на столик С гониометра призму так, чтобы одна из граней была перпендикулярна к плоскости столика (см. рисунок 6.5). Грань призмы, расположенную против преломляющего угла А (зачерненная грань), установить параллельно плоскости выходного отверстия коллиматора (то есть перпендикулярно падающему на призму лучу) так, чтобы она была обращена к объективу О зрительной трубы Т. Выходящий из коллиматора пучок света должен одновременно падать на обе преломляющие грани призмы.
6.5.2.2 Невооруженным глазом найти направление, в котором видно изображение щели в правой грани призмы (правая и левая грани призмы определяются со стороны падающего луча). Раскрепить винтом 11 зрительную трубу и, поворачивая ее в горизонтальной плоскости, найти положение, когда отраженные от этой грани лучи попадают в поле зрения трубы. Если изображение щели расплывчатое, то фокусировочным винтом 6 установить его на ясную видимость.
6.5.2.3 Совместить изображение щели коллиматора с вертикалью визирного креста и винтом 11 закрепить зрительную трубу. Микрометрическим винтом 12 добиться более точного совмещения середины изображения щели с центром визирного креста.
6.5.2.4 Вращением оправы окуляра микроскопа М (см. рисунок 6.5) нужно добиться отчетливого видения шкалы лимба и сделать по нему отсчет. Результат измерения записать в таблицу 6.2.
Таблица 6.2 − Результаты измерений преломляющего угла
|
Номер |
Отсчеты по лимбу |
А |
Аср |
||
|
α1 |
α2 |
||||
|
опыта |
|||||
|
(правая грань) |
(левая грань) |
||||
|
1 |
|||||
|
2 |
|||||
|
3 |
|||||
|
4 |
|||||
|
5 |
6.5.2.5 Повторить действия, предусмотренные в 6.5.2.2 − 6.5.2.4, для лучей, отраженных от левой грани призмы.
6.5.2.6 Опыт следует повторить не менее пяти раз для каждой из граней призмы, отсчитывая поочередно α1 и α2 .
6.5.2.7 По данным таблицы 6.2, воспользовавшись формулой (6.17) (при α1 < α2) или (7.18) (при α1 > α2), подсчитать в каждом опыте
66
преломляющий угол А и найти его среднее значение Аср. Результаты вычислений занести в таблицу 6.2.
6.5.2.8 Сформулировать вывод.
6.6 Задание 2. Определение показателя преломления призмы
6.6.1 Порядок выполнения работы
6.6.1.1 Поместить призму на столик так, чтобы свет падал на преломляющую грань под острым углом со стороны основания (зачерненной грани) призмы.
6.6.1.2 Невооруженным глазом найти направление, в котором видно разложенное в спектре изображение щели коллиматора или, что то же самое, направление преломленных призмой лучей. Освободить стопорный винт 11 (см. рисунок 6.5) и, поворачивая зрительную трубу, отыскать цветной спектр. Установить трубу так, чтобы желтые линии спектра оказались в поле зрения трубы.
6.6.1.3 Раскрепить винтом 16 столик гониометра и поворачивать его так, чтобы желтые линии спектра в поле зрения трубы приближались к направлению не отклоненного светового пучка (или, по другому, нулевому положению трубы); соответственно перемещать и зрительную трубу. Прекратить вращать столик с призмой в тот момент, когда линии спектра, достигнув крайнего положения, остановятся и начнут смещаться в противоположную сторону, хотя вращение столика производится в том же направлении. Если окажется, что при повороте столика наблюдаемые линии спектра совсем уходят из поля зрения, то зрительную трубу следует повернуть вслед за ними так, чтобы их место остановки оказалось в середине поля зрения трубы.
6.6.1.4 При раскрепленном винте 11 установить зрительную трубу так, чтобы ее визирная линия совпала с крайней желтой линией спектра (λ=579,1 нм). Стопорным винтом 11 зафиксировать трубу в этом положении. Тщательно сфокусировать линию винтом 6 (при плохой видимости − дополнительно винтом 2).
6.6.1.5 Небольшим поворотом столика проверить, соответствует ли положение призмы моменту остановки выбранной желтой линии. Если окажется, что наблюдаемая линия спектра смещается несколько правее визирной линии или не достигает ее слева, то необходимое перемещение зрительной трубы следует произвести при помощи ходового микрометрического винта 12, совместив середину спектральной линии с центром визирного креста. Положение призмы, при котором спект-
ральная линия останавливается, соответствует углу наименьшего отклонения для данной линии.
6.6.1.6 Проследить через окуляр микрометра, чтобы соответствующий отсчет по шкале лимба не выходил за пределы интервала углов от 900 до 2700. В противном случае, при раскрепленном винте 14 следует нажать
67

на маховичок 9 (см. рисунок 6.5) и, вращая его, вве сти требуемый участок лимба (это нужно только для того, чтобы при дальнейших измерениях не переходить через нуль шкалы лимба, что вызвало бы некоторые усложнения при определении разности отсчетов). В этом положении закрепить лимб на оси прибора винтом 14.
6.6.1.7 Сделать отсчет α на шкале лимба. Повторить это измерение (6.6.1.4, 6.6.1.5) не менее трех раз и найт и среднее значение αср. Все данные занести в таблицу 6.3.
6.6.1.8 Повторить действия, предусмотренные в 6.6.1.4 − 6.6.1.7, для всех остальных линий спектра, указанных в таблице 6.4 (всего 10 линий). При выборе спектральных линий руководствоваться их расположением, показанным на рисунке 6.9.
Таблица 6.3 − Результаты измерений показателей преломления
|
λ, |
Номер |
α |
αср |
αо |
αо ср |
δmin |
n |
υ, |
|
нм |
изм. |
м/с 108 |
||||||
|
579,1 |
1 |
|||||||
|
2 |
||||||||
|
3 |
||||||||
|
576,9 |
1 |
− | | − |
− | | − |
|||||
|
2 |
||||||||
|
3 |
||||||||
|
− | | − |
− | | − |
Примечание − Таблицу необходимо подготовить на отдельной странице для десяти спектральных линий, указанных в таблице 6.4.
6.6.1.9 Убрать призму со столика гониометра и, раскрепив винт 11, повернуть зрительную трубу так, чтобы видеть щель коллиматора (в поле зрительной трубы должна появиться белая линия). Совместить центр визирного креста с серединой этой линии и опять закрепить трубу винтом 11. Тщательно сфокусировать линию винтом 6 и винтом тонкой наводки 12 более точно совместить центр визирного креста с серединой линии. Сделать отсчет αо по лимбу. Это измерение также повторить не менее трех раз и найти среднее значение αо ср. Результаты занести в таблицу 6.3.
6.6.2 Обработка результатов измерений
6.6.2.1 На основе данных таблицы 6.3 для каждой линии спектра вычислить угол наименьшего отклонения по формуле:
δmin = αср −αо ср .
68
6.6.2.2 По формулам (6.10) и (6.12) вычислить соответственно показатель преломления n и фазовую скорость υ для всех λ. Результаты вычислений δmin, n и υ занести в таблицу 6.3.
6.6.2.3 По данным таблицы 6.3 построить дисперсионные кривые −
графики зависимости n и υ от λ. Графики выполнить на миллиметровой бумаге, градуированные кривые провести плавно с помощью лекала и карандаша.
6.6.2.4 Из графиков определить дисперсию материала n/Δλ для
желтой линии спектра и величину υ/Δλ − для зеленой.
6.6.2.5 По формуле (6.11) определить угловую дисперсию призмы
( δmin/Δλ)теор в угл. мин/нм для желтой линии спектра, а по формуле (6.13) − групповую скорость u для зеленой линии (значение u можно вычис-
лить также по формуле (6.14), предварительно определив из графика n=n(λ) дисперсию вещества n/Δλ для данной линии спектра).
6.6.2.6 По данным таблицы 6.3 вычислить угловую диспер-
сию (Δδmin/ λ) эксп для желтой линии (также в угл. мин/нм).
6.6.2.7 Сформулировать выводы, в которых сравнить теоретическое значение (Δδmin/ λ) теор с экспериментальным (Δ δmin/ λ) эксп, определить
по виду графика n=n(λ) тип дисперсии вещества (нормальная или аномальная), указать фазовую и групповую скорости света для зеленой линии спектра.
6.7 Справочные сведения
Таблица 6.4 − Длины волн наиболее характерных спектральных линий ртути
|
Длина волны, нм |
Линия спектра |
|
579,1 |
Желтая (крайняя) |
|
576,9 |
Желтая |
|
546,1 |
Зеленая |
|
495,9 |
Зелено-голубая |
|
491,6 |
Голубая |
|
435,8 |
Синяя (яркая) |
|
434,8 |
Синяя (слабая) |
|
433,9 |
Синяя (слабая) |
|
407,8 |
Фиолетовая (слабая) |
|
404,7 |
Фиолетовая (яркая) |
69

Спектр излучения ртути показан на рисунке 6.9.
|
желтые зеленая зел.-гол. голубая |
синие |
фиолетовые |
|
579.1 |
546.1 |
495.9 |
491.6 |
434.8 |
407.8 |
|||
|
576.9 |
435.8 |
433.9 |
404.7 |
Рисунок 6.9 − Спектр излучения ртути
6.8 Контрольные вопросы
6.8.1 Определение преломляющего угла призмы
6.8.1.1 Законы отражения и преломления света.
6.8.1.2 Абсолютный и относительный показатели преломления. Их физический смысл.
6.8.1.3 Зависимость показателя преломления от электрических и магнитных свойств среды.
6.8.1.4 Преломляющий угол призмы.
6.8.1.5 Изобразите ход монохроматического и белого света через призму.
6.8.1.6 Каково назначение и принцип действия гониометра?
6.8.1.7 Как производится фокусировка зрительной трубы и коллиматора?
6.8.1.8 Как снять отсчет по шкале лимба гониометра?
6.8.1.9 Вывести расчетную формулу для преломляющего угла призмы.
6.8.2 Определение показателя преломления призмы
6.8.2.1 Зависимость показателя преломления от длины волны. Дисперсия света.
6.8.2.2 Каким образом объясняется дисперсия света на основе электронной теории?
6.8.2.3 Что называют дисперсией вещества? Нормальная дисперсия. 6.8.2.4 Что называют угловой дисперсией призмы и от чего она
зависит?
6.8.2.5 Что характеризуют фазовая и групповая скорости света? Как экспериментально можно их определить?
70
6.8.2.6 Какова математическая запись формулы Рэлея для групповой скорости света?
6.8.2.7 Угол отклонения луча призмой и его наименьшее значение. 6.8.2.8 Объяснить метод измерения угла наименьшего отклонения
луча призмой на гониометре.
6.8.2.9 Теоретический и экспериментальный методы вычисления угловой дисперсии призмы.
Литература
1 Трофимова Т.И. Курс физики / Т.И. Трофимова − М.: Высшая школа, 2000. − 542 с.
2Фриш С.Э. Курс общей физики в 3-х т. / С.Э. Фриш, А.В. Тиморева
−М.: Физматгиз, 1968. − Т.3. −800 с.
3 Савельев И.В. Курс общей физики / И.В Савельев: учебное
пособие для ВТУзов: в 5 кн. − М.: Наука, 1998. − Кн.4: Волны. Оптика. −
256 с.
71
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основные характеристики спектральных приборов:
А) угловая и линейная дисперсии;
Б) разрешающая способность (и разрешающая сила)
В) дисперсионная область
Дисперсия
Угловой дисперсией прибора называется величина
, (7)
Где DJ — угол между лучами с длинами волн l и l + DL (см. рис. 1). Она характеризует скорость изменения угла отклонения светового пучка в приборе при изменении длины волны.
Линейной дисперсией называется величина
, (8)
Где DL — линейное расстояние на экране (см. рис. 1) между спектральными линиями, отличающимися по длине волны на DL. При малых углах j величина Dl @ F2 DJ, где F2 — фокусное расстояние камерного объектива O2.
Линейная дисперсия связана с угловой соотношением
. (9)
Дифференцированием (6) по l находим

Где Dn/DL — дисперсия материала призмы.
Угловая дисперсия призмы в положении наименьшего отклонения зависит от преломляющего угла q, показателя преломления N вещества призмы и дисперсии материала призмы.
Поэтому призмы спектральных приборов делают из стекол с возможно большим коэффициентом преломления и возможно большей дисперсией (из так называемых тяжелых флинтов). При данном материале призмы угловая дисперсия возрастает с увеличением угла преломления призмы q, но на практике q обычно берется равным 60°, так как при больших углах приходится иметь дело со слишком косо падающим на призму пучком света.
Соответственно для линейной дисперсии
В паспорте спектрального прибора обычно указывается величина обратная линейной дисперсии: Dl*- величина интервала длин волн, измеряемого в ангстремах (1 Å = 10-10 м), приходящегося на 1 мм длины спектра

Разрешающая способность.
Возможность разрешения (т. е. раздельного восприятия) двух близких монохроматических линий зависит не только от угловой или линейной дисперсии прибора, но также и от ширины этих спектральных линий. На рис. 4 сплошной линией показана результирующая интенсивность двух близких спектральных линий (штриховые кривые), полученные на приборах с одинаковой дисперсией, но с различной разрешающей способностью (l1 и l2 — длины волн, соответствующие каждой из линий).

Рис. 4
В первом случае (рис. 4А) линии очень широкие, они сильно перекрываются и воспринимаются как одна. В третьем случае (рис. 4В) линии узкие, они не перекрываются и воспроизводятся раздельно, т. е. разрешены заведомо. Во втором случае (рис. 4Б) считается, что линии находятся на пределе разрешения.
Для количественной характеристики возможности прибора разделять две близкие спектральные линии вводят величину, называемую разрешающей способностью:
, (12)
Где dlmin — предел разрешения — наименьшая разность длин волн, которые могут быть разрешены прибором;
L — длина волны, соответствующая центру провала интенсивности в суммарном контуре.
При определении предела разрешения Пользуются критерием Рэлея, согласно которому две спектральные линии считаются разрешенными, если максимум одной линии совпадает с минимумом другой (рис. 4Б). В этом случае при одинаковой интенсивности обеих исследуемых линий глубина провала интенсивности в суммарном контуре составляет около 20 %.
В реальных приборах происходит уширение спектральных линий, что приводит к снижению разрешающей способности (увеличение предела разрешения dlmin). Причин такого уширения несколько: конечный размер входной щели, аберрации объективов, несовершенство изготовления оптических деталей, неточная юстировка прибора и др. Все перечисленные причины являются техническими и их в той или иной мере можно исключить. Есть еще одна неустранимая причина, связанная с волновой природой света и обусловленная дифракцией световых пучков на различных ограничивающих оправах.
Дифракция имеет место во всех случаях, когда происходит ограничение световых пучков, но учитывается только дифракция на том элементе системы, который сильнее всего ограничивает световой пучок. Чаще всего этим элементом является диспергирующий элемент, в нашем случае призма.
Предел разрешения dlтеор, обусловленный только дифракционным уширением изображения входной щели, происходящим на оправе диспергирующего элемента, называется теорЕтическим пределом разрешения. Ему соответствует теоретическая разрешающая способность. Прибор с таким действием называется идеальным.
Рассчитаем теоретическую разрешающую способность прибора в предположении, что световые пучки сильнее всего ограничиваются оправой призмы, и призма установлена в положение наименьшего отклонения. Дифракция на призме уподобляется дифракции на щели, ширина которой определяется шириной волнового фронта, пропускаемого призмой по данному направлению (рис. 5).
,
Рис. 5
Согласно теории дифракции плоской волны на щели, угловая полуширина главного дифракционного максимума, или угловая величина dj уширения линии, определяется из условия
.
Поскольку B > > l, то угол дифракции мал, так что
. (13)
Величину B можно найти из рис. 5:

Откуда получаем

Где AC = T — длина основания (база) призмы.
Пусть у нас есть две близкие спектральные линии с длиной волны l и l + dlтеор, каждая из них испытывает дифракционное уширение, определяемое формулой (13). Угловое расстояние djтеор между этими линиями определяется угловой дисперсией прибора и равно
. (15)
Если угловое расстояние djтеор, обусловленное угловой дисперсией, будет равно дифракционному уширению dj , то такие линии, согласно критерию Рэлея, будут разрешены. Следовательно, условие разрешения запишется в виде
Dj = dj Теор . (16)
И тогда из (13-16) с учетом (10) следует, что
Или
, (17)
Т. е. разрешающая способность идеального призменного спектрального прибора зависит от размера ее базы T и дисперсии показателя преломления Dn/DL вещества призмы.
Реальная разрешающая способность всегда меньше теоретической, так как вследствие дополнительных причин уширения спектральных линий, реальный предел разрешения всегда больше теоретического.
|
ПРИЗМЕННЫЙ Цель работы: изучение и градуировка монохроматора, определение дисперсии и Приборы и принадлежности: монохроматор УМ-2, ртутная лампа. 1.
|
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
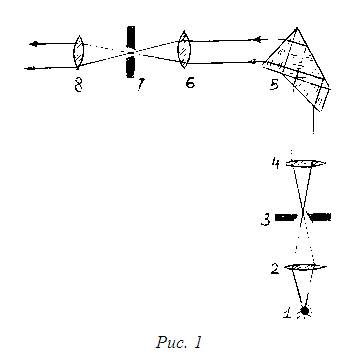
Схема состоит из трех основных частей: коллиматора 2–4, служащего для получения Основными характеристиками монохроматора являются дисперсия и Угловой дисперсией Dφ монохроматора называют
где δφ – угловое расстояние между спектральными линиями; Угловая дисперсия измеряется в радианах на нанометр (рад/нм) и Линейной дисперсией Dl
где δl – расстояние Линейная дисперсия измеряется в миллиметрах на нанометр (мм/нм).
Дисперсия спектральных аппаратов имеет различное значение в разных Разрешающая способность R монохроматора определяет возможность
где ‹λ› = (λ1+ λ2)/2. При малых углах δφ имеем δφ = λ/В, (6) где В – диаметр (или действующее отверстие) выходного объектива
Из формулы (4) имеем
где f = 280 мм – фокусное |
||||||||||||||||||||||||||||||||||||||||
|
2. Наблюдение спектральных линий и измерение их положения производится на Внешний вид монохроматора представлен на рис. 2. |
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
Монохроматор укреплен на рельсе, где также размещены источник света Основными частями монохроматора является коллиматор 7, диспергирующая призма 8 и выходная труба 2. В качестве входной щели 5 Диспергирующая призма 8 Лучи света, пройдя диспергирующую призму, попадают в объектив выходной Задачей данной работы является градуировка монохроматора, т.е. Для градуировки прибора служит ртутная лампа, установленная под |
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
Рис. 3 |
||||||||||||||||||||||||||||||||||||||||
|
Все интенсивные спектральные линии отмечены на стандартном спектре 3.
|
|
Окраска линии |
Относительная яркость |
Длина волны λ, нм |
Отсчет по барабану |
Среднее |
|
|
N1, …° |
N2, …° |
||||
|
Красная Оранжевая Желтая Желтая Зеленая Голубая Синяя Синяя Фиолетовая Фиолетовая |
8 4 10 10 10 10 10 7 7 7 |
690,7 623,2 579,0 577,0 546,1 491,6 435,8 434,7 407,8 404,7 |
3.1.6. Вычисляют среднее значение показаний барабана для каждой линии.
3.1.7. По данным таблицы строят градуировочную кривую монохроматора Nбар
= f1 (λ). Масштаб следует выбрать так, чтобы
диаграмма была достаточно большой и позволяла четко определить длину волны до
1 нм.
Задание 2. Рассчитать линейную дисперсию прибора.
3.2.1. По градуировочной кривой монохроматора определяют интервалы
значений показаний барабана ∆Nбар для следующих
участков спектра: 410, 450, 490, 530, 570, 610 нм. Величина ∆λ
берется по указанию преподавателя. Данные заносят в таблицу (форма
табл. 2).
3.2.2. Переводят интервалы показаний барабана ∆Nбар,
…° в интервалы угла поворота диспергирующей призмы ∆φ//,
учитывая, что 2° по барабану соответствуют 20// поворота призмы.
3.2.3. По формуле (1) вычисляют угловую
дисперсию монохроматора, заменяя малые интервалы δφ и δλ
на ∆φ и ∆λ.
Форма таблицы 2
|
Длина |
∆λ |
∆Nбар |
∆φ |
∆φ |
Dφ |
Dl |
|
нм |
нм |
…° |
// |
рад |
рад/нм |
мм/нм |
|
410 450 490 530 570 610 |
3.2.4. По формуле (4) и данным табл. 2 вычисляют линейную дисперсию
призмы монохроматора Dl для соответствующих участков спектра.
3.2.5. По полученным данным строят дисперсионную кривую
Dl = f2
(λ) на одном графике с градуировочной кривой.
Задание 3. Рассчитать разрешающую способность призмы
монохроматора для всех областей длин волн, в которых определялась линейная
дисперсия.
По формуле (8) разрешающая способность 
В = 40 мм, f = 280 мм, Dl – из дисперсионной кривой Dl = f2 (λ).
Данные заносят в таблицу (форма табл. 3).
Форма таблицы 3
|
Длина волны λ, нм |
Dl, мм/нм |
R |
|
410 450 490 530 570 610 |
По полученным данным строят кривую разрешающей способности R = f3
(λ).
ВОПРОСЫ
ДЛЯ ДОПУСКА К РАБОТЕ
1. Сформулируйте цель работы.
2. Каково назначение монохроматора?
3. Какие существуют способы монохроматизации света?
4. Как градуируется монохроматор?
5. Как рассчитать линейную дисперсию призмы монохроматора и определить
ее разрешающую способность?
ВОПРОСЫ
ДЛЯ ЗАЩИТЫ РАБОТЫ
1. Поясните оптическую схему монохроматора.
2. Каково назначение основных частей монохроматора?
3. По диаграммам Nбар= f1 (λ),
Dl = f2
(λ), R = f3 (λ) проанализируйте полученные
результаты и сделайте выводы.
4. Опишите практическое использование монохроматора.
5. Критические замечания к методу измерений.
ЛИТЕРАТУРА
1. Кортнев А.В., Рублев Ю.В., Куценко А.Н. Практикум по физике. – М.:
Высш. шк., 1963. – 568 с.
2. Ахматов А.С. и др. Лабораторный практикум по физике. – М.: Высш.
шк., 1980. – 307 с.
3. Барсуков К.А., Уханов Ю.И. Лабораторный практикум по физике. – М.:
Высш. шк., 1988. – 350 с.