Как найти угловую скорость вращения диска

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

если известно количество оборотов n за единицу времени t:
если задан угол поворота φ за единицу времени:
если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:

Количество оборотов за единицу времени [об/мин], [c^-1].
Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

Примеры расчета угловой скорости и ускорения
Скорости и ускорения точек вращающегося тела

Источник

Содержание

Тестирование онлайн
Угловая скорость
Период и частота
Линейная скорость
Центростремительное ускорение
Вращение Земли
Связь со вторым законом Ньютона
Как вывести формулу центростремительного ускорения
Движение по циклоиде*
Тестирование онлайн
Угловая скорость
Период и частота
Линейная скорость
Центростремительное ускорение
Вращение Земли
Связь со вторым законом Ньютона
Как вывести формулу центростремительного ускорения
Движение по циклоиде*
Номинальная скорость вращения
Угловая скорость
Угловая скорость в конкретных случаях
Как определить угловую скорость
Угол поворота и период обращения
Циклическая частота вращения (обращения)
Переход от угловой к линейной скорости
Видео

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Тестирование онлайн

Угловая скорость

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Центростремительное ускорение

Используя предыдущие формулы, можно вывести следующие соотношения

Вращение Земли

Связь со вторым законом Ньютона

Как вывести формулу центростремительного ускорения

Разница векторов есть . Так как , получим

Движение по циклоиде*

Мгновенная скорость определяется по формуле

Количество повторений каких-либо событий или их возникновения за одну единицу таймера называется частотой. Это физическая величина измеряется в герцах – Гц (Hz). Она обозначается буквами ν, f, F, и есть отношение количества повторяющихся событий к промежутку времени, в течение которого они произошли.

При обращении предмета вокруг своего центра можно говорить о такой физической величине, как частота вращения, формула:

где:

N – количество оборотов вокруг оси или по окружности,
t – время, за которое они были совершены.

В системе СИ обозначается как – с-1 (s-1) и именуется как обороты в секунду (об/с). Применяют и другие единицы вращения. При описании вращения планет вокруг Солнца говорят об оборотах в часах. Юпитер делает одно вращение в 9,92 часа, тогда как Земля и Луна оборачиваются за 24 часа.

Номинальная скорость вращения

Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:

К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.

Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.

Угловая скорость

Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.

Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.

Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:

где:

ω – угловая скорость (рад./с);
∆ϕ – изменение угла отклонения при повороте (рад.);
∆t – время, затраченное на отклонение (с).

Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.

Угловая скорость в конкретных случаях

На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.

Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.

где:

π – число, равное 3,14;
ν – частота вращения, (об./мин.).

В качестве примера могут быть рассмотрены угловая скорость и частота вращения колёсного диска при движении мотоблока. Часто необходимо уменьшить или увеличить скорость механизма. Для этого применяют устройство в виде редуктора, при помощи которого понижают скорость вращения колёс. При максимальной скорости движения 10 км/ч колесо делает около 60 об./мин. После перевода минут в секунды это значение равно 1 об./с. После подстановки данных в формулу получится результат:

ω = 2*π*ν = 2*3,14*1 = 6,28 рад./с.

К сведению. Снижение угловой скорости часто требуется для того, чтобы увеличить крутящий момент или тяговое усилие механизмов.

Как определить угловую скорость

Принцип определения угловой скорости зависит от того, как происходит движение по окружности. Если равномерно, то употребляется формула:

Если нет, то придётся высчитывать значения мгновенной или средней угловой скорости.

Величина, о которой идёт разговор, векторная, и при определении её направления используют правило Максвелла. В просторечии – правило буравчика. Вектор скорости имеет одинаковое направление с поступательным перемещением винта, имеющего правую резьбу.

Рассмотрим на примере, как определить угловую скорость, зная, что угол поворота диска радиусом 0,5 м меняется по закону ϕ = 6*t:

ω = ϕ / t = 6 * t / t = 6 с-1

Вектор ω меняется из-за поворота в пространстве оси вращения и при изменении значения модуля угловой скорости.

Угол поворота и период обращения

Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.

Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать 1/2, 1/4 оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.

Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.

Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.

В этом случае находят применения такие характеристики, как:

период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.

Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.

Циклическая частота вращения (обращения)

Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.

Циклическая частота вращения – это количество оборотов тела за 2*π секунды.

У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.

Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.

При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:

частоты питающей сети;
количества пар полюсов.

Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.

Переход от угловой к линейной скорости

Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:

ν = 2*π*R / Т = 2*π*R* ν.

Так как ω = 2*π*ν, то получается:

Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.

К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.

Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:

а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.

Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.

Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.

Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.

Видео

Источник

Содержание:

Определение и формула угловой скорости
Равномерное вращение
Формула, связывающая линейную и угловую скорости
Единицы измерения угловой скорости
Примеры решения задач

Определение и формула угловой скорости

Определение

Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность
с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.

Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.

Перемещение при вращении характеризуют при помощи угла поворота
$(varphi)$ . Часто используют вектор элементарного поворота
$bar{dvarphi}$ , который равен по величине элементарному углу поворота тела
$(d varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.

Определение

Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой
$omega$ . Математически определение угловой скорости записывают так:

$$bar{omega}=frac{d bar{varphi}}{d t}=dot{bar{varphi}}(1)$$

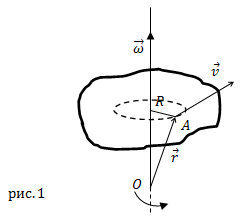
Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее
с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).

Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости),
так и за счет поворота оси вращения в пространстве ($bar{omega}$ при этом изменяет направление).

Равномерное вращение

Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:

$$omega=frac{varphi}{t}(2)$$

где $(varphi)$ – угол поворота, t – время, за которое этот поворот совершён.

Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот
($Delta varphi=2 pi$). Угловая скорость связана с периодом обращения как:

$$omega=frac{2 pi}{T}(3)$$

С числом оборотов в единицу времени ($nu) угловая скорость связана формулой:

$$omega=2 pi nu(4)$$

Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения,
но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно
с данной мгновенной величиной скорости.

Формула, связывающая линейную и угловую скорости

Линейная скорость $bar{v}$ точки А (рис.1), которая расположена
на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:

$$bar{v}=[bar{omega} bar{R}](5)$$

где $bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки
$A (bar{r})$ (рис.1). Вектор
$bar{r}$ проводят от точки, находящейся на оси вращения к рассматриваемой точке.

Единицы измерения угловой скорости

Основной единицей измерения угловой скорости в системе СИ является: [$omega$]=рад/с

В СГС: [$omega$]=рад/с

Примеры решения задач

Пример

Задание. Движение тела с неподвижной осью задано уравнением
$varphi=2 t-4 t^{3}$,
$(varphi)$ в рад, t в сек.
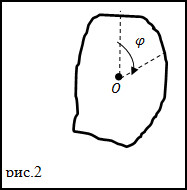
Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении (
относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.

Решение. Для нахождения модуля угловой скорости применим формулу:

$$omega=frac{d varphi}{d t}(1.1)$$

Используем заданную в условии задачи функцию
$varphi(t)$, возьмем производную от нее по времени, получим функцию
$omega(t)$:

$$omega(t)=2-8 t^{2}(1.2)$$

Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):

$$omega(t)=2-8(0,5)^{2}=0left(frac{r a d}{c}right)$$

Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Скорости вращения тела заданы системой уравнений:

$$left{begin{array}{c}bar{omega}_{1}=t^{2 bar{i}} \ bar{omega}_{2}=2 t^{2} bar{j}end{array}right.$$

где $bar{i}$ и
$bar{j}$ – единичные ортогональные векторы. На какой угол $(varphi)$ поворачивается тело за время равное 3 с?

Решение. Определим, какова функция, которая связывает модуль скорости вращения тела и время (t)
($omega(t)$). Так как вектора
$bar{i}$ и
$bar{j}$ перпендикулярны друг другу, значит:

$$omega=sqrt{omega_{1}^{2}+omega_{2}^{2}}=sqrt{left(t^{2}right)^{2}+left(2 t^{2}right)^{2}}=t^{2} sqrt{5}(2.2)$$

Модуль угловой скорости связан с углом поворота как:

$$omega=frac{d varphi}{d t}(2.3)$$

Следовательно, угол поворота найдем как:

$$varphi=int_{t_{1}}^{t_{2}} omega d t=int_{0}^{3} t^{2} sqrt{5} d t=left.sqrt{5} frac{t^{3}}{3}right|_{0} ^{3} approx 20(mathrm{rad})$$

Ответ. $varphi = 20$ рад.

Читать дальше: Формула удельного веса.

Источник

I. Механика

Тестирование онлайн

Угловая скорость

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Центростремительное ускорение

Используя предыдущие формулы, можно вывести следующие соотношения

Вращение Земли

Связь со вторым законом Ньютона

Как вывести формулу центростремительного ускорения

Движение по циклоиде*

Источник

Что такое угловая скорость

Угловая скорость (обозначается как (omega)) — векторная величина, характеризующая скорость и направление изменения угла поворота со временем.

Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.

Единица измерения

В Международной системе единиц (СИ) принятой единицей измерения угловой скорости является радиан в секунду (рад/с)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Формула угловой скорости

Вектор угловой скорости определяется отношением угла поворота ((varphi)) к интервалу времени ((mathcal t)), за которое произошел поворот:

(omega=frac{trianglevarphi}{trianglemathcal t})

Зависимость угловой скорости от времени

Зависимость (varphi ) от (mathcal t) наглядно показана на графике:

Зависимость угловой скорости от времени

Угол, на который повернулось тело, характеризуется площадью под кривой.

Угловая скорость вращения, формула

Через частоту

(omega=2pimathcal n)

(mathcal n) — частота вращения ((1/с))

(pi) — число Пи ((approx 3,14))

(mathcal n=frac1T)

(T )— период вращения (время, за которое тело совершает один оборот)

Через радиус

(omega=frac vR)

(v) — линейная скорость(м/с)

(R) — радиус окружности (м)

Как определить направление угловой скорости

Направление скорости в физике можно определять двумя способами:

Правило буравчика. Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.
Правило правой руки. Представим, что взяли тело в правую руку. Следует направлять и вращать его туда, куда указывают четыре пальца. Отведенный в сторону большой палец покажет направление угловой скорости при этом вращении.

Связь линейной и угловой скорости

Линейная скорость ((v)) тела, расположенного на расстоянии (R) от оси вращения, прямо пропорциональна угловой скорости.

(v=Romega)

(R) — радиус окружности (м)

Чему равна мгновенная угловая скорость

Мгновенную угловую скорость нужно находить как предел, к которому стремится средняя угловая скорость при (trianglemathcal trightarrow0) :

(omega=lim_{trianglerightarrow0}frac{trianglevarphi}{trianglemathcal t})

Измеряется в рад/с

Источник