Как найти угловую скорость вращения пули

ЛАБОРАТОРНАЯ
РАБОТА № 2

ОПРЕДЕЛЕНИЕ
СКОРОСТИ ПУЛИ МЕТОДОМ

ВРАЩАЮЩИХСЯ
ДИСКОВ

ЦЕЛЬ
РАБОТЫ:

1). Ознакомиться
со стробоскопическим методом измерения
угловых скоростей.

2). Измерить скорость
пули.

ОБОРУДОВАНИЕ:
экспериментальная установка, бумажные
диски, измерительные инструменты,
источник питания ИЭПП-1.

КРАТКАЯ ТЕОРИЯ

Вращательное
движение – самое распространенное
движение в технике. Для его описания
используются специальные физические
величины. Введём некоторые из них на
примере вращения материальной точки.

1. Положение
   материальной точки на окружности
   определяется углом
   ,
   который образует радиус-вектор
   материальной точки
   
   с некоторым неподвижным радиусом ОА.
   Зависимость угла поворота от времени
   
   — кинематический закон вращательного
   движения материальной точки. Угол
   
   обязательно измеряется в радианах.

2. Угловая скорость
   – физическая величина, определяемая
   соотношением

.
(2.1)

С точки зрения
физики соотношение (2.1) — это отношение
двух физически малых величин

и

— приращения угла поворота

за время
,
с точки зрения математики – единый
математический объект – производная
по времени от функции
.
Если вращение равномерное (),
то вместо уравнения (2.1) используют
другое

(2.2)

или

.
(2.3)

Единица угловой
скорости 1.
Малый угол поворота

— это векторная величина. Вектор

направлен по оси вращения и связан с
направлением вращения материальной
точки правилом правого винта. Естественно,
и угловая скорость векторная величина,
определяемая соотношением

.

3. Из известного
соотношения

следует другое

или

(2.4)

-связь линейной и
угловой скорости.

4. Если вращение
равномерное, то вводится период вращения
материальной точки на окружности

(2.5)

Отсюда следует
другой смысл угловой скорости.

— это число оборотов,
которые делает материальная точка за
промежуток времени

секунд.

5. Число оборотов
за одну секунду (частота вращения)
определяется соотношением
.
Следовательно,

и
.

Другие угловые
характеристики и связывающие их
соотношения в данной работе не понадобятся.

ТЕОРИЯ МЕТОДА

Стробоскопический
(от греческих слов strobos
– кружение, вихрь и skopeo – смотрю,
наблюдаю) эффект состоит:

1. в возможности
   видеть в условии прерывистого наблюдения
   быстро движущийся предмет неподвижным;

2. в восприятии
   быстрой смены изображений отдельных
   фаз движения тела (т.е. последовательности
   неподвижных положений тела) как
   непрерывного его движения.

Таким образом, в
первом случае движущийся предмет
становится неподвижным, во втором –
неподвижный предмет – движущимся.
Первая возможность реализуется в
контрольно-измерительных приборах для
наблюдения быстрых периодических
движений, вторая служит основой кино.

Принцип действия
стробоскопических приборов заключается
в том, что тело, совершающее быстрое
периодическое движение (вращение,
колебания) освещается и делается видимым
в отдельные, очень
малые по сравнению с периодом движения,
промежутки времени.

Идею стробоскопического
метода измерений можно показать на
очень простом примере. Пусть имеется
вращающееся колесо (рис.2.2) , на котором
проведён радиус ОА (например, это спица).
Пусть в момент времени

радиус занимает горизонтальное положение,
и колесо освещается кратковременной
вспышкой (мы радиус видим). Если через
промежуток времени

следует вторая вспышка лампы, то колесо
нам будет казаться неподвижным. Итак,
условие восприятия данного колеса как
неподвижного есть равенство периода
вращения и периода повторяемости вспышек
лампы. Если у колеса будет n
равноотстоящих спиц, то колесо будет
казаться неподвижным при условии
.
Если следующая вспышка произойдёт в
момент, когда радиус займёт положение
ОА₁,
а это будет, если
<
или
>,
то колесо нам будет казаться медленно
вращающимся в сторону истинного вращения.
Если в момент следующей вспышки радиус
окажется в положении ОА₂
(>,<
), то мы увидим вращение в противоположном
направлении.

В
данной работе стробоскопический эффект
используется для определения угловой
скорости электромотора. Для этого на
ось электромотора устанавливают диск,
разделённый на некоторое число одинаковых
тёмных и светлых секторов. Такой диск
называют стробоскопическим. Он освещается
лампой дневного света, питаемой от сети
переменного тока частотой
.
Напряжение в сети изменяется от нуля
до 220 В. Особенность этой лампы состоит
в том, что она зажигается только при
достижении определённого напря-жения
зажигания

и гаснет, когда напряжение упадёт
снова до такого же значения. На графике
зависимости напряжения от времени
(рис. 2.3) показано напряжение зажигания
лампы и промежутки времени
…,
когда лампа горит. За одну секунду таких
промежутков времени будет 100. Следовательно,
частота и период появления вспышек
равны
,
.
При постепенном увеличении угловой
скорости вращения диска, имеющего

тёмных и
светлых секторов, первая кажущаяся
остановка диска наблюдается, если
,
здесь
—
угол поворота диска за один световой
период. Следующая «остановка» будет
наблюдаться, если

и т.д. Общее условие наблюдения остановок
.
Здесь
=1,2,3…
Отсюда получаем

(2.6)

Пользуясь этим
соотношением, легко определить угловую
скорость вращения диска, которая нам
нужна для нахождения скорости пули.

Рис.
2.4

Экспериментальная
установка (рис.2.4) состоит из электромотора
М, питаемого от сети переменного тока
через источник питания

ИЭПП-1, позволяющий
изменять число оборотов мотора. С помощью
муфты 7 ось мотора соединяется с осью
1, на которую зажимами 6 укрепляются
тонкие бумажные диски 2 и 3. Вместе с
диском 2 устанавливается стробоскопический
диск 4. Перед диском 2 расположен
пневматический пистолет 5.

Определение
скорости пули в данной работе основано
на измерении угла, на который успевают
повернуться два тонких бумажных диска,
укреплённых на оси электромотора.
Сначала производится выстрел из пистолета
по неподвижным дискам и отмечаются
появившиеся отверстия, затем , подавая
напряжение на электромотор, добиваются
первой кажущейся остановки стробоскопического
диска, и снова производят выстрел. За
время

пролёта пули расстояния

между дисками они успевают повернуться
на угол
,
так что это время равно
.
Отсюда находим скорость
,
здесь
.

После остановки
электромотора снимают диски, совмещают
их начальное положение по отмеченным
отверстиям, а по смещению отверстия на
втором диске относительно первого
определяют угол
.
Расстояние

измеряют между зажимами 6. Теперь есть
все необходимые данные для определения
скорости пули.

ЗАДАНИЯ

1. Изучите теорию
   данного вопроса.

2. Изучите
   экспериментальную установку и сущность
   стробоскопического метода измерений.

3. Определите скорость
   пули при различных скоростях вращения
   дисков (или при различных стробоскопических
   дисках).

4. Оцените погрешность
   измерения скорости пули.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение
   следующим понятиям: материальной точки,
   радиус-вектора, вектора перемещения,
   вектора скорости.

2. Дайте определение
   угловых величин: углового перемещения,
   угловой скорости.

3. Установите связь
   между угловыми и линейными величинами.

4. Объясните явление
   стробоскопического эффекта.

5. В каком случае
   будет наблюдаться кажущая остановка
   стробоскопического диска?

6. Как определяется
   стробоскопическим методом угловая
   скорость вращения?

7. Что положено в
   основу метода определения скорости
   пули в работе?

8. Получите рабочую
   формулу расчёта скорости пули.

9. Как оценить
   погрешность измерения угловой скорости?

10. Как оценить
    погрешность в измерении скорости пули?

11. Почему при
    увеличении числа оборотов двигателя
    тёмные сектора кажутся размытыми?

Соседние файлы в папке Лаб.раб. по механике

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Решение.

Будем рассматривать движение системы «стержень – пуля»
относительно системы отсчета, начало которой расположено в центре стержня О,
а ось  совпадает с осью вращения и направлена «на
нас» (рис. 14). В момент удара на  систему действуют силы тяжести

и
реакции опоры – оси. Линии действия сил реакции оси и тяжести, действующих на стержень,
и силы тяжести, действующей на пулю, проходят через центр стержня О. Таким
образом, все внешние силы являются центральными, их моменты относительно центра
О равны нулю, следовательно, при столкновении выполняется закон
сохранения момента импульса:

,                                                          
(1)

где
 и – моменты
импульса системы относительно центра  непосредственно до удара
(рис. 14, а) и сразу после него (рис. 14, б) соответственно[1].

До
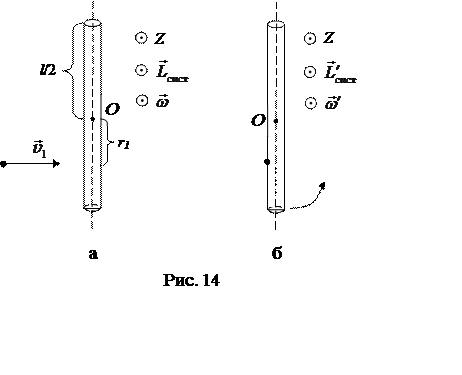
взаимодействия стержень был неподвижен, поэтому момент импульса системы равен
моменту импульса пули:

,             (2)

где
 – момент инерции пули относительно оси
вращения;

 – угловая скорость пули непосредственно
перед ударом.

Примем
пулю за материальную точку, тогда ее момент инерции относительно оси вращения

.                                       
    (3)

Модуль
угловой скорости пули выражается через модуль линейной скорости  и расстояние  от
точки попадания пули до оси

,                                                     
  (4)

где

Направление
 (рис. 14, а – «на нас») определяется по
правилу буравчика в соответствии с направлением вращения.

После
взаимодействия пули и стержня система начинает вращение как одно целое с
угловой скоростью  поэтому

,                          
 (5)

где
 – угловая скорость системы непосредственно
после удара.

Момент
инерции стержня относительно оси вращения, которая в рассматриваемом случае
совпадает с осью симметрии стержня, определяется по формуле:

.                                                   
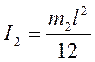
 (6)

Подставив
формулы (2) и (5) в уравнение (1), получим соотношение:

.                                          
    (7)

Отсюда

.                                             
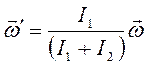
   (8)

Заметим, что моменты импульса пули до и после удара можно
вычислить, основываясь на определении момента импульса материальной точки:
 и .

При
анализе выражения (8) можно сделать два вывода:

1)
угловая скорость системы во втором состоянии сонаправлена с угловой скоростью пули
в первом состоянии: ;

2)
так как моменты инерции величины положительные, модуль угловой скорости  определяется по формуле:

.                                             
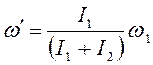
 (9)

Подставим
выражения (3), (4) и (6) в равенство (9):

.  (10)

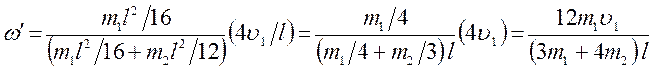
Подставим
данные задачи в уравнение (10) и получим:

 рад/с.

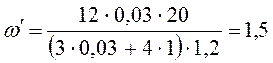
Ответ: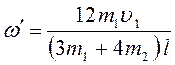,  рад/с.

Библиографический список

1. С
а в е л ь е в  И. В. Курс общей физики: В 5 кн. Кн. 1. Механика / И. В. С
а в е л ь е в. М., 1998. 336 с.

2. Я в о р с к и й  Б. М. Курс физики / Б. М.  Я в о
р с к и й, А. А.  Д е т л а ф, Л. Б.  М и л к о в с к а я. М., 2001. 718
с.

3. Т
р о ф и м о в а Т. И. Курс физики / Т. И.  Т р о ф и м о в а. М., 2004. 542
с.

4. Физический
энциклопедический словарь / Под ред. А. М. Прохорова. 
М., 1984. 940 с.

5.
Д ж а н к о л и  Д. Физика / Д.  Д ж а н к о л и.  М., 1989. Т. 1. 667 с.

6.
Н и к и т и н  Н. Н. Курс теоретической механики / Н. Н.  Н и к и т и н. М., 1990.
607 с.

_________________________________________________

Учебное
издание

ДРОЗДОВА Илга
Анатольевна,  ТОДЕР Георгий Борисович

ЗАКОНЫ  СОХРАНЕНИЯ  В  МЕХАНИКЕ

(ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ)

Редактор Т. С. Паршикова

***

Подписано в печать     . 02.2010.
Формат 60 ´ 84 ¹/₁₆.

Плоская печать. Бумага офсетная. Усл.
печ. л. 2,4. Уч.-изд. л. 2,6.

Тираж 800 экз.  Заказ         .

**

Редакционно-издательский
отдел ОмГУПСа

Типография ОмГУПСа

*

644046, г. Омск, пр. Маркса, 35

И. А.
ДРОЗДОВА,  Г. Б. ТОДЕР

ЗАКОНЫ 
СОХРАНЕНИЯ  В  МЕХАНИКЕ

(ПРИМЕРЫ 
РЕШЕНИЯ  ЗАДАЧ)

ОМСК  200

9

The problem is as follows:

The figure from below shows a cylinder spinning. Find the angular
speed of the cylinder so that the perforations made in a minimum time
by the bullet carrying a linear velocity $v$ make an angle with $O$ a
central angle of $120^{circ}$.

The alternatives given in my book are as follows:

$begin{array}{ll}
1.&frac{v}{pi R}\
2.&frac{3v}{R}\
3.&frac{3pi v}{R}\
4.&frac{pi v}{R^2}\
5.&frac{pi v}{6R}\
end{array}$

This problem is kind of confusing. I don’t know exactly how to understand what’s the central angle they are referring to. What would it be?.

The diagram is a bit confusing too, if the bullet is hitting the center of the cylinder, how can it make an angle?. What central angle is it referring?.

The only thing which I think it intended to say was that in a tiny fraction of time the cylinder and the bullet both have the same tangential speed. But would that idea help in the solution of this problem?.

Even if this is the case, how to use this logic?.

The only thing which I could do was to transform the given angle in rads as the angular displacement.

$theta=120^{circ}timesfrac{pi}{180^{circ}}=frac{2pi}{3}$

But again I don’t know what is the $O$ they are referring, could it be that $O$ is a point situated in the center or is it located at a certain distance from the center?. Would that matter?.

All and all can comeone help me with this question?. I’m very confused. Help please?.