Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:
Приняв вектор k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.
Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.
Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Содержание:
- Определение и формула угловой скорости
- Равномерное вращение
- Формула, связывающая линейную и угловую скорости
- Единицы измерения угловой скорости
- Примеры решения задач
Определение и формула угловой скорости
Определение
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность
с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота
$(varphi)$ . Часто используют вектор элементарного поворота
$bar{dvarphi}$ , который равен по величине элементарному углу поворота тела
$(d varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.
Определение
Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой
$omega$ . Математически определение угловой скорости записывают так:
$$bar{omega}=frac{d bar{varphi}}{d t}=dot{bar{varphi}}(1)$$
Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее
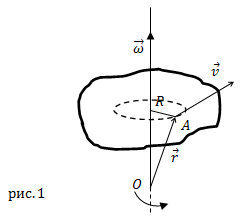
с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости),
так и за счет поворота оси вращения в пространстве ($bar{omega}$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
$$omega=frac{varphi}{t}(2)$$
где $(varphi)$ – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот
($Delta varphi=2 pi$). Угловая скорость связана с периодом обращения как:
$$omega=frac{2 pi}{T}(3)$$
С числом оборотов в единицу времени ($nu) угловая скорость связана формулой:
$$omega=2 pi nu(4)$$
Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения,
но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно
с данной мгновенной величиной скорости.
Формула, связывающая линейную и угловую скорости
Линейная скорость $bar{v}$ точки А (рис.1), которая расположена
на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:
$$bar{v}=[bar{omega} bar{R}](5)$$
где $bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки
$A (bar{r})$ (рис.1). Вектор
$bar{r}$ проводят от точки, находящейся на оси вращения к рассматриваемой точке.
Единицы измерения угловой скорости
Основной единицей измерения угловой скорости в системе СИ является: [$omega$]=рад/с
В СГС: [$omega$]=рад/с
Примеры решения задач
Пример
Задание. Движение тела с неподвижной осью задано уравнением
$varphi=2 t-4 t^{3}$,
$(varphi)$ в рад, t в сек.
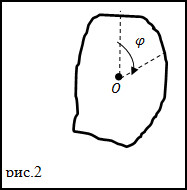
Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении (
относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.
Решение. Для нахождения модуля угловой скорости применим формулу:
$$omega=frac{d varphi}{d t}(1.1)$$
Используем заданную в условии задачи функцию
$varphi(t)$, возьмем производную от нее по времени, получим функцию
$omega(t)$:
$$omega(t)=2-8 t^{2}(1.2)$$
Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):
$$omega(t)=2-8(0,5)^{2}=0left(frac{r a d}{c}right)$$
Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Скорости вращения тела заданы системой уравнений:
$$left{begin{array}{c}bar{omega}_{1}=t^{2 bar{i}} \ bar{omega}_{2}=2 t^{2} bar{j}end{array}right.$$
где $bar{i}$ и
$bar{j}$ – единичные ортогональные векторы. На какой угол $(varphi)$ поворачивается тело за время равное 3 с?
Решение. Определим, какова функция, которая связывает модуль скорости вращения тела и время (t)
($omega(t)$). Так как вектора
$bar{i}$ и
$bar{j}$ перпендикулярны друг другу, значит:
$$omega=sqrt{omega_{1}^{2}+omega_{2}^{2}}=sqrt{left(t^{2}right)^{2}+left(2 t^{2}right)^{2}}=t^{2} sqrt{5}(2.2)$$
Модуль угловой скорости связан с углом поворота как:
$$omega=frac{d varphi}{d t}(2.3)$$
Следовательно, угол поворота найдем как:
$$varphi=int_{t_{1}}^{t_{2}} omega d t=int_{0}^{3} t^{2} sqrt{5} d t=left.sqrt{5} frac{t^{3}}{3}right|_{0} ^{3} approx 20(mathrm{rad})$$
Ответ. $varphi = 20$ рад.
Читать дальше: Формула удельного веса.
Самостоятельная работа Закон электромагнитной индукции. Изменение угла между контуром и полем. Вращение рамки в однородном магнитном поле 11 класс с ответами. Самостоятельная работа представлена в двух вариантах, в каждом варианте по 3 задания.
Вариант 1
1. Круговой контур диаметром 4 см помещен в однородное магнитное поле индукцией 0,2 Тл. Плоскость контура перпендикулярна направлению магнитного· поля, сопротивление контура 1 Ом. Какой заряд протечет по контуру при повороте его на 90°?
2. Угловая скорость вращения рамки в однородном магнитном поле 45 рад/с, а максимальный магнитный поток 2 Вб. Определите максимальное значение ЭДС индукции, возникающей в этой рамке.
3. Круглая рамка площадью 300 см2 имеет 100 витков и вращается в однородном магнитном поле с индукцией 0,2 Тл вокруг оси, проходящей через ее диаметр и перпендикулярной вектору индукции. Найдите угловую скорость вращения рамки, если максимальная величина ЭДС индукции равна 15 В.
Вариант 2
1. Катушка, имеющая 100 витков и расположенная перпендикулярно магнитному полю с индукцией 6 Тл, поворачивается за 1 с на угол 90°. За это время в катушке наводится ЭДС со средним значением 0,6 В. Определите площадь поперечного сечения катушки.
2. Определите максимальный магнитный поток через рамку, вращающуюся в однородном магнитном поле с частотой 10 Гц. Максимальная ЭДС, возникающая в рамке, 3 В.
3. Круглая рамка имеет 100 витков и вращается в однородном магнитном поле с индукцией 0,4 Тл вокруг оси, проходящей через ее диаметр и перпендикулярной вектору индукции. Найдите угловую скорость вращения рамки, если максимальная величина ЭДС индукции 20 В, а площадь рамки 0,08 м2.
Ответы на самостоятельную работу Закон электромагнитной индукции. Изменение угла между контуром и полем. Вращение рамки в однородном магнитном поле 11 класс
Вариант 1
1. 251,2 мкКл
2. 90 В
3. 25 рад/с
Вариант 2
1. 0,001 м2
2. 48 мВб
3. 6,25 рад/с
Опубликовано: 26.09.2022
Обновлено: 26.09.2022
Физическая величина
| Угловая скорость | |
|---|---|
| Общие символы | ω |
| В базовых единицах СИ | s |
| Расширенные ? | да (только для твердого тела) |
| Интенсивный ? | да |
| Сохраненный ? | no |
| Поведение при. преобразовании координат | псевдовектор |
| Выведение из. других величин | ω= d θ / d t |
| Размерность | T — 1 { displaystyle { mathsf {T}} ^ {- 1}} |
В физике угловая скорость относится к тому, насколько быстро объект вращается или вращается относительно другой точки, то есть насколько быстро угловое положение или ориентация объекта изменяется со временем. Есть два типа угловой скорости: орбитальная угловая скорость и угловая скорость вращения. Угловая скорость вращения относится к тому, насколько быстро твердое тело вращается относительно своего центра вращения. Орбитальная угловая скорость означает, насколько быстро точечный объект вращается вокруг фиксированного начала координат, то есть скорость изменения его углового положения относительно начала координат во времени. Угловая скорость вращения не зависит от выбора начала координат, в отличие от орбитальной угловой скорости, которая зависит от выбора начала координат.
Обычно угловая скорость измеряется в углах за единицу времени, например радиан в секунду (угол, заменяющий расстояние от линейной скорости с общим временем). Единица измерения угловой скорости СИ выражается в радианах в секунду, причем радиан имеет безразмерное значение, равное единице, поэтому единицы угловой скорости в системе СИ указаны как 1 / с или с. Угловая скорость обычно обозначается символом omega (ω, иногда Ω ). По соглашению, положительная угловая скорость означает вращение против часовой стрелки, а отрицательная — по часовой стрелке.
Например, геостационарный спутник совершает один оборот в день над экватором, или 360 градусов за 24 часа, и имеет угловую скорость ω = (360 °) / (24 ч) = 15 ° / ч, или (2π рад) / (24 ч) ≈ 0,26 рад / ч. Если угол измеряется в радианах, линейная скорость равна радиусу, умноженному на угловую скорость, v = r ω { displaystyle v = r omega}
В трех измерениях угловая скорость представляет собой псевдовектор с его величиной измерение скорости, с которой объект вращается или вращается, и его направление, указывающее перпендикулярно плоскости мгновенного вращения или углового смещения. Ориентация угловой скорости обычно определяется правилом правой руки .
Содержание
- 1 Орбитальная угловая скорость точечной частицы
- 1.1 Частица в двух измерениях
- 1.2 Частица в трех измерениях
- 1.2.1 Сложение векторов угловой скорости
- 2 Вектор угловой скорости для твердого тела или системы отсчета
- 2.1 Компоненты угловой скорости из базисных векторов неподвижной системы отсчета
- 2.2 Компоненты из углов Эйлера
- 3 Тензор угловой скорости
- 3.1 Расчет по матрице ориентации
- 4 Свойства тензоров угловой скорости
- 4.1 Двойственность по отношению к вектору скорости
- 4.2 Экспонента от W
- 4.3 W кососимметрична
- 4.4 Описание без координат
- 4.5 Угловая скорость как векторное поле
- 5 Соображения относительно твердых тел
- 5.1 Согласованность
- 6 См. Также
- 7 Ссылки
- 8 Внешние ссылки
Орбитальная угловая скорость точечной частицы
Двумерная частица

. В простейшем случае кругового движения на радиусе r { displaystyle r}






В общем случае частицы, движущейся в плоскости, орбитальная угловая скорость — это скорость, с которой вектор положения относительно выбранной точки отсчета «заметает» угол. На диаграмме показан вектор положения r { displaystyle mathbf {r}}







Угловая скорость ω — это скорость изменения углового положения относительно времени, которая может быть вычислена из поперечной радиальной скорости как:
- ω = d ϕ d t = v ⊥ r. { displaystyle omega = { frac {d phi} {dt}} = { frac {v _ { perp}} {r}}.}
Здесь поперечная радиальная скорость v ⊥ { displaystyle v _ { perp}}





- ω = v sin (θ) r. { displaystyle omega = { frac {v sin ( theta)} {r}}.}
Эти формулы могут быть получены из r = (x (t), y (t)) { Displaystyle mathbf {r} = (x (t), y (t))}




В двух измерениях угловая скорость — это число со знаком плюс или минус, указывающее ориентацию, но не указывающее в направлении. Знак традиционно считается положительным, если радиус-вектор вращается против часовой стрелки, и отрицательным, если по часовой стрелке. Тогда угловая скорость может быть названа псевдоскалярной, числовой величиной, которая меняет знак при инверсии четности, такой как инвертирование одной оси или переключение двух осей.
Частица в трех измерениях

В трехмерном пространстве мы снова имеем вектор положения r движущейся частицы. Здесь орбитальная угловая скорость представляет собой псевдовектор , величина которого представляет собой скорость, с которой r проходит под углом, и направление которого перпендикулярно мгновенной плоскости, в которой r выметает угол (т. е. плоскость, охватываемую r и v ). Однако, поскольку есть два направления, перпендикулярных любой плоскости, необходимо дополнительное условие, чтобы однозначно указать направление угловой скорости; обычно используется правило правой руки .
Пусть псевдовектор u { displaystyle mathbf {u}}


- ω знак равно ω U знак равно d ϕ dtu = v грех (θ) ru, { displaystyle { boldsymbol { omega}} = omega mathbf {u} = { frac {d phi} {dt }} mathbf {u} = { frac {v sin ( theta)} {r}} mathbf {u},}
где θ — угол между r и v . В терминах перекрестного произведения это:
- ω = r × v r 2. { displaystyle { boldsymbol { omega}} = { frac { mathbf {r} times mathbf {v}} {r ^ {2}}}.}
Из приведенного выше уравнения можно восстановить тангенциальная скорость как:
- v ⊥ = ω × r { displaystyle mathbf {v} _ { perp} = { boldsymbol { omega}} times mathbf {r}}
Обратите внимание, что Вышеприведенное выражение для ω { displaystyle { boldsymbol { omega}}}

Добавление векторов угловой скорости

Если точка вращается с орбитальной угловой скоростью ω 1 { displaystyle omega _ {1} }





Единственным неочевидным свойством вышеуказанного сложения является коммутативность. Это может быть доказано тем фактом, что тензор скорости W (см. Ниже) является кососимметричным, так что R = e W ⋅ dt { displaystyle R = e ^ {W cdot dt}}



Обратите внимание, что это также определяет вычитание как добавление отрицательного вектора.
Вектор угловой скорости для твердого тела или системы отсчета
Учитывая вращающуюся систему из трех единичных векторов координат, все три должны иметь одинаковую угловую скорость в каждый момент времени. В такой системе отсчета каждый вектор можно рассматривать как движущуюся частицу с постоянным скалярным радиусом.
Вращающаяся рамка появляется в контексте твердых тел, и для нее были разработаны специальные инструменты: угловая скорость вращения может быть описана как вектор или, что эквивалентно, как тензор .
В соответствии с общим определением, угловая скорость вращения кадра определяется как орбитальная угловая скорость любого из трех векторов (одинаковых для всех) относительно его собственного центра вращения. Добавление векторов угловой скорости для кадров также определяется обычным сложением векторов (композиция линейных перемещений) и может быть полезно для разложения вращения, как в подвесе. Все компоненты вектора могут быть вычислены как производные от параметров, определяющих движущиеся системы отсчета (углы Эйлера или матрицы вращения). Как и в общем случае, сложение коммутативно: ω 1 + ω 2 = ω 2 + ω 1 { displaystyle omega _ {1} + omega _ {2} = omega _ {2} + omega _ {1}}
Согласно теореме Эйлера о вращении, любая вращающаяся рамка имеет мгновенную ось вращения, которая является направлением вектора угловой скорости, и величиной угловая скорость согласуется с двумерным случаем.
Если мы выберем точку отсчета R { displaystyle { boldsymbol {R}}}

- r ˙ = R ˙ + (r — R) × ω { displaystyle { dot { boldsymbol {r}}} = { dot { boldsymbol {R}}} + ({ boldsymbol {r}} — { boldsymbol {R}}) times { boldsymbol { omega}}}
Компоненты угловой скорости из базисных векторов неподвижной системы отсчета
Рассмотрим твердое тело, вращающееся вокруг фиксированной точки O. Постройте систему отсчета в теле, состоящую из ортонормированного набора векторов e 1, e 2, e 3 { displaystyle mathbf {e} _ {1}, mathbf {e} _ {2}, mathbf {e} _ {3}}
- ω = (e ˙ 1 ⋅ e 2) e 3 + (e ˙ 2 ⋅ e 3) e 1 + (e ˙ 3 ⋅ е 1) е 2, { displaystyle { boldsymbol { omega}} = ({ dot { mathbf {e}}} _ {1} cdot mathbf {e} _ {2}) mathbf {e} _ {3} + ({ dot { mathbf {e}}} _ {2} cdot mathbf {e} _ {3}) mathbf {e} _ {1} + ({ точка { mathbf {e}}} _ {3} cdot mathbf {e} _ {1}) mathbf {e} _ {2},}
Здесь
- e ˙ i = deidt { displaystyle { dot { mathbf {e}}} _ {i} = { frac {d mathbf {e} _ {i}} {dt}}}
— скорость изменения вектор кадра ei, i = 1, 2, 3, { displaystyle mathbf {e} _ {i}, i = 1,2,3,}
из-за поворота.
Обратите внимание, что эта формула несовместима с выражением
- ω = r × vr 2. { displaystyle { boldsymbol { omega}} = { frac { mathbf {r} times mathbf {v}} {r ^ {2}}}.}
поскольку эта формула определяет только угловую скорость одной точки около O, тогда как формула в этом разделе применима к раме или твердому телу. В случае твердого тела один элемент ω { displaystyle { boldsymbol { omega}}}
Компоненты углов Эйлера

Компоненты псевдовектора спиновой угловой скорости были впервые рассчитаны Леонардом Эйлером с использованием его углов Эйлера и использование промежуточной системы отсчета:
- Одна ось системы отсчета (ось прецессии)
- Линия узлов подвижной системы отсчета относительно системы отсчета (ось нутации)
- Одна ось движущейся системы отсчета (ось собственного вращения)
Эйлер доказал, что проекции псевдовектора угловой скорости на каждую из этих трех осей являются производной соответствующего угла (что эквивалентно разложению мгновенного вращение в три мгновенных эйлерова вращения ). Следовательно:
- ω = α ˙ U 1 + β ˙ U 2 + γ ˙ U 3 { displaystyle { boldsymbol { omega}} = { dot { alpha}} mathbf {u} _ {1} + { dot { beta}} mathbf {u} _ {2} + { dot { gamma}} mathbf {u} _ {3}}
Этот базис не ортонормирован, и его трудно использовать, но теперь вектор скорости может быть изменен на фиксированную систему отсчета или на движущуюся рамку с помощью простой смены баз. Например, переход на мобильный фрейм:
- ω = (α ˙ sin β sin γ + β ˙ cos γ) i + (α ˙ sin β cos γ — β ˙ sin γ) j + (α ˙ соз β + γ ˙) К { Displaystyle { boldsymbol { omega}} = ({ точка { альфа}} грех бета грех гамма + { точка { бета}} cos gamma) mathbf {i} + ({ dot { alpha}} sin beta cos gamma — { dot { beta}} sin gamma) mathbf {j} + ({ точка { альфа}} соз бета + { точка { гамма}}) mathbf {k}}
где i, j, k { displaystyle mathbf {i}, mathbf { j}, mathbf {k}}
Тензор угловой скорости
Вектор угловой скорости ω = (ω x, ω y, ω z) { displaystyle { boldsymbol { omega}} = ( omega _ {x}, omega _ {y}, omega _ {z})}
- W = (0 — ω z ω y ω z 0 — ω x — ω y ω x 0) { displaystyle W = { begin {pmatrix} 0 — omega _ {z} omega _ {y} \ omega _ {z} 0 — omega _ {x} \ — omega _ {y} omega _ {x} 0 \ end {pmatrix}}}
Это матрица бесконечно малого вращения. Линейное отображение W действует как (ω ×) { displaystyle ({ boldsymbol { omega}} times)}
- ω × r = W ⋅ r. { displaystyle { boldsymbol { omega}} times mathbf {r} = W cdot mathbf {r}.}
Расчет по матрице ориентации
Вектор r { displaystyle mathbf {r}}
- drdt = ω × r = W ⋅ r { displaystyle { frac {d mathbf {r}} {dt}} = { boldsymbol { omega}} times mathbf {r} = W cdot mathbf {r}}
Дана матрица ориентации A (t) кадра, столбцы которой являются движущимися ортонормированные векторы координат e 1, e 2, e 3 { displaystyle mathbf {e} _ {1}, mathbf {e} _ {2}, mathbf {e} _ {3}}

- d A dt = W ⋅ A. { displaystyle { frac {dA} {dt}} = W cdot A.}
(Это верно, даже если A (t) не вращается равномерно.) Следовательно, тензор угловой скорости:
- W = d A dt ⋅ A — 1 знак равно d A dt ⋅ AT, { displaystyle W = { frac {dA} {dt}} cdot A ^ {- 1} = { frac {dA} {dt}} cdot A ^ { mathrm {T}},}
, поскольку инверсия ортогональной матрицы A { displaystyle A}

Свойства тензоров угловой скорости
В общем, угловая скорость в n-мерном пространстве является производной по времени от тензора углового смещения, который является вторым рангом кососимметричный тензор.
Этот тензор W будет иметь n (n − 1) / 2 независимых компонент, что является размерностью алгебры Ли из группы Ли из вращения n-мерного внутреннего пространства продукта.
Двойственность по отношению к вектору скорости
В трех измерениях угловая скорость может быть представлена псевдовектором, поскольку второй разряд десятки Или двойственны псевдовекторам в трех измерениях. Поскольку тензор угловой скорости W = W (t) является кососимметричной матрицей :
- W = (0 ω z — ω y — ω z 0 ω x ω y — ω x 0), { displaystyle W = { begin {pmatrix} 0 omega _ {z} — omega _ {y} \ — omega _ {z} 0 omega _ {x} \ omega _ {y} — omega _ {x} 0 \ end {pmatrix}},}
его дуал Ходжа является вектором, который в точности является предыдущим вектором угловой скорости ω = [ω x, ω y, ω z] { displaystyle { boldsymbol { omega}} = [ omega _ {x}, omega _ {y}, omega _ {z}]}![boldsymbolomega=[omega_x,omega_y,omega_z]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f418d52c41570663e22f7b19a8d3a427b69cab)
экспоненциальная от W
Если нам известна начальная система отсчета A (0) и дан тензор постоянной угловой скорости W, мы можем получить A (t) для любого заданного t. Напомним матричное дифференциальное уравнение:
- d A d t = W ⋅ A. { displaystyle { frac {dA} {dt}} = W cdot A.}
Это уравнение можно интегрировать, чтобы получить:
- A (t) = e W t A (0), { displaystyle A (t) = e ^ {Wt} A (0),}
, который показывает связь с группой Ли вращений.
W кососимметричен
Мы доказываем, что тензор угловой скорости кососимметричен, т.е. W = d A (t) dt ⋅ AT { displaystyle W = { frac {dA (t)} {dt}} cdot A ^ { text {T}}}

Матрица поворота A ортогональна, обратна ее транспонированию, поэтому мы имеем I = A ⋅ AT { displaystyle I = A cdot A ^ { text {T}} }

- 0 = d A dt AT + A d AT dt { displaystyle 0 = { frac {dA} {dt}} A ^ { text {T}} + A { frac {dA ^ { text {T}}} {dt}}}
Применение формулы (AB) T = BTAT { displaystyle (AB) ^ { text {T}} = B ^ { text {T}} A ^ { text {T}}}
- 0 знак равно d A dt AT + (d A dt AT) T = W + WT { displaystyle 0 = { frac {dA} {dt}} A ^ { text {T}} + left ({ frac { dA} {dt}} A ^ { text {T}} right) ^ { text {T}} = W + W ^ { text {T}}}
Таким образом, W является отрицательным транспонировать, что означает, что он асимметричен.
Бескординатное описание
В любой момент t { displaystyle t}


- v = W r. { displaystyle mathbf {v} = W mathbf {r}.}
Связь между этой линейной картой и угловой скоростью псевдовектор ω { displaystyle omega}
Поскольку W является производной от ортогонального преобразования, билинейная форма
- B (r, s) = (W r) ⋅ s { displaystyle B ( mathbf {r }, mathbf {s}) = (W mathbf {r}) cdot mathbf {s}}
является кососимметричным. Таким образом, мы можем применить тот факт, что внешней алгебры существует уникальная линейная форма L { displaystyle L}

- L (r ∧ s) = B (r, s) { displaystyle L ( mathbf {r} wedge mathbf {s) }) = В ( mathbf {r}, mathbf {s})}
где r ∧ s ∈ Λ 2 V { displaystyle mathbf {r} wedge mathbf {s} in Лямбда ^ {2} V}


Взяв диез L L, мы получаем
- (W r) ⋅ s = L ♯ ⋅ (r ∧ s) { displaystyle (W mathbf { r}) cdot mathbf {s} = L ^ { sharp} cdot ( mathbf {r} wedge mathbf {s})}
Представляем ω: = ⋆ (L ♯) { displaystyle omega: = { star} (L ^ { sharp})}
- (W r) ⋅ s = ⋆ (⋆ ( L ♯) ∧ р ∧ s) знак равно ⋆ (ω ∧ р ∧ s) знак равно ⋆ (ω ∧ r) ⋅ s = (ω × r) ⋅ s, { displaystyle (W mathbf {r}) cdot mathbf {s} = { star} ({ star} (L ^ { sharp}) wedge mathbf {r} wedge mathbf {s}) = { star} ( omega wedge mathbf {r } wedge mathbf {s}) = { star} ( omega wedge mathbf {r}) cdot mathbf {s} = ( omega times mathbf {r}) cdot mathbf {s },}
где
- ω × r: = ⋆ (ω ∧ r) { displaystyle omega times mathbf {r}: = { star} ( omega wedge mathbf {r}) }
по определению.
Поскольку s { displaystyle mathbf {s}}
- W r = ω × r { displaystyle W mathbf {r} = omega times mathbf {r}}
Угловая скорость как векторное поле
Поскольку тензор угловой скорости вращения твердого тела (в его система покоя) — это линейное преобразование, которое отображает положения в скорости (внутри твердого тела), его можно рассматривать как постоянное векторное поле . В частности, угловая скорость вращения — это векторное поле Киллинга , принадлежащее элементу алгебры Ли SO (3) из 3-мерной группы вращений SO (3).
Кроме того, можно показать, что векторное поле угловой скорости вращения составляет ровно половину rot линейного векторного поля скорости v(r) твердого тела. В символах
- ω = 1 2 ∇ × v { displaystyle { boldsymbol { omega}} = { frac {1} {2}} nabla times mathbf {v}}
Жесткое тело Соображения
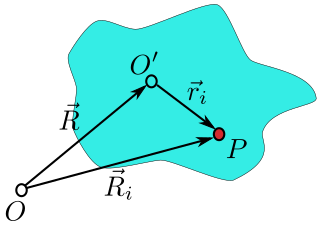
Те же уравнения для угловой скорости можно получить, рассуждая для вращающегося твердого тела . Здесь не предполагается, что твердое тело вращается вокруг начала координат. Вместо этого можно предположить, что он вращается вокруг произвольной точки, которая движется с линейной скоростью V (t) в каждый момент времени.
Чтобы получить уравнения, удобно представить твердое тело, прикрепленное к каркасам, и рассмотреть систему координат, которая зафиксирована по отношению к твердому телу. Затем мы изучим преобразования координат между этой координатой и фиксированной «лабораторной» системой.
Как показано на рисунке справа, начало координат лабораторной системы находится в точке O, начало системы твердого тела находится в точке O ‘, а вектор от O к O’ равен R . Частица (i) в твердом теле расположена в точке P, и положение вектора этой частицы Riв лабораторном кадре и в позиции riв кадре тела. Видно, что положение частицы можно записать:
- R i = R + ri { displaystyle mathbf {R} _ {i} = mathbf {R} + mathbf {r} _ {i} }
Определяющей характеристикой твердого тела является то, что расстояние между любыми двумя точками твердого тела не меняется во времени. Это означает, что длина вектора r i { displaystyle mathbf {r} _ {i}}







- R i = R + R rio { displaystyle mathbf {R} _ {i} = mathbf {R} + { mathcal {R}} mathbf {r } _ {io}}
Взяв производную по времени, получаем скорость частицы:
- V i = V + d R dtrio { displaystyle mathbf {V} _ {i} = mathbf {V} + { frac {d { mathcal {R}}} {dt}} mathbf {r} _ {io}}
где Vi- скорость частицы (в лабораторном кадре), а V — скорость O ‘(начало каркаса твердого тела). Поскольку R { displaystyle { mathcal {R}}}

- V i = V + d R dt I rio { displaystyle mathbf {V} _ {i} = mathbf {V} + { frac {d { mathcal {R}}} {dt}} { mathcal {I}} mathbf {r} _ {io}}
- V i = V + d R dt RTR rio { displaystyle mathbf {V} _ {i} = mathbf {V} + { frac {d { mathcal { R}}} {dt}} { mathcal {R}} ^ { text {T}} { mathcal {R}} mathbf {r} _ {io}}
- V i = V + d R dt RT ri { displaystyle mathbf {V} _ {i} = mathbf {V} + { frac {d { mathcal {R}}} {dt}} { mathcal {R}} ^ { text {T}} mathbf {r} _ {i}}
или
- V i = V + W ri { displaystyle mathbf {V} _ {i} = mathbf {V} + W mathbf {r} _ {i}}
где W = d R dt RT { displaystyle W = { frac {d { mathcal {R}}} {dt}} { mathcal {R}} ^ { text {T}}}
Можно доказать, что это кососимметричная матрица, поэтому мы можем взять его дуал, чтобы получить трехмерный псевдовектор, который в точности соответствует предыдущей угловой скорости вектор эффективности ω → { displaystyle { vec { omega}}}
- ω = [ω x, ω y, ω z] { displaystyle { boldsymbol { omega}} = [ omega _ {x}, omega _ {y}, omega _ {z}]}
Подставляя ω вместо W в приведенное выше выражение скорости, и заменяя матричное умножение на эквивалентное векторное произведение:
- V i = V + ω × ri { displaystyle mathbf {V} _ {i} = mathbf {V} + { boldsymbol { omega}} times mathbf {r} _ {i}}
Видно, что скорость точки в твердом теле может быть разделена на две точки — скорость опорной точки, установленной в твердом теле плюс сроке поперечного продукта, связанный с орбитальной скоростью частицы относительно опорной точки. Эта угловая скорость, что физики называют «спиновую угловую скорость» твердого тела, в отличии от орбитальной угловой скорости в опорной точке О ‘о происхождении О.
Последовательность
Мы предположили, что твердое тело вращается вокруг произвольной точки. Мы должны доказать, что ранее определенная угловая скорость спина не зависит от выбора начала отсчета, а это означает, что угловая скорость спина является внутренним свойством вращающегося твердого тела. (Обратите внимание на заметный контраст этого с орбитальной угловой скоростью точечной частицы, которая определенно зависит от выбора начала координат.)

См. График справа: начало лабораторной рамки — O, а O 1 и O 2 — две фиксированные точки на твердом теле, скорость которых равна v 1 { displaystyle mathbf {v} _ {1}}



- v 1 + ω 1 × r 1 = v 2 + ω 2 × r 2 { displaystyle mathbf {v} _ {1} + { boldsymbol { omega}} _ {1} times mathbf {r} _ {1} = mathbf {v} _ {2} + { boldsymbol { omega}} _ {2} times mathbf {r} _ {2}}
- v 2 = v 1 + ω 1 × r = v 1 + ω 1 × (r 1 — r 2) { displaystyle mathbf {v} _ {2} = mathbf {v} _ {1} + { boldsymbol { omega}} _ {1} times mathbf {r} = mathbf {v} _ {1} + { boldsymbol { omega}} _ {1} times ( mathbf {r} _ {1} — mathbf {r} _ {2})}
Два вышеуказанных результата дают, что
- (ω 2 — ω 1) × r 2 = 0 { displaystyle ({ boldsymbol { omega}} _ {2} — { boldsymbol { omega}} _ {1}) times mathbf {r} _ {2} = 0}
Поскольку точка P (и таким образом, r 2 { displaystyle mathbf {r} _ {2}}
- ω 1 = ω 2 { displaystyle { boldsymbol { omega} } _ {1} = { boldsymbol { omega}} _ {2}}
Если точкой отсчета является мгновенная ось вращения, выражение скорости точки в твердом теле будет только член постоянной скорости. Это потому, что скорость мгновенной оси вращения равна нулю. Пример мгновенной оси вращения — петля двери. Другой пример — точка контакта чисто катящегося сферического (или, в более общем смысле, выпуклого) твердого тела.
См. Также
- Угловое ускорение
- Угловая частота
- Угловой момент
- Площадная скорость
- Изометрия
- Ортогональная группа
- Динамика твердого тела
- Завихренность
Ссылки
- Саймон, Кейт (1971). Механика. Аддисон-Уэсли, Ридинг, Массачусетс. ISBN 978-0-201-07392-8 .
- Ландау, Л.Д. ; Лифшиц, Э.М. (1997). Механика. Баттерворт-Хайнеманн. ISBN 978-0-7506-2896-9 .
Внешние ссылки
| На Викискладе есть материалы, связанные с Угловой скоростью . |
- Учебник физики для колледжа Артур Лаланн Кимбалл (Угловая скорость частицы)
- Пикеринг, Стив (2009). «ω Скорость вращения [угловая скорость]». Шестьдесят символов. Брэди Харан для Ноттингемского университета.
| Angular velocity | |
|---|---|
|
Common symbols |
ω |
| In SI base units | s−1 |
| Extensive? | yes |
| Intensive? | yes (for rigid body only) |
| Conserved? | no |
|
Behaviour under |
pseudovector |
|
Derivations from |
ω = dθ / dt |
| Dimension |  |
In physics, angular velocity (ω or Ω), also known as angular frequency vector,[1] is a pseudovector representation of how fast the angular position or orientation of an object changes with time (i.e. how quickly an object rotates or revolves relative to a point or axis). The magnitude of the pseudovector represents the angular speed, the rate at which the object rotates or revolves, and its direction is normal to the instantaneous plane of rotation or angular displacement. The orientation of angular velocity is conventionally specified by the right-hand rule.[2]
There are two types of angular velocity.
- Orbital angular velocity refers to how fast a point object revolves about a fixed origin, i.e. the time rate of change of its angular position relative to the origin.[citation needed]
- Spin angular velocity refers to how fast a rigid body rotates with respect to its center of rotation and is independent of the choice of origin, in contrast to orbital angular velocity.
In general, angular velocity has dimension of angle per unit time (angle replacing distance from linear velocity with time in common). The SI unit of angular velocity is radians per second,[3] with the radian being a dimensionless quantity, thus the SI units of angular velocity may be listed as s−1. Angular velocity is usually represented by the symbol omega (ω, sometimes Ω). By convention, positive angular velocity indicates counter-clockwise rotation, while negative is clockwise.
For example, a geostationary satellite completes one orbit per day above the equator, or 360 degrees per 24 hours, and has angular velocity ω = (360°)/(24 h) = 15°/h, or (2π rad)/(24 h) ≈ 0.26 rad/h. If angle is measured in radians, the linear velocity is the radius times the angular velocity, 
Orbital angular velocity of a point particle[edit]
Particle in two dimensions[edit]
The angular velocity of the particle at P with respect to the origin O is determined by the perpendicular component of the velocity vector v.
In the simplest case of circular motion at radius 






In the general case of a particle moving in the plane, the orbital angular velocity is the rate at which the position vector relative to a chosen origin «sweeps out» angle. The diagram shows the position vector 







The angular velocity ω is the rate of change of angular position with respect to time, which can be computed from the cross-radial velocity as:
Here the cross-radial speed 





These formulas may be derived doing 









In two dimensions, angular velocity is a number with plus or minus sign indicating orientation, but not pointing in a direction. The sign is conventionally taken to be positive if the radius vector turns counter-clockwise, and negative if clockwise. Angular velocity then may be termed a pseudoscalar, a numerical quantity which changes sign under a parity inversion, such as inverting one axis or switching the two axes.
Particle in three dimensions[edit]
The orbital angular velocity vector encodes the time rate of change of angular position, as well as the instantaneous plane of angular displacement. In this case (counter-clockwise circular motion) the vector points up.
In three-dimensional space, we again have the position vector r of a moving particle. Here, orbital angular velocity is a pseudovector whose magnitude is the rate at which r sweeps out angle, and whose direction is perpendicular to the instantaneous plane in which r sweeps out angle (i.e. the plane spanned by r and v). However, as there are two directions perpendicular to any plane, an additional condition is necessary to uniquely specify the direction of the angular velocity; conventionally, the right-hand rule is used.
Let the pseudovector 


where θ is the angle between r and v. In terms of the cross product, this is:
[4]
From the above equation, one can recover the tangential velocity as:
Spin angular velocity of a rigid body or reference frame[edit]
Given a rotating frame of three unit coordinate vectors, all the three must have the same angular speed at each instant. In such a frame, each vector may be considered as a moving particle with constant scalar radius.
The rotating frame appears in the context of rigid bodies, and special tools have been developed for it: the spin angular velocity may be described as a vector or equivalently as a tensor.
Consistent with the general definition, the spin angular velocity of a frame is defined as the orbital angular velocity of any of the three vectors (same for all) with respect to its own center of rotation. The addition of angular velocity vectors for frames is also defined by the usual vector addition (composition of linear movements), and can be useful to decompose the rotation as in a gimbal. All components of the vector can be calculated as derivatives of the parameters defining the moving frames (Euler angles or rotation matrices). As in the general case, addition is commutative: 
By Euler’s rotation theorem, any rotating frame possesses an instantaneous axis of rotation, which is the direction of the angular velocity vector, and the magnitude of the angular velocity is consistent with the two-dimensional case.
If we choose a reference point 

Components from the basis vectors of a body-fixed frame[edit]
Consider a rigid body rotating about a fixed point O. Construct a reference frame in the body consisting of an orthonormal set of vectors 
where 

This formula is incompatible with the expression for orbital angular velocity
as that formula defines angular velocity for a single point about O, while the formula in this section applies to a frame or rigid body. In the case of a rigid body a single 
Components from Euler angles[edit]
Diagram showing Euler frame in green
The components of the spin angular velocity pseudovector were first calculated by Leonhard Euler using his Euler angles and the use of an intermediate frame:
- One axis of the reference frame (the precession axis)
- The line of nodes of the moving frame with respect to the reference frame (nutation axis)
- One axis of the moving frame (the intrinsic rotation axis)
Euler proved that the projections of the angular velocity pseudovector on each of these three axes is the derivative of its associated angle (which is equivalent to decomposing the instantaneous rotation into three instantaneous Euler rotations). Therefore:[5]
This basis is not orthonormal and it is difficult to use, but now the velocity vector can be changed to the fixed frame or to the moving frame with just a change of bases. For example, changing to the mobile frame:
where 
Tensor [edit]
The angular velocity vector 
This is an infinitesimal rotation matrix. The linear mapping W acts as 
Calculation of angular velocity tensor of a rotating frame[edit]
A vector 
Let ![{displaystyle A(t)=[mathbf {e} _{1}(t) mathbf {e} _{2}(t) mathbf {e} _{3}(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/961bf64c6fef578d15f27e1ffc086271e68721dd)



The angular velocity 

which holds even if A(t) does not rotate uniformly. Therefore the angular velocity tensor is:
since the inverse of an orthogonal matrix 

Properties[edit]
In general, the angular velocity in an n-dimensional space is the time derivative of the angular displacement tensor, which is a second rank skew-symmetric tensor.
This tensor W will have n(n−1)/2 independent components, which is the dimension of the Lie algebra of the Lie group of rotations of an n-dimensional inner product space.[6]
Duality with respect to the velocity vector[edit]
In three dimensions, angular velocity can be represented by a pseudovector because second rank tensors are dual to pseudovectors in three dimensions. Since the angular velocity tensor W = W(t) is a skew-symmetric matrix:
its Hodge dual is a vector, which is precisely the previous angular velocity vector ![boldsymbolomega=[omega_x,omega_y,omega_z]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f418d52c41570663e22f7b19a8d3a427b69cab)
Exponential of W[edit]
If we know an initial frame A(0) and we are given a constant angular velocity tensor W, we can obtain A(t) for any given t. Recall the matrix differential equation:
This equation can be integrated to give:
which shows a connection with the Lie group of rotations.
W is skew-symmetric[edit]
We prove that angular velocity tensor is skew symmetric, i.e. 

A rotation matrix A is orthogonal, inverse to its transpose, so we have 

Applying the formula 
Thus, W is the negative of its transpose, which implies it is skew symmetric.
Coordinate-free description[edit]
At any instant 


The relation between this linear map and the angular velocity pseudovector 
Because W is the derivative of an orthogonal transformation, the bilinear form
is skew-symmetric. Thus we can apply the fact of exterior algebra that there is a unique linear form 

where 


Taking the sharp L♯ of L we get
Introducing 

where
by definition.
Because 
Angular velocity as a vector field[edit]
Since the spin angular velocity tensor of a rigid body (in its rest frame) is a linear transformation that maps positions to velocities (within the rigid body), it can be regarded as a constant vector field. In particular, the spin angular velocity is a Killing vector field belonging to an element of the Lie algebra SO(3) of the 3-dimensional rotation group SO(3).
Also, it can be shown that the spin angular velocity vector field is exactly half of the curl of the linear velocity vector field v(r) of the rigid body. In symbols,
Rigid body considerations[edit]
Position of point P located in the rigid body (shown in blue). Ri is the position with respect to the lab frame, centered at O and ri is the position with respect to the rigid body frame, centered at O′. The origin of the rigid body frame is at vector position R from the lab frame.
The same equations for the angular speed can be obtained reasoning over a rotating rigid body. Here is not assumed that the rigid body rotates around the origin. Instead, it can be supposed rotating around an arbitrary point that is moving with a linear velocity V(t) in each instant.
To obtain the equations, it is convenient to imagine a rigid body attached to the frames and consider a coordinate system that is fixed with respect to the rigid body. Then we will study the coordinate transformations between this coordinate and the fixed «laboratory» system.
As shown in the figure on the right, the lab system’s origin is at point O, the rigid body system origin is at O′ and the vector from O to O′ is R. A particle (i) in the rigid body is located at point P and the vector position of this particle is Ri in the lab frame, and at position ri in the body frame. It is seen that the position of the particle can be written:
The defining characteristic of a rigid body is that the distance between any two points in a rigid body is unchanging in time. This means that the length of the vector 







Taking the time derivative yields the velocity of the particle:
where Vi is the velocity of the particle (in the lab frame) and V is the velocity of O′ (the origin of the rigid body frame). Since 

or
where 
It can be proved that this is a skew symmetric matrix, so we can take its dual to get a 3 dimensional pseudovector that is precisely the previous angular velocity vector 
Substituting ω for W into the above velocity expression, and replacing matrix multiplication by an equivalent cross product:
It can be seen that the velocity of a point in a rigid body can be divided into two terms – the velocity of a reference point fixed in the rigid body plus the cross product term involving the orbital angular velocity of the particle with respect to the reference point. This angular velocity is what physicists call the «spin angular velocity» of the rigid body, as opposed to the orbital angular velocity of the reference point O′ about the origin O.
Consistency[edit]
We have supposed that the rigid body rotates around an arbitrary point. We should prove that the spin angular velocity previously defined is independent of the choice of origin, which means that the spin angular velocity is an intrinsic property of the spinning rigid body. (Note the marked contrast of this with the orbital angular velocity of a point particle, which certainly does depend on the choice of origin.)
Proving the independence of spin angular velocity from choice of origin
See the graph to the right: The origin of lab frame is O, while O1 and O2 are two fixed points on the rigid body, whose velocity is 



The above two yields that
Since the point P (and thus 
If the reference point is the instantaneous axis of rotation the expression of the velocity of a point in the rigid body will have just the angular velocity term. This is because the velocity of the instantaneous axis of rotation is zero. An example of the instantaneous axis of rotation is the hinge of a door. Another example is the point of contact of a purely rolling spherical (or, more generally, convex) rigid body.
See also[edit]
- Angular acceleration
- Angular frequency
- Angular momentum
- Areal velocity
- Isometry
- Orthogonal group
- Rigid body dynamics
- Vorticity
References[edit]
- ^ Cummings, Karen; Halliday, David (2007). Understanding physics. New Delhi: John Wiley & Sons Inc., authorized reprint to Wiley – India. pp. 449, 484, 485, 487. ISBN 978-81-265-0882-2.(UP1)
- ^ Hibbeler, Russell C. (2009). Engineering Mechanics. Upper Saddle River, New Jersey: Pearson Prentice Hall. pp. 314, 153. ISBN 978-0-13-607791-6.(EM1)
- ^ Taylor, Barry N. (2009). International System of Units (SI) (revised 2008 ed.). DIANE Publishing. p. 27. ISBN 978-1-4379-1558-7. Extract of page 27
- ^ Singh, Sunil K. Angular Velocity. OpenStax. Rice University. Retrieved 21 May 2021.
- ^ K.S.HEDRIH: Leonhard Euler (1707–1783) and rigid body dynamics
- ^ Rotations and Angular Momentum on the Classical Mechanics page of the website of John Baez, especially Questions 1 and 2.
- Symon, Keith (1971). Mechanics. Addison-Wesley, Reading, MA. ISBN 978-0-201-07392-8.
- Landau, L.D.; Lifshitz, E.M. (1997). Mechanics. Butterworth-Heinemann. ISBN 978-0-7506-2896-9.
External links[edit]
- A college text-book of physics By Arthur Lalanne Kimball (Angular Velocity of a particle)
- Pickering, Steve (2009). «ω Speed of Rotation [Angular Velocity]». Sixty Symbols. Brady Haran for the University of Nottingham.