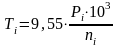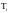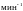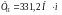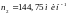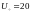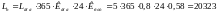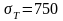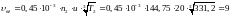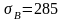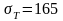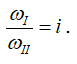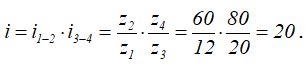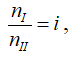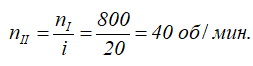Угловые скорости
валов определяются по формуле:
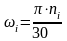
где i
– угловая скорость на расчетном
валу, с-1;
ni
– частота вращения расчетного вала,
об/мин.

Результаты расчетов
заносим в табл.2.1.
2.8 Крутящие моменты на валах привода
Крутящие моменты
на валах привода определяются по формуле:
;
где
– искомый крутящий момент на валу, Н·м;
Pi
– мощность на валу, Вт;
ni
– частота вращения вала, об/мин.
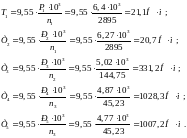
Результаты расчетов
заносим в табл.2.1.
Таблица 2.1
Значения частот
вращения, угловых скоростей, мощностей
и крутящих моментов на валах
-
Вал
Частота вращения
n,
Угловая
скоростьω,
с-1Мощность
P,
кВтКрутящий момент
T,
Н·м
2895
303,01
6,4
21,1
’
2895
303,01
6,27
20,7
144,75
15,15
5,02
331,2
45,23
4,73
4,87
1028,3
’
45,23
4,73
4,77
1007,2
3 Расчёт открытых передач
Для расчёта
звёздочки приводного вала выбираем
тяговую пластинчатую цепь М20-1-80-1 ГОСТ
588-81 [1(т.2);с.675;табл.24], у которой d1
= 6 мм; d2=9мм; b1=35мм;
b3= 15 мм; h = 18 мм; s =
2,5 мм.
Расчёт звёздочки
для пластинчатой цепи выполняем по ГОСТ
592-81 [1;с.683;табл.31]
Шаг цепи p
= 80 мм
Диаметр элемента
зацепления цепи Dц = d2 = 9 мм
Геометрическая
характеристика зацепления
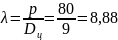
Число зубьев
звёздочки z = 10
Диаметр делительной
окружности звёздочки:
– в шагах

– в
миллиметрах
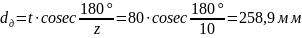
Диаметр окружности,
вписанной в шаговый многоугольник:
– в шагах
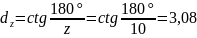
– в
миллиметрах
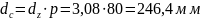
Высота зуба,
измеренная от шаговой линии:
– в шагах
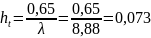
– в
миллиметрах
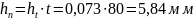
Диаметр окружности
выступов

Диаметр окружности
впадин
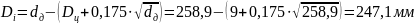
Смещение центров
дуг впадин
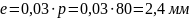
Радиус впадины
зубьев
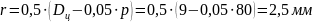
Половина угла
заострения зуба γ = 20˚
Угол впадины для
профилирования зубьев по впадине β
=2γ+360/z= 76˚
Предельно
допускаемое увеличение шага цепи по
зацеплению со звёздочкой Δt = 3%
Число ходов (число
зубьев на один шаг цепи t) m = 1
Ширина
основания зуба звёздочки
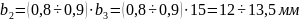
Принимаем
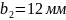
Ширина вершины
зуба
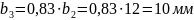
Радиус закругления
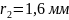
Диаметр
венца
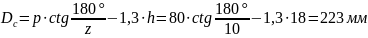
Принимаем
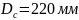
Радиус выпуклости
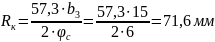
Расчётный угол
условного смещения звёздочек φс
= 6˚
4 Выбор материалов колёс, назначение твёрдости, расчёт допускаемых напряжений σНр, σFp, расчёт геометрических параметров и проверочные расчёты зубчатых передач по напряжениям σНр, σFр
4.1 Расчёт червячной передачи
Исходные данные:
– вращающий момент
на колесе;
– частота вращения
колеса;
– передаточное
число;
ч — время работы
передачи (ресурс).
4.1.1 Материалы
червяка и колеса
По рекомендациям
справочных таблиц для червяка принимаем
сталь марки 40Х, с улучшением и закалкой
ТВЧ с глубиной закаленного слоя 1,8 –
2,2 мм (т.к. для работы червяка предъявляются
высокие требования, а заданная в курсовом
проекте твердость невысокая) со следующими
характеристиками [8;с.11,табл.2.1]
твёрдость зубьев:
в сердцевине:
269-302 НВ < 350 НВ;
на поверхности:
45-50 НRCэ;
МПа.
Материал зубчатого
венца червячного колеса по мере
убывания антизадирных и антифрикционных
свойств и рекомендуемым для применения
скоростям скольжения относим к I
группе со скоростью скольжения:
м/c
и принимаем материал
БрО10Н1Ф1, со следующими характеристиками
[8;с.31;табл.2.14]:
МПа;
МПа.
Соседние файлы в папке 0091
- #
10.02.202369.96 Кб1Ведомость.frw
- #
10.02.2023262.36 Кб1Картер.cdw
- #
10.02.202391.92 Кб1Колесо зубчатое.cdw
- #
10.02.2023101.82 Кб1колесо.dwg
- #
10.02.202374.49 Кб1Компоновка.cdw
- #
- #
10.02.202368.04 Кб1Предворительная эскизаня компоновка.cdw
- #
10.02.2023326.59 Кб1привод.dwg
- #
10.02.2023152.35 Кб1рама.dwg
- #
- #
10.02.2023235.04 Кб1Редуктор.dwg
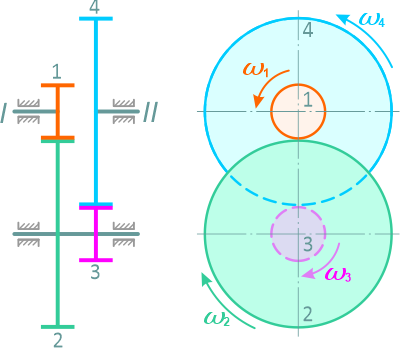
Пример решения задачи по определению угловой скорости шестерни ведомого вала редуктора по заданной угловой скорости колеса ведущего вала и передаточному числу
Задача
Редуктор обеспечивает вращение валов I и II, имеющих общую геометрическую ось, с различными угловыми скоростями (рисунок 1.10).
Рис. 1.10
Определить угловую скорость вала II, соответствующую угловой скорости вала I, равной n1=800 об/мин, если числа зубьев шестерен соответственно равны: z1=12, z2=60, z3=20, z4=80.
Другие примеры решений >
Помощь с решением задач >
Решение
Передаточное число редуктора равно отношению угловой скорости ведущего вала к угловой скорости ведомого:
При этом угловые скорости ведущего и ведомого валов равны угловым скоростям жестко соединенных с ними шестерен:
ωI = ω1, ωII = ω4.
Для получения зависимости между угловыми скоростями шестерен 1 и 4 следует определить передаточное число передачи, состоящей из двух пар колес:
Пользуясь угловыми скоростями, выраженными в об/мин, имеем:
откуда
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Одним из распространенных в природе и технике видов движения является вращение. Этот вид перемещения тел в пространстве характеризуется набором физических величин. Важная характеристика любого вращения — это частота. Формулу частоту вращения можно найти, зная определенные величины и параметры.
Что такое вращение?
Под ним в физике понимают такое перемещение материальной точки вокруг некоторой оси, при котором ее расстояние до этой оси остается постоянным. Оно называется радиусом вращения.

Примерами этого движения в природе является вращение планет вокруг Солнца и вокруг собственной оси. В технике вращение представлено движением валов, шестеренок, колеса автомобиля или велосипеда, перемещением лопастей ветровых мельниц.
Описывающие вращение физические величины
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.
В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:
n = θ/(2*pi);
L = θ*r.
Где r — радиус окружности или радиус вращения.
Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:
ω = θ/t
Угловая частота, период и угловая скорость
Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:
T = 2*pi/ω
Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:
f = 2*pi/T
Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.
Сравнивая две последние формулы, приходим к следующему равенству:
f = ω
Это равенство означает следующее:
- формулы угловой частоты и угловой скорости совпадают, поэтому эти величины равны численно между собой;
- так же как и скорость, частота показывает, на какой угол в радианах поворачивается тело за одну секунду.
Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.
Линейная скорость вращения, частота и частота угловая
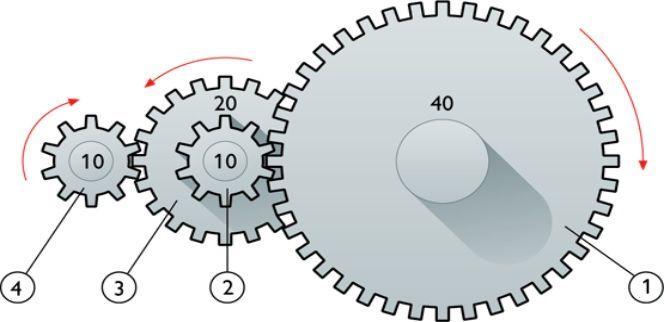
В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.
Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:
μ = 1/T
Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:
f = 2*pi*μ
Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.
Линейная скорость v связана со скоростью угловой ω следующим равенством:
v = ω*r
Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:
f = v/r
Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.
Задача на определение циклической частоты вращения вала
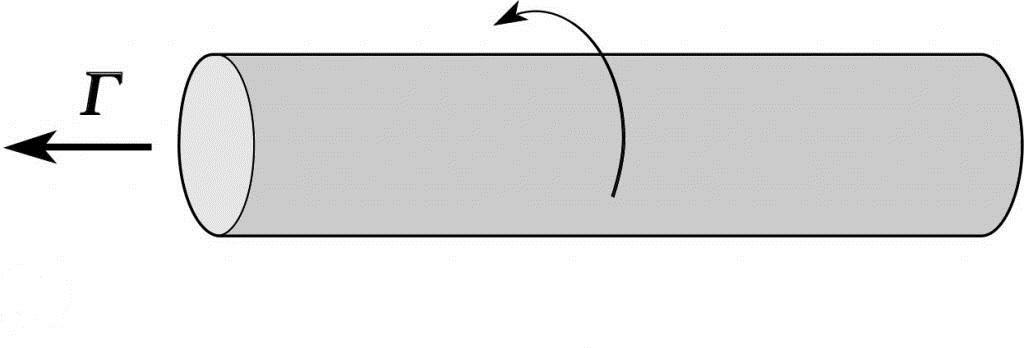
Угловые частоты вращения содержат полезную информацию, поскольку позволяют рассчитать такие важные физические характеристики, как момент импульса или угловую скорость. Решим такую задачу: известно, что рабочая частота вращения вала составляет 1500 оборотов в минуту. Чему равна циклическая частота для этого вала?
Из единиц измерения, приведенный в условии, понятно, что дана обычная частота μ. Поэтому формула частоты вращения вала циклической имеет вид:
f = 2*pi*μ
Прежде чем ею пользоваться, следует перевести указанную в условии цифру к стандартным единицам измерения, то есть к обратным секундам. Поскольку вал за минуту делает 1500 оборотов, то за секунду он сделает в 60 раз меньше оборотов, то есть 25. То есть частота его вращения равна 25 Гц. Подставляя это число в записанную выше формулу, получаем значение циклической частоты: f = 157 рад/с.
Что такое угловая скорость
Угловая скорость (обозначается как (omega)) — векторная величина, характеризующая скорость и направление изменения угла поворота со временем.
Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.
Единица измерения
В Международной системе единиц (СИ) принятой единицей измерения угловой скорости является радиан в секунду (рад/с)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формула угловой скорости
Вектор угловой скорости определяется отношением угла поворота ((varphi)) к интервалу времени ((mathcal t)), за которое произошел поворот:
(omega=frac{trianglevarphi}{trianglemathcal t})
Зависимость угловой скорости от времени
Зависимость (varphi ) от (mathcal t) наглядно показана на графике:
Угол, на который повернулось тело, характеризуется площадью под кривой.
Угловая скорость вращения, формула
Через частоту
(omega=2pimathcal n)
(mathcal n) — частота вращения ((1/с))
(pi) — число Пи ((approx 3,14))
(mathcal n=frac1T)
(T )— период вращения (время, за которое тело совершает один оборот)
Через радиус
(omega=frac vR)
(v) — линейная скорость(м/с)
(R) — радиус окружности (м)
Как определить направление угловой скорости
Направление скорости в физике можно определять двумя способами:
- Правило буравчика. Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.
- Правило правой руки. Представим, что взяли тело в правую руку. Следует направлять и вращать его туда, куда указывают четыре пальца. Отведенный в сторону большой палец покажет направление угловой скорости при этом вращении.
Связь линейной и угловой скорости
Линейная скорость ((v)) тела, расположенного на расстоянии (R) от оси вращения, прямо пропорциональна угловой скорости.
(v=Romega)
(R) — радиус окружности (м)
Чему равна мгновенная угловая скорость
Мгновенную угловую скорость нужно находить как предел, к которому стремится средняя угловая скорость при (trianglemathcal trightarrow0) :
(omega=lim_{trianglerightarrow0}frac{trianglevarphi}{trianglemathcal t})
Измеряется в рад/с