Как найти углы между кривыми - Исправление недочетов и поиск решений вместе с Examum.ru

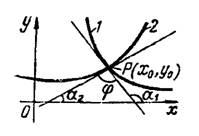
Угол между двумя пересекающимися кривыми определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения (рис. 1) по формуле

$displaystyle tg: varphi =frac{k_{1}-k_{2}}{1+k_{1}k_{2}},; ; (2)$

где $displaystyle k_{1}$ и $displaystyle k_{2}$ — угловые коэффициенты касательных к кривым в точке их пересечения $displaystyle P(x_{0},y_{0})$ ,
т. е. частные значения в точке $displaystyle x_{0}$ производных от по из уравнений этих кривых:

$displaystyle k_{1}=tg: alpha _{1}=left ( frac{dy_{1}}{dx} right )_{x=x_{0}};; k_{2}=tg: alpha _{2}=left ( frac{dy_{2}}{dx} right )_{x=x_{0}}.$

Рис.1

Пример 1. Найти углы, под которыми пересекаются следующие линии:
1) прямая displaystyle x+y-4=0 и парабола $displaystyle 2y=8-x^{2}$ ;
2) эллипс $displaystyle x^{2}+4y^{2}=4$ и парабола $displaystyle 4y=4-5x^{2}$ ;
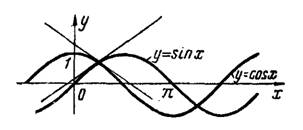
3) синусоида displaystyle y=sin x и косинусоида displaystyle y=cos x .
Решение.
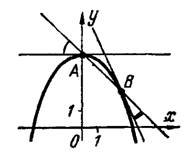
1) Совместно решая уравнения параболы и прямой, находим, что они пересекаются в двух точках: A(0;4) и B(2;2) , рис.2.

Рис.2

Далее находим производную от по из уравнения параболы: displaystyle 2y'=-2x,: y'=-x и определяем угловые коэффициенты касательных к параболе в точках и , как частные значения этой производной:

$displaystyle y'_{A}=k_{A}=0;; y'_{B}=k_{B}=-2.$

Угловой коэффициент прямой один и тот же во всех ее точках; у данной прямой он равен — 1.
Согласно формуле (2) получим

$displaystyle textrm{tg}: A=1,: A=45^{circ};; textrm{tg}: B=frac{-1+2}{1+2}=frac{1}{3},; Bapprox 18,5^{circ}.$

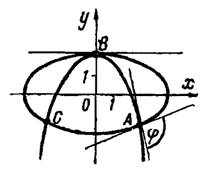
2) Решая совместно уравнения кривых, находим их общие точки: A(1,2;-0,8), B(0;1) и C(-1,2;-0,8) рис.3. Затем определяем угловые коэффициенты $displaystyle k_{1}$ и $displaystyle k_{2}$ касательных в любой точке эллипса и параболы как производные от по из их уравнений

$displaystyle k_{1}=-frac{x}{4y};; k_{2}=-frac{5}{2}x.$

Рис.3

Подставляя координаты точки , получим $displaystyle k_{1}=frac{3}{8}$ и $displaystyle k_{2}=-3$ . Следовательно, в точке :

$displaystyle textrm{tg}: varphi =frac{frac{3}{8}+3}{1-frac{9}{8}}=-27;; varphi approx 92^{circ}.$

Под таким же углом кривые пересекаются и в точке вследствие их симметричности относительно оси .
В точке имеем: $displaystyle k_{1}=k_{2}=0$ , следовательно, в точке кривые имеют общую касательную, т. е. касаются друг друга. В этой точке угол между кривыми равен нулю.
3) Абсциссы точек пересечения кривых (рис.4) определяются уравнением displaystyle sin x=cos x , решая которое, получим

$displaystyle x=frac{pi }{4}+pi n; (n=0,pm 1,pm 2,...).$

Дифференцированием находим угловые коэффициенты касательных к синусоиде и косинусоиде: $displaystyle k_{1}=cos x;: k_{2}=-sin x.$

Рис.4

Искомый угол между кривыми определяем по общей формуле (2)
$displaystyle textrm{tg}: varphi =frac{cos x+sin x}{1-cos xsin x}=pm frac{frac{sqrt{2}}{2}+frac{sqrt{2}}{2}}{1-frac{1}{2}}=pm 2sqrt{2}.$
Положительному знаку соответствует острый угол $displaystyle varphi approx 70,5^{circ}$ , отрицательному — тупой, смежный с ним угол $displaystyle varphi_{1} approx 109,5^{circ}$ .

Источник

Углом
между двумя кривыми
у
= f₁(x)
и у
= f₂(x)
в точке их пересечения М₀(х₀,
у₀)
называется угол между касательными к
этим кривым в точке М₀.
Этот угол определяется по формуле

=

.

Пример.
Найти угол между параболами

у
= 8 – х²
и у
= х².

□ Для
нахождения координат точек пересечения
заданных кривых решим систему уравнений

В
результате получим А(2;
4) и В(−2;
4). Продифференцируем уравнения парабол:

= −2х,

= 2х.
Найдем значения

для точки А(2;
4):

= −4,

= 4. Следовательно,

=

.

Аналогично
определяется угол между кривыми в точке
В(−2;
4):

.
■

§ 21. Формула тейлора

Теорема.
Пусть функция f(x)
имеет в точке а
и некоторой ее окрестности производные
порядка п
+ 1. Пусть х
– любое значение аргумента из указанной
окрестности, х
≠ а.
Тогда между точками а
и х
найдется точка

такая, что справедлива формула:

f(x)
= f(а)
+

(х
– а)
+
(х
– а)²+
…+

(х
– а)^п+

+
(х
– а)^п⁺¹.

Эту
формулу называют формулой
Тейлора.

Выражение

R_n₊₁(x)
=

(х
– а)^п⁺¹

называют
остаточным
членом

формулы Тейлора.

Запишем остаточный
член в другом виде:

так
как

(а,
х),
то найдется число

,
0 <

< 1, что

= а
+

(х
– а)
и тогда

R_n₊₁(x)
=

(х
– а)^п⁺¹,
0 <

< 1.

Эта
форма остаточного члена наиболее
употребительна в приложениях.

Если
в формуле Тейлора а
= 0, то получим формулу
Маклорена:

f(x)
= f(0)
+

х
+

х²+
… +

х^п+
R_n₊₁(x)

с
остаточным членом

R_n₊₁(x)
=

х^п⁺¹,
0 <

< 1.

Разложение
некоторых элементарных функций по
формуле Маклорена

1.
f(x)
= е^х.

Так как

f(x)
=

= … = f
^п⁺¹(x)
= е^х,

f(0)
=

= … = f
^п⁺¹(0)
= 1,

то
формула Маклорена имеет вид

е^х
= 1 +

+…+

+ R_n₊₁(x),

где

R_n₊₁(x)
=

х^п⁺¹,
0 <

< 1.

Аналогично
можно разложить по формуле Маклорена
следующие функции:

2.
f(x)
=

= х
−

−

+
…+ (−1)^т⁺¹

+ R₂_т(x),

где
R₂_т(x)
= (−1)^т
·
,
0 <

< 1.

3.
f(x)
=

= 1
−

−

+
…+ (−1)^т

+ R₂_т₊₁(x),

где
R₂_т₊₁(x)
= (−1)^т⁺¹
·
,
0 <

< 1.

4.
f(x)
= (1 + х)^т.

(1
+ х)^т
=1+
х+
х²+

х³+…+

+

х^п
+R_n₊₁(x),

где

R_n₊₁(x)=

х^п⁺¹(1
+

)^т^—^п-¹,
0 <

< 1.

Пример.
Вычислить число е.

□ Запишем
разложение е^х
по формуле Маклорена:

е^х
= 1+

+…+

+
х^п⁺¹,
0 <

< 1.

Если
заменить функцию е^х
ее многочленом Тейлора степени п
(отбросим остаточный член), то получим
приближенное равенство

е^х

1 +

+…+

,
(1)

абсолютная
погрешность которого

| R_n₊₁(x)
| =

| х
|^п⁺¹,
0 <

< 1.

Если
рассматривать функцию е^х
для −1 ≤ х
≤ 1, то

|
R_n₊₁(x)
| ≤

<

.

Полагая
в (1) х
= 1, получаем приближенное значение числа

е
≈ 1+

+ …+

.

При
этом | R_n₊₁(x)
| <

Если
требуется вычислить значение е
с точностью

= 0,001, то число п
определяется из неравенства

< 0,001, или (п
+ 1)! > 3000,

которое
выполняется при п
= 6. Следовательно,

е
≈ 1+

+ …+

.

Вычисляя
с четырьмя знаками после запятой, получим

е
≈ 2,7180.

Три
знака после запятой гарантированы.
■

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Задание. Найти тангенс угла между кривыми $y=x^2-1$ и
$y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.

Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:

$$begin{array}{c}
left{begin{array}{l}
y_{1}=x^{2}-1 \
y_{2}=x^{3}-1
end{array} Rightarrow x^{2}-1=x^{3}-1 Rightarrow x^{3}-x^{2}=0 Rightarrowright. \
Rightarrow x_{1,2}=0, x_{3}=1
end{array}$$

Таким образом, искомая точка $x=1$.

Далее находим производные заданных функций в найденной точке:

$$begin{array}{c}
y_{1}^{prime}=left(x^{2}-1right)^{prime}=left(x^{2}right)^{prime}-(1)^{prime}=2 x-0=2 x, y_{1}^{prime}(1)=2 \
y_{2}^{prime}=left(x^{3}-1right)^{prime}=left(x^{3}right)^{prime}-(1)^{prime}=3 x^{2}-0=3 x^{2}, y_{2}^{prime}(1)=3
end{array}$$

Итак, искомый тангенс:

$$operatorname{tg} phi=frac{3-2}{1+2 cdot 3}=frac{1}{7}$$

Ответ. $operatorname{tg} phi=frac{1}{7}$

Источник

Online trigonometry calculator, which helps to find angle between two curves with easy calculation.

Find Angle Between Two Curves

Curve Equation1 (y)

x²+

Curve Equation2 (y)

x²+

Angle between two curves

Calculator
Formula

Online trigonometry calculator, which helps to find angle between two curves with easy calculation.

Code to add this calci to your website

Formula

tan(θ) = (m2-m1)/(1+(m1.m2)) ∀ m2>m1
tan(θ) = (m1-m2)/(1+(m1.m2)) ∀ m1>m2
Where,
m1 = Curve 1 Tangent line slope
m2 = Curve 2 Tangent line slope

How to find angle between two curves?

Related Calculators:

Distance Between Two Points Calculator
Ratio Or Section
Mid Point
Point Slope Form Calculator
Find Acute Angle Between Two Lines And Plane
Date Calculator

Источник

Содержание

Длина дуги, угол между линиями, площадь области на поверхности

Краткие теоретические сведения

Зная первую квадратичную форму поверхности, мы можем решить три задачи:

1. Найти длину дуги на поверхности:
begin{equation*}
s=intlimits_{t_1}^{t_2}|vec{r’}(t)dt|=intlimits_{P_1}^{P_2}|dvec{r}(u,v)|=intlimits_{P_1}^{P_2}sqrt{I_1}.
end{equation*}
begin{equation*}
s=intlimits_{t_1}^{t_2}sqrt{Eleft(frac{du}{dt}right)^2+2Ffrac{du}{dt}frac{dv}{dt}+Gleft(frac{dv}{dt}right)^2}dt.
end{equation*}

2. Найти угол между двумя линиями на поверхности в точке их пересечения:

Если две линии, лежащие на поверхности с первой квадратичной формой $I_1=E,du^2+2F,du,dv+G,dv^2$, пересекаются в некоторой точке $P$ поверхности и имеют в этой точке направления $(du:dv)$ и $(delta u:delta v)$, то косинус угла между ними определяется по формуле:
begin{gather*}
mbox{cos},varphi = displaystylefrac{I_1(d,delta)}{sqrt{I_1(d)}cdotsqrt{I_1(delta)}} \
mbox{cos},varphi = displaystylefrac{E,du,delta u+F,(du,delta v+delta u,dv)+G,dv,delta v}{sqrt{E,du^2+2F,du,dv+G,dv^2}cdotsqrt{E,delta u^2+2F,delta u,delta v+G,delta v^2}}.
end{gather*}
Говорим, что кривая на поверхности $vec{r}=vec{r}(u,v)$ в точке $(u,v)$ имеет направление $(du:dv)$, если вектор $dvec{r}=vec{r}_udu+vec{r}_vdv$ является касательным вектором кривой в этой точке.

3. Найти площадь области $Omega$ на поверхности:
begin{equation*}
S = iintlimits_{D}sqrt{EG-F^2}du,dv,
end{equation*}
где $D$ — прообраз $Omega$ на плоскости $(u,v)$.

Решение задач

Задача 1 (почти Феденко 684)

Найти длину дуги кривой, заданной уравнениями $v=3u$ на поверхности с первой квадратичной формой
begin{equation*}
I_1=du^2+frac19,mbox{sh}^2u,dv^2
end{equation*}
между точками $M_1(u_1,v_1)$ и $M_2(u_2,v_2)$.

Решение задачи 1

begin{equation*}
E=1, ,, F=0,,, G=frac19,mbox{sh}^2u.
end{equation*}
begin{equation*}
v=3u ,, Rightarrow ,,dv=3du.
end{equation*}
begin{equation*}
I_1=du^2+frac19,mbox{sh}^2ucdot9,du^2=(1+mbox{sh}^2u)du^2=mbox{ch}^2u,du^2.
end{equation*}
begin{equation*}
s=left|intlimits_{u_1}^{u_2} mbox{ch},u,duright| = |mbox{sh},u_2-mbox{sh},u_1|.
end{equation*}

Задача 2 (почти Феденко 682)

Под каким углом пересекаются линии
$$ u+v=a, ,, u-v=a,$$
лежащие на поверхности:
begin{equation*}
x=u,mbox{cos}v, ,, y=u,mbox{sin},v, ,, z=au.
end{equation*}

Решение задачи 2

Первая квадратичная форма данной поверхности:
begin{equation*}
I_1=(1+a^2),du^2+u^2,dv^2.
end{equation*}

Данные линии пересекаются в точке:
begin{equation*}
left{
begin{aligned}
u+v&=a,\
u-v&=a.
end{aligned}
right. quad Rightarrow quad P(u=a,v=0).
end{equation*}

Направления данных линий:
begin{equation*}
du+dv=0, ,, delta u-delta v=0,, Rightarrow
end{equation*}
begin{equation*}
du = -dv, ,, delta u = delta v.
end{equation*}

Подставляем всё в формулу:
begin{gather*}
mbox{cos},varphi = displaystylefrac{(1+a^2),du,delta u + u^2,dv,delta v}{sqrt{(1+a^2),du^2+u^2,dv^2}cdotsqrt{(1+a^2),delta u^2+u^2,delta v^2}} = \
= left( dv = -du, ,, delta v = delta u right) = \
= displaystylefrac{(1+a^2- u^2),du,delta u}{sqrt{(1+a^2+u^2)^2,du,delta u}}= frac{1+a^2-u^2}{1+a^2+u^2}=\
= left(P(u=a,v=0)right) = \
= frac{1}{1+2a^2}.
end{gather*}

Задача 3

Дана поверхность:
$$z=axy.$$
Найти углы между координатными линиями.

Решение задачи 3

Координатные линии на данной поверхности задаются уравнениями: $x=x_0$, $y=y_0$.
Запишем коэффициенты первой квадратичной формы:
begin{align*}
&E=1+(z_x)^2=1+a^2y^2,\
&F=z_xz_y=a^2xy, \
&G=1+(z_y)^2=1+a^2x^2.
end{align*}

Направления координатных линий:
begin{align*}
&x=x_0 ,, Rightarrow dx=0,\
&y=y_0 ,, Rightarrow delta y=0.
end{align*}

Угол между линиями $x=x_0$, $y=y_0$ в точке $(x_0,y_0)$:
begin{align*}
&mbox{cos}, varphi = displaystylefrac{E,dx,delta x + F(dxdelta y+delta xdy)+Gdydelta y}{sqrt{Edx^2+2Fdxdy+Gdy^2}cdotsqrt{Edelta x^2+2Fdelta xdelta y+Gdelta y^2}}=\
&= displaystylefrac{Fdelta xdy}{sqrt{Gdy^2}cdotsqrt{Edelta x^2}}=displaystylefrac{(a^2x_0y_0)delta xdy}{sqrt{(1+a^2x_0^2)dy^2}cdotsqrt{(1+a^2y_0^2)delta x^2}}=\
& = displaystylefrac{a^2x_0y_0}{sqrt{(1+a^2x_0^2) }cdotsqrt{(1+a^2y_0^2) }}.
end{align*}

Задача 4 (Дополнение к Задаче 3)

Как мы вывели в примере выше, угол между координатными линиями равен

begin{equation*}
mbox{cos}, varphi = displaystylefrac{F}{sqrt{EG}}.
end{equation*}

Из формулы следует, что координатная сеть поверхности ортогональна (координатные линии пересекаются под прямым углом), тогда и только тогда, когда $F$=0.

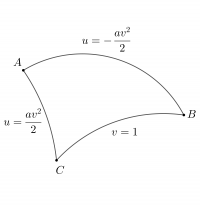
Задача 5 (Феденко 683)

Найти периметр и внутренние углы криволинейного треугольника
$$ u=pm av^2/2,,, v=1,$$
расположенного на поверхности
$$I_1=du^2+(u^2+a^2)dv^2.$$

Вершины треугольника:
begin{align*}
&A(u=0,, v=0),\
&B(u=-frac{a}{2},, v=1), \
&C(u=frac{a}{2},, v=1).
end{align*}

Зная координаты вершин и уравнения сторон, найдем длины дуг, составляющих стороны треугольника $ABC$, и углы между линиями в точках их пересечения, то есть в вершинах треугольника:
begin{align*}
&s_1 = |BC| = a,\
&s_2 = |AC| = frac76 a,\
&s_3 = |BC| = frac76 a,\
&P_{triangle ABC}=s_1+s_2+s_3=frac{10}{3}a.
end{align*}
begin{align*}
&mbox{cos},A = 1, ,, mbox{cos},B=mbox{cos},C=frac23.
end{align*}

Источник

§ 21. Формула тейлора

Find Angle Between Two Curves

Formula

Related Articles

Related Calculators:

Содержание

Длина дуги, угол между линиями, площадь области на поверхности

Краткие теоретические сведения

Решение задач

Задача 1 (почти Феденко 684)

Решение задачи 1

Задача 2 (почти Феденко 682)

Решение задачи 2

Задача 3

Решение задачи 3

Задача 4 (Дополнение к Задаче 3)

Задача 5 (Феденко 683)