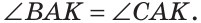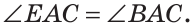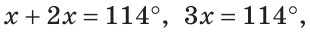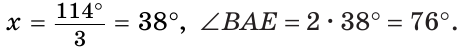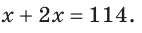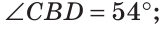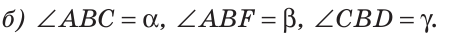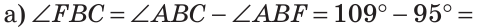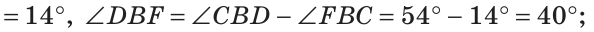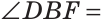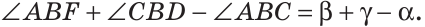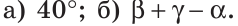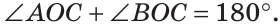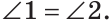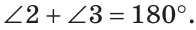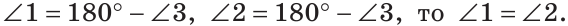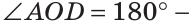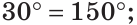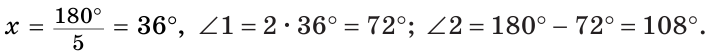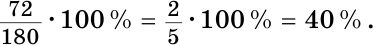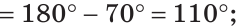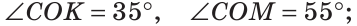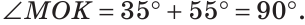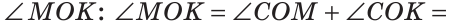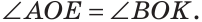Геометрия
7 класс
Урок №5
Измерение углов
Перечень рассматриваемых вопросов:
- Измерительные инструменты.
- Градусная мера угла; биссектриса.
- Транспортир.
- Классификация углов.
Тезаурус:
Градус – угол, равный одной сто восьмидесятой части развернутого угла.
Градусная мера угла – положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Минута – 1/60 часть градуса.
Секунда – 1/60 часть минуты.
Луч – часть прямой, состоящий из всех точек, лежащих по одну сторону от заданной точки, которая является началом луча.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Стороны угла – лучи, из которых состоит угол.
Вершина угла – общее начало сторон угла.
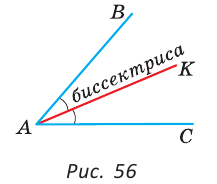
Биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее вы уже познакомились с геометрической фигурой – уголи его составными элементами.
Сегодня мы продолжим изучать углы, познакомимся с их классификацией и будем измерять углы с помощью транспортира.
Измерение углов аналогично измерению отрезков – оно основано на сравнении, только отрезки сравнивались с отрезком, принятым за единицу измерения, а углы с углом, тоже принятым за единицу измерения.
Обычно за единицу измерения углов принимают градус.
Градус – угол, равный 1/180 части развёрнутого угла.
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу, называется градусной мерой угла.
Для измерения углов используют транспортир. Вспомним, как проводить измерение углов с помощью транспортира.
Транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах на той же шкале.
Например:
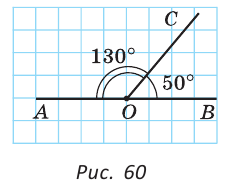
∠О = 50°
Но обычно говорят кратко – угол О равен 50 градусам.
Если масштабныйугол не укладываетсяцелое число раз в измеряемом угле, тоединицу измерения делят ещё на части.
Определённые части градуса носят специальные названия.
Части градуса.
Минута – 1/60 часть градуса.
Обозначается «´».
Секунда – 1/60 часть минуты.
Обозначается «´´».
Например:
∠А = 40 ° 15´ 16 ´´
Далее, аналогично понятию равные отрезки, ведём понятие равные углы.
Дваугла считаются равными, если градус и его части укладываются в этих углах одинаковое число раз, т.е. равные углы имеют равные градусные меры.
Если один угол меньше другого, то градус в нём (или его часть) укладываются в этом углу меньшее число раз, чем в другом, т.е. меньший угол имеет меньшую градусную меру.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
∠АОС =∠АОL + ∠LОС,
∠АОL = 64°,
∠LОС = 64°,
∠АОС = 64° + 64° = 128°.
Далее рассмотрим классификацию углов.
Мы уже знаем, что есть развёрнутый угол, его градусная мера сто восемьдесят градусов.
Но есть и другие углы.
Например, прямой угол, его градусная мера девяносто градусов;
острый угол, его градусная мера меньше девяноста градусов;
тупой угол, его градусная мера больше девяноста градусов, но меньше ста восьмидесяти.
Выполним практическое задание – построим биссектрису угла с помощью транспортира.
Мы знаем, что биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
∠АОС = 128°,
128° : 2 = 64°,
OL – биссектриса ∠АОС.
Поэтому для начала определим градусную меру ∠АОС, она составляет 128°, тогда биссектриса этого угла, исходя из определения, составит 64 °.
Итак, сегодня получили представление о том, как измерять и изображать угол с помощью транспортира. Перейдем к практическим заданиям.
Способы измерения на местности.
Измерение углов на местности проводят с помощью различных приборов. Один из таких – астролябия, она состоит из диска (лимб), разбитого на градусы и вращающейся вокруг центра диска линейки (алидады). На концах алидады есть окошечки, которые нужны, чтобы устанавливать её в определённом направлении.
Опишем, как происходит измерение углов с помощью этого прибора. При измерении углов астролябию устанавливают в его вершине, например, точке О, при этом лимб должен находится горизонтально плоскости угла, а отвес, в центе диска, совпадать с вершиной угла.
Затем устанавливаем алидаду вдоль одной из сторон угла, например, АО, отмечаем деление, напротив которого находится указатель алидады.
Далее поворачиваем алидаду по часовой стрелке, пока она не совпадёт со второй стороной угла, у нас это сторона ОВ, отмечаем деление, напротив которого оказался указатель алидады. Теперь можно найти градусную меру измеряемого угла, как разность второго и первого измерения.
Тренировочные задания.
1. Луч ВК делит развернутый ∠ОВС на два угла, разность которых равна 56°. Найдите образовавшиеся углы.
Решение: нарисуем рисунок, исходя из условия задачи.
Обозначим ∠СВК за х, тогда ∠ОВК= х + 56°, исходя из условия задачи (разность углов равна 56°). Развёрнутый угол равен 180°. Составим уравнение и решим его.
х + х +56 =180,
2х= 180 – 56,
2х= 124,
х = 124:2,
х = 62° (∠СВК).
Тогда ∠ОВК= х + 56°= 62° +56° = 118°.
Ответ: ∠СВК = 62°; ∠ОВК = 118°.
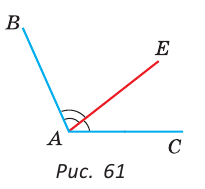
2. Чему равен ∠ЕОА, если ∠ВОА = 130° 54´, а ∠ВОЕ = 105° 76´?
Решение: Найдём ∠ЕОА = ∠ВОА – ∠ВОЕ, т.к. ОЕ – луч, проведённый из вершины ∠ВОА и делящий этот угол на 2 части. Подставим в выражение градусные меры углов и найдём градусную меру ∠ЕОА. Так как в градусе 60 минут, то 105° 76´ = 106° 16´.
∠ЕОА = 130° 54´ – 106° 16´ = 24° 38´.
Ответ: ∠ЕОА = 24° 38´.
Содержание:
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
Два угла называются равными, если их можно совместить наложением.
Биссектрисой угла называется луч, который выходит из вершины угла и делит его на два равных угла.
Определение. Развернутым углом называется угол, стороны которого являются дополнительными лучами.
На рисунке 56 луч АК — биссектриса угла ВАС и 
На рисунке 57 угол ABC — развернутый, лучи ВА и ВС — дополнительные. Другая (незакрашенная) полуплоскость относительно прямой АС также задает развернутый угол ABC.
Углы измеряются в градусах, минутах, секундах.
Развернутый угол равен 180°;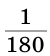 
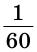
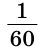
часть развернутого угла называется градусом и обозначается 1°; 
часть одного градуса называется минутой и обозначается 1′; 
часть минуты называется секундой и обозначается 1″.
Угол, равный 5 градусов 20 минут и 35 секунд, записывается так: 5°20’35».
Вместо «градусная мера угла равна 20°» часто говорят «угол равен 20°», вместо найти «градусную меру угла» говорят «найти угол».
Определения
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
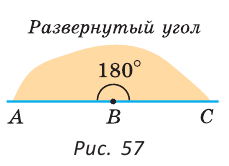
Определение: Угол, равный 90°, называется прямым; угол, меньший 90°, — острым; угол, больший 90°, но меньший 180°, — тупым; угол, равный 360°, называется полным (его стороны совпадают).
На рисунке 58 последовательно изображены: острый угол, равный 60°; прямой угол, равный 90°; тупой угол, равный 120°; угол, равный 270°; и полный угол, равный 360°.
Градусная мера угла является его важной характеристикой. Свойства градусной меры угла: любой угол имеет градусную меру, выраженную некоторым положительным числом; равным углам соответствуют равные градусные меры, а большему углу — большая градусная мера. И наоборот.
Аксиомы
Аксиома измерения углов. Если внутри угла из его вершины провести луч, то он разобьет данный угол на два угла, сумма градусных мер которых равна градусной мере данного угла.
Аксиома откладывания углов. От любого луча в данную полуплоскость можно отложить угол данной градусной меры, и притом только один.
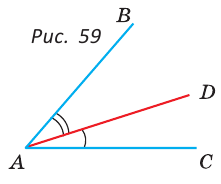
На рисунке 59 луч AD проходит внутри угла ВАС. По аксиоме измерения углов 
Например, если из вершины развернутого угла АОВ (рис. 60) провести ЛУЧ ОС, который составит со стороной ОВ угол 50°, то со стороной OA луч ОС составит 180° — 50° = 130°.
Два луча с общим началом задают на плоскости два угла. В дальнейшем будем рассматривать меньший из этих двух углов (если они неразвернутые). Такой угол меньше 180°.
Пример №1
Внутри угла ВАС, равного 114°, из его вершины проведен луч АЕ. Угол ВАЕ в 2 раза больше угла ЕАС. Найти величину угла ВАЕ.
Решение:
Пусть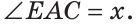 
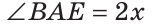
Тогда 
(рис. 61).
По аксиоме измерения углов 
Тогда 
Ответ: 76о
Замечания. 1. Возможен другой способ записи решения, когда рядом с буквой 
пишут знак градуса: 
Тогда в уравнении знак градуса писать не нужно: 
2. В дальнейшем при решении задач не будем ссылаться на аксиому измерения углов.
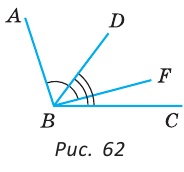
Пример №2
Внутри угла проведены лучи BD и BF (рис. 62).
Найти величину угла DBF, если:
Решение:
Если сложить углы ABF и CBD, то получим угол ABC плюс угол DBF.
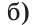
Отсюда 
Ответ: 
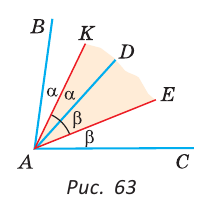
Пример №3
Луч AD делит угол ВАС на два угла BAD и CAD. Доказать, что угол между биссектрисами АК и АЕ углов BAD и CAD равен половине угла ВАС (рис. 63).
Доказательство:
Так как АК иАЕ — биссектрисы, то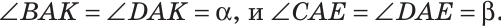 
Тогда 
Следовательно,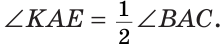 
Что и требовалось доказать.
Замечание. В данной задаче мы доказали свойство: «Если внутри угла из его вершины провести луч, то угол между биссектрисами полученных углов равен половине данного угла».
Геометрия 3D
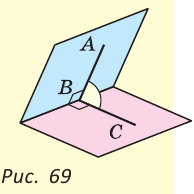
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 ZABC — линейный угол изображенного двугранного угла.
Геометрия 3D
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 
— линейный угол изображенного двугранного угла.
Смежные углы. Вертикальные углы
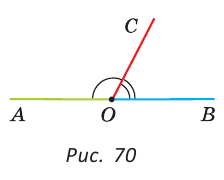
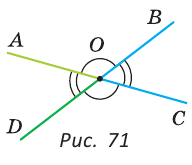
Определение. Два угла называются смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.
Если на рисунке 70 лучи OA и ОВ дополнительные, то углы АОС и ВОС — смежные.
Теорема (свойство смежных углов). Сумма смежных углов равна 180°.
Дано: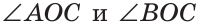 
— смежные.
Доказать: 
Доказательство:
Из определения смежных углов следует, что лучи OA и ОВ являются дополнительными и поэтому образуют развернутый угол АОВ, равный 180°. Луч ОС проходит между сторонами этого угла, и по аксиоме измерения углов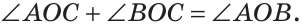 
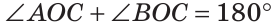
Поэтому 
. Теорема доказана.
Следствия.
- Если смежные углы равны, то каждый из них прямой.
- Если два угла равны, то равны и смежные с ними углы.
Замечание. Все теоремы курса геометрии 7—9 классов описывают свойства фигур на плоскости.
Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами к сторонам другого.
При пересечении двух прямых АС и DB в точке О (рис. 71) получим, что лучи OA и ОС, О В и OD — дополнительные. Поэтому углы AOD и BОС — вертикальные. Углы АОВ и DOC также вертикальные.
Теорема (свойство вертикальных углов). Вертикальные углы равны.
Дано: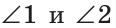 
— вертикальные (рис. 72).
Доказать: 
Доказательство:
Углы 1 и 3 смежные, так как лучи OA и OD — дополнительные по определению вертикальных углов. По свойству смежных углов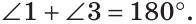 
Углы 2 и 3 также смежные, 
Так как 
Теорема доказана.
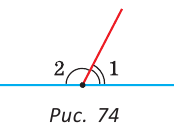
Углом между двумя пересекающимися прямыми называется меньший из образованных ими углов. Если при пересечении прямых АВ и CD (рис. 73)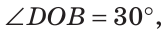 
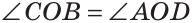
то 
как вертикальные. Угол между прямыми АВ и CD равен 30°. Говорят, что прямые пересекаются под углом 30°.
При пересечении двух прямых образуются четыре угла (не считая развернутых). Если один из них 90°, то и остальные по 90° (докажите самостоятельно). Говорят, что прямые пересекаются под прямым углом.
Угол между параллельными прямыми считается равным 0°.
Пример №4
Смежные углы относятся как 2:3. а) Найти величину каждого из углов, б) Определить, сколько процентов развернутого угла составляет меньший угол.
Решение:
а) Пусть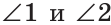 
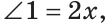
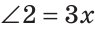
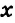
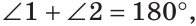
— данные смежные углы (рис. 74). Согласно условию 
(градусную меру одной части принимаем за 
). По свойству смежных углов
то есть 
б) Меньшим является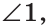 
а 72° от 180° составляют 
Ответ: 72°, 108°; 40 %.
Пример №5
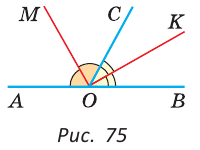
а) Найти угол между биссектрисами ОК и ОМ смежных углов ВОС и АОС (рис. 75), если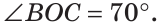 
б) Доказать, что биссектрисы смежных углов образуют прямой угол.
Решение:
а) Если 
б) Так как ОМ и ОК — биссектрисы, то
Найдем градусную меру 
По свойству смежных углов 
Тогда 
. Что и требовалось доказать.
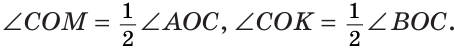
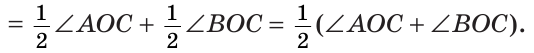
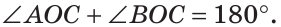
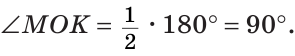
Замечание. Можно было сослаться на ключевую задачу 3* к § 5.
Пример №6
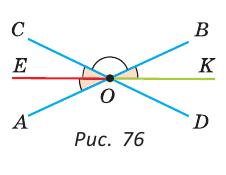
Доказать, что биссектрисы вертикальных углов образуют развернутый угол.
Решение:
а) Пусть ОЕ и ОК — биссектрисы вертикальных углов АОС и BOD (рис. 76). Докажем, что 
— развернутый. Известно, что биссектриса делит угол пополам. Так как вертикальные углы равны, то равны и их половины. Поэтому 
б) 
так как лучи OA и ОВ дополнительные, и поэтому 
— развернутый. Заменив в последнем равенстве 
на равный ему 
получим 
Отсюда следует, что — развернутый.
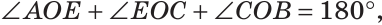
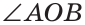
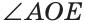
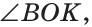
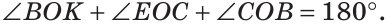
Замечание. Из решения задачи следует свойство: если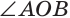 
— развернутый и 
— вертикальные.
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми
- Задачи на построение циркулем и линейкой
- Задачи на построение по геометрии
Загрузить PDF
Загрузить PDF
В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.
-
1
Сосчитайте число сторон многоугольника. Чтобы вычислить внутренние углы многоугольника, сначала нужно определить, сколько у многоугольника сторон. Обратите внимание, что число сторон многоугольника равно числу его углов.[1]
- Например, у треугольника 3 стороны и 3 внутренних углов, а у квадрата 4 стороны и 4 внутренних углов.
-
2
Вычислите сумму всех внутренних углов многоугольника. Для этого воспользуйтесь следующей формулой: (n — 2) x 180. В этой формуле n — это количество сторон многоугольника. Далее приведены суммы углов часто встречающихся многоугольников:[2]
- Сумма углов треугольника (многоугольника с 3-мя сторонами) равна 180°.
- Сумма углов четырехугольника (многоугольника с 4-мя сторонами) равна 360°.
- Сумма углов пятиугольника (многоугольника с 5-ю сторонами) равна 540°.
- Сумма углов шестиугольника (многоугольника с 6-ю сторонами) равна 720°.
- Сумма углов восьмиугольника (многоугольника с 8-ю сторонами) равна 1080°.
-
3
Разделите сумму всех углов правильного многоугольника на число углов. Правильный многоугольник это многоугольник с равными сторонами и равными углами. Например, каждый угол равностороннего треугольника вычисляется так: 180 ÷ 3 = 60°, а каждый угол квадрата находится так: 360 ÷ 4 = 90°.[3]
- Равносторонний треугольник и квадрат — это правильные многоугольники. А у здания Пентагона (Вашингтон, США) и дорожного знака «Стоп» форма правильного восьмиугольника.
-
4
Вычтите сумму всех известных углов из общей суммы углов неправильного многоугольника. Если стороны многоугольника не равны друг другу, и его углы также не равны друг другу, сначала сложите известные углы многоугольника. Теперь полученное значение вычтите из суммы всех углов многоугольника — так вы найдете неизвестный угол.[4]
- Например, если дано, что 4 угла пятиугольника равны 80°, 100°, 120° и 140°, сложите эти числа: 80 + 100 + 120 + 140 = 440. Теперь вычтите это значение из суммы всех углов пятиугольника; эта сумма равна 540°: 540 — 440 = 100°. Таким образом, неизвестный угол равен 100°.
Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны; в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.
Реклама
-
1
Помните, что в любом прямоугольном треугольнике один угол всегда равен 90°. Это так, даже если прямой угол никак не отмечен или его значение не указано. Таким образом, один угол прямоугольного треугольника всегда известен, а другие углы можно вычислить с помощью тригонометрии.[5]
-
2
Измерьте длину двух сторон треугольника. Самая длинная сторона прямоугольного треугольника называется гипотенузой. Прилежащая сторона это сторона, которая находится возле неизвестного угла. Противолежащая сторона — это сторона, которая находится напротив неизвестного угла. Измерьте две стороны, чтобы вычислить неизвестные углы треугольника.[6]
Совет: воспользуйтесь графическим калькулятором, чтобы решить уравнения, или найдите онлайн-таблицу со значениями синусов, косинусов и тангенсов.
-
3
Вычислите синус угла, если вам известны противолежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: sin(x) = противолежащая сторона ÷ гипотенуза. Например, противолежащая сторона равна 5 см, а гипотенуза равна 10 см. Разделите 5/10 = 0,5. Таким образом, sin(x) = 0,5, то есть x = sin-1 (0,5).[7]
- Если у вас есть графический калькулятор, введите 0,5 и нажмите клавишу sin-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 30°.
-
4
Вычислите косинус угла, если вам известны прилежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: cos(x) = прилежащая сторона ÷ гипотенуза. Например, прилежащая сторона равна 1,67 см, а гипотенуза равна 2 см. Разделите 1,67/2 = 0,83. Таким образом, cos(x) = 0,83, то есть x = cos-1 (0,83).[8]
- Если у вас есть графический калькулятор, введите 0,83 и нажмите клавишу cos-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 33,6°.
-
5
Вычислите тангенс угла, если вам известны противолежащая и прилежащая стороны. Для этого подставьте значения в уравнение: tg(x) = противолежащая сторона ÷ прилежащая сторона. Например, противолежащая сторона равна 75 см, а прилежащая сторона равна 75 см. Разделите 75/100 = 0,75. Таким образом, tg(x) = 0,75, то есть x = tg-1 (0,75).[9]
- Если у вас есть графический калькулятор, введите 0,75 и нажмите клавишу tg-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 36,9°.
Реклама
Советы
- Названия углов соответствуют их значениям. Угол в 90° — это прямой угол. Угол в 180° — это развернутый угол. Угол, который лежит между 0° и 90° — это острый угол. Угол, который лежит между 90° и 180° — это тупой угол. Угол, который лежит между 180° и 360° — это невыпуклый угол.
- Если сумма двух углов равна 90°, они называются дополнительными. Запомните: два острых угла прямоугольного треугольника всегда являются дополнительными. Если же сумма двух углов равна 180°, они называются смежными.
Реклама
Об этой статье
Эту страницу просматривали 237 189 раз.
Была ли эта статья полезной?
На прошлом уроке выяснилось, что единицей измерения углов и дуг является градус, равный $frac{1}{360}$ окружности. Измерение углов, следовательно, представляет из себя «процесс нахождения», сколько частей окружности ($frac{x}{360}$) заключено между сторонами угла.
Это отвечает на большую часть вопросов, что мы задавали ранее, однако не на все. Теперь, когда у нас есть единица измерения, нужно разобраться с правилами, определяющими, что в себя включает геометрия измерения углов.
Измерение углов — основное свойство
Начертим на плоскости угол $angle{BAC}$ и проведем между его сторонами $AB$ и $AC$ луч $AD$. Допустим, нам известна градусная мера $angle{DAC}$ и $angle{BAD}$.
Чему будет равен $angle{BAC}$?
Мы помним аксиому, задающую, что длина отрезка равняется сумме длин частей, на которые он разбивается любой его точкой. Измерение углов также подчиняется аксиоме «длины», только, конечно, вместо «длины» мы будем говорить «градусной меры»:
$A_8$. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Геометрия измерения углов: $0^circ$
Включает ли в себя геометрия измерения углов нулевые величины? Оказалось, что аксиома суммы частей применима как к отрезкам, так и к углам. А применима ли к углам аксиома «нулевой фигуры»? В отличие от отрезка, длина которого всегда задается строго больше нуля, о нулевых углах говорить можно.
Учтите, что в некоторых учебниках тем не менее встречается следующая аксиома: «Каждый угол имеет определенную градусную меру, бóльшую нуля». Это не совсем верно, поскольку тригонометрические функции могут принимать аргумент в виде нуля. Даже отрицательные аргументы.
Что это означает — не суть. Главное, что далее в курсе математики измерение углов может иметь дело с условным $angle{A}=0^circ$. Чтобы путаницу предупредить, аксиому углов $>0$ мы вводить не будем. А угол, равный нулю, будем представлять как угол, у которого стороны являются совпадающими лучами.
Измерение углов — основное свойство: задача
Условие. Проведено измерение углов, в результате которого получены следующие градусные меры: $angle{FDK}=38^circ$, $angle{KDM}=26^circ$, $angle{MDA}=32^circ$.
Чему равен $angle{FDA}$?
Дано:
$angle{FDK}=38^circ$
$angle{KDM}=26^circ$
$angle{MDA}=32^circ$
Решение. Воспользуемся аксиомой суммы градусных мер углов. Так, величина $angle{FDA}$ будет определяться суммой величин углов, его составляющих. Именно:
$$angle{FDA}=angle{FDK}+angle{KDM}+angle{MDA}$$
Градусные меры всех трех углов заданы по условию. Остается только их сложить. Имеем следующее:
$$angle{FDA}=38^circ+26^circ+32^circ=96^circ$$
Ответ: $96^circ$.
Измерение углов транспортиром
Измерительным инструментом углов является транспортир. Он представляет из себя пластину, выполненную в форме круга или полукруга, основанием которого иногда бывает линейка. Разметка полукругового транспортира состоит из 180 градусов, кругового — из 360. По своей сути транспортир — это конечный результат идеи о делении окружности на 360 ровных частей и нанесении на окружность соответствующей разметки.
Полукруговой транспортир
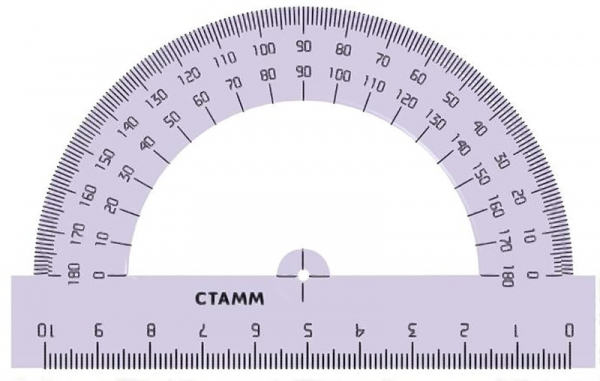
Круговой транспортир
Как пользоваться транспортиром для измерений
Измерение углов в школьном курсе геометрии вполне обходится упрощенной версией транспортира — полукруговой. На самом деле, транспортир используется не только для измерения, но и для построения углов. Вначале мы разберем, как проводить измерение углов транспортиром.
Шаг первый
Совместите точку отсчета инструмента с вершиной измеряемого угла. Одну из сторон угла расположите параллельно основанию транспорта: эта сторона должна указывать на нулевую отметку.
Шаг второй
Совместив основание со стороной угла, можно переходить к измерению угла. Вторая сторона угла будет указывать на некоторую отметку градусной шкалы. Если вдруг «поворотная» сторона не доходит до разметки, дорисуйте ее линейкой до необходимой длины.
Шаг третий
Зафиксируйте величину угла. Измерение углов транспортиром не допускает округление градусной меры без необходимости. Если транспортир показывает «$61^circ$», не стоит округлять значение до «$60^circ$».
В нашем же случае угол составляет ровно $60^circ$.
Как начертить угол транспортиром
Выше было продемонстрировано измерение углов с помощью транспортира без вспомогательной линейки. Транспортиры с основанием в виде сантиметровой линейки — тоже полезный инструмент, в особенности для откладывания углов. Давайте посмотрим, как начертить угол транспортиром, откладывая при этом на сторонах угла отрезки определенной длины.
Задача. Отложить $angle{BAC}=80^circ$ так, чтобы при этом отрезки $AC$ и $AB$ равнялись $4~см$ и $3~см$ соответственно.
☝️ Откладываем сторону на основании
В первую очередь на риске отсчета отметим точку $A$ — это будет вершина откладываемого угла. Проведем от точки $A$ луч, параллельный основанию транспортира. Первая часть откладывания угла выполнена.
✌️Откладываем вторую сторону угла
Чтобы начертить угол транспортиром, необходимо отметить еще одну точку на отметке $80^circ$. Отметим риску $80^circ$ небольшой вспомогательной точкой. Теперь проведем через эту вспомогательную точку и точку $A$ луч.
Нюанс!
Обратите внимание, что углы принято откладывать против часовой стрелки. Альтернативная разметка ниже основной — по часовой стрелке — предлагается на транспортире, чтобы было удобно проводить измерение углов. Ориентация углов на плоскости разная, и не всегда бывает хорошо иметь под рукой разметку, нанесенную только против часовой стрелки.
Построения линейкой
Руководствуясь условием поставленной задачи, отметим точку $C$ на основании таким образом, чтобы расстояние между точками $A$ и $C$ составляло $4~см$. Применим для этого линейку. Проделаем ту же самую последовательность действий с точкой $B$ с поправкой на $AB=3~см$.
Немного самостоятельной практики!
Возьмите карандаш, транспортир и лист бумаги. Отложите от стороны на основании транспортира два произвольных угла в границе $0^circ<x<180^circ$. Поделитесь в комментариях к уроку, какие градусные меры вы выбрали для углов.
Типы углов по градусам
Вероятно, ранее вам приходилось слышать определения для углов наподобие «острый», «тупой» и так далее. Эти определения задают типы углов по градусам. Зачем и кому это нужно? Цель очень даже приземленная: типы углов по градусам позволяют быстро сориентироваться, в каких границах значений располагается градусная мера угла. «Острый», «тупой» и прочее — это слова-маркеры.
Предлагаем с этими маркерами познакомимся поближе, дабы научиться проводить измерение углов на глаз.
Острый угол. Угол, градусная мера которого располагается в границах $0^circleq{x}<90^circ$. Заметьте, что угол, составляющий $0^circ$, считается острым. Пример острого угла: $angle{alpha}=50^circ$.
Тупой угол. Угол, градусная мера которого располагается в границах $90^circ<x<180^circ$. Пример тупого угла: $angle{beta}=130^circ$.
Развернутый и прямой углы. Заметьте, что выше границы для $90^circ$ и $180^circ$ устанавливаются строгими неравенствами. Это важные доли окружности, поэтому для них имеются отдельные названия. Так, угол, равный $90^circ$ ($frac{1}{4}$ окружности), называется прямым. Угол в $180^circ$ ($frac{1}{2}$ окружности) называется развернутым.
Прямой угол ($90^circ$)
Развернутый угол ($180^circ$)
Выпуклый угол. Когда градусная мера угла располагается в границах $180^circ<x<360^circ$, такой угол называется выпуклым.
Например, выпуклым углом является $angle{gamma}=260^circ$.
Выпуклые углы удобнее измерять круговым транспортиром. Однако если в наличии только полукруговой, можно вначале «отбить» развернутый угол ($180^circ$), а остальную часть измерить как острый угол. Полученное значение складывается с градусной мерой развернутого угла. На примере угла выше:
$$180^circ+80^circ=260^circ$$
Полный угол. Под полным углом понимается угол, равный полному обороту окружности, то есть составляющий $360^circ$.
Заметьте, что стороны полных и нулевых углов располагаются на одной прямой.
Угол между плоскостями
Содержание:
- Углы между плоскостями — обозначение
-
Расположение плоскостей и формула вычисления угла между ними
- Параллельность
- Перпендикулярность
- Угол между плоскостями
- Примеры решения задач
Углы между плоскостями — обозначение
Определение
Углом между плоскостями именуется такой угол, который образовался между перпендикулярными прямыми, опущенными в пределах этих плоскостей к линии их пересечения.
Рассмотрим данное понятие наглядно с помощью картинки:
Допустим, α и β — пересекающиеся плоскости. Проведем к линии с перпендикуляр a, который принадлежит α. Далее проведем прямую b, лежащую в β и образующую с прямой c угол в 90°. Угол между α и β равен углу, который образовался между а и b, обозначенному на картинке как φ. В записи это выглядит следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
∠(α, β)=∠(а, b)=φ
На схеме видно, что при пересечении α и β возникают четыре угла, но углом между плоскостями считается острый угол. В случае, когда плоскости при пересечении создают прямые углы, они считаются перпендикулярными друг другу.
Расположение плоскостей и формула вычисления угла между ними
Существует несколько вариаций взаимного расположения двух плоскостей.
Параллельность
Теорема
Две плоскости считаются параллельными в том случае, если у них отсутствуют общие точки.
Возьмем за условие, что плоскости α, расположенной в некоторой прямоугольной системе координат, соответствует общее уравнение: А1х+В1у+С1z+D1=0. А плоскость β определяется общим уравнением вида: А2х+В2у+С2z+D2=0.
Согласно теореме о параллельности плоскостей, чтобы α и β являлись параллельными, достаточно отсутствия решений системы линейных уравнений вида:
(left{begin{array}{l}A_1x+B_1y+C_1z+D_1=0\A_2x+B_2y+C_2z+D_2=0end{array}right.)
То есть приведенная выше система должна быть несовместной.
Доказательство
Допустим, указанные плоскости, соответствующие уравнениям А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0 параллельны друг другу, следовательно, у них отсутствуют общие точки. Это значит, что нет ни одной точки в прямоугольной системе координат, находящейся в трехмерном пространстве, чьи координаты отвечали бы условиям обоих уравнений одновременно или:
(left{begin{array}{l}A_1x+B_1y+C_1z+D_1=0\A_2x+B_2y+C_2z+D_2=0end{array}right.)
не имеет решения.
В случае, если данная система уравнений не имеет решений, то в прямоугольной системе координат трехмерного пространства отсутствуют точки с координатами, одновременно отвечающими условиям обоих уравнений, входящих в рассматриваемую систему. Отсюда можно сделать вывод, что плоскости α и β с соответствующими им уравнениями А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0 не обладают ни одной общей точкой, а значит, являются параллельными. Теорема доказана.
Перпендикулярность
Две плоскости перпендикулярны друг другу, в ситуации, когда они при взаимном пересечении образуют прямой угол, то есть угол в 90°.
Теорема
Если одна из двух плоскостей проходит через прямую, которая перпендикулярна другой плоскости, то такие плоскости являются перпендикулярными.
Доказательство
Пусть: AB∈α, AB⊥β, AB∩β=A.
Необходимо доказать, что α⊥β.
- α∩β=AC, причем AB⊥AC по условию.
- Проведем прямую AD, принадлежащую плоскости β и перпендикулярную AC.
- ∠BAD=90°, поскольку AB⊥β. Следовательно, заданные плоскости перпендикулярны, что и требовалось доказать.
Следствие
Плоскость, перпендикулярная к прямой, по которой пересекаются две заданные плоскости, перпендикулярна к каждой из этих плоскостей.
Теорема
Явность перпендикулярных пересекающихся плоскостей достигается при необходимом и достаточном условии, что нормальные векторы данных плоскостей при пересечении образовали прямой угол.
Доказательство
Допустим, в трехмерном пространстве существует некоторая прямоугольная система координат. При наличии нормальных векторов заданных плоскостей α и β с координатами:
(overrightarrow{n_1}=(A_1,B_1,C_1),)
(overrightarrow{n_2}=(A_2,B_2,C_2),)
то необходимо и достаточно, чтобы эти векторы приняли вид:
(left(overrightarrow{n_1},overrightarrow{;n_2}right)=0Leftrightarrow A_1times A_2+B_1times B_2+C_1times C_2=0)
Отсюда следует, что:
(overrightarrow{n_1}=(A_1,B_1,C_1),)
(overrightarrow{n_2}=(A_2,B_2,C_2))
— нормальные векторы плоскостей α и β. Чтобы заданные плоскости были перпендикулярными, достаточно, чтобы скалярное произведение данных векторов ровнялось нулю, то есть принимало вид:
(left(overrightarrow{n_1},overrightarrow{;n_2}right)=0Leftrightarrow A_1times A_2+B_1times B_2+C_1times C_2=0)
Равенство соблюдено.
Угол между плоскостями
Для вычисления угла между двумя пересекающимися плоскостями используют метод координат. Суть данного способа заключается в нахождении косинуса угла, образованного при пересечении плоскостей.
Предположим, что плоскости P1 и P2 заданы следующими уравнениями:
(P_1:;A_1x+B_1y+C_1z+D_1=0,;{overline N}_1=left(A_1,B_1,C_1right);)
(P_2:;A_2x+B_2y+C_2z+D_2=0,;{overline N}_2=left(A_2,B_2,C_2right))
Найдем косинус угла между P1 и P2 по формуле:
(cosleft(overbrace{P_1,P_2}right)=frac{overline{N_1}timesoverline{N_2}}{left|overline{N_1}right|timesleft|overline{N_2}right|}frac{A_1times A_2+B_1times B_2+C_1times C_2}{sqrt{A_1^2+B_1^2+C_1^2}timessqrt{A_2^2+B_2^2+C_2^2}})
Запишем в ответе модуль косинуса угла, поскольку за величину угла между плоскостями принимают острый угол.
Примеры решения задач
Задача №1
Плоскости заданы уравнениями:
(alpha:;x-y+1=0)
(beta:y-z+1=0)
Определить пересекаются ли α и β. В случае пересечения заданных плоскостей найти угол между ними.
Решение:
Найдем угол между заданными плоскостями:
(alpha:;x-y+1=0,Rightarrowoverline{N_1}=(1,-1,0);)
(beta:;y-z+1=0,Rightarrowoverline{N_2}=(0,1,-1))
Далее вычислим косинус угла между α и β:
(cosleft(overbrace{alpha,beta}right)=frac{overline{N_1}timesoverline{N_2}}{left|overline{N_1}right|timesleft|overline{N_2}right|}=frac{1times0+left(-1right)times1+0timesleft(-1right)}{sqrt{1^2+left(-1right)^2+0^2}timessqrt{0^2+1^2+left(-1right)^2}}=frac{-1}{sqrt4}=-frac12)
В ответе запишем модуль найденной величины.
Ответ: плоскости α и β пересекаются, а косинус угла между ними равен ½.
Задача №2
Плоскость α проходит через точку A(1,1,−1) и перпендикулярна к плоскостям, заданным уравнениями:
(beta:;2x-y+5z+3=0;)
(varphi:;x+3y-z-7=0)
Составьте уравнение плоскости α.
Решение:
Необходимым и достаточным условием перпендикулярности α к плоскостям β и φ является параллельность α к нормалям β и φ — N1 и N2, иными словами, α должна быть перпендикулярна к произведению векторов [N1,N2].
(x = {-b pm sqrt{b^2-4ac} over 2a}beta:;2x-y+5z+3=0,Rightarrow;overline{N_1}=left(2,-1,5right))
(varphi:;x+3y-z-73=0,Rightarrow;overline{N_2}=left(1,3,-1right))
(left[N_1,N_2right]=begin{vmatrix}i&j&k\2&-1&5\1&3&-1end{vmatrix}=ileft(1-15right)-jleft(-2-5right)+kleft(6+1right)=-14i+7j+7k)
Следующим шагом выпишем уравнение плоскости α, проходящей через точку A(1,1,−1) и перпендикулярную вектору [N1,N2]=(−14,7,7):
(-14left(x-1right)+7left(y-1right)+7left(z+1right)=left.0right|:7)
(-2left(x-1right)+y-1+z+1=0)
(−2x+y+z+2=0)
Ответ: (−2x+y+z+2=0.)