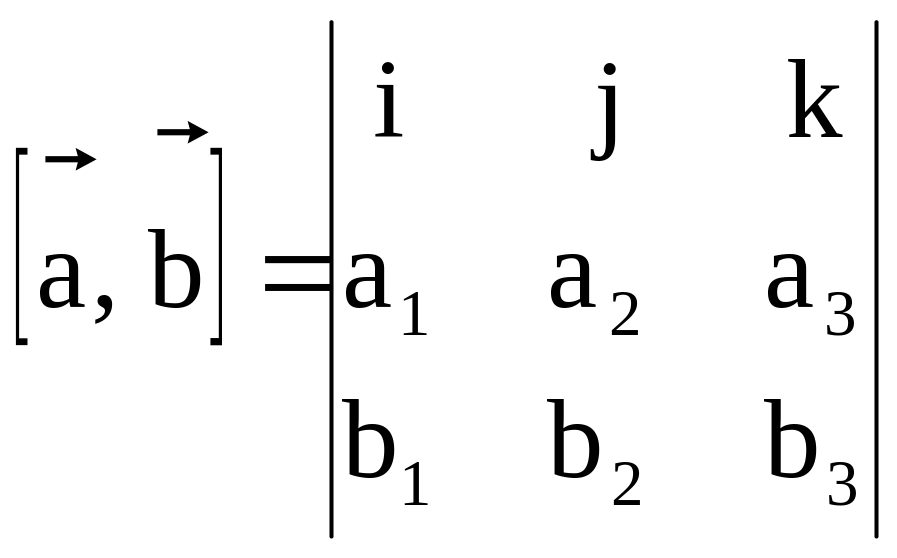Онлайн калькулятор. Вычисление угла между векторами
Этот онлайн калькулятор позволит вам очень просто найти угол между двумя векторами (косинус угла между векторами) для плоских и пространственных задач.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между векторами и закрепить пройденный материал.
Калькулятор для вычисления угла между векторами
Инструкция использования калькулятора для вычисления угла между векторами
Ввод даных в калькулятор для вычисления угла между векторами
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления угла между векторами
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Вычисление угла между векторами
Угол между двумя векторами a и b можно найти использовав следующую формулу:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Метод параллелограмма: примеры, решенные упражнения
Содержание:
В метод параллелограмма это графический метод сложения двух векторов на плоскости. Он часто используется, чтобы найти равнодействующую двух сил, приложенных к телу, или двух скоростей, как в случае пловца, который пытается пересечь реку перпендикулярно и отклоняется течением.
Чтобы построить параллелограмм, начала добавляемых векторов в масштабе должны совпадать в одной точке.
Затем параллельно каждому вектору проводят вспомогательные линии, доходящие до крайности другого, как показано на рисунке выше.
Сумма или результирующий вектор, также называемый чистой силой, является вектором Fсеть, который получается путем рисования вектора, идущего от общего начала координат F1 Y F2, до точки пересечения вспомогательных параллельных прямых. На схеме рисунка они представлены пунктирными линиями.
Метод получил свое название от фигуры, которая образована слагаемыми векторами и вспомогательными линиями, которая в точности представляет собой параллелограмм. Главная диагональ параллелограмма — это вектор суммы.
Очень важно отметить, что порядок, в котором размещаются слагаемые векторы, вообще не изменяет сумму, так как эта операция между векторами является коммутативной.
Пример пошагового метода параллелограмма
На следующем изображении показаны векторы v Y или в условных единицах. Вектор v измеряет 3,61 единицы и образует угол 56,3 ° с горизонтом, в то время как или он измеряет 6,32 единицы и угол 18.4º относительно указанной опорной линии.
Мы собираемся найти его векторную сумму, используя метод параллелограмма.
Необходимо выбрать соответствующий масштаб, например, показанный на следующем рисунке, в котором плоскость разделена сеткой. Ширина квадрата соответствует одной (1) единице.
Поскольку векторы не изменяются при преобразовании, они располагаются так, чтобы их начало совпадало с началом системы координат (левое изображение).
Теперь давайте выполним следующие шаги:
- Участок к концу вектора v сегментированная линия, параллельная вектору или.
- Повторите процедуру, но на этот раз с концом вектора. или.
- Нарисуйте главную диагональ, идущую от общего начала до точки пересечения сегментированных линий.
Результат виден на правом изображении, на котором появляется результирующий вектор. Р.
Если мы хотим узнать величину р, мы можем измерить его длину и сравнить с имеющимся у нас масштабом. Что касается его направления, то в качестве ориентиров можно использовать, например, горизонтальную или вертикальную ось.
При использовании горизонтальной оси или оси x угол, р форма с указанной осью измеряется транспортиром, и таким образом мы знаем направление р.
Кроме того, величина и направление р можно вычислить с помощью теорем косинусов и синусов, так как образовавшийся параллелограмм можно разделить на два равных треугольника, сторонами которых являются модули векторов или, v Y р. См. Рабочий пример 1.
Частный случай: сумма перпендикулярных векторов
Когда векторы перпендикулярны друг другу, образующаяся фигура представляет собой прямоугольник. Модуль полученного вектора соответствует длине диагонали, которую легко вычислить с помощью теоремы Пифагора.
Решенные упражнения
— Упражнение 1
У нас есть вектор v, который имеет размер 3,61 единицы и составляет угол 56,3 ° с горизонтом, а вектор или, размер которого составляет 6,32 единицы и составляет угол 18,4 ° (рисунок 2). Определите модуль результирующего вектора р = или + v и направление, которое указанный вектор образует с горизонтальной осью.
Решение
Метод параллелограмма применяется в соответствии с шагами, описанными выше, для получения вектора р. Как было сказано ранее, если векторы аккуратно нарисованы по шкале и с помощью линейки и транспортира, величина и направление р они измеряются прямо на чертеже.
Их также можно рассчитать напрямую, с помощью тригонометрии и свойств углов. Когда образованный треугольник не правильный, как в этом случае, применяется теорема косинусов, чтобы найти недостающую сторону.
В треугольнике справа стороны измеряют u, v и R. Чтобы применить теорему косинусов, необходимо знать угол между v Y или, который мы можем найти с помощью сетки, адекватно позиционируя углы, указанные в утверждении.
Этот угол равен α и состоит из:
α = (90-56.3º) + 90º +18.4º = 142.1º
Согласно теореме косинусов:
р 2 = v 2 + ты 2 — 2u⋅v⋅cos α = 3,61 2 + 6.32 2 — 2 × 3,61 × 6,32 × cos 142,1º = 88,98
Наконец, угол между р а по горизонтальной оси θ = 18,4 º + γ. Угол γ можно найти с помощью теоремы синусов:
грех α / R = грех γ / u
sin γ = v (sin α / R) = 3,61 x (sin 142,1º / 9,43)
θ = 18.4 º + 13.6 º = 32º
— Упражнение 2.
Пловец собирается пересечь реку, плывя перпендикулярно течению с постоянной скоростью 2,0 м / с. Пловец стартует из точки А, но заканчивается в точке В, расположенной ниже по течению, из-за отклонившего его течения.
Если скорость течения составляет 0,8 м / с, и все скорости предполагаются постоянными, найдите скорость пловца, которую видит наблюдатель, стоящий на берегу.
Решение
Наблюдатель, стоящий на берегу, увидит, как пловец отклоняется в зависимости от полученной скорости. Vр. Чтобы найти ответ, нам нужно векторно сложить скорость пловца относительно воды и скорость течения, которую мы называем V Река:
V р = V пловец + V Река
На рисунке, который не в масштабе, векторы были добавлены для получения V р. В этом случае можно применить теорему Пифагора, чтобы получить его величину:
Vр 2 = 2.0 2 + 0.8 2 = 4.64
Направление, в котором пловец отклоняется от перпендикулярного направления, легко вычислить, учитывая, что:
θ = arctg (2 / 0,8) = 68,2º
Затем пловец отклоняется на 90º — 68,2º = 27,2º от своего первоначального направления.
Ссылки
- Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
- Бедфорд, 2000. А. Инженерная механика: Статика. Эддисон Уэсли.
- Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB).
- Джамбаттиста, А. 2010. Физика. 2-й. Эд. Макгроу Хилл.
- Сирс, Земанский. 2016. Университетская физика с современной физикой. 14-го. Ред. Том 1.
EMB-агар: обоснование, подготовка и использование
Задача 32394 1. На векторах a = (9,1,1) и b = (1,1,9).
Условие
1. На векторах a = (9,1,1) и b = (1,1,9) построен параллелограмм.
Найти:
а) угол между диагоналями параллелограмма;
в) высоту параллелограмма, опущенную на вектор b.
Решение
По правилу сложения и вычитания векторов, одна диагональ является суммой векторов, вторая разностью.
vector=vector+vector=(10;2;10)
vector=vector-vector=(8;0;-8)
vector*vector=10*8+2*0+10*(-8)=0
Скалярное произведение равно 0, значит диагонали параллелограмма взаимно перпендикулярны, угол между диагоналями 90^(o)
С другой стороны
S=b*h
|vector|=sqrt(1^2+1^2+9^2)=sqrt(83)
h=8sqrt(102)/sqrt(83)
http://ru1.warbletoncouncil.org/metodo-del-paralelogramo-4263
http://reshimvse.com/zadacha.php?id=32394
Угол между векторами
Иногда студенты при решении задач аналитической геометрии сталкиваются с вопросом: «Как найти угол между векторами?». Чтобы решить такую задачу нужно сначала найти косинус угла между ними, а затем и сам угол. Для этого применяется такая формула: $$ phi = arccos(cos phi) $$
Если воспользоваться данной формулой, то сначала нужно найти угол между векторами $ cos phi $. Затем находим арккосинус от косинуса угла $ phi $. А чему равен $ cos phi $? Для его нахождения необходимо воспользоваться следующими формулами.
Формула
Если векторы расположены на плоскости и координаты их заданы в виде: $ overline{a} = (a_x; a_y) $ и $ overline{b} = (b_x; b_y) $, то найти угол между ними можно так:
$$ cos phi = frac{(overline{a},overline{b})}{|overline{a}| cdot |overline{b}|} = frac{a_xcdot b_x + a_y cdot b_y}{sqrt{a_x ^2 + a_y ^2}cdot sqrt{b_x ^2 + b_y ^2}} $$
Если вектора находятся в пространстве и координаты каждого из них заданы в виде: $ overline{a} = (a_x; a_y; a_z) $ и $ overline{b} = (b_x; b_y; b_z) $, то вычислить косинус угла следует по формуле:
$$ cos phi = frac{(overline{a},overline{b})}{|overline{a}| cdot |overline{b}|} = frac{a_xcdot b_x + a_y cdot b_y + a_z cdot b_z}{sqrt{a_x ^2 + a_y ^2 + a_z ^2}cdot sqrt{b_x ^2 + b_y ^2 + b_z ^2}} $$
Пояснение. В числителе расположено скалярное произведение векторов $ overline{a} $ и $ overline{b} $. Оно равно сумме произведений соответствующих координат. В знаменателе перемножаются модули (длины) векторов.
Примеры решений
| Пример 1 |
| Найти угол между векторами $ overline{a} = (2;4) $ и $ overline{b} = (3;1) $ |
| Решение |
|
Сначала находим косинус угла между векторами по формуле: $$ cos phi = frac{(overline{a},overline{b})}{|overline{a}| cdot |overline{b}|} = frac{2cdot 3 + 4 cdot 1}{sqrt{2^2 + 4^2} cdot sqrt{3^2 + 1^2} } = frac{10}{sqrt{20} cdot sqrt{10}} = $$ $$ = frac{10}{sqrt{200}} = frac{1}{sqrt{2}} = frac{sqrt{2}}{2} $$ Теперь искомый угол $ phi $ находим по другой формуле: $$ phi = arccos (cos phi) = arccos (cos frac{sqrt{2}}{2}) = 45^0 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Угол между двумя векторами равен $ phi = 45^0 $ |
| Пример 2 |
| Найти угол $ phi $ между двумя векторами $ overline{a} = (8;-11;7) $ и $ overline{b} = (-2;-7;8) $ |
| Решение |
|
Подставляем координаты в формулу и вычисляем: $$ cos phi = frac{8cdot (-2) + (-11)cdot (-7) + 7cdot 8}{sqrt{8^2+(-11)^2+7^2} cdot sqrt{(-2)^2+(-7)^2+8^2} } = $$ $$ = frac{-16+77+56}{sqrt{234} cdot sqrt{117}} = frac{117}{sqrt{234} cdot sqrt{117}} = $$ $$ = frac{sqrt{117}}{sqrt{234}} = frac{1}{sqrt{2}} = frac{sqrt{2}}{2} $$ Далее находим сам угол $ phi $ с помощью арккосинуса: $$ phi = arccos frac{sqrt{2}}{2} = 45^0 $$ |
| Ответ |
| Угол $ phi = 45^0 $ |
Как найти угол между диагоналями параллелограмма
Прежде чем искать решение поставленной задачи, следует выбрать наиболее подходящий метод ее решения. Геометрический метод требует тдополнительных построений и их обоснования, поэтому в данном случае наиболее удобным представляется использование векторной методики. Для этого используются направленные отрезки — векторы.
Вам понадобится
- — бумага;
- — ручка;
- — линейка.
Инструкция
Пусть параллелограмм задан векторами двух его сторон (остальные две попарно равны) в соответствии с рис. 1. Вообще-то равных векторов на плоскости сколь угодно много. Для этого требуется равенство их длин (точнее модулей – |a|) и направления, которое задается наклоном к какой-либо оси (в декартовых координатах это ось 0Х). Поэтому для удобства в задачах подобного типа векторы, как правило, задают их радиус-векторами r=а, у которых начало всегда лежит в начале координат.
Для нахождения угла между сторонами параллелограмма понадобится вычислить геометрическую сумму и разность векторов, а также их скалярное произведение (a,b). По правилу параллелограмма геометрическая сумма векторов a и b равна некоторому вектору с=а+b, который построен и лежит на диагонали параллелограмма AD. Разность a и b – вектор d=b-a, построенный на второй диагонали BD. Если векторы заданы координатами, а угол между ними составляет ф, тогда их скалярное произведение – это число, равное произведению модулей векторов и cosф (см. рис1): (a, b) = |a||b|cos ф
В декартовых координатах если а={x1, y1} и b={x2, y2}, то (a, b) = x1y2 +x2y1. При этом скалярный квадрат вектора (а,а)=|a|^2=x1^2 +x2^2. Для вектора b – аналогично. Тогда: |a||b|cos ф = x1y2 +x2y1. Следовательно cosф=(x1y2 +x2y1)/(|a||b|). Таким образом алгоритм решения задачи состоит в следующем:1. Нахождение координат векторов диагоналей параллелограмма как векторов суммы и разности векторов его сторон с=а+b и d=b-a. При этом соответствующие координаты a и b просто складываются или вычитаются. c= a+ b ={x3, y3}= { x1+x2, y1+y2},d= b-a ={x4, y4}={ x2 –x1, y2-y1}. 2. Нахождение косинуса угла между векторами диагоналей (назовем его фД) по приведенному общему правилу cosфд=(x3y3 +x4y4)/(|c||d|)
Пример. Найти угол между диагоналями параллелограмма, заданного векторами своих сторон a={1, 1} и b ={1, 4}. Решение. Согласно приведенному алгоритму вам необходимо найти векторы диагоналей c={1+1, 1+4}={2, 5} и d={1-1, 4-1}={0, 3}. Теперь вычислите cosфд =(0+15)/(sqrt(4+25)sqrt9)= 15/3sqrt29=0,92. Ответ: фд= arcos(0,92).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Примеры решения задач
Задача 1.
Определить длины диагоналей параллелограмма,
построенного на векторах
и
,
где
таковы, что
.
Решение.
Диагонали параллелограмма есть векторы
и
.
Вычислим длину вектора
:
.
Аналогично
вычисляется длина вектора
.
Задача 2.
Найдите вектор
,
коллинеарный вектору
и удовлетворяющий условию
.
Решение.
Обозначим вектор
,
тогда из условий задачи
или
,
тогда
.
Итак:
.
Задача 3.
Найти проекцию вектора
на направление вектора
.
Решение.
.
По формуле проекции вектора на ось будет
иметь место равенство
.
Задача 4.
Даны векторы:
.
П
роверить,
есть ли среди них коллинеарные. Найти
.
Решение.
Условие коллинеарности имеет вид
.
Этому условию удовлетворяют векторы
.
Следовательно, они коллинеарны. Найдем
длины
векторов
:
.
Угол между векторами
определяется по формуле
.
Т
огда
,
.
Используя формулу
,
получим
.
Задача 5.
На материальную точку действуют силы
.
Найти работу равнодействующей этих сил
при перемещении точки из положения
в положение
.
Решение.
Найдем силу
и вектор перемещения
.
,
тогда искомая работа
.
Задачи
1. Векторы
взаимно перпендикулярны, а вектор
образует с ними углы
.
Зная, что
,
найти: 1)
;
2)
.
2. Вычислить длину
диагоналей параллелограмма, построенного
на векторах
,
если известно, что
.
3. Доказать, что
вектор
перпендикулярен к вектору
.
4. Зная, что
,
определить, при каком значении коэффициента
векторы
окажутся перпендикулярными.
5. Даны вершины
четырехугольника:
.
Доказать, что его диагонали взаимно
перпендикулярны.
6. Найти острый
угол между диагоналями параллелограмма,
построенного на векторах
.
7. Даны силы
.
Найти работу их равнодействующей при
перемещении точки из начала координат
в точку
.
8. Даны вершины
треугольника:
.
Найти проекцию вектора
на вектор
.
9. Найти вектор
,
перпендикулярный векторам
,
если известно, что его проекция на вектор
равна единице.
10. Сила, определяемая
вектором
,
разложена по трем направлениям, одно
из которых задано вектором
.
Найти составляющую силы
в направлении вектора
.
11. Даны вершины
треугольника:
.
Найти его внутренний угол при вершине
А и внешний угол при вершине В.
12. Даны три
последовательные вершины параллелограмма:
.
Найти его четвертую вершину D
и угол между векторами
.
13. На оси
найти точку, равноудаленную от точек
.
14. Доказать, что
треугольник с вершинами
прямоугольный.
Домашнее задание
1. Вычислить
скалярное произведение двух векторов
,
зная их разложение по трем единичным
взаимно перпендикулярным векторам
;
.
2. Найти длину
вектора
,
зная, что
– взаимно перпендику-
лярные орты.
3. Векторы
попарно образуют друг с другом углы,
каждый из которых равен
.
Зная, что
,
определить модуль вектора
.
4. Доказать, что
вектор
перпендикулярен к вектору
.
5. Даны векторы
,
совпадающие со сторонами треугольника
АВС. Найти разложение вектора, приложенного
к вершине В этого треугольника и
совпадающего с его высотой BD
по базису
.
6. Вычислить угол
между векторами
,
где
—
единичные взаимно перпендикулярные
векторы.
7. Даны силы
,
приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда ее точка приложения,
двигаясь прямолинейно, перемещается
из положения
в положение
.
8. Даны вершины
треугольника
.
Определить его внутренний угол при
вершине В.
9. Вычислив
внутренние углы треугольника с вершинами
,
,
убедиться, что этот треугольник
равнобедренный.
10. Найти вектор
,
зная, что он перпендикулярен векторам
и
.
11. Найти вектор
,
коллинеарный вектору
и удовлетворяющий условию
,
где
.
12. Вычислить
проекцию вектора
на ось вектора
.
13. Даны векторы
.
Вычислить
.
14. Даны точки
.
Вычислить проекцию вектора
на ось вектора
.
Ответы к задачам
1) -7, 13. 2) 15,
.
4)
.
6)
.
7) 2. 
-1/3.
9)
.
10)
.
11)
.
12)
.
13)
.
Ответы к домашнему
заданию
1) 9. 2) 5. 3) 10. 5)
.
6)
.
7) 13.
.
10)
.
12) 6. 13) 5. 14) 3.
Занятие 3
Векторое
произведения векторов. Смешанное
произведение векторов
Определение1.
Тройка
некомпланарных векторов
называется правой (левой) если, находясь
внутри телесного угла, образованного
приведенными к общему началу векторами
и от него к
,
човершающимся против часовой стрелки
(по часовой стрелке)
Тройка правая
Тройка левая
Определение
2. Векторным
произведением вектора
на вектор
называется вектор
,
длина и направление которого определяются
условиями:
1.
,
где
— угол между
.
2.
.
3.
— правая тройка векторов.
Свойства
векторного произведения
1.
(свойство антиперестановочности
сомножителей);
2.
(распределительное относительно суммы
векторов);
3.
(сочетательное относиельно числового
множителя);
4.
(равенство нулю векторного произведения
означает коллинеарность векторов);
5.
,
т. е. момент сил равен векторному
произведению силы на плечо.
Если вектор
,
то
.
Определение
3. Смешанным
произведением
трех векторов называется число,
определяемое следующим образом:
.
Если векторы заданы своими координатами:
,
то
~
.
Свойства
смешанного произведения
1. Необходимым и
достаточным условием компланарности
векторов
является равенство
= 0.
2. Объем
параллелепипеда, построенного на
векторах
:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий
определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом 
или 
. Вектор 
называется противоположным
вектору и может быть
обозначен 
.
Сформулируем ряд базовых определений.
Длиной
или модулем
вектора называется
длина отрезка и обозначается 
. Вектор нулевой длины (его суть — точка) называется нулевым 
и направления
не имеет. Вектор 
единичной длины, называется единичным. Единичный вектор,
направление которого совпадает с направлением вектора , называется ортом вектора .
Векторы
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых, записывают
. Коллинеарные векторы могут иметь совпадающие или
противоположные направления. Нулевой вектор считают коллинеарным любому
вектору.
Векторы
называются равными 
, если они коллинеарны, одинаково направлены и имеют
одинаковые длины.
Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или на параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы
компланарны.
Рассмотрим в
пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и
обозначим их через 
соответственно.
Выберем произвольный вектор
пространства и совместим его начало с началом
координат. Спроектируем вектор
на координатные
оси и обозначим проекции через ax, ay, az
соответственно. Тогда нетрудно показать, что
. (2.25)
Эта
формула является основной в векторном исчислении и называется разложением
вектора по ортам координатных осей. Числа ax, ay, az называются координатами вектора . Таким образом, координаты вектора являются его
проекциями на оси координат. Векторное равенство (2.25) часто записывают в
виде
. Мы будем использовать обозначение вектора в фигурных
скобках, чтобы визуально легче различать координаты вектора и координаты точки.
С использованием формулы длины отрезка, известной из школьной геометрии, можно
найти выражение для вычисления модуля вектора
:
, (2.26)
то
есть модуль вектора равен корню квадратному из суммы квадратов его координат.
Обозначим углы между вектором
и осями
координат через α, β, γ соответственно. Косинусы этих углов называются
для вектора направляющими, и для них выполняется соотношение:
Верность данного равенства можно показать с помощью
свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем
пункте 4.
Пусть в трехмерном пространстве заданы векторы 
своими
координатами. Имеют место следующие
операции над ними: линейные (сложение, вычитание, умножение на число и
проектирование вектора на ось или другой вектор); не линейные – различные
произведения векторов (скалярное, векторное, смешанное).
1. Сложение двух векторов производится покоординатно, то
есть если
.
Данная
формула имеет место для произвольного конечного числа слагаемых.
Геометрически
два вектора складываются по двум правилам:
а) правило треугольника –
результирующий вектор суммы двух векторов соединяет начало первого из них с
концом второго при условии, что начало второго совпадает с концом первого
вектора; для суммы векторов –
результирующий вектор суммы соединяет начало первого из них с концом последнего
вектора-слагаемого при условии, что начало последующего слагаемого совпадает с
концом предыдущего;
б)
правило
параллелограмма (для двух
векторов) – параллелограмм строится на векторах-слагаемых как на сторонах,
приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой
векторов.
2. Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если 
, то
.
Геометрически два
вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов
является диагональ, соединяющая концы векторов, причем результирующий вектор
направлен из конца вычитаемого в конец уменьшаемого вектора.
Важным следствием
вычитания векторов является тот факт, что если известны координаты начала и
конца вектора, то для вычисления координат вектора необходимо из координат его конца
вычесть координаты его начала. Действительно, любой вектор пространства может быть
представлен в виде разности двух векторов, исходящих из начала координат: 
. Координаты векторов
и
совпадают с
координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу
вычитания векторов следует произвести вычитание координат точки А из координат точки В.
3. Умножение вектора на число λ покоординатно:
.
При λ>0
– вектор
сонаправлен ; λ<0 – вектор противоположно направлен ; |λ|>1 – длина вектора увеличивается в λ раз; |λ|<1 – длина вектора уменьшается в λ раз.
4. Пусть в пространстве задана
направленная прямая (ось l), вектор 
задан
координатами конца и начала. Обозначим проекции точек A и B на ось l
соответственно через A’ и B’.
Проекцией 
вектора на ось l называется длина вектора 
, взятая со
знаком «+», если вектор и ось l сонаправлены, и со
знаком «–», если и l противоположно направлены.
Если
в качестве оси l взять некоторый другой вектор 
, то получим проекцию вектора на вектор .
Рассмотрим некоторые
основные свойства проекций:
1) проекция вектора на ось l равна произведению модуля
вектора на косинус угла
между вектором и осью, то есть 
;
2.) проекция вектора на ось
положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и
равна нулю, если этот угол – прямой;
3) проекция суммы нескольких
векторов на одну и ту же ось равна сумме проекций на эту ось.
Сформулируем определения и
теоремы о произведениях векторов, представляющих нелинейные операции над
векторами.
5. Скалярным произведением 
векторов и называется
число (скаляр), равное произведению длин этих векторов на косинус угла φ между
ними, то есть
. (2.27)
Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол 
, поэтому его косинус (в 2.27) равен 1.
Теорема 2.2. Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения 
Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть 
Теорема 2.3. Скалярное произведение двух векторов 
,
заданных своими координатами, равно сумме произведений их одноименных координат, то есть
(2.28)
С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора
своими координатами , то косинус угла φ между ними:
(2.29)
Отсюда
следует условие перпендикулярности ненулевых векторов
и :
(2.30)
Нахождение проекции вектора на направление,
заданное вектором , может осуществляться по формуле
(2.31)
С помощью скалярного произведения векторов находят
работу постоянной силы 
на
прямолинейном участке пути.
Предположим, что под действием постоянной силы материальная точка перемещается прямолинейно из
положения А в положение B. Вектор силы образует угол φ с вектором перемещения 
(рис. 2.14). Физика утверждает, что работа силы при перемещении 
равна 
.
Следовательно, работа постоянной силы
при прямолинейном перемещении точки ее приложения равна скалярному произведению
вектора силы на вектор перемещения.
Пример
2.9. С
помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах 
Решение. Вычислим модули векторов и их скалярное произведение
по теореме (2.3):
Отсюда согласно формуле (2.29) получим косинус
искомого угла
Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых
на производство одной тонны творога, заданы в таблице 2.2 (руб.).
Какова общая цена этих ресурсов, затрачиваемых на изготовление одной
тонны творога?
Таблица 2.2
Решение. Введем в рассмотрение два вектора: вектор затрат
ресурсов на тонну продукции 
и вектор цены единицы
соответствующего ресурса 
.
Тогда 
. Общая цена
ресурсов 
, что представляет собой скалярное произведение
векторов 
. Вычислим его по формуле (2.28) согласно теореме 2.3:
Таким образом, общая цена затрат на производство одной
тонны творога составляет 279 541,5 рублей
Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix
Пример 2.11. Вычислить работу, произведенную силой 
, если точка ее приложения перемещается прямолинейно
из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила ?
Решение. Находим вектор перемещения, вычитая из координат его конца координаты
начала
. По формуле (2.28) 
(единиц работы).
Угол φ между и
находим по
формуле (2.29), то есть
6. Три некомпланарных вектора 
, взятые в указанном порядке, образуют правую
тройку, если при наблюдении из конца третьего вектора 
кратчайший
поворот от первого вектора ко второму
вектору совершается против часовой стрелки, и левую,
если по часовой стрелке.
Векторным
произведением 
вектора на вектор называется
вектор , удовлетворяющий следующим условиям:
– перпендикулярен векторам и ;
– имеет длину, равную 
, где φ – угол, образованный векторами
и ;
– векторы образуют правую
тройку (рис. 2.15).
Теорема 2.4. Необходимым и достаточным
условием коллинеарности двух векторов является равенство нулю их векторного
произведения
Теорема 2.5. Векторное произведение векторов 
, заданных своими координатами, равно определителю
третьего порядка вида
(2.32)
Примечание. Определитель (2.25)
раскладывается по свойству 7 определителей
Следствие 1. Необходимым и достаточным условием коллинеарности двух
векторов является пропорциональность их соответствующих координат
Следствие 2. Векторные произведения единичных орт равны 
Следствие 3. Векторный квадрат любого вектора равен нулю
Геометрическая
интерпретация векторного произведения состоит в том, что длина результирующего
вектора численно равна площади S
параллелограмма, построенного на векторах–сомножителях как на сторонах,
приведенных к одному началу. Действительно, согласно определению, модуль
векторного произведения векторов равен 
. С другой стороны, площадь параллелограмма,
построенного на векторах и , также равна 
. Следовательно,
. (2.33)
Также с помощью векторного произведения можно
определить момент силы относительно точки и линейную скорость вращения.
Пусть в точке A приложена
сила 
и пусть O –
некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом
силы относительно
точки O называется вектор 
, который проходит через точку O и удовлетворяет следующим условиям:
— перпендикулярен плоскости, проходящей через точки O, A, B;
— его модуль численно равен произведению силы на плечо 
.
— образует правую тройку с векторами и .
Следовательно,
момент силы относительно
точки O представляет собой векторное произведение
. (2.34)
Линейная скорость 
точки М твердого тела, вращающегося с
угловой скоростью 
вокруг
неподвижной оси, определяется формулой Эйлера 
, O – некоторая неподвижная
точка оси (рис. 2.17).
Пример 2.12. С помощью
векторного произведения найти площадь треугольника ABC, построенного на векторах
, приведенных к одному началу.
Решение. Найдем векторное произведение заданных векторов по
формуле (2.32).
. Согласно формуле (2.33) модуль векторного
произведения двух неколлинеарных векторов численно равен площади
параллелограмма, построенного на данных векторах как на сторонах, приведенных к
общему началу, то есть 
. Тогда площадь треугольника 
. Следовательно, искомая площадь равна 
(единиц
площади)
7. Рассмотрим произведение трех векторов , составленное следующим образом: 
. Здесь первые два вектора перемножаются векторно, а
результирующий вектор – скалярно на третий. Такое произведение 
называется смешанным
произведением трех векторов
(векторно–скалярным произведением).
Теорема 2.6. Необходимым и достаточным условием компланарности
трех векторов является равенство нулю их смешанного произведения
Теорема 2.7. Если три вектора 
заданы своими координатами, то их смешанное
произведение представляет собой определитель третьего порядка, составленный из
координат векторов- сомножителей соответственно, то есть
(2.35)
Нетрудно показать, что объем параллелепипеда,
построенного на векторах как на
сторонах, приведенных к общему началу, численно равен модулю смешенного
произведения этих векторов 
.
Объем треугольной пирамиды, построенной на этих же
векторах, равен
(2.36)
Пример 2.13. Вершинами пирамиды служат точки 
. Вычислить объем пирамиды.
Решение. Найдем
координаты векторов
. Вычислим смешанное произведение этих векторов: 
По формуле (2.36) объем пирамиды, построенной на
векторах 
равен
(единиц объема)
Рассмотрим очень важный вопрос о
разложении вектора по базису. Приведем
следующие определения.
Система векторов 
называется
линейно зависимой, если существуют такие числа 
, хотя бы одно из которых отлично от нуля, что имеет
место равенство
(2.37)
Отсюда всегда можно один из линейно
зависимых векторов выразить через линейную комбинацию остальных. Действительно,
допустим для определенности, что 
. Тогда на это число разделим равенство (2.37), имеем:
получим выражение вектора 
через
остальные векторы 
Линейно независимыми называют векторы, если равенство
(2.37) выполняется только тогда, когда
все
В системе векторов число линейно
независимых векторов равняется рангу матрицы, которая составлена из координат
этих векторов (смотри раздел I.5).
Базисом n – мерного
пространства En называют любую совокупность линейно независимых векторов n – мерного пространства.
Произвольный вектор 
n
– мерного пространства можно представить
в виде линейной комбинации векторов базиса
таким образом:
Числа
называются координатами
вектора в базисе
векторов .
Линейное пространство называется
конечномерным и имеет размерность n, если в этом
пространстве существует система из n линейно независимых векторов (базис) такая,
что каждое ее расширение приводит к линейной зависимости системы.
Например, в трехмерном пространстве
существует базис единичных орт такой, что любое расширение этой системы
линейно независимых векторов, то есть каждый вектор трехмерного
пространства, приводит к линейной зависимости векторов (является линейной
комбинацией орт ):
Коэффициенты {x1, x2, x3} такого разложения вектора
по ортам являются координатами вектора в трехмерном
пространстве.
Вопросы для самопроверки